应用回归分析第七章答案
第七章 相关回归分析 思考题及练习题

实用价值越小。
13、在相关分析中,要求相关的两个变量( )
A、都是随机变量
B、都不是随机变量
C、其中因变量是随机变量 D、其中自变量是随机变量
14、在简单回归直线
中,
表示( ) A、当
增加一个单位时,
增加
的数量 B、当
增加一个单位时,
增加
的数量 C、当
增加一个单位时,
的平均增加值 D、当
增加一个单位时,
按一定数额变化时,变量
也随之近似地按固定的数额变化,那么,这时变量
和
之间存在着( )
A、正相关关系
B、负相关关系
C、直线相关关系 D、曲线相关关系
18、两个变量间的相关关系称为( )
A、单相关
B、无相关
C、复相关
D、多相关
19、如果两个变量之间的相关系数
,说明这两个变量之间存在( )。 A、低度相关关系 B、高度相关关系 C、完全相关关系 D、显著相关关系 20、已知
第七章 思考题及练习题
(一) 填空题
1、 1、 在相关关系中,把具有因果关系相互联系的两个变
量中起影响作用的变量称为_______,把另一个说明观察结果的
变量称为________。
2、 2、 现象之间的相关关系按相关的程度分有________相
关、________相关和_______相关;按相关的方向分有________
E、 E、回归方程实用价值大小的指标 10、现象之间相互联系的类型有( )
A、函数关系 B、回归关系 C、相关关系 D、随机关系 E、结构关系 11、相关关系种类( ) A、从相关方向分为正相关和负相关 B、从相关形态分为线性相关和非线性相关 C、从相关程度分为完全相关、不完全相关和零相关
第七章回归与相关分析练习及答案

第七章回归与相关分析一、填空题1.现象之间的相关关系按相关的程度分为、和;按相关的形式分为和;按影响因素的多少分为和。
2.两个相关现象之间,当一个现象的数量由小变大,另一个现象的数量,这种相关称为正相关;当一个现象的数量由小变大,另一个现象的数量,这种相关称为负相关。
3.相关系数的取值X围是。
4.完全相关即是关系,其相关系数为。
5.相关系数,用于反映条件下,两变量相关关系的密切程度和方向的统计指标。
6.直线相关系数等于零,说明两变量之间;直线相关系数等1,说明两变量之间;直线相关系数等于—1,说明两变量之间。
7.对现象之间变量的研究,统计是从两个方面进行的,一方面是研究变量之间关系的,这种研究称为相关关系;另一方面是研究关于自变量和因变量之间的变动关系,用数学方程式表达,称为。
8.回归方程y=a+bx中的参数a是,b是。
在统计中估计待定参数的常用方法是。
9. 分析要确定哪个是自变量哪个是因变量,在这点上它与不同。
10.求两个变量之间非线性关系的回归线比较复杂,在许多情况下,非线性回归问题可以通过化成来解决。
11.用来说明回归方程代表性大小的统计分析指标是。
12.判断一条回归直线与样本观测值拟合程度好坏的指标是。
二、单项选择题1.下面的函数关系是( )A销售人员测验成绩与销售额大小的关系 B圆周的长度决定于它的半径C家庭的收入和消费的关系 D数学成绩与统计学成绩的关系2.相关系数r的取值X围( )A -∞<r<+∞B -1≤r≤+1C -1<r<+1D 0≤r≤+13.年劳动生产率z(干元)和工人工资y=10+70x,这意味着年劳动生产率每提高1千元时,工人工资平均( )A增加70元 B减少70元 C增加80元 D减少80元4.若要证明两变量之间线性相关程度是高的,则计算出的相关系数应接近于( )A+1 B 0 C 0.5 D [1]5.回归系数和相关系数的符号是一致的,其符号均可用来判断现象( ) A线性相关还是非线性相关 B正相关还是负相关C完全相关还是不完全相关 D单相关还是复相关6.某校经济管理类的学生学习统计学的时间(x)与考试成绩(y)之间建=a+b x。
第七章相关与回归分析习题答案

第七章 相关与回归分析习题答案一、填空题1.完全相关、不完全相关 、不相关2.—1≤r ≤1 3.函数、1=r4.无线性相关、完全正相关、完全负相关5. 密切程度6. 正相关、负相关7. 直线相关、曲线相关8.回归系数9.随机的、给定的10.最小二乘法,残差平方和二、单项选择题1.B 2.B 3.A 4.A 5.B6.C 7.D 8.B 9. A 10.C11.C 12.B 13.D 14.B 15.C三、多项选择题1.BCD 2.ACD 3.ABD 4.ABCD 5.ACE四、计算题1解:(1)7863.073.42505309.334229)())((ˆ22==---=∑∑X X X X Y Y ttt β 3720.4088.647*7863.08.549ˆˆ21=-=-=X Y ββ (2)∑∑∑----=2222)()(]))(([Y Y X X X X Y Y r t t t t999834.025.262855*73.42505309.3342292== 6340.43)()1(222=--=∑∑Y Y r e t0889.222=-=∑n e S te(3)0:,0:2120≠=ββH H003204.073.4250530889.2)(2ˆ2==-=∑X XS S t e β 4120.245003204.07863.0ˆ22ˆ2ˆ===βββS t 228.2)10()2(05.02/==-t n t αt 值远大于临界值2.228,故拒绝零假设,说明2β在5%的显著性水平下通过了显著性检验。
(4)41.669800*7863.03720.40=+=f Y (万元)1429.273.425053)88.647800(12110089.2)()(11222=-++=--++=∑X X X X n S S t f e f 所以,Y f 的置信度为95%的预测区间为:3767.241.6690667.1*228.214.696)2(2/±=±=-±f e f S n t Y α所以,区间预测为:18.46764.466≤≤f Y2解:(1)2222)())())((ˆ∑∑∑∑∑∑∑--=---=tt tt t t t t t X X N Y X Y X N X X X X Y Y β 0273.0472*47228158*9472*54.1302.803*9=--= 0727.09/472*0273.09/54.13ˆˆ21=-=-=X Y ββ (2)决定系数:9723.0)()(]))(([2222=----=∑∑∑Y X X X Y Y r t t t t 残差平方和 0722.0)()1(222=--=∑∑Y Y r e t (3)身高与体重的相关系数:9861.09723.02===R r不同时为零和211210:,0:ββββH H ==1016.022=-=∑n e S t e 检验统计量9134.245)(ˆ2222=-=∑e tS X F β)2(2,1-=-N t F NF 值远大于临界值2.365,故拒绝零假设,说明回归方程在5%的显著性水平下通过了显著性检验。
统计学第七章相关与回归分析试题及答案

统计学第七章相关与回归分析试题及答案第七章相关与回归分析(⼆) 单项选择题1、当⾃变量的数值确定后,因变量的数值也随之完全确定,这种关系属于( B )A 、相关关系B 、函数关系C 、回归关系D 、随机关系2、测定变量之间相关密切程度的代表性指标是(C )A 、估计标准误B 、两个变量的协⽅差C 、相关系数D 、两个变量的标准差3、现象之间的相互关系可以归纳为两种类型,即( A )A 、相关关系和函数关系B 、相关关系和因果关系C 、相关关系和随机关系D 、函数关系和因果关系4、相关系数的取值范围是( C )A 、10≤≤γB 、11<<-γC 、11≤≤-γD 、01≤≤-γ5、变量之间的相关程度越低,则相关系数的数值(B )A 、越⼩B 、越接近于0C 、越接近于-1D 、越接近于16、在价格不变的条件下,商品销售额和销售量之间存在着( D )A 、不完全的依存关系B 、不完全的随机关系C 、完全的随机关系D 、完全的依存关系7、下列哪两个变量之间的相关程度⾼( C )A 、商品销售额和商品销售量的相关系数是0.9;B 、商品销售额与商业利润率的相关系数是0.84;C 、平均流通费⽤率与商业利润率的相关系数是-0.94;D 、商品销售价格与销售量的相关系数是-0.918、回归分析中的两个变量(D )A 、都是随机变量B 、关系是对等的C 、都是给定的量D 、⼀个是⾃变量,⼀个是因变量9、每⼀吨铸铁成本(元)倚铸件废品率(%)变动的回归⽅程为:x y c 856+=,这意味着( C )A 、废品率每增加1%,成本每吨增加64元B 、废品率每增加1%,成本每吨增加8%C 、废品率每增加1%,成本每吨增加8元D 、如果废品率增加1%,则每吨成本为56元。
10、某校对学⽣的考试成绩和学习时间的关系进⾏测定,建⽴了考试成绩倚学习时间的直线回归⽅程为:x y c 5180-=,该⽅程明显有错,错误在于( C )A 、a 值的计算有误,b 值是对的B 、b 值的计算有误,a 值是对的C 、a 值和b 值的计算都有误D 、⾃变量和因变量的关系搞错了11、配合回归⽅程对资料的要求是(B )A 、因变量是给定的数值,⾃变量是随机的B 、⾃变量是给定的数值,因变量是随机的C 、⾃变量和因变量都是随机的D 、⾃变量和因变量都不是随机的。
《应用回归分析》课后习题部分答案何晓群版

第二章 一元线性回归2.14 解答:(1)散点图为:(2)x 与y 之间大致呈线性关系。
(3)设回归方程为01y x ββ∧∧∧=+1β∧=12217()ni ii nii x y n x yxn x --=-=-=-∑∑0120731y x ββ-∧-=-=-⨯=-17y x ∧∴=-+可得回归方程为(4)22ni=11()n-2i i y y σ∧∧=-∑ 2n 01i=11(())n-2i y x ββ∧∧=-+∑=2222213⎡⎤⨯+⨯+⨯⎢⎥+⨯+⨯⎣⎦(10-(-1+71))(10-(-1+72))(20-(-1+73))(20-(-1+74))(40-(-1+75)) []1169049363110/3=++++=6.1σ∧=≈ (5)由于211(,)xxN L σββ∧t σ∧==服从自由度为n-2的t 分布。
因而/2|(2)1P t n αασ⎡⎤⎢⎥<-=-⎢⎥⎣⎦也即:1/211/2(p t t ααβββ∧∧∧∧-<<+=1α-可得195%β∧的置信度为的置信区间为(7-2.3537+2.353 即为:(2.49,11.5)2201()(,())xxx Nn L ββσ-∧+t ∧∧==服从自由度为n-2的t 分布。
因而/2(2)1P t n αα∧⎡⎤⎢⎥⎢⎥<-=-⎢⎥⎢⎥⎢⎥⎢⎥⎣⎦即0/200/2()1p βσββσα∧∧∧∧-<<+=- 可得195%7.77,5.77β∧-的置信度为的置信区间为()(6)x 与y 的决定系数22121()490/6000.817()nii nii y y r y y ∧-=-=-==≈-∑∑(7)由于(1,3)F F α>,拒绝0H ,说明回归方程显著,x 与y 有显著的线性关系。
(8)t σ∧==其中2221111()22n ni i i i i e y y n n σ∧∧====---∑∑ 7 3.661==≈ /2 2.353t α= /23.66t t α=>∴接受原假设01:0,H β=认为1β显著不为0,因变量y 对自变量x 的一元线性回归成立。
第七章相关分析与回归分析
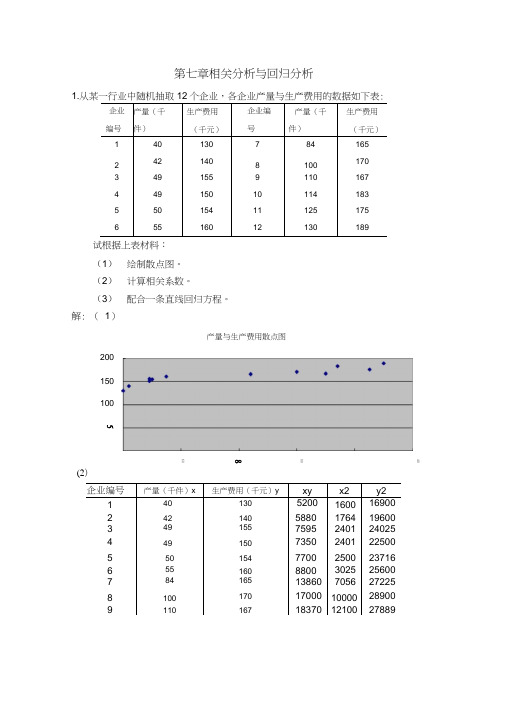
第七章相关分析与回归分析1.企业 编号 产量(千 件)生产费用 (千元)企业编 号 产量(千 件)生产费用 (千元) 1 40 130 7 84 165 2 42 140 8 100 170 3 49 155 9 110 167 4 49 150 10 114 183 550 154 11 125 175 65516012130189试根据上表材料: (1) 绘制散点图。
(2) 计算相关系数。
(3) 配合一条直线回归方程。
解: ( 1)(2) 企业编号产量(千件)x生产费用(千元)yxy x2 y2 1 40 130 **** **** 16900 2 42 140 5880 1764 19600 3 49 155 **** **** 24025 4 49 150 **** **** 22500 5 50 154 7700 2500 23716 6 55 160 8800 3025 25600 784 165 138607056272258 100170 17000 10000 28900 911016718370 12100 278896080040200 150 100产量与生产费用散点图512x159062 -948x1938.12 88368 -9482、12 316190 -19382(3)设回归方程为? = a bxb』甞7n Z x 一(送 x)12 159062-948 1938 12y -bx =1^ -0.4423948=126.558312 12所以回归方程为$ =126.5583 0.4423x2.某县城研究居民月家庭人均生活费支出和月家庭收入的相互关系,随机抽样 10利用上表材料:(1) 绘制散点图并观察两变量之间是否存在线性关系 (2) 计算相关系数,建立回归方程。
(3) 计算估计标准误差。
(4) 测算人均收入为200时,其人均生活费应为多少元 解: ( 1)12 88368-9482_ n 瓦xy-任x)任y) n' x 2 -r x)2. n' y 2 -(' y)2 71520 78838.84-0.907271520 161712二 0.4423(2) 家庭序号月人均收入(元)x月人均生活费(元)yxy x2y21 100 85 8500 10000 72252 110 88 968012100 77443 120 90 10800 14400 81004 130 94 12220 16900 88365 140 96 13440 19600 9216 6 150 100 15000 22500 100007 160 106 16960 25600 112368 170 118 20060 28900 13924 9180 120 21600 32400 14400 10 190 124 23560 36100 15376合计14501021151820 218500 106057n' xy-C x)(' y)10 151820 -1450 1021设回归方程为bxn £ xy-(£ x)(£ y) 10 汇 151820 —1450 乂 1021 n' x 2-C x)2 n' y 2-(' y)2 _ 10 218500 -14502a-bx=1021-0.45761450=35.74810 10所以回归方程为? =35.748 0.4576x (3)、10 218500 -14502 一 10 106057 -10212费活生均人月200-C x)2 .. n'y 2-c y)2 3775038673.54= 0.97613775082500 = 0.4576月人均生活费与人均收入散点图120140160月人均收入180oo oooooo 4 2 0 8 6 4 2' y2-a' y-b' xy _ 106057-35.748 1021-0.4576 151820 目二n-2 「10-2= 3.2684(4)当x=200 时,人均生活费为:y =35.748 0.4576 200 =127.2683. 已知x、y两变量的相关系数r = 0.8 , X =20, y = 50,二y为二x的两倍,求y 对x 的回归方程。
最新应用回归分析-第7章课后习题参考答案
第7章 岭回归思考与练习参考答案7.1 岭回归估计是在什么情况下提出的?答:当自变量间存在复共线性时,|X’X |≈0,回归系数估计的方差就很大, 估计值就很不稳定,为解决多重共线性,并使回归得到合理的结果,70年代提出了岭回归(Ridge Regression,简记为RR)。
7.2岭回归的定义及统计思想是什么?答:岭回归法就是以引入偏误为代价减小参数估计量的方差的一种回归方法,其统计思想是对于(X ’X )-1为奇异时,给X’X 加上一个正常数矩阵D, 那么X’X+D接近奇异的程度就会比X ′X 接近奇异的程度小得多,从而完成回归。
但是这样的回归必定丢失了信息,不满足blue 。
但这样的代价有时是值得的,因为这样可以获得与专业知识相一致的结果。
7.3 选择岭参数k 有哪几种方法?答:最优k 是依赖于未知参数β和2σ的,几种常见的选择方法是: ○1岭迹法:选择0k 的点能使各岭估计基本稳定,岭估计符号合理,回归系数没有不合乎经济意义的绝对值,且残差平方和增大不太多; ○2方差扩大因子法:11()()()c k X X kI X X X X kI --'''=++,其对角线元()jj c k 是岭估计的方差扩大因子。
要让()10jj c k ≤;○3残差平方和:满足()SSE k cSSE <成立的最大的k 值。
7.4 用岭回归方法选择自变量应遵循哪些基本原则? 答:岭回归选择变量通常的原则是:1. 在岭回归的计算中,我们通常假定涉及矩阵已经中心化和标准化了,这样可以直接比较标准化岭回归系数的大小。
我们可以剔除掉标准化岭回归系数比较稳定且绝对值很小的自变量;2. 当k 值较小时,标准化岭回归系数的绝对值并不很小,但是不稳定,随着k 的增加迅速趋近于零。
像这样岭回归系数不稳定、震动趋于零的自变量,我们也可以予以剔除;3. 去掉标准化岭回归系数很不稳定的自变量。
如果有若干个岭回归系数不稳定,究竟去掉几个,去掉那几个,要根据去掉某个变量后重新进行岭回归分析的效果来确定。
应用回归分析(第三版)何晓群 刘文卿 课后习题答案 完整版
资料范本本资料为word版本,可以直接编辑和打印,感谢您的下载应用回归分析(第三版)何晓群刘文卿课后习题答案完整版地点:__________________时间:__________________说明:本资料适用于约定双方经过谈判,协商而共同承认,共同遵守的责任与义务,仅供参考,文档可直接下载或修改,不需要的部分可直接删除,使用时请详细阅读内容第二章一元线性回归分析思考与练习参考答案2.1 一元线性回归有哪些基本假定?答:假设1、解释变量X是确定性变量,Y是随机变量;假设2、随机误差项ε具有零均值、同方差和不序列相关性:E(εi)=0 i=1,2, …,nVar (εi)=s2 i=1,2, …,nCov(εi, εj)=0 i≠j i,j= 1,2, …,n假设3、随机误差项ε与解释变量X之间不相关:Cov(Xi, εi)=0 i=1,2, …,n假设4、ε服从零均值、同方差、零协方差的正态分布εi~N(0, s2 ) i=1,2, …,n2.2 考虑过原点的线性回归模型Yi=β1Xi+εi i=1,2, …,n误差εi(i=1,2, …,n)仍满足基本假定。
求β1的最小二乘估计解:得:2.3 证明(2.27式),Sei =0 ,SeiXi=0 。
证明:其中:即: Sei =0 ,SeiXi=02.4回归方程E(Y)=β0+β1X的参数β0,β1的最小二乘估计与最大似然估计在什么条件下等价?给出证明。
答:由于εi~N(0, s2 ) i=1,2, …,n所以Yi=β0 + β1Xi + εi~N(β0+β1Xi , s2 )最大似然函数:使得Ln(L)最大的,就是β0,β1的最大似然估计值。
同时发现使得Ln(L)最大就是使得下式最小,上式恰好就是最小二乘估计的目标函数相同。
值得注意的是:最大似然估计是在εi~N(0, s2 )的假设下求得,最小二乘估计则不要求分布假设。
所以在εi~N(0, s2 ) 的条件下,参数β0,β1的最小二乘估计与最大似然估计等价。
第七章相关与回归分析
函数关系
(几个例子)
某种商品的销售额 y 与销售量 x 之间的关系 可表示为 y = px (p 为单价)
圆的面积S与半径R之间的关系可表示为 S=R2 企业的原材料消耗额y与产量x1 、单位产量 消耗x2 、原材料价格x3之间的关系可表示为 y = x1 x2 x3
相关关系
(correlation)
1. 是一一对应的确定关系 2. 设有两个变量 x 和 y ,变量 y 随变量 x 一起变化,并完 y 全依赖于 x ,当变量 x 取某 个数值时, y 依确定的关系 取相应的值,则称 y 是 x 的 函数,记为 y = f (x),其中 x 称为自变量,y 称为因变量 3. 各观测点落在一条线上
二.相关关系的种类 1、按相关的程度划分 完全相关 不完全相关 不相关 正相关 负相关 线性相关 非线性相关 单相关 4、按影响因素的多少划分 复相关 3、按相关的形式划分
2、按相关的方向划分
散点图
(scatter diagram)
第七章 相关与回归分析
教学目的与要求 掌握相关关系的含义,以及相关关系与 函数关系的区别,了解相关分析的内容,掌 握相关关系的判别方法和类型,理解回归分 析的实质,熟悉回归分析与相关分析的区别 与联系,掌握一元线性回归分析方法和应用
本章主要内容 第一节 相关分析 第二节 回归分析
第一节
相关分析
客观存在的各种现象之间的相互联系,都可以 表现为一定的数量关系,研究现象之间的数量关系 ,则是回归分析和相关分析的宗旨。现象之间的相 互联系,在许多情况下,表现为一定的因果关系, 将这些现象数量化,则成为变量,其中起着影响作 用的变量称为自变量,受自变量影响而发生变动的 变量称为因变量。 现象之间的相互关系,可以概括为两种不同的类 型,即函数关系和相关关系。
《应用回归分析》课后题答案[整理版]
《应用回归分析》课后题答案[整理版] 《应用回归分析》部分课后习题答案第一章回归分析概述 1.1 变量间统计关系和函数关系的区别是什么, 答:变量间的统计关系是指变量间具有密切关联而又不能由某一个或某一些变量唯一确定另外一个变量的关系,而变量间的函数关系是指由一个变量唯一确定另外一个变量的确定关系。
1.2 回归分析与相关分析的联系与区别是什么, 答:联系有回归分析和相关分析都是研究变量间关系的统计学课题。
区别有a.在回归分析中,变量y称为因变量,处在被解释的特殊地位。
在相关分析中,变量x和变量y处于平等的地位,即研究变量y与变量x的密切程度与研究变量x与变量y的密切程度是一回事。
b.相关分析中所涉及的变量y与变量x全是随机变量。
而在回归分析中,因变量y是随机变量,自变量x可以是随机变量也可以是非随机的确定变量。
C.相关分析的研究主要是为了刻画两类变量间线性相关的密切程度。
而回归分析不仅可以揭示变量x 对变量y的影响大小,还可以由回归方程进行预测和控制。
1.3 回归模型中随机误差项ε的意义是什么, 答:ε为随机误差项,正是由于随机误差项的引入,才将变量间的关系描述为一个随机方程,使得我们可以借助随机数学方法研究y与x1,x2…..xp的关系,由于客观经济现象是错综复杂的,一种经济现象很难用有限个因素来准确说明,随机误差项可以概括表示由于人们的认识以及其他客观原因的局限而没有考虑的种种偶然因素。
1.4 线性回归模型的基本假设是什么,答:线性回归模型的基本假设有:1.解释变量x1.x2….xp是非随机的,观测值xi1.xi2…..xip是常数。
2.等方差及不相关的假定条件为{E(εi)=0 i=1,2….Cov(εi,εj)=,σ^23.正态分布的假定条件为相互独立。
4.样本容量的个数要多于解释变量的个数,即n>p.1.5 回归变量的设置理论根据是什么,在回归变量设置时应注意哪些问题,答:理论判断某个变量应该作为解释变量,即便是不显著的,如果理论上无法判断那么可以采用统计方法来判断,解释变量和被解释变量存在统计关系。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第七章岭回归1.岭回归估计是在什么情况下提出的?答:当解释变量间出现严重的多重共线性时,用普通最小二乘法估计模型参数,往往参数估计方差太大,使普通最小二乘法的效果变得很不理想,为了解决这一问题,统计学家从模型和数据的角度考虑,采用回归诊断和自变量选择来克服多重共线性的影响,这时,岭回归作为一种新的回归方法被提出来了。
2.岭回归估计的定义及其统计思想是什么?答:一种改进最小二乘估计的方法叫做岭估计。
当自变量间存在多重共线性,∣X'X∣≈0时,我们设想给X'X加上一个正常数矩阵kI(k>0),那么X'X+kI 接近奇异的程度小得多,考虑到变量的量纲问题,先对数据作标准化,为了计算方便,标准化后的设计阵仍然用X表示,定义为()()1ˆ''X X I X yβκκ-=+,称为β的岭回归估计,其中k称为岭参数。
3.选择岭参数k有哪几种主要方法?答:选择岭参数的几种常用方法有1.岭迹法,2.方差扩大因子法,3.由残差平方和来确定k值。
4.用岭回归方法选择自变量应遵从哪些基本原则?答:用岭回归方法来选择变量应遵从的原则有:(1)在岭回归的计算中,我们假定设计矩阵X已经中心化和标准化了,这样可以直接比较标准化岭回归系数的大小,我们可以剔除掉标准化岭回归系数比较稳定且绝对值很小的自变量。
(2)当k值较小时标准化岭回归系数的绝对值并不是很小,但是不稳定,随着k的增加迅速趋于零。
像这样的岭回归系数不稳定,震动趋于零的自变量,我们也可以予以删除。
(3)去掉标准化岭回归系数很不稳定的自变量,如果有若干个岭回归系数不稳定,究竟去掉几个,去掉哪几个,这并无一般原则可循,这需根据去掉某个变量后重新进行岭回归分析的效果来确定。
5.对第5章习题9的数据,逐步回归的结果只保留了3个自变量x1,x2,x5,用y对这3个自变量做岭回归分析。
答:依题意,对逐步回归法所保留的三个自变量做岭回归分析。
程序为:include'C:\Program Files\SPSSEVAL\Ridge regression.sps'.ridgereg dep=y/enter x1 x2 x5/start=0.0/stop=1/inc=0.01.岭迹图如下:1.200001.000000.800000.600000.400000.200000.000004.0000003.0000002.0000001.0000000.000000-1.000000-2.000000x5Kx2Kx1Kx5Kx2Kx1KKR IDG E TR AC E计算结果为:可以看到,变量x1、x2迅速由负变正,x5迅速减小,在0.01-0.1之间各回归系数的岭估计基本稳定,重新做岭回归。
岭迹图如下:先取k=0.08:语法命令如下:include'C:\Program Files\SPSSEVAL\Ridge regression.sps'. ridgereg dep=y/enter x1 x2 x5 /k=0.08.运行结果如下:得到回归方程为:123ˆ0.160.080.06738.84yx x x =+++再取k=0.01: 语法命令如下:include'C:\Program Files\SPSSEVAL\Ridge regression.sps'. ridgereg dep=y/enter x1 x2 x5 /k=0.01.运行结果:****** Ridge Regression with k = 0.01 ******Mult R .9931857RSquare .9864179Adj RSqu .9840210SE 329.6916494ANOVA tabledf SS MSRegress 3.000 134201841 44733947Residual 17.000 1847841.9 108696.58F value Sig F411.5487845 .0000000--------------Variables in the Equation----------------B SE(B) Beta B/SE(B)x1 .0556780 .0615651 .0981355 .9043751x2 .0796395 .0218437 .3291293 3.6458814x5 .1014400 .0108941 .5621088 9.3114792Constant 753.3058478 121.7381256 .0000000 6.1879205回归方程为:y=753.3058-0.05568x1-0.0796x2+0.1014x5从上表可看出,方程通过F检验,R检验,经查表,所有自变量均通过t检验,说明回归方程通过检验。
从经济意义上讲,x1(农业增加值)、x2(工业增加值)x5(社会消费总额)的增加应该对y(财政收入)有正方向的影响,岭回归方程中三个自变量的系数均为正值,与实际的经济意义相符。
比逐步回归法得到的方程有合理解释。
6.对习题3.12的问题,分别用普通最小二乘和岭回归建立GDP对第二产业增加值x2,和第三产业增加值x3的二元线性回归,解释所得到的回归系数?答:(1)普通最小二乘法:根据上表得到y 与x2,x3的线性回归方程为:yˆ=4352.859+1.438x2+0.679x3 上式中的回归系数得不到合理的解释. 3ˆβ的数值应该大于1,实际上,x 3的年增长幅度大于x 1和x 2的年增长幅度,因此合理的3ˆβ的数值应大于1。
这个问题产生的原因仍然是存在共线性, 所以采用岭回归来改进这个问题。
(2)岭回归法:程序为:include'C:\Program Files\SPSSEVAL\Ridge regression.sps'. ridgereg dep=GDP/enter x2 x3 /start=0.0/stop=0.5/inc=0.01.根据岭迹图(如下图)可知,)(ˆ2k β和)(ˆ3k β很不稳定,但其和大体上稳定,说明x2和x3存在多重共线性。
取k=0.1,SPSS 输出结果为:Mult R .998145, RSquare .996294 Adj RSqu .995677,SE 2364.837767ANOVA tabledf SS MS Regress 2.000 1.80E+010 9.02E+009 Residual 12.000 67109492 5592457.7 F value Sig F1613.140715 .000000--------------Variables in the Equation----------------B SE(B) Beta B/SE(B)x2 .907990 .021842 .489067 41.571133x3 1.393800 .035366 .463649 39.410560Constant 6552.305986 1278.903452 .000000 5.123378x7.一家大型商业银行有多家分行,近年来,该银行的贷款额平稳增长,但不良贷款额也有较大比例的提高,为弄清楚不良贷款形成的原因,希望利用银行业务的有关数据做些定量分析,以便找出控制不良贷款的办法,表7.5是该银行所属25家分行2002年的有关业务数据。
(1)计算y与其余四个变量的简单相关系数。
(2)建立不良贷款y对4个自变量的线性回归方程,所得的回归系数是否合理?(3)分析回归模型的共线性。
(4)采用后退法和逐步回归法选择变量,所得回归方程的回归系数是否合理,是否还存在共线性?(5)建立不良贷款y对4个自变量的岭回归。
(6)对第4步剔除变量后的回归方程再做岭回归。
(7)某研究人员希望做y对各项贷款余额,本年累计应收贷款.贷款项目个数这三个变量的回归,你认为这种做是否可行,如果可行应该如何做?逐步回归得R-SQUARE AND BETA COEFFICIENTS FOR ESTIMATED VALUES OF KK RSQ x1 x2 x3 x4______ ______ ________ ________ ________ ________.00000 .79760 .891313 .259817 .034471 -.324924 .05000 .79088 .713636 .286611 .096624 -.233765 .10000 .78005 .609886 .295901 .126776 -.174056 .15000 .76940 .541193 .297596 .143378 -.131389 .20000 .75958 .491935 .295607 .153193 -.099233 .25000 .75062 .454603 .291740 .159210 -.074110 .30000 .74237 .425131 .286912 .162925 -.053962 .35000 .73472 .401123 .281619 .165160 -.037482 .40000 .72755 .381077 .276141 .166401 -.023792 .45000 .72077 .364000 .270641 .166949 -.012279 .50000 .71433 .349209 .265211 .167001 -.002497 .55000 .70816 .336222 .259906 .166692 .005882 .60000 .70223 .324683 .254757 .166113 .013112 .65000 .69649 .314330 .249777 .165331 .019387 .70000 .69093 .304959 .244973 .164397 .024860 .75000 .68552 .296414 .240345 .163346 .029654 .80000 .68024 .288571 .235891 .162207 .033870 .85000 .67508 .281331 .231605 .161000 .037587 .90000 .67003 .274614 .227480 .159743 .040874 .95000 .66508 .268353 .223510 .158448 .043787 1.0000 .66022 .262494 .219687 .157127 .046373Run MATRIX procedure:****** Ridge Regression with k = 0.4 ******Mult R .802353780RSquare .643771588Adj RSqu .611387187SE 2.249999551ANOVA tabledf SS MS Regress 2.000 201.275 100.638 Residual 22.000 111.375 5.062F value Sig F19.87906417 .00001172--------------Variables in the Equation----------------B SE(B) Beta B/SE(B) x1 .025805860 .003933689 .574462395 6.560218798 x4 .004531316 .007867533 .050434658 .575951348 Constant .357087614 .741566536 .000000000 .481531456------ END MATRIX -----Y对x1 x2 x3 做岭回归Run MATRIX procedure:****** Ridge Regression with k = 0.4 ******Mult R .850373821RSquare .723135635Adj RSqu .683583583SE 2.030268037ANOVA tabledf SS MSRegress 3.000 226.089 75.363Residual 21.000 86.562 4.122F value Sig F 18.28313822 .00000456--------------Variables in the Equation----------------B SE(B) Beta B/SE(B) x1 .016739073 .003359156 .372627316 4.983118685 x2 .156806656 .047550034 .275213878 3.297719120 x3 .067110931 .032703990 .159221005 2.052071673 Constant -.819486727 .754456246 .000000000 -1.086195166------ END MATRIX -----由图及表可知,(1)y 与x1 x2 x3 x4 的相关系数分别为0.844,0.732,0.700,0.519.(2)y 对其余四个变量的线性回归方程为1234ˆy =-1.022+0.40x 0.1480.0150.029x x x ++- 由于4x 的系数为负,说明存在共线性,固所得的回归系数是不合理的。
