含容电路的分析和计算
含容电路和电路故障分析

含容电路和电路故障分析一、含电容电器的分析与计算方法在直流电路中,当电容器充、放电时,电路里有充、放电电流.一旦电路达到稳定状态,电容器在电路中就相当于一个阻值无限大(只考虑电容器是理想的不漏电的情况)的元件,在电容器处电路可看作是断路,简化电路时可去掉它.简化后若要求电容器所带电量时,可接在相应的位置上.分析和计算含有电容器的直流电路时,需注意以下几点:(1)电路稳定后,由于电容器所在支路无电流通过,所以在此支路中的电阻上无电压降,因此电容器两极间的电压就等于该支路两端的电压.(2)当电容器和电阻并联后接入电路时,电容器两极间的电压与其并联电阻两端的电压相等.(3)电路的电流、电压变化时,将会引起电容器的充(放)电.如果电容器两端电压升高,电容器将充电;如果电压降低,电容器将通过与它连接的电路放电.【例1】如图所示,电源电动势E =12V ,内阻r =1Ω,电阻R 1=3Ω,R 2=2Ω,R 3=5Ω,电容器的电容C 1=4μF ,C 2=1μF 。
求:(1)当S 闭合时间足够长时,C 1和C 2所带的电量各是多少?(2)然后把S 断开,S 断开后通过R 2的电量是多少?解:(1)当S 闭合时间足够长时,C 1两端的电压等于R 2两端的电压;C 2两端的电压等于路端电压 回路电流122E I A r R R ==++ C 1两端的电压U C1=U 2=IR 2=4VC 1的带电量为:Q 1=C 1U C1=4×10-6×4C =1.6×10-5CC 2两端的电压U C2=U =I (R 1+R 2)=10VC 2的带电量为:Q 2=C 2U C2=1×10-6×10C =1.0×10-5C(2)断开S 后,电容器C 1通过电阻R 2、R 3放电;电容器C 2通过电阻R 1、R 2、R 3放电,放电电流均流过R 2,且方向相同。
因此,通过R 2的电量为:Q =Q 1+Q 2=1.6×10-5C +1.0×10-5C =2.6×10-5C【例2】如图,已知源电动势E =12V ,内电阻不计。
含电容器电路的分析与计算

含电容器电路的分析与计算电容器是一个储存电能的元件.在直流电路中,当电容器充放电时,电路里有充放电电流,一旦电路达到稳定状态,电容器在电路中就相当于一个阻值无限大(只考虑电容器是理想的不漏电的情况)的元件,在电容器处电路看作是断路,简化电路时可去掉它.简化后若要求电容器所带电荷量时,可在相应的位置补上.分析和计算含有电容器的直流电路时,需注意以下几点:(1)电路稳定后,由于电容器所在支路无电流通过.所以在此支路中的电阻上无电压降,因此电容器两极间的电压就等于该支路两端的电压.(2)当电容器和用电器并联后接入电路时,电容器两极间的电压与其并联用电器两端的电压相等.(3)电路的电流、电压变化时,将会引起电容器的充(放)电.如果电容器两端电压升高,电容器将充电,如果电压降低,电容器将通过与它并联的电路放电.电容器两根引线上的电流方向总是相同的,所以要根据正极板电荷变化情况来判断电流方向。
⑷如果变化前后极板带电的电性相同,那么通过每根引线的电荷量等于始末状态电容器电荷量的差;如果变化前后极板带电的电性改变,那么通过每根引线的电荷量等于始末状态电容器电荷量之和。
含有电容器的电路解题方法(1)先将含电容器的支路去掉(包括与它串在同一支路上的电阻),计算各部分的电流、电压值。
(2)电容器两极扳的电压,等于它所在支路两端点的电压。
(3)通过电容器的电压和电容可求出电容器充电电量。
(4)通过电容器的电压和平行板间距离可求出两扳间电场强度,再分析电场中带电粒子的运动。
例1:如图所示的电路,水平放置的平行板电容器中有一个带电液滴正好处于静止状态,现将滑动变阻器的滑片P向左移动,则()A.电容器中的电场强度将增大B.电容器上的电荷量将减少C.电容器的电容将减小D.液滴将向上运动由题意可知,电容器与R2并联,根据闭合电路欧姆定律可确定随着滑片左移,电阻的变化,导致电压的变化,从而判定电阻R2的电压变化,再根据可得,电容器的电量及由E=知两极间的电场强度如何变化.【解析】A、电容器两板间电压等于R2两端电压.当滑片P向左移动时,R2两端电压U减小,由E=知电容器中场强变小,A错误;B、根据可得,电容器放电,电荷量减少,B项正确;C、电容器的电容与U的变化无关,保持不变,C项错误.D、带电液滴所受电场力变小,使液滴向下运动,D项错误;故选:B例2:在如图所示的电路中,电源两端A、B 间的电压恒定不变,开始时S断开,电容器上充有电荷.闭合S后,以下判断正确的是()A.C1所带电量增大,C2所带电量减小B.C1所带电量减小,C2所带电量增大C.C1、C2所带电量均减小D.C1、C2所带电量均增大S断开时,外电路中没有电流,两电容器的电压都等于电源的电动势,S闭合后,两电容器的电压都小于电源的电动势,根据Q=CU分析电容器电量的变化.【解析】S断开时,外电路中没有电流,两电容器的电压都等于电源的电动势.S闭合后,两电阻串联,电容器C1的电压等于R1的电压,电容器C2的电压等于R2的电压,可知两电容器的电压都小于电源的电动势,根据Q=CU分析可知两电容器电量均减小.故C正确,ABD错误.故选C例3:如图所示的电路中,R1、R2、R3是固定电阻,R4是光敏电阻,其阻值随光照的强度增强而减小.当开关S闭合且没有光照射时,电容器C 不带电.当用强光照射R4且电路稳定时,则与无光照射时比较()A.电容器C的上极板带正电B.电容器C的下极板带正电C.通过R4的电流变小,电源的路端电压增大D.通过R4的电流变大,电源提供的总功率变小电容在电路稳定时可看作开路,故由图可知,R1、R2串联后与R3、R4并联,当有光照射时,光敏电阻的阻值减小,由闭合电路欧姆定律可得出电路中总电流的变化及路端电压的变化,再分析外电路即可得出C两端电势的变化,从而得出电容器极板带电情况;同理也可得出各电阻上电流的变化.【解析】因有光照射时,光敏电阻的阻值减小,故总电阻减小;由闭合电路的欧姆定律可知,干路电路中电流增大,由E=U+Ir可知路端电压减小;R1与R2支路中电阻不变,故该支路中的电流减小;则由并联电路的电流规律可知,另一支路中电流增大,即通过R2的电流减小,而通过R4的电流增大,故C、D错误;当没有光照时,C不带电说明C所接两点电势相等,以电源正极为参考点,R1上的分压减小,而R3上的分压增大,故上极板所接处的电势低于下极板的电势,故下极板带正电;故A错误,B正确;故选B.例4:如图所示的电路中,两平行金属板A、B水平放置,极板长L=80cm,两板间的距离d=40cm.电源电动势E=40V,内电阻r=1Ω,电阻R=15Ω,闭合开关S,待电路稳定后,将一带负电的小球从B板左端且非常靠近B 板的位置以初速度v=4m/s水平向右射入两板间,该小球可视为质点.若小球带电量q=1×10-2C,质量为m=2×10-2kg,不考虑空气阻力,电路中电压表、电流表均是理想电表.若小球恰好从A板右边缘射出(g取10m/s2).求:(1)滑动变阻器接入电路的阻值为多少?(2)此时电流表、电压表的示数分别为多少?(3)此时电源的输出功率是多少?(1)小球进入电场中做类平抛运动,小球恰好从A板右边缘射出时,水平位移为L,竖直位移为d,根据运动学和牛顿第二定律结合可求出板间电压,再根据串联电路分压特点,求解滑动变阻器接入电路的阻值.(2)根据闭合电路欧姆定律求解电路中电流,由欧姆定律求解路端电压,即可求得两电表的读数.(3)电源的输出功率P=UI,U是路端电压,I是总电流.【解析】(1)小球进入电场中做类平抛运动,水平方向做匀速直线运动,竖直方向做匀加速运动,则有:水平方向:L=vt竖直方向:d=由上两式得:a===20m/s2又根据牛顿第二定律得:a=联立得:U==V=24V根据串联电路的特点有:=代入得:=解得,滑动变阻器接入电路的阻值为 R′=24Ω(2)根据闭合电路欧姆定律得电流表的示数为:I==A=1A电压表的示数为:U=E-Ir=(40-1×1)V=39V(3)此时电源的输出功率是 P=UI=39×1W=39W.答:(1)滑动变阻器接入电路的阻值为24Ω.(2)此时电流表、电压表的示数分别为1A和39V.(3)此时电源的输出功率是39W.每日一练解析C为板间距离固定的电容器,电路连接如图所示,当滑动触头P向右缓慢滑动的过程中,下列说法中正确的是()A.电容器C充电B.电容器C放电C.流过电流计G的电流方向为a→G→bD.流过电流计G的电流方向为b→G→a首先明确含电容器的支路等效为断路,且两端的电压为并联部分的电压相等;当滑动触头P向右缓慢滑动的过程中,该电路的总电阻不变,但与电容器并联部分的电阻减少,即电容器两端的电压减少,根据C=可知,电容器极板电量减少,即放电;电容器右极板与电源负极相连,所以自由电子从a移动到b,故流过电流计G的电流方向为b→G→a.【解析】AB、含电容器的支路等效为断路,且两端的电压为并联部分的电压相等;当滑动触头P向右缓慢滑动的过程中,该电路的总电阻不变,但与电容器并联部分的电阻减少,即电容器两端的电压减少,根据C=可知,电容器极板电量减少,即放电,故A错误,B正确.CD、以上分析可知,电容器放电,且电容器右极板与电源负极相连,所以自由电子从a移动到b,电流的方向与电子的方向相反,故流过电流计G的电流方向为b→G→a,故C错误,D正确.故选:BD.。
高二物理电学专题提升专题20含容电路的分析及计算(2021年整理)

专题20 含容电路的分析及计算一:专题概述解决含电容器的直流电路问题的一般方法:(1) 不分析电容器的充、放电过程时,把电容器处的电路视为断路,简化电路时可以去掉,求电荷量时再在相应位置补上。
(2)电路稳定后,与电容器串联的电路中没有电流,同支路的电阻相当于导线,即电阻不起降压的作用,但电容器两端可能出现电势差.(3)电路中电流、电压的变化可能会引起电容器的充、放电。
若电容器两端电压升高,电容器将充电;若电压降低,电容器将通过与它连接的电路放电.(4)如果电容器与电源并联,且电路中有电流通过,则电容器两端的电压不是电源电动势E,而是路端电压U.(5) 如果变化前后极板带电的电性相同,那么通过每根引线的电荷量等于始、末状态电容器带电荷量之差;如果变化前后极板带电的电性改变,那么通过每根引线的电荷量等于始、末状态电容器带电荷量之和.二:典例精讲1.电容器与滑动变阻器的电路分析典例1:在如图所示的电路中,闭合电键S,将滑动变阻器滑片P向a端移动一段距离,下列结论正确的是A.灯泡L变亮B.电流表读数变大C.电容器C上的电荷量增多D.电压表读数变小【答案】C2.电容与传感器结合的电路分析典例2:如图所示的电路中,R1、R2、R3是固定电阻,R4是光敏电阻,其阻值随光照强度的增强而减小。
当开关S闭合且没有光照射时,电容器C不带电。
当用强光照射R4且电路稳定时,则与无光照射时比较A.电容器C的上极板带正电B.电容器C的下极板带正电C.通过R4的电流变小,电源的路端电压增大D.通过R4的电流变大,电源提供的总功率变小【答案】B3.电容器与二极管电路的分析典例3:如图所示的电路中,电源电动势E=6V,内阻r=1Ω,电阻R1=3Ω,R2=6Ω,电容器的电容C=3。
6μF,二极管D具有单向导电性。
开始时,开关S1闭合,S2断开.(1)合上S2,待电路稳定以后,求电容器上电荷量变化了多少.(2)合上S2,待电路稳定以后再断开S1,求断开S1后流过R1的电荷量是多少.【答案】(1) 减少1.8×10—6C(2) 9.6×10—6C【解析】(1) 设开关S1闭合,S2断开时,电容器两端的电压为U1,干路电流为I1,根据闭合电路欧姆定律有I1==1。
含容电路分析(公)

A.增大R1 B.增大R2 C.增大R3 D.减小R2.
R1 m R2 R3 E
解 这 类 题 的 关 键 : 据 E=U/d 和 E=4π kQ/(ε · S)讨论E的变化情况。根 C 据场强的变化情况就可以分析电容器 中带电粒子的受力情况,从而判定带 电粒子的运动情况。 《走向高考》:P230 第10题
同理可得电容C1的电压为:
U=I (R1+R2)=2×(3+2 )V=10 V 所以根据电容的定义式可分别求出电容C1和C2的带电量为: Q1=C1U=4×10-6×10 C=4×10-5 C Q2=C2U2=1×10-6×2 C=2×10-6 C
电容与电场知识的综合问题 :3、讨论平行板 电容器内部场强的变化,从而判定带电粒子的 运动情况。
R1
C2 C1 R3
R2
求解这类问题关键要知道:电路稳定后,电容器 是断路的,同它串联的电阻均可视为短路,电容 器两端的电压等于同它并联电路两端的电压。
《走向高考》:P230 第6题
解:E=12V,r=1Ω,R1=3Ω,R2=2Ω,R3= 5Ω, C1=4 μF=4×10-6 F,C2=1 μF=1×10-6 F。根据闭合电路的 欧姆定律得到通过R1、R2的电流为: I=E/( R1+ R2+r)=12/(3+2+1) A=2 A 由于电容C2与R2并联,所以根据欧姆定律得到它的电压为: U2=I R2=2×2 V=4 V
U1= UR1 /R= 18×6/(6+3) V=12V
高中物理含电容器电路的分析方法学法指导
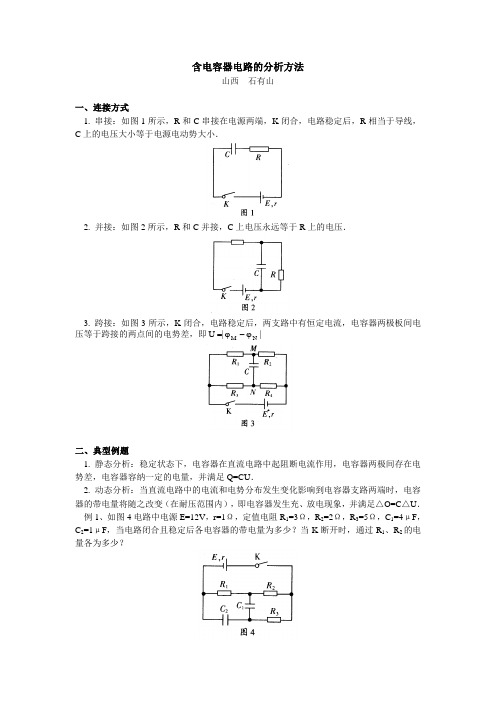
含电容器电路的分析方法山西 石有山一、连接方式1. 串接:如图1所示,R 和C 串接在电源两端,K 闭合,电路稳定后,R 相当于导线,C 上的电压大小等于电源电动势大小.2. 并接:如图2所示,R 和C 并接,C 上电压永远等于R 上的电压.3. 跨接:如图3所示,K 闭合,电路稳定后,两支路中有恒定电流,电容器两极板间电压等于跨接的两点间的电势差,即||U N M ϕ-ϕ=二、典型例题1. 静态分析:稳定状态下,电容器在直流电路中起阻断电流作用,电容器两极间存在电势差,电容器容纳一定的电量,并满足Q=CU .2. 动态分析:当直流电路中的电流和电势分布发生变化影响到电容器支路两端时,电容器的带电量将随之改变(在耐压范围内),即电容器发生充、放电现象,并满足△O=C △U . 例1、如图4电路中电源E=12V ,r=1Ω,定值电阻R 1=3Ω,R 2=2Ω,R 3=5Ω,C 1=4μF ,C 2=1μF ,当电路闭合且稳定后各电容器的带电量为多少?当K 断开时,通过R 1、R 2的电量各为多少?解析:静态分析:R 3相当于导线,C 2与R 1、R 2串联起来的部分并联,C 1和R 2并联.V 10)R R (I U ,V 4IR U ,A 2r R R E I 212C 21C 21=+====++= C 100.1U C Q ,C 101.6U C Q 52C 225C111--⨯==⨯==,且C 1的下极板,C 2的右极板带正电.动态分析:断开K 后,C 1通过R 3、R 2放电,C 2通过R 3、R 2和R 1放电,最后电压都为0,电容上电量也都为0.故通过R 2的电量为Q=Q 1+Q 2=2.6x10-5C ,通过R 1的电量为Q 2=C 100.15-⨯. 例2、如图5所示的电路中,电源电动势为E ,内阻不计,电容器的电容为C ,R 2=R 3=R 4=R 5=R ,R 1为滑动变阻器,其阻值可在0~2R 范围内变化,则当滑动头从最左端向最右端滑动的过程中,通过R 5的电量是多少?解析:动态分析:本题电容器的接法为跨接,且电阻R 1连续变化,C 上电压为连续变化,不妨设电源负极为零电势点.则有2E N =ϕ 当P 置于R 1的最左端时2E U ,E MN M ==ϕ 当P 置于R 1中间某位置时0U ,2E MN M ==ϕ 当P 置于R 1的最右端时6E U ,3E MN M -==ϕ 当滑动头P 从最左端向最右端滑动的过程中,电容器上下极板电势差改变为3E 22E 6E U =--=∆ 则通过R 5的电量CE 32U C Q =∆=∆。
原创1:含容电路的分析与计算

由欧姆定律得通过R1的电流
E
10
I
A 1A
R1 R2 4 6
(2)S断开前,C两端电压U1=IR2=6 V C所带电量Q1=CU1=30×10-6×6 C=1.8×10-4 C 开关S断开稳定后,总电流为零, 电容器两端电压为E, 所带电量Q2=CE=30×10-6×10 C=3×10-4 C 通过R1的电量,即为电容器增加的电量 ΔQ=Q2-Q1=1.2×10-4 C. 答案:(1)1 A (2)1.2×10-4 C 规律总结:处于稳定状态时,电容器相当于断路,与之串联的电阻不
例1.如图所示,电路中E=10 V,R1=4 Ω,R2=6 Ω,C=30 μF.电 池内阻可忽略. (1)闭合开关S,求稳定后通过R1的电流. (2)然后将开关S断开,求这以后通过R1的总电量.
解析:(1)电路稳定后,电容器所在的支路上无电流通过,
因此R1与R2串联,C两端的电压即为R2两端的电压.
R0为定值电阻,R1、R2为可调电阻,用绝缘细线 将质量为m、带正电的小球悬于电容器内部.闭合 电键S,小球静止时受到悬线的拉力为F,下列关 于F的大小变化的判断正确的是( ) A.保持R2不变,缓慢增大R1时,F将变大 B.保持R1不变,缓慢增大R2时,F将变小 C.保持R1、R2不变,减小平行板MN的间距,F将变大 D.保持R1、R2不变,减小平行板MN的间距,F将变小
·R2=3 V.
Q=CU2=12×10-6 C,且a板带正电,b板带负电.
SQ闭′=合C,U1C=两7端.2×电1压0-即6 RC1.两且端a电板压带,负由电电,路b分板析带:正U电1=.R1
R1 R2
·r
E R外
·R外=1.8 V.
据此通过电流表电量ΔQ=Q+Q′=1.92×10-5 C. 答案:1.92×10-5 C
含电容器电路的分析与计算
含电容器电路的分析与计算电容器是一种重要的电子元件,广泛应用于电路中。
在电容器电路的分析与计算中,我们需要了解电容器的基本原理、参数和特性,以及如何计算电容器电路中的电压、电流和时间常数等。
首先,电容器是一种能够储存电荷的电子元件,由两个导体板和介质组成。
常用的电容器有金属箔电容器、陶瓷电容器和电解电容器等,其容值单位是法拉(F)。
电容器的容量取决于其两个导体板之间的面积、板间的距离和介质的电容常数。
在电容器电路中,电容器的两个导体板分别连接到电路的两个节点,形成一个开回路。
当电容器充电时,电容器两个板之间的电荷会积累,并且在两个板之间形成一个电势差。
根据库仑定律,电容器的电压与其所储存的电荷量成正比。
电容器的电压-电荷关系可以表示为V=Q/C,其中V 是电容器的电压,Q是电容器所储存的电荷量,C是电容器的容值。
在电容器电路中,常用于分析和计算的是RC电路和RLC电路。
1.RC电路:RC电路由电阻和电容器组成,常用于滤波和积分电路。
在RC电路中,电容器会充电和放电,形成一个充放电过程。
当电容器充电时,电流通过电阻,电压逐渐上升。
当电容器放电时,电流从电容器流向电阻,电压逐渐下降。
在RC电路中,电容器的充放电过程遵循指数衰减的规律,其电压变化可以用指数函数来描述。
2.RLC电路:RLC电路由电感、电阻和电容器组成,常用于振荡、滤波和谐振电路。
在RLC电路中,电容器和电感可以形成共振回路,当外部输入信号频率等于回路共振频率时,电流最大。
RLC电路的分析和计算可利用电压-电流关系和频率响应等进行求解。
在电容器电路分析和计算时,我们可以通过以下步骤进行:1.确定电容器电路的拓扑结构:确定电容器的连接方式、电阻和电感的位置等。
2.建立电容器电路的数学模型:通过电压和电流的关系、电容器的电压-电荷关系等,建立电容器电路的数学方程。
3.求解电容器电路的初始条件:根据电路的初始状态,确定初始电荷量、电压和电流。
含容电路的分析与计算
D.不论开关 S 断开还是闭合,C1 带的电荷量总比 C2 带的电荷量 大
3、含容电路上的电阻
稳定时,与电容器串联的定 值电阻对电路有没有影响?
第二章 恒定电流
含容电路的分析与计算
稳定时,电容器中有“电流”流过吗?
Hale Waihona Puke R1 E,r CR3 R2 bP a
一、含容电路处理方法
1、含容电路的简化
直流电路中,稳定后电容器可视为断路,简化
电路时可先去掉.
R1 E,r C
R2 bP a
如图所示,R 是光敏电阻,当它受到的光照强度增大 时( )
考
向
互
动
探
究
A.灯泡 L 变暗
B.光敏电阻 R 上的电压增大
C.电压表 V 的读数减小
D.电容器 C 的带电荷量减小
2、含容电路的电压 电容器两端电压等于什么?
R1 E,r C
R2 bP a
2、电容器两端的电压:与其并联支路两端的电压相等 可将其当作一理想电压表
(多选)如图所示,C1=6 μF,C2=3 μF,R1=3 Ω,R2=6 Ω, 电源电动势 E=18 V,内阻不计.下列说法正确的是( )
A.增大R1
B.增大R4
C.减小R2
D.减小R3
R4
C2
C1
R2
R3
R1
E,r
3.如图所示的电路中,电源电动势E=3V,内阻忽略不
计,R1=5Ω, R2=4Ω, C=50μF ,先闭后开关S,当电 路稳定后,断开开关,求开关断开后流过电阻R1的电 量?
含电容器直流电路分析计算问题
含电容器直流电路的分析与计算问题摘要:初次接触电路问题的中学生在利用欧姆定律和串、并联电路的特点进行定性分析和定量计算时,往往觉得很”繁”、很”乱”、很”难”。
其实,解决电路问题的关键在于掌握思路和方法:一般是先对电路进行变形、整理,组成简单的串、并联电路,然后利用欧姆定律及串联的特点建立方程。
学生的问题大多不是出在电路分析阶段,而是建立方程阶段。
关键词:含电容器,直流电路;分析,计算中图分类号:g633.7 文献标识码:e 文章编号:1006-5962(2013)01-0194-01电学是中学物理的重点,也是难点。
欧姆定律又是电学的基础。
初次接触电路问题的中学生在利用欧姆定律和串、并联电路的特点进行定性分析和定量计算时,往往觉得很”繁”、很”乱”、很”难”。
其实,解决电路问题的关键在于掌握思路和方法:一般是先对电路进行变形、整理,组成简单的串、并联电路,然后利用欧姆定律及串联的特点建立方程。
学生的问题大多不是出在电路分析阶段,而是建立方程阶段,在教学中,发现学生”乱”就乱在不知先用哪个公式算什么量.后用哪个公式算什么量。
往往花很长时间还理不出头绪,于是,越想越糊涂,简单的问题也变难了,当然解决不了,怎么办呢?很简单,只要有一种能迅速获得计算结果的方法就行了。
本文以两个用电器串、并联电路为例,介绍一种简单快捷的电器计算方法。
直流电路中,当电容器充放电时,电路里有充、放电电流。
一旦电路达到稳定状态,电容器在电路中就相当于一个阻值无限大(只考虑电容器是理想的不漏电情况)的元件,电容器所在支路可视为断路,简化电路时可去掉,简化后若要求电容器所带电荷量,可接在相应的位置。
【例1】如图1所示,两个电阻r1=5ω,r2=10ω,两电容器c1=5μf,c2=10μf,电路两端电压恒定,u=18v,求:(1)当s断开时,a、b两点间的电压为多大?(2)当s闭合时,两电容器的带电量分别改变了多少?【解析】(1)直流电不能通过c1、c2,所以当s断开时,电路中无电流。
微专题65 含电容器电路分析问题-2025版高中物理微专题
微专题65含电容器电路分析问题【核心考点提示】1.电路的简化:不分析电容器的充、放电过程时,把电容器所处的支路视为断路,简化电路时可以去掉,求电荷量时再在相应位置补上.2.处理方法:电路稳定后,与电容器串联的电路中没有电流,同支路的电阻相当于导线,即电阻不起降低电压的作用,与电容器串联的电阻视为等势体.电容器的电压为与之并联的电阻两端的电压.3.电容器所带电荷量的变化的计算:(1)如果变化前后极板带电的电性相同,那么通过所连导线的电荷量等于初、末状态电容器所带电荷量之差;(2)如果变化前后极板带电的电性相反,那么通过所连导线的电荷量等于初、末状态电容器所带电荷量之和.分析和计算含有电容器的直流电路时,关键是准确判断和求出电容器两端的电压,其具体方法是:(1)确定电容器和哪个电阻并联,该电阻两端电压即为电容器两端电压.(2)当电容器和某一电阻串联后接在某一电路两端时,此电路两端电压即为电容器两端电压.(3)当电容器与电源直接相连,则电容器两极板间电压即等于电源电动势.【微专题训练】(2016·全国卷Ⅱ,17)阻值相等的四个电阻、电容器C 及电池E (内阻可忽略)连接成如图所示电路。
开关S 断开且电流稳定时,C 所带的电荷量为Q 1;闭合开关S ,电流再次稳定后,C 所带的电荷量为Q 2。
Q 1与Q 2的比值为()A.25B.12C.35D.23【解析】S 断开时等效电路如图甲所示。
图甲电容器两端电压为U 1=E R +23R ×23R ×12=15E ;S 闭合时等效电路如图乙所示。
图乙电容器两端电压为U 2=E R +12R ×12R =13E ,由Q =CU 得Q 1Q 2=U 1U 2=35,故选项C 正确。
【答案】C【变式】(多选)如图所示,C 1=6μF ,C 2=3μF ,R 1=3Ω,R 2=6Ω,电源电动势E =18V ,内阻不计,下列说法正确的是()A .开关S 断开时,a 、b 两点电势相等B .开关S 闭合后,a 、b 两点间的电流是2AC .开关S 断开时C 1带的电荷量比开关S 闭合后C 1带的电荷量大D .不论开关S 断开还是闭合,C 1带的电荷量总比C 2带的电荷量大【解析】S 断开时外电路处于断路状态,两电阻中均无电流通过,电阻两端电势相等,由题图知a 点电势与电源负极电势相等,而b 点电势与电源正极电势相等,A 错误.S 断开时两电容器两端电压都等于电源电动势,而C 1>C 2,由Q =CU 知此时Q 1>Q 2.当S 闭合时,稳定状态下C 1与R 1并联,C 2与R 2并联,电路中电流I =E R 1+R 2=2A ,此时两电阻两端电压分别为U 1=IR 1=6V 、U 2=IR 2=12V ,则此时两电容器所带的电荷量分别为Q 1′=C 1U 1=3.6×10-5C 、Q 2′=C 2U 2=3.6×10-5C ,对电容器C 1来说,S 闭合后其两端电压减小,所带的电荷量也减小,故B 、C 正确,D 错误.【答案】BC【巩固习题】1.(2014·天津·2)如图所示,电路中R1、R2均为可变电阻,电源内阻不能忽略,平行板电容器C的极板水平放置,闭合电键S,电路达到稳定时,带电油滴悬浮在两板之间静止不动.如果仅改变下列某一个条件,油滴仍能静止不动的是()A.增大R1的阻值B.增大R2的阻值C.增大两板间的距离D.断开电键S【解析】增大R1的阻值,稳定后电容器两板间的电压升高,带电油滴所受电场力增大,将向上运动,A错误.电路稳定后,电容器相当于断路,无电流通过电阻R2,故R2两端无电压,所以,增大R2的阻值,电容器两板间的电压不变,带电油滴仍处于静止状态,B正确.增大两板间的距离,两板间的电压不变,电场强度减小,带电油滴所受电场力减小,将向下运动,C错误.断开电键S后,两板间的电势差为0,带电油滴只受重力作用,将向下运动,D错误.【答案】B2.如图所示电路中,电源的电动势为E,内阻为r,R1、R3为定值电阻,R2为滑动变阻器,C 为平行板电容器,开关S闭合后,电容器两板正中央有一个带电液滴恰好静止.电流表和电压表都可以视为理想电表.当滑动变阻器滑片P向b端滑动过程中,下述说法中正确的是()A.电压表示数变大,电流表示数变小B.电压表示数变小,电流表示数变大C.电容器C所带电荷量增加,液滴向上加速运动D.电容器C所带电荷量减小,液滴向下加速运动【解析】当滑动变阻器滑片P向b端滑动过程中,接入电路的电阻减小,R2与R3并联的电阻减小,总电阻减小,则总电流增大,R1两端电压增大,则电压表示数变大;R2与R3并联的电压减小,通过R3电流减小,则电流表示数变大,故A、B错误;R2与R3并联的电压减小,电容器板间的电压减小,板间场强减小,液滴所受的电场力减小,则液滴将向下加速运动,故C错误,D正确.【答案】D3.在如图所示的电路中,R 1=11Ω,r =1Ω,R 2=R 3=6Ω,当开关S 闭合且电路稳定时,电容器C 带电荷量为Q 1;当开关S 断开且电路稳定时,电容器C 带电荷量为Q 2,则()A .Q 1∶Q 2=1∶3B .Q 1∶Q 2=3∶1C .Q 1∶Q 2=1∶5D .Q 1∶Q 2=5∶1【解析】当开关S 闭合时,电容器两端电压等于R 2两端的电压,U 2=ER 2R 1+R 2+r =E 3,Q 1=E 3C ;当开关S 断开时,电容器两端电压等于电源电动势,U =E ,Q 2=EC ,所以Q 1∶Q 2=1∶3,选项A 正确.【答案】A4.如图所示,E 为内阻不计的电源,MN 为同种材料制成的粗细均匀的长电阻丝,C 为电容器。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
闭合电路欧姆定律应用二
含容电路
1、如图所示的电路中,电源的电动势恒定,要想使灯泡变暗,可以 ( )
(A )增大R1 (B )减小R1
(C )增大R2 (D )减小R2
2、如图所示,一平行板电容器C ,极板是水平放置的,它和三个可
变电阻及电源连接成如图所示电路.今有一质量为m 的带电油滴悬
浮在两极板之间静止不动.要使油滴上升,可采用的办法是:
A.增大R 1
B.增大R 2
C.增大R 3
D.减小R 2
3、在如图5电路中,电键K 1、K 2、K 3、K 4均闭合,C 是极板水平放置的平行
板电容器,板间悬浮着一油滴P.断开哪一个电键后P 会向下运动?
A.K 1
B.K 2
C.K 3
D.K 4
4、电容器C 1、C 2和可变电阻器R 1、R 2以及电源ε连接成如图所示的电路。
当R 1的滑动触头在图示位置时,C 1、C 2的电量相等。
要使C 1的电量大于C 2
的电量,应
(A)增大R 2 (B)减小R 2
(C)将R 1的滑动触头向A 端移动 (D)将R 1的滑动触头向B 端移动
5、如图所示电路中,已知电容C=2μF ,电源电动势ε=12V ,内电阻不计,
R 1:R 2:R 3:R 4=1:2:6:3,则电容器极板b 所携带的电量为:
A.-8×10-6C
B.4×10-6C
C.-4×10-6C
D.8×10-6C
6、如图所示,ε=10V ,C 1=C 2=30μF ,R 1=4.0Ω,R 2=6.0Ω,电池
内阻可忽略.先闭合开关K ,待电路稳定后,再将K 断开,则断开K
后流过电阻R l 的电量为 .C .
7、在如图所示的电路中,电源电动势为E ,开关S 闭合后,电流表A 的示数为I ,电压表
1V 、2V 的示数分别为1U 、2U ,电容为C 的电容器所带的电荷量为Q 。
现将滑动变阻器1R 的滑动触头P 向上移动一段距离,待电路稳定后,与P 移动前相比( )
A .若电源内阻不能忽略,则
1U 减小,Q 变大,C 不变 B .若电源内阻不能忽略,则
1U 减小,Q 减小,C 变小 C .若电源内阻可以忽略,则
1U 、2U 、I 、Q 和C 中至 少有一个量发生变化
D .不论电源内阻忽略与否,2U 、I 、C 均不变
8、如图所示,电源电动势ε=12伏,内阻r=1欧,电阻R 1=3欧,R 2=2欧,R 3=5欧,电容器的电容量C 1=4μF,C 2=1μF,求C 1、C 2所带电量。
9、如图所示的电路中,两平行金属板A 、B 水平放置,两板间的距离d =40 cm.电源电动势E =24 V ,内电阻r =1 Ω,电阻R =15 Ω.闭合开关S ,待电路稳定后,将一带正电的小球从B 板小孔以初速度v 0=4 m/s 竖直向上射入板间.若小球带电荷量为q =1×10-2C ,质量为m =2×10-
2kg ,不考虑空气阻力.那么,滑动变阻器接入电路的阻值为多大时,小球恰能到达A 板?此时,电源的输出功率是多大?(取g =10 m/s 2)
10、如图所示,将一电动势为E =6 V 、内阻r =0.5 Ω的电源,与一粗细均匀的电阻丝AB 相连,
电阻丝的长度为L =0.30 m ,阻值为R =4 Ω,电容器的电容为C =3 μF.闭合开关S 使其达到稳定状态后,将滑动触头P 向右以速度v =0.6 m/s 匀速滑动的过程中,电流计的读数为多少?流过电流计的电流方向如何?。
