运筹学试题及答案解析
运筹学试卷及参考问题详解
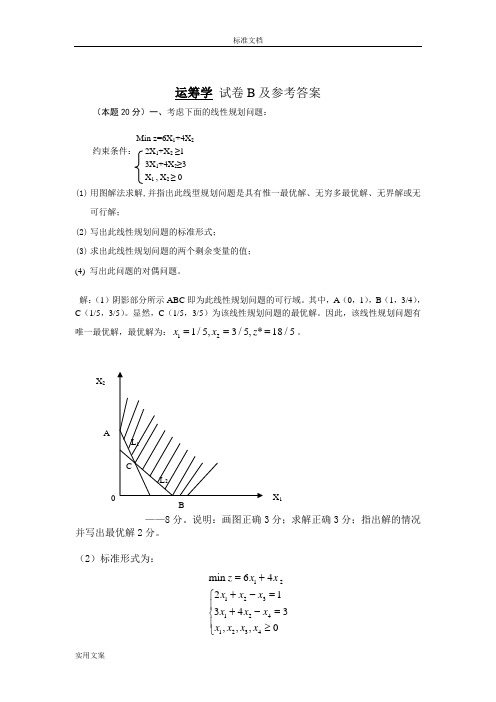
运筹学 试卷B 及参考答案(本题20分)一、考虑下面的线性规划问题:Min z=6X 1+4X 2约束条件: 2X 1+X 2 ≥13X 1+4X 2≥3 X 1 , X 2 ≥ 0(1) 用图解法求解,并指出此线型规划问题是具有惟一最优解、无穷多最优解、无界解或无可行解;(2) 写出此线性规划问题的标准形式; (3) 求出此线性规划问题的两个剩余变量的值; (4) 写出此问题的对偶问题。
解:(1)阴影部分所示ABC 即为此线性规划问题的可行域。
其中,A (0,1),B (1,3/4),C (1/5,3/5)。
显然,C (1/5,3/5)为该线性规划问题的最优解。
因此,该线性规划问题有唯一最优解,最优解为:121/5,3/5,*18/5x x z ===。
——8分。
说明:画图正确3分;求解正确3分;指出解的情况并写出最优解2分。
(2)标准形式为:121231241234min 6421343,,,0z x x x x x x x x x x x x =++-=⎧⎪+-=⎨⎪≥⎩ X 1 X 2 AB——4分 (3)两个剩余变量的值为:340x x =⎧⎨=⎩——3分(4)直接写出对偶问题如下:12121212max '323644,0z y y y y y y y y =++≤⎧⎪+≤⎨⎪≥⎩——5分(本题10分)二、前进电器厂生产A 、B 、C 三种产品,有关资料下表所示:学模型,不求解)解:设生产A 、B 、C 三种产品的数量分别为x 1,x 2和x 3,则有:——1分123123123123123max 810122.0 1.5 5.030002.0 1.5 1.21000200250100,,0z x x x x x x x x x x x x x x x =++++≤⎧⎪++≤⎪⎪≤⎪⎨≤⎪⎪≤⎪≥⎪⎩ ——14分,目标函数和每个约束条件2分(本题10分)三、某电子设备厂对一种元件的年需求为2000件,订货提前期为零,每次订货费为25元。
运筹学试题及详细答案

运筹学试题及详细答案
一、选择题
1、Nash均衡的定义是:
A、每位参与者的行为均达到最佳利益的状态
B、每位参与者的行为均达到得到最大胜利的状态
C、每位参与者的行为均达到合作的最佳状态
D、每位参与者的行为均达到合作的最大胜利的状态
答案:A
2、决策就是参与者用来实现选择的:
A、计划
B、机构
C、程序
D、工具
答案:D
3、运筹学可以分为:
A、组合数学
B、运动学
C、博弈论
D、概率论
答案:A、B、C、D
4、非线性规划有:
A、分支定界法
B、梯度下降法
C、基于格法的解法
D、对偶法
答案:A、B、C、D
5、关于迭代法,下列表述正确的有:
A、可以求解非凸优化问题
B、单次迭代过程简单
C、收敛性较好
D、用于非线性规划
答案:A、B、C
二、填空题:
1、博弈论是研究__参与者之间的__的科学。
答案:多,竞争。
运筹学试卷及参考答案

运筹学试卷及参考答案运筹学试卷一、选择题(每小题2分,共20分)1、下列哪个不是线性规划的标准形式?() A. min z = 3x1 + 2x2B. max z = -4x1 - 3x2C. s.t. 2x1 - x2 <= 1D. s.t. x1 + x2 >= 0答案:C2、以下哪个是最小生成树的Prim算法?() A. 按照权值从小到大的顺序选择顶点 B. 按照权值从大到小的顺序选择顶点 C. 按照距离从小到大的顺序选择顶点 D. 按照距离从大到小的顺序选择顶点答案:B3、下列哪个不是网络流模型的典型应用?() A. 道路交通流量优化 B. 人员部署 C. 最短路径问题 D. 生产计划答案:C4、下列哪个是最小化问题中常用的动态规划解法?() A. 自顶向下的递推求解 B. 自底向上的递推求解 C. 分治算法 D. 回溯法答案:A5、下列哪个是最大流问题的 Ford-Fulkerson 算法?() A. 增广路径的寻找采用深度优先搜索 B. 增广路径的寻找采用广度优先搜索 C. 初始流采用最大边的二分法求解 D. 初始流采用最小边的二分法求解答案:B二、简答题(每小题10分,共40分)1、请简述运筹学在现实生活中的应用。
答案:运筹学在现实生活中的应用非常广泛。
例如,线性规划可以用于生产计划、货物运输和资源配置等问题;网络流模型可以用于解决道路交通流量优化、人员部署和生产计划等问题;动态规划可以用于解决最短路径、货物存储和序列安排等问题;图论模型可以用于解决最大流、最短路径和最小生成树等问题。
此外,运筹学还可以用于医疗资源管理、金融风险管理、军事战略规划等领域。
总之,运筹学的理论和方法可以帮助人们更好地解决实际生活中的问题,提高决策的效率和准确性。
2、请简述单纯形法求解线性规划的过程。
答案:单纯形法是一种求解线性规划问题的常用方法。
它通过不断迭代和修改可行解,最终找到最优解。
具体步骤如下: (1) 将线性规划问题转化为标准形式; (2) 根据标准形式构造初始可行基,通常选取一个非基变量,使其取值为零,其余非基变量的取值均为零; (3) 根据目标函数的系数,计算出目标函数值; (4) 通过比较目标函数值和已选取的非基变量的取值,选取最优的非基变量进行迭代; (5) 在迭代过程中,不断修正基变量和非基变量的取值,直到找到最优解或确定无解为止。
《运筹学》课程考试试卷试题(含答案)

《运筹学》课程考试试卷试题(含答案)一、选择题(每题5分,共25分)1. 运筹学的核心思想是()A. 最优化B. 系统分析C. 预测D. 决策答案:A2. 在线性规划中,约束条件可以用()表示。
A. 等式B. 不等式C. 方程组D. 矩阵答案:B3. 以下哪个不是运筹学的基本模型?()A. 线性规划B. 整数规划C. 非线性规划D. 随机规划答案:D4. 在目标规划中,以下哪个术语描述的是决策变量的偏离程度?()A. 目标函数B. 约束条件C. 偏差变量D. 权重系数答案:C5. 在动态规划中,以下哪个概念描述的是在决策过程中,某一阶段的最优决策对后续阶段的影响?()A. 最优子结构B. 无后效性C. 最优性原理D. 阶段性答案:B二、填空题(每题5分,共25分)1. 运筹学是一门研究在复杂系统中的______、______和______的科学。
答案:决策、优化、实施2. 在线性规划中,若目标函数为最大化,则其标准形式为______。
答案:max z = c^T x3. 在非线性规划中,若目标函数和约束条件均为凸函数,则该规划问题为______。
答案:凸规划4. 在目标规划中,若决策变量x_i的权重系数为w_i,则目标函数可以表示为______。
答案:min Σ(w_i d_i^+ + w_i d_i^-)5. 在动态规划中,若状态变量为s_n,决策变量为u_n,则状态转移方程可以表示为______。
答案:s_{n+1} = f(s_n, u_n)三、判断题(每题5分,共25分)1. 线性规划问题的最优解一定在可行域的顶点处取得。
()答案:正确2. 在整数规划中,若决策变量为整数,则目标函数和约束条件也必须为整数。
()答案:错误3. 目标规划中的偏差变量可以是负数。
()答案:正确4. 在动态规划中,最优策略具有最优子结构。
()答案:正确5. 在非线性规划中,若目标函数为凸函数,则约束条件也必须为凸函数。
运筹学考研真题及答案

运筹学考研真题及答案运筹学考研真题及答案一、选择题1. 在线性规划中,若最优化问题的对偶问题有最优解,则原始问题也有最优解。
(正确)解析:线性规划理论中对偶定理:“若原始问题的对偶问题有可行解,且存在最优解,则原始问题也有最优解。
”2. 若在线性规划的单纯形法中,某一回路上的所有非基变量(非基变量为0)均为0,则这一问题无有限最优解。
(错误)解析:所有非基变量为0时,相应的基变量可以任意非负,问题有无穷多最优解。
3. 在线性规划中,若某元组在原始问题和对偶问题下都是可行解,则该元组是原始问题和对偶问题的最优解。
(错误)解析:若某元组在原始问题和对偶问题下都是可行解,则该元组满足原始问题的可行性和对偶问题的可行性,但并不一定是最优解。
4. 线性规划的最优性条件是原始问题的可行解和对偶问题的可行解所对应的目标函数值相等。
(正确)解析:线性规划理论中最优性条件:“若原始问题的可行解与对偶问题的可行解所对应的目标函数值相等,则解是原始问题和对偶问题的最优解。
”5. 线性规划的可行性要求约束条件为不等式约束。
(错误)解析:线性规划的可行性要求是所有约束条件都满足,包括等式约束和不等式约束。
二、填空题1. 与线性规划的相对论证法相对应的是(单纯形法)。
解析:线性规划的相对论证法和单纯形法是互为相对的两种求解方法。
2. 在线性规划中,若最优差异为0,则最优解是(非唯一)。
解析:最优差异为0意味着最优解是非唯一的,有多个最优解。
3. 线性规划的最优性条件是(对偶定理)与最优条件相对应。
解析:线性规划的最优性条件是对偶定理,而最优条件是原始问题的可行解和对偶问题可行解所对应的目标函数值相等。
4. 在线性规划中,若一个可行解在原始问题和对偶问题下都是最优解,则称为(互补性)条件。
解析:若一个可行解在原始问题和对偶问题下都是最优解,则满足互补性条件。
三、应用题1.某公司生产两种产品A和B,每个产品的制造工序及所需时间如下表,在一天内,公司有8小时的工时可用,每个工序只能由一名员工负责完成。
运筹学考试试卷及答案

运筹学考试试卷及答案一、选择题(每题2分,共20分)1. 线性规划问题的标准形式是:A. 所有变量都非负B. 目标函数是最大化C. 所有约束条件都是等式D. 所有约束条件都是不等式答案:A2. 单纯形法中,如果某个变量的检验数为负数,那么:A. 该变量可以增大B. 该变量可以减小C. 该变量保持不变D. 该变量不能进入基答案:A3. 在运输问题中,如果某种资源的供应量大于需求量,那么应该:A. 增加供应量B. 减少需求量C. 增加需求量D. 减少供应量答案:C4. 动态规划的基本原理是:A. 递归B. 迭代C. 回溯D. 分解答案:D5. 决策树中,每个节点代表:A. 一个决策B. 一个状态C. 一个结果D. 一个概率答案:A6. 排队论中,M/M/1队列的特点是:A. 到达时间服从泊松分布,服务时间服从指数分布,且只有一个服务台B. 到达时间服从指数分布,服务时间服从泊松分布,且只有一个服务台C. 到达时间服从泊松分布,服务时间服从指数分布,且有两个服务台D. 到达时间服从指数分布,服务时间服从泊松分布,且有两个服务台答案:A7. 网络流问题中,最大流最小割定理说明:A. 最大流等于最小割B. 最大流小于最小割C. 最大流大于最小割D. 最大流与最小割无关答案:A8. 整数规划问题中,分支定界法的基本思想是:A. 将问题分解为多个子问题B. 将问题转化为线性规划问题C. 将问题转化为非线性规划问题D. 将问题转化为动态规划问题答案:A9. 在多目标决策中,如果目标之间存在冲突,通常采用的方法是:A. 目标排序B. 目标加权C. 目标合并D. 目标替换答案:B10. 敏感性分析的目的是:A. 确定最优解的稳定性B. 确定最优解的唯一性C. 确定最优解的可行性D. 确定最优解的最优性答案:A二、填空题(每题2分,共20分)1. 线性规划问题的可行域是由所有_________约束条件构成的集合。
答案:可行2. 在单纯形法中,如果目标函数的系数都是正数,则该问题为_________问题。
运筹学复习试题和参考答案解析

《运筹学》一、判断题:在下列各题中,您认为题中描述的内容为正确者,在题尾括号内写“T”,错误者写“F”。
1、 T2、 F3、 T4、T5、T6、T7、 F8、 T9、 F10、T 11、 F 12、 F 13、T 14、 T 15、 F1、线性规划问题的每一个基本可行解对应可行域的一个顶点。
( T )2、用单纯形法求解一般线性规划时,当目标函数求最小值时,若所有的检验数C j-Z j≤0,则问题达到最优。
( F )3、若线性规划的可行域非空有界,则其顶点中必存在最优解。
( T )4、满足线性规划问题所有约束条件的解称为可行解。
( T )5、在线性规划问题的求解过程中,基变量与非机变量的个数就是固定的。
( T )6、对偶问题的对偶就是原问题。
( T )7、在可行解的状态下,原问题与对偶问题的目标函数值就是相等的。
( F )8、运输问题的可行解中基变量的个数不一定遵循m+n-1的规则。
( T )9、指派问题的解中基变量的个数为m+n。
( F )10、网络最短路径就是指从网络起点至终点的一条权与最小的路线。
( T )11、网络最大流量就是网络起点至终点的一条增流链上的最大流量。
( F)12、工程计划网络中的关键路线上事项的最早时间与最迟时间往往就是不相等。
( F )13、在确定性存贮模型中不许缺货的条件下,当费用项目相同时,生产模型的间隔时间比订购模型的间隔时间长。
(T )14、单目标决策时,用不同方法确定的最佳方案往往就是不一致的。
( T )15、动态规则中运用图解法的顺推方法与网络最短路径的标号法上就是一致的。
( F )二、单项选择题1、A2、B3、D4、B5、A6、C7、B8、C9、 D 10、B11、A 12、D 13、C 14、C 15、B1、对于线性规划问题标准型:maxZ=CX, AX=b, X≥0, 利用单纯形法求解时,每作一次迭代,都能保证它相应的目标函数值Z必为( A )。
A、增大B、不减少C、减少D、不增大2、若线性规划问题的最优解不唯一,则在最优单纯形表上( B )。
运筹学复习试题和参考答案解析

《运筹学》一、判断题:在下列各题中,你认为题中描述的内容为正确者,在题尾括号内写“T”,错误者写“F”。
1. T2. F3. T4.T5.T6.T7. F8. T9. F10.T 11. F 12. F 13.T 14. T 15. F1. 线性规划问题的每一个基本可行解对应可行域的一个顶点。
( T )2. 用单纯形法求解一般线性规划时,当目标函数求最小值时,若所有的检验数C j-Z j≤0,则问题达到最优。
( F )3. 若线性规划的可行域非空有界,则其顶点中必存在最优解。
( T )4. 满足线性规划问题所有约束条件的解称为可行解。
( T )5. 在线性规划问题的求解过程中,基变量和非机变量的个数是固定的。
( T )6. 对偶问题的对偶是原问题。
( T )7. 在可行解的状态下,原问题与对偶问题的目标函数值是相等的。
( F )8. 运输问题的可行解中基变量的个数不一定遵循m+n-1的规则。
( T )9. 指派问题的解中基变量的个数为m+n。
( F )10. 网络最短路径是指从网络起点至终点的一条权和最小的路线。
( T )11. 网络最大流量是网络起点至终点的一条增流链上的最大流量。
( F)12. 工程计划网络中的关键路线上事项的最早时间和最迟时间往往是不相等。
( F )13. 在确定性存贮模型中不许缺货的条件下,当费用项目相同时,生产模型的间隔时间比订购模型的间隔时间长。
(T )14. 单目标决策时,用不同方法确定的最佳方案往往是不一致的。
( T )15. 动态规则中运用图解法的顺推方法和网络最短路径的标号法上是一致的。
( F )二、单项选择题1.A2.B3.D4.B5.A6.C7.B8.C9. D 10.B11.A 12.D 13.C 14.C 15.B1、对于线性规划问题标准型:maxZ=CX, AX=b, X≥0, 利用单纯形法求解时,每作一次迭代,都能保证它相应的目标函数值Z必为( A )。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
运筹学试题及答案一、填空题:(每空格2分,共16分)1、线性规划的解有唯一最优解、无穷多最优解、 无界解 和无可行解四种。
2、在求运费最少的调度运输问题中,如果某一非基变量的检验数为4,则说明 如果在该空格中增加一个运量运费将增加4 。
3、“如果线性规划的原问题存在可行解,则其对偶问题一定存在可行解”,这句话对还是错? 错4、如果某一整数规划: MaxZ=X 1+X 2X 1+9/14X 2≤51/14 -2X 1+X 2≤1/3 X 1,X 2≥0且均为整数所对应的线性规划(松弛问题)的最优解为X 1=3/2,X 2=10/3,MaxZ=6/29,我们现在要对X 1进行分枝,应该分为 X1≤1 和 X1≥2 。
5、在用逆向解法求动态规划时,f k (s k )的含义是: 从第k 个阶段到第n 个阶段的最优解 。
6. 假设某线性规划的可行解的集合为D ,而其所对应的整数规划的可行解集合为B ,那么D 和B 的关系为 D 包含 B7. 已知下表是制订生产计划问题的一张LP 最优单纯形表(极大化问题,约束条件均为“≤”型不等式)其中X3,X4,X5为松驰变量。
问:(1)写出B -1=⎪⎪⎪⎭⎫ ⎝⎛---1003/20.3/1312(2)对偶问题的最优解: Y =(5,0,23,0,0)T8. 线性规划问题如果有无穷多最优解,则单纯形计算表的终表中必然有___某一个非基变量的检验数为0______;9. 极大化的线性规划问题为无界解时,则对偶问题_ 无解_____;10. 若整数规划的松驰问题的最优解不符合整数要求,假设X i =b i 不符合整数要求,INT (b i )是不超过b i 的最大整数,则构造两个约束条件:Xi ≥INT (b i )+1 和 Xi ≤INT (b i ) ,分别将其并入上述松驰问题中,形成两个分支,即两个后继问题。
11. 知下表是制订生产计划问题的一张LP 最优单纯形表(极大化问题,约束条件均为“≤”型不等式)其中X4,X5,X6为松驰变量。
问:(1)对偶问题的最优解: Y =(4,0,9,0,0,0)T (2)写出B -1=⎪⎪⎪⎭⎫⎝⎛611401102二、计算题(60分) 1、已知线性规划(20分) MaxZ=3X 1+4X 2 X 1+X 2≤5 2X 1+4X 2≤12 3X 1+2X 2≤8 X 1,X 2≥0其最优解为:1)写出该线性规划的对偶问题。
2)若C2从4变成5,最优解是否会发生改变,为什么?3)若b2的量从12上升到15,最优解是否会发生变化,为什么?4)如果增加一种产品X6,其P6=(2,3,1)T,C6=4该产品是否应该投产?为什么?解:1)对偶问题为Minw=5y1+12y2+8y3y1+2y2+3y3≥3y1+4y2+2y3≥4y1,y2≥02)当C2从4变成5时,σ4=-9/8σ5=-1/4由于非基变量的检验数仍然都是小于0的,所以最优解不变。
3)当若b2的量从12上升到15X=9/829/81/4由于基变量的值仍然都是大于0的,所以最优解的基变量不会发生变化。
4)如果增加一种新的产品,则 P 6’=(11/8,7/8,-1/4)T σ6=3/8>0所以对最优解有影响,该种产品应该生产2、已知运输问题的调运和运价表如下,求最优调运方案和最小总费用。
(共15分)。
解:初始解为计算检验数由于存在非基变量的检验数小于0,所以不是最优解,需调整调整为:重新计算检验数所有的检验数都大于等于0,所以得到最优解3、某公司要把4个有关能源工程项目承包给4个互不相关的外商投标者,规定每个承包商只能且必须承包一个项目,试在总费用最小的条件下确定各个项目的承包者,总费用为多少?各承包商对工程的报价如表2所示:(15分)答最优解为:X= 0 1 0 01 0 0 00 0 1 00 0 0 1总费用为504. 考虑如下线性规划问题(24分)Max z=-5x1+5x2+13x3s.t. -x1+x2+3x3≤2012x1+4x2+10x3≤90x1,x2, x3≥0回答以下问题:1)求最优解2)求对偶问题的最优解3)当b1由20变为45,最优解是否发生变化。
4)求新解增加一个变量x6,c6=10,a16=3,a26=5,对最优解是否有影响5)c2有5变为6,是否影响最优解。
答:最优解为1)最优解为X1=185/33, X3=35/112)对偶问题最优解为Y=(1/22,1/11,68/33,0,0)T3)当b1=45时X= 45/11-11/90由于X2的值小于0,所以最优解将发生变化4)P6’=(3/11,-3/4)Tσ6=217/20>0所以对最优解有影响。
5)当C2=6σ1=-137/33σ4=4/11σ5=-17/22由于σ4大于0所以对最优解有影响5. 求如图所示的网络的最大流和最小截集(割集),每弧旁的数字是(c ij , f ij)。
(15分)V1(5,0) (3,3)(3,3)V S (4,1) V2(4,0)(9,3) (8,4)V3 Vt(6,0)最大流为:14Vs (4,4)(4,1)(9,7) (8,8) VtV3 (6,6)6. 考虑如下线性规划问题(20分)Max z=3x1+x2+4x3s.t. 6x1+3x2+5x3≤93x1+4x2+5x3≤8x1,x2, x3≥0回答以下问题:1)求最优解;2)直接写出上述问题的对偶问题及其最优解;3)若问题中x2列的系数变为(3,2)T,问最优解是否有变化;4)c2由1变为2,是否影响最优解,如有影响,将新的解求出。
最优解为X1=1/3,X3=7/5,Z=33/52)对偶问题为Minw=9y1+8y26y1+3y2≥33y1+4y2≥15y1+5y2≥4y1,y2≥0对偶问题最优解为y1=1/5,y2=3/53) 若问题中x2列的系数变为(3,2)T则P2’=(1/3,1/5)Tσ2=-4/5<0所以对最优解没有影响4)c2由1变为2σ2=-1<0所以对最优解没有影响7. 求如图所示的网络的最大流和最小截集(割集),每弧旁的数字是(c ij , f ij)。
(10分)V1 (4,4 ) V3(9,5) (6,3)V S (3,1) (3,0) (4,1) Vt(5,3) (7,5)V2 (5,4) V4解:V1 (4,4) V3(5,4) (7,7)V2 (5,5) V4最大流=118.某厂Ⅰ、Ⅱ、Ⅲ三种产品分别经过A、B、C三种设备加工。
已知生产单位各种产品所需的设备台时,设备的现有加工能力及每件产品的预期利润见表:1)建立线性规划模型,求获利最大的产品生产计划。
(15分)2)产品Ⅲ每件的利润到多大时才值得安排生产?如产品Ⅲ每件利润增加到50/6元,求最优计划的变化。
(4分)3)产品Ⅰ的利润在多大范围内变化时,原最优计划保持不变。
(2分)4)设备A的能力在什么范围内变化时,最优基变量不变。
(3分)5)如有一种新产品,加工一件需设备A、B、C的台时各为1、4、3h,预期每件为8元,是否值得生产。
(3分)6)如合同规定该厂至少生产10件产品Ⅲ,试确定最优计划的变化。
(3分)解:1)建立线性规划模型为:MaxZ=10x1+6x2+4x3x1+x2+x3≤10010x1+4x2+5x3≤6002x1+2x2+6x3≤300xj≥0,j=1,2,3获利最大的产品生产计划为:X*=(x1,x2,x3,x4,x5,x6)’=(100/3,200/3,0,0,0,100)’ Z*=2200/3 2)产品Ⅲ每件利润到20/3才值得生产。
如果产品Ⅲ每件利润增加到50/6元,最优计划的变化为:X*=(x1,x2,x3,x4,x5,x6)’=(175/6,275/6,25,0,0,0)’ Z*=7753)产品Ⅰ的利润在[6,15]变化时,原最优计划保持不变。
4)设备A的能力在[60,150]变化时,最优基变量不变。
5)新产品值得生产。
6)最优计划的变化为:X*=(x1,x2,x3,x4,x5,x6)’=(190/6,350/6,10,0,0,60 )’ Z*=706.79.给出成性规划问题:(15分)Min z=2x1+3x2+6x3x1+2x2+x3≥2-2x1+x2+3x3≤-3x j≥0 j=1,…,4要求:(1)写出其对偶问题。
(5分)(2)利用图解法求解对偶问题。
(5分)(3)利用(2)的结果,根据对偶问题性质写出原问题最优解。
(5分)解:1)该问题的LD为:MaxW=2y1-3y2y1-2y2≤22y1+y2≤3y1+3y2≤6y1≥0,y2≤02)用图解法求得LD的最优解为:Y*=(y1,y2)’=(8/5,-1/5)’ W*=19/53)由互补松弛定理:原问题的最优解为:X*=(x1,x2,x3)’=(8/5,1/5,0)’10. 某部门有3个生产同类产品的工厂(产地),生产的产品由4个销售点(销地)出售,各工厂的生产量,各销售点的销售量(单位.t)以及各工厂到各销售点的单位运价(元/t)示于下表中,要求研究产品如何调运才能使总运量最小?(10分)A1-B3和B4 28t 和4t A2-B1和B4 16t 和4t A3-B2和B4 28t 和16t 最小总运费为:460元11. 求解下列0-1规划问题 maxz=3x 1+2x 2-5x 3-2x 4+3x 5 x 1+x 2+x 3+2x 4+x 5≤4 7x 1+3x 3-4x 4+3x 5≤8 11x 1-6x 2+3x 4-3x 5≥3 x j =0或1 (j=1, (5)解:最优解为:x1=x2=1,其他为0 ,最优目标函数值为5销产。
