第3章 爆轰波、爆燃波的经典理论
燃烧学 复习重点

第三章 着火和灭火理论一、谢苗诺夫自燃理论 1. 基本思想:某一反应体系在初始条件下,进行缓慢的氧化还原反应,反应产生的热量,同时向环境散热,当产生的热量大于散热时,体系的温度升高,化学反应速度加快,产生更多的热量,反应体系的温度进一步升高,直至着火燃烧。
2.着火的临界条件:放、散热曲线相切于C 点。
3.∆T=ER 20B T T T ≈-① 改变散热条件 ②增加放热二、区别弗兰克-卡门涅茨基热自燃理论与谢苗诺夫热自燃理论的异同点1.谢苗诺夫热自燃理论适用范围:适用于气体混合物,可以认为体系内部温度均一;对于比渥数 Bi 较小的堆积固体物质,也可认为物体内部温度大致相等; 不适用于比渥数Bi 大的固体.2。
弗兰克-卡门涅茨基热自燃理论:适用于比渥数Bi 大的固体(物质内部温度分布的不均匀性 ); 以体系最终是否能得到稳态温度分布作为自燃着火的判断准则 ;Tq αT自燃临界准则参数 δcr 取决于体系的几何形状。
三、链锁自然理论 1。
反应速率与时间的关系 2.运用链锁自燃理论解释着火半岛现象 在第一、二极限之间的爆炸区内有一点P(1)保持系统温度不变而降低压力,P 点则向下垂直移动自由基器壁消毁速度加快,当压力下降到某一数值后,f < g, φ < 0 -—-------———-—--—--——-第一极限(2)保持系统温度不变而升高压力,P 点则向上垂直移动自由基气相消毁速度加快,当压力身高到某一数值后,f 〈 g , φ 〈 0 —-——-——-——————-—-—-———第二极限(3)压力再增高,又会发生新的链锁反应导致自由基增长速度增大,于是又能发生爆炸。
---3.基于f (链传递过程中链分支引起的自由基增长速率)和g (链终止过程中自由基的消毁w0w123M HO M O H +→++⋅22⋅⋅+→+OH O H H HO 222速率 )分析链锁自燃着火条件a.在低温时, f 较小(受温度影响较大),相比而言,g 显得较大,故:这表明,在 的情况下,自由基数目不能积累,反应速率不会自动加速,反应速率随着时间的增加只能趋势某一微小的定值,因此,f<g系统不会着火。
第3章 爆轰波的经典理论

1 2 j D u j U j Pj D u j j D u j D u j 2
… (3)
16
3.1.1 爆轰波的基本关系式
由(1)、(2)式可得:
D u 0 v0 p j p0 v0 v j
p j p0 v0 v j
4
第3章 爆轰波的经典理论
Chapman和Jouguet在20世纪初分别提出了关于爆
轰波的平面一维流体动力学理论,简称爆轰波的
CJ理论。
前苏联的泽尔多维奇(Zeldovich,1940年),美 国的冯纽曼(Von Neumann,1942年),德国的道 尔令(Doering,1943年)各自对CJ理论进行了改 进,提出了ZND模型。
P0 O
0
v0
v
爆轰波:
e e0
1 p p0 v0 v Qe 2
22
3.1.2 爆轰波稳定传播的条件
3.Rayleigh线和Hugoniot曲线的关系
(1)dc段:v>v0,p>p0 D为虚数 (2)c点: v>v0,p=p0 D=0,定压燃烧 (3)CGAI段: v>v0,p<p0 D>0,u<0;爆燃 其中,CGA段(p-p0)负压值较小, 称弱爆燃支; AI段(p-p0)负压值较大, 称强爆燃支。 A点的爆燃速度最大。
D v0
p p0 v0 v
D2 D2 p 2 v p0 v v0 0
D2 tg tg 2 v0
21
3.1.2 爆轰波稳定传播的条件
2. Hugoniot (雨贡纽、雨果尼奥)曲线
P 1 2
爆轰学第3章_爆轰波、爆燃波的经典理论

pp0 v0 v
pD v022vD v02 p0
tgtg D v0 22
21
3.1.2 爆轰波稳定传播的条件 2. Hugoniot (雨贡纽、雨果尼奥)曲线
12 P
冲击波: ee01 2pp0v0v
P0
O
0
v0
爆轰波: e e01 2pp 0v0 v Q e
v 22
3.1.2 爆轰波稳定传播的条件
由(3)、(6)、(7)式可推导出:
e j e 0 1 2p j p 0v 0 v j Q e ……(8)
这就是爆轰波的Hugoniot方程,也称放热的 Hugoniot方程。
18
3.1.1 爆轰波的基本关系式
➢ 如果已知爆轰产物的状态方程:
eep,v
或
pp,s
……(9)
➢ 从数学上来说,爆轰波应满足什么条件才能使爆
16
3.1.1 爆轰波的基本关系式
由(1)、(2)式可得:
Du0 v0
pj p0 v0 vj
uj u0v0vj
pj p0 v0vj
在u0 0 时,(4)、(5)式可变为:
Dv0
pj p0 v0 vj
uj v0vj
pj p0 v0vj
……(4) ……(5) ……(6) ……(7)
17
3.1.1 爆轰波的基本关系式
➢ ZND模型把爆轰波阵面看成是由前沿冲击波和紧 跟其后的化学反应区构成,它们以同一速度沿爆 炸物传播,反应区的末端平面对应CJ状态,称 为CJ面。
39
3. 2 爆轰波的ZND模型
图3-4 ZND模型
40
3. 2 爆轰波的ZND模型
➢ 按照这一模型,爆轰波面内发生的历程为:原始爆 炸物首先受到前导冲击波的强烈冲击压缩,立即由 初始状态O(v0,p0)被突跃压缩到N(vN,pN)点的状态, 温度和压力突然升高,高速的爆轰化学反应被激发, 随着化学反应连续不断地展开,反应进程变量λ从 N(vN,pN)点(λ=0)开始逐渐增大,所释放的反应热λQe 逐渐增大,状态由点N沿瑞利线逐渐向反应终态点M 变化,直至反应进程变量λ=1 ,到达反应区的终态, 化学反应热Qe全部放出。
爆轰学 第1章_绪论

1.1基本概念
▪ 一些宇宙学家认为,当今宇宙是在一次大爆 炸中开始形成和发展的,而且至今这一过程 尚未结束,宇宙的年龄大约为137亿年,地球 也是在一次大爆炸中产生的,距今已46亿年。
12
1.1基本概念
2011年诺贝尔物理学奖 美国加州大学伯克利分校教授索尔-佩尔马特、澳大利亚国 立大学教授布莱恩-施密特,以及美国约翰斯霍普金斯大学
8
1.1基本概念
(4)燃烧产物移动的方向与燃烧波传播 的方向相反。
(5)凝聚物的燃烧要经过熔化、蒸发、升 华、热分解、混合和扩散等中间阶段,才能 通过燃烧化学反应转变为燃烧的最终产物。
(6)与其他化学反应相似,燃烧反应速度 受到反应物浓度和温度的影响,燃速对外界 条件(如压力、初温、扩散速度等)的变化 敏感。
2
爆炸物理学 ➢ 主要内容
第1章 绪论 第2章 炸药的起爆机理 第3章 爆轰(爆热)波的经典理论 第4章 气体爆轰理论 第5章 凝聚炸药爆轰理论 第6章 爆轰产物的流动及其与物体的相互作用
3
第1章 绪论
4
第1章 绪论
本章内容 ➢ 燃烧、爆炸、炸药、爆轰的基本概念; ➢ 炸药爆炸的特点; ➢ 炸药发生化学变化的类型; ➢ 爆轰学的研究历史。
5
1.1基本概念
6
1.1基本概念
1.燃烧(Combustion,Deflagration) ➢ 物质间发生剧烈氧化还原的化学反应,并
伴随放热和发光,产生大量高温气体的过 程,称为燃烧。
➢ 燃烧具有以下的基本特征: (1)燃烧体系中,必须有燃烧化学反
应所需要的氧化元素和可燃元素。
7
1.1基本概念
▪ 烟火剂:通常由氧化剂、有机可燃物(或金 属粉)加入少量粘合剂混合而成。军事上, 利用其速燃时产生的光、热、烟、色、声等 效应用于各种用途,如照明弹中的照明剂、 烟幕弹、燃烧弹等。
3.3炸药的爆轰理论
炸药径向间隙效应
视频1 视频2
可采取选用爆速大的炸药和大直径药 卷及坚固外壳等措施,实现稳定爆轰。
视频1
视频2
七、爆速的测定方法
炸药的爆速是衡量炸药爆炸性能的重 要标志量,也是目前可以比较准确测定的 一个爆轰参数。
测量方法 (1)导爆索法 (2)电测法 (3)高速摄影法
视频1 视频2
l
h
导爆索法测爆速
一、冲击波的基本概念
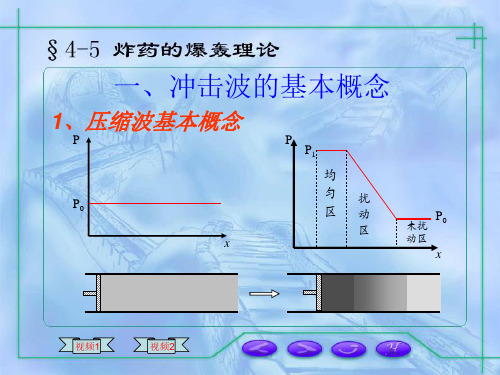
1、压缩波基本概念
P P
P1
P0 x
均 匀 区
扰 动 区
未扰 动区
P0 x
视频1
视频2
在无限长气筒活塞右侧充满压力为P0 的气体,当活塞在F力的作用下向右运动 时,活塞右侧气体存在三个区域: 压力为P1的均匀区 压力介于P1与P0之间的扰动区 压力仍为P0的未扰动区
视频1
视频2
视频1 视频2
2
1 0
使介质运动的力是波阵面两边的压力差 PH P0 在单位时间内流进波阵面的介质质量为 0 ( D u0 ) 其速度的变化为 ( D u 0 ) ( D u H ) u H u 0 根据动量守恒定律有:
PH P0 0 ( D u 0 )( u H u 0 )
已反应的药包
视频1 视频2
未反应的药包
1)炸药达到稳定爆轰前有 一个不稳定的爆炸区。
2)在特定的条件下,每种 炸药都会有一个不变的炸 药特征爆速Di。 3) 每种炸药都存在一个最 小的临界爆速Dc。波速低 于Dc后,冲击波将衰减为 音波而导致爆轰熄灭。
炸药包在冲击波激发下的爆轰过程
视频1 视频2
(2)爆轰波模型
H ( D u H )[ E H
炸药与爆炸的基本理论

第一章本章小结本章集中介绍了与炸药爆炸相关的一些基本概念、基本理论和基本实验,这些内容是后续章节的基础。
现将其中的要点归纳如下:1.炸药发生化学变化的三种基本形式,炸药爆炸的三要素,炸药的分类。
炸药、单质炸药、混合炸药、起爆药、猛炸药和炸药爆炸的概念。
2.炸药氧平衡的概念极其计算方法。
爆热、爆温、爆容、爆炸压力的概念。
3.波、横波、纵波、音波、压缩波、稀疏波、冲击波的概念。
冲击波的基本特性。
4.爆轰波、爆轰压力、爆轰温度的概念和爆轰波的结构。
凝聚炸药的爆轰反应机理。
5.炸药的使用感度、危险感度、热感度、爆发点、机械感度、撞击感度、摩擦感度、起爆感度和雷管感度的概念。
炸药的物理状态和装药条件对炸药感度的影响。
6.炸药的热点起爆理论,爆炸物直接作用于炸药的起爆机理。
7.炸药的爆速、影响爆速的主要因素、爆速的测定方法。
作功能力、猛度、殉爆距离的概念及其试验测定方法。
炸药的理想爆速、临界爆速、极限直径、临界直径、最佳密度、临界密度的概念。
8.沟槽效应,产生沟槽效应的机理,消除沟槽效应的措施。
9.聚能效应及其应用。
复习题1.计算硝化甘油和梯恩梯的氧平衡。
2.在铵油炸药中(硝酸铵与柴油的混合炸药),假如 4%木粉作疏松剂,试按零氧平衡设计炸药配方。
3•已知凝聚炸药的绝热指数 K值一般取为3,试推导计算凝聚炸药爆轰波参数的方程式。
4•已测得某种岩石铵梯炸药的密度0 1.0g/cm,爆速D=3750m/s。
经计算得到其爆温 Tb 2592 C。
试求这种炸药的其余各项爆轰波参数uH、PH、H、cH和TH。
5•如果采用理想气体状态方程来计算爆炸压力P,则存在关系P 0(K 1)Qv。
试证明:爆轰压力近似等于爆炸压力的2倍。
6•试推导实验测定炸药爆速的导爆索法中计算爆速的公式。
3。
第3章 炸药的起爆机理

Ea Tc2 Tc T0 0
12
1 1 4RT0 Ea 它的解为: Tc 2R Ea
3.2.1 均温分布的定常热爆炸理论
对于大多数炸药,取负号的解,因为正号的解 不符合实际情况。 由于 RT0 Ea 的值很小,取上式在 RT0 Ea 附近 的级数展开:
2 Tc RT0 RT0 RT0 2 4 Ea Ea Ea 2R Ea
35
3.2.2 炸药的热感度
根据试验作出T与τ ,lnτ 与1/T的关系图,由 τ -T图可求得5s延滞期爆发点。 试验得到的凝聚炸药爆发点与延滞期的关系为: lnτ =A+E/RT 式中 τ 为延滞期(s);E为与爆炸 反应相应的炸药活化能(J/mol);R为通用气体 常数;A为与炸药有关的常数;T为爆发点(K)。 测得的爆发点越低,说明炸药的感度越大,反 之则感度越小。
Q1 m q A exp Ea RT
……(2)
式中
m ——炸药质量; Ea ——炸药活化能;
16
R
——气体常数。
3.2.1 均温分布的定常热爆炸理论
由(2)式可知,炸药进行放热化学反应而产 生的热量与温度的关系符合指数曲线,该曲线 称为得热线,如图3-2所示。
17
3.2.1 均温分布的定常热爆炸理论
22
3.2.1 均温分布的定常热爆炸理论
Tc Tc T02
表示热爆炸前的升温情况。
从数学上看,切点必须满足两个条件,即不但 Q1和Q2在该点的数值相等,且两条曲线的斜率 也相等,即 Q 1=Q 2 ……(4) ……(5)
dQ1 dT dQ2 dT
23
爆轰波PPT课件

冲击波+化学反应区=爆轰波 “爆速”(detonation velocity)定义: 爆轰波沿炸药装药传播的速度------爆速。
29.07.2020
第 4页
29.07.2020
第 10 页
C-J理论
从λ=0到λ=1是瞬间完成的,期间没有时间间隔。用e(λ) 表示单位质量(或mol)的化学反应能,则e(λ)可写为:
e()(1)Q
比内能e可表示为: e e (P ,V ,) e (P ,V ) e ()
Q:炸药爆轰热(爆轰化学反应放出的热量),
e 1 (P 1 ,V 1 , 1 ) e (P 1 ,V 1 ),e 0 (P 0 ,V 0 , 0 ) e (P 0 ,V 0 ) Q
②在Ⅱ区, PP0 0 , VV0 0 , 对应于爆轰过程。
Ⅱ区, 爆轰
③在Ⅳ区,PP0 0 ,VV0 0 , 对应于爆燃过程。
І区, 无物理 意义
29.07.2020
A(P0,V0)
Ш区,无物理 意义
பைடு நூலகம்
Ⅳ区,爆燃
V
第 13 页
对爆轰波, PP0 0 ,由(2)可知:D u0 与 u1 u0 同号,
说明爆轰波通过后,介质质点在爆轰波方向受到加速,如果
u0 0 ,则介质质点运动速度u1与D同向。
C、爆轰波绝热曲线——Hugoniot曲线(由3个守恒方程得到的 P-V关系在P-V平面上的几何表示)
(4)式在P-V平面上的曲线为双曲线:
e1
P1V 1 1
, e0 P0V01(爆轰前后均为理想气体,且 不变)
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(5)
所以
D uj cj
31
3.1.2 爆轰波稳定传播的条件
5.CJ点的性质 (1)在Hugoniot曲线上,CJ点的爆速最小。 证明:可由Rayleigh线的斜率来证明。
P K
M P0
L
O
0
v0
v 32
3.1.2 爆轰波稳定传播的条件 (2)在Hugoniot曲线上,CJ点的熵值最小。
4
第3章 爆轰波、爆燃波的经典理论
Chapman和Jouguet在20世纪初分别提出了关于爆
轰波的平面一维流体动力学理论,简称爆轰波的
CJ理论。 前苏联的泽尔多维奇(Zeldovich,1940年),美 国的冯纽曼(Von Neumann,1942年),德国的道 尔令(Doering,1943年)各自对CJ理论进行了改 进,提出了ZND模型。
6
3.1 爆轰波的CJ理论
7
3.1 爆轰波的CJ理论
19世纪末研究发现,爆炸物的爆炸过程是爆轰波 沿爆炸物的传播过程,并且发现爆轰一旦被激发, 其传播速度很快趋向该爆炸物所具有的特定数值, 即所谓理想特性爆速。在通常情况下,爆轰波以 该特征速度稳定传播下去。 在揭示爆轰波稳定传播的理论探索中, Chapman和Jouguet各自独立地提出了爆轰流 体动力学理论,提出并论证了爆轰波稳定传播的 条件及其表达式。此理论简称为爆轰波的C-J理 论。
27
3.1.2 爆轰波稳定传播的条件
由该式可知,爆轰波阵面后的稀疏波就不会 传入爆轰反应区之中,因此反应区内所释放 出来的能量就不会发生损失,而全部用来支 持爆轰波的定常传播。
28
3.1.2 爆轰波稳定传播的条件
该CJ条件可由Rayleigh线和Hugoniot曲线相 切来证明。
dp dp dv H dv R
第3章 爆轰波、爆燃波的 经典理论
1
主要内容
3.1 爆轰波的CJ理论 3.2爆轰波的ZND模型 3.3爆轰和爆燃状态的基本性质 (Jouguet法则)
3.4反应区流动的定常解
2
第3章 爆轰波、爆燃波的经典理论
1881年贝尔特劳(Berthelot)、维也里(Vieille) 发现了爆轰现象,即爆轰波的传播现象。 从此,人们对气相爆炸物(2H2+O2,CH4+2O2) 和凝聚相爆炸物(硝基甲烷、TNT、RDX)的 爆轰过程进行了大量的实验观察。 实验表明:爆轰过程乃是爆轰波沿爆炸物一层一 层地进行传播的,同时还发现,不同的爆炸物爆 轰之后,爆轰波都趋向于该爆炸物所特有的爆速 进行传播。
p p0 v0 v
D v0
D2 D2 p 2 v v p0 v0 0
D2 tg tg 2 v0
21
3.1.2 爆轰波稳定传播的条件
2. Hugoniot (雨贡纽、雨果尼奥)曲线
P 1 2
冲击波: e e0 1 p p0 v0 v 2
1 2
… (3)
j D u j U j Pj D u j
1 j D u j D u j 2 2
16
3.1.1 爆轰波的基本关系式
由(1)、(2)式可得:
D u 0 v0 p j p0 v0 v j
p j p0 v0 v j
和Qj分别表示爆炸物和产物单位质量含有的化 学能,以e0和ej代表相应物质的状态内能。则
U 0 e 0 Qe U j ej Qj
14
3.1.1 爆轰波的基本关系式
因此,波阵面前后物质总的比内能的变化为:
U j U 0 e j e0 Q j Qe
5
第3章 爆轰波、爆燃波的经典理论
对于通常的气相爆炸物爆轰波的传播速度一般约 为1500m/s~4000m/s,爆轰终了断面所达到的 压力和温度分别为数个兆帕和2000K~4000K。 对于军用高猛炸药,爆速通常在6000m/s~ 10000m/s的范围,波阵面穿过后产物的压力高达 数十个吉帕,温度高达3000K~5000K,密度增 大1/3。
dv R dv H dv s
30
3.1.2 爆轰波稳定传播的条件
由于
p p0 dp dv R v0 v
p p0 dp dp 因此 c j v v d v0 v dv s s p p0 D v0 v0 v
证明:
1 e e0 p p0 v0 v Qe 2 1 de v0 v dp p p0 dv 2
Tds de pdv
Tds
1 v0 v dp p p0 dv 2 2 p p0 2Tds v 0 v d v v 0 p p0 tg v0 v
其中 Q j Qe 就是爆轰反应放出的化学能称 为爆热。
15
3.1.1 爆轰波的基本关系式
由于爆轰产物中化学能Qj为零,因此:
U j U 0 e j e0 Qe
按照能量守恒定律,单位时间、单位面积上从波阵
面前流入的能量等于从波阵面后流出的能量,即
0 D u 0 U 0 P0 D u 0 0 D u 0 D u 0 2
P0 O
0
v0
v
爆轰波:
e e0
1 p p0 v0 v Qe 2
22
3.1.2 爆轰波稳定传播的条件
3.Rayleigh线和Hugoniot曲线的关系
(1)dc段:v>v0,p>p0 D为虚数 (2)c点: v>v0,p=p0 D=0,定压燃烧 (3)CGAI段: v>v0,p<p0 D>0,u<0;爆燃 其中,CGA段(p-p0)负压值较小, 称弱爆燃支; AI段(p-p0)负压值较大, 称强爆燃支。 A点的爆燃速度最大。
33
3.1.2 爆轰波稳定传播的条件
Tds v0 v 1 tg 2 d
2
2T
ds d 2 v0 v 1 tg 2 dv dv
1 P
2 K
M
a
P0 O
L
0
v0
v 34
3.1.2 爆轰波稳定传播的条件
在切点M以上,当v沿Hugoniot曲线逐渐增大时,a角 逐渐减小。即da/dv<0。 因此ds/dv<0,即在M以上,熵s是随v的增大而减小的。 在切点M以下,当 v 沿Hugoniot曲线逐渐增大时, a 角逐渐增大。即da/dv>0。 因此ds/dv>0,即在M以下,熵s是随v的增大而增大 的。
……(4) ……(5) ……(6) ……(7)
17
u j u 0 v0 v j
在u 0 0 时,(4)、(5)式可变为:
D v0 p j p0 v0 v j
u j v 0 v j
p j p0 v0 v j
3.1.1 爆轰波的基本关系式
由(3)、(6)、(7)式可推导出:
(2)该点应具备什么特点呢?
26
3.1.2 爆轰波稳定传播的条件
4.爆轰波稳定传播的CJ条件 Chapman首先提出,稳定爆轰的状态应对应于 Rayleigh线和Hugoniot曲线的相切点M。 Jouguet进一步阐明,爆轰波相对波后产物的传 播速度等于当地声速,即
D uj cj
பைடு நூலகம்
此式即为爆轰波稳定传播的CJ条件,该切点M对 应的爆轰也叫CJ爆轰。
证了爆轰波稳定传播的条件及其表达式。
9
3.1.1 爆轰波的基本关系式
10
3.1.1 爆轰波的基本关系式
CJ理论将爆轰波视为带有化学反应的冲击波, 其波阵面上仍满足质量、动量和能量守恒。
设爆轰波传播速度为D,把坐标系建立在波阵
面上,则原始爆炸物以D-u0的速度流入波阵面, 而以D-uj的速度从波阵面流出,如图3-1所示, 其中下标j代表波阵面后的参数。
由图示可知:D>C0 该段为爆轰段
24
3.1.2 爆轰波稳定传播的条件
其中,MLd段(p-p0)值较小, 称弱爆轰支; MK段(p-p0)值较大, 称强爆轰支。 M点的爆轰速度最小。
25
3.1.2 爆轰波稳定传播的条件
问题:
(1)稳定传播的爆轰波传过后爆 轰产物的状态究竟对应K、M、L三 点的哪一点呢?
1 e j e0 p j p0 v0 v j Qe 2
……(8)
这就是爆轰波的Hugoniot方程,也称放热的 Hugoniot方程。
18
3.1.1 爆轰波的基本关系式
如果已知爆轰产物的状态方程:
e e p, v
p p , s 从数学上来说,爆轰波应满足什么条件才能使爆
因此:
de p dv H
(3)
由热力学第一定律: Tds de pdv
对于等熵线, ds 0
de p dv s
(4)
因此,Rayleigh线、Hugoniot曲线和等熵线在 M点相切, 即 dp dp dp
8
3.1 爆轰波的CJ理论
CJ理论假设:流动是一维的,不考虑热传导、热 辐射及其粘滞摩擦等耗散效应;把爆轰波视为一 强间断面;爆轰波通过后化学反应瞬间完成并放 出化学反应热,反应产物处于热化学平衡及热力 学平衡状态;爆轰波阵面传播过程是定常的。
Chapman和Jouguet在以上假设基础上,提出并论
