新编物理基础学全册(王少杰版)课后习题答案及详解

合集下载

新编基础物理学上册1-2单元课后答案

新编物理基础学(上、下册)课后习题详细答案王少杰，顾牡主编第一章1-1.质点运动学方程为：cos()sin(),r a t i a t j btk ωω=++r r r r其中a ，b ，ω均为正常数，求质点速度和加速度与时间的关系式。

分析：由速度、加速度的定义，将运动方程()r t r对时间t 求一阶导数和二阶导数，可得到速度和加速度的表达式。

解：/sin()cos()==-++r r r r rv dr dt a t i a t j bk ωωωω2/cos()sin()a dv dt a t i t j ωωω⎡⎤==-+⎣⎦r r r r1-2. 一艘正在沿直线行驶的电艇，在发动机关闭后，其加速度方向与速度方向相反，大小与速度平方成正比，即2/d d v v K t -=，式中K 为常量．试证明电艇在关闭发动机后又行驶x 距离时的速度为 0Kx v v e -= 。

其中0v 是发动机关闭时的速度。

分析：要求()v v x =可通过积分变量替换dxdvvdt dv a ==，积分即可求得。

证：2d d d d d d d d v x vv t x x v t v K -==⋅= d Kdx v =-v⎰⎰-=x x K 0d d 10v v v v , Kx -=0ln v v0Kx v v e -=1-3．一质点在xOy 平面内运动，运动函数为22,48x t y t ==-。

（1）求质点的轨道方程并画出轨道曲线；（2）求t =1 s t =2 s 和时质点的位置、速度和加速度。

分析：将运动方程x 和y 的两个分量式消去参数t ，便可得到质点的轨道方程。

写出质点的运动学方程)(t r ρ表达式。

对运动学方程求一阶导、二阶导得()v t r 和()a t r ，把时间代入可得某时刻质点的位置、速度、加速度。

解：（1）由2,x t =得：,2x t =代入248y t =-可得：28y x =-，即轨道曲线。

新编基础物理学(王少杰、顾牡)版本)上册

1、质点作曲线运动[ D ]（3）v dtds =；（D ）只有（3）是对的。

2、质点沿半径为R [ B ](B) 0，t R π2 3、一运动质点在[ D ](D) 22)()(dt dy dt dx +4、一小球沿斜面[ B]（B ）t=2s ；5、一质点在平面（B ）变速直线运动；6.质量为m 的小球在向心力作用下j mv B 2)(-7.一质点作匀速率圆周运动(C)它的动量不断改变，对圆心的角动量不变；8、质点在外力作用下运动时（B ）外力的冲量为零，外力的功一定为零;9.选择正确答案(A)物体的动量不变，则动能也不变;10.人造卫星绕地球作圆运动(D)角动量守恒，动能不守恒;11.质点系内力可以改变 (C )系统的总动能;12.一力学系统由两个质点组成（C 动量守恒、但机械能和角动量守恒与否不能断定;13.对功的概念说法正确的是(C) 质点沿闭合路径运动，保守力对质点做的功等于零;14.用绳子系着一物体;（D ）重力、张力都没对物体做功;15.狭义相对论中的相对性原理;(C) (3)，(4);16.狭义相对论中的光速不变原理;(C) (3)，(4);17.边长为a 的正方形薄板静止于惯性系S ;(B)0.62a ;18.有一直尺固定在系中; 45)(等于C ;19.电场强度qF E =;（D ）任何电场。

; 20.下面列出的真空中静电场的场强公式[ D ] 半径为R ..r rR E 302εσ=; 21.一个带负电荷的质点22.如图所示，闭合面S 内有一点电荷q(B) S 面的电通量不变， P 点场强改变 23.若匀强电场的电场强度为E ；（B ）E a 221π;24.下列说法正确的是（C)通过闭合曲面S 的总电通量，仅仅由S 面内所包围的电荷提供；24.静电场的环路定理⎰=∙0l d E 说明静电场的性质是;（D ）静电场是保守场.25.下列叙述中正确的是(D) 场强方向总是从电势高处，指向电势低处。

新编物理学基础课后习题答案

i AB CD
0 I vl 1 1 ( ) 2 a vt a b vt
I
aA b D l
方向为顺时针方向。 (2) 选面积元dS = ldr a b 0 I 0 l I a b Φ a l dr ln 2 r 2 a
r v
B
C
dr
I aA b D l B C
v
解：(1) 任意时刻 t，AB、CD边到导线的距离分别为 a +v t 和 a +b + v t 0 I 0 I BAB BCD 2 (a vt ) 2 (a b vt )
AB l vBAB (A B)
CD l vBCD (D C)
0 0 0
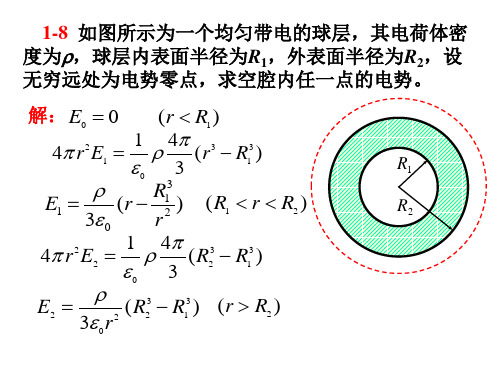
3-7 如图所示，长直导线AB中的电流 I沿导线向上，并以 dI/dt＝2A/s的变化率均匀增长。导线附近放一个与之共面的直角三角形线框，其一边与导线平行，位置及线框尺寸如图（设a =10cm, b=20cm, c = 5.0cm）所示。求此线框中产生的感应电动势的大小和方向。 A Y 0 I 解： dx 处的B 2 x I 0.15 0 I Φ s B dS 0.05 y dx b 2 x y 0.15 x y y 2(0.15 x ) O x dx X 0.1 0.2 a B c

k
R rk 2eR (2k 1) 2 rk2 1 12 1 k 50.5 50 (条) 4 R 2 0.5 10 400 2
2
4-15 波长范围在450~650nm之间的复色平行光垂直照射在每厘米有5000条刻线的光栅上，屏幕放在透镜的焦平面处，屏上第二级光谱各色光在屏上所占范围的宽度为35.1cm，求透镜的焦距f 。 1 cm 解： a b (a b)sin k 2 5000 21 2 450 0 sin 1 0.45 26.74 1 a b 2 103

新编基础物理学课后答案

习题一1-1.质点运动学方程为：cos()sin(),r a t i a t j btk ωω=++其中a ，b ，ω均为正常数，求质点速度和加速度与时间的关系式。

分析：由速度、加速度的定义，将运动方程()r t 对时间t 求一阶导数和二阶导数，可得到速度和加速度的表达式。

解：/sin()cos()==-++v dr dt a t i a t j bk ωωωω2/cos()sin()a dv dt a t i t j ωωω⎡⎤==-+⎣⎦1-2. 一艘正在沿直线行驶的电艇，在发动机关闭后，其加速度方向与速度方向相反，大小与速度平方成正比，即2/d d v v K t -=，式中K 为常量．试证明电艇在关闭发动机后又行驶x 距离时的速度为 0Kx v v e -= 。

其中0v 是发动机关闭时的速度。

分析：要求()v v x =可通过积分变量替换dxdvv dt dv a ==，积分即可求得。

证：2d d d d d d d d v x vv t x x v t v K -==⋅= d Kdx v =-v⎰⎰-=x x K 0d d 10v v v v , Kx -=0ln v v 0Kx v v e -=1-3．一质点在xOy 平面内运动，运动函数为22,48x t y t ==-。

（1）求质点的轨道方程并画出轨道曲线；（2）求t =1 s t =2 s 和时质点的位置、速度和加速度。

分析：将运动方程x 和y 的两个分量式消去参数t ，便可得到质点的轨道方程。

写出质点的运动学方程)(t r表达式。

对运动学方程求一阶导、二阶导得()v t 和()a t ，把时间代入可得某时刻质点的位置、速度、加速度。

解：（1）由2,x t =得：,2x t =代入248y t =-可得：28y x =-，即轨道曲线。

画图略（2）质点的位置可表示为：22(48)r ti t j =+- 由/v dr dt =则速度：28v i tj =+ 由/a dv dt =则加速度：8a j =则：当t=1s 时，有24,28,8r i j v i j a j =-=+=当t=2s 时，有48,216,8ri j v i j a j =+=+=1-4．一质点的运动学方程为22(1)x t y t ==-，，x 和y 均以m 为单位，t 以s 为单位。

新编基础物理学(王少杰、顾牡)版本)答案

1．已知质点的运动方程为; a = 4i j -+。

2．说明质点做何种运动时; 变速率曲线运动；变速率直线运动 3.一质点运动方程为26x t t =-; 8m;10m 4.飞轮作加速转动时； 26m s ; 24m s ;5.一个力F 作用在质量为kg 0.1的质点上;16N S ; 176J ;6.如图为一圆锥摆; 0 ;2m g πω ;2m gπω;7.一质量为m 的物体；0m v ；竖直向下； 8.一质量为m 小球；竖直向上；mgt;9.一颗子弹在枪筒里前进时; 0.003s; 0.6N*S; 2g ; 10.一质点在几个力同时作用下; 38J ; 11.一人把质量为10kg 的物体; 196 ; 216; 12.二质点的质量各为; 1211()G m m ab--;13.狭义相对论是建立在; 伽利略 ; 14.一光子以速度c 运动; c; 15.在测量物体长度中; 最长 ; 最短 ; 16.一观察者测量得沿尺长;32c ;17.静止时边长为a 的立方体;3221a u c -;18.一点电荷q 位于一立方体中心;6Oq ε; 0 ;24Oq ε;19.描述静电场性质的两个物理量是;E ;u ;F E q=;0u Pu E dl ==⎰;20.如图，真空中两个点电荷;O Q ε;0;201094QR πε;21.如图示，两个平行的无限大;2Oσε;32O σε;2Oσε; 方向向右; 方向向右; 方向向左;22.图中曲线表示一种球对称性静电场;均匀带电实心球; 23.真空中有一半径为R 的半圆细环;4O Q Rπε;4O qQ Rπε-;24.如图示，在带电量为q 的点电荷;11()4O abqq r r πε-;25.如图所示，负电荷Q 的电场中有b a ,两点;b; a ; 增加; 26.在点电荷q 的电场中;7210C --⨯;27一带电量为Q 的导体环;Q - ; Q ;28.一孤立金属球带电量Q +;径向方向向外;0;电荷均匀分布于金属球的外表面;29.在带电量为Q +的金属球外面;24Q rπ; Q ;204r Q rπεε;0rQεε;30.一平行板电容器，充电后与电源保持连接;r ε; 1; r ε; 31.半径为0.5cm 的无限长的直圆柱形导体上; 0 ;32.在安培环路定理;_环路所包围的所有稳恒电流的代数和；环路上的磁感应强度；环路内外全部电流所产生的磁场的叠加；33.在均匀磁场中放置两个面积相等；相等；34.一平面实验线圈的磁矩大小为；0.5T ；沿y 轴正向；35.如右图，无限长直导线中流有的电流分别为；不相等；0123()I I I μ--；01()I μ-；36.无限长直圆筒入在相对磁导率为；2Irπ；02r Irμμπ；37.三根无限长载流直导线；5I; 38.一自感线圈中;0.4H;39.产生动生电动势的非静电场力;洛伦兹 ; 涡旋电场;。

《新编基础物理学》第2章习题解答和分析2

《新编基础物理学》第2章习题解答和分析2-CAL-FENGHAI-(2020YEAR-YICAI)_JINGBIAN第2章质点动力学2-30 一物体在介质中按规律2x ct =作直线运动，c 为一常量。

设介质对物体的阻力正比于速度的平方。

试求物体由x 0=0运动到x =l 时，阻力所做的功。

（已知阻力系数为k ）分析本题是一个变力做功问题，按功的定义式d W F x =⋅⎰来求解。

解由运动学方程2x ct =，可得物体速度d 2d xct t==v 物体所受阻力大小为22244F k kc t kcx ===v阻力做的功为200d d 4d 2llW F x F x kcx x kcl =⋅=-=-=-⎰⎰⎰2-31．一辆卡车能沿着斜坡以115km h -⋅的速率向上行驶，斜坡与水平面夹角的正切tan 0.02α=，所受的阻力等于卡车重量的0.04，如果卡车以同样的功率匀速下坡，则卡车的速率是多少？分析：求出卡车沿斜坡方向受的牵引力，再求瞬时功率。

注意：牵引力和速度同方向。

解：如解图2-31所示，由于斜坡角度很小所以有sin 0.02tg αα≈=且阻力0.04f G =上坡时牵引力为sin 0.06F f G G α=+=下坡时牵引力为sin 0.02F f G G α'==－由于上坡和下坡时功率相同，故P F F ''==v v所以1145km h 12.5m s --'=⋅=⋅v2-32．某物块重量为P ，用一与墙垂直的压力N F 使其压紧在墙上，墙与物块间的滑动摩擦系数为μ，试计算物块沿题图2-32所示的不同路径：弦AB ，劣弧AB ，折线AOB 由A 移动到B 时，重力和摩擦力的功。

已知圆弧半径为r 。

解图2-31α分析：保守力做功与路径无关，非保守力做功与路径有关。

解：重力是保守力，而摩擦力是非保守力，其大小为f N μ=。

（1）物块沿弦AB 由A 移动到B 时，重力的功1G W mgh Pr ==摩擦力的功12f W f AB Nr μ=⋅=（2）物块沿圆弧AB 由A 移动到B 时，重力的功2G W mgh Pr ==摩擦力的功212f W f AB Nr πμ=⋅=2（3）物块沿折线AOB 由A 移动到B 时，重力的功3G W mgh Pr ==。

新编物理基础学下册(9-17章)课后习题(每题都有)详细答案

题9-2解图新编物理基础学下册（9-17章）课后习题（每题都有）详细答案之阿布丰王创作王少杰，顾牡主编第九章9-1 两个小球都带正电，总共带有电荷55.010C -⨯,如果当两小球相距时，任一球受另一球的斥力为1.0N.试求总电荷在两球上是如何分配的？分析：运用库仑定律求解。

解：如图所示，设两小球分别带电q 1，q 2则有q 1+q 2×10-5C ① 由题意，由库仑定律得：912122091014π4q q q q F r ε⨯⨯⨯===②由①②联立得：5152 1.210C3.810Cq q --⎧=⨯⎪⎨=⨯⎪⎩ 9-2 两根×10-2m 长的丝线由一点挂下，每根丝线的下端都系着一个质量为×10-3kg 的小球.当这两个小球都带有等量的正电荷时，每根丝线都平衡在与沿垂线成60°角的位置上。

求每一个小球的电量。

分析：对小球进行受力分析，运用库仑定律及小球平衡时所受力的相互关系求解。

解：设两小球带电q 1=q 2=q ，小球受力如图所示220cos304πq F T R ε==︒①sin30mg T =︒②联立①②得：2o 024tan30mg R qπε=③ 3sin 6062r l =︒=⨯⨯其中代入③式，即： q ×10-7CF E q =，9-3 电场中某一点的场强定义为若该点没有试验电荷，那么该点是否存在场强？为什么？答：若该点没有试验电荷，该点的场强不变.因为场强是描述电场性质的物理量，仅与场源电荷的分布及空间位置有关，与试验电荷无关，从库仑定律知道，试验电荷q 0所受力F与q 0成正比，故0F E q =是与q 0无关的。

9-4直角三角形ABC 如题图9-4所示，AB 为斜边，A 点上有一点荷91 1.810C q -=⨯，B 点上有一点电荷92 4.810C q -=-⨯，已知BC =0.04m ，AC ，求C 点电场强度E的大小和方向(cos37°≈0.8,sin37°≈0.6). 分析：运用点电荷场强公式及场强叠加原理求解。

《新编基础物理学》第二章习题解答和分析报告

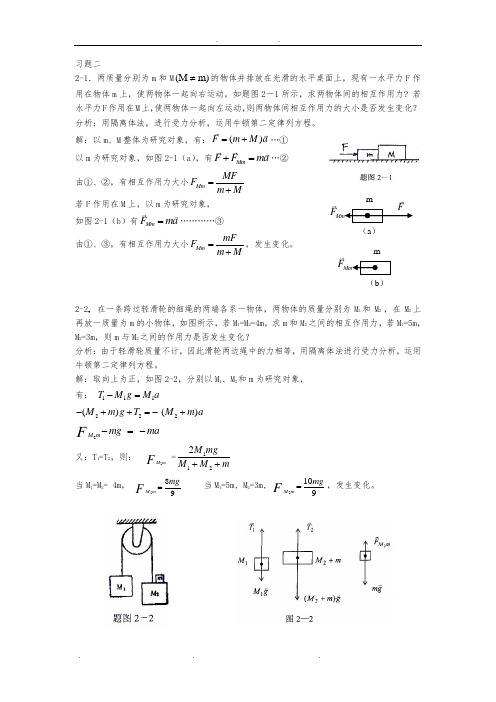
习题二2-1．两质量分别为m 和M (M m)≠的物体并排放在光滑的水平桌面上，现有一水平力F 作用在物体m 上，使两物体一起向右运动，如题图2－1所示，求两物体间的相互作用力? 若水平力F 作用在M 上，使两物体一起向左运动，则两物体间相互作用力的大小是否发生变化？分析：用隔离体法，进行受力分析，运用牛顿第二定律列方程。

解：以m 、M 整体为研究对象，有：()F m M a =+…① 以m 为研究对象，如图2-1（a ），有Mm F F ma +=…② 由①、②，有相互作用力大小Mm MFF m M=+若F 作用在M 上，以m 为研究对象，如图2-1（b ）有Mm F ma =…………③ 由①、③，有相互作用力大小Mm mFF m M=+，发生变化。

2-2. 在一条跨过轻滑轮的细绳的两端各系一物体，两物体的质量分别为M 1和M 2 ，在M 2上再放一质量为m 的小物体，如图所示，若M 1=M 2=4m ，求m 和M 2之间的相互作用力，若M 1=5m ，M 2=3m ，则m 与M 2之间的作用力是否发生变化？分析：由于轻滑轮质量不计，因此滑轮两边绳中的力相等，用隔离体法进行受力分析，运用牛顿第二定律列方程。

解：取向上为正，如图2-2，分别以M 1、M 2和m 为研究对象，有： 111T M g M a -=222() ()M m g T M m a -++=-+2 M mmg ma F-=-又：T 1=T 2，则： 2M mF =1122M mgM M m++当M 1=M 2= 4m ， 289M mmg F = 当M 1=5m, M 2=3m, 2109M mmg F =，发生变化。

m（a ）MmF Fm（b ）MmF2-3.质量为M 的气球以加速度a 匀加速上升，突然一只质量为m 的小鸟飞到气球上，并停留在气球上。

若气球仍能匀加速向上，求气球的加速度减少了多少？分析：用隔离体法受力分析，运用牛顿第二定律列方程。

新编基础物理学王少杰第二版习题解答

新编基础物理学王少杰第二版习题解答习题八8-1 位于委内瑞拉的安赫尔瀑布是世界上落差最大的瀑布，它高979m.如果在水下落的过程中，重力对它所做的功中有50％转换为热量使水温升高，求水由瀑布顶部落到底部而产生的温差.( 水的比热容c 为3114.1810J kg K --)解由上述分析得水下落后升高的温度8-2 在等压过程中，0.28kg 氮气从温度为293K 膨胀到373K ，问对外做功和吸热多少?内能改变多少?解：等压过程气体对外做功为气体吸收的热量内能的增量为8-3 一摩尔的单原子理想气体，温度从300K 加热到350K 。

其过程分别为体积保持不变和压强保持不变。

在这两种过程中：(1) 气体各吸取了多少热量？(2) 气体内能增加了多少？(3) 气体对外界做了多少功？解：已知气体为1 摩尔单原子理想气体(1) 体积不变时，气体吸收的热量压强保持不变时，气体吸收的热量(2) 由于温度的改变量一样，气体内能增量是相同的(3) 体积不变时，气体对外界做功压强保持不变时，根据热力学第一定律，气体对外界做功为8-4 一气体系统如题图8-4所示,由状态A 沿ACB 过程到达B 状态,有336J 热量传入系统,而系统做功126J,试问:(1) 若系统经由ADB 过程到B 做功42J,则有多少热量传入系统?(2) 若已知168J D A E E -=,则过程AD 及DB 中,系统各吸收多少热量?(3)若系统由B 状态经曲线BEA 过程返回状态A ,外界对系统做功84J,则系统与外界交换多少热量?是吸热还是放热?解：已知ACB 过程中系统吸热336J Q =,系统对外做功126J W =,根据热力学第一定律求出B 态和A 态的内能增量(1) ADB 过程，42J W =, 故(2) 经AD 过程,系统做功与ADB 过程做功相同,即42J W =，故经DB 过程,系统不做功,吸收的热量即内能的增量所以，吸收的热量为(3)因为是外界对系统做功，所以BEA 过程210J BEA E E ?=-?=-,故系统放热.8-5 如题图8-5所示，压强随体积按线性变化，若已知某种单原子理想气体在A,B 两状态的压强和体积,题图8-4题图8-5问:(1)从状态A 到状态B 的过程中,气体做功多少?(2)内能增加多少?(3)传递的热量是多少?解：(1) 气体做功的大小为斜线AB 下的面积(2) 对于单原子理想气体气体内能的增量为由状态方程 m pV RT M=代入得 (3)气体传递的热量为8-6一气缸内储有10mol 的单原子理想气体,在压缩过程中,外力做功200J,气体温度升高o 1C ,试计算:(1) 气体内能的增量;(2) 气体所吸收的热量;(3) 气体在此过程中的摩尔热容量是多少?解：(1) 气体内能的增量(2) 气体吸收的热量(3) 1mol 物质温度升高(或降低) o 1C 所吸收的热量叫摩尔热容量,所以 8-7一定量的理想气体，从A 态出发，经题图8-7所示的过程经C 再经D 到达B 态，试求在该过程中，气体吸收的热量．解：由题图8-7可得A 状态： 5810A A p V =?B 状态： 5810B B p V =? 题图8-7因为A AB B p V p V =，根据理想气体状态方程可知所以气体内能的增量根据热力学第一定律得8-8 一定量的理想气体，由状态A 经B 到达C ．如题图8-8所示，ABC 为一直线。

新编基础物理学(王少杰版)章末测验及答案汇总.

专业班级学号姓名机械振动本章知识点：简谐振动的特征及其运动方程，简谐振动的旋转矢量表示法，振动的能量，简谐运动的合成，阻尼振动，受迫振动，共振本章重点：简谐振动的特征及其运动方程，简谐振动的旋转矢量表示法，振动的能量，同方向同频率简谐运动的合成一、填空题1．一个给定系统做简谐振动时，其振幅和初相位决定于、和；弹簧振子做简谐振动时，其频率决定于和．2．一弹簧振子，弹簧的劲度系数为0.32 N/m ，重物的质量为0.02 kg ，则这个系统的固有角频率为 rad/s ，相应的振动周期为 s ．3．在两个相同的弹簧下各悬挂一物体，两物体的质量比为4：1，则两者做简谐运动的周期之比为． 4．质点做简谐运动的位移和时间关系如图1所示，则其运动方程为． 5．两个同频率的简谐运动曲线如图2所示，则2x 的相位比1x 的相位落后．6．两个简谐振动曲线如图3所示，两个简谐振动的频率之比12:νν= ，加速度最大值之比a 1m ：a 2m = ，初始速率之比1020:=v v ．7．简谐振动的方程为)cos(ϕω+=t A x ，势能最大时位移x= ，此时动能E k = ．8．已知一质点做简谐运动曲线如图4所示，由图可确定振子在t= s 时速度为零；在t= s 时弹性势能最小；在(__________)s 时加速度取正的最大值．9．两个同方向同频率的简谐振动，其合振动的振幅为0.20m ，合振动与第一分振动的相位差为60度，已知第一分振动的振幅为0.10m ，则第二分振动的振幅为 m ，第二分振动与第一分振动的相位差为．10．某谐振子同时参与两个同方向的简谐运动，其运动方程分别为))(3/4cos(10321m t x ππ+⨯=-；))(4cos(10422m t x ϕπ+⨯=-当ϕ= 时合振动的振幅最大，其值max A = ；当ϕ= 时合振动的振幅最小，其值min A = ．11．图5中所示为两个简谐振动的振动曲线，若以余弦函数表示这两个振动的合成结果，则合振动的方程为=+=11x x xt/s7x/m0.050.10 图1x 1xx 2to图32 1xt/s图4图5x 2x 1 xt图2(____________________)。

《新编基础物理学》第1章习题解答和分析

第1章质点运动学1-1. 一质点沿x 轴运动，坐标与时间的变化关系为x ＝8t 3－6t （m ），试计算质点 (1) 在最初2s 内的平均速度，2s 末的瞬时速度；(2) 在1s 末到3s 末的平均加速度，3s 末的瞬时加速度. 分析：平均速度和瞬时速度的物理含义不同，分别用x t ∆=∆v 和d d xt=v 求得；平均加速度和瞬时加速度的物理含义也不同，分别用a t∆=∆v和d d a t =v 求得.解：(1) 在最初2s 内的平均速度为31(2)(0)(8262)026(m s )2x x x t t -∆-⨯-⨯-====⋅∆∆v2s 末质点的瞬时速度为212d 24690(m s )d xt t-==-=⋅v (2) 1s 末到3s 末的平均加速度为22(3)(1)(2436)(246)96(m s )2a t t -∆-⨯---====⋅∆∆v v v3s 末的瞬时加速度23d 48144(m s )d a t t-===⋅v1-2．一质点在xOy 平面内运动，运动方程为22(m),48(m)x t y t ==-. （1）求质点的轨道方程并画出轨道曲线；（2）求=1 s =2 s t t 和时质点的位置、速度和加速度.分析：将运动方程x 和y 的两个分量式消去参数t ，便可得到质点的轨道方程.写出质点的运动学方程)(t r表达式.对运动学方程求一阶导、二阶导得()t v 和()a t ，把时间代入可得某时刻质点的位置、速度、加速度.解：（1）由2,x t = 得：,2xt =代入248y t =- 可得：28y x =-，即轨道方程. 画图略（2）质点的位置矢量可表示为22(48)r ti t j =+-则速度d 28d ri t j t==+v 加速度d 8d a j t==v当t =1s 时，有1224(m),28(m s ),8m s r i j i j a j --=-=+⋅=⋅v当t =2s 时，有1248(m),216(m s ),8m s r i j i j a j --=+=+⋅=⋅v1-3．一质点的运动学方程为22(1)x t y t ==-，，x 和y 均以m 为单位，t 以s 为单位. 求：（1）质点的轨迹方程；（2）在2s t =时质点的速度和加速度. 分析：同1-2.解：（1）由题意可知：x ≥ 0，y ≥ 0，由2x t =，可得t =,代入2(1)y t =- 整理得：1=即轨迹方程（2）质点的运动方程可表示为22(1)r t i t j =+-则d 22(1)d rti t j t ==+-v d 22d a i j t==+v因此, 当2s t =时，有1242(m s ),22(m s )i j a i j --=+⋅=+⋅v1-4．一枚从地面发射的火箭以220m s -⋅的加速度竖直上升后，燃料用完，于是像一个自由质点一样运动. 略去空气阻力并设g 为常量，试求：（1）火箭达到的最大高度；（2）它从离开地面到再回到地面所经过的总时间.分析：分段求解：030s t ≤≤时，220m s a -=⋅，可求出11,x v ；t ＞30s 时，g a -=.可求出2()t v ，2()x t .当20=v 时，火箭达到的最大高度, 求出t 、x . 再根据0x =，求出总时间.解：（1）以地面为坐标原点，竖直向上为x 轴正方向建立一维坐标系，设火箭在坐标原点时，t =0s ，且=30s.则当0≤ t ≤30s，由d d xx a t=v ,得 3020d d xx t =⎰⎰v v ，解得 20x t =v当130s =v 时11600m s -=⋅v由d d x xt=v ，得 13020d d x t t x =⎰⎰，则19000m x =当火箭未落地, 且t ＞30s, 又有221309.8d d x tx t -=⎰⎰v v v解得28949.8x t =-v同理由d d x x t=v 得 130(8949.8)d d txx t t x -=⎰⎰解得24.989413410x t t =-+- … ①由20x =v ，得91.2s t =，代入①得max 27.4km x ≈（2）由①式可知，当0x =时，解得1166s t ≈216s<30s t ≈（舍去）1-5．质点沿直线运动，加速度24a t =-，式中a 的单位为2m s -⋅，t 的单位为s ，如果当t =3s时，x =9m ，12m s -=⋅v ，求质点的运动方程.分析本题属于第二类运动学问题，可通过积分方法求解. 解由分析可知0200d d (4)d tta t t t ==-⎰⎰⎰vv v 积分得30143t t =+-v v 由030001d d (4)d 3xt tx x t t t t ==+-⎰⎰⎰v v 得24001212x x t t t =+-+v 将t =3s 时，x =9m ，12m s -=⋅v 代入上两式中得101m s -=-⋅v ，x 0=0.75m所以质点的运动方程为2410.752(m)12x t t t =-+-1-6. 一艘正在沿直线行驶的电艇，在发动机关闭后，其加速度方向与速度方向相反，大小与速度大小平方成正比，即2d /d t k =-v v ，式中k 为常量．试证明电艇在关闭发动机后又行驶x 距离时的速度大小为 0kxe-=v v . 其中0v 是发动机关闭时的速度大小.分析：要证明~x v 关系，可通过积分变量替换将时间变量替换掉，即d d d d a t x==v vv ，积分即可证明. 证： 2d d d d d d d d k =⋅==-v v vv v x t x t x分离变量得d d k x =-vv两边积分001d d x k x =-⎰⎰vv v v , 0lnkx =-v v 证得0kxe -=v v1-7．一质点沿半径为R 做圆周运动，运动学方程为2012s t bt =+v ，其中v 0，b 都是大于零的常量.求：（1）t 时刻质点的加速度大小及方向；（2）在何时加速度大小等于；分析：由质点在自然坐标系下的运动学方程()t s s =，求导可求出质点的运动速率d d st=v ，而切向加速度d d t a t=v ，法向加速度2n a ρ=v ，总加速度22n a a a +=τ，当a =时，即可求出t .解：（1）质点的运动速率0d d sbt t==+v v 切向加速度d d t a b t ==v 法向加速度220()n bt a Rρ+==v v 加速度大小a ==方向()211tantan ntbt a a bRθ--+==v（2）当a =时，可得22220()2bt b b R ⎡⎤++=⎢⎥⎣⎦v解出t b=v 1-8. 物体以初速度120m s -⋅被抛出，抛射仰角60°，略去空气阻力，问：（1）物体开始运动后的末，运动方向与水平方向的夹角是多少末的夹角又是多少（2）物体抛出后经过多少时间，运动方向才与水平成45°角这时物体的高度是多少（3）在物体轨迹最高点处的曲率半径有多大（4）在物体落地点处，轨迹的曲率半径有多大分析：（1）建立坐标系，写出初速度0v ，求出()t v 、θtan ，代入t 求解.（2）由（1）中的θtan 关系，求出时间t ；再根据y 方向的运动特征写出()t y ，代入t 求y . （3）根据物体在轨迹最高点处，0y =v ，且加速度2n a a g ρ===v ，可求出ρ.（4）由对称性，落地点与抛射点的曲率相同 2cos n a g θρ==v ，求出ρ.解：以水平向右为x 轴正向，竖直向上为y 轴正向建立二维坐标系（1）初速度001020cos6020sin6010103(m s )i j i j -=+=+⋅v ，加速度29.8(m s ),a j -=-⋅则任一时刻10(1039.8)at i t j =+=+-v v ………………①与水平方向夹角有1039.8tan 10tθ-=……………………………②当t =时tan 0.262,1441'θθ==︒当t =时tan 0.718,3541'θθ=-=-︒（2）此时tan 1θ=, 由②得t =物体的高度22111030.759.80.7510.23(m)22yo y t gt =-=⨯-⨯⨯=v （3）在最高处2110m s ,n a g ρ-=⋅==v v得210.2m gρ==v （4）由对称性可知，落地点的曲率与抛射点的曲率相同. 由解图1-8得210cos cos 4.9(m s )20x n a a g gg θθ-=====⋅v v240082(m)4.9n a ρ===v1-9．汽车在半径为400m 的圆弧弯道上减速行驶，设在某一时刻，汽车的速率为110m s -⋅，切向加速度的大小为20.2m s -⋅.求汽车的法向加速度和总加速度的大小和方向. 分析：由某一位置的ρ、v 求出法向加速度n a ，再根据已知切向加速度τa 求出总加速度a 的大小和方向.解：法向加速度的大小222100.25(m s ),400n a ρ-===⋅v 方向指向圆心总加速度的大小222220.20.250.32(m s )n a a a τ-=+=+=⋅由解图1-9得tan 0.8,3840'na a ταα===︒ 则总加速度与速度夹角9012840'θα=︒+=︒1-10. 质点在重力场中作斜上抛运动，初速度的大小为0v ，与水平方向成α角．求质点到达抛出点的同一高度时的切向加速度、法向加速度以及该时刻质点所在处轨迹的曲率半径（忽略空解图1-8解图1-9气阻力）．已知法向加速度与轨迹曲率半径之间的关系为2n a ρ=v .分析：在运动过程中，质点的总加速度 a g =.由于无阻力作用，所以回落到抛出点高度时，质点的速度大小0=v v ，其方向与水平线夹角也是α.可求出n a ，如解图1-10所示.再根据法向加速度与轨迹曲率半径之间的关系2n a ρ=v ，解出曲率半径.解：切向加速度t sin a g a =法向加速度a g a n cos =因为2n a ρ=v ，所以220cos n a g ρα==v v1-11．在生物物理实验中用来分离不同种类的分子的超级离心机的转速为313.1410rad s -⨯⋅.在这种离心机的转子内，离轴10cm 远的一个大分子的向心加速度是重力加速度的几倍分析根据定义可得向心加速度的大小2n a r ω=.解所求倍数2222425244(610)0.1=410609.8rn r g g ωππ⨯⨯==⨯⨯1-12. 一质点在半径为0.10m 的圆周上运动，其角位置变化关系为324(rad)t θ=+.试求：(1) 在t =2s 时，质点的法向加速度和切向加速度大小各为多少； (2) 当切向加速度大小恰等于总加速度大小的一半时，θ值为多少 (3) 在什么时刻，切向加速度和法向加速度恰好大小相等分析本题为物体作圆周运动的角坐标表示下的第一类运动学问题，求导可得到角速度和角加速度，再由角量与线量的关系求得切向加速度t a 和法向加速度n a .解图1-10解 (1) 角速度和角加速度分别为2d 12d t t θω== d 24d t tωβ==法向加速度22222n 0.1(12) 2.3010(m s )a r t ω-==⨯=⨯⋅切向加速度2t d 2.4 4.8(m s )d a r t tβ-====⋅v (2) 由 t /2a a =，2222t n t 4a a a a =+= 得22t n3a a = 22243(24)(12)r t r t =33t = 332424 3.15(rad)t θ=+=+⨯= (3) 由 n t a a =，即22(12)24r t rt =，解得 0.55s t =1-13．离水面高度为h 的岸上有人用绳索拉船靠岸，人以恒定速率0v 拉绳子，求当船离岸的距离为s 时，船的速度和加速度的大小.分析：收绳子速度和船速是两个不同的概念.小船速度的方向为水平方向，由沿绳的分量与垂直绳的分量合成，沿绳方向的收绳的速率恒为0v .可以由0v 求出船速v 和垂直绳的分量1v .再根据21n a ρ=v 关系，以及n a 与a关系来求解a .解：如解图1-13，小船速度沿绳的分量20=v v ，船速2sec θ=v v当船离岸的距离为s 时，船速22s h s+=v v 解图1-13船速垂直绳的分量012tan hsθ==v v v 则船的法向加速度2211n 2222cos a a as hs hθρ====++v解得2203h a s =v1-14. A 船以130km h -⋅的速度向东航行，B 船以145km h -⋅的速度向正北航行，求A 船上的人观察到的B 船的速度和航向.分析：关于相对运动，必须明确研究对象和参考系.同时要明确速度是相对哪个参照系而言.画出速度矢量关系图求解. 解：如解图1-14所示11A B 30km h ,45km h i j --=⋅=⋅v vB 船相对于A 船的速度1BA B A 4530(km h )j i -=-=-⋅v v v则速度大小221BA B A 54.1(km h )-=+=⋅v v v方向BAarctan56.3θ==︒v v ，既西偏北56.3︒1-15. 一个人骑车以118km h -⋅的速率自东向西行进时，看见雨滴垂直落下，当他的速率增加至136km h -⋅时，看见雨滴与他前进的方向成120°角下落，求雨滴对地的速度.解图1-14分析：这是一个相对运动的问题，雨对地的速度不变，画出速度矢量图，就可根据几何关系求解.解：如解图1-15所示，r v 为雨对地的速度， 12,p p v v 分别为第一次，第二次人对地的速度，12,rp rp v v 分别为第一次，第二次雨对人的速度，120θ=︒由三角形全等的知识，可知18012060αβ==︒-︒=︒三角形ABC 为正三角形，则2136km h r p -==⋅v v ，方向竖直向下偏西30︒.1-16如题图1-16所示，一汽车在雨中以速率1v 沿直线行驶，下落雨滴的速度方向偏于竖直方向向车后方θ角，速率为2v ，若车后有一长方形物体，问车速为多大时，此物体刚好不会被雨水淋湿分析：相对运动问题，画矢量关系图，由几何关系求解.解：如解图1-16（a ），车中物体与车蓬之间的夹角 arctan l h α=若θ＞α，无论车速多大，物体均不会被雨水淋湿若θ＜α，如解图1-16（b ）则有||||||BC AC AB ==-v 车=sin sin cos tan sin αθθαθ-=-v v v v 雨雨雨雨对车又2=v v 雨则2cos (sin )l h θθ=-v v 车题图1-16 解图1-16 解图1-151-17 人能在静水中以11.10m s -⋅的速度划船前进.今欲横渡一宽为m 10.0013⨯、水流速度10.55m s -⋅的大河.他若要从出发点横渡该河而到达正对岸的一点，那么应如何确定划行方向到达正对岸需多少时间分析船到达对岸所需时间由船相对于岸的速度v 决定，而v 由水流速度u 和船在静水中划行速度'v 确定.画出矢量图由几何关系求解.解根据解图1-17，有'v =u+v ，解得 0.551sin 1.102u α==='v 030α= 即应沿与正对岸方向向上游偏300方向划行.船到达正对岸所需时间为 31.0510s cos d d t α===⨯'v v 1-18．一升降机以2g 的加速度从静止开始上升，在末时有一小钉从顶板下落，若升降机顶板到底板的距离h=2.0m ，求钉子从顶板落到底板的时间t , 它与参考系的选取有关吗分析：选地面为参考系，分别列出螺钉与底板的运动方程，当螺丝落到地板上时，两物件的位置坐标相同，由此可求解.解：如解图1-18建立坐标系，y 轴的原点取在钉子开始脱落时升降机的底板处，此时，升降机、钉子速度为0v ,钉子脱落后对地的运动方程为21012y h t gt =+-v 升降机底板对地的运动方程为220122y t gt =+⨯v 且钉子落到底板时，有12=y y ，即2012h t gt +-=v 20t gt +v αuv 'v 解图1-17解图1-18解出t0.37s t与参考系的选取无关.。

新编基础物理学第1章习题解答和分析

第1章质点运动学1-1. 一质点沿x 轴运动，坐标与时间的变化关系为 x = 8t 3— 6t ( m ),试计算质点(1)在最初2s 内的平均速度，2s 末的瞬时速度；⑵ 在1s 末到3s 末的平均加速度，3s 末的瞬时加速度分析：平均速度和瞬时速度的物理含义不同，分别用V ―和v dx 求得；平均加速度和瞬时 tdt加速度的物理含义也不同，分别用 a v 和ta 史求得. dt 解：(1)在最初2s 内的平均速度为2s 末质点的瞬时速度为21-2.一质点在xOy 平面内运动，运动方程为x 2t(m), y 4t 8(m).(1 )求质点的轨道方程并画出轨道曲线； (2 )求t = 1 s 禾口 t= 2 s 时质点的位置、速度和加速度• 分析：将运动方程 x 和y 的两个分量式消去参数 t ，便可得到质点的轨道方程•写出质点的运动学方程r(t)表达式•对运动学方程求一阶导、二阶导得v(t)和a(t),把时间代入可得某时刻质点的位置、速度、加速度.解：(1) 由 x 2t,得：t —, 代入 y 4t 282 2 可得：y x 8，即轨道方程.画图略 (2)质点的位置矢量可表示为v 2 v (4t 8)jv2ti 则速度\/v dr v v v 2i 8t j 加速度dt \/v dv v 8ja 当t=1s 时，有dt r r r r r r 1 r r 4 j (m), v 2i 8j (m s ), a 8j m s r 2ix x(2) x(0) t t (8 23 6 2) 0 2 26(m s 1)V 2等 24t 2 6 190(m s ) (2) 1s 末到3s 末的平均加速度为v(3) v(1) (24 32 6) (24 6) 96(m s 2)3s 末的瞬时加速度a 3dv dt48t 2 144 (m s )r r r r r r 1 r r 2 r 4i 8j(m), v 2i 16j(m s 1), a 8j m s 21-3.一质点的运动学方程为x t 2, y (t 1)2 , x 和y 均以m 为单位，t 以s 为单位.求: (1) 质点的轨迹方程；(2) 在t 2s 时质点的速度和加速度•分析：同1-2.解：(1)由题意可知：x X), y 由x t 2,可得t , x ,代入y (t 1)2 整理得：一 y x 1即轨迹方程(2)质点的运动方程可表小为 1)2[ r r t 2i r i (t 则v d v r rv 2ti 2(t 1)jdtv dv r ra 2i 2jdt 因此 ,当t 2s 时，有r r r 1 r r r 2v 4i 2j(m s ), a 2i 2j(m s ) 1-4. 一枚从地面发射的火箭以 20m s 2的加速度竖直上升后，燃料用完，于是像一个自由质点一样运动•略去空气阻力并设 g 为常量，试求：(1 )火箭达到的最大高度；(2 )它从离开地面到再回到地面所经过的总时间分析：分段求解：0 t 30s 时，a 20m s 2，可求出v 1,x 1 ；t > 30s 时，a g .可求出v 2(t),v x 2894 9.8t 当t =2s 时，有 X 2(t) •当V 2 0时，火箭达到的最大高度解：(1)以地面为坐标原点，竖直向上为求出t 、x .再根据x 0，求出总时间 x 轴正方向建立一维坐标系，设火箭在坐标原点时,t=0s ，且=30s.则当 0wt < 30,由 a xdv x dt ，得 300 20dt V x0 dv x , 解得v x 20t当W 由V x 则当火箭未落地解得30s 时v 1 600m sdxdt ，得3020tdt 0 为 9000m且t > 30s,又有t30 9.8dtx 1 dx ,同理由v x dt 得t30(894 9.8t)dtxdxx1解得x 4.9t2 894t13410…①由v x20，得t91.2s, 代入①得x max27.4km(2)由①式可知, 当x0时，解得t1166st216s<30s (舍去)2 21-5•质点沿直线运动，加速度a 4 t ,式中a的单位为m s , t的单位为s,如果当t=3s 时，x=9m，v 2m s 1，求质点的运动方程.分析本题属于第二类运动学问题，可通过积分方法求解解由分析可知v dv v0t0atdt 0(4t2)dt积分得v v°4t It33由x t t 1 3x dx x0°vdt0(v°4t t )dt3得2 1 4x X o + V o t 2t t12将t=3s时，x=9m，v 2m s1代入上两式中得v01m s 1，x o=O.75m所以质点的运动方程为2 1 4x 0.75 t 2t2t4(m) 121-6. 一艘正在沿直线行驶的电艇，在发动机关闭后，其加速度方向与速度方向相反，大小与速度大小平方成正比，即dv/dt kv2，式中k为常量•试证明电艇在关闭发动机后又行驶xkx距离时的速度大小为v v°e .其中v o是发动机关闭时的速度大小.分析：要证明v〜x关系，可通过积分变量替换将时间变量替换掉，即 a 史v包，积分即dt dx '常量•求：（1） t 时刻质点的加速度大小及方向；（2）在何时加速度大小等于、、2b ；可证明•证：分离变量得两边积分证得dv dv dx dv — --- ----- v - dt dx dt dxdv kdxvv 1 xdv kdx V o v 0 v v 0e kxln — v o 1-7.—质点沿半径为 R 做圆周运动，运动学方程为kxs v o t -bt 2，其中v o ，b 都是大于零的 2 分析：由质点在自然坐标系下的运动学方程s s t ，求导可求出质点的运动速率v 兰，而 dt切向加速度a t 牛，法向加速度a n 2 __________________________________ —，总加速度a .. a 2 a 2，当a 2b 时，即可求解：（1 ）质点的运动速率五 v 0 bta t法向加速度 a n加速度大小a方向业b dtvt (v 。

新编物理学基础课后习题答案

02
简答题：简述热力学第一定律和第二定律的内容，并指出它们在物理学中的意义。
热力学基础习题答案
简答题
简述分子动理论的基本内容，并说明气体分子平均自由程与哪些因素有关。
答案
分子动理论的基本内容包括分子在永不停息地做无规则运动，分子之间存在着引力和斥力，分子之间存在着空隙。气体分子平均自由程与气体压强、温度和分子的平均碰撞频率有关。
总结词
能够运用动量和角动量的知识解决实际问题。
总结词
理解动量守恒和角动量守恒的条件和意义。
动量与角动量习题答案
动量与角动量习题答案
01
02
03
详细描述
动量是描述物体运动状态的物理量，计算公式为 $p = mv$，其中 $m$ 是物体的质量，$v$ 是物体的速度。
角动量是描述物体旋转运动的物理量，计算公式为 $L = mr^2omega$，其中 $m$ 是物体的质量，$r$ 是物体到旋转轴的距离，$omega$ 是物体的角速度。
法拉第电磁感应定律描述了当磁场发生变化时会在导体中产生感应电动势的现象。楞次定律指出感应电流的方向总是阻碍引起感应电流的磁通量的变化。
磁场
安培环路定律
法拉第电磁感应定律
磁场与电磁感应习题答案
光学部分习题答案
04
在此添加您的文本17字
在此添加您的文本16字
在此添加您的文本16字
在此添加您的文本16字
康普顿散射证明了光的粒子性，并为量子力学的发展奠定了基础。
光的量子性习题答案
量子力学部分习题答案
05
不确定性原理
由海森堡提出，指在量子力学中无法同时精确测量某些物理量，如位置和动量。
测量
在量子力学中，测量是一个重要的概念，它会影响到量子态的塌缩和结果的不确定性。

新编基础物理学上册7-8单元课后答案

第七章7-1 氧气瓶的容积为瓶内充满氧气时的压强为130atm 。

若每小时用的氧气在1atm 下体积为400L 。

设使用过程温度保持不变，当瓶内压强降到10atm 时，使用了几个小时?分析氧气的使用过程中，氧气瓶的容积不变，压强减小。

因此可由气体状态方程得到使用前后的氧气质量。

进而将总的消耗量和每小时的消耗量比较求解。

解已知。

质量分别为，，,由题意可得: 11m PV RT M= ○1 22m PV RT M= ○2 233m PV RT M = ○3 所以一瓶氧气能用小时数为: ()121233313010329.61.0400m m PV PV n m PV -⨯--====⨯小时 7-2 一氦氖气体激光管，工作时管内温度为 27。

压强为2.4mmHg ，氦气与氖气得压强比是7:1.求管内氦气和氖气的分数密度.分析先求得氦气和氖气各自得压强，再根据公式求解氦气和氖气的分数密度。

所以 ,根据所以 2139.6610P n m kT -=⨯氖氖7-3 氢分子的质量为克。

如果每秒有个氢分子沿着与墙面的法线成角的方向以厘米/秒的速率撞击在面积为的墙面上,如果撞击是完全弹性的,求这些氢分子作用在墙面上的压强.分析压强即作用在单位面积上的平均作用力，而平均作用力由动量定理求得。

解:单位时间内作用在墙面上的平均作用力为:27522342 3.3101010102cos 4522330210F mv N p Pa S S---⨯⨯⨯⨯︒====⨯ 7-4 一个能量为的宇宙射线粒子,射入一氖气管中,氖管中含有氦气0.10mol,如果宇宙射线粒子的能量全部被氖气分子所吸收而变为热运动能量,问氖气的温度升高了多少?分析对确定的理想气体，其分子能量是温度的单值函数，因此能量的变化对应着温度的变化。

由能量守恒求解氖气的温度变化。

2312193 0.1 6.0210 k T 10 1.6102-⨯⨯⨯∆=⨯⨯ 771.610 1.28100.1 6.02 1.5 1.38T K -=⨯∆==⨯⨯⨯⨯ 7-5 容器内贮有1摩尔某种气体。