ABAQUS简支梁分析报告(梁单元和实体单元)
ABAQUS简支梁分析报告(梁单元和实体单元)

基于ABAQUS简支梁受力和弯矩的相关分析(梁单元和实体单元)对于简支梁,基于 ABAQUS2016,首先用梁单元分析了梁受力作用下的应力,变形,剪力和力矩;对同一模型,并用实体单元进行了相应的分析。
另外,还分析了梁结构受力和弯矩作用下的剪力及力矩分析。
对于CAE仿真分析具体细节操作并没有给出详细的操作,不过在后面上传了对应的cae,odb,inp文件。
不过要注意的是本文采用的是ABAQUS2016进行计算,低版本可能打不开,可以自己提交inp文件自己计算即可。
可以到小木虫搜索:“基于ABAQUS简支梁受力和弯矩的相关分析”进行相应文件下载。
对于一简支梁,其结构简图如下所示,梁的一段受固支,一段受简支,在梁的两端受集中载荷,梁的大直径D=180mm,小直径d=150mm,a=200mm,b=300mm,l=1600mm,F=300000N。
现通过梁单元和实体单元分析简支梁的受力情况,变形情况,以及分析其剪力和弯矩等。
材料采用45#钢,弹性模量E=2.1e6MPa,泊松比v=0.28。
图1 简支梁结构简图1.梁单元分析ABAQUS2016中对应的文件为beam-shaft.cae ,beam-shaft.odb,beam-shaft.inp。
在建立梁part的时候,采用三维线性实体,按照图1所示尺寸建立,然后在台阶及支撑梁处进行分割,结果如图2所示。
图2 建立part并分割接下来为梁结构分配材料,创建材料,定义弹性模量和泊松比,创建梁截面形状,如图3,非别定义两个圆,圆的直接分别为180和150mm。
然后创建两个截面,截面选择梁截面,再选择图2中的所有梁,定义梁的方向矢量为(0,0,-1)(点击图3中的n2,n1,t那个图标即可创建梁的方向矢量),最后把创建好的梁赋给梁结构。
图3 创建梁截面形状接下来装配实体,再创建分析步,在创建分析步的时候,点击主菜单栏的Output,编辑Edit Field Output Request,在SF前面打钩,这样就可以在结果后处理中输出截面剪力和力矩,如图4所示。
(完整版)Abaqus分析实例(梁单元计算简支梁的挠度)精讲

Abaqus分析实例(梁单元计算简支梁的挠度)精讲对于梁的分析可以使用梁单元、壳单元或是固体单元。
Abaqus的梁单元需要设定线的方向,用选中所需要的线后,输入该线梁截面的主轴1方向单位矢量(x,y,z),截面的主轴方向在截面Profile设定中有规定。
注意:因为ABAQUS软件没有UNDO功能,在建模过程中,应不时地将本题的CAE模型(阶段结果)保存,以免丢失已完成的工作。
简支梁,三点弯曲,工字钢构件,结构钢材质,E=210GPa,μ=0.28,ρ=7850kg/m3(在不计重力的静力学分析中可以不要)。
F=10k N,不计重力。
计算中点挠度,两端转角。
理论解:I=2.239×10-5m4,w中=2.769×10-3m,θ边=2.077×10-3。
文件与路径:顶部下拉菜单File, Save As ExpAbq00。
一部件1 创建部件:Module,Part,Create Part,命名为Prat-1;3D,可变形模型,线,图形大约范围10(程序默认长度单位为m)。
2 绘模型图:选用折线,从(0,0)→(2,0)→(4,0)绘出梁的轴线。
3 退出:Done。
二性质1 创建截面几何形状:Module,Property,Create Profile,命名为Profile-1,选I型截面,按图输入数据,l=0.1,h=0.2,b l=0.1,b2=0.1,t l=0.01,t2=0.01,t3=0.01,关闭。
2 定义梁方向:Module,Property,Assign Beam Orientation,选中两段线段,输入主轴1方向单位矢量(0,0,1)或(0,0,-1),关闭。
3 定义截面力学性质:Module,Property,Create Section,命名为Section-1,梁,梁,截面几何形状选Profile-1,输入E=210e9(程序默认单位为N/m2,GPa=109N/m2),G=82.03e9,ν=0.28,关闭。
ABAQUS简支梁分析梁单元和实体单元

ABAQUS简支梁分析梁单元和实体单元梁单元是ABAQUS中常用的一种单元类型,适用于对梁结构进行分析。
它是一维元素,具有沿一个坐标轴的长度、截面积和转动惯量等属性。
梁单元适用于对纤维偏离主轴较小的梁进行建模。
与梁单元相比,实体单元更适用于对复杂几何形状的梁进行建模。
实体单元是三维元素,它在三个坐标轴上都具有长度,并且可以定义复杂的几何形状。
实体单元适用于对纤维偏离主轴较大的梁、异形梁和复杂梁进行建模。
梁单元的建模步骤如下:1.创建部件:在ABAQUS中创建一个新部件,并设定其属性,如截面形状、材料参数等。
2.创建草图:使用ABAQUS提供的工具创建梁单元的草图,定义梁的几何形状和尺寸。
3.定义截面:将截面属性应用到梁单元上,包括截面形状和尺寸。
4.创建网格:使用ABAQUS的网格划分工具将梁的草图划分为网格,生成梁单元。
5.设置材料属性:为梁单元定义材料属性,包括弹性模量、泊松比等。
6.施加边界条件:为梁单元定义边界条件,如支撑和加载情况。
7.定义分析类型:选择适当的分析类型,如静力分析或动力分析。
8.执行分析:运行分析,并获取梁的响应结果,如位移、应变和应力。
实体单元的建模步骤如下:1.创建部件:在ABAQUS中创建一个新部件,并设定其属性,如材料参数等。
2.创建草图:使用ABAQUS提供的工具创建梁的草图,定义梁的几何形状和尺寸。
3.创建几何图形:使用ABAQUS的几何模块创建复杂的实体几何形状。
4.定义材料属性:为实体单元定义材料属性,包括弹性模量、泊松比等。
5.生成网格:使用ABAQUS的网格划分工具将实体几何形状划分为网格,生成实体单元。
6.施加边界条件:为实体单元定义边界条件,如支撑和加载情况。
7.定义分析类型:选择适当的分析类型,如静力分析或动力分析。
8.执行分析:运行分析,并获取梁的响应结果,如位移、应变和应力。
梁单元和实体单元在ABAQUS中都提供了丰富的分析功能和选项,可以根据实际需要使用不同的单元类型来建模和分析梁结构。
Abaqus单元小结

Abaqus单元小结1、单元表征单元族:单元名字里开始的字母标志着这种单元属于哪一个单元族。
C3D8I是实体单元;S4R是壳单元;CINPE4是无限元;梁单元;刚体单元;膜单元;特殊目的单元,例如弹簧,粘壶和质量;桁架单元。
自由度dof(和单元族直接相关):每一节点处的平动和转动1 1方向的平动2 2方向的平动3 3方向的平动4 绕1轴的转动5 绕2轴的转动6 绕3轴的转动7 开口截面梁单元的翘曲8 声压或孔隙压力9 电势11 度(或物质扩散分析中归一化浓度)12+梁和壳厚度上其它点的温度轴对称单元1 r方向的平动2 z方向的平动6 r-z方向的转动节点数:决定单元插值的阶数数学描述:定义单元行为的数学理论积分:应用数值方法在每一单元的体积上对不同的变量进行积分。
大部分单元采用高斯积分方法计算单元内每一高斯点处的材料响应。
单元末尾用字母“R”识别减缩积分单元,否则是全积分单元。
ABAQUS拥有广泛适用于结构应用的庞大单元库。
单元类型的选择对模拟计算的精度和效率有重大的影响;节点的有效自由度依赖于此节点所在的单元类型;单元的名字完整地标明了单元族、单元的数学描述、节点数及积分类型;所用的单元都必须指定单元性质选项。
单元性质选项不仅用来提供定义单元几何形状的附加数据,而且用来识别相关的材料性质定义;对于实体单元,ABAQUS参考整体笛卡尔坐标系来定义单元的输出变量,如应力和应变。
可以用*ORIENTATION选项将整体坐标系改为局部坐标系;对于三维壳单元,ABAQUS参考建立在壳表面上的一个坐标系来定义单元的输出变量。
可以用*ORIENTATION选项更改这个参考坐标系。
2.实体单元(C)实体单元可在其任何表面与其他单元连接起来。
C3D:三维单元CAX:无扭曲轴对称单元,模拟3600的环,用于分析受轴对称载荷作用,具有轴对称几何形状的结构;CPE:平面应变单元,假定离面应变ε33为零,用力模拟厚结构;CPS:平面应力单元,假定离面应力σ33为零,用力模拟薄结构;广义平面应变单元包括附加的推广:离面应变可以随着模型平面内的位置线性变化。
abaqusABAQUS中的实体单元

线性单元 (如:CPS4R)
北京怡格明思工程技术有限公司
二次单元 (如:CPS8R)
Innovating through simulation
线性的减缩积分单元由于存在着来自本身的所谓沙漏(hourglassing)数值 问题而过于柔软。为了说明这个问题,再次考虑用单一减缩单元模拟受纯弯 曲载荷的一小块材料 :
产生这种伪剪应力的原因是因为单元的边不能弯曲,它的出现意味着应变能正在产 生剪切变形,而不是产生所希望的弯曲变形,因此总的挠度变小:即单元是过于的 刚硬。
剪力自锁仅影响受弯曲载荷的完全积分的线性单元的行为。在受轴向或剪切载荷时, 这些单元的功能表现很好。而二次单元的边界可以弯曲,故它没有剪力自锁的问题。 二次单元预测的自由端位移接近于理论解答。
第二讲 ABAQUS中的实体单元
王慎平 北京怡格明思工程技术有限公司
北京怡格明思工程技术有限公司
Innovating through simulation
ห้องสมุดไป่ตู้
ABAQUS中的单元
北京怡格明思工程技术有限公司
Innovating through simulation
ABAQUS中的单元
ABAQUS单元库中大量的单元为不同几何体和结构建模提供了非常大 的灵活性。
剪力自锁引起单元在弯曲时过于刚硬,对此解释如下。考虑受纯弯曲结构中的一 小块材料,如图4-4所示,材料产生弯曲,变形前平行于水平轴的直线成为常曲 率的曲线,而沿厚度方向的直线仍保持为直线,水平线与竖直线之间的夹角保持 为90o 。
受弯矩M作用下材料的变形 线性单元的边不能弯曲;所以,如果应用单一单元来模拟这一小块材料, 其变形后的形状如图所示。
受弯矩M作用下完全积分、线性单元的变形
ABAQUS计算指导0应用梁单元计算简支梁的挠度

ABAQUS计算指导0:应用梁单元计算简支梁的挠度对于梁的分析可以使用梁单元、壳单元或是固体单元。
Abaqus的梁单元需要设定线的方向,用选中所需要的线后,输入该线梁截面的主轴1方向单位矢量(x,y,z),截面的主轴方向在截面Profile设定中有规定。
注意:因为ABAQUS软件没有UNDO功能,在建模过程中,应不时地将本题的CAE模型(阶段结果)保存,以免丢失已完成的工作。
简支梁,三点弯曲,工字钢构件,结构钢材质,E=210GPa,μ=0.28,ρ=7850kg/m3(在不计重力的静力学分析中可以不要)。
F=10kN,不计重力。
计算中点挠度,两端转角。
理论解:I=2.239×10-5m4,w中=2.769×10-3m,θ边=2.077×10-3。
文件与路径:顶部下拉菜单File, Save As ExpAbq00。
一部件1 创建部件:Module,Part,Create Part,命名为Prat-1;3D,可变形模型,线,图形大约范围10(程序默认长度单位为m)。
2 绘模型图:选用折线,从(0,0)→(2,0)→(4,0)绘出梁的轴线。
3 退出:Done。
二性质1 创建截面几何形状:Module,Property,Create Profile,命名为Profile-1,选I型截面,按图输入数据,l=0.1,h=0.2,b l=0.1,b2=0.1,t l=0.01,t2=0.01,t3=0.01,关闭。
2 定义梁方向:Module,Property,Assign Beam Orientation,选中两段线段,输入主轴1方向单位矢量(0,0,1)或(0,0,-1),关闭。
3 定义截面力学性质:Module,Property,Create Section,命名为Section-1,梁,梁,截面几何形状选Profile-1,输入E=210e9(程序默认单位为N/m2,GPa=109 N/m2),G=82.03e9,ν=0.28,关闭。
abaqus实体单元、壳单元、梁单元的定义与用法

abaqus实体单元、壳单元、梁单元的定义与用法文章标题:深度了解abaqus实体单元、壳单元、梁单元的定义与用法一、引言在工程领域中,模拟和分析结构力学行为是非常重要的。
ABAQUS作为有限元分析软件,在工程结构分析和仿真中扮演着重要的角色。
在ABAQUS中,实体单元、壳单元和梁单元是常用的元素类型,它们可以用来模拟各种不同类型的结构和力学行为。
本文将深入探讨这些单元的定义与用法。
二、实体单元的定义与用法1. 实体单元是ABAQUS中最基本的有限元单元之一,通常用于模拟具有三维结构的实体物体。
它能够准确描述物体的体积和构造。
2. 实体单元适用于模拟压力容器、机械零件、汽车车身等实体结构的力学行为。
它能够有效分析结构的应力、应变、变形等力学特性。
3. 在实际工程中,使用实体单元时需要注意单元的类型、材料特性、边界条件和加载方式,以确保分析结果的准确性和可靠性。
三、壳单元的定义与用法1. 壳单元是ABAQUS中常用的二维有限元单元,适用于模拟薄壁结构和板材。
它能够准确描述结构的曲率和变形。
2. 壳单元适用于模拟飞机机翼、船体、薄膜结构等薄壁结构的力学行为。
它能够有效分析结构的弯曲、剪切、挠曲等力学特性。
3. 在实际工程中,使用壳单元时需要注意单元的厚度、材料特性、边界条件和加载方式,以确保分析结果的准确性和可靠性。
四、梁单元的定义与用法1. 梁单元是ABAQUS中用于模拟杆件和梁结构的有限元单元,适用于描述结构的轴向变形和弯曲变形。
2. 梁单元适用于模拟桥梁、支撑结构、梁柱结构等杆件和梁结构的力学行为。
它能够有效分析结构的弯曲、扭转、轴向变形等力学特性。
3. 在实际工程中,使用梁单元时需要注意单元的截面特性、材料特性、边界条件和加载方式,以确保分析结果的准确性和可靠性。
五、个人观点和理解在工程结构分析中,选择合适的有限元单元对于准确模拟和分析结构的力学行为是至关重要的。
实体单元、壳单元和梁单元都有各自的优缺点,工程师需要根据具体的结构特点和分析要求来选取合适的单元类型。
abaqus梁结构分析
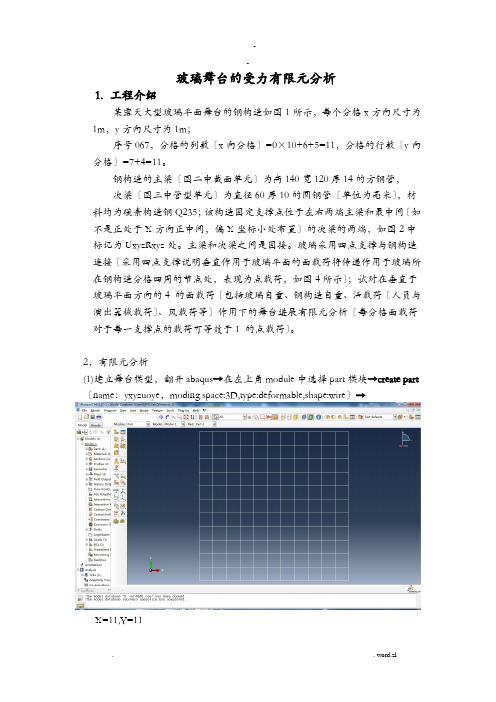
玻璃舞台的受力有限元分析1.工程介绍某露天大型玻璃平面舞台的钢构造如图1所示,每个分格x方向尺寸为1m,y方向尺寸为1m;序号067,分格的列数〔x向分格〕=0×10+6+5=11,分格的行数〔y向分格〕=7+4=11。
钢构造的主梁〔图二中截面单元〕为高140宽120厚14的方钢管,次梁〔图三中管型单元〕为直径60厚10的圆钢管〔单位为毫米〕,材料均为碳素构造钢Q235;该构造固定支撑点位于左右两端主梁和最中间〔如不是正处于X方向正中间,偏X坐标小处布置〕的次梁的两端,如图2中标记为UxyzRxyz处。
主梁和次梁之间是固接。
玻璃采用四点支撑与钢构造连接〔采用四点支撑说明垂直作用于玻璃平面的面载荷将传递作用于玻璃所在钢构造分格四周的节点处,表现为点载荷,如图4所示〕;试对在垂直于玻璃平面方向的4 的面载荷〔包括玻璃自重、钢构造自重、活载荷〔人员与演出器械载荷〕、风载荷等〕作用下的舞台进展有限元分析〔每分格面载荷对于每一支撑点的载荷可等效于1 的点载荷〕。
2,有限元分析(1)建立舞台模型,翻开abaqus→在左上角module中选择part模块→create part 〔name:yxyzuoye,moding space:3D,type:deformable,shape:wire〕→X=11,Y=11图一(2)定义材料属性和截面形状,在module中选择property模块→create material(Y=2.06Gpa,E=0.3)→create section主梁截面形状及尺寸如图二图二次梁截面形状及尺寸如图三图三→赋予截面属性assign section→assign beam orientation→done(3)装配:进入assembly模块→create instance→点击ok完成装配。
(4)进入step模块设置步:进入step模块→create step(initial,static,general) →点击continue→点击ok完成。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于ABAQUS简支梁受力和弯矩的相关分析
(梁单元和实体单元)
对于简支梁,基于 ABAQUS2016,首先用梁单元分析了梁受力作用下的应力,变形,剪力和力矩;对同一模型,并用实体单元进行了相应的分析。
另外,
还分析了梁结构受力和弯矩作用下的剪力及力矩分析。
对于CAE仿真分析具体细节操作并没有给出详细的操作,不过在后面上
传了对应的cae,odb,inp文件。
不过要注意的是本文采用的是ABAQUS2016
进行计算,低版本可能打不开,可以自己提交inp文件自己计算即可。
可以到
小木虫搜索:“基于ABAQUS简支梁受力和弯矩的相关分析”进行相应文件
下载。
对于一简支梁,其结构简图如下所示,梁的一段受固支,一段受简支,在
梁的两端受集中载荷,梁的大直径D=180mm,小直径d=150mm,a=200mm,
b=300mm,l=1600mm,F=300000N。
现通过梁单元和实体单元分析简支梁的受
力情况,变形情况,以及分析其剪力和弯矩等。
材料采用45#钢,弹性模量
E=2.1e6MPa,泊松比v=0.28。
图1 简支梁结构简图
1.梁单元分析
ABAQUS2016中对应的文件为beam-shaft.cae ,beam-shaft.odb,beam-shaft.inp。
在建立梁part的时候,采用三维线性实体,按照图1所示尺寸建立,然后
在台阶及支撑梁处进行分割,结果如图2所示。
图2 建立part并分割
接下来为梁结构分配材料,创建材料,定义弹性模量和泊松比,创建梁截
面形状,如图3,非别定义两个圆,圆的直接分别为180和150mm。
然后创建
两个截面,截面选择梁截面,再选择图2中的所有梁,定义梁的方向矢量为(0,0,-1)(点击图3中的n2,n1,t那个图标即可创建梁的方向矢量),最后把
创建好的梁赋给梁结构。
图3 创建梁截面形状
接下来装配实体,再创建分析步,在创建分析步的时候,点击主菜单栏的Output,编辑Edit Field Output Request,在SF前面打钩,这样就可以在结果后
处理中输出截面剪力和力矩,如图4所示。
在Load加载中,在固支处剪力边界
条件,约束x,y,z,及绕x和y轴的转动,如图5所示,同理,在固支另一处约束y,z,及绕x和y轴的转动。
在梁的两端添加集中力,集中力的大小为300000N。
最后对实体部件进行分网,采用B32梁单元,网格尺寸为10。
完成
以上工作后,创建作业并提交分析。
(由于操作比较简单,故没有详细列下所有操作步骤。
)
图4 Step中SF输出编辑
图5 边界条件约束
图6为等效应力云图,可知最大应力为181.1MPa ,最大位置出现在梁台阶处(梁直径变化处)。
根据材料力学,最大弯矩应力产生在C 截面,同时根据材料力学知道AB 段处的最大应力,其应力为
max 33
3232300000200181.083150c C c M Fa MPa W d σσππ⨯⨯=====⨯ (1) 33
3232300000300157.19180AB AB AB M Fb MPa W D σππ⨯⨯====⨯ (2) 从图6和图7可以知道,梁的最大应力以及AB 段的应力都与理论解一致。
图8为梁的等效应力图,可见最大位移出现在梁的两端,最大有1.639mm 。
沿着梁的轴线建立路径,然后绘制出梁的变形,图9和图10分别给出了截面剪力和力矩沿路径的变化情况。
值得注意的是,图9中剪力图与材料力学的剪力图有区别,其并不是按照设正法画的剪力图,不过其数值的绝对值与材料力学上的一致。
图10的弯矩图也材料力分析一致,图11为等效位移沿路径的变化情况。
图6 等效应力
图7 中间段等效应力图
图8 等效位移图
图9 剪力SF2沿路径情况
图10 弯矩SM1沿路径情况
图11 等效位移U沿路径情况
2.实体单元分析
ABAQUS2016中对应的文件为beam-solid.cae ,beam-solid.odb,beam-solid.inp。
按照图1建立相应的实体单元,然后在支撑处切割实体,再建立材料属性,装配,设置步,在创建分析步的时候,点击主菜单栏的Output,编辑Edit Field Output Request,在SF前面打钩,同梁设置操作一样。
图12 实体单元结构
图13给出了力载荷及边界条件加载情况,在梁左右两端加载力载荷,可以选择对应的面,然后加载界面切应力(F/S=300000/(3.1414*75^2=16.9765MPa,S为圆的面积),也可以在加载面的中心建立参考点,然后把加载面与参考点相耦合,然后直接在参考点加载300000N的力即可。
在支撑处选择对应的面,然后加载对应的边界条件约束即可。
最后完成相应的分网并提交分析。
图13 载荷及边界条件
图14 等效应力图
图15 等效位移图
图16 输出剪力弯矩操作
图17 输出剪力弯矩操作
图18 剪力数据数据输出
图14给出了等效应力图,其数值结果与梁给出的结果一致,与理论计算也一致,但是图15给出的等效位移图与梁单元计算的等效位移图不同,因此在具体问题分析的时候,我们应该判断具体使用什么单元进行分析。
图16到图18给出了如何把沿轴向方向各个截面的剪力和弯矩输出到一个txt文件的操作。
在图16中打开主菜单Tools中的View Cut Manager,然后在轴线平面前面打钩,
结果如16所示,然后单击图16中的Options,再单击Slicing进入到图17,设
置实体切割的数目,然后单击OK即可。
再在主菜单中单击Report的Free Body Cut,然后按照图18中设置,然后单击OK,这样就可以在ABAQUS的当前文
件夹找到moment.txt文件,里面记录了各个截面的力矩和弯矩,把里面的数据
复制到excel中就可以绘制出弯矩和剪力图。
3. 梁同时受集中力和弯矩分析
ABAQUS2016中对应的文件为beam-force-moment.cae ,beam-force-moment.odb,beam-force-moment.inp。
对于该分析,还给出用Workbench给
出的对应分析,其文件为beam-force-moment.wbpj,Workbench版本为15.0。
图19为梁在中间受集中载荷和弯矩的结构简图,梁的长度l=1000mm,梁
的直径d=100mm,M e=9e7N·mm,F=300000N,E=210000MPa,v=0.28。
现采
用梁单元进行剪力和弯矩等相关分析。
图19 梁受力和弯矩结构简图
其建模等分析过程与前面第一个实例的梁单元分析一样,在梁的中点部分
进行切割。
为了对比分析只有集中力,弯矩以及集中力和弯矩同时作用在梁上
的几种情形,如图20,对应Load处右键单击,然后选择Suppress,可以抑制
载荷作用,选择Resume,可以激活抑制的载荷。
通过载荷抑制或者激活的设置,然后提交分析,就可以得到对应载荷情况下的结果。
图20 载荷加载情况
(1)梁中部只受集中力情形
下面四个图给出了只受集中力载荷作用下的等效应力,等效位移,剪力和弯矩图,剪力和弯矩图与材料力学分析一致。
图21 等效应力图
图22 等效位移图
图23 轴线方向剪力图
图24 轴线方向弯矩图
(2)梁中部只受弯矩作用
下面四个图给出了在梁的中部只加载弯矩作用下的等效应力,等效位移,力矩和弯矩图。
从剪力和弯矩图可以知道,整个梁受到90000N(M e*l=9e7 N·mm *1000mm=90000N)的剪力作用,这与材料力学分析不一致,这应该引起关注。
在材料力学分析中,只受到弯矩作用时,应该没有剪力作用,不过按
照这思路也可以做出有弯矩作用下的剪力和弯矩图。
在弯矩图中可以知道,弯矩中部处出现了突变,有均匀剪力作用处,其弯矩呈现线性变化。
图25 等效应力图
图26 等效位移图
图27 轴线方向剪力图
图29 轴线方向弯矩图
(3)梁中部同时受集中力和弯矩作用
下面四图给出了梁在中部同时受到集中力和弯矩作用下的等效应力,等效位移,剪力和弯矩图。
从剪力图知道,当给梁加载弯矩后,改变了梁的剪力和弯矩,不过在梁的中部,梁的弯矩图出现了突变,这与材料力学的分析变化趋势相一致。
图30 等效应力图
图31 等效位移图
图32 轴线方向剪力图
图33 轴线方向弯矩图。
