第18章 多相流模拟
通气超空泡多相流场数值仿真方法

通气超空泡多相流场数值仿真方法佚名【摘要】通气超空泡流动涉及多相流动、湍流、相变及可压缩等流体力学难点问题,流动机理非常复杂。
其中多相流模型是通气超空泡数值仿真研究工作的重点,将严重影响通气超空泡数值仿真结果的精度。
本文有针对性地对比了目前广泛采用的均质平衡流模型和欧拉双流体模型,结合作者所在课题组多年来在水洞试验和数值仿真方面的研究成果,从空泡形态和流体动力两方面分析了欧拉双流体模型在预测通气超空泡方面的优势。
随着研究的进一步深入,通气超空泡数值仿真方法有望成为超空泡减阻技术的重要研究手段,可以为工程设计提供参考。
%Ventilated supercavitating flow involves such topics in fluid mechanics as multiphase flow, turbulence, phase change and compressibility, its mechanism is very complex. The multiphase flow model has attracted much more atten-tion in the study of numerical simulation of supercavitating flow, however its accuracy in simulation is not satisfactory. In this paper, the homogeneous model, which are widely used in the world, are compared with the Euler two-fluid model by combining with the authors′ research by means of water tunnel experiments and numerical simulation. The advan-tages of the Euler two-fluid model in predicting ventilated supercavitation is analyzed in terms of cavity shape and hy-drodynamics of a vehicle. Numerical simulation of ventilated supercavitation is expected to become an important ap-proach of drag-reduction technology through supercavitation.【期刊名称】《鱼雷技术》【年(卷),期】2013(000)003【总页数】6页(P165-170)【关键词】通气超空泡;多相流;数值仿真方法;均值平衡流模型;欧拉双流体模型【正文语种】中文【中图分类】TJ630.1;O351.2对于通气超空泡流动的研究, 最早可以追溯到上个世纪40年代。
多相流模型数值模拟(中文)
va
po r
– 欧拉显式
po r
liq
Байду номын сангаасui
d
Actual interface shape
Geo-reconstruct (piecewise linear) Scheme
– 欧拉隐式
• 定常和非定常都使用相同的求解器,在差的网格 单元上有固定的数值差分方法 –使用高阶VOF离 散(HRIC, CICSAM)
Stokes数
• 系统载入媒介粒子时, 根据Stokes数选择合适的模型。
– Stokes数(St)是粒子(分散内相)时间松弛系数(τd)和流动特征 时间比例(τc)的比值。
St =
2 ρd d d 其中 . τ d = 18 μ c
τd τc
,τ c =
D U
– D 和 U 是问题中的特征长度和速度标量。 – 如果 St << 1, 粒子流动将会跟随流场流动。 – 如果 St > 1, 粒子流动独立于流场流动。
• 几种有效的子模型方法:
– 散布相的加热/冷却 – – – – 流体液滴的汽化和蒸发 燃烧粒子的挥发演变和燃烧 喷雾模型中液滴的分裂和融合 腐蚀/衍生
DPM模型的适用条件
• 流域: • 填充体积: • 填充粒子: • 建立湍流模型: • Stokes数: • 案例
– – – – – – 气旋 喷雾干燥器 粒子的分离和分类 浮质散布 液体燃料 媒的燃烧
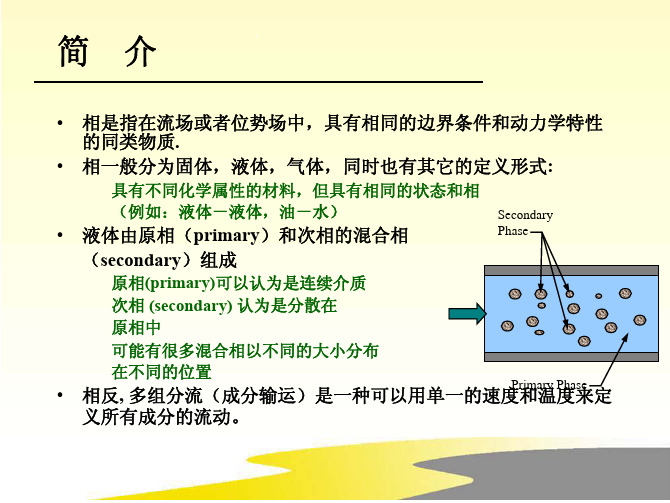
Primary Phase
选择多相流模型
• 为能选择合理的模型,用户需要推理得到下列 形式的一些流动参数:
– 流动域
• 微粒 (连续介质中的气泡,液滴和固体颗粒) • 分层 (流体分界面的长度和域的长度成正比)
多相流体力学的数值模拟及其应用

多相流体力学的数值模拟及其应用引言多相流体力学是研究多种不同物质在相互作用下流动行为的学科领域。
它在工程、环境、生物等多个领域都有重要的应用价值。
随着计算机技术的不断发展,数值模拟成为研究多相流体力学的重要手段之一。
本文将介绍多相流体力学数值模拟的基本原理和方法,并探讨其在工程和科学研究中的应用。
一、多相流体力学的基本概念1.1 多相流体的定义多相流体是指由两种或更多种不同物质组成的流体系统。
它们可以是气体和液体的组合,也可以是液体和固体的组合。
在多相流体中,不同相之间存在各种各样的相互作用,如表面张力、颗粒间作用力等。
1.2 多相流体的分类根据不同的分类标准,多相流体可以分为不同的类型。
按照相间分布的均匀性,可以将多相流体分为均质和非均质两类。
均质多相流体是指各相之间存在均匀分布的情况,如气泡在液体中的分布。
非均质多相流体是指各相之间存在不均匀分布的情况,如液滴在气体中的分布。
1.3 多相流体的力学性质多相流体的力学性质是研究多相流体力学的重要内容。
它包括各个相的速度分布、压力分布、浓度分布等。
多相流体的力学性质直接影响多相流体的流动行为,并对多相流体的应用产生重要影响。
二、多相流体力学的数值模拟方法2.1 多相流体力学方程多相流体力学方程是研究多相流体力学的基本方程。
它从守恒性原理出发,通过质量守恒、动量守恒和能量守恒等方程来描述多相流体的运动行为。
2.2 多相流体的计算模型多相流体的计算模型是进行多相流体力学数值模拟的基础。
常见的多相流体计算模型包括欧拉法、拉格朗日法和亚欧拉法等。
2.3 多相流体力学的数值方法多相流体力学的数值方法是进行多相流体力学数值模拟的关键环节。
常见的多相流体力学数值方法包括有限体积法、有限元法、边界元法等。
2.4 多相流体力学的边界条件多相流体力学的边界条件在数值模拟中起着重要作用。
它们可以分为速度边界条件、压力边界条件和浓度边界条件等。
三、多相流体力学数值模拟的应用3.1 多相流体流动的数值模拟多相流体流动的数值模拟在工程和科学研究中有着广泛的应用。
流体力学中的多相流模型与仿真

流体力学中的多相流模型与仿真在流体力学领域中,多相流模型和仿真技术在研究和应用中发挥着重要的作用。
多相流模型是描述多个不同物理相互作用的数学模型,而仿真技术则是利用计算机来模拟和预测多相流体的行为。
本文将探讨多相流模型和仿真技术在流体力学中的应用和发展。
一、多相流模型多相流模型是流体力学中研究多相流体行为的重要工具。
多相流是指在同一空间中存在着两种或多种物质相的流动状态。
常见的多相流包括气固流动、气液流动和固液流动等。
1. 气固流动模型气固流动模型是研究气体和颗粒物质相互作用的模型。
这种流动模型在煤矿爆炸、粉尘扬尘、颗粒输送等领域有着广泛的应用。
常用的气固流动模型有Euler-Euler模型和Euler-Lagrange模型。
2. 气液流动模型气液流动模型是研究气体和液体相互作用的模型。
气液两相流动在石油、化工、环保等行业中具有重要的应用价值。
常用的气液流动模型有两流体模型、体积力平衡模型和界面平衡模型等。
3. 固液流动模型固液流动模型是研究固体颗粒和液体相互作用的模型。
这种流动模型在颗粒床反应器、混凝土输送等领域有着广泛的应用。
常用的固液流动模型有物理模型、经验模型和计算流体动力学模型等。
二、多相流仿真技术多相流仿真技术是利用计算机来模拟和预测多相流体行为的方法。
仿真技术可以通过数值计算的方式,将多相流动的数学模型转化为离散的数值计算模型,并通过迭代求解来获得流体的相关参数。
1. 传统的数值模拟方法传统的数值模拟方法基于有限差分法、有限元法等数值计算方法,通过网格划分和离散化,将流体力学方程数值化求解。
这种方法在处理简单的流动问题时有效,但对于复杂的多相流问题,计算效率较低。
2. 基于粒子的仿真方法基于粒子的仿真方法是通过跟踪流体颗粒的运动轨迹,模拟多相流体的流动行为。
这种方法可以精确地模拟颗粒与流体之间的相互作用,并考虑颗粒的密度、粒径等特性。
常用的基于粒子的仿真方法有离散元法和分子动力学方法等。
基于相场模型及涡量流函数形式的一种多相流数值模拟方法

基于相场模型及涡量-流函数形式的一种多相流数值模拟方法1)黄军杰2),王时龙重庆大学机械传动国家重点实验室,重庆400044摘要:本文提出一种基于相场(Phase-Field)模型及涡量-流函数形式的二维多相流模拟数值方法。
基于相场的多相流数值模拟需求解两组方程:流动控制方程(具体为不可压Navier-Stokes方程)及界面演化方程(这里使用Cahn-Hilliard方程)。
与常见方法不同的是,对于流动控制方程,本文采用其涡量-流函数形式,并且给出涡量-流函数形式下包含界面张力作用的涡量演化方程及适当的边界条件。
两组方程都使用有限差分法进行空间离散,采用四阶龙格库塔(Runge-Kutta)法进行时间推进。
另外本方法采用空间交错网格,涡量和流函数定义于网格节点,而相场变量(包括相序参数和化学势)定义于网格中心。
对于相场变量的空间导数,本文尝试使用了一般二阶中心差分以及各向同性的九点差分格式(借鉴格子玻尔兹曼方法(Lattice-Boltzmann Method, LBM))。
通过三个基本的多相流算例(平整界面,静止液滴的表面张力平衡以及接触角),本方法得以初步验证;此外,以一种格子玻尔兹曼方法作为参考,本文亦对一般中心差分以及各向同性的差分格式作以比较。
本文认为涡量-流函数形式的多相流模拟方法有其一定的优势,可作为现有常见基于压力-速度形式方法的一种替代来研究某些多相流问题(特别是二维和轴对称问题)。
关键词:多相流;数值模拟;相场模型;涡量-流函数引言很多工业问题中(如石油,化工,食品,化妆品及制药等)都涉及到多相流。
对于不可混合的液-液两相流系统的研究在理论和工程应用中都有重要意义。
基于相场模型的多相流模拟方法近年来发展迅速,颇受关注。
这类方法基于流体临界点附近的理论,使用狭窄但具有有限厚度的区域来代表界面,可以更自然的处理界面的拓扑变化(如液滴融合和分离)[1,2,3,4]。
现有相场多相流模拟方法大多采用基于速度-压力形式的流体控制方程[3,4]。
多相流动的基础知识和数值模拟方法

多相流动的基础知识和数值模拟方法多相流动是指在同一空间中存在两种及以上物质的流动现象。
在工程领域中,多相流动具有广泛应用,如化工反应器中的气液流动、石油勘探中的油水混合流动等。
本文将介绍多相流动的基础知识,并探讨一些常用的数值模拟方法。
一、多相流动的分类多相流动可以根据不同的分类标准进行分类,常见的分类方法包括:1.根据组分:固液流动、气液流动、固气流动等;2.根据速度:稳定流动、不稳定流动、湍流等;3.根据形态:离散相、连续相、两相界面等。
二、多相流动的基础知识1.多相流动的基本方程多相流动的基本方程包括连续性方程、动量方程和能量方程。
在连续性方程中,考虑到多相流动中各相的质量守恒关系;在动量方程中,引入各相之间的相互作用力和速度差等因素;在能量方程中,考虑到各相之间的相变、传热等现象。
2.多相流动的相互作用多相流动中的不同相之间存在相互作用力,如液固两相之间的颗粒间碰撞力、气液两相之间的表面张力等。
这些相互作用力对多相流动的行为和特性具有重要影响。
3.多相流动的模型为了更好地描述多相流动的行为,研究者们提出了多种多相流动模型,如两流体模型、Eulerian-Eulerian模型和Eulerian-Lagrangian模型等。
不同的模型适用于不同的多相流动情况,选择合适的模型对于准确描述多相流动至关重要。
三、多相流动的数值模拟方法数值模拟是研究多相流动的重要手段之一,常用的数值模拟方法包括:1.有限体积法有限体积法是常用的求解多相流动的数值方法之一,它将流动域划分为网格单元,通过离散化各个方程,利用差分格式求解模拟区域内的物理量。
2.多尺度方法多尺度方法考虑到多相流动中存在不同尺度的现象和作用力,通过将流动域划分为不同的区域进行求解,以更好地描述多相流动的行为。
常见的多尺度方法有多尺度网格方法和多尺度时间方法。
3.相场方法相场方法是一种常用的描述多相流动界面的方法,它通过引入相场函数来表示相界面,并利用Cahn-Hilliard方程等对相场函数进行求解,从而获得界面位置和形状等信息。
FLUENT教程--20-27章

20.通用多相流模型(General Multiphase Models)本章讨论了在FLUENT中可用的通用的多相流模型。
第18章提供了多相流模型的简要介绍。
第19章讨论了Lagrangian离散相模型,第21章讲述了FLUENT中的凝固和熔化模型。
20.1选择通用多相流模型(Choosing a General Multiphase Model)20.2VOF模型(Volume of Fluid(VOF)Model)20.3混合模型(Mixture Model)20.4欧拉模型(Eulerian Model)20.5气穴影响(Cavity Effects)20.6设置通用多相流问题(Setting Up a General Multiphase Problem)20.7通用多相流问题求解策略(Solution Strategies for General Multiphase Problems)20.8通用多相流问题后处理(Postprocessing for General Multiphase Problems)20.1选择通用的多相流模型(Choosing a General Multiphase Model)正如在Section 18.4中讨论过的,VOF模型适合于分层的或自由表面流,而mixture和Eulerian 模型适合于流动中有相混合或分离,或者分散相的volume fraction超过10%的情形。
(流动中分散相的volume fraction小于或等于10%时可使用第19章讨论过的离散相模型)。
为了在mixture模型和Eulerian模型之间作出选择,除了Section18.4中详细的指导外,你还应考虑以下几点:★ 如果分散相有着宽广的分布,mixture模型是最可取的。
如果分散相只集中在区域的一部分,你应当使用Eulerian模型。
★ 如果应用于你的系统的相间曳力规律是可利用的(either within FLUENT or through a user-defined function),Eulerian模型通常比mixture模型能给出更精确的结果。
多相流动动力学的数值模拟与分析

多相流动动力学的数值模拟与分析多相流动是指在流体中同时存在两种或两种以上的物质,这些物质可以是气体、液体或固体。
由于多相流动的复杂性,数值模拟成为研究多相流动的有效手段之一。
数值模拟可以通过计算机模拟多相流动的各种特性,如相互作用、相变、物理效应等,以更深入地理解多相流动动力学行为。
本文将介绍多相流动动力学的数值模拟与分析方法和应用,包括模型、算法以及重要应用领域。
多相流动动力学模型在数值模拟中,多相流动动力学模型是处理多相流动问题的基础。
多相流动模型可以大致分为两类:欧拉-欧拉模型和欧拉-拉格朗日模型。
欧拉-欧拉模型使用两个或多个连续性方程对每个相的物质守恒和动量守恒进行建模。
这些方程用于描述不同相之间的相互作用,包括不同相之间的质量和能量传递。
欧拉-欧拉模型被广泛应用于处理多孔介质中的多相流,如油藏、地下水系统等。
欧拉-拉格朗日模型则使用一个欧拉方程对流体整体进行建模,用于描述流体的运动和相互作用。
该模型建立在欧拉方程的基础上,使用另一种拉格朗日方程来描述固体颗粒运动。
欧拉-拉格朗日模型通常用于研究一个或多个固体颗粒在流体中的运动,例如颗粒悬浮在液体中的情况。
多相流动动力学算法在多相流动动力学数值模拟中,有多种算法可供选择。
以下是几种常用的多相流动动力学算法:Lattice-Boltzmann方法:Lattice-Boltzmann方法是Lattice-Gas方法的一种改进。
该算法将连续性方程转化为离散空间和时间的微分方程,从而简化了计算过程。
Lattice-Boltzmann方法已经被广泛应用于湍流数值模拟、多孔流动和多相流动等领域。
有限元法:有限元法通过将流场划分为多个小区域来离散化流 field。
这种方法对任意复杂的几何形状和流动条件都有一个准确的数值解,已被广泛用于数值模拟和工程设计中。
元胞自动机方法:元胞自动机方法是一种离散事件方法,通过定义哪些工作单元(mesh cell)可以容纳颗粒,颗粒在各个时间步长内向相邻工作单元的移动,来模拟多相流动的行为。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
王巍雄——2003-6-1918.多相流模拟介绍自然界和工程问题中会遇到大量的多相流动。
物质一般具有气态、液态和固态三相,但是多相流系统中相的概念具有更为广泛的意义。
在多项流动中,所谓的“相”可以定义为具有相同类别的物质,该类物质在所处的流动中具有特定的惯性响应并与流场相互作用。
比如说,相同材料的固体物质颗粒如果具有不同尺寸,就可以把它们看成不同的相,因为相同尺寸粒子的集合对流场有相似的动力学响应。
本章大致介绍一下Fluent中的多相流建模。
第19章和第20章将会详细介绍本章所提到的内容。
第20章会介绍一下融化和固化方面的内容•18.1多相流动模式•18.2多相系统的例子•18.3多相建模方法•18.4多相流模型的选择18.1多相流动模式我们可以根据下面的原则对多相流分成四类:•气-液或者液-液两相流:o气泡流动:连续流体中的气泡或者液泡。
o液滴流动:连续气体中的离散流体液滴。
o活塞流动:在连续流体中的大的气泡o分层自由面流动:由明显的分界面隔开的非混合流体流动。
•气-固两相流:o充满粒子的流动:连续气体流动中有离散的固体粒子。
o气动输运:流动模式依赖诸如固体载荷、雷诺数和粒子属性等因素。
最典型的模式有沙子的流动,泥浆流,填充床,以及各向同性流。
o流化床:由一个盛有粒子的竖直圆筒构成,气体从一个分散器导入筒内。
从床底不断充入的气体使得颗粒得以悬浮。
改变气体的流量,就会有气泡不断的出现并穿过整个容器,从而使得颗粒在床内得到充分混合。
•液-固两相流o泥浆流:流体中的颗粒输运。
液-固两相流的基本特征不同于液体中固体颗粒的流动。
在泥浆流中,Stokes数(见方程18.4-4)通常小于1。
当Stokes数大于1时,流动成为流化(fluidization)了的液-固流动。
o水力运输:在连续流体中密布着固体颗粒o沉降运动:在有一定高度的成有液体的容器内,初始时刻均匀散布着颗粒物质。
随后,流体将会分层,在容器底部因为颗粒的不断沉降并堆积形成了淤积层,在顶部出现了澄清层,里面没有颗粒物质,在中间则是沉降层,那里的粒子仍然在沉降。
在澄清层和沉降层中间,是一个清晰可辨的交界面。
•三相流(上面各种情况的组合)上述的各种流动模式如图18.1.1所示:图18.1.1多相流动模式18.2多相系统的例子18.1节给出的各流动模式对应的例子如下:•气泡流例子:抽吸,通风,空气泵,气穴,蒸发,浮选,洗刷•液滴流例子:抽吸,喷雾,燃烧室,低温泵,干燥机,蒸发,气冷,刷洗•活塞流例子:管道或容器内有大尺度气泡的流动•分层自由面流动例子:分离器中的晃动,核反应装置中的沸腾和冷凝•粒子负载流动例子:旋风分离器,空气分类器,洗尘器,环境尘埃流动泥浆流气泡,液滴,或颗粒负载流分层自由面流动气动输运、水力输运、或泥浆流沉降流化床•风力输运例子:水泥、谷粒和金属粉末的输运•流化床例子:流化床反应器,循环流化床•泥浆流例子:泥浆输运,矿物处理•水力输运例子:矿物处理,生物医学及物理化学中的流体系统•沉降例子:矿物处理18.3多相建模方法计算流体力学的进展为深入了解多相流动提供了基础。
目前有两种数值计算的方法处理多相流:欧拉-拉格朗日方法和欧拉-欧拉方法。
•18.3.1欧拉-拉格朗日方法•18.3.2欧拉-欧拉方法18.3.1欧拉-拉格朗日方法在Fluent中的拉格朗日离散相模型(详见第19章)遵循欧拉-拉格朗日方法。
流体相被处理为连续相,直接求解时均纳维-斯托克斯方程,而离散相是通过计算流场中大量的粒子,气泡或是液滴的运动得到的。
离散相和流体相之间可以有动量、质量和能量的交换。
该模型的一个基本假设是,作为离散的第二相的体积比率应很低,即便如此,较大的质量加载率()仍能满足。
粒子或液滴运行轨迹的计算是独立的,它们被安排在流相计算的指定的间隙完成。
这样的处理能较好的符合喷雾干燥,煤和液体燃料燃烧,和一些粒子负载流动,但是不适用于流-流混合物,流化床和其他第二相体积率不容忽略的情形。
18.3.2欧拉-欧拉方法在欧拉-欧拉方法中,不同的相被处理成互相贯穿的连续介质。
由于一种相所占的体积无法再被其他相占有,故此引入相体积率(phasic volume fraction)的概念。
体积率是时间和空间的连续函数,各相的体积率之和等于1。
从各相的守恒方程可以推导出一组方程,这些方程对于所有的相都具有类似的形式。
从实验得到的数据可以建立一些特定的关系,从而能使上述方程封闭,另外,对于小颗粒流(granular flows),则可以通过应用分子运动论的理论使方程封闭。
在FLUENT中,共有三种欧拉-欧拉多相流模型,分别为:流体体积模型(VOF),混合物模型,以及欧拉模型。
VOF模型所谓VOF模型(详见第20.2节),是一种在固定的欧拉网格下的表面跟踪方法。
当需要得到一种或多种互不相融流体间的交界面时,可以采用这种模型。
在VOF 模型中,不同的流体组分共用着一套动量方程,计算时在全流场的每个计算单元内,都记录下各流体组分所占有的体积率。
VOF模型的应用例子包括分层流,自由面流动,灌注,晃动,液体中大气泡的流动,水坝决堤时的水流,对喷射衰竭(jet breakup)(表面张力)的预测,以及求得任意液-气分界面的稳态或瞬时分界面。
混合物模型混和物模型(详见第20.3节)可用于两相流或多相流(流体或颗粒)。
因为在欧拉模型中,各相被处理为互相贯通的连续体,混和物模型求解的是混合物的动量方程,并通过相对速度来描述离散相。
混合物模型的应用包括低负载的粒子负载流,气泡流,沉降,以及旋风分离器。
混合物模型也可用于没有离散相相对速度的均匀多相流。
欧拉模型欧拉模型(详见第20.4节)是Fluent中最复杂的多相流模型。
它建立了一套包含有n个的动量方程和连续方程来求解每一相。
压力项和各界面交换系数是耦合在一起的。
耦合的方式则依赖于所含相的情况,颗粒流(流-固)的处理与非颗粒流(流-流)是不同的。
对于颗粒流,可应用分子运动理论来求得流动特性。
不同相之间的动量交换也依赖于混合物的类别。
通过FLUENT的客户自定义函数(user-defined functions),你可以自己定义动量交换的计算方式。
欧拉模型的应用包括气泡柱,上浮,颗粒悬浮,以及流化床。
18.4多相流模型的选择解决多相流问题的第一步,就是从18.1节中挑选出最能符合实际流动的模式。
在18.4.1节中,将对如何根据不同的模式,挑选恰当的模型给出最基本的原则,然后在18.4.2节中,将就以下的问题给出具体的方法:即如何给定相与相之间(包括气泡,液滴,和粒子)耦合的程度,以及如何针对不同程度的耦合情况选择恰当的模型。
•18.4.1基本原则•18.4.2细节指导18.4.1基本原则通常,你一旦决定了采用何种模式最能符合实际的流动,那么就可以根据以下的原则来挑选最佳的模型。
更为具体的指导,包括如何选择含有气泡,液滴和粒子的流动模型可以参见第18.4.2节。
•对于体积率小于10%的气泡、液滴和粒子负载流动,采用离散相模型。
具体内容参见第19章。
•对于离散相混合物或者单独的离散相体积率超出10%的气泡、液滴和粒子负载流动,采用混合物模型(详见20.3)或者欧拉模型(详见20.4)。
具体采用何种模型,可参考18.4.2和20.1所述。
•对于活塞流,采用VOF模型。
详见20.2。
•对于分层/自由面流动,采用VOF模型。
详见20.2。
•对于气动输运,如果是均匀流动(详见20.3),则采用混合物模型;如果是粒子流(详见20.4),则采用欧拉模型。
具体采用何种模型,可参考18.4.2和20.1节内容。
•对于流化床,采用欧拉模型模拟粒子流。
详见20.4。
•对于泥浆流和水力输运,采用混合物模型(详见20.3)或欧拉模型(详见20.4)。
具体采用何种模型,可参考18.4.2和20.1节内容。
•对于沉降,采用欧拉模型。
详见20.4。
•对于更加一般的,同时包含若干种多相流模式的情况,应根据最感兴趣的流动特征,选择合适的流动模型。
此时由于模型只是对部分流动特征做了较好模拟,其精度必然低于只包含单个模式的流动。
18.4.2细节指导对于分层流和活塞流,最直接的就是选择VOF模型,如18.4.1所述。
选择其他的模型就不那么直接。
一般来说,下面的一些参数可以帮助选择合适的多相流模型:粒子的加载率,,和斯托克斯数,St。
(注意:这里“颗粒”一词泛指粒子,液滴和气泡)粒子加载率的影响粒子加载率对相之间的影响具有很大的作用。
颗粒加载率定义为离散相的质量密度(d)和载体相的质量密度(c)之比:(18.4.1)物质密度比为:(18.4.2)气-固两相流中它大于1000,液-固两相流中在1左右,而气-液两相流中小于0.001。
利用这些参数,就可以估计粒子相中粒子之间的平均间隔距离。
下面是由Crowe et al.给出的一种估计方法[42]:(18.4.3)其中。
这些参数的信息对于决定如何来处理离散相是非常重要的。
例如,对于某种气体-颗粒流动,其粒子加载率为1,那么粒子间距就等于8;于是粒子就可以看成相互孤立的(也就是说,粒子加载率很低)。
根据粒子加载率的不同,相之间的影响程度可以分为三类:•对于低加载率,相之间的耦合作用是单向的;就是说,作为载体的流体介质可以通过推动和涡漩影响粒子的运动,但是粒子对流体运动却没有影响。
离散相,混合物以及欧拉模型都可以很好的处理这一类问题。
由于欧拉模型是最消耗资源的,故此离散相和混合物模型相对更为合适。
•对于中等的加载率,耦合作用成为双向的;就是说,流体通过推动和涡漩影响粒子运动的同时粒子反过来也通过消耗平均动量和涡漩来影响流动。
离散相,混合物和欧拉模型都可以应用于这种情况,但是你需要考虑其他的一些影响因素来决定采用何种模型更为合适。
可利用下文将要介绍的斯托克斯数作为判断的准则。
•对于高加载率,在双向影响的基础上还有粒子压力和由粒子引起的粘性应力的耦合(是四向的耦合)。
只有欧拉模型才能正确的处理此类问题了。
斯托克斯数的重要意义对于具有中等粒子加载率的系统,通过估计斯托克斯数的大小可以帮助你选择合适的模型。
斯托克斯数可以根据粒子响应时间和系统响应时间的关系来定义:(18.4.4)其中,而ts 是根据所考察系统的特征长度(Ls)和特征速度(Vs)来定义的。
对于的情况,对载流而言,粒子将具有很好的跟随性,所以三种模型(离散相,混合物和欧拉模型)都可以采用,于是你可以选择最节省资源的模型(通常为混合物模型),或者根据到其他的因素选择最为合适的。
对于的情况,粒子将独立于流场运动,此时选用离散相模型和欧拉模型比较合适。
对于的情况,三种模型又都可以采用了,可以根据情况选择最节省资源的或者最为合适的的模型。
例子某选矿器,特征长度为1m,特征速度为10m/s,于是对于直径为30微米的粒子,其斯托克斯数为0.04,而对于300微米的粒子,其斯托克斯数为4.0。
