(完整版)初四第一学期期末数学试题.docx
山东2022-2023第一学期初四数学期末考试试题

2022-2023第一学期初四数学期末考试试题一.选择题(每题3分,12道题共36分)1.在﹣1,﹣2,0,0.1这四个数中,最小的数是()A.﹣1B.﹣2C.0D.0.12.一季度,面对国际环境更趋复杂严峻和国内疫情频发带来的多重考验,在以习近平同志为核心的党中央坚强领导下,科学统筹疫情防控和经济社会发展,初步核算,一季度国内生产总值约为27万亿元,按不变价格计算,同比增长4.8%.数据27万亿元用科学记数法表示为()A.2.7×1013元B.2.7×1014元C.0.27×1014元D.27×1012元3.函数的自变量x 的取值范围是()A.x ≥﹣3B.x >﹣3C.x ≥﹣3且x ≠0D.x ≠0且x ≠﹣34.下列说法:①三点确定一个圆,②平分弦的直径垂直于弦,③相等的圆心角所对的弦相等,④三角形的外心到三个顶点的距离相等,⑤弧长相等的弧是等弧;其中正确的有()A.1个B.2个C.3个D.4个5.如图,一个底部呈球形的烧瓶,球的半径为5cm ,瓶内液体的最大深度CD =1cm ,则截面圆中弦AB 的长为()cm .A.4B.6C.8D.8.46.如图,点A ,B ,C 是⊙O 上的三点.若∠AOC =90°,∠BAC =35°,则∠AOB 的大小为()A.10°B.20°C.35°D.40°7.设A (0,y 1),B (-1,y 2),C (2,y 3)是抛物线y =﹣(x +2)2+k 上的三点,则y 1,y 2,y 3的大小关系为()A.y 3>y 2>y 1B.y 2>y 1>y 3C.y 1>y 2>y 3D.y 3>y 1>y 28.飞机着陆后滑行的距离s (米)关于滑行的时间t (秒)的函数解析式是s =60t ﹣1.5t 2,则飞机着陆后滑行到停止下来,滑行的距离为()A.500米B.700米C.600米D.800米9.已知二次函数y =ax 2+bx +c 的图象如图所示,有以下结论:①abc >0;②a ﹣b +c <0;③4a +2b +c >0;④2a =b ;⑤3a +c <0;⑥若实数m ≠1,则a +b >am 2+bm 其中正确结论的个数是()A.1个B.2个C.3个D.4个10.如图,正方形ABCD 、等边三角形AEF 内接于同一个圆,则的度数为()A.15°B.20°C.25°D.30°11.如图,ABC 的内切圆⊙O 与,,AB BC AC 分别相切于点D ,E ,F ,连接OE ,OF ,90C ∠=︒,AC=3,BC=4,则阴影部分的面积为()A.122π-B.142π-C.4π-D.114π-12.如图,正六边形ABCDEF 的边长为12,连接AC ,以点A 为圆心,AC 为半径画弧CE ,得扇形ACE ,将扇形ACE 围成一个圆锥,则圆锥的高为()A.3B.6C.D.2二.填空题(每题3分,8道题共24分)13.计算:(﹣2)0﹣()﹣1+|﹣1|+2sin30°=。
学年度烟台市莱阳第一学期初四期末考试初中数学

2007-2008学年度烟台市莱阳第一学期初四期末考试数学试卷一、选择题(本题共60分,每题5分)答案的四个选项中,只有一个是正确的。
1.已知α为锐角,且cos (90°-α)=21,则cos α等于A .30°B .60°C .21D .23 2.某水池现有水100m 3,每小时进水20m 3,排水15m 3,t 小时后水池中的水为Qm 3,它的解析式为 A .Q=100+20t B .Q=100—15t C .Q=100+5tD .Q=100—5t3.将抛物线221x y =作适当的移动后就可以得到抛物线3212-=x y ,那么下面移动正确的是A .向上平移3个单位B .向下平移3个单位C .向右平移3个单位D .向左平移3个单位4.如图,∠BAC=35°,∠EDC=50°,则∠BOE 的度数为A .85°B .135°C .170°D .175°5.大圆的半径是小圆的半径的2倍,当两圆内切时,圆心距为3cm ,那么这两圆外切时,圆心距为A .6cmB .9cmC .12cmD .18cm6.若扇形的圆心角是150°,扇形的面积是240πcm 2,那么该扇形的弧长是A .5πcmB .10πcmC .20πcmD .40πcm7.若二次函数c=2,当x取x l,x2(x l≠x2)时,函数值相等,那么当axy+x取x l+x2时,函数值为A.c B.一c C.a—c D.a+c8.根据如图的程序,计算当输入值x=-2时,输出结果y为A.1 B.5 C.7 D.以上都有可能9.若∠A为锐角,则下列三角函数值可能为2的是A.sinA B.sin2A C.cosA D.tanA 10.甲、乙、丙三个梯字斜靠在同一堵墙上(梯子顶端靠墙),小明测得甲与地面的夹角为60°;乙的底端距离墙脚移3米,顶端距离墙脚3米;丙的坡度为3,那么这三个梯子的倾斜程度是A.甲较陡B.乙较陡C.丙较陡D.一样陡11.如图,一个含有30°角的直角三角板ABC,在水平桌面上绕点C按顺时针方向旋转到△A’B’C的位置,若BC的长为15cm,那么AA’的长为A.103cm B.153cmC.303cm D.30cm12.如图,已知正方形ABCD的边长为I,E,F,G,H分别为各边上的点,且AE=BF=CG=DH,设小正方形EFGH的面积为S,AE=x,则S关于x的函数图象大致为二、填空题(本题共30分,每题5分)13.在R t △ABC 中,∠C=90°,已知c ,∠A ,求b 的关系式为_______ 14.抛物线1)1(22+--=x y 的顶点坐标为_______15.在⊙O 中,直径AB=4,弦CD ⊥AB ,垂足为E ,若OE=3,则CD 的长为_______16.在R t △ABC 中,∠C=90°,△ABC 的面积为24cm 2,斜边长为10cm ,则tanA+tanB 的值为_______17.如图,是中央电视台大风车栏目的图标,其中心为O ,半圆ACB 的半径为2r ,车轮为中心对称图形,轮片也是半圆形,那么车轮旋转至如图位置时,留在半圆ACB 内的轮片面积为_______18.已知二次函数3)(32+-=m x y ,当4>x 时,y 随x 的增大而增大;当x <4时,y 随x 的增大而减小,则m 为_______ 三、解答题(共60分) 19.(本题8分)自由落体运动是由于地球引力的作用造成的,在地球上,物体自由下落的时间t (秒)和下落的距离h (米)之间的关系是h=4.9t 2. (1)求一物体从高空下落3秒时,下落的距离是多少?(2)求物体下落10米所需要的时间. 20.(本题10分)如图,小河边有一棵树AB ,在小河对岸C 处用高为1米的测角仪测得树顶A 的仰角为60。
第一学期初四期末检测数学试卷

第一学期初四期末检测数学试卷说明:考试时间120分钟,满分150分。
一、选择题(本题共14小题,在每小题所给出的四个选项中,只有一个是正确的,请把正确的选项选出来。
每小题4分,共56分,错选、不选或选出的答案超过一个,均记0分) 1.抛物线32+=x y 的顶点是A .(3,0)B .(-2,3)C .(2,-3)D .(0,3)2.已知α为锐角,且23sin =α,则α等于 A .30°B .45°C .60°D .90°3.在△ABC 中,∠C=90°,AC=2,AB=3,则B sin 等于A .35B .23C .43 D .32 4.已知抛物线12--=x x y 过点(m ,-1),则20082+-m m 的值为A .2006B .2007C .2008D .20095.在一个晴朗的上午,小丽拿着一块矩形木板在阳光下做投影实验,矩形木板在地面上形成的投影不可能是6.一直角三角形的两直角边分别为3和4,则较小角的正切值为A .43B .34 C .54 D .53 7.如下图,在平地上植树时,要求株距(相邻两树间的水平距离)为4m .如果在坡度为0.5的山坡上植树,也要求株距为4m ,那么相邻两树间的坡面距离为A .52mB .5mC .2mD .8m8.在同一直角坐标系中,函数m mx y +=和222++-=x mx y (m 是常数,且0≠m )的图像可能是9.已知,在△ABC 中,∠C=90°,∠A=30°,AC 32=,则AB 的长是A .2B .3C .4D .510.下列结论正确的是A .弦是直径B .圆外一点到圆心的距离等于半径C .垂直于直径的直线是圆的切线D .三角形的内心是三条角平分线的交点11.若A (-2,1y ),B (0,2y ),C (1,3y )为二次函数542-+=x x y 的图像上的三点,则321y y y ,,的大小关系是 A .312y y y << B .321y y y <<C .213y y y <<D .231y y y <<12.下列结论正确的是A .过不在同一直线上的四个点确定一个圆B .经过三个点一定可以作圆C .过不在同一直线上的三个点确定一个圆D .三角形的外心到三边的距离相等13.一个圆锥的底面半径为3,母线长5,则圆锥的侧面积是A .π24B .π15C .π30D .π5.2214.如下图,在平面直角坐标系中,四边形OABC 为正方形,顶点A 、C 在两坐标轴上,以边AB 为弦的⊙M 与x 轴相切,若点A 的坐标为(0,8),则圆心M 的坐标为A .(4,5)B .(-5,4)C .(-4,6)D .(-4,5)二、填空题(本题共7小题,每小题4分,共28分,只要求填写最后结果)15.边长为2的正方形,若边长增加x ,则正方形的面积S 与x 之间的函数关系为__________。
初四第一学期期末学业水平测试数学试卷

初四第一学期期末学业水平测试数学试卷一、选择题(本题共12小题,在每小题所给出的四个选项中,只有一个是正确的,每小题3分,共36分,错选、不选或选出的答案超过一个,均记0分) 1.如下图,在Rt △ABC 中,23B tan =,32BC =,则AC 等于A .3B .4C .34D .62.把抛物线2x y =向右平移2个单位得到的抛物线是A .22+=x yB .22-=x yC .2)2(+=x yD .2)2(-=x y3.二次函数c bx ax y ++=2)0(≠a 的图像如下图所示,当0<y 时,x 的取值范围是A .31<<-xB .3>xC .1-<xD .3>x 或1-<x4.桌面上放着1个长方体和1个圆柱体,按下图所示的方式摆放在一起,其左视图是5.下列图形中的曲线不表示y 是x 的函数的是6.二次函数c bx ax y ++=2)0(≠a 的图像如下图所示,则下列结论:①0>ac ;②0>b ;③042>-ac b ,其中正确的个数是A .0个B .1个C .2个D .3个7.如下图,在⊙O 中,AB 是弦,OC ⊥AB ,垂足为C ,若AB=16,OC=6,则⊙O 的半径OA 等于A .16B .10C .12D .88.下列说法正确的是A .垂直于半径的直线是圆的切线B .过三点A 、B 、C 一定可以确定一个圆 C .平分弦的直径垂直于弦D .相等的弦所对的弧不一定相等9.一个函数的图像如下图,给出以下结论:①当0=x 时,函数值最大;②当20<<x 时,函数y 随x 的增大而减小;③存在100<<x ,当0x x =时,函数值为0。
其中正确的结论是 A .①②B .①③C .②③D .①②③10.如下图,正方形ABCD 中,E 是BC 边上一点,以E 为圆心、EC 为半径的半圆与以A 为圆心,AB 为半径的圆弧外切,则EAB sin ∠的值为A .34B .43 C .54 D .53 11.若同一个圆的内接正三角形、正方形、正六边形的边心距分别为643r r r ,,,则643::r r r等于A .3:2:1B .1:2:3C .1︰2︰3D .3︰2︰112.如下图,路灯距地面8米,身高1.6米的小明从距离灯的底部(点O )20米的点A 处,沿AO 所在的直线行走14米到点B 时,人影长度A .变长3.5米B .变短3.5米C .变长2.5米D .变短2.5米二、填空题(本题共5小题,满分20分,只要求填写最后结果,每小题填对,得4分) 13.一名滑雪运动员从坡比为1︰5的山坡上滑下.如果这名运动员滑行的距离是150米,那么他下滑的高度是_________米(用精确值表示)。
上学期期末初四数学试题附答案

A. 0.4x100B 0.9x1011C.3.9x1013D. 0.39x1014
姓名
班级
初中初四学年上学期期末质考试
数学试题
题分
一
二
三
总分
得分
19
20
21
22
23
24
25
26
27
28
考生注意:1.考试时间120分钟。
2.全卷共三道大题,28个小题,总分120分。
一.选择题(本大题共10小题,每小题3分,共30分,在每小题所给出的四个选项中,只有一项是符合题目要求的,请将正确选项的序号填在后面的括号里)
(1)求n,k的值;(2)若抛物线y=x2-2mx+m2+m+1的顶点在反比例函数
y= 的图象上,求这条抛物线的顶点坐标.
23.(8分)如图,从地面上的点A看一山坡上的电线杆PQ,测得杆顶端点P的仰角是45°,向前走6 m到达B点,测 得杆顶端点P和杆底端点Q的仰角分别是60°和30°.(1)求∠BPQ的度数;(2)求该电线杆PQ的高度.
16.如图,直线y=mx+n与抛物线y=ax2+bx+c交于A(﹣1,p),B(4,q)两点,则关于x的不等式mx+n>ax2+bx+c的解集是.
(16题图) (17题图) (18题图)
17.如上图AB是⊙O的直径AC是⊙O的弦,过点C作⊙O的切线交AB的延长线于D,∠A=∠D,CD=3,则图中阴影部分的面积_______
初四上学期期末数学试题
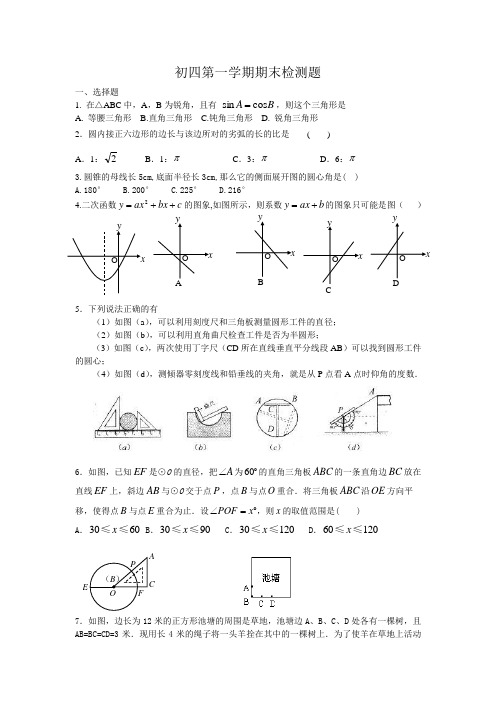
初四第一学期期末检测题一、选择题1. 在△ABC 中,A ,B 为锐角,且有 B A cos sin =,则这个三角形是A. 等腰三角形B.直角三角形C.钝角三角形D. 锐角三角形2.圆内接正六边形的边长与该边所对的劣弧的长的比是 ( )A .1:2B .1:πC .3:πD .6:π3.圆锥的母线长5cm,底面半径长3cm,那么它的侧面展开图的圆心角是( )A.180°B.200°C.225°D.216°4.二次函数c bx ax y ++=2的图象,如图所示,则系数b ax y +=的图象只可能是图( )5.下列说法正确的有(1)如图(a ),可以利用刻度尺和三角板测量圆形工件的直径;(2)如图(b ),可以利用直角曲尺检查工件是否为半圆形;(3)如图(c ),两次使用丁字尺(CD 所在直线垂直平分线段AB )可以找到圆形工件的圆心;(4)如图(d ),测倾器零刻度线和铅垂线的夹角,就是从P 点看A 点时仰角的度数.6.如图,已知EF 是⊙O 的直径,把A ∠为60 的直角三角板ABC 的一条直角边BC 放在直线EF 上,斜边AB 与⊙O 交于点P ,点B 与点O 重合.将三角板ABC 沿OE 方向平 移,使得点B 与点E 重合为止.设POF x ∠= ,则x 的取值范围是( )A .3060x ≤≤B .3090x ≤≤C .30120x ≤≤D .60120x ≤≤7.如图,边长为12米的正方形池塘的周围是草地,池塘边A 、B 、C 、D 处各有一棵树,且AB=BC=CD=3米.现用长4米的绳子将一头羊拴在其中的一棵树上.为了使羊在草地上活动A区域的面积最大,应将绳子拴在( )。
A . A 处B . B 处C .C 处D .D 处8.如图,在△ABC 中,BC =4,以点A 为圆心、2为半径的⊙A 与BC 相切于点D ,交AB 于E ,交 AC 于F ,点P 是⊙A 上的一点,且∠EPF =40°,则图中阴影部分的面积是( )。
初四第一学期期末数学试题

初四第一学期期末数学试题(第Ⅰ卷)一、 选择题(每小题3分,共60分)1、下列函数中,y 是x 的反比例函数的是( )A 、 1)1(=-y xB 、11+=x yC 、21xy = D 、 x y 31=2、若A (-3,y 1),B (-2,y 2),C (1,y 3)三点都在函数y =-x1的图象上,则y 1,y 2,y 3的大小关系是( ).A 、y 1>y 2>y 3B 、y 1<y 2<y 3C 、y 1=y 2=y 3D 、y 3<y 1<y 2 3、若反比例函数22)12(--=mx m y 的图象在第二、四象限,则m 的值是( )A 、 -1或1B 、小于21的任意实数 C 、 -1 D、 不能确定 4、在Rt △ABC 中∠C=90°,BC=2,AB=22 ,则∠A=( )A.30° B.45° C.60° D.90° 5、下列命题是真命题的是( )A .垂直于圆的半径的直线是圆的切线B .经过半径外端的直线是圆的切线C .直线上一点到圆心的距离等于圆的半径的直线是圆的切线D .到圆心的距离等于圆的半径的直线是圆的切线6、如图,在两建筑物之间有一旗杆,高15米,从A 点经过旗杆顶点恰好看到矮建筑物的墙角C 点,且俯角α为60º,又从A 点测得D 点的俯角β为30º,若旗杆底点G 为BC 的中点, 则矮建筑物的高CD 为( )A .20米B .103米C .153米D .56米7、 抛物线22(1)3y x =+-的顶点坐标是( )A .(1,3)B .(-1,3)C .(1,-3)D .(-1,-3) 8、一个不透明的袋子里装有2个黑球,2个白球,这些球除颜色外其余都完全相同。
小明同学做摸球试验,将球搅匀后,从中随机摸出一个球,记下它的颜色后不放回袋中, 然后再重复进行下一次试验,当摸球次数很大时,摸到两个白球的概率为( ) A .21B .31 C .41 D . 619、在同一坐标系中,函数xky =和 ( )A B C D10、二次函数y =mx 22-m 有最低点,则m =( ). A 、2 B 、 2 C 、﹣2 D 、±2 11、下列几何体,主视图和俯视图都为矩形的是( )A .B .C .D .12、如图AC 是电杆AB 的一根拉线,测得BC=6米,∠ACB=52°,则拉线AC 长为 ( )A.︒526sin 米 B. ︒526tan 米 C. 6·cos52°米 D. ︒526cos 米13、如图,抛物线y=﹣2x 2+8x ﹣6与x 轴交于点A 、B ,把抛物线在x 轴及其上 方的部分记作C 1,将C 1向右平移得C 2,C 2与x 轴交于点B ,D .若直线y=x+m 与C 1、C 2共有3个不同的交点,则m 的取值范围是( )BA C 北东ABC ┐A.﹣2<m <B.﹣3<m <﹣C.﹣3<m<﹣2 D.﹣3<m<﹣14、已知α为锐角,tan(90°-α)=3,则α的度数为()A.75°B.60°C.45°D.30°15.在同一坐标系中一次函数y ax b=+和二次函数2y ax bx=+的图象可能为()16、已知抛物线的顶点为(-1,-2),且通过(1,10),则这条抛物线的表达式为()A.y=32(1)x--2 B.y=32(1)x++2 C.y=32(1)x+-2 D.y=-32(1)x+-2 17、如图是二次函数y=ax2+bx+c图象的一部分,图象过点A(-3,0),对称轴为x=-1.给出四个结论:①b2>4ac;②2a+b=0;③a-b+c=0;④5a<b.其中正确结论是().A.②④ B.①④ C.②③ D.①③18、如图,△OAB中,C是AB的中点,反比例函数xky=(k>0)在第一象限的图象经过A、O xyO xyO xyO xy AC 两点,若△OAB 面积为6,则k 的值为( ) A 、2B 、4C 、6D 、819、若y 与-3x 成反比例,x 与z4成正比例,则y 是z 的( ) A 、 正比例函数 B 、 反比例函数 C 、 一次函数 D 、 不能确定20、如图,AB 、CD 是⊙O 的直径,⊙O 的半径为R ,AB ⊥CD ,以B 为圆心,以BC为半径作弧CED ,则弧CED 与 弧CAD 围成的新月形ACED 的面积为 ( )平方单位.A 、()21R -π B 、2R C 、()21R +π D 、2R π(请将你认为正确的选项填入第Ⅱ卷选择题相应答案栏内)ACDE O初四第一学期期末数学试题(第Ⅱ卷)一 二2526272829总分题号 1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 答案二. 填空题(每小题3分,共12分)21、如图,正方形ABOC 的边长为2,反比例函数y =kx 的图象经过点A , 则k 的值是22、如图,在圆内接四边形ABCD 中,O 为圆心,∠BOD=160°,则∠BCD= 度. 23、将抛物线3)3(22+-=x y 向右平移2个单位后,再向下平移5个单位后所得抛物线表达式为_______ 。
初四期末数学试题及答案

初四期末数学试题及答案一、选择题(每题3分,共30分)1. 下列哪个数是最小的正整数?A. -1B. 0C. 1D. 2答案:C2. 计算下列表达式的结果:\[ \frac{2}{3} + \frac{1}{2} \]A. 1B. \(\frac{7}{6}\)C. \(\frac{5}{6}\)D. \(\frac{4}{3}\)答案:B3. 一个圆的半径是5厘米,那么它的面积是多少平方厘米?A. 25B. 50C. 100D. 200答案:C4. 一个等腰三角形的底角是45度,那么它的顶角是多少度?A. 45B. 90C. 135D. 180答案:B5. 下列哪个选项表示的是一次函数?A. \(y = 3x + 2\)B. \(y = 3x^2 + 2\)C. \(y = \frac{1}{x}\)D. \(y = x^2 + 3x + 2\)答案:A6. 一个数的平方根是4,那么这个数是多少?A. 16B. -16C. 4D. -4答案:A7. 一个长方体的长、宽、高分别是2厘米、3厘米、4厘米,那么它的体积是多少立方厘米?A. 24B. 12C. 8D. 6答案:A8. 一个数的绝对值是5,那么这个数可以是下列哪个?A. 5B. -5C. 5和-5D. 0答案:C9. 计算下列表达式的结果:\[ 3^2 - 2^3 \]A. 1B. 5C. 7D. 9答案:B10. 一个直角三角形的两条直角边分别是3厘米和4厘米,那么它的斜边是多少厘米?A. 5B. 6C. 7D. 8答案:A二、填空题(每题4分,共20分)1. 一个数的立方是-27,那么这个数是______。
答案:-32. 一个数的倒数是\(\frac{1}{4}\),那么这个数是______。
答案:43. 一个数的平方是25,那么这个数是______。
答案:±54. 一个数的绝对值是8,那么这个数可以是______。
答案:8或-85. 一个数的平方根是2.5,那么这个数是______。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
箱.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8分
8
22.解:(1)CD的延 交MN于E点,MN
xm,ME
( x
1.6)m.
∵
450,∴DE ME x
1.6.∴CE
x 1.6
18.6 x
17 .
∵ME
tantan 350,∴x
1.6
数学试题
第Ⅱ卷 (非选择题共84分)
二、填空题:
13.分解因式:ax2a.
14.
已知两圆的半径分别是2和3,圆心距为6,那么这两圆的位置关系是
.
15.
在等腰梯形
ABCD中,AD∥BC
AD=
3cm,
AB=
4cm,
∠B=°
,
则下底BC的长为
,
60
cm .
y
16.
如图,⊙A和⊙B都与x轴和y轴相切,圆心A
∴OA在旋 程中所 的面
45
22
.⋯⋯⋯⋯⋯4分
360
2
(2)解:∵MN∥AC,
∴
BMN
BAC 45 ,
BNMBCA
45
.
∴
BMN
BNM .∴BM BN.
又∵BA
BC,∴AM
CN .
又∵OA
OC , OAM
OCN ,∴OAM
OCN .
10
∴AOMCON .∴AOM1(90 45.
2
∴旋 程中,当MN和AC平行 ,正方形OABC旋 的度数
有
个 .
第1个第2个第3个
(第18题)
三、解答题:
19.(6分)
计算:(π-1)°+(1)
1+5-27-23.
2
20.(6分)
解方程:x
3
1
3
.
x
2
2 x
3
21.(8分)
作为一项惠农强农应对当前国际金融危机、拉动国内消费需求的重要措施, “家电下乡”工作已经国务院批准从2008年12月1日起在我市实施.我市某家电公司营销点自去年12月份至今年5月份销售两种不同品牌冰箱的数量如下图:
A. 2 cm
2
B. 4 cm
2
C. 8 cm
2
D. 16 cm
2
(第7题)
8.已知a为实数,那么
a2
等于
A.a
B.
a
C.-1
D. 0
9.将一正方形纸片按下列顺序折叠,然后将最后折叠的纸片沿虚线(直角三角形的中位线)剪去上面的小直角三角形.
1
将留下的纸片展开,得到的图形是
ABCD
10.“赵爽弦图”是四个全等的直角三角形与中间一个小正方形拼成的大正方形
.
NP的长为am(如图2),你能
;
23.(8分)
阅读下面的材料:
在平面几何中,我们学过两条直线平行的定义.下面就两个一次函数的图象所确定的两条直线,
给 出 它 们 平 行 的 定 义 : 设 一 次 函 数y k1x
b1(k1
0)的 图 象 为 直 线l1, 一 次 函 数
y k2x b2(k20)的图象为直线l2,若
和圆心
B都在反比例函数y
1的图象上,则图中阴影部
A
分的
.
x
O
x
面积等于
B
17.
请你阅读下面的诗句:“栖树一群鸦,鸦树不知
数,三
只栖一树,五只没去处,五只栖一树,闲了一棵
(第16题)
树,请你仔细数, 鸦
树各几何?”
诗句中谈到的鸦为
只、
树为
棵.
18.观察图中每一个大三角形中白色三角形的排列规律,则第
5个大三角形中白色三角形
A
的延长
D
C150°
(第2题)
A.93B.(a2)3a6C.3a 2a6aD.326
4.山东省地矿部门经过地面磁测,估算济宁磁异常铁矿的内蕴经济资源量为
10 800 000 000
吨.
这个数据用科学记数法表示为
A. 108
×108吨
B. 10 .8
×109吨
C. 1 .08
×10
10吨
D. 1 .08
×10
11吨
5.下列图形中,既是轴对称图形又是中心对称图形的是(
)
A.
B
.
C
.
D
.
(
第5题)
6.在函数y
1
中,自变量x的取值范围是
x
3
A、x≠0
B、x>3 C
、x≠ -3
D、x≠3
7.如图,在长为8 cm、宽为4 cm的矩形中,截去一个矩形,使得留下
的矩形(图中阴影部分)与原矩形相似,则留下矩形的面积是()
初四第一学期期末数学试题
出题人:
一、选择题(下列各题的四个选项中,只有一顶符合题意,每小题
1.2的倒数是
A.
1
B.
-1
C.2D.
-2
2
2
2.如图,△ABC中,∠A=70°,∠B=60°,点D在BC
线上,
则∠ACD等于
B
A. 100°
B. 120°C. 130°
D.
3.下列运算中,正确的是
3分,共36分)
y
正方形
OABC旋转的度数;
y x
(3)设MBN的周长为p,在旋转正方形
A
OABC
M
的过程中,p值是否有变化?请证明你的
B
结论.
O
N
x
C
(第26题)
7
数学 参考答案及 分 准
一、
号123456789101112
ACBCDDCDACBC
二、填写
13.a( x 1)( x 1)14.外离15.7 16.
2
∵t>0,∴tf 0.
-2
O2
46x
2
∴C点在x的正半 上.
当C点在B点的左,
-2
(第23题)
S
1(3
t) 6 9
3t;
2
2
2
1
t
3t
当C点在B点的右 ,
.
S
(3)6
9
2
2
2
∴△ABC的面S关于t的函数表达式
9
3t
p t p 6),
(0
S
2
⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8分
3t
9(t
f 6).
2
24.(1)解:当⊙P在移 中与AB相切 , 切点M,PM,
π17. 20,5 18.121
三、解答
19.解:原式=1+2+(27-5)-23⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
=3+33-5-23⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯5分
=3-2.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6分
20.解:方程两 同乘以(x-2),得⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯1分
x-3+(x-2)=-3.
45.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯8分
(3)答:p无 化.
明:延BA交y于E点,AOE450AOM,
CON900450AOM450AOM,
∴AOECON .
又∵OAOC,OAE1800900900OCN.
∴OAEOCN .
∴OE ON,AE CN.
又∵MOEMON450, OMOM ,
∴OMEOMN .∴MNMEAMAE.
3
3
12.
5
5
∵ADP∽ABC,∴PD
AP.∴PD
16
5,
BC
AC
3
4
∴PD
12.∴PD
BE.
5
∴当t
16
s,四 形PDBE平行四 形.
⋯⋯⋯⋯⋯9分
5
25.解:(1)(130-100)×80=2400(元);⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯4分
(2) 将售价定
x元, 售利
y (x 100)(80
130
x
∴MN AM CN,
∴p MN BN BM AM CN BN BM AB BC 4.
∴在旋 正方形OABC的 程中,p无 化.⋯⋯⋯⋯⋯12分
y
E
yx
A
M
B
O
N
x
C
(第26题)
11
点C,求出△
ABC的面积S关于t的函数表达式.
24.(9分)
5
如图,ABC中,C900,AC4,BC3.半径为1的圆的圆心P以1个单位/s的速度由
点A沿AC方向在AC上移动,设移动时间为t(单位:s).(1)当t为何值时,⊙P与AB相切;
(2)作PD
AC交AB于点D,如果⊙P和线段BC交于点E,证明:当t
y
k1
k2,且b1
b2,
我们就称直线l1与直线l2互相平行.
6
解答下面的问题:
4
(1)求过点P(1,4)且与已知直线
2
y
2x 1
平 行
的直线l的函数表达式,并画出直线l的
图象;
-2
O
24
6x
(2)设直线l分别与y轴、x轴交于点A、
B,如果直线m:
-2
y kx t (t 0)与直线l平行且交x轴于
(第23题)
分
5
20)⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯6
4x2
1000 x
60000
4( x
125)2
2500.⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯⋯
8分
当x 125,y有最大2500.
