系统的状态变量分析法共47页文档
质点动量定理.pptx

1
Yc m
1 yCdm m
R
0 y边 (2x边dy边)
1 R
m
0
y边 (2
R2
y边2 dy边 )
4R 3π
dy边
yC
y边
即质心位置为
0,
4R 3π
。
8
第9页/共47页
(4) 多个规则形状物体组成系统的质心 多个规则形状物体组成系统的质心,可先找到每
个物体的质心,再用分立质点系质心的求法,求出公 共质心。
它们置于一质量也为 m 的槽的底部。槽置于光滑的水
平面上。释放后,球最终静止于槽的底部,问此时槽移
动了多远?
解:水平方向动量守恒,质心位置不变
xC0 xC
xC 0
2m 0 3m
mR
3mx xC 3m
解得: x 1 R 0 向右移动
3 27 第28页/共47页
例4.1.2-2 一物体在光滑水平面上以 5m/s的速度沿 x
由牛顿第二定律原始表达式:
对上式积分得:
F d(mv) dt
定义:
t t
Fdt mv(t t) mv(t) t P mv 称为质点的动量
tt
I Fdt
称为力在 t 时间内的冲量
t
质点的动量定理: 外力冲量等于质点动量的改变量
16
第17页/共47页
例4.2.1-1 一质量为 0.15 千克的棒球以 v0 40m/s 的
(3)
1
yc
mA yA mB yB mD yD mA mB mD
4mD (2) 2mD (1) mD (8) 4mD 2mD mD
2
zc
mA zA mB zB mD mA mB mD
2024年大数据应用及处理技术能力知识考试题库与答案

2024年大数据应用及处理技术能力知识考试题库与答案一、单选题1.当图像通过信道传输时,噪声一般与()无关。
A、信道传输的质量B、出现的图像信号C、是否有中转信道的过程D、图像在信道前后的处理参考答案:B2.在留出法、交叉验证法和自助法三种评估方法中,()更适用于数据集较小、难以划分训练集和测试集的情况。
A、留出法B、交叉验证法C、自助法D、留一法参考答案:C3.在数据科学中,通常可以采用()方法有效避免数据加工和数据备份的偏见。
A、A/B测试B、训练集和测试集的划分C、测试集和验证集的划分D、图灵测试参考答案:A4.下列不属于深度学习内容的是(_)oA、深度置信网络B、受限玻尔兹曼机C、卷积神经网络D、贝叶斯学习参考答案:D5.在大数据项目中,哪个阶段可能涉及使用数据工程师来优化数据查询性能?A、数据采集B、数据清洗C、数据存储与管理D、数据分析与可视化参考答案:C6.假定你现在训练了一个线性SVM并推断出这个模型出现了欠拟合现象,在下一次训练时,应该采取下列什么措施()A、增加数据点B、减少数据点C、增加特征D、减少特征参考答案:C7.两个变量相关,它们的相关系数r可能为0?这句话是否正确0A、正确B、错误参考答案:A8.一幅数字图像是()。
A、一个观测系统B、一个由许多像素排列而成的实体C、一个2-D数组中的元素D、一个3-D空间中的场景参考答案:C9.以下说法正确的是:()。
一个机器学习模型,如果有较高准确率,总是说明这个分类器是好的如果增加模型复杂度,那么模型的测试错误率总是会降低如果增加模型复杂度,那么模型的训练错误率总是会降低A、1B、2C、3D、land3参考答案:c10.从网络的原理上来看,结构最复杂的神经网络是0。
A、卷积神经网络B、长短时记忆神经网络C、GRUD、BP神经网络参考答案:B11.LSTM中,(_)的作用是确定哪些新的信息留在细胞状态中,并更新细胞状态。
A、输入门B、遗忘门G输出门D、更新门参考答案:A12.Matplotiib的核心是面向()。
连续控制部分第五章状态反馈与观测

有关系数 的选择
从收敛性的观点出发,特征值实部绝对值希望取得大一点。 但是,实部变大的时候,输入也要变大等问题也就出现了。 并且,当系统发生变化的时候,稳定性的保持问题也会出现。(鲁棒、稳定性)
收敛性
输入的大小
最优控制 鲁棒控制
鲁棒稳定性 其他需要考虑的特性
更加一般的鲁棒 Advanced control 。。。。。。。
输出反馈: u = Ky + Gv
闭环系统: x ( A BKC)x BGv y Cx
x Ax Bv y Cx Du ( A A BKC, B BG)
因为静态输出反馈很难实现极点的自由配置,提出了动态输出反馈的概念 → 「状态反馈」 + 「状态观测」
观测器(概念)
状态观测器(状态估计):状态x不能被直接地观测或者测量的时候,通过系统 输出y 和系统输入 u 对系统状态x 进行估计或者推测所构建的模型。
设计坐标变换矩阵T:
p
T
pA
pAn1
坐标变换后的能控性 矩阵
0 0 1
可以得到、 rank{T b
Ab
An1b } rank0
1 *
* *
n
1
* *
因此T是一个正则矩阵。
得到闭环系统:
x ( A BF)x BGv
0 0 0
1 12
0
0 0
1
0 1000
6 1
~x 是x 的估计値 该拷贝模型不能保证初期推测误差收敛到0。所以引入系统输出差:
~y y C~x y
可以修正控制对象的直接拷贝模型的运动。
全维状态观测器:
~x A~x Bu K(C~x y) ~y C~x
演示文稿信号与系统
第59页,共128页。
2.13 在如题图2.7所示电路中,试分别求出响应i1(t)、 i2(t)、i3(t)对激励f(t)的传输算子H1(p)、H2(p)、H3(p)。
题图 2.7
第60页,共128页。
解 画出算子模型,并标记网孔电流i1、i2和i3如题解图 2.13所示。列出网孔方程:
第37页,共128页。
(3) 因为ε(-∞)=0, 故有 所以
第38页,共128页。
(4) 由于tε(t)|t=-∞=0,有 所以
第39页,共128页。
2.8 已知f1(t)和f2(t)如题图2.4所示。设f(t)=f1(t)*f2(t),试求 f(-1)、f(0)和f(1)的值。
题图 2.4
其一、二阶导函数为 代入初始条件,整理得
第72页,共128页。
联立求解得 最后得系统零输入响应为
第73页,共128页。
2.16 如题图2.9所示电路。已知iL(0-)=0, uC(0-)=1 V, C=1 F, L=1 H, 求i(t)(t>0)。
题图 2.9
第74页,共128页。
解 算子电路模型如题解图2.16所示。列出回路KVL方程, 并代入元件参数,得
解 设连续系统的输入为f(t), 输出为y(t)。 (1) 因为系统传输算子 算子方程 所以系统微分方程为
第48页,共128页。
(2) 因为系统传输算子 算子方程 所以系统微分方程为
第49页,共128页。
(3) 因为系统传输算子 算子方程 所以系统微分方程为
第50页,共128页。
(4) 因为系统传输算子 算子方程 或写成 所以,系统微分方程为
第100页,共128页。
(3) 当f(t)=e-3tε(t)时,有零状态响应: 系统全响应:
状态方程_电路分析基础_[共2页]
![状态方程_电路分析基础_[共2页]](https://img.taocdn.com/s3/m/df1756bea45177232e60a211.png)
第13章 电路方程的矩阵形式 277思考与练习13-5-1 列写割集电压方程的矩阵形式的步骤是什么?13-5-2 节点电压方程和割集电压方程有何区别和联系?13.6 状态方程一、状态和状态变量状态是指电路在任何时刻所必需的最少信息,它们和自该时刻以后的输入(激励)足以确定该电路的性状。
选定系统中一组最少数量的变量X = [x 1,x 2,…,x n ]T ,如果当t =t 0时这组变量X (t 0)和 t ≥t 0后的输入为已知,就可以确定t 0及t 0以后任何时刻系统的响应。
称这一组最少数目的变量为状态变量。
状态变量是描述电路的一组最少数目的独立变量,如果某一时刻这组变量已知,且自此时刻以后电路的输入亦已知,则可以确定此时刻以后任何时刻电路的响应。
状态变量是电路的一组独立的动态变量,它们在任何时刻的值组成了该时刻的状态,如独立的电容电压(或电荷),电感电流(或磁通链)就是电路的状态变量。
二、状态方程称描述输入信号和状态变量之间的关系的一阶微分方程为状态方程,其解是待求的状态变量。
借助于状态变量,建立一组联系状态变量和激励函数的一阶微分方程组。
只要知道状态变量在某一时刻0t 的值0()X t ,再知道输入激励,就可以确定0t t >后电路的全部性状(响应)。
在每个状态方程中只含有一个状态变量的一阶导数。
状态方程的标准形式如下:x =+ Ax Bv (13-28)式(13-28)又称为向量微分方程。
其中,x 称为状态向量,它的分量21x x 、是状态变量,v 称为输入向量。
在一般情况下,设电路具有n 个状态变量,m 个独立源,A 和B 是常数矩阵。
A 为n×n 方阵,B 为n×m 矩阵。
三、状态方程的列写列写电路状态方程有直观法和系统法两种方法。
前者适用于简单电路,后者适用于复杂电路。
1.直观法对于简单的网络,用直观法比较容易,列写状态方程的步骤如下。
(1)状态变量的选择:选择独立的电容电压和电感电流作为状态变量。
第2章 2-1物理系统的微分方程

共计58页
20
此外,在工程实践中,控制系统都有一 个额定的工作状态和工作点,当变量在 工作点附近作小范围的变化,且变量在给 定的区域间有各阶导数时,便可在给定 工作点的邻域将非线性函数展开为泰勒 级数,忽略级数中高阶无穷小项后,就 可得到只包含偏差的一次项的线性方程。 这种线性化方法称为小偏差法。
共计58页 21
例如,设非线性函数y=f(x)如图所示, 其输入量为x,输出量为y,如果在给定工 作点y0=f(x0)处各阶导数均存在,则在 y0=f(x0)附近将y展开成泰勒级数:
共计58页
22
如果偏差Δx=x-x0很小,则可忽略级数中高阶无穷小项, 上式可写为
K表示y=f(x)曲线在(x0,y0)处切线的斜率。因此非线性函数在工作点处可以用该点 的切线方程线性化。
N1
2
(2 - 9)
[ f f ( N 1 ) 2 ] ( N 1 )T T [J1 J 2 ( ) ] 1 1 2 1 L M N2 N2 N2 N2 N 2 N 2 2 ) J 1 J 2 ]2 [ f 1 ( 2 ) f 2 ]2 T L ( 2 ) T M N1 N1 N1
共计58页
24
附录: 用拉普拉斯变换求解线性微分方程
建立了系统的微分方程以后,对微分方程求解 就可以得到表示系统动态性能的时间响应。微分方 程的求解可以用经典方法或借助于计算机进行,也 可以采用拉普拉斯变换法。 一、拉普拉斯变换定义:设有函数f (t), t为实变量, s=ζ+jω为复变量。 如果线性积分
共计58页 1
第二章 控制系统的数学模型
§2.1物理系统的微分方程 §2.2传递函数 §2.3系统框图及其简化 §2.4典型信号分析 §2.5信号流程图 §2.6线性系统的状态方程
第二章双闭环直流调速系统

•系统原理图
+
RP1 Un R0
-
R0
Ufn
-
Rn Cn
U+fi
R0
ASR
-
+
+
Ui
LM
R0
-
TA
Ri Ci
L
ACR
LM GT
-
+
+
Uc
V
Id
UPE +Ud
MM
+TGG -
双闭环直流调速系统电路原理图
第15页/共199页
调节器输出限幅值的整定
图中表出,两个调节器的输出都是带限 幅作用的。
(2) 转速调节器饱和
这时,ASR输出达到限幅值Uim ,转速外环呈 开环状态,转速的变化对系统不再产生影响。双 闭环系统变成一个电流无静差的单电流闭环调节 系统。稳态时
Id
Uim
Idm
式中,最大电流 Idm 是由设计者选定的,取决于 电机的容许过载能力和拖动系统允许的最大加速 度。
第36页/共199页
第28页/共199页
2.2 双闭环调速系统的稳态结构图及其静特 性
为了分析双闭环调速系统的静特性,必须先绘出它的稳态结构图, 如下图。它可以很方便地根据上图的原理图画出来,只要注意用带限幅的输 出特性表示PI 调节器就可以了。分析静特性的关键是掌握这样的 PI 调节器 的稳态特征。
第29页/共199页
第11页/共199页
1. 系统的组成
TA
L
内环
Un +-
Ufi
V
Ui ASR +
ACR Uc UPE
+
现代控制理论浙大
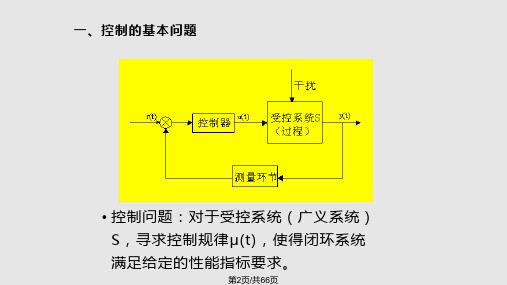
三、现代控制理论与古典控制理论的对比
• 共同 对象-系统 主要内容 分析:研究系统的原理和性能 设计:改变系统的可能性(综合性能)
用 • 区别
古典
研究对象:单入单出(SIS0)系统,线性定常 工具:传递函数(结构图),已有初始条件为零时才适
试探法解决问题 : PID串联、超前、滞后、反馈
整理得一阶微分方程组为
Ri (t )
L
di(t) dt
uc
u(t)
duc(t) 1 i(t) dt C
i(t) C duc dt
di(t) dt
1 L
uc
(t)
R L
i(t)
1 L
u(t)
即
x1 (t )
1 C
x2 (t)
状态方程
x2
(t)
1 L
x1 (t )
R L
x2
(t)
1 L
u(t)
状态空间 表达式
研究对象:多入多出(MIMO)系统、
线性定常、非线性、时变、
第9页/共66页
现代控制理论预览
可控性 可观性 稳定性
建模 分析 设计
状态空间 表达式
建立 求解 转换
状态反馈 状态观测器 最优控制
第10页/共66页
第一章 控制系统的状态空间表达式
主要内容: • 状态变量及状态空间表达式 • 状态变量及状态空间表达式的系统结构图 • 状态变量及状态空间表达式的建立 • 状态矢量的线性变换 • 从状态空间表达式求传递函数阵
(1) 专家系统;(2)模糊控制,人工智能 (3) 神经网络,人脑模型;(4)遗传算法 控制理论与计算机技术相结合→计算机控制技术
第7页/共66页
