等效均布荷载
楼面等效均布荷载 B-1 计算结果
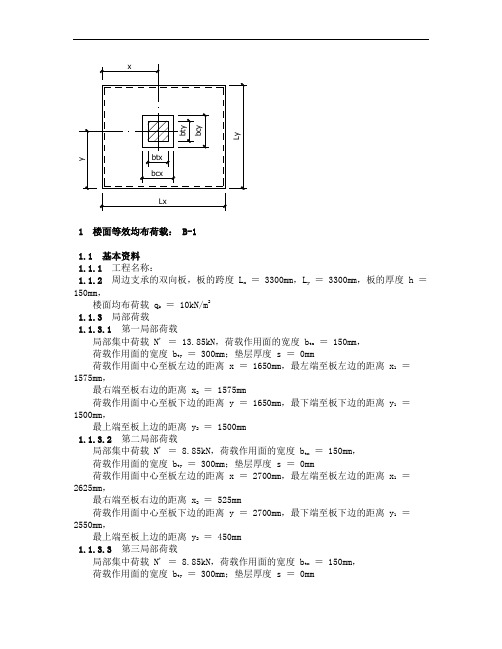
1 楼面等效均布荷载: B-11.1 基本资料1.1.1 工程名称:1.1.2 周边支承的双向板,板的跨度 L x = 3300mm ,L y = 3300mm ,板的厚度 h = 150mm ,楼面均布荷载 q k = 10kN/m 21.1.3 局部荷载1.1.3.1 第一局部荷载局部集中荷载 N' = 13.85kN ,荷载作用面的宽度 b tx = 150mm , 荷载作用面的宽度 b ty = 300mm ;垫层厚度 s = 0mm荷载作用面中心至板左边的距离 x = 1650mm ,最左端至板左边的距离 x 1 = 1575mm ,最右端至板右边的距离 x 2 = 1575mm荷载作用面中心至板下边的距离 y = 1650mm ,最下端至板下边的距离 y 1 = 1500mm ,最上端至板上边的距离 y 2 = 1500mm1.1.3.2 第二局部荷载局部集中荷载 N' = 8.85kN ,荷载作用面的宽度 b tx = 150mm , 荷载作用面的宽度 b ty = 300mm ;垫层厚度 s = 0mm荷载作用面中心至板左边的距离 x = 2700mm ,最左端至板左边的距离 x 1 = 2625mm ,最右端至板右边的距离 x 2 = 525mm荷载作用面中心至板下边的距离 y = 2700mm ,最下端至板下边的距离 y 1 = 2550mm ,最上端至板上边的距离 y 2 = 450mm1.1.3.3 第三局部荷载局部集中荷载 N' = 8.85kN ,荷载作用面的宽度 b tx = 150mm , 荷载作用面的宽度 b ty = 300mm ;垫层厚度 s = 0mm荷载作用面中心至板左边的距离 x = 1650mm,最左端至板左边的距离 x1=1575mm,最右端至板右边的距离 x2= 1575mm荷载作用面中心至板下边的距离 y = 2700mm,最下端至板下边的距离 y1=2550mm,最上端至板上边的距离 y2= 450mm1.1.3.4第四局部荷载局部集中荷载 N' = 13.85kN,荷载作用面的宽度 b tx= 150mm,荷载作用面的宽度 b ty= 300mm;垫层厚度 s = 0mm荷载作用面中心至板左边的距离 x = 2700mm,最左端至板左边的距离 x1=2625mm,最右端至板右边的距离 x2= 525mm荷载作用面中心至板下边的距离 y = 1650mm,最下端至板下边的距离 y1=1500mm,最上端至板上边的距离 y2= 1500mm1.2局部荷载换算为局部均布荷载1.2.1第一局部荷载 P = N' / (b tx·b ty) - q k= 13.85/(0.15*0.3)-10 =297.78kN/m21.2.2第二局部荷载 P = N' / (b tx·b ty) - q k= 8.85/(0.15*0.3)-10 =186.67kN/m21.2.3第三局部荷载 P = N' / (b tx·b ty) - q k= 8.85/(0.15*0.3)-10 =186.67kN/m21.2.4第四局部荷载 P = N' / (b tx·b ty) - q k= 13.85/(0.15*0.3)-10 =297.78kN/m21.3第一局部荷载1.3.1荷载作用面的计算宽度1.3.1.1 b cx= b tx + 2s + h = 150+2*0+150 = 300mm1.3.1.2 b cy= b ty + 2s + h = 300+2*0+150 = 450mm1.3.2局部荷载的有效分布宽度1.3.2.1按上下支承考虑时局部荷载的有效分布宽度当 b cy≥ b cx, b cx≤ 0.6L y时,取 b x= b cx+ 0.7L y= 300+0.7*3300 = 2610mm 当 0.5b x> 0.5e x2时,取 b x= 1305 + 0.5e x2= 1305+0.5*1050 = 1830mm 1.3.2.2按左右支承考虑时局部荷载的有效分布宽度当 b cx< b cy, b cy≤ 2.2L x时,取b y= 2b cy / 3 + 0.73L x= 2*450/3+0.73*3300 = 2709mm当 0.5b y> 0.5e y2时,取 b y= 1355 + 0.5e y2= 1355+0.5*1050 = 1880mm 1.3.3绝对最大弯矩1.3.3.1按上下支承考虑时的绝对最大弯矩1.3.3.1.1将局部均布荷载转换为 Y 向线荷载q y= P·b tx= 297.78*0.15 = 44.67kN/m1.3.3.1.2 M maxY= q y·b ty·(L y - y)·[y1 + b ty·(L y - y) / 2L y] / L y。
等效均布荷载

等效均布荷载通常,荷载可以分为均布荷载和非均布荷载两大类。
其中,均布荷载指的是荷载施加在构件上,荷载分布形式是连续变化,但是每个位置上荷载的大小是一致的或者有一定的规律变化,其作用与构件一般线性变形,构件上的变形和位置有关,使得等效的整体变形和位置的变形和位置的变化量最小。
等效均布荷载是指均布荷载可以通过一个与之等效的非均布荷载来表达。
这样的荷载主要是构件面的均布荷载,它可以通过把构件的单个面上的均布荷载折合成多个独立的点荷载,实现等效均布荷载。
等效均布荷载用来模拟均布荷载可以有效地减少计算时间,减少计算量,提高计算效率。
但是,等效均布荷载也可能会产生误差,需要用户对计算结果进行检验,以确保计算结果的准确性。
在建筑结构设计过程中,等效均布荷载的使用范围很广,可以用来计算集中荷载的效应,也可以用来计算悬臂构件的剪力,曲线梁的弯矩,屋面构件的弯矩,地面及地基的沉降等。
等效均布荷载的基本计算方法是:计算均布荷载施加在构件上的总力,然后把总力均分到各个面上,再将每个面上的力采用与之等效的非均布荷载来表示,如结构柱或梁上,可以采用一定数量的集中荷载,把均布荷载折合到集中荷载上,或者可以采用施加结构面上的等效矩形均布荷载,把均布荷载折合到等效矩形均布荷载上。
在计算不同面上的等效均布荷载时,还可以进行以下处理:在一定范围内,把一个面上荷载(例如受拉梁)的均布荷载折合成多个等效的集中荷载;在另一定范围内,把一个面上荷载(例如受压梁)的均布荷载折合成多个等效的非集中荷载;在其他范围内,把一个面上荷载(例如受拉或受压梁)的均布荷载折合成等效的矩形均布荷载。
综上所述,等效均布荷载是一种经常被使用的一种方法,它在结构设计中具有重要的意义,用以模拟均布荷载,减少计算量和提高计算效率。
但需要注意的是,计算结果一定要经过校验,确保准确。
等效均布荷载计算

等效均布荷载计算
等效均布荷载是一种用于计算结构物受力的方法。
在实际工程中,结构物往往需要承受各种不同的荷载,如雪荷载、风荷载、地震荷载等。
而等效均布荷载的作用就是将这些不同的荷载转化成一个等效的均布荷载,方便进行计算。
等效均布荷载的计算方法有多种。
其中一种常用的方法是根据结构物的形态及其所受荷载的类型,采用经验公式计算出该类型荷载对应的等效均布荷载系数,再将设计荷载乘以该系数得到等效均布荷载。
例如,在计算风荷载时,可以根据结构物的高度、形态、所处地区的风速等因素,使用相应的经验公式计算出风荷载系数。
然后将设计风荷载乘以该系数得到等效均布荷载,再将其施加到结构物上进行计算。
还有一种常用的方法是使用有限元分析软件进行计算。
在该方法中,首先需要将结构物的几何模型建立成有限元模型,并指定结构物所受荷载的类型及其大小。
然后,通过有限元分析软件进行计算,得到结构物受力情况及其变形情况。
最后,可以根据计算结果得到等效均布荷载。
需要注意的是,等效均布荷载只是一种简化计算方法,其结果并不一定完全准确。
在实际工程中,为了得到更加准确的计算结果,还
需要考虑各种不同荷载的相互作用、结构物的实际受力情况等因素。
等效均布荷载是一种常用的结构物受力计算方法,其优点是简化了计算过程,便于工程师进行设计。
但在使用该方法时,需要注意计算准确性,并结合实际情况进行综合考虑。
等效均布荷载的概念

等效均布荷载的概念下载温馨提示:该文档是我店铺精心编制而成,希望大家下载以后,能够帮助大家解决实际的问题。
文档下载后可定制随意修改,请根据实际需要进行相应的调整和使用,谢谢!Download Tip: This document has been carefully written by the editor. I hope that after you download, they can help you solve practical problems. After downloading, the document can be customized and modified. Please adjust and use it according to actual needs. Thank you!等效均布荷载概念如下:①定义:在结构工程中,等效均布荷载是一种简化计算方法,即将实际作用在结构上的非均匀分布荷载(如集中荷载、线性荷载等),转换为作用面积上均匀分布的荷载,以便于结构分析与设计。
②目的:简化计算,通过等效处理,可以使用基本的结构力学公式,如梁的弯曲理论,快速求解结构的内力、位移等问题,提高设计效率。
③转换原则:转换时需保持原荷载产生的效应(如弯矩、剪力等)在关键截面处相等。
通常采用积分法或分段近似法确定等效均布荷载的大小。
④应用前提:适用于荷载作用范围相对较大且变化平缓的情况,确保等效过程中的误差在允许范围内,不影响结构安全与性能评价。
⑤计算步骤:a. 确定实际荷载分布;b. 分析控制截面受力特点;c. 计算并调整等效荷载值,使之在关键部位产生的效应与实际荷载相同;d. 应用等效均布荷载进行结构分析。
⑥注意事项:实际应用中,需考虑等效带来的误差,特别是当荷载高度集中或分布不均时,需仔细校核结果,必要时进行局部精细化分析。
等效均布荷载 梁集中力

等效均布荷载梁集中力
等效均布荷载是指在结构分析中,将集中力转化为作用在梁上
的均布荷载,以便于进行统一的计算和分析。
梁集中力则是指作用
在梁上的集中力,通常是指集中在某一点或某几个点上的力的合力。
从结构分析的角度来看,将集中力转化为等效均布荷载有利于
简化计算。
当梁上受到集中力作用时,我们可以通过将集中力转化
为均布荷载来进行等效静力分析,这样可以将原本不规则的受力情
况转化为均匀的受力分布,从而方便进行弯矩、剪力等参数的计算。
另外,从设计和施工的角度来看,等效均布荷载的概念也具有
重要意义。
在实际工程中,由于集中力可能对梁产生局部的集中应力,为了减小这种局部应力对梁的影响,我们可以将集中力转化为
等效均布荷载,从而在设计和施工中更好地考虑梁的受力性能和安
全性。
总的来说,等效均布荷载和梁集中力是结构分析和设计中常见
的概念,它们在简化计算、考虑梁的受力性能和安全性等方面起着
重要的作用。
在工程实践中,合理地处理和应用这些概念对于确保
结构的安全可靠具有重要意义。
汽车等效均布荷载的简化计算(可编辑)

汽车等效均布荷载的简化计算Building Structure设计交流汽车等效均布荷载的简化计算朱炳寅/中国建筑设计研究院汽车(消防车)轮压以其荷载数值大、作用位置不确定够厚,轮压扩散足够充分时,汽车轮压荷载可按均布荷载考及一般作用时间较短而倍受结构设计者关注。
结构设计的关虑。
当覆土层厚度足够时,可按汽车在合理投影面积范围内键问题在于汽车轮压等效均布荷载数值的确定。
轮压荷载作的平均荷重计算汽车的轮压荷载,见表2。
用位置的不确定性,给等效均布荷载的确定带来了一定难覆土厚度足够时消防车的荷载表2度,一般情况下,要精确计算轮压的等效均布荷载是比较困汽车类型 100kN 150kN 200kN 300kN 550kN2难的,且从工程设计角度看,也没有必要。
“等效”和“折荷载/kN/m 4.3 6.3 8.5 11.3 11.4覆土厚度最小值hmin/m 2.5 2.4 2.4 2.3 2.6减”的本质都是“近似”,且其次数越多,误差就越大。
本文推荐满足工程设计精度需要的汽车轮压等效均布荷载的足够的覆土厚度指:汽车轮压通过土层的扩散、交替和简化计算方法,供读者参考。
重叠,达到在某一平面近似均匀分布时的覆土层厚度。
足够1 影响等效均布荷载的主要因素的覆土厚度数值应根据工程经验确定,当无可靠设计经验1.1跨度时,可按后轴轮压的扩散面积不小于按荷重比例划分的汽车等效均布荷载的数值与构件的跨度有直接的关系,在相投影面积(图 1)确定相应的覆土厚度为 hmin ,当实际覆土同等级的汽车轮压作用下,板的跨度越小,则等效均布荷载厚度 h≥hmin 时,可认为覆土厚度足够。
的数值越大;而板的跨度越大,则等效均布荷载数值越小。
以300kN级汽车为例(图1):结构设计中应注意“等效均布荷载”及“效应相等”的特点,考虑汽车合理间距(每侧600mm)后汽车的投影面积为(8+0.6 )×(2.5+0.6 )=26.66m2汽车轮压荷载具有荷载作用位置变化的特性,是移动的活荷载,其最大效应把握困难,且效应类型(弯矩、剪力等)不后轴轮压占全车重量的比例为 240/300=0.8同,等效均布荷载的数值也不相同,等效的过程就是一次近取后轴轮压的扩散面积为 0.8×26.66=21.33m2似的过程。
楼面双向板等效均布活荷载的计算方法

楼面双向板等效均布活荷载的计算方法这个题目来自于《建筑结构荷载规范GB50009-2001》的附录B,要弄清它需要先知道楼面等效均布活荷载。
规范中虽然介绍了计算的原则,但究其本源,其实就是为了方便地统一处理各种类型的局部活荷载,也就是说寻找一个均布面荷载值,使它对结构产生的效果与局部活荷载产生的效果相同(也就是等效的含义),这样我们对结构荷载问题的处理就比较统一,因为我们进行结构分析时,已习惯输入KN/m2这样的荷载方式,甚至有时候对某些楼面(比如地下室顶板)进行荷载值限定时,会写下该处的荷载不能超过多少KN/m2这样的说明文字。
所谓“等效”,主要是指内力的等值,而且对于连续跨也常常是按单跨简支来考虑。
在处理单向板和悬臂板时,很容易理解,规范中也给出了计算的原则。
但是对于双向板而言,规范中仅给出一条简单的说明:“按四边简支板的绝对最大弯矩等值来确定”,让很多人望而却步。
有些耐心的结构工程师在针对具体的工程项目时,还是可以得到一些关于这个问题的结果的。
他可以近似地让局部荷载作用于双向板的跨中,因为这种荷载布置以及均布荷载下的四边简支双向板的绝对最大弯矩都可以在《建筑结构静力计算手册》中查表得到。
有多些耐心的结构工作者还可以通过有限元分析来得到结果,这些结构人士以高校老师诸多。
其实学过《板壳理论》的力学专业出身的人可能会有这样的印象,那就是薄板理论中首先推导的就是双向板局部荷载下的挠曲面方程,对其偏导就可以得到弯矩方程,结果是一个级数方程式。
我们可以在程序中取前面几项,就可以得到足够近似的值。
你可以通过访问的在线计算部分得到结果。
这里有两个问题需要特别强调一下,有些程序处理双向板时,可能是因为规范的嘎然而止,导致其武断地用两个方向的单向板来分别计算,取其中大者作为结果,这是偏不安全的。
(Morgain好像是这样计算的)。
还有个问题是关于绝对最大弯矩的问题,这是针对当局部荷载不是作用在板的正中间的情况。
等效均布荷载计算

等效均布荷载计算
等效均布荷载计算是指将不规则的荷载分布转化为等效的均布荷载,以便于结构分析和设计。
在建筑结构分析和设计中,等效均布荷载计算是一项重要的工作,它可以简化复杂的荷载分析,提高分析的准确性和可靠性。
等效均布荷载计算的基本原理是将不规则荷载分布转化为等效的均布荷载,使得结构受到的荷载分布变得均匀,从而方便进行结构分析和设计。
等效均布荷载计算的方法有很多种,其中常用的方法包括:
1. 静力等效法:将不规则荷载分布转化为等效的均布荷载,使得结构受到的荷载分布变得均匀。
这种方法适用于简单的结构,如梁、柱等。
2. 动力等效法:将不规则荷载分布转化为等效的均布荷载,使得结构受到的荷载分布变得均匀。
这种方法适用于复杂的结构,如桥梁、塔架等。
3. 基于有限元分析的等效法:将不规则荷载分布转化为等效的均布荷载,使得结构受到的荷载分布变得均匀。
这种方法适用于复杂的结构,如高层建筑、大型桥梁等。
在进行等效均布荷载计算时,需要注意以下几点:
1. 荷载的分布应该尽可能地准确,以便于计算出更为准确的等效均布荷载。
2. 等效均布荷载的大小应该与实际荷载的大小相当,以便于分析和设计的准确性。
3. 等效均布荷载的分布应该符合实际情况,以便于分析和设计的可靠性。
总之,等效均布荷载计算是建筑结构分析和设计中的一项重要工作,它可以简化复杂的荷载分析,提高分析的准确性和可靠性。
在进行等效均布荷载计算时,需要注意荷载分布的准确性、等效均布荷载的大小和分布的符合实际情况等问题,以便于得到更为准确和可靠的分析和设计结果。
