数学实验 12:回归分析
数学建模-回归分析

一、变量之间的两种关系 1、函数关系:y = f (x) 。
2、相关关系:X ,Y 之间有联系,但由 其中一个不能唯一的确定另一个的值。 如: 年龄 X ,血压 Y ; 单位成本 X ,产量 Y ; 高考成绩 X ,大学成绩 Y ; 身高 X ,体重 Y 等等。
二、研究相关关系的内容有
1、相关分析——相关方向及程度(第九章)。 增大而增大——正相关; 增大而减小——负相关。 2、回归分析——模拟相关变量之间的内在 联系,建立相关变量间的近似表达式 (经验 公式)(第八章)。 相关程度强,经验公式的有效性就强, 反之就弱。
三、一般曲线性模型 1、一般一元曲线模型
y = f ( x) + ε
对于此类模型的转换,可用泰勒展开 公式,把 在零点展开,再做简单的变 f ( x) 换可以得到多元线性回归模型。 2、一般多元曲线模型
y = f ( x1 , x2源自,⋯ , xm ) + ε
对于此类模型也要尽量转化为线性模 型,具体可参考其他统计软件书,这里不 做介绍。
ˆ ˆ ˆ ˆ y = b0 + b1 x1 + ⋯ + bm x m
2、利用平方和分解得到 ST , S回 , S剩。 3、计算模型拟合度 S ,R ,R 。 (1)标准误差(或标准残差)
S =
S剩 ( n − m − 1)
当 S 越大,拟合越差,反之,S 越小, 拟合越好。 (2)复相关函数
R =
2
仍是 R 越大拟合越好。 注: a、修正的原因:R 的大小与变量的个数以及样本 个数有关; 比 R 要常用。 R b、S 和 R 是对拟合程度进行评价,但S与 R 的分 布没有给出,故不能用于检验。 用处:在多种回归模型(线性,非线性)时, 用来比较那种最好;如:通过回归方程显著性检验 得到:
回归分析的基本思路

回归分析的基本思路回归分析是一种统计学方法,用于研究自变量与因变量之间的关系。
它的基本思路是通过建立一个数学模型,利用已知的自变量数据来预测因变量的值。
回归分析主要有两个目标,一是确定自变量和因变量之间的函数关系,二是利用这个函数关系进行预测。
本文将详细介绍回归分析的基本思路。
一、数据收集:首先需要收集与研究主题相关的数据,包括自变量和因变量的观测值。
数据可以通过实验、调查或者已有的数据集来获取。
二、变量选择:在进行回归分析前,需要选择适当的自变量和因变量。
自变量是用来预测因变量的变量,而因变量是需要被预测的变量。
选择合适的变量对于回归分析的结果至关重要。
三、建立数学模型:在回归分析中,需要通过建立一个数学模型来描述自变量和因变量之间的关系。
最常用的数学模型是线性回归模型,表示因变量和自变量之间存在一个线性关系。
线性回归模型的一般形式是:Y=β0+β1X1+β2X2+...+βnXn+ε,其中Y是因变量,X1、X2、..、Xn是自变量,β0、β1、β2、..、βn是回归系数,ε是误差项。
四、参数估计:在回归分析中,需要估计回归系数的值。
常见的参数估计方法有最小二乘法、最大似然估计等。
最小二乘法是一种常用的参数估计方法,它通过最小化观测值与模型预测值之间的差异来估计回归系数的值。
五、模型检验:在回归分析中,需要对建立的模型进行检验,以评估模型的拟合程度和可靠性。
常用的模型检验方法有残差分析、方差分析、Hypothesis Check等。
残差分析是一种常用的检验方法,它通过分析模型的预测误差来判断模型是否符合要求。
六、模型解释:回归分析的一个重要目标是解释自变量和因变量之间的关系。
模型解释可以通过回归系数的符号和大小来实现。
回归系数的符号表示自变量和因变量之间的正相关还是负相关,而回归系数的大小表示自变量对因变量的影响程度。
七、模型应用:通过建立回归模型,可以利用已知的自变量数据来预测因变量的值。
这种预测可以用于决策和规划,例如使用回归模型来预测销售额、股票价格等。
spass回归分析实验报告
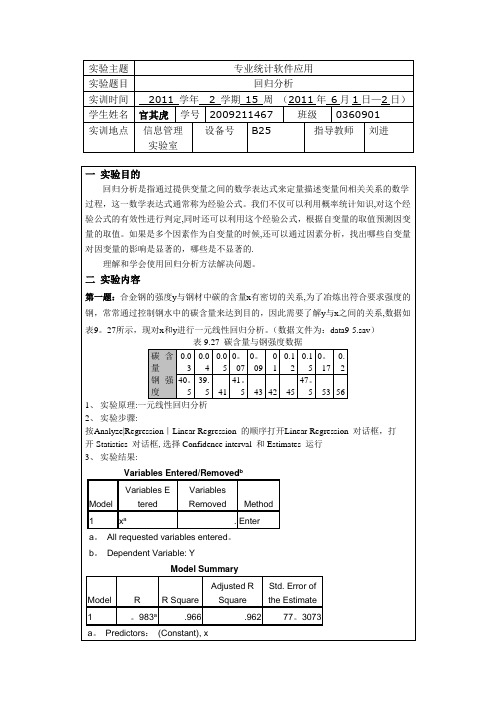
上,看哪种模型拟合效果更好从拟合优度(Rsq 即R2)来看,QUA,CUB,POW 效果较好(因为其Rsq 值较大),于是就选QUA,CUB,POW来进行。
重新进行上面的过程,只选以上三种模型。
3、实验结果:Model Summary and Parameter EstimatesDependent Variable:远视率EquationModel Summary Parameter EstimatesRSquare F df1 df2 Sig。
Constant b1 b2 b3Linear。
674 22。
7101 11 .001 74.006—4。
768Logarith mic .793 42.251 1 11 。
000 156。
773-57.574Inverse。
883 83.244 1 11 。
000 -40。
567 615.321Quadrati c .94382。
1142 10 .000 192.085-26.567。
908Cubic.959 69。
5383 9 .000 290.851—54。
7173.398 —。
069Compound。
794 42.445 1 11 .000 308。
120 .731Power.861 68.413 1 11 .000 49462.724—3。
638S .877 78.119 1 11 .000 -1。
502 37.175Growth.794 42。
4451 11 。
000 5。
730 —。
314Exponen tial .79442。
4451 11 。
000 308.120 -.314Logistic 。
794 42.445 1 11 。
000 .003 1。
369The independent variable is 年龄.分析:可以用Cubic拟合曲线图的拟合效果最好.第四题:棉花单株在不同时期的成铃数(y)与初花后天数(x)存在非线性的关系,假设这一非线性关系可用Gompertz模型表示:y=b1*exp(-b2*exp(—b3*x))。
回归分析 实验报告

回归分析实验报告1. 引言回归分析是一种用于探索变量之间关系的统计方法。
它通过建立一个数学模型来预测一个变量(因变量)与一个或多个其他变量(自变量)之间的关系。
本实验报告旨在介绍回归分析的基本原理,并通过一个实际案例来展示其应用。
2. 回归分析的基本原理回归分析的基本原理是基于最小二乘法。
最小二乘法通过寻找一条最佳拟合直线(或曲线),使得所有数据点到该直线的距离之和最小。
这条拟合直线被称为回归线,可以用来预测因变量的值。
3. 实验设计本实验选择了一个实际数据集进行回归分析。
数据集包含了一个公司的广告投入和销售额的数据,共有200个观测值。
目标是通过广告投入来预测销售额。
4. 数据预处理在进行回归分析之前,首先需要对数据进行预处理。
这包括了缺失值处理、异常值处理和数据标准化等步骤。
4.1 缺失值处理查看数据集,发现没有缺失值,因此无需进行缺失值处理。
4.2 异常值处理通过绘制箱线图,发现了一个销售额的异常值。
根据业务经验,判断该异常值是由于数据采集错误造成的。
因此,将该观测值从数据集中删除。
4.3 数据标准化为了消除不同变量之间的量纲差异,将广告投入和销售额两个变量进行标准化处理。
标准化后的数据具有零均值和单位方差,方便进行回归分析。
5. 回归模型选择在本实验中,我们选择了线性回归模型来建立广告投入与销售额之间的关系。
线性回归模型假设因变量和自变量之间存在一个线性关系。
6. 回归模型拟合通过最小二乘法,拟合了线性回归模型。
回归方程为:销售额 = 0.7 * 广告投入 + 0.3回归方程表明,每增加1单位的广告投入,销售额平均增加0.7单位。
7. 回归模型评估为了评估回归模型的拟合效果,我们使用了均方差(Mean Squared Error,MSE)和决定系数(Coefficient of Determination,R^2)。
7.1 均方差均方差度量了观测值与回归线之间的平均差距。
在本实验中,均方差为10.5,说明模型的拟合效果相对较好。
回归分析实验报告

回归分析实验报告实验报告:回归分析摘要:回归分析是一种用于探究变量之间关系的数学模型。
本实验以地气温和电力消耗量数据为例,运用回归分析方法,建立了气温和电力消耗量之间的线性回归模型,并对模型进行了评估和预测。
实验结果表明,气温对电力消耗量具有显著的影响,模型能够很好地解释二者之间的关系。
1.引言回归分析是一种用于探究变量之间关系的统计方法,它通常用于预测或解释一个变量因另一个或多个变量而变化的程度。
回归分析陶冶于20世纪初,经过不断的发展和完善,成为了数量宏大且复杂的数据分析的重要工具。
本实验旨在通过回归分析方法,探究气温与电力消耗量之间的关系,并基于建立的线性回归模型进行预测。
2.实验设计与数据收集本实验选择地的气温和电力消耗量作为研究对象,数据选取了一段时间内每天的气温和对应的电力消耗量。
数据的收集方法包括了实地观测和数据记录,并在数据整理过程中进行了数据的筛选与清洗。
3.数据分析与模型建立为了探究气温与电力消耗量之间的关系,需要建立一个合适的数学模型。
根据回归分析的基本原理,我们初步假设气温与电力消耗量之间的关系是线性的。
因此,我们选用了简单线性回归模型进行分析,并通过最小二乘法对模型进行了估计。
运用统计软件对数据进行处理,并进行了以下分析:1)描述性统计分析:计算了气温和电力消耗量的平均值、标准差和相关系数等。
2)直线拟合与评估:运用最小二乘法拟合出了气温对电力消耗量的线性回归模型,并进行了模型的评估,包括了相关系数、残差分析等。
3)预测分析:基于建立的模型,进行了其中一未来日期的电力消耗量的预测,并给出了预测结果的置信区间。
4.结果与讨论根据实验数据的分析结果,我们得到了以下结论:1)在地的气温与电力消耗量之间存在着显著的线性关系,相关系数为0.75,表明二者之间的关系较为紧密。
2)构建的线性回归模型:电力消耗量=2.5+0.3*气温,模型参数的显著性检验结果为t=3.2,p<0.05,表明回归系数是显著的。
一元线性回归分析研究实验报告

一元线性回归分析研究实验报告一元线性回归分析研究实验报告一、引言一元线性回归分析是一种基本的统计学方法,用于研究一个因变量和一个自变量之间的线性关系。
本实验旨在通过一元线性回归模型,探讨两个变量之间的关系,并对所得数据进行统计分析和解读。
二、实验目的本实验的主要目的是:1.学习和掌握一元线性回归分析的基本原理和方法;2.分析两个变量之间的线性关系;3.对所得数据进行统计推断,为后续研究提供参考。
三、实验原理一元线性回归分析是一种基于最小二乘法的统计方法,通过拟合一条直线来描述两个变量之间的线性关系。
该直线通过使实际数据点和拟合直线之间的残差平方和最小化来获得。
在数学模型中,假设因变量y和自变量x之间的关系可以用一条直线表示,即y = β0 + β1x + ε。
其中,β0和β1是模型的参数,ε是误差项。
四、实验步骤1.数据收集:收集包含两个变量的数据集,确保数据的准确性和可靠性;2.数据预处理:对数据进行清洗、整理和标准化;3.绘制散点图:通过散点图观察两个变量之间的趋势和关系;4.模型建立:使用最小二乘法拟合一元线性回归模型,计算模型的参数;5.模型评估:通过统计指标(如R2、p值等)对模型进行评估;6.误差分析:分析误差项ε,了解模型的可靠性和预测能力;7.结果解释:根据统计指标和误差分析结果,对所得数据进行解释和解读。
五、实验结果假设我们收集到的数据集如下:经过数据预处理和散点图绘制,我们发现因变量y和自变量x之间存在明显的线性关系。
以下是使用最小二乘法拟合的回归模型:y = 1.2 + 0.8x模型的R2值为0.91,说明该模型能够解释因变量y的91%的变异。
此外,p 值小于0.05,说明我们可以在95%的置信水平下认为该模型是显著的。
误差项ε的方差为0.4,说明模型的预测误差为0.4。
这表明模型具有一定的可靠性和预测能力。
六、实验总结通过本实验,我们掌握了一元线性回归分析的基本原理和方法,并对两个变量之间的关系进行了探讨。
Exp12

0 β2
x
待定系数 β1 (最终反应速度)
β2 (半速度点)
2
例4 酶促反应
为研究酶促反应中嘌呤霉素对反应速度与底物浓度 之间关系的影响, 设计了两个实验 :使用的酶经过嘌 呤霉素处理; 使用的酶未经嘌呤霉素处理。
实验数据
底物浓度(ppm) 0.02
0.06
0.11
0.22
0.56
1.10
反应 处理 76 47 97 107 123 139 159 152 191 201 207 200 速度 未处理 67 51 84 86 98 115 131 124 144 158 160 /
140 120
由数据确定系数 β0 , β1
100
10
20
30
40
50
60
70
的估计值 βˆ0 , βˆ1
• 曲线拟合(求超定线性方程组的最小二乘解);
• 从统计推断角度讨论β0 ,β1 的置信区间和假设检验; • 对任意的年龄 x 给出血压 y 的预测区间。
例2 血压与年龄、体重指数、吸烟习惯
又调查了例1中30个成年人的体重指数、吸烟习惯:
对于身高72英寸的父亲,
O
儿子身高多数不到73英寸;
对于身高64英寸的父亲, 儿子身高多数超过65英寸;
回归直线 y=0.516 x+33.73 Pearson: 1078个父亲和儿子身高的散点图
回归分析是数学建模的有力工具
• 由于客观事物内部规律的复杂及人们认识程度的限制, 无法分析实际对象内在的因果关系;
资历~ 从事专业工作的年数;管理~ 1=管理人员,0=
非管理人员;教育~ 1=中学,2=大学,3=研究生
利用回归分析预测实验结果的趋势

利用回归分析预测实验结果的趋势在科学研究和实验中,预测实验结果的趋势是一项重要的任务。
回归分析作为一种常用的统计方法,可以帮助我们探索变量之间的关系,并通过数学模型预测未来的结果。
本文将介绍回归分析的基本原理和应用,以及如何利用回归分析预测实验结果的趋势。
一、回归分析的基本原理回归分析是一种统计方法,用于研究自变量与因变量之间的关系。
在回归分析中,自变量是我们想要用来预测和解释因变量的变化的变量,因变量是我们想要预测的变量。
回归分析的目标是建立一个数学模型,可以通过自变量的取值预测因变量的取值。
回归分析的基本原理是最小二乘法。
最小二乘法通过将自变量与因变量的观测值代入数学模型,计算出预测值与观测值之间的差异(残差),然后调整模型参数,使得残差的平方和最小化。
最小二乘法可以得出最优的模型参数,并基于这个模型来预测未来的结果。
二、回归分析的应用回归分析广泛应用于各个领域的科学研究和实验中。
它可以帮助我们更好地理解变量之间的关系,预测未来的趋势,并作出更合理的决策。
以下是几个常见的应用领域:1. 经济学:回归分析可以用来研究经济变量之间的关系,如GDP与通货膨胀率、利率与投资额等。
通过回归分析,我们可以预测未来的经济趋势,评估政策的效果,并制定相应的经济政策。
2. 医学研究:回归分析可以用来研究生物医学的相关性,如药物剂量与疗效、生活方式与慢性疾病的关系等。
通过回归分析,我们可以预测治疗效果,指导临床决策,并优化治疗方案。
3. 社会科学:回归分析可以用来研究社会学、心理学、教育学等领域的问题,如家庭收入对子女学业成绩的影响、领导风格对员工满意度的影响等。
通过回归分析,我们可以预测社会现象的发展趋势,为政策制定和管理提供依据。
三、利用回归分析预测实验结果的趋势在科学研究和实验中,我们经常需要通过实验数据来预测未来的趋势。
回归分析可以帮助我们利用历史数据或实验结果,建立一个模型,并用这个模型来预测未来的结果。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
实验 12:回归分析习题7:在有氧锻炼中人的耗氧能力y(ml/(min ·kg))是衡量身体状况的重要指标,它可能与以下因素有关:年龄x1,体重x2(kg),1500m 跑的时间x3(min),静止时心跳速度x4(次/min ),跑步后心速x5(次/min ).对24名40至57岁的志愿者进行了测试,结果如下表(节选),试建立耗氧能力y 与诸因素的之间的回归模型。
(1)若x1~x5中只许选择1个变量,最好的模型是什么? (2)若x1~x5中只许选择2个变量,最好的模型是什么? (3)若不限制变量的个数,最好的模型是什么?(4)对最终模型观察残查,有无异常点,若有,剔除后如何?1. 模型建立本题不同小问需要建立不同模型,由于专业知识所限,并且提供的数据较少,难以做出精确符合现实情况的模型,因此这里采用最简单的线性回归法进行拟和,模型基本形式如下:0111,m m jk j k j k my x x x x ββββε≤≤=+++++∑事实上,∑中的项(高次项和交互项)对于本题目来讲意义不大,因为所给定的5个自变量和因变量之间关系比较模糊,几个变量彼此之间的联系也很难说清,因此用自变量的一次线性拟和就足以适应本题的要求。
但作为练习,还是将每种回归方法都使用到了,可以用于参考。
具体采用的各个模型将在下面单独说明,这里不再重复。
2. 程序设计由于本题需要建立多组模型,并且要在不断的调试中发现最合理的,很多命令都要在这个过程中不断使用,这里仅仅给出使用的最基本的命令。
◆ 数据 clearA=[…]; %数据矩阵,略 n=24; y=A(2,:); %提取各个数据x1=A(3,:);x2=A(4,:);x3=A(5,:);x4=A(6,:);x5=A(7,:);◆ 绘制散点图(大致判断影响情况) for i=1:5subplot(2,3,i),plot(A(i+2,:),y,'+'),grid序号 1 2 3 4 … 21 22 23 24 Y 44.6 45.3 54.3 59.6 … 39.4 46.1 45.4 54.7 X1 44 40 44 42 … 57 54 52 50 X2 89.5 75.1 85.8 68.2 … 73.4 79.4 76.3 70.9 X3 6.82 6.04 5.19 4.9 … 7.58 6.7 5.78 5.35 X4 62 62 45 40 … 58 62 48 48 X5178 185 156 166 … 174 156 164 146pauseendpause◆单参数回归(第一问)X=[ones(n,1),x4']; %这里检验的是自变量x4,实际操作时要分别检验x1~x5 [b,bint,r,rint,s]=regress(y',X); %回归分析程序( =0.05)b,bint,s, %输出回归系数估计值、置信区间、以及统计量rcoplot(r,rint) %残差图Polytool(x3',y',2) %检验一元多项式回归的结果,输出交互式画面◆双参数回归(第二问):用逐步回归法找出最合理的两个变量X5=[x1',x2',x3',x4',x5'];stepwise(X5,y');%利用输出的交互式画面,可以选出最佳的两个变量XX=[x3',x1']; %当得到了最佳的两个变量后(这里假设是x3\x1)rstool(XX,y','linear') %检验二元情况下的交互项和高次项◆全部参数回归(第三问):X5=[x1',x2',x3',x4',x5']; %仍然用逐步回归法找出最合理的组合方式stepwise(X5,y')第五问要求对残差进行分析,并且剔除异常点,可以在该问得到最终模型后,采用regress 得到的残差值和置信区间并根据其绘制残差图,然后再进行剔除操作重新检验。
3.运行结果及分析散点图从左上到右下的顺序为x1~x5.可以由点的分布大致看出,除了x3自变量呈现比较明显的负相关趋势以外,对于其他的各个自变量都难以直接观测出其对于因变量的影响。
根据这种结果,可以假设自变量x3(1500m 跑后心速)最直接的与锻炼耗氧能力相关,下面通过对各个自变量的单参数回归进行检验。
由单参数回归的结果可以证明X3(1500m 跑后心速)可以最好的反映出y(锻炼耗氧能力)的情况。
由β1置信区间可以看出,x1、x2包含0在内,即y 可能与该参数无关,所以不选择,并且两者的p 值已经明显的大于 =0.05,则不考虑x1、x2。
比较x3~x5后发现,x3的2R -决定系数明显的大于x4、x5的,决定系数反映的是在因变量的总变化中自变量引起的那部分的比例,2R 大说明x3自变量对因变量起的决定作用最大。
并且x3的p 和s^2值也都比较小,所以最终确定x3可以最好的反映出y 的情况。
55.566.577.588.5可以同之前的仅含一次项的结果进行比较,发现各个参量的置信区间都很宽,且β2的置信区间过0。
可以认为二次项的引入是不重要的。
因此采用如下单参数模型描述y 是最准确地:033y x ββ=+ 其中:0383.4438,-5.6682ββ==双参数回归:用stepwise 作逐步回归,部分过程和最终结果如下图:Coeff. t-stat p-val12Model HistoryR M S E-6-4-2X XX X X Coefficients with Error Bars只取x3自变量的回归结果Coeff. t-stat p-val123Model HistoryR M S E-6-4-2X X X X X Coefficients with Error Bars取x3和x5自变量的回归结果Coeff. t-stat p-val123Model HistoryR M S E-6-4-2X X X X X Coefficients with Error Bars取x3和x1自变量的回归结果根据题目要求,最终得到取双参量时的最佳结果(RMSE 参量最小)是取x3(1500m 跑后心速)和x1(年龄)自变量。
但事实上,实际的逐步回归过程在此时并没有结束,最终的最优结果是只取x3参量。
这说明取x3、x1参量同只取x3相比优势并不明显。
通过rstool 命令检验二元情况下的交互项和高次项情况,下图是linear 情况下固定单参数进5.566.577.584042444648505254可以看到高次项和相关项的系数都非常小,说明其对于y 的影响不大。
根据rmse 的结果进行比较,仍然选择linear 回归方式,即只用二元自变量的一次项。
01133y x x βββ=++ 其中:01390.8529,=-0.1870,-5.4671βββ==全参数回归根据以上的分析可以验证模型建立时的猜想,本题中5个字变量和y 的关系都不是很直接的,除x3外其他变量的影响很小,所以在最终完整模型中,不再考虑高次项和交互项的影响,一方面简化模型,一方面大大节省的筛选的时间。
所以采用stepwise 命令,仅对五元变量x1~x5的一次项进行回归分析,结果如下:Coeff. t-stat p-val1234Model HistoryR M S E-6-5-4-3-2-1X X X X X Coefficients with Error BarsF=29.2364 RMSE=2.66669 P=1.64368*e-7最终取以下三个参数得到最佳回归结果:x3(1500m 跑后心速)、x1(年龄)以及x5(跑步后心速)。
但仍需要进行一般回归分析(regress )确定常数项并观察残差,结果如下:5101520-8-6-4-20246810R e s i d u a l sCase Number残差图(全部点)可以看到10和15号数据异常,剔除,再次观察残差,结果如下246810121416182022-6-4-22468Residual Case Order PlotR e s i d u a l sCase Number残差图(剔除10,15号点)可以看到4号数据变为异常,再次剔除,结果仍然有异常点。
过程从略,最终经过4次剔除,去掉5个点(4,10,15,17,23)以后,得到没有异常点的模型:24681012141618-4-3-2-101234R e s i d u a l sCase Number去掉所有异常点之后的结果最终得到的结果整体上优越于剔除异常点之前的结果(不再粘贴结果)。
但是事实上,由于数据点经过剔除不断的结果,模型最终的形式和实际统计到的24组数据的整体情况偏离越来越大,也就是说:剔除异常点虽然能够一应程度上降低其对于整体情况的干扰作用,而剔除的过程也放大了其他原本正常数据点的异常性,所以异常点可能会不断产生,但是剔除的数量增加即采样数据的减少也会削弱模型反省整体性能的能力。
是一对矛盾,在数据点较少的时候尤其明显。
比较科学的做法是:只进行1次或少次剔除,保证整体性,又去掉了最主要的异常点。
这里的最终结果采用剔除最初两个异常点(10,15号)后的结果,在此也附上完整数据(剔除之前)的结果,作为第3问的答案:0113355y x x x ββββ=+++其中:0135118.0135,=-0.3254,-4.5694,0.1561ββββ===-0113355y x x x ββββ=+++其中:0135119.4955,=-0.03623,-4.0411,0.1774ββββ===-1500m 跑后心速、年龄以及跑步后心速三个参数最能够反映锻炼耗氧量这个重要的身体状态指标。
三种心跳速度越快,说明耗氧量越大;速度越慢,即时间越长,说明耗氧量越小。
习题11:一个医药公司的新药研究部门为了掌握一种新型止痛剂的疗效,设计了一个药物试验,给24名患有同种痛病的病人使用这种新止痛剂的以下4个剂量中的某一:2、5、7、10,(g ),并记录每个病人病痛明显减轻的时间(min ).为了了解新药的疗效与病人性别和血压有什么关系,试验过程中研究人员把柄热男性别集血压的低中高3档平均分配来进行测试。
通过比较每个病人血压的历史数据,从低到高分成3组,分别记作0.25,0.0,0.75。
实验结束后,公司的记录结果见表格(略). 请为公司建立一个模型,根据病人用药的计量、性别和血压组别,预测出服1. 模型建立本题共提供了三种不同的自变量,设为性别-x1,血压-x2和用药计量-x3。
