青岛版八年级下册数学期末测试卷(基础题)

合集下载

青岛版八年级下册数学期末测试卷及含答案(有一套)

青岛版八年级下册数学期末测试卷及含答案一、单选题(共15题，共计45分)1、已知a=.b=的关系是（）A.a＞bB.a＜bC.a=bD.无法确定2、若二次根式在实数范围内有意义，则实数x的取值范围是( )A.x<3B.x＞3C.x≠3D.x≤33、下列运算正确的是（）A. B. C. D.4、已知一次函数的图象与轴交于点A，将直线= -1绕点A逆时针旋转90°后的直线表达式为( )A. B. C. D.5、汽车是人们出行的一种重要的交通工具。

下列汽车标志中，既是轴对称图形又是中心对称图形的是( )A. B. C. D.6、如果不等式组的解集是x＜2，那么m的取值范围是（）A.m=2B.m＞2C.m＜2D.m≥27、已知实数a，b，c所对应的点在数轴上的位置如图所示.求=（）A.aB.-aC.a+bD.b-a+c8、下列各式中，正确的是（）A. =﹣3B.（﹣）2=9C.±=±3D. =﹣29、若有意义，则x的取值范围是（）A.x＞B.x≥C.x＞D.x≥10、如图，是的中线，四边形是平行四边形，增加下列条件，能判断是菱形的是( )A. B. C. D.11、在数学拓展课《折叠矩形纸片》上，小林折叠矩形纸片ABCD进行如下操作：①把△ABF翻折，点B落在CD边上的点E处，折痕AF交BC下边于点F；②把△ADH翻折，点D落在AE边上的点G处，折痕AH交CD边于点H．若AD=6，AB=10，则的值是( )A. B. C. D.12、矩形ABCD的周长为56，对角线AC，BD交于点O，△ABO与△BCO的周长差为4，则AB的长是（）A.12B.22C.16D.2613、下列函数中，一定是一次函数的是A. B. C. D.14、已知a＞b,则下列不等式成立的是（）A. a-c ＞b-cB.a+c ＜b+cC.ac ＞bcD. ＞15、如图，点O是菱形ABCD对角线的交点，DE∥AC，CE∥BD，连接OE，设AC ＝12，BD＝16，则OE的长为（）A.8B.9C.10D.12二、填空题(共10题，共计30分)16、计算的结果是________.17、如图，正方形ABCD的边长为5，连接BD，在线段CD上取一点E，在线段BD上取点F，使得∠BEC=∠DEF，当S△DEF = S△EFB时，在线段BC上有一点G，使FG+EG最短，则CG=________．18、不等式组的解集是________ ；这个不等式组的整数解是________．19、如图，在四边形ABCD中，AC平分∠BAD，BC=CD=10，AC=17，AD=9，则AB=________.20、计算×结果是________21、如图，x轴、y轴上分别有两点、，以点A为圆心，为半径的弧交x轴负半轴于点C，则点C的坐标为________.22、如图，O为矩形ABCD的对角线交点，DF平分∠ADC交AC于点E，交BC于点F，∠BDF=15°，则∠COF=________°．23、若x，y为实数，且满足|x﹣3|+=0，则（）2012的值是________24、x的与12的差不小于6，用不等式表示为________．25、如图，在矩形ABCD中，BC=4，CD=3，将△ABE沿BE折叠，使点A恰好落在对角线BD上的点F处，则DE的长是________．三、解答题(共5题，共计25分)26、计算27、如图，在正方形ABCD中，E为DC边上的点，连接BE，将绕点C 顺时针方向旋转得到，连结EF，若，求的度数．28、一个直角三角形的两条直角边的长分别为cm与cm，求这个直角三角形的面积和周长．29、直线y=kx﹣3经过点A（﹣1，﹣1），求关于x的不等式kx﹣3≥0的解集．30、为了打造区域中心城市，实现攀枝花跨越式发展，我市花城新区建设正按投资计划有序推进．花城新区建设工程部，因道路建设需要开挖土石方，计划每小时挖掘土石方540m3，现决定向某大型机械租赁公司租用甲、乙两种型号的挖掘机来完成这项工作，租赁公司提供的挖掘机有关信息如下表所示：租金（单位：元/台•时）挖掘土石方量（单位：m3/台•时）甲型挖掘机100 60乙型挖掘机120 80（1）若租用甲、乙两种型号的挖掘机共8台，恰好完成每小时的挖掘量，则甲、乙两种型号的挖掘机各需多少台？（2）如果每小时支付的租金不超过850元，又恰好完成每小时的挖掘量，那么共有哪几种不同的租用方案？参考答案一、单选题(共15题，共计45分)1、C2、D3、D4、C5、C6、D7、B8、C9、D10、A11、D12、C13、A14、A15、C二、填空题(共10题，共计30分)16、18、19、20、21、23、25、三、解答题(共5题，共计25分)26、27、28、29、30、。

青岛版八年级下册数学期末测试卷【通用】

青岛版八年级下册数学期末测试卷一、单选题(共15题，共计45分)1、若平行四边形的一边长为2,面积为，则此边上的高介于( )A.3与4之间B.4与5之间C.5与6之间D.6与7之间2、小亮家与姥姥家相距24km，小亮8：00从家出发，骑自行车去姥姥家妈妈8：30从家出发，乘车沿相同路线去姥姥家在同一直角坐标系中，小亮和妈妈的行进路程与北京时间的函数图象如图所示，根据图象得到如下结论，其中错误的是（）A.9：00妈妈追上小亮B.妈妈比小亮提前到达姥姥家C.小亮骑自行车的平均速度是D.妈妈在距家13km处追上小亮3、下列说法中正确的是（）A.平移和旋转都不改变图形的形状和大小B.任意多边形都可以进行镶嵌C.有两个角相等的四边形是平行四边形D.对角线互相垂直的四边形是菱形4、如图，在直角坐标系中有线段AB，AB＝50cm，A、B到x轴的距离分别为10cm和40cm，B点到y轴的距离为30cm，现在在x轴、y轴上分别有动点P、Q，当四边形PABQ的周长最短时，则这个值为（）A.50B.50C.50 －50D.50 ＋505、如图，将绕点逆时针旋转得到点的对应点分别为则的长为（）A. B. C. D.6、下列命题中：真命题的个数是（）①两条对角线互相平分且相等的四边形是正方形；②菱形的一条对角线平分一组对角；③顺次连结四边形各边中点所得的四边形是平行四边形；④两条对角线互相平分的四边形是矩形；⑤平行四边形对角线相等．A.1B.2C.3D.47、对于一次函数y=x+6，下列结论错误的是（）A.函数值随自变量增大而增大B.函数图象与两坐标轴围成的三角形面积为18.C.函数图象不经过第四象限D.函数图象与x轴交点坐标是（0，﹣6）8、关于的不等式只有2个正整数解，则的取值范围为A. B. C. D.9、的立方根是（）A.8B.2C.4D.±410、如图，在平面直角坐标系xOy中，已知点A（3，4），将OA绕坐标原点O 逆时针旋转90°至OA′，则点A′的坐标是（）．A.（-4，3）B.（-3，4）C.（3，-4）D.（4，-3）11、下列选项中，对任意实数a都有意义的二次根式是（）A. B. C. D.12、下列运算错误的是（）A. B. C. D.13、在实数，，，中，最大的数是（）A. B. C. D.14、甲、乙两人沿相同的路线由A地到B地匀速前进，A、B两地间的路程为20km．他们前进的路程为s(km)，甲出发后的时间为t(h)，甲、乙前进的路程与时间的函数图象如图所示．根据图象信息，下列说法正确的是( )A.甲的速度是4km/hB.乙的速度是10km/hC.乙比甲晚出发1h D. 甲比乙晚到B地3h15、一次函数y＝－3x－2的图象不经过（）A.第一象限B.第二象限C.第三象限D.第四象限二、填空题(共10题，共计30分)16、如图，三角形DEF是三角形ABC沿射线BC平移的得到的，BE=2，DE与AC 交于点G，且满足DG=2GE．若三角形CEG的面积为1，CE=1，则点G到AD的距离为________．17、不等式组的解集为________.18、的平方根是________，已知一个数的平方是，则这个数的立方是________.19、如图，在平面直角坐标系中，▱ABCD的顶点B位于y轴的正半轴上，顶点C，D位于x轴的负半轴上，双曲线y＝（k＜0，x＜0）与▱ABCD的边AB，AD交于点E、F，点A的纵坐标为10，F（﹣12，5），把△BOC沿着BC所在直线翻折，使原点O落在点G处，连接EG，若EG∥y轴，则△BOC的面积是________.20、等腰三角形底边长10cm，周长为36cm，则一底角的正切值为________21、如图，Rt△ABC≌Rt△DCB，两斜边交于点O，如果AC=3，那么OD的长为________．22、在Rt△ABC中，∠C＝90°，CA＝8，CB＝6，则△ABC内切圆的面积为________．23、如图，在Rt△ABC中，∠ACB = 90°，，点D、E分别在边AB上，且AD = 2，∠DCE = 45°，那么DE =________．24、如图，折叠直角三角形纸片的直角，使点C落在斜边AB上的点E处，已知CD=1，∠B=30°，则AC的长是________．25、如图，Rt△ABC中，∠ACB=90°，AC=4，将斜边AB绕点A逆时针旋转90°至AB′，连接B′C，则△AB′C的面积为________三、解答题(共5题，共计25分)26、解不等式组：．27、如果一个正数的两个平方根是a+1和2a﹣22，求出这个正数的立方根.28、解不等式组，并把它的解集在数轴上表示出来.29、如图，菱形ABCD的对角线AC，BD相交于点O，AC=6，BD=8，且DE∥AC，AE∥BD．求OE的长．30、如图，矩形ABCD中，E为BC上一点，DF⊥AE于F．若AB=6,AD=12,BE=8，求：DF的长，以及四边形DCEF的面积。

2023-2024学年山东省青岛市市南区八年级下学期期末数学试题

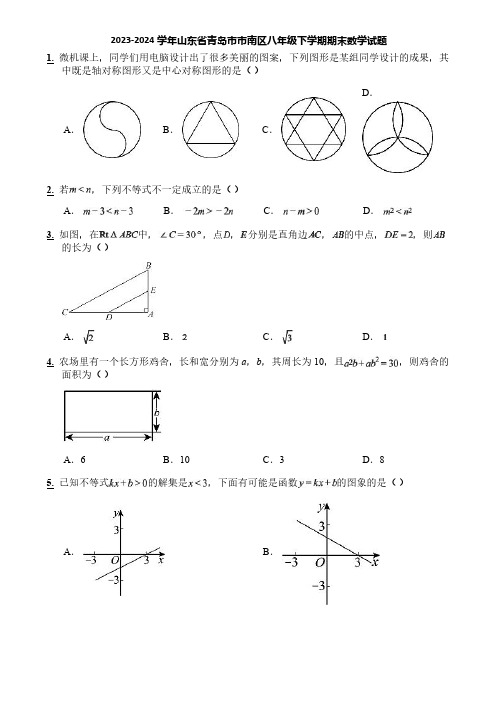
2023-2024学年山东省青岛市市南区八年级下学期期末数学试题1.微机课上，同学们用电脑设计出了很多美丽的图案，下列图形是某组同学设计的成果，其中既是轴对称图形又是中心对称图形的是（）A．B．C．D．2.若，下列不等式不一定成立的是（）A．B．C．D ．3.如图，在中，，点，分别是直角边，的中点，，则的长为（）A．B．C ．D ．4.农场里有一个长方形鸡舍，长和宽分别为a ，b ，其周长为10，且，则鸡舍的面积为（）A ．6B ．10C ．3D ．8 5.已知不等式的解集是，下面有可能是函数的图象的是（）A ．B ．C．D．6.某学校八年级同学到劳动基地进行实践活动，第一天的任务是用100斤黄豆磨豆浆．由于操作不熟练，开始的半小时只磨完9斤黄豆，基地要求完成全部任务的时间不超4小时，若设在剩余时间内每小时需磨完x斤黄豆，则可列不等式为（）A．B．C．D．7.小明在解关于x的分式方程时，发现墨水不小心把其中一个数字污染了，翻看答案上说此方程有增根无解，则被污染的数字为（）A．B．1C．2D．8.如图，中，对角线和交于点，，是对角线上的点，添加以下条件，不能判定四边形是平行四边形的是（）A．B．C．D．9.商场搞促销活动，某件商品的原售价为m元，现7折出售，仍获利，则该商品的进价为（）A．B．C．D．10.如图，中，，，，将进行平移得到，若点D到三边的距离相等，则平移后重叠部分图形的周长为()A．B．C．D．11.将因式分解的结果为________．12.一个正n边形，其内角和是外角和的三倍，则n的值为__________．13.用地砖铺地，用瓷砖贴墙，都要求砖与砖严丝合缝，不留空隙，把地面或墙面全部覆盖．通常把这类问题叫做平面镶嵌．现施工材料里有几种边长相同的多边形瓷砖：①正三角形；②正方形；③正六边形；④正五边形；⑤正八边形，需要从中选择三种进行组合镶嵌，它们是（填序号）_________．14.不等式组无解，则a的取值范围为________．15.若关于x的方程解为正数，则m的取值范围是_____．16.如图，把绕直角顶点C顺时针旋转后得到，点F在线段上，延长交于点G，若，，则的面积为_______．17.请用直尺、圆规作图，不写作法，但要保留作图痕迹．在公园中有一块四边形的空地，需要规划栽种不同品种的植物，空地图纸如图所示，已知四边形，，在边上求作一点M，在边上求作一点N，使得、、的面积都相等．18.（1）因式分解：；（2）解不等式组：19.（1）化简：（2）解分式方程：20.在如图所示的平面直角坐标系中，三个顶点的坐标分别为，，．(1)作出将向左平移5个单位得到的图形；(2)作出将绕点A顺时针旋转得到的图形；(3)若与成中心对称图形写出对称中心的坐标_______．21.如图，等腰中，是腰上的高，在底边上截取，过点E作交于F．(1)求证：(2)若，求的度数．22.八年级研学小组的同学从学校出发参加课外实践活动，目的地距学校120千米．部分同学乘甲车先行，出发半小时后，另一部分同学乘乙车前往，乙车的速度是甲车的倍，结果乙车比甲车提前10分钟到达目的地，求甲车的速度．23.如图，F是线段和的中点，连接、，延长至点A，使，连接．(1)求证：四边形是平行四边形；(2)连接，已知_________（从以下两个条件中选择一个作为已知，填写序号）条件①：；条件②：平分．求证：（注：如果选择条件①条件②分别都进行解答，则按第一个解答计分）24.如图1，在中，是的角平分线．(1)若，，，可得到结论：__________；(2)若，，，可得到结论：__________；(3)图2中，，，，若是的外角平分线，与的延长线交于点E，可得到结论：__________．25.航空航天技术是一个国家综合国力的反映．我国航天事业的飞速发展引发了航空航天模型的热销，某航模店购进了“神舟”和“天宫”两款航空模型共套．设购进“神舟”模型x套，销售完这两种模型所获得的利润为y（元），已知这两种模型的进价与售价如下表所示：“神舟”模型“天宫”模型进价（元/套）售价（元/套）(1)求y与x之间的函数关系式；(2)若购进“神舟”模型的套数不少于“天宫”模型套数的4倍，求销售完这两种模型该航模店所获得的最大利润．26.如图①②，在四边形中，，顶点坐标分别为，，，，，动点从开始以每秒个单位长度的速度沿线段向运动，另一个动点以每秒个单位长度的速度从开始运动，、同时出发，当其中一点到达终点时，另一点也随之停止运动，设运动时间为秒．请回答下列问题：(1)__________，___________；(2)如图①，若点沿折线向运动，①为何值时，，请说明理由；②为何值时，以点、和四边形的任意两个顶点为顶点的四边形是平行四边形，请说明理由；(3)如图②，若点沿射线运动，当线段被平分时，直接写出点坐标为_______．。

青岛版2024年八年级数学下册期末检测题+答案2

八年级下学期期末检测题一、选择题1、若()2x 24,x 2+=+则的平方根为（）A.16B.±16C.2D.±22、一直角三角形的斜边长比一直角边长大1，另一直角边长为4，则斜边长为（）A.4B.8C.10D.123、下列命题正确的是（）A.矩形不是平行四边形B.相似三角形不一定是全等三角形C.等腰梯形的对角线未必相等D.两直线平行，同位角不一定相等4、如图，在菱形ABCD 中，∠ADC=120°，则OD ：OC 等于（）A.3：2B.3：3C.1：2D.3：15、119的估算结果应在（）之间.A 、9到10B 、10到11C 、11到12D 、12到136、如图中字母M 所代表的正方形的面积为（）A.4B.8C.16D.647、甲、乙、丙、丁四人进行射击测试，每人10次射击成绩的平均数都是9.2环，方差分别为20.52S =甲，20.61S =乙，20.49S =丙，45.02=丁S ，则成绩最稳定的是（）A 、甲B 、乙C 、丙D 、丁8、如图，点O 王明家的位置，他家门前有一条东西走向的公路，水塔A 位于他家北偏东60°的300米处，那么水塔所在的位置到公路的距离是（）A.150米B.1503C.1003D.15029、如图△ABC 中，AD 垂直BC 于点D,BE 垂直AC 于点E ，AD 与BE 相交于点F ，若BF=AC ，那么∠ABC 的大小是（）AB C DEFA.40°B.45°C.50°D.60° 10、如图所示，在□ABCD 中，E 为AD 中点，已知△DEF 的面积为S ，则△ABE 的面积为（）A.SB.2SC.3SD.4S11、一组数据的方差为S 2，将这组数据的每个数据都加上2，所得到的一组新数据的方差为（）A.S 2B.2+S 2C.2S 2D.4S 212、在Rt △ABC 中，各边长度都扩大10倍，则锐角B 的正弦值（）A.扩大4倍B.扩大2倍C.不变D.缩小2倍二、填空题13、已知最简二次根式a +1与a 24-是同类二次根式，则a=____________.A B C DEF14、如图，已知AB=BE ，BC=BD ，∠1=∠2，那么图中 ≌ ，AC= ，∠ABC= .15、如图E 、F 、G 、H 分别是矩形ABCD 四边上的点，EF 垂直于GH ，若AB=2，BC=3，则EF ：GH=____.A B C DEFG H 16、已知正方形的面积为3，点E 为DC 边上一点，DE=1，将线段AE 绕点A 旋转，使点E 落在直线BC 上，落点记为F ,则FC 的长为___________.17、如图：直角三角形纸片ABC 中，∠ABC=90o ，AC=8，BC=6,折叠该纸片使点B 与点C 重合，折痕与AB 、BC 的交点分别为D 、E ，（1）DE 的长为_________；（2）将折叠后的图形沿直线AE 剪开，原纸片被剪成3快，其中最小一块的面积为________________.AB C DE三、解答题18、计算：222sin30tan 60cos 45︒+︒-︒19、如图所示，已知点A 、E 、F 、D 在同一条直线上，AE=DF ，BF ⊥AD ，CE ⊥AD ，垂足分别为F 、E ，BF=CE ，求证：AB ∥CD.A 2 1 DC B14EAFC EB D20、在△ABC 中，∠C=90o ，∠CAB=60°，AD 是∠BAC 的平分线，已知AB=23.求AD 的长.AB CD21、如图所示，在□ABCD 中，对角线AC 、BD 交于点O ，过点O 作直线EF ⊥BD ，分别交AD 、BC 于点E 和点F ，求证：BEDF 是菱形.A BC DE F O参考答案：1-5BCBBB 6-12DDABAAC13.1 14.略 15.3：217.4 4 18.41219.略 21.略。

(基础题)青岛版八年级下册数学期末测试卷

青岛版八年级下册数学期末测试卷一、单选题(共15题，共计45分)1、如图，在方格纸中，△ABC经过变换得到△DEF，正确的变换是( )A.把△ABC绕点C逆时针方向旋转90°，再向下平移2格B.把△ABC 绕点C顺时针方向旋转90°，再向下平移5格C.把△ABC向下平移4格，再绕点C逆时针方向旋转180°D.把△ABC向下平移5格，再绕点C顺时针方向旋转180°2、如图，在矩形中，点是的中点，点在上，且若在此矩形上存在一点，使得是等腰三角形，则点的个数是（）A. B. C. D.3、若数a使关于x的不等式组有解且所有解都是2x+6＞0的解，且使关于y的分式方程+3= 有整数解，则满足条件的所有整数a的个数是（）A.5B.4C.3D.24、下列实数是无理数的是（）A.1.732B.C.D.05、估算× +2的值应在（）A.4和5之间B.5和6之间C.6和7之间D.7和8之间6、亮亮准备用自己节省的零花钱买一台英语复读机，他现在已存有45元，计划从现在起以后每个月节省30元，直到他至少有300元．设x个月后他至少有300元，则可以用于计算所需要的月数x的不等式是（）A.30x－45≥300B.30x＋45≥300C.30x－45≤300 D.30x+45≤3007、三个正方形ABCD，BEFG，RKPF的位置如图所示，点G在线段DK上，正方形BEFG的边长为4，则△DEK的面积为（）A.14B.16C.18D.208、直角三角形纸片的两直角边长分别为6，8，现将△ABC如图那样折叠，使点A与点B重合，折痕为DE，则tan∠CBE的值是（）A. B. C. D.9、下列图形是轴对称而不是中心对称图形的是（）A.平行四边形B.等边三角形C.菱形D.正方形10、说法错误的个数是（）①只有正数才有平方根；②-8是64的一个平方根③；④与数轴上的点一一对应的数是实数。

【新】青岛版八年级下册数学期末测试卷及含答案

青岛版八年级下册数学期末测试卷及含答案一、单选题(共15题，共计45分)1、下列四个数中，无理数是（）A.﹣B.﹣C.0D.|﹣2|2、化简的结果是（）A.4B.C.D.3、如图，已知四边形ABCD为菱形，AD＝5cm，BD＝6cm，则此菱形的面积为（）A.12cm 2B.24cm 2C.48cm 2D.96cm 24、一个四边形，对于下列条件，不能判定为平行四边形的是（）A.对角线交点分别是两对角线的中点B.一组对边平行，一组对角相等 C.一组对边相等，一条对角线被另一条对角线平分 D.一组对边平行，一条对角线被另一条对角线平分5、已知是的一次函数，下表列出了部分与的对应值：-1 0 1 2-2 -1 0则的值为（）A.-2B.1C.2D.36、已知一次函数y＝（k+1）x+b的图象如图所示，则k的取值范围是（）A.k＜0B.k＜﹣1C.k＜1D.k＞﹣17、如图，在平行四边形中，，平分交于点E，若，则的度数是（）A.10°B.15°C.20°D.25°8、一次函数y=mx+n的图象如图所示，则方程mx+n=0的解为（）A.x=2B.y=2C.x=-3D.y=-39、小明的父亲饭后出去散步，从家中走20min到一个离家900m的报亭看10min报纸后，用15min返回家里，图中表示小明父亲离家的时间与距离之间的关系是（）A. B. C.D.10、-27的立方根与的算术平方根的和是( )A.0B.6C.6或一1D.0或611、在实数﹣3，0，5，3中，最小的实数是（）A.﹣3B.0C.5D.312、如图，矩形ABCD中，AB＝3，BC＝4，点E是AB边上一点，且AE＝2，点F 是边BC上的任意一点，把BEF沿EF翻折，点B的对应点为G，连接AG，CG，则四边形AGCD的面积的最小值为（）A. B. C. D.813、下列图形中，既是轴对称图形，又是中心对称图形的是（）A. B. C. D.14、如图，一次函数的图象经过A、B两点，则关于x的不等式的解集（）A. B. C. D.15、如图是某机器零件的设计图纸，用不等式表示零件长度的合格尺寸，则长度L的取值范围是（）A.40＜L≤40.2B.38≤L≤42C.39.8≤L≤40.2D.39.8＜L＜40.2二、填空题(共10题，共计30分)16、如图，在矩形ABCD的边AB上有一点E，且，DA边上有一点F，且EF＝18，将矩形沿EF对折，A落在边BC上的点G，则AB＝________.17、如果一个数的平方根是a+6和2a﹣15，则这个数为________．18、如图，∠MAN=90°，点C在边AM上，AC=4，点B为边AN上一动点，连接BC，△A′BC与△ABC关于BC所在直线对称，点D，E分别为AC，BC的中点，连接DE并延长交A′B所在直线于点F，连接A′E．当△A′EF为直角三角形时，AB的长为________．19、当a=2时，二次根式的值是________。

山东省青岛市青岛大学附属中学2023-2024学年八年级下学期期末数学试题

山东省青岛市青岛大学附属中学2023-2024学年八年级下学期期末数学试题一、单选题1．下列图形中，既是轴对称图形又是中心对称图形的是（）A ．B ．C ．D ． 2．若关于x 的不等式2x －a ≤－1的解集是x ≤－1，则a 的值是( )A ．0B ．－3C ．－2D ．－13．下列分解因式正确的是（）A ．24(4)x x x x -+=-+B ．2()x xy x x x y ++=+C ．2()()()x x y y y x x y -+-=-D ．244(2)(2)x x x x -+=+-4．如图，将ABC V 绕点A 逆时针旋转40︒得到ADE V ，AD 与BC 相交于点F ，若80E ∠=︒且AFC V 是以线段FC 为底边的等腰三角形，则BAC ∠的度数为( )A ．55︒B ．60︒C ．65︒D ．70︒5．如图，在平行四边形ABCD 中，按以下步骤作图：①以A 为圆心，任意长为半径作弧，分别交AB AD ，于点M N ，；②分别以M N ，为圆心，以大于12MN 的长为半径作弧，两弧相交于点P ；③作射线AP ，交边CD 于点Q ，若34DC QC BC ==，，则平行四边形ABCD 周长为（）A ．10B ．18C ．16D ．206．若关于x 的分式方程122x x a x x --=--有增根，则a 的值为（） A ．4- B ．4 C ．2- D ．27．已知点()23A -，， ()51B -，，将线段AB 平移至A B ''，点A 的对应点A '在x 轴上，点B 的对应点B '在y 轴上，点A '的横坐标为a ，点B '的纵坐标为b ，则a b -的值为（） A ．7- B ．1- C ．7 D ．18．我们知道，四边形具有不稳定性，如图，在平面直角坐标系中，边长为2的正方形ABCD 的边AB 在x 轴上，AB 的中点是坐标原点O ，固定点A ，B ，把正方形沿箭头方向推，使点D 落在y 轴正半轴上点D ¢处，则点C 的对应点C '的坐标为（）A ．)B ．()2,1C ．(D ．( 9．定义：若一个正整数能表示为两个连续自然数的平方差，那么就称这个正整数为“明德数”．如：22110=-，2321=-，22532=-，因此1，3，5这三个数都是“明德数”．则介于1到200之间的所有“明德数”之和为 ( )A ．10000B ．40000C ．200D ．2500二、填空题10．当x= 时，分式33||x x -+的值等于零． 11．一个正多边形的一个内角比它的外角的2倍多60°，则它的边数是．12．如图，已知直线1y x a =+与2y kx b =+相交于点()1,2P -，则关于x 的不等式kx x a b -≥-的解集是13．正六边形ABCDEF 与平行四边形GHMN 的位置如图所示，若18ABG ∠=︒，则N M D ∠的度数是°．14．中山公园有很多长方形草地，草地里修了很多有趣的小路，如图长方形草地ABCD 长为50米，宽为30米，非阴影部分为1米宽的小路，沿着小路的中间从入口E 处走到出口F 处，所走的路线（图中虚线）长为．15．为了进一步优化环境，某区计划对长3000米的河道进行整治，原计划每天修x 米，为减少施工对居民生活的影响，实际施工时，每天的工作效率比原计划提高20%，那么实际整治这段河道的工期比原计划缩短了天．（结果化为最简）16．如图是五四广场用正六边形、正方形和正三角形地板砖铺设的图案，图案中央是一块正六边形地板砖，周围是正方形和正三角形的地板砖．从里向外第一层包括6块正方形和6块正三角形地板砖；第二层包括6块正方形和18块正三角形地板砖；以此递推．第n 层中含有块正三角形地板砖（用含n 的代数式表示）．现打算在一个新建广场中央，采用如图样式的图案铺设地面，现有1块正六边形、150块正方形和420块正三角形地板砖，问：铺设这样的图案，最多能铺层．三、解答题17．作图题：请用直尺和圆规作图，不写作法，但要保留作图痕迹已知，线段a ，直线l 及l 外一点A ，求作：ABC V ，使AB AC =，BC a =，且点B C 、在直线l 上．18．（1）因式分解：32244b ab a b -+；（2）解分式方程：()222111x x x-+=--；（3）解不等式组()21511325131x x x x -+⎧-≤⎪⎨⎪-<+⎩，并写出所有的整数解；（4）化简：2321222a a a a a ⎛⎫ ⎪⎝⎭-++-÷++，并在2-，1，3三个数中选取一个合适的数值作为a 的值，求出化简后的值．19．如图，ABC V 中，BE 平分ABC ∠，E 在AC 垂直平分线上，EF BC ⊥于F ，EG AB ⊥于G ．(1)求证：AG CF =；(2)若10BC =，4AB =，求FC 的长．20．小丽有慢跑的习惯，她常使用某种运动软件来记录她的跑步数据．下面是她4次慢跑的具体数据．如你所见，她的慢跑速度相对稳定，基本不变．我们把小丽跑步的千米数记为()km x ，把她在此过程中消耗的总热量记为 y （大卡）．(1)根据上述表格提供的数据，在下面的平面直角坐标系中描点、连线．按照这4次的规律，求：y 与x 之间的函数关系式；(2)某日，小丽购买面包和酸奶共计8件食品，已知每袋面包产生110大卡的热量，每杯酸奶产生50大卡的热量．她要跑步10km 才能将这8件食品所产生的热量全部消耗掉．跑步10km ，她消耗的总热量是多少大卡？她最多购买了几袋面包？请说明你的理由．21．已知：如图，在四边形ABCD 中，90BAC ACD ∠=∠=︒，12AB CD =，点E 是CD 的中点．（1）求证：四边形ABCE 是平行四边形；（2）若4AC =，AD =ABCE 的面积．22．今年荆州马拉松比赛召开前，某体育用品专卖店抓住商机，计划购进A B ，两种跑鞋共80双进行销售．已知9000元全部购进B 种跑鞋数量是全部购进A 种跑鞋数量的1.5倍，A 种跑鞋的进价比B 种跑鞋的进价每双多150元，A B ，两种跑鞋的售价分别是每双550元，500元． (1)求A B ，两种跑鞋的进价分别是多少元？(2)该体育用品专卖店根据以往销售经验，决定购进A 种跑鞋的数量不多于B 种跑鞋的23，销售时对B 种跑鞋每双降价25%出售．若这批跑鞋能全部售完，则如何购货才能获利最大？最大利润是多少？23．【图形定义】连接三角形两边中点的线段叫做三角形的中位线．类似的，我们把连接四边形对边中点的线段叫做四边形的中位线．例如：如图1，在四边形ABCD 中，点M 是AB 的中点，点N 是CD 的中点，MN 是四边形ABCD 的中位线．【方法探究】如图2，已知MN 是ABC V 的中位线，以点N 为中心将ABC V 旋转180︒得到CB A '△，可证12MN BC =．【方法应用】(1)如图3，MN 是梯形ABCD 的中位线．若35AD BC ==，，则MN =；若AD a =，BC b =，且b a >，则MN =．(2)如图4，MN 是四边形ABCD 的中位线．若35AD BC ==，，AD 与BC 不平行，则MN 的取值范围是；若AD a BC b ==，，且b a >，AD 与BC 不平行，则MN 的取值范围是．(3)如图5，在五边形ABCDE 中，AE CD ∥，6120AB AE A ==∠=︒，，4CD =，若点F G ，分别是边BC DE ，的中点，则线段FG 的长是．24．如图1，在ABC V 中，90C ∠=︒，30ABC ∠=︒，12AB =，DEF V 中，90DFE ∠=︒，6EF DF ==，DEF V 从点C 开始沿射线CB 平移，直角边EF 始终在射线CB 上，连接AD 、BD ，如图2，设CE 的长度为(0x x <<．(1)是否存在点A 在BD 垂直平分线上的情况？存在，求x 的值；不存在，说明理由；(2)连接AE ，当x 为何值时，四边形AEBD 是平行四边形？说明理由；(3)将ABD △绕点B 逆时针旋转60︒，得到A BD ''V ，是否存在x 的值，使点D ¢落在ABC V 的边上？若存在，直接写出x 的值为；若不存在，说明理由．。

(基础题)青岛版八年级下册数学期末测试卷

青岛版八年级下册数学期末测试卷一、单选题(共15题，共计45分)1、将一副三角板按如图①的位置摆放，将△DEF绕点A（F）逆时针旋转60°后，得到如图②，测得CG=6 ，则AC长是（）A.6+2B.9C.10D.6+62、若方程有两个不等的实数根，则m的取值范围是( )A.m=1B.C. 且D. 且3、不等式组的整数解是（）A.15B.16C.17D.15，14、二次根式在实数范围内有意义，则x的取值范围是（）A.x≥3B.x＞3C.x≥0D.x＞05、9的平方根是（）A.±3B.3C.81D.±816、地铁是城市生活中的重要交通工具，地铁标志作为城市地铁的形象和符号，出现在城市的每个角落，它是城市文化的缩影．下列城市地铁的标志图案中（文字部分除外），既是轴对称图形又是中心对称图形的是（）A. B. C. D.7、在函数自变量x的取值范围是( )A. B. C. D.8、如图，在中，对角线与相交于点O，点分别是的中点，连接.若，则的长为（）A.8B.6C.4D.29、从3，﹣1，，1，﹣3这5个数中，随机抽取一个数记为a，若数a使关于x的不等式组无解，且使关于x的分式方程﹣=﹣1有整数解，那么这5个数中所有满足条件的a的值之积是（）A. B.﹣2 C.﹣3 D.﹣10、如图，△ABC沿BC方向平移得到△DEF，已知BC＝7，EC＝4，那么平移的距离为（）A.2B.3C.5D.711、如果关于x的不等式组的整数解仅为3，4，5，那么适合这个不等式组的整数对共有（）A.8对B.12对C.15对D.20对12、下列说法中，不正确的个数有( )．①所有的正数都是整数. ② 一定是正数. ③无限小数一定是无理数.④ 没有平方根. ⑤不是正数的数一定是负数. ⑥带根号的一定是无理数.A.3个B.4个C.5个D.6个13、实数0是（）A.有理数B.无理数C.正数D.负数14、如图，在菱形ABCD中，DE⊥AB，cosA＝，BE＝2，则tan∠CDB的值是（）A. B.2 C. D.15、如图所示的四边形，与选项中的四边形一定相似的是（）A. B. C. D.二、填空题(共10题，共计30分)16、如图，正方形ABCD中，AB＝6，点E在边CD上，且CD＝3DE，将△ADE沿AE对折至△AEF，延长EF交边BC于点G，连结AG，CF，则下列结论：①△ABG≌△AFG；②BG＝CG；③AG∥CF；④S△EGC ＝S△AFE；⑤S△FGC＝；其中正确的结论有________.17、在平面直角坐标系xOy中，点P（2，﹣3）关于原点O对称的点的坐标是________.18、如图，将矩形ABCD绕点C沿顺时针方向旋转90°到矩形A′B′CD′的位置，AB=2，AD=4，则阴影部分的面积为________．19、解：（1）观察与归纳：在如图1所示的平面直角坐标系中，直线l与y轴平行，点A与点B是直线l上的两点（点A在点B的上方）．①小明发现：若点A坐标为（2，3），点B坐标为（2，﹣4），则AB的长度为________ ；②小明经过多次取l上的两点后，他归纳出这样的结论：若点A坐标为（t，m），点B坐标为（t，n），当m＞n时，AB的长度可表示为________ ；（2）如图2，正比例函数y=x与一次函数y=﹣x+6交于点A，点B是y=﹣x+6图象与x轴的交点，点C在第四象限，且OC=5．点P是线段OB上的一个动点（点P不与点0、B重合），过点P与y轴平行的直线l交线段AB于点Q，交射线OC于R，设点P横坐标为t，线段QR的长度为m．已知当t=4时，直线l 恰好经过点C．①求点A的坐标________②求OC所在直线的关系式________③求m关于t的函数关系式________20、如图，在正方形ABCD中，E是AB上一点，BE=2，AE=3，P是AC上一动点，则PB+PE的最小值是________．21、已知△ABC中，点D为BC边上一点，且BD：CD=7：4，点A、E均在CD的垂直平分线上，BG⊥BD，连接GD交AB于点F，若∠AFD=45°，EC=GD，∠GDB+∠ECB=90°，AC= ，则CD=________．22、如图，在Rt△ABC中，∠ACB=90°，AC=BC=1，将Rt△ABC绕A点逆时针旋转30°后得到Rt△ADE，点B经过的路径为，则图中阴影部分的面积是________．23、观察下列各组勾股数，并寻找规律：①4，3，5；②6，8，10；③8，15，17；④10，24，26 ……请根据你发现的规律写出第⑦组勾股数：________.24、如图，O是矩形ABCD的对角线AC的中点，M是AD的中点．若AB=5，AD=12，则四边形ABOM的周长为________ ．25、如图，在平面直角坐标系中，三角形②是由三角形①绕点P旋转后所得的图形，则旋转中心P的坐标是________.三、解答题(共5题，共计25分)26、解不等式组，并把解集在数轴上表示出来．27、如图，在△ABC中，CD⊥AB于D，AC＝20，BC＝15，AD＝16，求AB的长．28、某电梯的额定限载量为1000kg．两人要用电梯把一批货物从底层搬到顶层，已知这两个人的体重分别为70kg和60kg，货物每箱重50kg，问他们每次最多只能搬运货物多少箱？29、如图，E是▱ABCD的边AD的中点，连接CE并延长交BA的延长线于F，若CD=6，求BF的长．30、某学校组织八年级学生参加社会实践活动，若单独租用35座客车若干辆，则刚好坐满；若单独租用55座客车，则可以少租一辆，且余45个空座位．（1）求该校八年级学生参加社会实践活动的人数；（2）已知35座客车的租金为每辆320元，55座客车的租金为每辆400元．根据租车资金不超过1500元的预算，学校决定同时租用这两种客车共4辆（可以坐不满）．请你计算本次社会实践活动所需车辆的租金．参考答案一、单选题(共15题，共计45分)1、A2、D3、B4、A5、A6、D7、A9、C10、B11、C12、D13、A14、B15、D二、填空题(共10题，共计30分)16、17、18、19、20、21、22、23、24、三、解答题(共5题，共计25分)26、27、28、30、。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

青岛版八年级下册数学期末测试卷
一、单选题(共15题，共计45分)
1、如图，一棵树在一次强台风中于离地面4米处折断倒下，倒下部分与地面成30°夹角，这棵树在折断前的高度为（）米．
A.4
B.8
C.12
D.
2、在中，，两直角边，，在三角形内有一点到各边的距离相等，则这个距离是（）
A.1
B.2
C.3
D.4
3、下列函数是一次函数的是（）
A.y=﹣8x
B.y=﹣
C.y=
D.y=﹣+2
4、下列函数图象中，当x＞0时，y随x的增大而减小的是（）
A.y=﹣
B.y=x
C.y=x 2
D.y=﹣（x+1）2
5、如图，有a、b、c三户家用电路接入电表，相邻电路的电线等距排列，则三户所用电线（）
A.a户最长
B.b户最长
C.c户最长
D.三户一样
6、如图所示的车标，可以看作由“基本图案”经过平移得到的是（）
A. B. C. D.
7、下列说法中不正确的是（）
A.-1的平方是1
B.-1的立方是-1
C.-1的平方根是-1
D.-1的立方根是-1
8、点A ， B ， C是平面内不在同一条直线上的三点，点D是平面内任意一点，若A ， B ， C ， D四点恰能构成一个平行四边形，则在平面内符合这样条件的点D有（）
A.1个
B.2个
C.3个
D.4个
9、如图，在平行四边形中，，，，则
的长是（）
A. B. C.3 D.5
10、某市为了鼓励节约用水，按以下规定收水费：每户每月用水量不超过
，则每立方米水费为元，每户用水量超过，则超过的部分每立方米水费2元，设某户一个月所交水费为元，用水量为，则y与x的函数关系用图象表示为（）
A. B. C.
D.
11、下列实数中，是无理数的是（）
A.﹣0.101001
B.
C.
D.﹣
12、正比例函数图象y=（1-m)x的图像经过第一，三象限，则m的取值范围是（）
A.m=1
B.m>1  
C.m<1
D.m≥1
13、如图，已知点A（﹣8，0），B（2，0），点C在直线y=﹣上，则使△ABC是直角三角形的点C的个数为（）
A.1
B.2
C.3
D.4
14、如图，正方形ABCD和正方形CEFG中，点D在CG上，BC＝1，CE＝3，H是AF的中点，那么CH的长是（）
A.2
B.
C.
D.
15、估计的结果在（）.
A.6至7之间
B.7至8之间
C.8至9之间
D.9至10之间
二、填空题(共10题，共计30分)
16、如图，在▱ABCD中，对角线AC，BD交于点O，AB⊥AC，AH⊥BD于点H，若AB＝2，BC＝2 ，则AH的长为________．
17、计算6 -15 的结果是________.
18、计算________.
19、比较大小：________ ．
20、如图，正五边形ABCDE绕点A顺时针旋转后得到正五边形
AB′C′D′E′，旋转角为α（0°≤α≤90°），若DE⊥B′C′，则∠α＝________°
21、一辆汽车由A地开往B地，它距离B地的路程s(km)与行驶时间t(h)之间的关系如图所示，如果汽车一直快速行驶，那么可以提前________小时到达B 地．
22、如图，，，，，，
，垂足分别为D，E，则的长为________.
23、不等式组的解集是________ .
24、已知，矩形ABCO的对角线AC、BO相交于点D，△ADO是等边三角形，且A 点的坐标为（0，2），则点D的坐标为________．
25、）如图，Rt△ABC中，C= 90o，以斜边AB为边向外作正方形 ABDE，且正方形对角线交于点D，连接OC，已知AC=5，OC=6 ，则另一直角边BC的长为________．
三、解答题(共5题，共计25分)
26、先化简，再求值：，其中X的值从不等式组
的整数解中选取.
27、如图，在△ABC中，∠BAC=90°，AD是中线，E是AD的中点，过点A作AF∥BC交BE的延长线于F，连接CF，求证：四边形ADCF是菱形．
28、某超市店庆期间开展了促销活动，出售A，B两种商品，A种商品的标价为60元/件，B种商品的标价为40元/件，活动方案有如下两种，顾客购买商品时只能选择其中的一种方案：
A B
方案一按标价的“七折”优惠按标价的“八折”优惠
方案二若所购商品达到或超过35件（不同商品可累计），均按标价的“七五折”优惠
若某单位购买A种商品x件（x＞15），购买B种商品的件数比A种商品件数多10件，求该单位选择哪种方案才能获得更多优惠？
29、判断下列各式哪些是等式，哪些是不等式，哪些既不是等式也不是不等式．
① x＋y；② 3x＞7；③ 5＝2x＋3；④ x2＞0；⑤ 2x－3y＝1；⑥ 52；⑦ 2＞
3.
30、计算：（）﹣2+（π﹣3.14）0﹣| |﹣2cos30°．
参考答案
一、单选题(共15题，共计45分)
1、C
2、B
3、A
4、D
5、D
6、B
7、C
9、B
10、C
11、B
12、C
13、C
14、D
15、B
二、填空题(共10题，共计30分)
16、
17、
18、
19、
20、
21、
22、
23、
24、
25、
三、解答题(共5题，共计25分)
29、
30、。