中南大学信息论与编码讲义-第七章
信息论与编码原理第7章信道编码的基本概念PPT课件

二进制:每个码元的信息含量为 1 比特,二进制的波特率与比特 率在数值上是相等的。
M进制:每一个码元的信息含量为 log2M。如果码元传输速率为 rs
波特,相应的比特率 rb 为:rb = rs log2M (bit/s)
05.08.2020
Department of Electronics and Information, NCUT Song Peng
▼ 在电报传送时,允许的比特差错率约为 10-4~10-5; ▼ 计算机数据传输,一般要求比特差错率小于 10-8~10-9; ▼ 遥控指令和武器系统指令中,要求误比特率更小。
05.08.2020
Department of Electronics and Information, NCUT Song Peng
第8页
7.1 信道编码在数字通信系统中的地位和作用
(2) 通信系统的主要技术指标
差错率:差错率是衡量传输质量的重要指标之一,有几种不同的定义 码元差错率:指在传输的码元总数中发生差错的码元数所占的比例 (平均值),简称误码率。 比特差错率(比特误码率):指在传输的比特总数中发生差错的比 特数所占的比例(平均值)。在二进制传输系统中,码元差错率就是 比特差错率。 码组差错率:指在传输的码组总数中发生差错的码组数所占的比例 (平均值)。 根据不同的应用场合对差错率有不同的要求。
信息论与编码原理
(第七章)
──────────────
信道编码的基本概念
05.08.2020
Department of Electronics and Information, NCUT So点击此处输入相关文本内容 点击此处输入相关文本内容
概况二
点击此处输入相关文本内容 点击此处输入相关文本内容
信息论与编码课件910PPT

信源消息中的信息是一个时变的不可预知的函数,因 此,描述信源消息或对信源建模,随机过程是一个有效的 工具,随机过程的特性依赖于信源的特性。
离散信源和连续信源
信源的输出被抽象为一个随机变量序列(随机过程)
离散信源:如果信源输出的随机变量取值于某一离散符号集 合,消息在时间和幅值上均是离散的,就叫做离散信源。
pi
log
[
1] pi
自信息量的单位取决于对数选取的底。
单位:比特bit、奈特nat、笛特Det 。
当对数的底取2时,单位为比特bit
当以自然数e为底时,单位为奈特nat(理论推导常用)
当以10为底时,单位为笛特Det(工程计算常用)
表
对数及常用公式
y=log10x y=logbx
x=10y x=by
➢ 离散(数字)消息,一组未知量,可用随机序列来描述: X=(X1…Xi…Xn)
➢ 连续(模拟)消息,未知量,它可用随机过程来描述: X(t)
信息:它是更高层次哲学上的抽象,是信号与消 息的更高表达层次。
信息、消息和信号
❖ 信息、消息和信号是既有区别又有联系的三 个不同的概念。
消息中包含信息,是信息的载体。 信号携带着消息,它是消息的运载工具。
什么是信息?
就狭义而言,在通信中对信息的表达分为 三个层次:信号、消息、信息。 信号:是信息的物理表达层,是三个层次 中最具体的层次。它是一个物理量,是一 个载荷信息的实体,可测量、可描述、可 显示。
消息:(或称为符号)是信息的数学表达层,它虽 不是一个物理量,但是可以定量地加以描述,它 是具体物理信号的进一步数学抽象,可将具体物 理信号抽象为两大类型:
中南大学信息论与编码讲义-第三章

3.1率失真函数
• R(δ)的计算
0 1 D= 1 0
例3.1(续)P{U=0}=p,P{U=1}=q。 d(u,v)=0 ● δmin=∑up(u) minv d(u,v)=0。 ● δmax=minv ∑up(u) d(u,v)=min{p,q}=p。 ●对于δmin≤δ≤δmax,选择达到了R(δ)试验信道。即, E(d)=P(U≠V)=δ,求I的最小值。 方法1:由定理1.2知,H(U|V)≤H(δ)。故有 I(U;V)=H(U)-H(U|V)=H(p)-H(U|V)≥H(p)-H(δ)。下面通过证 明可以找到一个试验信道达到这个值H(p)-H(δ)。 定义一个反向试验信道,即给定转移概率p(u|v)。如 图所示:
u v v
= ∑ p (u ) min d (u , v)
u v
率失真函数的性质
• R(δ)是δ≥δmin的下降函数
如果δ1>δ2,则满足E(d)≤kδ2的所有试验信道,一定是满足 E(d)≤kδ1的试验信道,所以Rk (δ1) ≤ Rk (δ2) 。所以 Rk (δ)在δ≥δmin范围内是下降函数。
第三章
离散无记忆信源及率失真函数
离散无记忆信源及率失真函数
一 般 可以 对 信源 输出的信息进行失真处理 , 降 低信 息率 , 提 高传输 效率那么允许在一定程度的失真 条件下 , 能够把信源信 息压 缩到什 么程 度 , 至少需 要 多 少比特的 信 息 率 才 能 描 述 信 源 呢 ? 本章主要讨论在一定程度的失真情况下,所需的最 少信息率。
证明:(略)
率失真函数的性质
• R (δ)在δ≥δmin范围内是连续的。 • 存在一个δmax,当δ≥δmax时,R(δ)=0。
中南大学信息论与编码编码部分实验报告

信息论与编码编码部分实验报告课程名称:信息论与编码实验名称:关于香农码费诺码Huffman码的实验学院:信息科学与工程学院班级:电子信息工程1201姓名:viga学号:指导老师:张祖平日期:2014年1月3日目录⊙实验目的及要求1.1 实验目的 (4)1.2 开发工具及环境 (4)1.3 需求分析与功能说明 (4)⊙实验设计过程2.1 用matlab实现香农码、费诺码和Huffman编码2.1.1 说明 (6)2.1.2 源代码 (7)2.1.3 运行结果(截图) (19)2.2 用C\C++ 实现香农码2.2.1 说明 (22)2.2.2 源代码 (23)2.2.3 运行结果(截图) (26)2.3 用C\C++ 实现Huffman码2.3.1 说明 (26)2.3.2 源代码 (29)2.3.3 运行结果(截图) (36)2.4 用C\C++ 实现费诺码2.4.1 说明 (37)2.4.2 源代码 (37)2.4.3运行结果结果(截图) (40)⊙课程设计总结 (42)⊙参考资料4.1 课程设计指导书 (43)实验目的及要求1.1 实验目的1.掌握香农码、费诺码和Huffman编码原理和过程。
2.熟悉matlab软件的基本操作,练习使用matlab实现香农码、费诺码和Huffman编码。
3.熟悉C/C++语言,练习使用C/C++实现香农码、费诺码和Huffman编码。
4.应用Huffman编码实现文件的压缩和解压缩。
1.2 开发工具及环境MATLAB 7.0、wps文字、红精灵抓图精灵2010Windows7 系统环境1.3 需求分析与功能说明1、使用matlab实现香农码、费诺码和Huffman编码,并自己设计测试案例。
2、使用C\C++实现香农码、费诺码和Huffman编码,并自己设计测试案例。
3、可以用任何开发工具和开发语言,尝试实现Huffman编码应用在数据文件的压缩和解压缩中,并自己设计测试案例。
彭代渊王玲-信息论与编码理论-第七章习题解答

7 c6=1100111, c7=1110000。 又因伴随式有 24=16 种组合, 差错图样为 1 的有 7种 , 1 7 T T 差错图样为 2 的有 21种 ,而由 Hr He ,则计算陪集首的伴随式,构造伴 2
随表如下: 伴随式 0000 1101 1010 0111 1000 0100 0010 0001 陪集首 0000000 1000000 0100000 0010000 0001000 0000100 0000010 0000001 伴随式 0101 1001 1111 1100 1110 1011 0011 0110 陪集首 1001000 1000100 0011000 0001100 0100100 0100001 0010100 0000110
0 1 0 1 0 1 0 G 0 0 1 0 1 1 1 1 0 0 1 1 0 1
(1)求系统生成矩阵; (2)求校验矩阵; (3)求最小汉明距离; (4)列出伴随式表。 3.已知一个(6, 3)线性码 C 的生成矩阵为:
1 0 0 1 0 1 G 0 1 0 0 1 1. 0 0 1 1 1 0
得到线性码 C 的系统生成矩阵为
1 0 0 1 1 GS 0 1 0 1 0 0 1 1 1 0 0 1 1 1 0 1 0 0 1 1 1
(2)码字 c (c0 , c1 , , c n1 ) 的编码函数为 生成了的 8 个码字如下 信息元 000 001 010 011 100 101 110 111
(1)求校验矩阵,并校验 10110 是否为一个码字; (2)求生成矩阵,并由信息码元序列 101 生成一个码字。 解: (1)由监督方程直接得监督矩阵即校验矩阵为:
《信息论与编码》部分课后习题参考答案

P ( y1 = 0 | M 1 ) P ( y1 = 0)
因为信道为无记忆信道,所以
P( y1 = 0 | M 1 ) = P( y1 = 0 | x11 x12 = 00) = P( y1 = 0 | x11 = 0) = P(0 | 0) = p
同理,得 I ( y1 = 0 | M i ) = P ( y1 = 0 | xi1 xi 2 ) = P ( y1 = 0 | xi1 ) 输出第一个符号是 y1=0 时, 有可能是四个消息中任意一个第一个数字传送来的。 所以
第二章
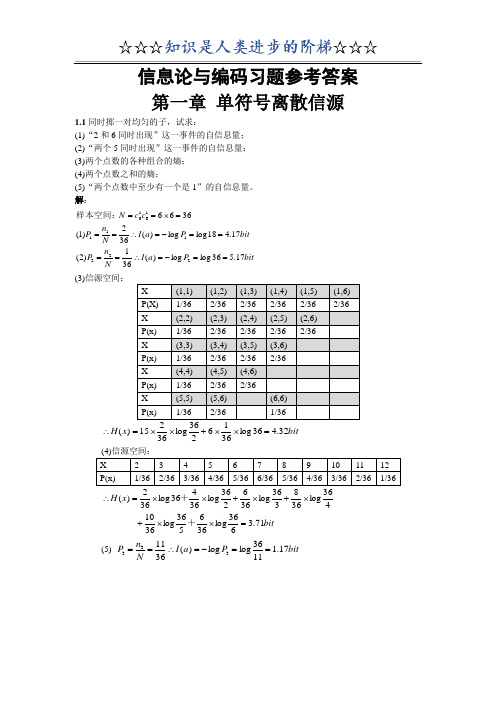
2.1 同时掷两个骰子,设每个骰子各个面向上的概率都是 1/6。试求: (1)事件“2 和 6 同时出现”的自信息量; (2)事件“两个 3 同时出现”的自信息量; (3)事件“两个点数中至少有一个是 5”的自信息量; (4)两个点数之和的熵。 答: (1)事件“2 和 6 同时出现”的概率为:
《信息论与编码》
部分课后习题参考答案
1.1 怎样理解消息、信号和信息三者之间的区别与联系。 答:信号是一种载体,是消息的物理体现,它使无形的消息具体化。通信系统中传输的是 信号。 消息是信息的载体, 信息是指消息中包含的有意义的内容, 是消息中的未知成分。 1.2 信息论的研究范畴可以分成哪几种,它们之间是如何区分的? 答:信息论的研究范畴可分为三种:狭义信息论、一般信息论、广义信息论。 1.3 有同学不同意“消息中未知的成分才算是信息”的说法。他举例说,他从三岁就开始背 诵李白诗句“床前明月光,疑是地上霜。举头望明月,低头思故乡。 ” ,随着年龄的增长, 离家求学、远赴重洋,每次读到、听到这首诗都会带给他新的不同的感受,怎么能说这 些已知的诗句没有带给他任何信息呢?请从广义信心论的角度对此现象作出解释。 答:从广义信息论的角度来分析,它涉及了信息的社会性、实用性等主观因素,同时受知识 水平、文化素质的影响。这位同学在欣赏京剧时也因为主观因素而获得了享受,因此属于广 义信息论的范畴。
信息论与编码习题参考答案(全)
111
(1)在W4=011中,接到第一个码字“0”后获得关于a4的信息量I(a4;0);
(2)在收到“0”的前提下,从第二个码字符号“1”中获取关于a4的信息量I(a4;1/0);
(3)在收到“01”的前提下,从第三个码字符号“1”中获取关于a4的信息量I(a4;1/01);
(4)从码字W4=011中获取关于a4的信息量I(a4;011)。
其中N=2FT,б2X是信号的方差(均值为零),б2N是噪声的方差(均值为零).
再证:单位时间的最大信息传输速率
信息单位/秒
(证明详见p293-p297)
5.12设加性高斯白噪声信道中,信道带宽3kHz,又设{(信号功率+噪声功率)/噪声功率}=10dB.试计算改信道的最大信息传输速率Ct.
解:
5.13在图片传输中,每帧约有2.25×106个像素,为了能很好的重现图像,需分16个量度电平,并假设量度电平等概率分布,试计算每分钟传输一帧图片所需信道的带宽(信噪功率比为30dB).
(2)求信源的极限熵H∞;
(3)求当p=0,p=1时的信息熵,并作出解释。
解:
3.10设某马尔柯夫信源的状态集合S:{S1S2S3},符号集X:{α1α2α3}。在某状态Si(i=1,2,3)下发发符号αk(k=1,2,3)的概率p(αk/Si) (i=1,2,3; k=1,2,3)标在相应的线段旁,如下图所示.
证明:
3.5试证明:对于有限齐次马氏链,如果存在一个正整数n0≥1,对于一切i,j=1,2,…,r,都有pij(n0)>0,则对每个j=1,2,…,r都存在状态极限概率:
(证明详见:p171~175)
3.6设某齐次马氏链的第一步转移概率矩阵为:
信息论与编码教学课件(全)

目录
• 课程介绍与背景 • 信息论基础 • 编码理论基础 • 信道编码技术 • 数据压缩技术 • 多媒体信息编码技术 • 课程总结与展望
01
课程介绍与背景
Chapter
信息论与编码概述
信息论的基本概念
01
信息、信息量、信息熵等
编码的基本概念
02
信源编码、信道编码、加密编码等
02
极化码(Polar Codes)
一种新型信道编码方式,通过信道极化现象实现高效可靠的信息传输。
03
深度学习在信道编码中的应用
利用深度学习技术优化传统信道编码算法,提高编码性能和效率。
05
数据压缩技术
Chapter
数据压缩概述与分类
数据压缩定义
通过去除冗余信息或使用更高效的编码方式,减小数据表示所需存储空间的过 程。
线性分组码原理:线性分组码是一 种将信息序列划分为等长的组,然 后对每组信息进行线性变换得到相 应监督位的编码方式。
具有严谨的代数结构,易于分析和 设计;
具有一定的检错和纠错能力,适用 于各种通信和存储系统。
循环码原理及特点
循环码原理:循环码是一种特殊的线 性分组码,其任意两个码字循环移位
后仍为该码的码字。
03
编码理论基础
Chapter
编码的基本概念与分类
编码的基本概念
编码是将信息从一种形式或格式转换为另一种形式的过程,以 满足传输、存储或处理的需要。
编码的分类
根据编码的目的和原理,可分为信源编码、信道编码、加密编 码等。
线性分组码原理及特点
线性分组码特点
监督位与信息位之间呈线性关系, 编码和解码电路简单;
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
7.2 q进制对称信道上的伴随式 译码
对应于qn-k个伴随式s,码C一共有qn-k个陪集;每个陪集包 含qk个元素。因此一旦接收方计算出s,就可以将z的搜寻范 围从qn种可能降低到qk种可能,即搜寻范围是与s相对应的陪 集元素。
7.2 q进制对称信道上的伴随式 译码
假设信道是q进制对称信道(qSC),即如果X是表示信道 输入的随机矢量,Y是表示信道输出的随机矢量,则Y=X+Z, Z是一个随机矢量,它的分量是独立、同分布的随机变量,具 有相同的分布: P{Z=0}=1-(q-1)ε。 P{Z=z且z≠0}= ε 对于这个信道,z∈Vn(Fq),则 P(Z=z)=[1-(q-1)ε]n-WH(Z) εWH(Z) wH(Z)为z的汉明重量,被定义为z中非零分量的个数,即出现 错误的个数。
7.1 生成和一致校验矩阵
将这k个基底码字排列成一个k×n的矩阵G
g11 g G = 21 ... g k1 g12 g 22 ... gk 2 ... g1n ... g 2 n ... ... ... g kn
则G称为C的生成矩阵。
7.1 生成和一致校验矩阵
定义:令C是Fq上的一个(n,k)线性码。一个行空间等于C的k × n阶矩阵G称为C的生成矩阵。相反,如果G是元素取自Fq的一 个矩阵,则它的行空间称为由G生成的码。 由于k个基底即G的k个行矢量线性无关 , 矩阵G的秩一定等 于 k。当信息元确定后,码字仅由G矩阵决定, 因此称这k×n矩 阵 G为该 ( n, k ) 线 性分组码的生成矩阵。 将信息u映射为码字x的规则是: x=uG
第二部分 编码理论
第七章 线性码
第七章 线性码
• • • • • • 7.1 生成和一致校验矩阵 7.2 q进制对称信道上的伴随式译码 7.3 汉明几何和码的性能 7.4 汉明码 7.5 一般q进制对称信道上的伴随式译码 7.6 重量牧举多项式和MacWilliams恒等 式
7.1 生成和一致校验矩阵
7.1 生成和一致校验矩阵
如果G不具有这种形式,则可以通过列置换为[IkA]形式,然后 再对[-ATIn-k]进行逆置换而得到H。 例如有G1,G2和G3生成的一致校验矩阵是:
1 1 H1 = 1 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1
1 1 0 0 0 H2 = 1 0 1 1 1
7.2 q进制对称信道上的伴随式 译码
• 伴随式
如果传输的是x,输出的是y。引进矢量s=HyT,称为y的伴 随式。伴随式最重要的特性是,它只依赖于错误图案z而不依 赖于所传输的码字,即 s=HyT=H(x+z)T=HzT 由于y是已知的,则只要知道了z,就能求得x。伴随式 提供了z的一些信息,但不够充分。因为对于一个固定的s, 方程HzT=s的解的集合形成了码C的一个陪集,即一个具有如 下形式的Vn(Fq)的子集:C+z0={x+z0:x∈C}
7.2 q进制对称信道上的伴随式 译码
• 错误图案
假定信道输出符号集AY=Fq,即输入与输出符号集相同。 因此如果传输的是x=(x1,x2,…,xn)∈Vn(Fq),则接收矢量 y=(y1,y2,…,yn)也属于Vn(Fq);两者的差值z=y-x称为错误图案。 如果zi≠0,我们就称在第i个位置上出现了一个错误。
0 1 1 1 1 0 0 H 3 = 1 0 1 1 0 1 0 生成和一致校验矩阵
• 定理7.1
令C是Fq上的一个(n,k)线性码,则存在唯一的一个k×n阶RRE 矩阵G,满足x∈C,当且仅当x在G的行空间内。另外,存在一 个(n-k)×n阶矩阵H,满足x∈C当且仅当HxT=0。如果码C被用 于一个无记忆信道,则不失一般性,可以假设存在一个k ×(n-k)阶矩阵A,使得: G=[IkA], H=[-ATIn-k] 在这种情况下,矢量u∈Vk(Fq)的编码由u→(u,uA)给出。
例 考虑码C2,它的一致校验矩阵是: 只有四个可能的伴随式:00,01,10,11。
伴随式 00 01 10 11 陪集首 00000 00100 01000 10000
1 1 0 0 0 H2 = 1 0 1 1 1
0 0 0 11 0 0 11 1 0 1 0 11 1 0 0 11
7.2 q进制对称信道上的伴随式 译码
如果ε≤1/q,则上式就是wH(Z)的递减函数,因此最有 可能的z是具有最小重量的z。 所以q进制对称信道上的伴随式译码算法如下: 1. 计算伴随式s=HyT 2. 在对应于s的陪集中找出最小重量矢量,称为z0。 3. 输出码字x=y-z0。
7.2 q进制对称信道上的伴随式 译码
7.3 汉明几何和码的性能
如果C是线性码,则x-x′也是C的一个码字, 因为dH(x, x′)=wH(x-x′),则dmin(C)=wmin(C)。 这样计算量从qk(qk-1)/2减少到qk 。 定理7.3 如果C是Fq上的一个(n,k)线性码,具有一致校验矩 阵H,则dmin(C)=H中线性相关列的最小数目。因此如果H中 任意2t及更少的列所组成的子集都是线性无关的,则这个 码能够纠正所有重量≤t的错误图案。 推论:如果q=2,且H中≤e列的所有可能线性组合都不同,则 dmin(C) ≥2e+1,由此可知C能纠正重量≤e的错误图案。
00101 00001 0 11 0 1 10101
0 0 11 0 00010 0 11 1 0 1 0 11 0
11 0 0 1 111 0 1 10001 01001
11 0 1 0 111 1 0 10010 01010
111 0 0 11 0 0 0 10100 0 11 0 0
111 11 11 0 1 1 1 0 11 1 0 11 11
7.1 生成和一致校验矩阵
与任何一个(n,k)分组线性码的码空间C相对应,一定存在一 个对 偶空间D。事实上, 码空间基底数k只是 n维n重空间全部 n 个基底的一部分,若能找出另外n-k个基底,也就找到了对偶空间 D。 既然用k个基底能产生一个(n,k)分组线性码,那么也就能用 n-k个 基底产生包含2n-k个码字的(n,n-k)分组线性码,称(n,n-k)码 是(n,k )码的对偶码。 将D空间的n-k个基底排列起来可构成一个(n-k) ×n矩阵,将 这个矩阵称为码空间C的校验矩阵H,而它正是(n,n-k )对偶码的 生成矩阵,它的每一行是对偶码的一个码字。 C和D的对偶是相互的,G是C的生成矩阵又是D的校验矩阵, 而H是D的生 成矩阵,又是C的校验矩阵.
7.3 汉明几何和码的性能
• 例题
1 1 H1 = 1 1 1 0 0 0 0 1 0 0 0 0 1 0 0 0 0 1
1 1 0 0 0 H2 = 1 0 1 1 1
0 1 1 1 1 0 0 H 3 = 1 0 1 1 0 1 0 1 1 0 1 0 0 1
7.1 生成和一致校验矩阵
例7.1 一个(5,1)线性码C1,具有生成矩阵G1=[1,1,1,1,1]. 显然C1仅含有两个码字00000和11111;速率R=1/5。 (重复编码) 例7.2 一个(5,3)线性码C2,具有生成矩阵
1 1 1 0 0 G2 = 0 0 1 1 0 1 1 1 1 1
7.3 汉明几何和码的性能
定义:码C的最小距离为: dmin(C)=min{dH(x,x′): x,x′∈C, x≠x′} 定理7.2 码C={x1,x2,...,xM}能够纠正所有重量≤e的错误图案, 当且仅当dmin(C)≥2e+1。 定义:码C的最小重量 wmin(C)=min{wH(x):x∈C,x≠0}
7.3 汉明几何和码的性能
• 汉明几何
假设希望码C能够纠正汉明重量≤e的错误图案,即如果发 送xi, 接收到y= xi+z,如果wH(z)≤e,则译码器的输出x′=xi。 对于qSC,译码的最佳策略是使dH(xi,y)最小的那个码字。 如果采用这种几何译码策略,则码能够纠正所有重量≤e 的错误图案的充分必要条件是,每一对码字之间的距离都 ≥2e+1。 xi y xi xi y xi
7.1 生成和一致校验矩阵
可见G1和G3是RRE形式了,当G2不是。G2的唯一RRE生成矩 阵为:
1 1 0 0 1 ′ G2 = 0 0 1 0 1 0 0 0 1 1
7.1 生成和一致校验矩阵
定义:存在一个编码规则,使信息符号独立地出现在码字中, 就称为它是系统的。 反之,不具备“系统”特性的码叫非系统码。非系统码与 系 统码并无本质的区别,它的生成矩阵可以通过行运算转变为 系统形式,这个过程叫系统化。系统化不改变码集 , 只改变映射 规则。 所有的线性码都是系统的。 对于无记忆信道,对G进行列置换并不会改变码的性能, 因此在这种情况下总可以假设G=[IkA]。
7.3 汉明几何和码的性能
• 汉明距离
定义两个矢量x和y之间的汉明距离为: dH(x,y)={分量xi≠yi的个数}=wH(y-x) 它满足真正的测度所具有的下列性质: (a)d(x,x)=0 (b)如果x≠y,则d(x,y)>0 (c)d(x,y)=d(y,x) (d)d(x,y)≤d(x,z)+d(z,y)
1 0 G3 = 0 0 0 0 0 0 1 1 1 0 0 1 0 1 0 1 0 1 1 0 0 0 1 1 1 1
例7.3 一个(7,4)线性码C3,具有生成矩阵 ((7,4)含明码)
7.1 生成和一致校验矩阵
基底不是惟一的,生成矩阵也就不是惟一的。事实上,将k 个基底线性组合后产生另一组 k 个矢量 , 只要满足线性无关 的条件 , 依然可以作为基底张成一个码空间。不同的基底有 可能生成同一码集 , 但因编码涉及码集和映射两个因素 , 码 集一样而映射方法不同也不能说是同样的码。 基底的线性组合等效于生成矩阵 G 的行运算 , 可以 产生 一组 新的基底。
