第2章作业解答
第2章 递归与分治_作业答案讲解

具体执行过程:求最大值
0 1 2 3 4 5 6 7 8 9 10 11 12 13 24 -13 29 113 87 65 -9 36 14 76 44 83 67 5 0 1 2 3 4 5 6 24 -13 29 113 87 65 -9 0 1 2 3 24 -13 29 113 0 1 24 -13 2 3 29 113 4 5 6 87 65 -9 7 8 9 10 11 12 13 36 14 76 44 83 67 5 7 8 9 10 36 14 76 44 7 8 36 14 7 36 9 10 76 44 11 12 13 83 67 5 11 12 83 67 11 83 12 67 13 5
课后练习
• 练习2:分析如下时间函数的复杂度,并说明 原因。 1. 利用递归树说明以下时间函数的复杂度:
O(1) T ( n) 3T ( n ) O( n) 4 n1 n1
2. 利用主定理说明以下时间函数的复杂度:
T(n) = 16T(n/4) + n
T(n) = T(3n/7) + 1
课后练习
• 练习1:给定数组a[0:n-1], 1. 试设计一个分治法算法,找出a[0:n-1]中元素最 大值和最小值; 2. 写出该算法时间函数T(n)的递推关系式; 3. 分析该算法的时间复杂度和空间复杂度。
0 1 2 3 4 5 6 7 8 9 10 11 12 13 24 -13 29 113 87 65 -9 36 14 76 44 83 67 5
• 递归公式:
– 设n个元素的集合可以划分为F(n,m)个不同的由 m个非空子集组成的集合。 F(n,m) = 1, when n=0, n=m, n=1, or m=1 F(n,m) = 0, when n<m 否则 F(n,m)=F(n-1,m-1)+m*F(n-1,m)
第2章作业-2 参考答案

二、综合题
1. 若X=-0.1110,Y=-0.1101,采用原码一位乘法运算求 X·Y=? 给出计算过程。
2.若X=-0.1101,Y=-0.1011 试利用补码Booth算法(比较 法)求X·Y=? 给出计算过程。
3. 将十进制数+76.75存入某微机中,试写出其IEEE754标准规 格化单精度浮点数形式。
第2章作业-2 参考答案
一、单项选择题: 1、两个浮点数相加,一个数的阶码值为7 ,另一个数的阶码值为9 ,则需要将阶码
值较小的浮点数的小数点( )。 A .左移1 位 B .右移1 位 C .左移2 位 D .右移2 位29 .
答案: C
2、如果某单精度浮点数、某原码、某补码、某移码的32位机器数均为 OxF0000000 。这些数从大到小的顺序是()。 A .浮原补移 B .浮移补原 C .移原补浮 D . 移补原浮 答案: D
说明
初始值,最后一位补0 Y4Y5=10 +[-X]补
右移一位 Y3Y4=01
+[X]补
右移一位 Y2Y3=10
+[-X]补
右移一位 Y1Y2=01
+[X]补
右移一位 Y0Y1=10 不移位
+[-X]补
3. 解:76.75 = 1001100.11 = 1.00110011 ×26 指数E = 7 + 127 = 133 = 1000 0101B 127是单精度浮点数应加的指数偏移量。
4. 某微机内存有一个单精度规格化浮点数(IEEE754标准)为 C2308000H,试写出其真值。
计算机组成原理
1. 解: X=-0.1110,Y=-0.1101 ,X*=0.1110,Y*=0.1101。 其中寄存器 B=X* ,计数器Cd=4。计算过程:
第2章拉压作业参考解答

aEADj + 4.5aEADj = 2aF , Dj = 2F 5.5EA
4. 再由 Hooke 定律:
FN1
=
EADj
=
2F 5.5
=
0.3636F
FN 2
= 1.5EADj
=
1.5´ 2F 5.5
2
(1)图(a)为开槽拉杆,两端受力 F=14kN,b=20mm,b0=10mm,δ=4mm。 (2)图(b)为阶梯形杆,AB 段杆横截面面积为 80mm2,BC 段杆横截面面积为 20mm2, CD 段杆横截面面积为 120mm2。 (3)图(c)为变截面拉杆,上段 AB 的横截面面积为 40mm2,下段 BC 的横截面面积为
DG
=
Dl2
-
2 3
Dl1
-
1 3
Dl3=6.89 ´10-4
m
5
2-15 求附图示圆锥形杆在轴向力 F 作用下的伸长量。弹性模量为 E。
解答 对于截面缓变的圆锥形杆可假设横截面上正应力均匀分布。横截面面积为
A(x)
=
1 4
p [d1l
-
(d1
-
d2 )x]2
/l2
ò ò ò Dl =
l
edx =
FN1
FN3
FN2
D
(2)
(b) 整体分析,示力图见附图(3)。
å M Ai = 0 : FN1 ´1 + 3´ 3´1.5 = 0
FN1 = -13.5kN
FAx A
FAy FN1
B
s1
=
FN 1 A1
=
-13.5 ´103 850 ´10-6
=
-15.88MPa
第二章作业 参考答案
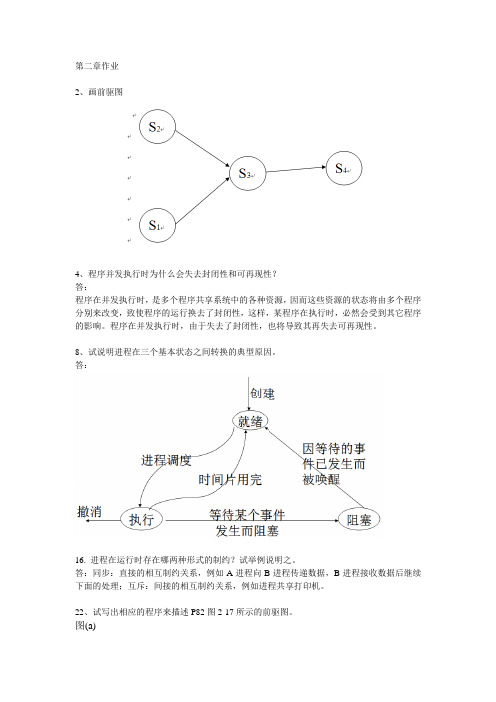
第二章作业2、画前驱图4、程序并发执行时为什么会失去封闭性和可再现性?答:程序在并发执行时,是多个程序共享系统中的各种资源,因而这些资源的状态将由多个程序分别来改变,致使程序的运行换去了封闭性,这样,某程序在执行时,必然会受到其它程序的影响。
程序在并发执行时,由于失去了封闭性,也将导致其再失去可再现性。
8、试说明进程在三个基本状态之间转换的典型原因。
答:16. 进程在运行时存在哪两种形式的制约?试举例说明之。
答:同步:直接的相互制约关系,例如A进程向B进程传递数据,B进程接收数据后继续下面的处理;互斥:间接的相互制约关系,例如进程共享打印机。
22、试写出相应的程序来描述P82图2-17所示的前驱图。
图(a)int a1=0,a2=0,a3=0,a4=0,a5=0,a6=0;a7=0;a8=0;parbeginbegin S1;V(a1);V(a2);end;begin P(a1);S2;V(a3);V(a4);end;begin P(a2);S3;V(a5);end;begin P(a3);S4;V(a6);end;begin P(a4);S5;V(a7);end;begin P(a5);S6;V(a8);end;begin P(a6);P(a7);P(a8);S7;end;parend图(b)int a1=0,a2=0,a3=0,a4=0,a5=0,a6=0;a7=0;a8=0;a9=0;a10=0;parbeginbegin S1;V(a1);V(a2);end;begin P(a1);S2;V(a3);V(a4);end;begin P(a2);S3;V(a5);V(a6);end;begin P(a3);S4;V(a7);end;begin P(a4);S5;V(a8);end;begin P(a5);S6;V(a9);end;begin P(a6);S7;V(a10);end;begin P(a7);P(a8);P(a9);P(a10);S8;end;parend28、在测量控制系统中的数据采集任务,把所采集的数据送一单缓冲区;计算任务从该单缓冲中取出数据进行计算。
第2章作业参考答案

2. 一批晶体管中有个 9 个合格品和 3 个不合格品,从中任取一个安装在电子设备上。若取 出不合格品不再放回,求取得合格品前已取出的不合格品个数的分布律和分布函数。 解:
X0 1 2
3
p 3/4 9/44 9/220 1/220
⎧ 0,
x<0
F (x) = ⎪⎪⎪⎨321/ 4/ ,22,
0≤ x <1 1≤ x < 2
求: (1) 系数 A,B; (2) X 落在区间(-1,1)的概率; (3) X 的概率密度。 解:
x∈R
7. 从一批子弹中任意抽出 5 发试射,若没有一发子弹落在靶心 2 厘米以外,则接受该批子 弹。设弹着点与靶心的距离 X(厘米)的概率密度为
f
(
x)
=
⎪⎧ ⎨
Axe−
x2
,
⎪⎩ 0,
0< x<3 其他
X
~
B
⎛ ⎜⎝
4,
1 5
⎞ ⎟⎠
, 故分布律为
P( X = k) = C4k (0.2)k (0.8)4−k , k = 0,1, 2, 3, 4
( ) (2)P X = k
=
C5k
*
C 4− 20
k
C245
k = 0,1,2,3,4
5. 临床观察表明,某药物产生副作用的概率为 0.002。现在 900 个患者服用该药物,求至 少有3例患者出现副作用的概率.
试求:(1)系数 批子弹被接受的概率。 解:
⎧ 0,
x<0
∫ ∫ (2) F(x) =
x −∞
f
(t)dt
=
⎪⎪ ⎨ ⎪
x2 0 1 − e−9
第二章作业题解答

第二章静电场习题解答2-1.已知半径为F = Cl的导体球面上分布着面电荷密度为A = p s0 cos的电荷,式中的炖0为常数,试计算球面上的总电荷量。
解取球坐标系,球心位于原点中心,如图所示。
由球面积分,得到2用打Q =护= J j p50cos OrsmOd Od(p(S) 0 0In x=j j psQSefsinGded00 0In n=PsF j J cos ageded(p0 0丸=sin20d0 = 0o2-2.两个无限人平面相距为d,分别均匀分布着等面电荷密度的异性电荷,求两平面外及两平面间的电场强度。
解对于单一均匀带电无限人平面,根据对称性分析,计算可得上半空间和卞半空间的电场为常矢量,且大小相等方向相反。
由高斯定理,可得电场大小为E = ^-2e0对于两个相距为的d无限大均匀带电平面,同样可以得到E] = E“耳=E3题2-2图因此,有2-3.两点电荷q、= 8C和q2 = -4C ,分别位于z = 4和),=4处,求点P(4,0,0)处的电场强度。
解根据点电荷电场强度叠加原理,P点的电场强度矢量为点Si和Si处点电荷在P处产生的电场强度的矢量和,即E r = Qi 弘 | ① R?4T V£0/?/ 4TT£0R] = r — r L = 4e v — 4e., R 、= J 4-0 " + 0-4 ~ = 4>/2 R 2 =r —r 2 =4e v -4e v , R 2 = J 4-0 ' + 0-4 ' = 4>/22-7. 一个点电荷+q 位于(-a, 0,0)处,另一点电荷-2q 位于(a,0,0)处,求电位等于零的 面;空间有电场强度等于零的点吗?解根据点电荷电位叠加原理,有々)=丄]鱼+鱼4矶丄忌」式中Rj =r-r L = x-\-a e v + ye v +e. R i = yl x + a 2 + r+^2 R 2 =r-r 2 = x ~a e v + ),e y+e r R? — yj x — ci + )r +代入得到式中代入得到心孟 _______ 1^x + a)2+ y 2+ z 22JaS+b+z 2(3x+d )(x+3a ) + 3),+3z ,=0根据电位与电场强度的关系,有电位为零,即令简化可得零电位面方程为要是电场强度为零,必有E x = 0, E y = 0, E : = 0一 (x+ d)[(x + d)2 + y 2 + ^2p + 2(—d)[(—d)2+ y 2 + 疋 -)^(x+n)2 + y 2 + z 2 2 +2y^(x-a)2 + y 2+ z 2丄-z[(x + d)2 + + 疋 2+2z[(x-d)2 +)*此方程组无解,因此,空间没有电场强度为零的点。
第二章课后作业答案

第二章线性表习题(答案)1.描述以下三个概念的区别:头指针,头结点,首元素结点。
首元结点是指链表中存储线性表中第一个数据元素a1的结点。
为了操作方便,通常在链表的首元结点之前附设一个结点,称为头结点,该结点的数据域中不存储线性表的数据元素,其作用是为了对链表进行操作时,可以对空表、非空表的情况以及对首元结点进行统一处理。
头指针是指向链表中第一个结点(或为头结点或为首元结点)的指针。
若链表中附设头结点,则不管线性表是否为空表,头指针均不为空。
否则表示空表的链表的头指针为空。
2.填空:(1)在顺序表中插入或删除一个元素,需要平均移动一半元素,具体移动的元素个数与插入或删除的位置有关。
(2)在顺序表中,逻辑上相邻的元素,其物理位置也相邻。
在单链表中,逻辑上相邻的元素,其物理位置不一定相邻。
(3)在带头结点的非空单链表中,头结点的存储位置由头指针指示,首元素结点的存储位置由头结点的next域指示,除首元素结点外,其它任一元素结点的存储位置由其直接前趋的next域指示。
3.已知L是无表头结点的单链表,且P结点既不是首元素结点,也不是尾元素结点。
按要求从下列语句中选择合适的语句序列。
a. 在P结点后插入S结点的语句序列是:(4)、(1)。
b. 在P结点前插入S结点的语句序列是:(7)、(11)、(8)、(4)、(1)。
c. 在表首插入S结点的语句序列是:(5)、(12)。
d. 在表尾插入S结点的语句序列是:(11)、(9)、(1)、(6)。
供选择的语句有:(1)P->next=S; (2)P->next= P->next->next; (3)P->next= S->next;(4)S->next= P->next; (5)S->next= L; (6)S->next= NULL;(7)Q= P; (8)while(P->next!=Q) P=P->next;(9)while(P->next!=NULL) P=P->next; (10)P= Q;(11)P= L; (12)L= S; (13)L= P;4.设线性表存于a[n]中且递增有序。
第二章作业解答

(3)动态分析:h参数微变等效电路如
解图2.11所示。
rbe
rbb'
(1
)
26mV I EQ
≈2.73k
A u
(Rc ∥ RL ) rbe (1 )Rf
≈-7.7
Ri Rb1 ∥ Rb2 ∥[rbe (1 )Rf ] ≈3.7k
Ro Rc 5k
若电容Ce开路,则Re串入电路
A u=- rbe+(β1(+ Rcβ∥ )(R ReL+ )Rf )≈- 1.92 Ri =Rb1∥ Rb2∥ [rbe+(1+β)(Re+Rf )]≈4.1Ω k
2.5 在图P2.5所示电路中,已知晶体管的=80,rbe=1kΩ,U=i
20mV;静态时UBEQ=0.7V,UCEQ=4V,IBQ=20μA。判断下列 结论是否正确,凡对的在括号内打“”,否则打“×”。
(1) ( ) Au
4
20103
200
(2)Au
4 0.7
5.71
(
)
(3)
Au
805400( 1
=
I CQ β
=
2 ×10 -3 100
= 20 μA
Rb
= VCC- U BEQ I BQ
12-0.7 =
0.02
≈ 565 kΩ
(2)求解RL:
图P2.9
Au
Uo Ui
100100 1
Au
R' L
rbe
100R'L 1.4
R'L 1.4k
Rc // RL 1.4 RL 2.625k
2.10 在图P2.9所示电路中,设静态时ICQ=2mA,晶体管饱和管压 降UCES=0.6V。试问:当负载电阻RL=∞和RL=3kΩ时电路的最大 不失真输出电压各为多少伏? 解:由于ICQ=2mA,所以UCEQ=VCC-ICQRc=6V。 空载时,输入信号增大到一定幅值,电路首先出现饱和失真。故
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2.3 将题2.3
模型。
解题提示:
解答:图(a)变换如下:
''S
S S
s S R R R I U =⋅=a b ab
电压源电流源ab
a
b
(b)
题2.3 图
图(b)变换如下:
2.4 将题2.4图所示电路变换为等效电压源模型。
解题提示:
等效互换的条件:对外的电压电流相等。
电压源与电流源的等效变换条件如下:
''S
S S
s S R R R I U =⋅=a b
ab
电压源
电流源
ab
a
b
(a)
(b)
题2.4图
解答:图(a)变换如下:
(a)
图(b)变换如下:
(b)
2.5 用电源等效变换的方法,求题2.5图中的电流I。
24V
题2.5 图
ab
a
b
2A
2.6 用支路电流法求题2.6图中的I 和U 。
A 212
题2.6图
解题提示:
以支路电流为未知数,根据基氏定律,列结点电流和回路电压方程,然后联立求解。
具有n 个结点,m 条支路的电路。
独立的电流方程个数:()1-n 个,独立的电压方程:()1+-n m 个,通常用网孔列写电压方程。
解答:支路电流方向如上图所示。
⎪⎩
⎪
⎨⎧=+--=-+=+0243 BEDCB 01236211U I KVL I I KVL ABEFA
I I KCL 方程:的回路方程:的回路方程:结点
联立求解得:
⎪⎩⎪⎨⎧
==V
U A
I 638
2.9 用网孔电流法求题2.9图中的电流I 和电压U 。
A 2
3 题2.9图
解题提示:
以网孔电流为未知数,列写网孔KVL 方程,求解出网孔电流,再根据网孔电流与支路电流关系,求解出支路电流。
解答:网孔电流如上图所示: 可得:A I m 31
=,A I m 23
=
列写网孔2的KVL 方程: ()15443883
2
1
-=++++-m m m I I I
解得:A I
m 15
12
=
A I I m 15
12=
=
()V
I I U m m 153528*15138*21=⎪⎭
⎫ ⎝⎛
-=-=
2.10 用结点电压法求题2.10图中各支路的电流。
解题提示:
假设一个参考点,令其电压为零,各支路的电流用相关结点电压表示,根据基氏电流定律,列结点电流方程,然后联立求解。
解答:电流参考方向如上图所示:
⎪⎪⎩⎪⎪⎨
⎧-=⎪⎭⎫ ⎝⎛++-+=-⎪⎭⎫ ⎝⎛+5221414
15341411B A
B A U U U U
解得:V
U
A
6=,V
U
B
2-=
A U I A 61
6
11===
A 23
题2.10图
A U U I
B A 242
642=+=-=
A
U I B 12223-=-==
2.12用弥尔曼定理求题2.12图所示电路中开关S 断开和闭合时的各支路电流。
解题提示:
具有两个结点电路的结点电压法(弥尔曼定理):对只有两个结点的电路,可任取一个结点为参考结点,另一个结点的电压1
U 满足的方程为:
题2.12图
11
111S I U G =
∑∑∑∑==k
Sk Sk
k Sk R
R U R I U 111
解答:
S 断开:
V U ON 340050
150150150100
5010050200-=++---=
A
U I ON 3
450200
3400502001=+-=+=
A
U I I ON 3
250100
34005010032-=+-=+==
S 闭合:
A U I ON
4.250
20080502001
=+-=+= A U I I ON
4.050
100
80501003
2=+-=+== A U I ON
N
2.325
8025-=-==
2.14 利用叠加定理求题2.14图所示电路中电流源上的电压U 。
V U ON
8025
150150150150100
5010050200-=+
++---=
题2.14图
解题提示:
在多个独立电源同时作用的线性电路中,任何支路的电流或任意两点间的电压,都是各个独立源单独作用时所得结果的代数和。
一个独立源单独作用,意味着其他独立源不作用,不作用的电压源的电压为零,
可用短路代替;不作用的电流源的电流为零,可用开路代替。
解答:原电路可以分解为如下两个子电路:
V U 28*8
8123*3612-=+-+=' V U 12)8//83//6(*2=+='' V U U U 10122=+-=''+'=
2Ω3Ω=+
2.15 在题2.15图所示电路中,两电源1
S U 和2
S U
对负载L
R 供电,已知当02=S U 时,mA I 20=,当V U S 62
-=时,mA I 40-=,求:
1)若此时令01
=S U ,I 为多少? 2)若将2
S U 改为V 8,I 又为多少?
解题提示:
利用叠加原理求解。
解答:
1)mA I U U S S 20,01
2
='=单独作用,
mA I U U V U S S S 40,6212-==共同作用,和 I U S '
'单独作用时为2
mA
I I I I I I 602040-=--='-=''⇒''+'=
2)mA I I 808
60
6=''⇒'
'=-- mA I I I 1008020=+=''+'=
2.17 用戴维宁定理求题2.17图所示电路中的I 。
题2.15图
题2.17图
10
Ω
解题提示:
在复杂电路中,只需计算某一支路的电压或电流常用戴维宁定理求解。
等效电压源的电压(U OC)等于有源二端网络的开端电压;等效电压源的内阻等于有源二端网络相应无源二端网络的输入电阻。
(有源网络变无源网络的原则是:电压源短路,电流源断
路) 解答:
⑴将待求支路分离出来,端口做好标记;
(2)求出有源二端电路的开路电压U OC 10V 单独作用:
V U AB
88*8
6//310
=+=' 6V 单独作用:
V
U AB 5
16
8//6*8//636-=+-=''
V U U U AB
AB AB
5
24
5168=-=''+'=
(3)除源后从端口看入的等效电阻R O 。
Ω10
Ω
Ω==6.16//3//8O R
(4)画出原电路的戴维宁等效电路,
求解等效
电路。
Ω
524
6.1
A I 5.086.1524
=+=
2.19图示电路中D 为二极管,当Uab>0时,二极管导通,当Uab<0时,二极管截止(相当于开路)。
设二极管导通时的压降为0.6V ,试利用戴维宁定理计算电流I 。
解题提示:
在复杂电路中,只需计算某一支路的电压或电流常用戴维宁定理求解。
等效电压源的电压(U OC )等于有源二端网络的开端电
题2.19图
压;等效电压源的内阻等于有源二端网络相应无源二端网络的输入电阻。
(有源网络变无源网络的原则是:电压源短路,电流源断路)
解答:
⑴将待求支路分离出来,端口做好标记;
(2)求出有源二端电路的开路电压U OC ()()()()V U U ab OC 42266262262662262=⨯++++⨯-⨯++++⨯==
(3)除源后从端口看入的等效电阻R O 。
(4)画出原电路的戴维宁等效电路,求解等效电路。
A I 85.04
6.04=-=
2.20 用戴维宁定理求题2.20图所示电路中的I 。
44 题2.20图
2
解题提示:
在复杂电路中,只需计算某一支路的电压或电流常用戴维宁定理求解。
等效电压源的电压(U OC)等于有源二端网络的开端电压;等效电压源的内阻等于有源二端网络相应无源二端网络的输入电阻。
(有源网络变无源网络的原则是:电压源短路,电流源断路)
解答:
原电路可画为如下形式:
V U U U B A AB 1311214112244861312161239-=+++--+++-=-= Ω=+=5.23//12//46//3//2O R
Ω2
Ω Ω1-5.2
A I 7215.21=+=。
