八年级数学下《一次函数及几何综合》专题练习题.doc

合集下载

(word)新人教版八年级下《一次函数》测试题及答案,文档

2021—2021学年度第二学期八年级〔下〕第十九章一次函数单元检测题班级＿＿＿＿姓名＿＿＿＿＿得分＿＿＿＿＿一、选择题〔本大题共12个小题，每题3分，共36分。

在每题给出的四个选项中，只有一项为哪一项满足题目要求的，请把其代号填在答题栏中相应题号的下面〕。

题号123456789101112答案1 .假设点A〔2，4〕在函数ykx2的图象上，那么以下各点在此函数图象上的是〔〕．A．〔0，2〕B．〔3，0〕C．〔8，20〕D．〔1，1〕2222 .变量x,y有如下关系：①x+y=10②y=5③y=|x-3④y2=8x.其中y是x的函数的是xA.①②②③④ B.①②③ C.①② D.①3 .以下各曲线中不能表示y是x的函数是〔〕．A．B．C．D．4.一次函数y 2x a与y x b的图象都经过A〔2，0〕，且与y轴分别交于B、C两点，那么△ABC的面积为〔〕．A．4B．5C．6D．7正比例函数y=(k+5)x,且y随x的增大而减小，那么k的取值范围是＞5＜5＞-5＜-56.在平面直角坐标系xoy中，点M(a,1)在一次函数y=-x+3的图象上，那么点N(2a-1,a)所在的象限是A.一象限B.二象限C.四象限D.不能确定7.如果通过平移直线y x x5yx〕．得到y的图象，那么直线必须〔333A．向上平移5个单位B．向下平移5个单位C．向上平移5个单位D．向下平移5个单位338.经过一、二、四象限的函数是A.y=7B.y=-2xC.y=7-2xD.y=-2x-79.正比例函数y=kx(k≠0)的函数值y随x的增大而减小，那么函数y=kx-k的图象大致是10.假设方程x-2=0的解也是直线y=(2k-1)x+10与x轴的交点的横坐标，那么D.±2k的值为11.根据如图的程序，计算当输入x 3时，输出的结果y．输y x5(x1)输入出x y x5(x≤1)y12.直线y1=2x与直线y2=-2x+4相交于点 A.有以下结论：①点A的坐标为A(1,2);②当x=1时，两个函数值相等；③当x＜1时，y1＜y2④直线y1=2x与直线y2=2x-4在平面直角坐标系中的位置关系是平行.其中正确的选项是A.①③④B.②③C.①②③④D.①②③二、填空题〔本大题共5个小题，每题4分，共20分。

(完整版)《一次函数与几何图形综合》专题

《一次函数与几何图形综合》专题总论：函数与几何是初中数学中的重点内容,是中考命题重点考查的内容之一；函数中的几何问题，能使代数知识图形化，而几何中的函数问题，能使图形性质代数化；由于函数与几何结合的综合题的形式灵活、立意新颖，能更好地考查学生的思维水平和数学思想方法，因而成为近几年各地中考的一类热门试题；函数知识与几何知识有机结合的综合题，根据构成命题的主要要素可分为以下两类：一类是几何元素间的函数关系问题（这类问题不妨称简称为“几函”问题），这类问题的特点是：根据已知几何图形间的位置和数量关系（如平行、全等、相似，特别是成比例）建立自变量与函数所表示的几何元素间的等量关系，求出函数关系式，运用函数的性质解决几何图形中的问题；另一类是函数图像中的几何图形的问题（如三角形、四边形，特别是圆）（这类问题不妨简称为“函几”问题），这类问题的特点是：根据已知函数图像中的几何图形的位置特征，运用数形结合方法解决有关函数、几何问题。

一次函数与几何综合题是八年级学生初次接触一种用代几综合解决问题的方法，这种方法和能力是九年级解决中考压轴题所必须具备的。

1.代数（1）表达什么函数（包括其系数的代数意义、几何意义、物理意义）（2）显现怎样的图形（自身、与坐轴、与其他图形）（3）既是一个方程，也是一个坐标4）藏有那些数据，含有什么些关系（5）要建立某种代数关系缺少那些数据2.几何（1）基本图象有几个（2）图象之间有怎样关系（3）图象与所要证明（求解）的结论怎样的关联（4）要建立图象与图象之间的关系缺少那些数据3.代数与几何（1）代数（几何）在那些地方为几何（代数）提供了怎样的数据（2）几何（代数）通过什么方式为几何（代数）提供关系式（3）怎样设数据（坐标或线段长）函数与几何综合题的解题思想方法：“函几问题”与“几函问题”涉及的知识面广、知识跨度大、综合性强，应用数学方法多、纵横联系较复杂、结构新颖灵活、注重基础能力、探索创新和数学思想方法，它要求学生有良好的心理素质和过硬的数学基本功，能从已知所提供的信息中提炼出数学问题，从而灵活地运用所学知识和掌握的基本技能创造性的解决问题，正因如此，解决这类问题时，要注意解决问题的策略，常用的解题策略一般有以下几种：1.综合使用分析法和综合法。

(word版)八年级下册数学《一次函数》测试题及答案,文档

第十九章一次函数时间：120分钟总分值：120分姓名班级分数一、选择题(每题3分，共30分)1．假设函数y=〔2m+1〕x 2+〔1-2m 〕x 〔m 为常数〕是正比例函数，那么 m 的值为〔〕A ．m>1B ．m=1C ．m<1D ．m=-122222．假设一次函数y=〔3-k 〕x-k 的图象经过第二、三、四象限，那么 k 的取值范围是〔〕A ．k>3B．0<k ≤3 C ．0≤k<3D．0<k<33．一次函数的图象与直线 y=-x+1平行，且过点〔8，2〕，那么此一次函数的解析式为〔〕A ．y=-x-2B ．y=-x-6C ．y=-x+10D ．y=-x-14．一次函数y=kx+b 的图象经过点〔 2，-1〕和〔0，3〕，?那么这个一次函数的解析式为〔〕A ．y=-2x+3B．y=-3x+2C．y=3x-2D．y=1x-325．李老师骑自行车上班，最初以某一速度匀速行进，?中途由于自行车发生故障，停下修车耽误了几分钟，为了按时到校，李老师加快了速度，仍保持匀速行进，如果准时到校．在课堂上，李老师请学生画出他行进的路程 y?〔千米〕与行进时间 t 〔小时〕的函数图象的示意图，同学们画出的图象如下列图，你认为正确的选项是〔〕6．假设直线 y ＝－x ＋a 与直线y ＝x ＋b 的交点坐标为 (2，8)，那么a －b 的值为(A ．2B ．4C ．6D ．87．假设一次函数 y ＝ax ＋b 的图象经过第一、二、四象限，那么以下不等式一定成立的是)()A ．a ＋b ＜0B ．a －b ＞0C ．ab ＞0bD.a ＜08．等腰三角形的周长是10，底边长 y 是腰长x 的函数，那么以下列图象中，能正确反映y 与x 之间函数关系的图象是()9．如是某复印店复印收y(元)与复印面数(8开)x(面)的函数象，那么从象中可看出，复印超A．元100面的局部，每面收B．元C．元()D．元第9第10210．如，直y＝3x＋4与x、y分交于A点和点B，点C，D分段AB，OB的中点，点POA上一点，当PC＋PD最小，点P的坐()A．(－3，0)B．(－6，0)C.－3，0 D.－5，022二、填空(每小3分，共24分)11．直y＝2x＋1点(0，a)，a＝________．12．直l点M(－2，0)，直的解析式可以写______________(只写出一个即可)．13．直y＝x＋4与x、y所成的三角形的面________．14．一次函数y＝(m－1)x＋m2的象点(0，4)，且y随x的增大而增大，m＝________．15．直y＝2x－1沿y平移3个位度，平移后直与y的交点坐______________．16．如，直l1：y＝－2x＋4与直l2：y＝kx＋b(k≠0)在第一象限交于点M.假设直l2与x的交点A(－2，0)，k的取范是__________．第16第17第1817．甲、乙两点分从段AB的两端点同出，甲从点A出，向点 B运，乙从点B出，向点A运．段 AB90cm，甲的速度运x(s)，甲、乙两点之的距离y(cm)，y与x的函数象如所示，中段DE所表示的函数关系式____________________(并写出自量的取范)．18．正方形A1B1C1O，A2B2C2C1，A3B3C3C2，⋯按如所示的方式放置，点A1，A2，A3，⋯和点C1，C2，C3，⋯分在直y＝x＋1和x上，点B2021的坐是________．三、解答(共66分)19．(8分)y与x＋1成正比例关系，当x＝2，y＝1.求：当x＝－3，y的．20．(9分)一次函数y＝2x＋4.(1)在如所示的平面直角坐系中，画出函数的象；(2)求象与x的交点A的坐，与y交点B的坐；(3)在(2)的条件下，求出△AOB的面；(4)利用象直接写出：当y＜0，x的取范．21.(8分)一次函数y＝kx＋b的象点A(0，－2)，B(3，4)，C(5，m)．求：(1)个一次函数的解析式；(2)m的．22．(9分)某途汽客运公司定旅客可免携一定量的行李，当行李的量超定，需付的行李y(元)是行李量x(kg)的一次函数．行李量20k需付g 行李2元，行李量50kg需付行李8元．(1)当行李的量x超定，求y与x之的函数解析式；(2)求旅客最多可免携行李的量．23．(10分)如，直l1：y＝2x＋1与直l2：y＝mx＋4相交于点P(1，b)．(1)求b，m的；(2)垂直于x的直x＝a与直l1，l2分交于点C，D，假设段CD2，求a的．24．(10分)“五一〞期，小明一家乘坐高前往某市旅游，划第二天租用新能源汽自出游．根据以上信息，解答以下：(1)租 x小，租用甲公司的所需用y2元，分求出y1，y2关于x的函数解析式；(2)你帮助小明算并哪个出游方案合算．y1元，租用乙公司的所需用25．(12分)小慧根据学函数的，函数y＝|x－1|的象与性行了探究．下面是小慧的探究程，充完整：(1)函数y＝|x－1|的自量x的取范是(2)列表，找出y与x的几.____________；x y ⋯⋯－1b112132⋯⋯其中，b＝________；(3)在如所示的平面直角坐系xOy中，描出上表中以各坐的点，并画出函数的象；(4)写出函数的一条性：____________________.答案CDACB BDDC11．1 ＝x ＋2(答案不唯一) 13． 15.(0，2)或(0，－4) 16．0<k<2 ＝－90(20≤x ≤36)18．2202119．解：∵y 与x ＋1成正比例关系，∴设y ＝k(x ＋1)，(1分)将x ＝2，y ＝1 代入得1 1 1 1 1 1 1 ＝3k ，解得k ＝，∴函数解析式为y ＝(x ＋1)＝ x ＋ .(5分)当x ＝－3时，y ＝－3×＋＝－33 33 3 323.(8分)20．解：(1)当x ＝0时，y ＝4，当y ＝0时，x ＝－2，那么该函数的图象如下列图．(3分)(2)由(1)可知点A 的坐标为(－2， 0)，点B 的坐标为(0，4)．(5分)(3)∵OA ＝2，OB ＝4，∴S＝ 2OA ·OB ＝2×2×4＝4.(7分)△AOB1 1(4)x ＜－2.(9分)21．解：(1)∵一次函数y ＝kx ＋b 的图象经过点A(0，－2)，B(3，4)，∴b ＝－2，(23k ＋b ＝4，分)解得k ＝2，y ＝2x －2.(4分)∴这个一次函数的解析式为b ＝－2，(2)把C(5，m)代入y ＝2x －2，得m ＝2×5－2＝8.(8分)22．解：(1)设y 与x 的函数解析式为y ＝kx ＋b.(1分)将(20，2)，(50，8)代入y ＝kx ＋b1中，得20k ＋b ＝2，(3分)解得k ＝5，∴当行李的质量x 超过规定时，y 与x 之间的函数50k ＋b ＝8，b ＝－2，1解析式为 y ＝5x －2.(5分) 1 (2)当y ＝0时，5x －2＝0，(7分)解得x ＝10.答：旅客最多可免费携带行李10kg.(9分)23．解：(1)∵点P(1，b)在直线l 1：y ＝2x ＋1 上，∴ b ＝2×1＋1＝3.(2分)∵点P(1，3)在直线l 2：y ＝mx ＋4上，∴3＝m ＋4，∴m ＝－1.(4分)(2)当x ＝a 时，y C ＝2a ＋1.当x ＝a 时，y D ＝4－a.(6分)∵CD ＝2，∴|2a ＋1－(4－a)|＝2，15(8分)解得a ＝或.(10分)24．解：(1)设y 1＝k 1x ＋80，把点(1，95)代入，可得95＝k 1＋80，解得k 1＝15，∴y 1＝15x ＋80(x ≥0)．(2分)设y 2＝k 2x ，把(1，30)代入，可得k 2＝30，∴y 2＝30x(x ≥0)．(4分)(2)当y 1＝y 2时，15x ＋80＝30x ，解得x ＝163；当y 1＞y 2时，15x ＋80＞30x ，解得x ＜163；当y 121616小时，选择甲、乙公司一＜y 时，15x＋80＜30x ，解得x ＞3.(7分)∴当租车时间为3样合算；当租车时间小于16小时，选择乙公司合算；当租车时间大于16小时，选择甲公司合33算．(10 分)25．解：(1)任意实数(3分)(2)2(6分)(3)如下列图．(9分)(4)函数的最小值为 0(答案不唯一)(12分)。

人教版八年级数学下《一次函数与几何综合》专题练习题

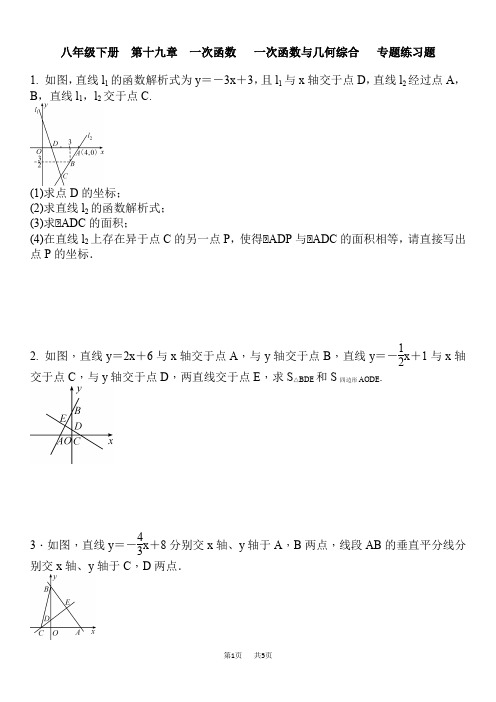
八年级下册第十九章一次函数一次函数与几何综合专题练习题1. 如图，直线l1的函数解析式为y＝－3x＋3，且l1与x轴交于点D，直线l2经过点A，B，直线l1，l2交于点C.(1)求点D的坐标；(2)求直线l2的函数解析式；(3)求△ADC的面积；(4)在直线l2上存在异于点C的另一点P，使得△ADP与△ADC的面积相等，请直接写出点P的坐标．2. 如图，直线y＝2x＋6与x轴交于点A，与y轴交于点B，直线y＝－12x＋1与x轴交于点C，与y轴交于点D，两直线交于点E，求S△BDE和S四边形AODE.3．如图，直线y＝－43x＋8分别交x轴、y轴于A，B两点，线段AB的垂直平分线分别交x轴、y轴于C，D两点．(1)求点C的坐标；(2)求直线CE的解析式；(3)求△BCD的面积．4. 如图，在平面直角坐标系中，点A(－1，0)，B(0，3)，直线BC交坐标轴于B，C两点，且△CBA＝45°.求直线BC的解析式．5. 如图，A(0，4)，B(－4，0)，D(－2，0)，OE⊥AD于点F，交AB于点E，BM⊥OB 交OE的延长线于点M.(1)求直线AB和直线AD的解析式；(2)求点M的坐标；(3)求点E，F的坐标．6. 如图，正方形OBAC中，O(0，0)，A(－2，2)，B，C分别在x轴、y轴上，D(0，1)，CE⊥BD交BD延长线于点E，求点E的坐标．7. 如图，在平面直角坐标系中，A(0，1)，B(3，12)，P 为x 轴上一动点，则PA ＋PB 最小时点P 的坐标为________．8. 如图，直线y ＝x ＋4与坐标轴交于点A ，B ，点C(－3，m)在直线AB 上，在y 轴上找一点P ，使PA ＋PC 的值最小，求这个最小值及点P 的坐标．答案：1. 分析：(1)令y ＝－3x ＋3＝0，求出x 可得点D 的坐标；(2)设直线l 2的解析式为y ＝kx ＋b ，把A ，B 的坐标代入求出k ，b 可得；(3)先求出点C 的坐标，再求S △ADC ；(4)在l 2上且到x 轴的距离等于点C 纵坐标的相反数的点即为点P.解：(1)由y ＝－3x ＋3，令y ＝0，得－3x ＋3＝0，∴x ＝1，∴D(1，0) (2)y ＝32x －6 (3)由⎩⎨⎧y ＝－3x ＋3，y ＝32x －6，解得⎩⎪⎨⎪⎧x ＝2，y ＝－3，△C(2，－3)，△AD ＝3，△S △ADC ＝12×3×|－3|＝92 (4)P(6，3)2. 解：易求A (－3，0)，B(0，6)，C(2，0)，D(0，1)，△BD ＝5，解⎩⎨⎧y ＝2x ＋6，y ＝－12x ＋1，得⎩⎪⎨⎪⎧x ＝－2，y ＝2， △E(－2，2)，△S △BDE ＝5，S 四边形AODE ＝S △AOB －S △BDE ＝9－5＝43. 解：(1)易得A(6，0)，B(0，8)，设C 点坐标为(x ，0)，则BC ＝AC ＝6－x ，由勾股定理得x 2＋82＝(6－x)2，△x ＝－73，△C(－73，0) (2)△点E 是AB 的中点，△点E 的坐标为(3，4)，易得直线CE 的解析式为y ＝34x ＋74 (3)由CE 解析式得，点D 坐标为(0，74)，S △BCD ＝12×(8－74)×73＝175244. 分析：过点A 作AD△AB ，AD 交BC 于点D ，可得△BAD 是等腰直角三角形，再过点D 作DE△x 轴于点E ，通过证△DEA△△AOB 求出点D 的坐标，最后由点B ，D 的坐标利用待定系数法可求出直线BC 的解析式．解：过点A 作AD△AB ，AD 交BC 于点D ，可得AD ＝AB ，过点D 作DE△x 轴于点E ，可证△DEA△△AOB ，△DE ＝OA ＝1，EA ＝OB ＝3，△D(－4，1)，可求直线BC的解析式为y ＝12x ＋35. 解：(1)AB ：y ＝x ＋4，AD ：y ＝2x ＋4 (2)由△OBM△△AOD 得BM ＝OD ，△M(－4，2) (3)由(2)得OM ：y ＝－12x ，联立⎩⎨⎧y ＝－12x ，y ＝x ＋4，得E(－83，43)；联立⎩⎨⎧y ＝2x ＋4，y ＝－12x ，得F(－85，45)6. 解：延长CE 交x 轴于点F ，则有△BOD△△COF ，△OD ＝OF ＝1，△F(1，0)，△C(0，2)，△CF ：y ＝－2x ＋2，△B(－2，0)，D(0，1)，△BD ：y ＝12x ＋1，由⎩⎨⎧y ＝12x ＋1，y ＝－2x ＋2，得E(25，65)7. (2，0) 分析：先作出点A 关于x 轴对称的点A′，再连接A′B 交x 轴于点P ，则点P 即为所求．由题中条件易求出直线A′B 的解析式，再求出直线A′B 与x 轴的交点坐标即可．8. 解：作点A 关于y 轴的对称点A′，连接CA′交y 轴于P ，此时PA ＋PC 值最小，最小值为CA′，易求C(－3，1)，△A′(4，0)，△CA′：y ＝－17x ＋47，△P(0，47)，作CE△x 轴于E ，△CA′＝CE 2＋A′E 2＝52。

人教版八年级的数学下《一次函数》期末典型题型练习试卷含答案.doc

一次函数1、下列问题中，变量y 与x 成一次函数关系的是( )A. 路程一定时，时间y 和速度x 的关系B. 长 10 米的铁丝折成长为C. 圆的面积y 与它的半径xy 米，宽为x 米的长方形D. 斜边长为 5 的直角三角形的直角边y 和x2、函数A.x ≠1B.x ＞－ 1 的自变量C.x≥－x 的取值范围为（1 D.x≥－ 1 且）x≠13、图象中所反映的过程是：小敏从家跑步去体育场，在那里锻炼了一阵后，又去早餐店吃早餐，然后散步走回家，其中 x 表示时间， y 表示小敏离家的距离，根据图象提供的信息，以下说法错误的是（）A. 体育场离小敏家 2.5 千米B. 体育场离早餐店 4 千米C. 小敏在体育场锻炼了15 分钟D.小敏从早餐店回到家用时30 分钟4、已知如图，正比例函数y=kx （k≠0）的函数值y 随 x 的增大而增大，则一次函数y=x+k 的图象大致是（）A. B. C. D.5、一次函数y=-x+6 的图像不经过（）A. 第一象限B.第二象限C.第三象限D.第四象限6、已知A（﹣ 4， y1）， B（ 2，y2）在直线y=﹣1/2x+20 上，则y1、 y2大小关系是（）A.y 1＞ y2B.y 1=y2C.y 1＜y2D. 不能比较7、已知某一次函数的图象与直线y=﹣x+1 平行，且过点（8， 2），那么此一次函数为（）A.y= ﹣x﹣2B.y= ﹣x+10C.y=﹣x﹣6D.y=﹣x﹣108、在同一平面直角坐标系中，直线与直线的交点不可能在（）A. B. C. D.9、如图，已知函数y=3x+b 和 y=ax﹣3的图象交于点P（﹣ 2，﹣ 5），则根据图象可得不等式3x+b＞ax﹣3的解集是（）A.x ＞﹣5B.x ＞﹣2C.x ＞﹣3D.x ＜﹣210、某学校组织团员举行申奥成功宣传活动，从学校骑车出发，先上坡到达 A 地后，宣传 8 分钟；然后下坡到 B 地宣传 8 分钟返回，行程情况如图 . 若返回时，上、下坡速度仍保持不变，在 A 地仍要宣传 8 分钟，那么他们从 B 地返回学校用的时间是（）A.45.2分钟B.48分钟C.46分钟D.33分钟11、已知直线y=﹣x+8 与 x 轴、 y 轴分别交于点 A 和点 B， M是 OB上的一点，若将△ ABM 沿 AM折叠，点B 恰好落在x 轴上的点B′处，则直线AM的函数解析式是（）A.y= ﹣x+8B.y= ﹣x+8C.y=﹣x+3D.y=﹣x+312、如图，直线y= x+4 与x 轴、 y 轴分别交于点 A 和点B，点C、D 分别为线段AB、OB的中点，点P 为直线OA上一动点，PC+PD值最小时点P 的坐标为（）A.（﹣ 3， 0）B. （﹣ 6， 0）C. （﹣，0）D. （﹣， 0）13、“五四”青年节期间，校团委对团员参加活动情况进行表彰，计划分为优秀奖和贡献奖，为此联系印刷公司设计了两种奖状，A，B 两家公司都为学校提出了相同规格和单价的两种奖状，其中优秀奖的奖状 6 元/ 张，贡献奖的奖状 5 元 / 张，经过协商， A 公司的优惠条件是：两种奖状都打八折，但要收制版费50 元；B 公司的优惠条件是：两种奖状都打九折；根据学校要求，优秀奖的个数是贡献奖的2 倍还多10 个，如果设贡献奖的个数是x 个 .（1）分别写出校团委购买A， B 两家印刷厂所需要的总费用y1（元）和y2（元）与贡献奖个数x 之间的函数关系式；（2）校团委选择哪家印刷公司比较合算？请说明理由.14、某超市鸡蛋供应紧张，需每天从外地调运鸡蛋1200 斤 . 超市决定从甲、乙两大型养殖场调运鸡蛋，已知甲养殖场每天最多可调出800 斤，乙养殖场每天最多可调出900 斤，从甲、乙两养殖场调运鸡蛋到该超市的路程和运费如下表：到超市的路程(千米) 运费 ( 元/ 斤·千米 )甲养殖场200 0.012乙养殖场140 0.015设从甲养殖场调运鸡蛋x 斤，总运费为W元（1）试写出 W与 x 的函数关系式 .（2）怎样安排调运方案才能使每天的总运费最省？参考答案1、 B2、 D3、 B4、 A5、 C6、 A7、 B.8、 D9、 B10、 A11、 C12、 C13、解：（ 1）由题意y1=4.8 （2x+10 ） +4x+50=13.6x+98 ，y2 =5.4 （ 2x+10） +4.5x=15.3x+54.（2）当 y1＞y2时， 13.6x+98 ∴当贡献奖个数小于等于＞15.3x+54 ，解得 x＜25，∵x为整数，25 个时，选 B 公司比较合算；当贡献奖个数大于25 个时，选 A 公司比较合算.14、解：从甲养殖场调运了x 斤鸡蛋，从乙养殖场调运了（1200﹣x）斤鸡蛋，根据题意得：解得： 300≤x≤800，总运费 W=200×0.012x+140×0.015 ×（1200﹣x）=0.3x+2520∵W随 x 的增大而增大，∴当x=300 时， W最小 =2610 元，，（ 300≤x≤800），∴每天从甲养殖场调运了300 斤鸡蛋，从乙养殖场调运了900 斤鸡蛋，每天的总运费最省.。

人教版八年级下一次函数与几何综合训练(PDF,无答案)

«一次函数»几何综合专题训练卷班级:㊀姓名:㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀㊀１.如图ꎬ直线ｌ１:ｙ１＝－２３ｘ＋ｂ过点Ａ(６ꎬ０)ꎬ交ｙ轴于点Ｂꎬ直线ｌ２:ｙ２＝１３ｘ＋１与ｘ轴交于点Ｃꎬ两直线ｌ１㊁ｌ２相交于点Ｄꎬ连接ＢＣ.㊀(１)求直线ｌ１的解析式及点Ｄ的坐标ꎻ㊀(２)求әＢＣＤ的面积ꎻ㊀(３)根据图象ꎬ直接写出当ｙ１>时ｘ的取值范围.㊀２.在平面直角坐标系中ꎬＯ为原点ꎬ点Ｐ的坐标为(３ꎬ３)ꎬ点Ａ坐标为(２ꎬ０)ꎬ平行于ｙ轴动直线ｌ交ｘ轴于Ｍꎬ交直线ＯＰ于Ｆꎬ交直线ＡＰ于Ｅ.㊀(１)求直线ＯＰꎬ直线ＡＰ的解析式ꎻ㊀(２)若设Ｍ点的横坐标为ｔꎬ试用含ｔ的式子表示ＥＦꎬ并求当ＥＦ＝２时Ｍ点的坐标ꎻ㊀(３)当әＯＥＦ是直角三角形时ꎬ试求Ｍ１３.如图ꎬ直线ｌ１的函数表达式为ｙ１＝－３ｘ＋３ꎬ且ｌ１与ｘ轴交于点Ｄꎬ直线ｌ２:ｙ２＝ｋｘ＋ｂ经过点ＡꎬＢꎬ与直线ｌ１交于点Ｃ.㊀(１)求直线ｌ２的函数表达式ꎬ并利用图象回答ꎬ何时ｙ１>ｙ２ꎻ㊀(２)求әＡＤＣ的面积ꎻ㊀(３)在直角坐标系中有点Ｅꎬ和ＡꎬＣꎬＤ构成平行四边形ꎬ请直接写出Ｅ点的坐标.４.如图ꎬ在平面直角坐标系ｘＯｙ中ꎬ直线ｙ＝－４３ｘ＋８与ｘ轴ꎬｙ轴分别交于点Ａꎬ点Ｂꎬ点Ｄ在ｙ轴的负半轴上ꎬ若将әＤＡＢ沿直线ＡＤ折叠ꎬ点Ｂ恰好落在ｘ轴正半轴上的点Ｃ处.㊀(１)求ＡＢ的长和点Ｃ的坐标ꎻ㊀(２)求直线ＣＤ的解析式.５.已知一次函数ｙ＝ｋｘ＋ｂ的图象与ｘ轴㊁ｙ轴分别交于点Ａ(－２ꎬ０)㊁Ｂ(０ꎬ４)ꎬ直线ｌ经过点Ｂꎬ并且与直线ＡＢ垂直.点Ｐ在直线ｌ上ꎬ且әＡＢＰ是等腰直角三角形.㊀(１)求直线ＡＢ的解析式ꎻ㊀(２)求点Ｐ的坐标ꎻ㊀(３)点Ｑ(ａꎬｂ)在第二象限ꎬ且ＳәＱＡＢ＝ＳәＰＡＢ.㊀①用含ａ的代数式表示ｂꎻ㊀②若ＱＡ＝ＱＢꎬ求点Ｑ的坐标.６.如图ꎬ已知点Ａ(０ꎬａ)ꎬＢ(ｂꎬ０)ꎬＣ(０ꎬｃ)ꎬ且∣ａ＋４∣＋ｂ２－８ｂ＋１６＝０ꎬ(ｃ＋１)２ɤ０ꎬ点Ｄ与点Ｃ关于直线ＡＢ对称.㊀(１)求直线ＡＢ的解析式和点Ｃ㊁Ｄ的坐标ꎻ㊀(２)点Ｅ在直线ＡＢ上ꎬ直接写出∣ＥＯ－ＥＤ∣的最大值和最小值及对应的点Ｅ的坐标..３７.如图ꎬ在平面直角坐标系ｘＯｙ中ꎬ一次函数ｙ＝ｋ１ｘ＋ｂ的图象与ｘ轴交于点Ａ(－３ꎬ０)ꎬ与ｙ轴交于点Ｂꎬ且与正比例函数ｙ＝ｋｘ的图象交点为Ｃ(３ꎬ４).求:㊀(１)求ｋ值与一次函数ｙ＝ｋ１ｘ㊀(２)若点Ｄ在第二象限ꎬәＤＡＢ是以ＡＢ为直角边的等腰直角三角形ꎬ请求出点Ｄ的坐标ꎻ㊀(３)在ｙ轴上求一点Ｐ使әＰＯＣ为等腰三角形ꎬ请求出所有符合条件的点Ｐ的坐标.角әＰＢＣꎬ求点Ｃ的坐标.㊀８.如图ꎬ平面直角坐标系中ꎬ直线ＡＢ:ｙ＝－ｘ＋ｂ交ｙ轴于点Ａ(０ꎬ４)ꎬ交ｘ轴于点Ｂ.㊀(１)求直线ＡＢ的表达式和点Ｂ的坐标ꎻ㊀(２)直线ｌ垂直平分ＯＢ交ＡＢ于点Ｄꎬ交ｘ轴于点Ｅꎬ点Ｐ是直线ｌ上一动点ꎬ且在点Ｄ的上方ꎬ设点Ｐ的纵坐标为ｎ.㊀①用含ｎ的代数式表示әＡＢＰ的面积ꎻ㊀②当ＳәＡＢＰ＝８时ꎬ求点Ｐ的坐标ꎻ㊀③在②的条件下ꎬ以ＰＢ为斜边在第一象限作等腰直９.(１６绍兴)如图ꎬ在矩形ＡＢＣＤ中ꎬ点Ｏ为坐标原点ꎬ点Ｂ的坐标为(４ꎬ３)ꎬ点Ａ㊁Ｃ在坐标轴上ꎬ点Ｐ在ＢＣ边上ꎬ直线ｌ１:ｙ＝２ｘ＋３ꎬ直线ｌ２:ｙ＝２ｘ－３.㊀(１)分别求直线ｌ１与ｘ轴ꎬ直线ｌ２与ＡＢ的交点坐标ꎻ㊀(２)已知点Ｍ在第一象限ꎬ且是直线ｌ２上的点ꎬ若әＡＰＭ是等腰直角三角形ꎬ求点Ｍ的坐标.１０.如图ꎬ长方形ＡＢＣＯ位于直角坐标平面ꎬＯ为原点ꎬＡ㊁Ｃ分别在坐标轴上ꎬＢ的坐标为(８ꎬ６)ꎬ线段ＢＣ上有一动点Ｐꎬ已知点Ｄ在第一象限.(１)Ｄ是直线ｙ＝２ｘ＋６上一点ꎬ若әＡＰＤ是等腰直角三角形ꎬ求点Ｄ的坐标ꎻ(２)Ｄ是直线ｙ＝２ｘ－６上一点ꎬ若әＡＰＤ是等腰直角三角形.求点Ｄ的坐标.５１１.(１７盘锦)如图ꎬ在平面直角坐标系中ꎬ直线ｌ:ｙ＝－３３ｘ＋４与ｘ轴㊁ｙ轴分别交于点ＭꎬＮꎬ高为３的等边三角形ＡＢＣꎬ边ＢＣ在ｘ轴上ꎬ将此三角形沿着ｘ轴的正方向平移ꎬ在平移过程中ꎬ得到әＡ１Ｂ１Ｃ１ꎬ当点Ｂ１与原点重合时ꎬ解答下列问题:(１)求出点Ａ１的坐标ꎬ并判断点Ａ１是否在直线ｌ上ꎻ(２)求出边Ａ１Ｃ１所在直线的解析式ꎻ(３)在坐标平面内找一点Ｐꎬ使得以Ｐ㊁Ａ１㊁Ｃ１㊁Ｍ为顶点的四边形是平行四边形ꎬ请直接写出Ｐ点坐标.１２.(１７无锡)操作: 如图１ꎬＰ是平面直角坐标系中一点(ｘ轴上的点除外)ꎬ过点Ｐ作ＰＣʅｘ轴于点Ｃꎬ点Ｃ绕点Ｐ逆时针旋转６０ʎ得到点Ｑ. 我们将此由点Ｐ得到点Ｑ的操作称为点的Ｔ变换.(１)点Ｑ的坐标为㊀㊀㊀㊀ꎻ若点Ｍ经过Ｔ变换后得到点Ｎ(６ꎬ－３)ꎬ则点Ｍ的坐标为㊀㊀㊀㊀.(２)Ａ是函数ｙ＝３２ｘ图象上异于原点Ｏ的任意一点ꎬ经过Ｔ变换后得到点Ｂ.①求经过点Ｏꎬ点Ｂ的直线的函数表达式ꎻ②如图２ꎬ直线ＡＢ交ｙ轴于点Ｄꎬ求әＯＡＢ的面积与әＯＡＤ的面积之比.６。

八年级数学下一次函数综合练习题

1999 2000
） C.
2000 2001
B.1
D.
2001 2002
13.一个一次函数的图象与直线 y
5 95 平行，与 x 轴、 y 轴的交点分别为 A、 B，并且过点（-1， -25）， x 4 4
则在线段 AB 上（包括端点 A、B），横、纵坐标都是整数的点有（ A.4 个 B.5 个 C.6 个
C． k<0, ）
4.关于函数 y 2 x 1 下列结论正确的是（ A．图象必经过点（﹣2，1） C．当 x
B．图象经过第一、二、三象限 D． y 随 x 的增大而增大
1 时， y 0 2
5.已知一次函数 y=ax+4 与 y=bx-2 的图象在 x 轴上相交于同一点,则 A．4 B．-2 C． 1 2 D． 1 2
6
18.如图，在直角坐标系中，矩形 OABC 的顶点 B 的坐标为（15，6），直线 y 成面积相等的两部分，那么 b=
1 x b 恰好将矩形 OABC 分 3
19.在直角坐标系中，x 轴上的动点 M（x，0）到顶点 P(5,5)、Q(2,1)的距离分别为 MP 和 MQ，当 MP+MQ 最小值时，点 M 的横坐标 x=
a 的值是( b
)
6.已知关于 x 的一次函数 y mx 2m 7 在 1 x 5 上的函数值总是正的，则 m 的取值范围（ A. m>7 B. m>1 C. 1 m 7 D.以上都不对
）
7.把直线 y 2 x 向上平移后得到直线 AB，直线 AB 经过点（m，n），且 2m+n=6，则直线 AB 的解析式是（） B. y 2 x 6 C. y 2 x 3 D. y 2 x 6

一次函数与几何图形综合题(含答案)

一次函数与几何图形综合题(含答案)近日，举行了一次关于一次函数与几何图形综合的专题讲座。

在思想方法方面，介绍了函数方法和数形结合法。

函数方法是通过观察运动和变化来分析数量关系，并将其抽象升华为函数模型，从而解决问题的方法。

数形结合法则是将数与形结合起来，分析研究并解决问题的一种思想方法，对于与函数有关的问题，使用数形结合法能够事半功倍。

在知识规律方面，讲座介绍了常数k和b对直线y=kx+b(k≠0)位置的影响。

当b大于0时，直线与y轴的正半轴相交；当b等于0时，直线经过原点；当b小于0时，直线与y轴的负半轴相交。

当k和b异号时，即b大于0时，直线与x轴正半轴相交；当k和b同号时，即k和b的乘积小于0时，直线与x轴负半轴相交。

当k大于0且b大于0时，图象经过第一、二、三象限；当k大于0且b等于0时，图象经过第一、三象限；当b大于0且b小于0时，图象经过第一、三、四象限；当k小于0且b大于0时，图象经过第一、二、四象限；当k小于0且b等于0时，图象经过第二、四象限；当b小于0且b小于0时，图象经过第二、三、四象限。

讲座还介绍了直线y=kx+b(k≠0)与直线y=kx(k≠0)的位置关系。

当b大于0时，将直线y=kx向上平移b个单位，即可得到直线y=kx+b；当b小于0时，将直线y=kx向下平移|b|个单位，即可得到直线y=kx+b。

另外，当k1不等于k2时，y1与y2相交；当k1等于k2且b1不等于b2时，y1与y2平行但不重合；当k1等于k2且b1等于b2时，y1与y2重合。

最后，讲座还通过一个例题对知识规律进行了精讲。

题目是直线y=－2x+2与x轴、y轴交于A、B两点，C在y轴的负半轴上，且OC=OB。

要求求出AC的解析式。

的性质，需要灵活运用几何知识和代数知识。

在解答过程中，要注意清晰的逻辑思路和准确的计算，避免出现错误。

2) 在OA的延长线上任取一点P，作PQ⊥BP，交直线AC于Q。

我们来探究一下BP与PQ的数量关系，并证明结论。

(完整版)青岛版八年级数学下册一次函数专项训练

一次函数专题一次函数知识点总结（一）函数1、变量：在一个变化过程中能够取不一样数值的量。

常量：在一个变化过程中只好取同一数值的量。

2、函数：一般的，在一个变化过程中，假如有两个变量x 和 y，而且对于x 的每一个确立的值，y 都有独一确立的值与其对应，那么我们就把x 称为自变量，把 y 称为因变量， y 是 x 的函数。

*判断 Y 能否为 X 的函数，只需看X 取值确立的时候，Y 能否有独一确立的值与之对应3、函数的分析式：用含有表示自变量的字母的代数式表示因变量的式子叫做函数的分析式4、函数的图像一般来说，对于一个函数，假如把自变量与函数的每对对应值分别作为点的横、纵坐标，那么坐标平面内由这些点构成的图形，就是这个函数的图象．5、描点法画函数图形的一般步骤第一步：列表（表中给出一些自变量的值及其对应的函数值）；第二步：描点（在直角坐标系中，以自变量的值为横坐标，相应的函数值为纵坐标，描出表格中数值对应的各点）；第三步：连线（依照横坐标由小到大的次序把所描出的各点用光滑曲线连结起来）。

6、函数的表示方法列表法：了如指掌，使用起来方便，但列出的对应值是有限的，不易看出自变量与函数之间的对应规律。

分析式法：简单了然，能够正确地反应整个变化过程中自变量与函数之间的相依关系，但有些实质问题中的函数关系，不可以用分析式表示。

图象法：形象直观，但只好近似地表达两个变量之间的函数关系。

（二）一次函数1、一次函数的定义一般地，形如y kx b（ k ， b 是常数，且 k 0 ）的函数，叫做一次函数，此中x是自变量。

当 b 0 时，一次函数ykx ，又叫做正比率函数。

⑴一次函数的分析式的形式是y kx b ，要判断一个函数是不是一次函数，就是判断能否能化成以上形式．⑵当 b 0 ， k 0 时，y kx还是一次函数．⑶当 b 0 ， k0 时，它不是一次函数．⑷正比率函数是一次函数的特例，一次函数包含正比率函数．2、正比率函数及性质一般地，形如y=kx(k 是常数， k≠0)的函数叫做正比率函数，此中k 叫做比率系数.注：正比率函数一般形式y=kx (k 不为零 )① k不为零② x指数为1③b 取零当 k>0 时，直线 y=kx 经过三、一象限，从左向右上涨，即随x 的增大 y 也增大；当k<0 时， ?直线 y=kx 经过二、四象限，从左向右降落，即随x 增大 y 反而减小．(1)分析式： y=kx （ k 是常数， k≠ 0）(2)必过点：（ 0， 0）、（ 1， k）(3) 走向： k>0 时，图像经过一、三象限；k<0 时， ?图像经过二、四象限13、一次函数及性质一般地，形如y=kx ＋b(k,b 是常数， k≠0)，那么 y 叫做 x 的一次函数 .当 b=0 时， y=kx ＋ b 即 y=kx ，因此说正比率函数是一种特别的一次函数.注：一次函数一般形式y=kx+b (k 不为零 )① k不为零②x指数为1③ b取随意实数一次函数y=kx+b 的图象是经过（0， b）和（ - b，0）两点的一条直线，我们称它为直线y=kx+b, 它能够k看作由直线y=kx 平移 |b| 个单位长度获得. （当 b>0 时，向上平移；当b<0 时，向下平移）（ 1）分析式： y=kx+b(k 、b 是常数， k 0)（2）必过点：（0，b）和（-b，0）k（3）走向： k>0 ，图象经过第一、三象限； k<0，图象经过第二、四象限b>0，图象经过第一、二象限；b<0，图象经过第三、四象限k0 b 0 k0 b 0 直线经过第一、二、三象限直线经过第一、二、四象限k0b 0k0b 0直线经过第一、三、四象限直线经过第二、三、四象限（ 4）增减性： k>0 ， y 随 x 的增大而增大；k<0， y 随 x 增大而减小 .（ 5）倾斜度： |k| 越大，图象越靠近于y 轴； |k| 越小，图象越靠近于x 轴 . （ 6）图像的平移：当 b>0 时，将直线 y=kx 的图象向上平移 b 个单位；当 b<0 时，将直线 y=kx 的图象向下平移 b 个单位 .一次k kx b k函数k ， b k 0符号 b 0 b 0y y图象O x Oxk 0b 0 b 0 b 0b 0y y y yO x O x O x O x性质y 随x的增大而增大y 随x的增大而减小4、一次函数y=kx ＋ b 的图象的画法.依据几何知识：经过两点能画出一条直线，而且只好画出一条直线，即两点确立一条直线，因此画一次函数的图象时，只需先描出两点，再连成直线即可.一般状况下：是先选用它与两坐标轴的交点：（0，b），.即横坐标或纵坐标为0 的点 .b>0b<0b=0经过第一、二、三象限经过第一、三、四象限经过第一、三象限k>0图象从左到右上涨，y 随 x 的增大而增大经过第一、二、四象限经过第二、三、四象限经过第二、四象限k<0图象从左到右降落，y 随 x 的增大而减小5、正比率函数与一次函数之间的关系一次函数y=kx ＋ b 的图象是一条直线，它能够看作是由直线y=kx 平移 |b|个单位长度而获得（当b>0 时，向上平移；当b<0 时，向下平移）6、正比率函数和一次函数及性质正比率函数一次函数概念一般地，形如 y=kx(k 是常数，k ≠0) 一般地，形如 y=kx ＋b(k,b 是常数， k ≠0)，那么的函数叫做正比率函数，此中k y 叫做 x 的一次函数 .当 b=0 时，是 y=kx ，因此叫做比率系数说正比率函数是一种特别的一次函数.自变量 X 为全体实数范围图象一条直线必过点（ 0， 0）、（ 1， k ）（ 0， b ）和（ - b， 0）k走向k>0 时，直线经过一、三象限； k ＞ 0， b ＞0, 直线经过第一、二、三象限 k<0 时，直线经过二、四象限k ＞ 0， b ＜0 直线经过第一、三、四象限 k ＜ 0， b ＞0 直线经过第一、二、四象限k ＜ 0， b ＜0 直线经过第二、三、四象限增减性 k>0， y 随 x 的增大而增大；（从左向右上涨） k<0， y 随 x 的增大而减小。

2020—2021年人教版初中数学八年级下册一次函数综合检测题及答案(精品试题).docx

八年级下册一次函数综合练习1.已知直线6y,解下列各题：=x3-+(1)若x>0,则y的取值范围为；(2)若y>0,则x的取值范围为；(3)若2-x，则y的取值范围为；<4≤(4)若2-y，则x的取值范围为；<4≤2.y=-2x+3先向右平移2个单位,再向下平移5个单位后的解析式为;(1)平移后的直线与x轴、y轴的交点A,B坐标分别为、;(2)平移后的直线与坐标轴围成的三角形的面积为.(3)若点P在直线AB上为一动点,当△OBP的面积是△OAB面积的2倍,则此时点P的坐标为.3.已知y=2x+b向左平移1个单位,再向上平移3个单位后经过点A(-2,4),则b=;(1)原直线关于y轴对称的直线解析式为；(2)原直线关于x轴对称的直线解析式为；(3)若直线y=mx-1与y=2x+b垂直,则m=.4.等腰三角形的周长是40cm,腰长y(cm)，底边长x(cm)，y与x的函数解析式wie ,底边长x的取值范围为.5.一次函数y=（m2-4）x+（1-m）和y=（m-1）x+m2-3的图象与y轴分别交于点P和点Q，若点P与点Q关于x轴对称，则m=．6.函数y=-3x＋2的图象上存在点P,使得点P•到x轴的距离等于3，则点P•的坐标为.7.已知一次函数y=ax+4与y=bx-2的图象在x 轴上相交于同一点,则b a 的值是( )A ．4B ．-2C ． 12D ． - 128.“五一节”期间，王老师一家自驾游去了离家170千米的某地，下面是他们家的距离y （千米）与汽车行驶时间x （小时）之间的函数图象，当他们离目的地还有20千米时，汽车一共行驶的时间是（）A.2小时B.2.2小时C.2.25小时D.2.4小时9.在如图所示的平面直角坐标系中，点P 是直线y=x 上的动点，A （1，0），B （2，0）是x 轴上的两点，则PA+PB 的最小值为．此时点P 的坐标为.10.已知直线221+=x y ,点P 在直线上一点,且点P 到x 轴、y 轴的距离相等,则点P 作为.11.为了响应国家节能减排的号召，鼓励市民节约用电，我市从2012年7月1日起，居民用电实行“一户一表”的“阶梯电价”，分三个档次收费，第一档是用电量不超过180千瓦时实行“基本电价”，第二、三档实行“提高电价”，具体收费情况如右折线图，请根据图象回答下列问题；（1）档用地阿亮是180千瓦时时，电费是元；（2）第二档的用电量范围是；（3）“基本电价”是元/千瓦时；（4）小明家8月份的电费是328.5元，这个月他家用电多少千瓦时？12.某工厂现有甲种原料280千克，乙种原料290千克，计划用这两种原料生产A、B两种产品共50件．已知生产一件A产品需要甲种原料9千克，乙种原料3千克，可获利700元；生产一件B产品需要甲种原料4千克，乙种原料10千克，可获利1200元．设生产A、B两种产品总利润为y元，其中A种产品生产件数是x．（1）写出y与x之间的函数关系式；（2）如何安排A、B两种产品的生产件数，使总利润y有最大值，并求出y的最大值．13.已知C坐标为(2,0),P坐标为(x,y),直线y=-x+4与x轴、y轴分别交于A、B两点.若点P(a,b)在直线y=-x+4上.(1)求出A、B坐标,并求出△AOB的面积;(2)若点P在第一象限内,连接PC,OP,△OPC的面积为S,请找出S与a之间的函数关系式,并求出a的取值范围;(3)当△OPC的面积等于6时,求P点坐标.(4)点P在移动的过程中,若△BCP为等腰三角形,求找出满足条件的点P坐标.(直接写出答案)14.已知矩形OABC,O为坐标原点,A(8，0),C(0，4),D(1，0)，点P为一动点,从A-B-C-O运动,点P速度为2个单位/秒,时间为t.(1)若△PAD的面积为S,请找出S与t的函数关系式,并写出对应的t的取值范围；(2)当直线PD平分矩形OABC的周长时,求点P的坐标;(3)当直线PD平分矩形OABC的面积时,求点P的坐标.答案详解1解:(1)6,06,0,36<<-∴>--=y y x y x Θ;(2)y>0时,-3x+6>0,-3x>-6,x<2; (3)当x=-4时,y=12+6=18,当x=2时,y=0,所以0≤y<18;(4)当y=-4时,-4=-3x+6,310,103=-=-x x ,当y=2时,34,43,263=-=-=+-x x x ,所以31034<≤x .2解:y=-2(x-2)+3-5=-2x+4+3-5=-2x+2（1）A(1，0),B(0，2);(2)三角形OAB 的面积为1；(3)P(-1，4)或(3，-4)3.解:y=2(x+1)+b+3,将(-2,4)代入,4=2(-2+1)+b+3,4=-2+b+3,b=3 (1)y=-2x+3;(2)y=-2x-3;(3)m=-21. 4.解:y=-2x+40,10<x<20.5.解:P(0，1-m),Q(0，m 2-3),因为P 与Q 关于x 轴对称,则m 2-3+1-m=0,m 2-m-2=0.(m-2)(m+1)=0，m=2或m=-1.因为m 2-4≠0,所以m ≠±2.所以m=-1.6.解:35,53,323,3;31,13,323,3=-=--=+--=-==-=+-=x x x y x x x y 时当时当,)335)(331(--，，P .7.解:.2,24,2,02;4,04-==-==--==+ba b a b x bx a x ax 8.解：设AB 段的函数解析式是y=kx+b ，y=kx+b 的图象过A （1.5，90），B （2.5，170），⎩⎨⎧=+=+1705.2905.1b k b k ，解得⎩⎨⎧-==3080b k ∴AB 段函数的解析式是y=80x ﹣30，离目的地还有20千米时，即y=170﹣20=150km ，当y=150时，80x ﹣30=150x=2.25h ，故选：C ．9.解：如图所示：作A 点关于直线y=x 的对称点A ′，连接A ′B ，交直线y=x 于点P ，此时PA+PB 最小，由题意可得出：OA ′=1，BO=2，PA ′=PA ，∴PA+PB=A ′B=52122=+．故答案为：5．10.解:)44(,4,221,221),,(,，所以设在第一象限时当P m m m m m m P P ==+= )34,34(,34,223,221),,(,---==-+-=-P m m m m m m P P 设在第二象限时当 11.解：（1）由函数图象，得当用电量为180千瓦时，电费为：108元．故答案为：108；（2）由函数图象，得设第二档的用电量为x °，则180＜x ≤450．故答案为：180＜x ≤450（3）基本电价是：108÷180=0.6；故答案为：0.6（4）设直线BC 的解析式为y=kx+b ，由图象，得，解得：，y=0.9x ﹣121.5．y=328.5时，x=500．答：这个月他家用电500千瓦时． 12解：（1）y=700x+1200（50﹣x ），即y=﹣500x+60000；（2）由题意得，解得16≤x ≤30y=﹣500x+60000，y随x 的增大而减小，当x=16时，y 最大=58000，生产B 种产品34件，A 种产品16件，总利润y 有最大值，y 最大=58000元．13.解:(1)A(4，0),B(0，4);S △OAB =8(2)将P(a,b)代入y=-x+4得,b=-a+4,S △OPC =)40(4)4(221<<+-=+-⨯⨯a a a(3)10,64;2,646)4(221=-=+--==+-=+-⨯⨯a a a a a ，,P(-2,6)或(10,6) (4)(2,2),(4-2,2),(24+,-2)14.解:(1))86(567)216(721,)62(144721,)20(72721,≤<+-=-⨯⨯=≤<=⨯⨯=≤≤=⨯⨯=t t t S OC P t S BC P t t t S AB P 上时在当上时在当上时在当 )4,5.3(,5.3,72,84714),4,()2(P x x x x x P ==-++=++设3232.32,32,23,0,24)0,1(),2,4(,)2,4(,)3(-=-====+=++=x y b k k b k b k b kx y PD AC 所以代入将直线解析式为设的中点坐标为由题意可知。

一次函数与几何图形综合专题练习(附答案)

一次函数与几何图形综合专题练习1.如图①所示，直线L ：5y mx m =+与x 轴负半轴、y 轴正半轴分别交于A 、B 两点。

(1)当OA=OB 时，试确定直线L 的解析式；(2)在(1)的条件下，如图②所示，设Q 为AB 延长线上一点，作直线OQ ，过A 、B 两点分别作AM ⊥OQ 于M ，BN ⊥OQ 于N ，若AM=4，BN=3，求MN 的长。

(3)当m 取不同的值时，点B 在y 轴正半轴上运动，分别以OB 、AB 为边，点B 为直角顶点在第一、二象限内作等腰直角△OBF 和等腰直角△ABE ，连EF 交y 轴于P 点，如图③。

问：当点B 在 y 轴正半轴上运动时，试猜想PB 的长是否为定值，若是，请求出其值，若不是，说明理由。

2、如图，直线1l 与x 轴、y 轴分别交于A 、B 两点，直线2l 与直线1l 关于x 轴对称，已知直线1l 的解析式为3y x =+，（1）求直线2l 的解析式；（2）过A 点在△ABC 的外部作一条直线3l ，过点B 作BE ⊥3l 于E,过点C 作CF ⊥3l 于F 分别，请画出图形并求证：BE ＋CF ＝EF（3）△ABC 沿y 轴向下平移，AB 边交x 轴于点P ，过P 点的直线与AC 边的延长线相交于点Q ，与y 轴相交与点M ，且BP ＝CQ ，在△ABC 平移的过程中，①OM 为定值；②MC 为定值。

在这两个结论中，有且只有一个是正确的，请找出正确的结论，并求出其值。

第2题图第2题图② 第2题图③CB A l 2l 10x yC BA0x y Q M PCBA 0xy3.如图，在平面直角坐标系中，A(a，0)，B(0，b)，且a、b满足.(1)求直线AB的解析式；(2)若点M为直线y=mx上一点，且△ABM是以AB为底的等腰直角三角形，求m值；(3)过A点的直线交y轴于负半轴于P，N点的横坐标为-1，过N点的直线交AP于点M，试证明的值为定值．4.如图，直线AB：y=-x-b分别与x、y轴交于A（6，0）、B两点，过点B的直线交x轴负半轴于C，且OB：OC=3：1。

第19章专题20：一次函数与几何综合题(四)-通用版八年级下册数学专题练

19章专题：一次函数与几何综合题（三）1.如图，把长方形纸片OABC 放入平面直角坐标系中，使OA ，OC 分别落在x ，y 轴的的正半轴上，连接AC ，且AC=45，AO=2CO ．（1）求点A ，C 的坐标；（2）将纸片OABC 折叠，使点A 与点C 重合（折痕为EF ），求折叠后纸片重叠部分△CEF 的面积；（3）求EF 所在直线的函数表达式，并求出对角线AC 与折痕EF 交点D 的坐标．（1）∵AC=45，AO=2CO ，∵AC 2=OC 2+OA 2， ∴80=OC 2+4OC 2，∴OC=4，OA=8，∴A （8，0），C （0，4）；（2）设AC 的解析式为y=kx+b ，则⎩⎨⎧=+=084b k b ，解得：⎪⎩⎪⎨⎧=-=421b k ， ∴AC 的解析式为y=-21x+4；设AC 与EF 交于点D ，由折叠知EF 垂直平分AC ，所以D 是矩形ABOC 的中心， ∴FD=DE ，∴EF 、AC 互相垂直平分， ∴重合部分AECF 是菱形，设CF=x ，则AF=x ，BF=8-x ， ∵AB=4，∠B=90°， ∴x 2=42+（8-x ）2， ∴x=5，即CF=5， ∴重合部分的面积=5×4=20；（3）∵AC ⊥EF ，直线AC 表达式中的k 值为：-21，∴直线EF 表达式中的k 值为2， ∵A （8，0），C （0，4），且D 为AC 中点， ∴D （4，2），设直线EF 的表达式为：y=2x+b ，将点D 的坐标代入上式并解得：则直线EF 解析式为：y=2x-6．2. 如图1，在平面直角坐标系中，直线AB 分别交x 轴、y 轴于点A （-2，0）点B （0，4）；点P 在直线AB 的右侧，且∠APB=45°．（1）若△ABP 为直角三角形，求点P 的坐标；（2）如图2，若点P 在第四象限，且∠BAP=90°，AP 与y 轴交于点M ，BP 与x 轴交于点N ，连接MN ，求证：P 是△OMN 的一个外角平分线交点．【解答】（1）∵△ABP 是直角三角形，且∠APB=45°，∴只有∠ABP=90°或∠BAP=90°，如图3，Ⅰ、当∠ABP=90°时，∵∠APB=∠BAP=45°，∴AB=PB ，过点P 作PC ⊥OB 于C ，∴∠BPC+∠CBP=90°， ∵∠CBP+∠ABO=90°，∴∠ABO=∠BPC ，在△AOB 和△BCP 中，∠AOB=∠BCP=90°，∠ABO=∠BPC ，AB=BP ，∴△AOB ≌△BCP （AAS ），∴PC=OB=4，BC=OA=2， ∴OC=OB-BC=2，∴P （4，2）；Ⅱ、当∠BAP=90°时，过点P'作P'D ⊥OA 于D ，同Ⅰ的方法得，△ADP'≌△BOA ，∴DP'=OA=2，AD=OB=4，∴OD=AD-OA=2，∴P'（2，-2）；即：满足条件的点P （4，2）或（2，-2）；（2）如图2，由（2）知点P （2，-2），∵A （-2，0），∴直线AP 的解析式为y=-21x-1，∴M （0，-1），∴BM=5，同理：直线BP 的解析式为y=-3x+4，∴N （34，0），∴MN=35，过点P 作PH ∥AB 交x 轴于H ，∵∠BAP=90°，∴∠BAO+∠PAH=90°，∴∠BAO+∠ABM=90°，∴∠ABM=∠PAH ，在△ABM 和△PAH 中，∠ABM=∠PAH ，AB=AP ，∠BAM=∠APH=90°， ∴△ABM ≌△PAH （ASA ），∴∠AMB=∠PHA ，AH=BM=5，∴∠PMG=∠PHA ，OH=AH-OA=3，∴H （3，0），∴NH=3-34=35=MN ，∵P （2，-2），M （0，-1），H （3，0），∴PM=5，PH=5，∴PM=PH ， ∴△PNM ≌△PNH （SSS ），∴∠AHP=∠PMN ，∴∠PMG=∠PMN ，即：MP 是△BMN 的一个外角的平分线．3. 如图1，在平面直角坐标系中，直线y=21x+4经过点A （310，m ），与x 轴，y 轴分别交于B ，C 两点，点D （0，-1），P （t ，0）（t ＞-8）（1）求m 的值和直线AD 的函数表达式；（2）连结CP ，当△BPC 是等腰三角形时，求t 的值；（3）若t=-4，点M ，N 分别在线段AB ，线段AD 上，当△PMN 是等腰直角三角形且∠MPN=45°时，求△PMN 的面积（1）直线y=21x+4经过点A （310，m ），则m=21×310+4=317， y=21x+4，令y=0，则x=-8，令x=0，则y=4，故点B 、C 的坐标分别为：（-8，0）、（0，4）；设直线AD 的表达式为：y=kx-1，将点A 的坐标代入上式并解得：k=2，故直线AD 的表达式为：y=2x-1；（2）点P （t ，0），点B 、C 的坐标分别为：（-8，0）、（0，4），PB 2=（t+8）2，PC 2=t 2+16，BC 2=80；当PB=PC 时，（t+8）2=t 2+16，解得：t=-3，当PB=BC 时，同理可得：t=-8+45（不合题意的值已舍去）；当PC=BC 时，同理可得：t=±8（舍去-8）；故t=-3或-8+45或8；（3）点P （-4，0），设点M （m ，21m+4），点N （n ，2n-1），①当∠PMN=90°时，如图1，PM=MN ，过点M 作MH ⊥x 轴于点H ，作GN ⊥MH 于点G ， ∵∠PMH+∠NMH=90°，∠NMH+∠MNG=90°， ∴∠PMH=∠MNG ，∠NGM=∠MHP=90°， ∴△NGM ≌△MHP （AAS ），∴GN=MH ，MG=PH ，即n-m=21m+4，21m+4-2n+1=m+4，解得：m=-2，故点M （-2，3）；△PMN 的面积=21PM 2=21（4+9）=213；②当∠MNP=90°时，MN=PN ，过点N 作x 轴的平行线交过点P 与y 轴的平行线于点H ，交过点M 与y 轴的平行线于点G ，同理可得：△MGN ≌△NHP （AAS ），则PH=GN ，HM=MG ，即1-2n=m-n ，n+4=21m+4-2n+1，解得：m=74，故点M （74，730），△PMN 的面积=21×（22PM ）2=49481；故答案为：213或49481．4. 直线y=-43x+6与x 轴相交于点B ，与y 轴相交于点A ．（1）求直线AB 与坐标轴围成的面积；（2）在x 轴上一动点P ，使△ABP 是等腰三角形；请直接写出所有P 点的坐标，并求出如图所示AP=PB 时点P 的坐标；（3）直线y=x+3与直线AB 相交于点C ，与x 轴相交于点D ；点Q 是直线CD 上一点，若△BQD 的面积是△BCD 的面积的两倍，求点Q 的坐标．（1）在当y=-43x+6中，令y=0时，x=8；当x=0时，y=6；∴△AOB 的面积=6×6×21=24；（2）如图，由（1）知A （0，6），B （8，0）， ∴OA=6，OB=8，∴AB=10， ∵△ABP 是等腰三角形；∴当AB=PB=10时，OP=18或2， ∴P （18，0）或（-2，0），当AB=AP 时，OP=OB=8， ∴P （-8，0），当AP=PB 时，如图所示：设OP=x ，则AP=BP=8-x ，由AO 2+OP 2=AP 2，得：62+x 2=（8-x ）2，∴x=47此时P （47，0）；综上所述，点P 的坐标为（18，0）或（-2，0）或（-8，0）或P （47，0）；（3）由y=-43x+6以及y=x+3联立方程组求得x=712，y=733，∴C （712，733），∵△BQD 的面积是△BCD 的面积的两倍，∴Q 点的纵坐标为766或-766，把y=766代入y=x+3得x=745，把y=-766代入y=x+3得x=-787，因此Q （745，766）或（-787，-766）．5. 如图，在平面直角坐标系中，直线l 1：y 1=kx+b 经过A （a ，0），B （0，b ）两点，且a 、b 满足（a-4）2+2-b =0，过点B 作BP ∥x 轴，交直线l 2：y 2=x 于点P ，连接PA ．（1）求直线AB 的函数表达式；（2）在直线l 2上是否存在一点Q ，使得S △BPQ =S △BPA ？若存在，求出点Q 的坐标；若不存在，请说明理由．（3）点C （n ，0）是x 轴上的一个动点，点D 是y 轴上的一个动点，过点C 作x 轴的垂线交直线l 1、l 2于点M 、N ，若△MND 是等腰直角三角形，请直接写出符合条件的n 的值．（1）（a-4）2+2-b =0，则a=4，b=2，点A 、B 的坐标分别为：（4，0）、（0，2），把点A 、B 的坐标代入一次函数表达式：y=kx+b 并解得：y=-21x+2；（2）存在，理由：点B （0，2），点P （2，2），则BP=2，S △APM =2， S △BPQ =S △BPA ，则点Q 的纵坐标为：0或4，故点Q （0，0）或（4，4）；0，0）或（4，4）；（3）MN=|-21n+2-n|=|-23n+2|，x M =x N =n ，①当∠MDN=90°时，则x M =21MN ，即：21|-23n+2|=n ，解得：n=74或-4；②当∠DNM=90°（或∠DMN=90°）时，则x M =MN ，即|-23n+2|=n ，解得：n=54或4；符合条件的n 的值为：4或54或74或-4．。

人教版数学八年级下册第十九章一次函数一次函数与几何综合专题练习题

人教版数学八年级下册第十九章一次函数一次函数与几何综合专题练习题
1.如图，直线1］的函数解析式为y=—3x+3,且1］与x轴交于点D,直线12经过点A,B,直线1］,12交于点C.
1
D
(1)求点D的坐标；
(2)求直线12的函数解析式；
(3)求厶ADC的面积；
(4)在直线12上存在异于点C的另一点P,使得△ADP与厶ADC的面积相等，请直接写出点P的坐标.
2.如图，直线y=2x+6与x轴交于点A,与y轴交于点B,直线y=—；x+l与x轴交于点C,与y轴交于点D,两直线交于点E,求和S四边形AODE-
4
3.如图，直线y=—萨+8分别交x轴、y轴于A,B两点，线段AB的垂直平分线分别交x 轴、y轴于C,D两点.
(1)求点C的坐标；
(2)求直线CE的解析式;
(3)求厶BCD的面积.。

部编数学八年级下册专题09一次函数与几何图形综合的七种考法(解析版)含答案

专题09 一次函数与几何图形综合的七种考法类型一、面积问题例．如图，直线AB 的表达式为364y x =-+，交x 轴，y 轴分别与B ，A 两点，点D 坐标为()4,0-点C 在线段AB 上，CD 交y 轴于点E ．(1)求点A ，B 的坐标．(2)若CD CB =，求点C 的坐标．(3)若ACE △与DOE V 的面积相等，在直线AB 上有点P ，满足DOC △与DPC △的面积相等，求点P 坐标．∵CD CB =，∴DF BF =，∵点D 坐标为()4,0-，点B 的坐标为(∴12BD =，8OB =，∴6BF =，∴2OF =，∵DOC △与DPC △的面积相等，∴点O 和点P 到距离相等，此时OP ∥∴直线OP 的解析式为35y x =，联立得：36435y x y xì=-+ïïíï=ïî，解得：x y ì=ïïíï=ïî【变式训练1】如图，直线1:1l y kx =+与x 轴交于点D ，直线2:l y x b =-+与x 轴交于点A ，且经过定点(1,5)B -，直线1l 与2l 交于点(2,)C m ．(1)填空：k =________；b =________；m =________；(2)在x 轴上是否存在一点E ，使BCE V 的周长最短？若存在，请求出点E 的坐标；若不存在，请说明理由；(3)若动点P 在射线DC 上从点D 开始以每秒1个单位的速度运动，连接AP ，设点P 的运动时间为t 秒．是否存在t 的值，使ACP △和ADP △的面积比为1:2？若存在，直接写出t 的值；若不存在，请说明理由．（3）∵点P 在射线DC 上从点∴(2,0)D -，∵(2,2)C ，∴22(22)225CD =++=，∵点P 的运动时间为t 秒．②点P 在线段DC 的延长线上，∵ACP △和ADP △的面积比为1:∴12CP DP =，∴22545DP =´=，综上：存在t 的值，使ACP △和【变式训练2】在平面直角坐标系中，O 为原点，点()4,0A ，()2,0B -，()3,2C -，点D 是y 轴正半轴上的动点，连接CD 交x 轴于点E ．(1)如图①，若点D 的坐标为()0,2，求ACD V 的面积；(2)如图②，若12ABD ABC S S =V V ，求点D 的坐标．(3)如图③，若BDE ACE S S =△△，请直接写出点D 的坐标．【变式训练3】如图，平面直角坐标系中，直线AB ：13y x b =-+交y 轴于点()0,1A ，交x 轴于点B ．过点()1,0E 且垂直于x 轴的直线DE 交AB 于点D ，P 是直线DE 上一动点，且在点D 的上方，设()1,P n ．(1)求直线AB 的解析式和点B 的坐标；(2)求ABP V 的面积（用含n 的代数式表示）；(3)当ABP V 的面积为2时，以PB 为边在第一象限作等腰直角三角形BPC ，求出点C 的坐标．，则90PEB BP CGB Ð=Ð=Ð=°，PB BC =，∴90PBE BPE Ð+Ð=°，90BPE CPG Ð+Ð=°，∴BPE CPG Ð=Ð，∴()AAS BEP PGC ≌V V ，∴2BE PG ==，2PE CG ==，∴点()3,4C ；②以PB 为底时，如图，过点C 作CG PE ^于点G ，作CH x ^轴于点H ，则90PGC CGE CHB PEB PCB Ð=Ð=Ð=°=Ð=Ð，CP CB =，∴90GCH PCB Ð=°=Ð，∴PCG BCH Ð=Ð，∴∴()AAS BCH PCG ≌V V ，∴BH PG =，CH CG =，∴BE BH PE PG +=-，即22BH BH +=-，∴0BH PG ==，∴点()3,2C ；综上，符合题意的点C 坐标为()5,2或()3,4或()3,2．类型二、最值问题例．如图，在平面直角坐标系xOy 中，一次函数()0y kx b k =+¹的图像经过()4,0A 、()0,4B 两点．(1)k =______，b =______．(2)已知()1,0M -、()3,0N ，①在直线AB 上找一点P ，使PM PN =．用无刻度直尺和圆规作出点P （不写画法，保留作图痕迹）；②点P 的坐标为______；③点Q 在y 轴上，那么PQ NQ +的最小值为______．【答案】(1)1-，4；(2)①见解析；②()1,3；③5【详解】（1）解：将()4,0A 、()0,4B 代入()0y kx b k =+¹中，得：044k b b =+ìí=î，解得；14k b =-ìí=î，故答案为：1-，4；（2）①如图，点P 即为所求；【变式训练1】在平面直角坐标系中，已知直线l经过1,32Aæöç÷èø和()3,2B-两点，且与x轴，y轴分别相交于C，D两点．(1)求直线l的表达式；V的面积等于2时，求点E的坐标；(2)若点E在直线AB上，当ODE-的值最小，则点P的坐标为______；(3)①在x轴上找一点P，使得PA PB-的值最大，则点Q的坐标为______．②在x轴上找一点Q，使得QA QB【变式训练2】如图，一次函数2y x =+的图象分别与x 轴和y 轴交于C ，A 两点，且与正比例函数y kx=的图象交于点()1,B m -．(1)求正比例函数的表达式；(2)点D 是一次函数图象上的一点，且OCD V 的面积是4，求点D 的坐标；(3)点P 是y 轴上一点，当BP CP +的值最小时，若存在，点P 的坐标是______．取点C 关于y 轴的对称点C ¢，则PC PC =CP BP C P BP C B ¢¢\+=+³，即点P 位于C B ¢与x 轴的交点时，BP +∵点(2,0)C - ，【变式训练3】如图，在平面直角坐标系内，()3,4A -，()3,2B ，点C 在x 轴上，AD x ^轴，垂足为D ，BE x ⊥轴，垂足为E ，线段AB 交y 轴于点F ．若AC BC =，ACD CBE Ð=Ð．(1)求点C 的坐标；(2)如果经过点C 的直线y kx b =+与线段BF 相交，求k 的取值范围；(3)若点P 是y 轴上的一个动点，当PA PC -取得最大值时，求BP 的长．类型三、等腰三角形存在性问题例．如图，在平面直角坐标系中，一次函数21y x =--的图像分别交x 轴、y 轴于点A 和B ．已知点C 的标为()3,0-，若点P 是x 轴上的一个动点．(1)A 的坐标是______，B 的坐标是______；(2)过点P 作y 轴的平行线交AB 于点M ，交BC 于点N ，当点P 恰好是MN 的中点时，求出P 点坐标．(3)若以点B 、P 、C 为顶点的BPC △为等腰三角形时、请求出所有符合条件的P 点坐标．【变式训练1】直线8y kx =-与x 轴、y 轴分别交于B C 、两点，且43OC OB =．(1)求OB 的长和k 的值：(2)若点A 是第一象限内直线8y kx =-上的一个动点，当它运动到什么位置时，AOB V 的面积是12？(3)在（2）成立的情况下，y 轴上是否存在点P ，使POA V 是等腰三角形？若存在，求出点P 的坐标；若不存在，请说明理由．（写过程）由题意得，12OB AD ´´=6OB =Q ，\解得，AD当21294OA OP =+==当397OA OP ==时，3P 当22AP OP =时，作2P H ^22AP OP =Q Q 2P 为线段OA 垂直平分线与【变式训练2】在平面直角坐标系中，直线MN 交x 轴正半轴于点M ，交y 轴负半轴于点()0,3N -，30Ð=°ONM ，作线段MN 的垂直平分线交x 轴于点A ，交y 轴于点B ．(1)如图1，求直线MN 的解析式和A 点坐标；(2)如图2，过点M 作y 轴的平行线l ，P 是l 上一点，若ANP S =△P 坐标；(3)如图3，点Q 是y 轴的一个动点，连接QM 、AQ ，将MAQ V 沿AQ 翻折得到1M AQ △，当1M MN △是等腰三角形时，求点Q 的坐标．过T 作TS AM ^于S ，则AT ∴22333322AS æö=-=ç÷èø，同理2315Q P y x =--：，综上：()3,6P ，(3,P -（3）①如图，当MN MM =由轴对称的性质可得：AM ∵()223323AN =+=，∴()0,1Q ．②当1NM NM =时，如图，由23AN NM AM ===，∴ANM V 为等边三角形，此时Q ，N 重合，∴()0,3Q -；③当11M M M N =时，1M 在直线∵30OAB Ð=°，【变式训练3】如图，一次函数()0y kx b k =+¹的图象与x 轴交于点C ，与y 轴交于点()0,5A ，与正比例函数12y x =的图象交于点B ，且点B 的横坐标为2，点P 为y 轴上的一个动点．(1)求B 点的坐标和k 、b 的值；(2)连接CP ，当ACP △与AOB V 的面积相等时，求点P 的坐标；(3)连接BP ，是否存在点P 使得PAB V 为等腰三角形?若存在，请求出点P 的坐标；若不存在，请说明理由．③当PA PB =时，如图2，设(0,P m 22(5)PA m =-，1PH m =-，所以PB 所以222(5)(1)2m m -=-+，解得m类型四、直角三角形存在性问题例．如图1，在平面直角坐标系xOy 中，点O 为坐标原点，直线AB :3y 4x b =+与直线AC ：9y kx =+交于点(2,)A n ，与x 轴分别交于点0()6,B -和点C ．点D 为线段BC 上一动点，将ABD △沿直线AD 翻折得到ADE V ，线段AE 交x 轴于点F ．(1)直线AC 的函数表达式．(2)当点D 在线段BO 上，点E 落在y 轴上时，求点E 的坐标．(3)若DEF V 为直角三角形，求点D 的坐标．【变式训练1】综合与探究：如图，在平面直角坐标系中，直线2y x =+与x 轴，y 轴分别交于点A ，B ，与直线11433y x =-+交于点C ．直线11433y x =-+与x 轴交于点D ，若点P 是线段AD 上的一个动点，点P 从点D 出发沿DA 方向，以每秒2个单位长度匀速运动到点A （到 A 停止运动）．设点P 的运动时间为s t ．(1)求点A 和点B 的坐标；△的面积为12时，求t的值；(2)当ACP△为直角三角形？若存在，请直接写出t的值；(3)试探究，在点P运动过程中，是否存在t的值，使ACP若不存在，请说明理由．【变式训练2】如图，平面直角坐标系中，直线AB 与x 轴交于点()30A -，与y 轴交于点()06B ，，点C 是直线AB 上的一点，它的坐标为()4m ，，经过点C 作直线CD x ∥轴交y 轴于点D ．(1)求点C 的坐标；(2)已知点P 是直线CD 上的动点，①若POC △的面积为4，求点P 的坐标；②若POC △为直角三角形，请求出所有满足条件的点P 的坐标．②Q OCP Ð一定不是直角，当90OPC Ð=°时，点P 恰好在点D ，\()04P ，，当90POC Ð=°时，，由题可得221417OC =+=，2222416OP DP DP =+=+，()221CP DP =+，Q 222CP OC OP =+，\()2211716DP DP +=++，\16DP =，\()164P ，，综上所述，所有满足条件的点P 的坐标为()04，或()164P ，．【变式训练3】如图，已知函数1y x =+的图象与y 轴交于点A ，一次函数y kx b =+的图象经过点()0,1B -，与x 轴以及1y x =+的图象分别交于点C ，D ，且点D 的坐标为()1,n ．(1)则k =______，b =______，n =______；(2)关于x ，y 的二元一次方程组y =x +1,y =kx +b的解为______；(3)求四边形AOCD 的面积；(4)在x 轴上是否存在点P ，使得以点P ，C ，D 为顶点的三角形是直角三角形，请求出点P 的坐标．①当P D DC ¢^时，22P C P D ¢¢=类型五、等腰直角三角形存在性问题例．模型建立：如图1，等腰直角三角形ABC 中，90ACB Ð=°，CB CA =，直线ED 经过点C ，过A 作AD ED ^于D ，过B 作BE ED ^于E ．(1)求证：BEC CDA V V ≌．(2)模型应用：已知直线14:43l y x =+与y 轴交与A 点，将直线1l 绕着A 点顺时针旋转45°至2l ，如图2，求2l 的函数解析式．(3)如图3，矩形ABCO ，O 为坐标原点，B 的坐标为()8,6，A 、C 分别在坐标轴上，P 是线段BC 上动点，设PC m =，已知点D 在第一象限，且是直线26y x =-上的一点，若APD △是不以A 为直角顶点的等腰直角三角形，请直接写出点D 的坐标．∵45BAC Ð=°，∴ABC V 为等腰直角三角形，由（1）得：CBD BAO V V ≌∴BD AO =，CD OB =，∵直线4:4l y x =+，∴()626122AE x =--=-由（1）得：ADE DPF △△≌∴DF AE =，即1228x x -=-，解得：4x =；∴()4,2D ；∴266212BF x x =--=-；同（1）得，APB PDF △≌△∴8AB PF ==，PB DF ==∴()88BF PF PB x =-=--=∴21216x x -=-，解得：283x =；∴2838,33D æöç÷èø；【变式训练1】综合与探究：如图1，平面直角坐标系中，一次函数334y x =-+的图像分别与x 轴、y 轴交于点A ，B ，点C 是线段OA 的中点，点D 与点C 关于y 轴对称，作直线BD ．(1)求A ，B 两点的坐标；(2)求直线BD 的函数表达式；(3)若点P 是直线BD 上的一个动点．请从A ，B 两题中任选一题作答．我选择______题．A ．如图2，连接AP ，CP ．直接写出ACP △为直角三角形时点P 的坐标．B ．如图3，连接CP ，过点P 作PQ x ^轴于点Q ．直接写出CPQ V 为等腰直角三角形时点P 的坐标．【变式训练2】如图，平面直角坐标系中，直线1:3AB y x b =-+交y 轴于点()0,1A ，交x 轴于点B ．直线1x =交AB 于点D ，交x 轴于点E ，P 是直线1x =上一动点，且在点D 的上方，设()1,P n ．(1)求直线AB 的解析式；(2)当2ABP S =△时，在第一象限内找一点C ，使BCP V 为等腰直角三角形，求点C 的坐标．∵1x =时，12133y x =-+=，P 在点∴23PD n =-，∴12PAB APD BPD S S S PD AM =+=×+V V V ∵2ABP S =△，3∵90,45CPB EPB Ð=°Ð=°，∴45NPC EPB Ð=Ð=°．又∵90,CNP PEB BP PC Ð=Ð=°=，∴CNP BEP ≌V V ，∴2PN =NC =EB =PE =，∴224NE NP+PE ==+=，∴()3,4C ；若90,PBC BP BC Ð=°=，如图，过点C 作CF x ^轴于点F ．∵90,45PBC EBP Ð=°Ð=°，∴45CBF PBE Ð=Ð=°．又∵90,CFB PEB BC BP Ð=Ð=°=，∴CBF PBE ≌V V ．∴2BF CF PE EB ====，∴325OF OB BF =+=+=，∴()5,2C ；若90,PCB CP EB Ð=°=，如图，∴45CPB EBP Ð=Ð=°，∵,,CP EB CPB EBP BP BP =Ð=Ð=，∴PCB PEB ≌V V ，∴2PC CB PE EB ====，∴()3,2C ；∴点C 的坐标是()3,4或()5,2或()3,2．【变式训练3】如图，在平面直角坐标系xOy 中，直线AP 交x 轴于点(),0P p ，与y 轴交于点()0,A a ，且a ，p ()230a +=．(1)求直线AP 的解析式；(2)如图1，直线2x =-与x 轴交于点N ，点M 在x 轴上方且在直线2x =-上，若MAP △的面积等于6，请求出点M 的坐标；(3)如图2，已知点()2,4C -，若点B 为射线AP 上一动点，连接BC ，在坐标轴上是否存在点Q ，使BCQ △是以BC 为底边，点Q 为直角顶点的等腰直角三角形，若存在，请直接写出点Q 坐标；若不存在，请说明理由．∵MD AP P ，MAP △的面积等于∴DAP V 的面积等于6，∴162A DP y ××=，即12DP ×∴4DP =，∴()3,0D -，y∴,33OE t BE t ==-，∵BCQ △是以BC 为底边的等腰直角三角形，∴BQ CQ =，90BQC Ð=∴90BQE NQC Ð=°-Ð=又∵BEQ QNC Ð=Ð，∴()AAS BEQ QNC V V ≌，∴BG t =，33OG t =-，∴BT t =，33OT t =-，同②可证CFQ QTB V V ≌∴QF BT t ==，QT CF =∴OQ OT QT OF =+=+∴52t =，∴513422OQ =+=，类型六、平行四边形存在性问题例．在平面直角坐标系xOy 中，直线36y x =+分别与x 、y 轴相交于A 、B 两点，将线段AB 绕点A 顺时针旋转90°得到线段AC ．连接BC 交x 轴于点D ．(1)求点C 的坐标；(2)P 为x 轴上的动点，连接PB ，PC ，当PB PC -的值最大时，求此时点P 的坐标．(3)点E 在直线AC 上，点F 在x 轴上，若以B 、D 、E 、F 为顶点的四边形是平行四边形，请直接写出点F 的坐标；【答案】(1)点C 的坐标为()4,2-(2)()6,0P (3)点F 的坐标为()17,0-或()13,0或()23,0【详解】（1）解：令0y =，则2x =-，()2,0A \-，令0x =，则6y =，()0,6B \，26OA BO \==，，过点C 作CH x ^轴于H ，9090CAD BAO BAO ABO ÐÐÐÐ+=°+=°Q ，，CAD ABO ÐÐ\=，90AHC BOA ÐÐ\==°，由旋转得AB AC =，()AAS ABO CAH \V V ≌，26CH OA AH BO \====，，4OH AH OA \=-=，\点C 的坐标为()4,2-；（2）作点C 关于x 轴的对称点C ¢，连接BC ¢延长交x 轴于点P ，则点P 就是所求的最大值点，\()4,2C ¢设直线BC ¢的解析式为y kx b =+，\642b k b =ìí+=î，解得16k b =-ìí=î，6y x \=-+，()6,0P \；（3）()()()2,04,20,6A C B --Q ，，，设直线AC 的解析式为y mx n =+，则2042m n m n -+=ìí+=-î【变式训练1】如图1，在平面直角坐标系中，直线AB 与x 轴交于点(),0A m ，与y 轴交于点()0,B n ，且m n ，满足：()260m n n ++-=．(1)求：AOB S V 的值；(2)D 为OA 延长线上一动点，以BD 为直角边作等腰直角BDE V ，连接EA ，求直线EA 与y 轴交点F 的坐标；(3)在（2）的条件下，当2AD =时，在坐标平面内是否存在一点P ，使以B E F Р、、、为顶点的四边形是平行四边形，如果存在，直接写出点Р的坐标，若不存在，说明理由．∵EDB △为等腰直角三角形，∴,90DE DB EDB =Ð=°，∴18090EDG ODB Ð+Ð=°-。

八年级下学期一次函数单元测试题(含答案)(K12教育文档)

八年级下学期一次函数单元测试题(含答案)(word版可编辑修改)编辑整理：尊敬的读者朋友们：这里是精品文档编辑中心，本文档内容是由我和我的同事精心编辑整理后发布的，发布之前我们对文中内容进行仔细校对，但是难免会有疏漏的地方，但是任然希望（八年级下学期一次函数单元测试题(含答案)(word版可编辑修改)）的内容能够给您的工作和学习带来便利。

同时也真诚的希望收到您的建议和反馈，这将是我们进步的源泉，前进的动力。

本文可编辑可修改，如果觉得对您有帮助请收藏以便随时查阅，最后祝您生活愉快业绩进步，以下为八年级下学期一次函数单元测试题(含答案)(word版可编辑修改)的全部内容。

一次函数测试题一、选择1．下列函数中，自变量x 的取值范围是x ≥2的是（） A ．y=2x - B ．y=2x - C ．y=24x - D ．y=2x +·2x - 2．下面哪个点在函数y=12x+1的图象上（）A ．（2,1）B ．（-2，1）C ．（2，0）D ．（—2,0) 3．下列函数中，y 是x 的正比例函数的是（）A ．y=2x —1B ．y=3x C ．y=2x 2D ．y=-2x+14．一次函数y=—5x+3的图象经过的象限是（） A ．一、二、三 B ．二、三、四 C ．一、二、四 D ．一、三、四5．若函数y=(2m+1）x 2+（1-2m ）x （m 为常数）是正比例函数，则m 的值为（ )A ．m>12B ．m=12C ．m 〈12D ．m=—126．若一次函数y=（3-k)x-k 的图象经过第二、三、四象限,则k 的取值范围是( ） A ．k 〉3 B ．0<k ≤3 C ．0≤k<3 D ．0<k 〈3 7．已知一次函数的图象与直线y=-x+1平行，且过点（8，2），那么此一次函数的解析式为（ ) A ．y=—x —2 B ．y=—x —6 C ．y=-x+10 D ．y=-x-1⑧．汽车开始行驶时，油箱内有油40升，如果每小时耗油5升，则油箱内余油量y （升）与行驶时间t （时）的函数关系用图象表示应为下图中的( ）9．李老师骑自行车上班，最初以某一速度匀速行进，•中途由于自行车发生故障,停下修车耽误了几分钟，为了按时到校，李老师加快了速度，仍保持匀速行进，如果准时到校．在课堂上，李老师请学生画出他行进的路程y•（千米）与行进时间t （小时）的函数图象的示意图,同学们画出的图象如图所示，你认为正确的是（）10．一次函数y=kx+b 的图象经过点（2，—1）和（0，3)，•那么这个一次函数的解析式为（）A ．y=-2x+3B ．y=—3x+2C ．y=3x —2D ．y=12x —3二、填空11．已知自变量为x 的函数y=mx+2—m 是正比例函数，则m=________,•该函数的解析式为_________．12．若点（1,3）在正比例函数y=kx 的图象上，则此函数的解析式为________． 13．已知一次函数y=kx+b 的图象经过点A （1,3)和B(—1,-1），则此函数的解析式为_________． 14．若解方程x+2=3x —2得x=2,则当x_________时直线y=x+•2•上的点在直线y=3x-2上相应点的上方．15．已知一次函数y=—x+a 与y=x+b 的图象相交于点（m ，8），则a+b=_________．16．若一次函数y=kx+b 交于y•轴的负半轴,•且y•的值随x•的增大而减少,•则k____0,b______0．（填“>”、“<”或“＝”）17．已知直线y=x-3与y=2x+2的交点为（-5，—8），则方程组30220x y x y --=⎧⎨-+=⎩的解是________． 18．已知一次函数y=-3x+1的图象经过点（a ，1)和点（—2，b)，则a=________，b=______． 19．如果直线y=-2x+k 与两坐标轴所围成的三角形面积是9，则k 的值为_____． 20．如图，一次函数y=kx+b 的图象经过A 、B 两点，与x 轴交于点C ，则此一次函数的解析式为__________，△AOC 的面积为_________．三、解答21．根据下列条件，确定函数关系式：（1）y+1与x —2成正比，且当x=9时，y=16；（2)y=kx+b 的图象经过点（3，2）和点（-2,1）． 566-2xy1234-2-15-14321O22。

八年级数学下册专题11一次函数几何压轴训练(原卷版)

专题11 一次函数几何压轴训练1．（2023秋•东阳市期末）如图，在平面直角坐标系中，直线分别交x轴，y轴于点B，A，直线OC⊥AB，垂足为点C，D为线段OA上一点（不与端点重合），过点D 作直线l∥x轴，交直线AB于点E，交直线OC点F．（1）求线段OC的长；（2）当DE＝EF时，求点D的坐标；（3）若直线l过点C，点M为线段OC上一点，N为直线l上的点，已知OM＝CN，连结AN，AM，求线段AN+AM的最小值．2．（2023秋•和平县期末）如图1，在平面直角坐标系xOy中，点O是坐标原点，直线AB：y＝kx+与直线AC：y＝﹣2x+b交于点A，两直线与x轴分别交于点B（﹣3，0）和C （2，0）．（1）求直线AB和AC的表达式．（2）点P是y轴上一点，当P A+PC最小时，求点P的坐标．（3）如图2，点D为线段BC上一动点，将△ABD沿直线AD翻折得到△ADE，线段AE 交x轴于点F，若△DEF为直角三角形，求点D坐标．3．（2023秋•槐荫区期末）如图，直线和直线l2与x轴分别相交于A，B两点，且两直线相交于点C，直线l2与y轴相交于点D（0，﹣4），OA＝2OB．（1）求出直线l2的函数表达式；（2）E是x轴上一点，若S△ABC＝2S△BCE，求点E的坐标；（3）若F是直线l1上方且位于y轴上一点，∠ACF＝2∠CAO，判断△BCF的形状并说明理由．4．（2023秋•巴中期末）如图，在平面直角坐标系中，直线y＝﹣x+3与x轴、y轴分别交于点A、B，直线BC与x轴负半轴交于点C，且CO＝2AO．（1）求线段AC的长；（2）动点P从点C出发沿射线CA以每秒1个单位的速度运动，连接BP，设点P的运动时间为t（秒），△BPO的面积为S，求S与t的函数关系式，并直接写出自变量t的取值范围；（3）在（2）的条件下，在线段BC上是否存在点D，连接DP，使得△BDP是以BP为直角边的等腰直角三角形，若存在，请求出t的值，若不存在，请说明理由．5．（2023秋•金牛区期末）如图1，在平面直角坐标系中，直线y＝2x+b与x轴、y轴分别交于点A、点B，S△AOB＝4，点C（3，m）是直线AB上一点，在直线AB左侧过点C的直线交y轴于点D，交x轴于点E．（1）求m和b的值；（2）当∠ACD＝45°时，求直线CD的解析式；（3）如图2，在（2）的条件下，过C作CM⊥x轴，在直线AC上一点P，直线CD上一点Q，直线CM上一点H，当四边形AHQP为菱形时，求P点的坐标．6．（2023秋•咸阳期末）如图，已知一次函数y＝kx+b（k、b为常数，且k≠0）的图象与x 轴交于点A（﹣6，0），与y轴交于点B（0，8）．（1）求该一次函数的表达式；（2）点C为点B上方y轴上的点，在该一次函数的图象上是否存在点P，使得以点P、B、C为顶点的三角形与△OAB全等？若存在，求出所有符合条件的点P的坐标；若不存在，请说明理由．7．（2023秋•历城区期末）如图1，直线AB：y＝﹣x+b分别与x，y轴交于A（3，0），B两点，点A沿x轴向右平移3个单位得到点D．（1）分别求直线AB和BD的函数表达式．（2）在线段BD上是否存在点E，使△ABE的面积为，若存在，求出点E坐标；若不存在，说明理由．（3）如图2，P为x轴上A点右侧的一动点，以P为直角顶点，BP为腰在第一象限内作等腰直角△BPQ，连接QA并延长交y轴于点K．当点P运动时，点K的位置是否发生变化？如果不变请求出它的坐标；如果变化，请说明理由．8．（2023秋•江门期末）如图所示，直线AB交x轴于点A（a，0），交y轴于点B（0，b），且a，b满足+（a﹣4）2＝0．（1）a＝，b＝；（2）如图1，若点C的坐标为（﹣1，0），且AH⊥BC于点H，AH交OB于点P，试求点P的坐标；（3）如图2，若点D为AB的中点，点M为y轴正半轴上一动点，连接MD，过点D作DN⊥DM交x轴于点N，当点M在y轴正半轴上运动的过程中，式子S△BDM﹣S△ADN的值是否发生改变？如发生改变，求出该式子的值的变化范围；若不改变，求出该式子的值．9．（2023秋•简阳市期末）如图，在平面直角坐标系xOy中，一次函数y＝﹣x+8分别与x 轴、y轴交于A、B两点，过点B作BC⊥AB交x轴于点C．（1）求点C的坐标；（2）点D为直线AB上一点，且∠DCA＝∠DAC，求直线CD的解析式；（3）若点Q是x轴上一点，连接BQ，将△ABQ沿着BQ所在直线折叠，当点A落在y 轴上时，求点Q的坐标．10．（2023秋•天桥区期末）如图1，已知函数y＝x+3与x轴交于点A，与y轴交于点B，点C与点A关于y轴对称．（1）请写出点A坐标，点B坐标，直线BC的函数解析式；（2）设点M是x轴上的一个动点，过点M作y轴的平行线，交直线AB于点P，交直线BC于点Q．①若△PQB的面积为，求点Q的坐标；②点M在线段AC上，连接BM，如图2，若∠BMP＝∠BAC，直接写出P的坐标．11．（2023秋•万州区期末）如图1，在平面直角坐标系中，一次函数y＝2x+4的图象与x轴，y轴分别交于A、B两点，点C是OB的中点．（1）求直线AC的解析式；（2）如图2，若点M是直线AC上的一动点，当S△ABM＝2S△AOC时，求点M的坐标；（3）将直线AB向右平移3个单位长度得到直线l，若点E为平移后直线l上的一点，在平面直角坐标系中是否存在点F，使以点A、C、E、F为顶点，AE为边的四边形为菱形，若存在，请直接写出所有满足条件的点F的坐标；若不存在，请说明理由．12．(2023秋•盐都区期末）如图，直线AB：y＝x+b分别与x、y轴交于A，B两点，点A的坐标为（−4，0），过点B的直线交x轴正半轴于点C，且OB：OC＝4：3．（1）求直线BC的函数表达式；（2）在x轴上方是否存在点D，使以点A，B，D为顶点的三角形与△ABC全等．若存在，画出△ABD，并求出点D的坐标，若不存在，请说明理由；（3）点P是y轴上的一点，连接CP，将△BCP沿直线CP翻折，当点B的对应点B′恰好落在x轴上时，请直接写出此时直线CP的函数表达式．13．（2023春•阳江期末）如图，在平面直角坐标系中，直线l1：y＝﹣x+5与y轴交于点A，直线l2与x轴、y轴分别交于点B（﹣4，0）和点C，且与直线l1交于点D（2，m）．（1）求直线l2的解析式；（2）若点E为线段BC上一个动点，过点E作EF⊥x轴，垂足为F，且与直线l1交于点G，当EG＝6时，求点G的坐标；（3）若在平面上存在点H，使得以点A，C，D，H为顶点的四边形是平行四边形，请直接写出点H的坐标．14．(2023春•潮阳区期末）如图，直线y＝x﹣3交x轴于A，交y轴于B，（1）求A，B的坐标和AB的长（直接写出答案）；（2）点C是y轴上一点，若AC＝BC，求点C的坐标；（3）点D是x轴上一点，∠BAO＝2∠DBO，求点D的坐标．15．（2023春•武穴市期末）如图，在平面直角坐标系xOy中，直线l1：y＝x+2与x轴交于点A，直线l2：y＝3x﹣6与x轴交于点D，与l1相交于点C．（1）求点D的坐标；（2）在y轴上一点E，若S△ACE＝S△ACD，求点E的坐标；（3）直线l1上一点P（1，3），平面内一点F，若以A、P、F为顶点的三角形与△APD 全等，求点F的坐标．16．（2023春•淅川县期末）如图，已知直线y＝kx+b经过A（6，0）、B（0，3）两点．（1）求直线y＝kx+b的解析式；（2）若C是线段OA上一点，将线段CB绕点C顺时针旋转90°得到CD，此时点D恰好落在直线AB上．①求点C和点D的坐标；②若点P在y轴上，Q在直线AB上，是否存在以C、D、P、Q为顶点的四边形是平行四边形？若存在，直接写出所有满足条件的点Q坐标，否则说明理由．17．（2023春•拜泉县期末）综合与探究．如图，平面直角坐标系中，矩形OABC的两条邻边分别在x轴、y轴上，对角线，点B的坐标为B（2a，a）．（1）A，C．（2）把矩形OABC沿直线DE对折使点C落在点A处，直线DE与OC、AC、AB的交点分别为D，F，E，求直线DE的解析式（问题（1）中的结论可直接使用）．（3）若点M在y轴上，则在平面直角坐标系中的x轴及x轴的下方，是否存在这样的点N，使得以A、D、N、M为顶点的四边形是菱形？若存在，请直接写出点N的坐标；若不存在，请说明理由．18．（2023春•唐县期末）（1）基本图形的认识：如图1，在四边形ABCD中，∠B＝∠C＝90°，点E是边BC上一点，AB＝EC，BE＝CD，连结AE、DE，求证：△AED是等腰直角三角形．（2）基本图形的构造：如图2，在平面直角坐标系中，A（2，0），B（0，3），连结AB，过点A在第一象限内作AB的垂线，并在垂线截取AC＝AB，求点C的坐标；（3）基本图形的应用：如图3，一次函数y＝﹣2x+2的图象与y轴交于点A，与x轴交于点B，直线AC交x轴于点D，且∠CAB＝45°，求点D的坐标．19．（2023春•新罗区期末）数形结合作为一种数学思想方法，数形结合包括两个方面：第一种情形是“以数解形”，而第二种情形是“以形助数”．例如：在我们学习数轴的时候，数轴上任意两点，A表示的数为a，B表示的数为b，则A，B两点的距离可用式子|a﹣b|表示．研一研：如图，在平面直角坐标系中，直线AB分别与x轴正半轴、y轴正半轴交于点A（a，0）、点B（0，b），且a、b满足（a﹣6）2+|b﹣4|＝0．（1）直接写出以下点的坐标：A（，0），B（0，）．（2）若点P、点Q分别是y轴正半轴（不与B点重合）、x轴负半轴上的动点，过Q作QC∥AB，连接PQ．已知∠BAO＝34°，请探索∠BPQ与∠PQC之间的数量关系，并说明理由．（3）已知点D（3，2）是线段AB的中点，若点H为y轴上一点，且，求S△AHD＝S△AOB，求点H的坐标．20．（2023春•红安县期末）如图，在平面直角坐标系中，直线l1：y＝kx+8分别交x轴，y 轴于点A，B，点A（8，0）．直线l2：经过线段AB的中点Q，分别交x轴，y 轴于点C，D．（1）请直接写出k的值；（2）请求出直线l2的解析式；（3）点P（t，0）为x轴上一动点，过点P作PE∥y轴交l1，l2于点E，F；①当EF＝2EP时，求t的值．②连接BC，当∠OBC＝∠ABF时，求t的值．21．（2023春•樊城区期末）如图，在平面直角坐标系中，一次函数y1＝ax+b的图象与x轴，y轴交于A，B；与直线y2＝kx交于P（2，1），且PO＝P A．（1）求点A的坐标；（2）求函数y1，y2的解析式；（3）点D为直线y1＝ax+b上一动点，其横坐标为t（t＜2），DF⊥x轴于点F，交y2＝kx于点E，且DF＝2EF，求点D的坐标；（4）在（3）的条件下，如果点D在第一象限内，过点P的直线y＝mx+n将四边形OBDE 分为两部分，两部分的面积分别设为S1，S2．若≤2，直接写出m的取值范围．22．（2023春•松北区期末）如图，直线y＝x+10交x轴于点A，交y轴于点B，直线y＝kx+b 过点A，交y轴于点C，且C为线段OB的中点．（i）求k、b的值；（2）点P为线段AC延长线上一点，连接PB，设点P的横坐标为t，△P AB的面积为S，求S与t的函数关系式；（3）在（2）的条件下，点D在线段AO的延长线上，连接CD、PD，且，点E在AD上，且∠DPE＝45°，过点C作CF∥PE，交x轴于点F，若AF＝DE，求P点的坐标．23．（2023春•碑林区校级期末）如图，在平面直角坐标系中，直线y＝﹣2x+b与x轴，y轴分别交于A、B两点．直线交线段AB于点C（1，m），且S△AOB＝2S△BOC．（1）求b的值；（2）若点D是y轴上一点，点E为平面上一点，是否存在以点A，B，D，E为顶点的四边形是矩形？若存在，请求出点E的坐标，若不存在请说明理由．24．（2023春•台江区期末）已知直线与x轴交于点A，与y轴交于点B，P为直线AB上的一个动点，过点P分别作PF⊥x轴于点F，PE⊥y轴于点E，如图所示．（1）若点P为线段AB的中点，求OP的长；（2）若四边形PEOF为正方形时，求点P的坐标；（3）点P在AB上运动过程中，EF的长是否有最小值，若有，求出这个最小值；若没有，请说明理由．25．（2023春•舞阳县期末）如图，在平面直角坐标系中，直线y＝﹣x+6与x轴、y轴分别交于点D、C，直线AB与y轴交于点B（0，﹣3），与直线CD交于点A（m，3）．（1）求直线AB的解析式；（2）点E是射线CD上一动点，过点E作EF∥y轴，交直线AB于点F．若以O、C、E、F为顶点的四边形是平行四边形，请求出点E的坐标；（3）设P是射线CD上一点，在平面内是否存在点Q，使以B、C、P、Q为顶点的四边形是菱形？若存在，请直接写出点Q的坐标；若不存在，请说明理由．26．(2023秋•新都区期末）如图所示，直线l1：y＝x﹣1与y轴交于点A，直线l2：y＝﹣2x ﹣4与x轴交于点B，直线l1与l2交于点C．（1）求点A，C的坐标；（2）点P在直线l1上运动，求出满足条件S△PBC＝S△ABC且异于点A的点P的坐标；（3）点D（2，0）为x轴上一定点，当点Q在直线l1上运动时，请直接写出|DQ﹣BQ|的最大值．27．(2023秋•金华期末）如图，在平面直角坐标系中，直线l1：y＝kx+1交y轴于点A，交x轴于点B（4，0），过点E（2，0）的直线l2平行于y轴，交直线l1于点D，点P是直线l2上一动点（异于点D），连接P A、PB．（1）直线l1的表达式为，点D的坐标为；（2）设P（2，m），当点P在点D的下方时，求△ABP的面积S的表达式（用含m的代数式表示）；（3）当△ABP的面积为3时，则以点B为直角顶点作等腰直角△BPC，请直接写出点C 的坐标．28．(2023秋•新都区校级期末）如图，已知直线y＝x﹣2分别与x轴，y轴交于A，B两点，直线OG：y＝kx（k＜0）交AB于点D．（1）求A，B两点的坐标；（2）如图1，点E是线段OB的中点，连接AE，点F是射线OG上一点，当OG⊥AE，且OF＝AE时，在x轴上找一点P，当PE+PD的值最小时，求出△APE的面积；（3）如图2，若k＝﹣2，过B点BC∥OG，交x轴于点C，此时在x轴上是否存在点M，使∠OBM+∠OBC＝45°，若存在，求出点M的坐标；若不存在，请说明理由．29．(2023春•巴中期末）如图，在平面直角坐标系中，直线y＝2x+10与x轴交于点A，与y轴交于点B，过点B的另一直线交x轴正半轴于点C，且△ABC面积为60．（1）求点C的坐标及直线BC的表达式；（2）若M为线段BC上一点，直线AM把△ABC的面积分成两部分，这两部分的面积之比为1：2，求M的坐标；（3）当△ABM的面积为20时，点E为直线AM上一动点，在x轴上是否存在点D，使以点D、E、B、C为顶点的四边形为平行四边形？若存在，直接写出点D的坐标；若不存在，请说明理由．30．(2023春•湘潭县期末）如图，长方形OABC，是一张放在平面直角坐标系中的长方形纸片，O为原点，点A在x轴上，点C在y轴上，OA＝10，OC＝6，在AB上取一点M使得△CBM沿CM翻折后，点B落在x轴上，记作B′点．（1）求B'点的坐标；（2）求折痕CM所在直线的表达式；（3）求折痕CM上是否存在一点P，使PO+PB'最小？若存在，请求出最小值，若不存在，请说出理由．。

初二下学期压轴题练习- 一次函数与几何变换(含答案)

专题09一次函数与几何变换一．选择题1．（2021春•大同期末）对于一次函数y＝﹣2x+4，下列结论正确的是（）A．函数的图象与y轴的交点坐标是（4，0）B．函数的图象不经过第三象限C．函数的图象向上平移4个单位长度得y＝﹣2x的图象D．若A（x1，y1），B（x2，y2）两点在该函数图象上，且x1＜x2，则y1＜y22．（2021•扬州）如图，一次函数y＝x+的图象与x轴、y轴分别交于点A，B，把直线AB绕点B顺时针旋转30°交x轴于点C，则线段AC长为（）A．+B．3C．2+D．+3．（2020秋•天桥区期末）如图1，将正方形ABCD置于平面直角坐标系中，其中AD边在x轴上，其余各边均与坐标轴平行，直线l：y＝x﹣3沿x轴的负方向以每秒1个单位的速度平移，在平移的过程中，该直线被正方形ABCD的边所截得的线段长为m，平移的时间为t（秒），m与t的函数图象如图2所示，则图2中b的值为（）A．5B．4C．3D．24．（2020秋•碑林区校级期中）将直线y＝﹣3x沿着x轴向右平移2个单位，所得直线的表达式为（）A．y＝﹣3x+6B．y＝﹣3x﹣6C．y＝﹣3x+2D．y＝﹣3x﹣2 5．（2020•碑林区校级模拟）若直线y＝kx+3与直线y＝2x+b关于直线x＝1对称，则k、b值分别为（）A．k＝2、b＝﹣3B．k＝﹣2、b＝﹣3C．k＝﹣2、b＝1D．k＝﹣2、b＝﹣1 6．（2019•嘉祥县三模）在平面直角坐标系中，将直线y1：y＝2x﹣2平移后，得到直线y2：y＝2x+4，则下列平移作法正确的是（）A．将y1向上平移2个单位长度B．将y1向上平移4个单位长度C．将y1向左平移3个单位长度D．将y2向右平移6个单位长度7．（2018春•雨花区校级月考）如图，A（0，1），M（3，2），N（4，4）．点P从点A出发，沿y轴以每秒1个单位长度的速度向上移动，且过点P的直线l：y＝﹣x+b也随之移动，设移动时间为t秒，当M、N位于直线l的异侧时，t应该满足的条件是（）A．3＜t＜6B．4＜t＜7C．3＜t＜7D．＜t＜7二．填空题8．（2021春•安丘市期末）在平面直角坐标系xOy中，Rt△AOB的直角顶点B在y轴上，点A的坐标为（1，），将Rt△AOB沿直线y＝﹣x翻折，得到Rt△A'OB'，过A'作A'C垂直于OA′交y轴于点C，则点C 的坐标为．9．（2021春•东台市月考）如图1，在平面直角坐标系中，将▱ABCD放置在第一象限，且AB∥x轴．直线y＝﹣x从原点出发沿x轴正方向平移，在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示，那么ABCD面积为．10．（2021•广东模拟）如图，已知一条直线经过点A（﹣1，0），B（0，﹣2），将这条直线向右平移与x 轴、y轴分别交于点C、D，若AB＝AD，则直线CD的函数表达式为．11．（2020春•黄陂区期末）将直线y＝2x﹣3沿y轴向上平移2个单位后，所得直线的解析式是．12．（2018秋•福田区校级期中）如图，过点A1（1，0）作x轴的垂线，交直线y＝2x于点B1；点A2与点O关于直线A1B1对称；过点A2（2，0）作x轴的垂线，交直线y＝2x于点B2；点A3与点O关于直线A2B2对称；过点A3（4，0）作x轴的垂线，交直线y＝2x于点B3；…，按此规律作下去，则点B n的坐标为．13．（2017秋•碑林区校级期末）如图，一次函数y＝，的图象向下平移2个单位后得直线l，直线l交x轴于点A、交y轴于点B，在线段AB上有一动点P（不与点A、B重合），过点P分别作PE⊥x 轴点E，PF⊥y轴于点F，当线段EF的长最小时，点P的坐标为．14．（2018春•丰南区期末）如图，将八个边长为1的小正方形摆放在平面直角坐标系中，若过原点的直线l将图形分成面积相等的两部分，则将直线l向右平移3个单位长度后所得直线l′的函数解析式为．15．（2019春•西湖区校级期中）在平面直角坐标系中，平行四边形OABC的边OC落在x轴的正半轴上，且点C（4，0），B（6，2），直线y＝4x+1以每秒2个单位的速度向下平移，经过秒该直线可将平行四边形OABC的面积平分．16．（2019•天津二模）将函数y＝3x+1的图象平移，使它经过点（1，1），则平移后的函数表达式是．17．（2019春•常州期中）如图，在平面直角坐标系中，平行四边形OABC的边OC落在x轴的正半轴上，且点B（6，2），C（4，0），直线y＝2x+1以每秒1个单位长度的速度沿y轴向下平移，经过秒该直线可将平行四边形OABC分成面积相等的两部分．三．解答题18．（2021春•古丈县期末）如图，直线l是一次函数y＝kx+b的图象．（1）求出这个一次函数的解析式；（2）将该函数的图象向下平移5个单位，求出平移后一次函数的解析式，并写出平移后的图象与x轴的交点坐标．19．（2021春•武汉月考）已知，在平面直角坐标系中，函数y1＝2|x﹣a|，（1）若该函数经过点A（1，0），求该函数的解析式，并在图1中画出函数图象；（2）在（1）的条件下，将函数y2＝x向上平移m个单位后与函数y1的图象相交于点B和C点，若BC ＝，求m；（3）如图2，设直线y3＝6n与直线y4＝2n分别与函数y1＝2|x﹣a|相交于点E、F和M、N，点P为直线y3＝6n上一点，连接PM、PN并延长交直线y5＝kn于点G、H，若2EF＝3GH，求k．20．（2021春•河北区期末）如图，在平面直角坐标系中，边长为3的正方形ABCD在第一象限内，AB∥x 轴，点A的坐标为（5，4）经过点O、点C作直线l，将直线l沿y轴上下平移．（1）当直线l与正方形ABCD只有一个公共点时，求直线l的解析式；（2）当直线l在平移过程中恰好平分正方形ABCD的面积时，直线l分别与x轴、y轴相交于点E、点F，连接BE、BF，求△BEF的面积．21．（2019秋•罗湖区校级期末）如图，在平面直角坐标系中，直线l1：y＝x与直线l2：y＝kx+b相交于点A，点A的横坐标为3，直线l2交y轴于点B，且OA＝OB．（1）试求直线l2的函数表达式；（2）若将直线l1沿着x轴向左平移3个单位，交y轴于点C，交直线l2于点D．试求△BCD的面积．22．（2018秋•宿迁期末）如图，一次函数y＝（m+1）x+4的图象与x轴的负半轴相交于点A，与y轴相交于点B，且△OAB面积为4．（1）则m＝，点A的坐标为（，）．（2）过点B作直线BP与x轴的正半轴相交于点P，且OP＝4OA，求直线BP的解析式；（3）将一次函数y＝（m+1）x+4的图象绕点B顺时针旋转45°，求旋转后的对应的函数表达式．23．（2019•大渡口区模拟）如图，在平面直角坐标系中，边长为2的正方形ABCD在第一象限内，AD∥y轴，点A的坐标为（5，3），已知直线l：y＝x﹣2．（1）将直线l向上平移m个单位，使平移后的直线恰好经过点A，求m的值；（2）在（1）的条件下，平移后的直线与正方形的边长BC交于点E，求△ABE的面积．24．（2018春•沙坪坝区校级期末）如图：一次函数y＝x+2交y轴于A，交y＝3x﹣6于B，y＝3x﹣6交x轴于C，直线BC顺时针旋转45°得到直线CD．（1）求点B的坐标；（2）求四边形ABCO的面积；（3）求直线CD的解析式．25．（2017春•武昌区期末）已知一次函数y＝kx+b的图象过点A（﹣4，﹣2）和点B（2，4）（1）求直线AB的解析式；（2）将直线AB平移，使其经过原点O，则线段AB扫过的面积为．26．（2017春•安岳县期中）已知直线y＝（m+1）x|m|﹣1+（2m﹣1），当x1＞x2时，y1＞y2，求该直线的解析式．并求该直线经过怎么的上下平移就能过点（2，5）？27．（2016春•大兴区期末）阅读材料：通过一次函数的学习，小明知道：当已知直线上两个点的坐标时，可以用待定系数法，求出这个一次函数的表达式．有这样一个问题：直线l1的表达式为y＝﹣2x+4，若直线l2与直线l1关于y轴对称，求直线l2的表达式．下面是小明的解题思路，请补充完整．第一步：求出直线l1与x轴的交点A的坐标，与y轴的交点B的坐标；第二步：在平面直角坐标系中，作出直线l1；第三步：求点A关于y轴的对称点C的坐标；第四步：由点B，点C的坐标，利用待定系数法，即可求出直线l2的表达式．小明求出的直线l2的表达式是．请你参考小明的解题思路，继续解决下面的问题：（1）若直线l3与直线l1关于直线y＝x对称，则直线l3的表达式是；（2）若点M（m，3）在直线l1上，将直线l1绕点M顺时针旋转90°．得到直线l4，求直线l4的表达式．28．（2016•河北模拟）如图，直线l1在平面直角坐标系中，直线l1与y轴交于点A，点B（﹣3，3）也在直线l1上，将点B先向右平移1个单位长度，再向下平移2个单位长度得到点C，点C恰好也在直线l1上．（1）求点C的坐标和直线l1的解析式；（2）若将点C先向左平移3个单位长度，再向上平移6个单位长度得到点D，请你判断点D是否在直线l1上；（3）已知直线l2：y＝x+b经过点B，与y轴交于点E，求△ABE的面积．29．（2015秋•栖霞区期末）课本P152有段文字：把函数y＝2x的图象分别沿y轴向上或向下平移3个单位长度，就得到函数y＝2x+3或y＝2x﹣3的图象．【阅读理解】小尧阅读这段文字后有个疑问：把函数y＝﹣2x的图象沿x轴向右平移3个单位长度，如何求平移后的函数表达式？老师给了以下提示：如图1，在函数y＝﹣2x的图象上任意取两个点A、B，分别向右平移3个单位长度，得到A′、B′，直线A′B′就是函数y＝﹣2x的图象沿x轴向右平移3个单位长度后得到的图象．请你帮助小尧解决他的困难．（1）将函数y＝﹣2x的图象沿x轴向右平移3个单位长度，平移后的函数表达式为．A．y＝﹣2x+3；B．y＝﹣2x﹣3；C．y＝﹣2x+6；D．y＝﹣2x﹣6【解决问题】（2）已知一次函数的图象与直线y＝﹣2x关于x轴对称，求此一次函数的表达式．【拓展探究】（3）一次函数y＝﹣2x的图象绕点（2，3）逆时针方向旋转90°后得到的图象对应的函数表达式为．（直接写结果）专题09一次函数与几何变换一．选择题1．（2021春•大同期末）对于一次函数y＝﹣2x+4，下列结论正确的是（）A．函数的图象与y轴的交点坐标是（4，0）B．函数的图象不经过第三象限C．函数的图象向上平移4个单位长度得y＝﹣2x的图象D．若A（x1，y1），B（x2，y2）两点在该函数图象上，且x1＜x2，则y1＜y2【思路引导】代入y＝0求出与之对应的x值，即可得出A不正确；根据一次函数的系数结合一次函数的性质，即可得知B选项正确、D选项不正确，根据平移的规律求得平移后的解析式，即可判断C不正确，此题得解．【完整解答】解：A、令y＝﹣2x+4中y＝0，则x＝2，∴一次函数的图象与x轴的交点坐标是（2，0），故本选项不符合题意；B、∵k＝﹣2＜0，b＝4＞0，∴一次函数的图象经过第一、二、四象限，即函数的图象不经过第三象限，故本选项符合题意；C、根据平移的规律，函数的图象向上平移4个单位长度得到的函数解析式为y＝﹣2x+4+4，即y＝﹣2x+8，故本选项不符合题意；D、∵k＝﹣2＜0，∴一次函数中y随x的增大而减小，∴若A（x1，y1），B（x2，y2）两点在该函数图象上，且x1＜x2，则y1＞y2，故本选项不符合题意．故选：B．【考察注意点】本题考查了一次函数的图象以及一次函数的性质，解题的关键是逐条分析四个选项．本题属于基础题，难度不大，解决该题时，熟悉一次函数的性质、一次函数图象上点的坐标特征以及一次函数图象与系数的关系是解题的关键．2．（2021•扬州）如图，一次函数y＝x+的图象与x轴、y轴分别交于点A，B，把直线AB绕点B顺时针旋转30°交x轴于点C，则线段AC长为（）A．+B．3C．2+D．+【思路引导】根据一次函数表达式求出点A和点B坐标，得到△OAB为等腰直角三角形和AB的长，过点C作CD⊥AB，垂足为D，证明△ACD为等腰直角三角形，设CD＝AD＝x，结合旋转的度数，用两种方法表示出BD，得到关于x的方程，解之即可．【完整解答】解：∵一次函数y＝x+的图像与x轴、y轴分别交于点A、B，令x＝0，则y＝，令y＝0，则x＝﹣，则A（﹣，0），B（0，），则△OAB为等腰直角三角形，∠ABO＝45°，∴AB＝＝2，过点C作CD⊥AB，垂足为D，∵∠CAD＝∠OAB＝45°，∴△ACD为等腰直角三角形，设CD＝AD＝x，∴AC＝＝x，由旋转的性质可知∠ABC＝30°，∴BC＝2CD＝2x，∴BD＝＝x，又BD＝AB+AD＝2+x，∴2+x＝x，解得：x＝+1，∴AC＝x＝（+1）＝，故选：A．【考察注意点】本题考查了一次函数与坐标轴的交点问题，等腰直角三角形的判定和性质，直角三角形的性质，勾股定理，二次根式的混合运算，知识点较多，解题的关键是作出辅助线，构造特殊三角形．3．（2020秋•天桥区期末）如图1，将正方形ABCD置于平面直角坐标系中，其中AD边在x轴上，其余各边均与坐标轴平行，直线l：y＝x﹣3沿x轴的负方向以每秒1个单位的速度平移，在平移的过程中，该直线被正方形ABCD的边所截得的线段长为m，平移的时间为t（秒），m与t的函数图象如图2所示，则图2中b的值为（）A．5B．4C．3D．2【思路引导】先根据△AEF为等腰直角三角形，可得直线l与直线BD平行，即直线l沿x轴的负方向平移时，同时经过B，D两点，再根据BD的长即可得到b的值．【完整解答】解：如图1，连接BD并且两端延长，直线y＝x﹣3中，令y＝0，得x＝3；令x＝0，得y ＝﹣3，即直线y＝x﹣3与坐标轴围成的△OEF为等腰直角三角形，∴直线l与直线BD平行，即直线l沿x轴的负方向平移时，同时经过B，D两点，由图2可得，t＝2时，直线l经过点A，∴AO＝3﹣2×1＝1，∴A（1，0），由图2可得，t＝12时，直线l经过点C，∴当t＝+2＝7时，直线l经过B，D两点，∴AD＝（7﹣2）×1＝5，∴等腰Rt△ABD中，BD＝5，即当a＝7时，b＝5．故选：A．【考察注意点】本题考查了动点问题的函数图象，一次函数图象与几何变换，用图象解决问题时，要理清图象的含义即会识图．解决问题的关键是掌握正方形的性质以及平移的性质．4．（2020秋•碑林区校级期中）将直线y＝﹣3x沿着x轴向右平移2个单位，所得直线的表达式为（）A．y＝﹣3x+6B．y＝﹣3x﹣6C．y＝﹣3x+2D．y＝﹣3x﹣2【思路引导】根据平移性质可由已知的解析式写出新的解析式．【完整解答】解：根据题意，得直线向右平移2个单位，即对应点的纵坐标不变，横坐标减2，所以得到的解析式是y＝﹣3（x﹣2）＝﹣3x+6．故选：A．【考察注意点】此题主要考查了一次函数图象与几何变换，解题时注意：y＝kx左右平移|a|个单位长度的时候，即直线解析式是y＝k（x±|a|）；当直线y＝kx上下平移|b|个单位长度的时候，则直线解析式是y ＝kx±|b|．5．（2020•碑林区校级模拟）若直线y＝kx+3与直线y＝2x+b关于直线x＝1对称，则k、b值分别为（）A．k＝2、b＝﹣3B．k＝﹣2、b＝﹣3C．k＝﹣2、b＝1D．k＝﹣2、b＝﹣1【思路引导】先求出一次函数y＝kx+3与y轴交点关于直线x＝1的对称点，得到b的值，再求出一次函数y＝2x+b与y轴交点关于直线x＝1的对称点，代入一次函数y＝kx+3，求出k的值即可．【完整解答】解：∵一次函数y＝kx+3与y轴交点为（0，3），∴点（0，3）关于直线x＝1的对称点为（2，3），代入直线y＝2x+b，可得4+b＝3，解得b＝﹣1，一次函数y＝2x﹣1与y轴交点为（0，﹣1），（0，﹣1）关于直线x＝1的对称点为（2，﹣1），代入直线y＝kx+3，可得2k+3＝﹣1，解得k＝﹣2．故选：D．【考察注意点】本题考查的是一次函数图象与几何变换，待定系数法求函数解析式，先根据题意得出直线与坐标轴的交点是解决问题的关键．6．（2019•嘉祥县三模）在平面直角坐标系中，将直线y1：y＝2x﹣2平移后，得到直线y2：y＝2x+4，则下列平移作法正确的是（）A．将y1向上平移2个单位长度B．将y1向上平移4个单位长度C．将y1向左平移3个单位长度D．将y2向右平移6个单位长度【思路引导】利用一次函数图象的平移规律，左加右减，上加下减，得出即可．【完整解答】解：∵将直线y1：y＝2x﹣2平移后，得到直线y2：y＝2x+4，∴2（x+a）﹣2＝2x+4，解得：a＝3，故将y1向左平移3个单位长度．故选：C．【考察注意点】此题主要考查了一次函数图象与几何变换，正确把握变换规律是解题关键．7．（2018春•雨花区校级月考）如图，A（0，1），M（3，2），N（4，4）．点P从点A出发，沿y轴以每秒1个单位长度的速度向上移动，且过点P的直线l：y＝﹣x+b也随之移动，设移动时间为t秒，当M、N位于直线l的异侧时，t应该满足的条件是（）A．3＜t＜6B．4＜t＜7C．3＜t＜7D．＜t＜7【思路引导】分别求出直线l经过点M、点N时的t值，即可得到t的取值范围．【完整解答】解：当直线y＝﹣x+b过点M（3，2）时，2＝﹣3+b，解得：b＝5，5＝1+t，解得t＝4．当直线y＝﹣x+b过点N（4，4）时，4＝﹣4+b，解得：b＝8，8＝1+t，解得t＝7．故若点M，N位于l的异侧，t的取值范围是：4＜t＜7．故选：B．【考察注意点】本题考查了坐标平面内一次函数的图象与性质，关键是利用一次函数图象上点的坐标特征解答．二．填空题8．（2021春•安丘市期末）在平面直角坐标系xOy中，Rt△AOB的直角顶点B在y轴上，点A的坐标为（1，），将Rt△AOB沿直线y＝﹣x翻折，得到Rt△A'OB'，过A'作A'C垂直于OA′交y轴于点C，则点C 的坐标为（0，﹣4）．【思路引导】依据轴对称的性质可得OB'＝OB＝，A′B′＝AB＝1，OA′＝OA＝2，进而通过证得△A′OB′∽△COA′，求得OC＝4，即可证得C的坐标为（0，﹣4）．【完整解答】解：∵点A的坐标为（1，），∴AB＝1，OB＝，∴OA＝＝＝2，∵将Rt△AOB沿直线y＝﹣x翻折，得到Rt△A'OB'，∴OB'＝OB＝，A′B′＝AB＝1，OA′＝OA＝2，∴A'（﹣，﹣1），∵过A'作A'C垂直于OA'交y轴于点C，∴∠A′OC+∠A′CO＝90°，∵∠A′OB′+∠A′OC＝90°，∴∠A′CO＝∠A′OB′，∵∠A′B′O＝∠OA′C＝90°，∴△A′OB′∽△OCA′，∴＝，即＝，∴OC＝4，∴C（0，﹣4），故答案是：（0，﹣4）．【考察注意点】本题考查了轴对称的性质，正比例函数的性质，求得对称点的坐标是解题的关键．9．（2021春•东台市月考）如图1，在平面直角坐标系中，将▱ABCD放置在第一象限，且AB∥x轴．直线y＝﹣x从原点出发沿x轴正方向平移，在平移过程中直线被平行四边形截得的线段长度l与直线在x轴上平移的距离m的函数图象如图2所示，那么ABCD面积为8．【思路引导】通过图象中（4，0），（7，2），（8，2）可得直线运动到A，D，B三点时所移动距离，从而求出AB长度，再通过添加辅助线构造直角三角形求出平行四边形的高而求解．【完整解答】解：由图象可知，直线经过A时移动距离为4，经过D时移动距离为7，经过B时移动距离为8，∴AB＝8﹣4＝4．如图，当直线经过点D时，交AB于点E，作DF垂直于AB于点F，由图2可知DE＝2，∵直线与AB夹角为45°，∴DF＝EF＝2，∴ABCD面积为AB•DF＝4×2＝8．故答案为：8．【考察注意点】本题考查一次函数图象与图形结合问题，解题关键是掌握k＝﹣1时直线与x轴所夹锐角为45°．10．（2021•广东模拟）如图，已知一条直线经过点A（﹣1，0），B（0，﹣2），将这条直线向右平移与x 轴、y轴分别交于点C、D，若AB＝AD，则直线CD的函数表达式为y＝﹣2x+2．【思路引导】先求出直线AB的解析式，再根据平移的性质求直线CD的解析式．【完整解答】解：设直线AB的解析式为y＝kx+b（k≠0），∵点A（﹣1，0）点B（0，﹣2）在直线AB上，∴，解得，∴直线AB的解析式为y＝﹣2x﹣2，∵AB＝AD，AO⊥BD，∴OD＝OB，∴D（0，2），∴直线CD的函数解析式为：y＝﹣2x+2，故答案为：y＝﹣2x+2．【考察注意点】本题考查的是一次函数的图象与几何变换，熟知函数图象平移的法则是解答此题的关键．11．（2020春•黄陂区期末）将直线y＝2x﹣3沿y轴向上平移2个单位后，所得直线的解析式是y＝2x﹣1．【思路引导】直接根据“上加下减，左加右减”的原则进行解答即可．【完整解答】解：由“上加下减”的原则可知，直线y＝2x﹣3沿y轴向上平移2个单位，所得直线的函数关系式为y＝2x﹣3+2，即y＝2x﹣1；故答案为y＝2x﹣1．【考察注意点】本题考查的是一次函数的图象与几何变换，熟知函数图象平移的法则是解答此题的关键．12．（2018秋•福田区校级期中）如图，过点A1（1，0）作x轴的垂线，交直线y＝2x于点B1；点A2与点O关于直线A1B1对称；过点A2（2，0）作x轴的垂线，交直线y＝2x于点B2；点A3与点O关于直线A2B2对称；过点A3（4，0）作x轴的垂线，交直线y＝2x于点B3；…，按此规律作下去，则点B n的坐标为（2n﹣1，2n）．【思路引导】先根据题意求出A2点的坐标，再根据A2点的坐标求出B2的坐标，以此类推总结规律便可求出点B n的坐标．【完整解答】解：∵点A1坐标为（1，0），∴OA1＝1，过点A1作x轴的垂线交直线于点B1，可知B1点的坐标为（1，2），∵点A2与点O关于直线A1B1对称，∴OA1＝A1A2＝1，∴OA2＝1+1＝2，∴点A2的坐标为（2，0），B2的坐标为（2，4），∵点A3与点O关于直线A2B2对称．故点A3的坐标为（4，0），B3的坐标为（4，8），依此类推便可求出点A n的坐标为（2n﹣1，0），点B n的坐标为（2n﹣1，2n）．故答案为：（2n﹣1，2n）．【考察注意点】本题考查了一次函数图象上点的坐标特征：一次函数图象上点的坐标满足其解析式．也考查了轴对称的性质．13．（2017秋•碑林区校级期末）如图，一次函数y＝，的图象向下平移2个单位后得直线l，直线l交x轴于点A、交y轴于点B，在线段AB上有一动点P（不与点A、B重合），过点P分别作PE⊥x轴点E，PF⊥y轴于点F，当线段EF的长最小时，点P的坐标为（﹣，）．【思路引导】利用勾股定理和一次函数图象上点的坐标特征，列出二次函数关系式，结合二次函数最值的求法解答．【完整解答】解：由已知条件得到直线l解析式为：y＝﹣2，即y＝，设P（a，），所以EF2＝a2+（）2＝a2+a+．当EF取最小值时，a＝﹣＝﹣，此时，＝，即P（﹣，），故答案是：（﹣，）．【考察注意点】考查了一次函数图象与几何变换，解题时，利用了二次函数最值的求法，熟记二次函数顶点坐标公式是解题的关键．14．（2018春•丰南区期末）如图，将八个边长为1的小正方形摆放在平面直角坐标系中，若过原点的直线l将图形分成面积相等的两部分，则将直线l向右平移3个单位长度后所得直线l′的函数解析式为y＝x﹣．【思路引导】设直线l和八个正方形的最上面交点为A，过点A作AB⊥y轴于点B，过点A作AC⊥x 轴于点C，易知OB＝3，利用三角形的面积公式和已知条件求出A的坐标，再利用待定系数法可求出该直线l的解析式，再根据平移规律即可得到直线l′的函数解析式．【完整解答】解：设直线l和八个正方形的最上面交点为A，过A作AB⊥OB于B，过A作AC⊥OC于C，∵正方形的边长为1，∴OB＝3，∵经过原点的一条直线l将这八个正方形分成面积相等的两部分，∴两边分别是4，∴三角形ABO面积是5，∴OB•AB＝5，∴AB＝，∴OC＝，由此可知直线l经过（，3），设直线l为y＝kx，则3＝k，k＝，∴直线l解析式为y＝x，∴直线l向右平移3个单位长度后所得直线l′的函数解析式为y＝（x﹣3），即y＝x﹣，故答案为：y＝x﹣．【考察注意点】此题考查了面积相等问题、用待定系数法求一次函数的解析式以及正方形的性质，解题的关键是作AB⊥y轴，作AC⊥x轴，根据题意即得到：直角三角形ABO，利用三角形的面积公式求出AB的长．15．（2019春•西湖区校级期中）在平面直角坐标系中，平行四边形OABC的边OC落在x轴的正半轴上，且点C（4，0），B（6，2），直线y＝4x+1以每秒2个单位的速度向下平移，经过6秒该直线可将平行四边形OABC的面积平分．【思路引导】首先连接AC、BO，交于点D，当y＝4x+1经过D点时，该直线可将▱OABC的面积平分，然后计算出过D且平行直线y＝4x+1的直线解析式，从而可得直线y＝4x+1要向下平移，进而可得答案．【完整解答】解：连接AC、BO，交于点D，当y＝4x+1经过D点时，该直线可将▱OABC的面积平分；∵四边形AOCB是平行四边形，∴BD＝OD，∵B（6，2），点C（4，0），∴D（3，1），设DE的解析式为y＝kx+b，∵平行于y＝4x+1，∴k＝4，∵过D（3，1），∴DE的解析式为y＝4x﹣11，∴直线y＝4x+1要向下平移12个单位，∴时间为6秒，故答案为：6【考察注意点】此题主要考查了平行四边形的性质，以及一次函数，关键是正确掌握经过平行四边形对角线交点的直线平分平行四边形的面积．16．（2019•天津二模）将函数y＝3x+1的图象平移，使它经过点（1，1），则平移后的函数表达式是y＝3x﹣2．【思路引导】根据函数图象平移的性质得出k的值，设出相应的函数解析式，再把经过的点代入即可得出答案．【完整解答】解：新直线是由一次函数y＝3x+1的图象平移得到的，∴新直线的k＝3，可设新直线的解析式为：y＝3x+b．∵经过点（1，1），则1×3+b＝1，解得b＝﹣2，∴平移后图象函数的解析式为y＝3x﹣2；故答案为：y＝3x﹣2．【考察注意点】此题考查了一次函数图形与几何变换，求直线平移后的解析式时要注意平移时k和b的值的变化．17．（2019春•常州期中）如图，在平面直角坐标系中，平行四边形OABC的边OC落在x轴的正半轴上，且点B（6，2），C（4，0），直线y＝2x+1以每秒1个单位长度的速度沿y轴向下平移，经过6秒该直线可将平行四边形OABC分成面积相等的两部分．【思路引导】首先连接AC、BO，交于点D，当y＝2x+1经过D点时，该直线可将▱OABC的面积平分，然后计算出过D且平行直线y＝2x+1的直线解析式，从而可得直线y＝2x+1要向下平移6个单位，进而可得答案．【完整解答】解：连接AC、BO，交于点D，当y＝2x+1经过D点时，该直线可将▱OABC的面积平分；∵四边形AOCB是平行四边形，∴BD＝OD，∵B（6，2），点C（4，0），∴D（3，1），设DE的解析式为y＝kx+b，∵平行于y＝2x+1，∴k＝2，∵过D（3，1），∴DE的解析式为y＝2x﹣5，∴直线y＝2x+1要向下平移6个单位，∴时间为6秒，故答案为：6．【考察注意点】此题主要考查了平行四边形的性质，以及一次函数，关键是正确掌握经过平行四边形对角线交点的直线平分平行四边形的面积．三．解答题18．（2021春•古丈县期末）如图，直线l是一次函数y＝kx+b的图象．（1）求出这个一次函数的解析式；（2）将该函数的图象向下平移5个单位，求出平移后一次函数的解析式，并写出平移后的图象与x轴的交点坐标．【思路引导】（1）利用待定系数法确定该一次函数的解析式；（2）根据平移规律“上加下减”写出平移后一次函数解析式，然后根据一次函数图象上点的坐标特征求直线与x轴的交点坐标．【完整解答】解：（1）∵一次函数y＝kx+b的图象经过点（﹣2，0）和点（2，2），∴．解得k＝，b＝1．∴一次函数的解析式为：y＝x+1；（2）∵一次函数y＝x+1向下平移5个单位的解析式为y＝x+1﹣5＝x﹣4，即y＝x﹣4．∴当y＝0时，x＝8，∴平移后的图象与x轴的交点坐标为（8，0）．【考察注意点】本题考查的是一次函数的图象与几何变换，熟知函数图象平移的性质是解答此题的关键．19．（2021春•武汉月考）已知，在平面直角坐标系中，函数y1＝2|x﹣a|，（1）若该函数经过点A（1，0），求该函数的解析式，并在图1中画出函数图象；（2）在（1）的条件下，将函数y2＝x向上平移m个单位后与函数y1的图象相交于点B和C点，若BC＝，求m；（3）如图2，设直线y3＝6n与直线y4＝2n分别与函数y1＝2|x﹣a|相交于点E、F和M、N，点P为直线y3＝6n上一点，连接PM、PN并延长交直线y5＝kn于点G、H，若2EF＝3GH，求k．【思路引导】（1）把点A坐标代入函数，求出a，得到函数y1的解析式，画出图象；（2）设出函数y2的解析式，得到B、C的坐标，根据BC＝列出方程，求m的值；（3）由三角形相似得出MN和GH的比例，求出k的值．【完整解答】解：（1）把点A（1，0）代入y1＝2|x﹣a|，得：2|1﹣a|＝0，解得：a＝1，∴y1＝2|x﹣1|，图象如右所示．（2）由题意得y2＝x+m（m＞0），x≤1时，y1＝﹣2x+2，x＞1时，y1＝2x﹣2，由，解得：，∴B（，），由，解得：，∴C（m+2，2m+2），∵BC＝，∴（m+2﹣）2+（2m+2﹣）2＝128，解得：m1＝5，m2＝﹣7（舍），∴m＝5．（3）∵直线y3＝6n与直线y4＝2n间的距离为4n，直线y4＝2n与x轴间的距离为2n，∴EF＝3MN，∵2EF＝3GH，∴MN：GH＝1：2，∴MN是△PGH的中位线，∴y3＝6n与y4＝2n间的距离和y3＝6n与y5＝kn间的距离相等，∴k＝﹣2．【考察注意点】本题考查了分段函数图象和函数图象变换，画图的关键顺序是“列表﹣描点﹣连线”，需要注意的是连线的时候要用平滑的曲线连接．20．（2021春•河北区期末）如图，在平面直角坐标系中，边长为3的正方形ABCD在第一象限内，AB∥x 轴，点A的坐标为（5，4）经过点O、点C作直线l，将直线l沿y轴上下平移．（1）当直线l与正方形ABCD只有一个公共点时，求直线l的解析式；（2）当直线l在平移过程中恰好平分正方形ABCD的面积时，直线l分别与x轴、y轴相交于点E、点F，连接BE、BF，求△BEF的面积．【思路引导】（1）根据题意求得正方形各顶点的坐标，然后根据待定系数法求得直线l的解析式，直线平移，斜率不变，设平移后的直线方程为y＝x+b；把点B和D的坐标代入进行解答即可；（2）根据正方形是中心对称图形，当直线l经过对角线的交点时，恰好平分正方形ABCD的面积，求得交点坐标，代入y＝x+b，根据待定系数法即可求得直线l此时的解析式，然后求得E、F的坐标，根据待定系数法求得直线BE的解析式，得到与y轴的交点Q的坐标，根据三角形面积公式即可求得．【完整解答】解：（1）∵长为3的正方形ABCD中，点A的坐标为（5，4），∴B（2，4），C（2，1），D（5，1），设直线l的解析式为y＝kx，把C（2，1）代入得，1＝2k，解得k＝，∴直线l为y＝，设平移后的直线方程为y＝x+b，。

初二一次函数与几何题(附答案)

初二一次函数与几何题（附答案）1、平面直角坐标系中，点A 的坐标为（4，0），点P 在直线y=-x-m 上，且AP=OP=4，则m的值是多少？2、如图，已知点A 的坐标为（1，0），点B 在直线y=-x 上运动，当线段AB 最短时，试求点B 的坐标。

3、如图，在直角坐标系中，矩形OABC 的顶点B 的坐标为（15，6），直线y=1/3x+b 恰好将矩形OABC 分为面积相等的两部分，试求b 的值。

4、如图，在平面直角坐标系中，直线y= 2x —6与x 轴、y 轴分别相交于点A 、B ，点C 在x 轴上，若△ABC 是等腰三角形，试求点C 的坐标。

5、在平面直角坐标系中，已知A （1，4）、B （3，1），P 是坐标轴上一点，（1）当P 的坐标为多少时，AP+BP 取最小值，最小值为多少? 当P 的坐标为多少时，AP-BP 取最大值，最大值为多少？A B C O x y xyA B O6、如图，已知一次函数图像交正比例函数图像于第二象限的A点，交x轴于点B（-6，0），△AOB的面积为15，且AB=AO，求正比例函数和一次函数的解析式。

7、已知一次函数的图象经过点（2，20），它与两坐标轴所围成的三角形的面积等于1，求这个一次函数的表达式。

8、已经正比例函数Y=k1x的图像与一次函数y=k2x-9的图像相交于点P(3,-6)求k1,k2的值如果一次函数y=k2x-9的图象与x轴交于点A 求点A坐标9、正方形ABCD的边长是4，将此正方形置于平面直角坐标系中，使AB在x轴负半轴上，A 点的坐标是（-1，0），（1）经过点C的直线y=-4x-16与x轴交于点E，求四边形AECD的面积；（2）若直线L经过点E且将正方形ABCD分成面积相等的两部分，求直线L的解析式。

10、在平面直角坐标系中，一次函数y=Kx+b(b小于0）的图像分别与x轴、y轴和直线x=4交于A、B、C，直线x=4与x轴交于点D，四边形OBCD的面积为10，若A的横坐标为-1/2，求此一次函数的关系式11、在平面直角坐标系中,一个一次函数的图像过点B(-3,4),与y 轴交于点A ，且OA=OB ：求这个一次函数解析式12、如图，A 、B 分别是x 轴上位于原点左右两侧的点，点P （2，m ）在第一象限，直线PA 交y 轴于点C （0，2），直线PB 交y 轴于点D ，S AOP =6.求：（1）△COP 的面积（2）求点A 的坐标及m 的值；（3）若S BOP =S DOP ，求直线BD 的解析式13、一次函数y=-33x+1的图像与x 轴、y 轴分别交于点A 、B ，以AB 为边在第一象限内做等边△ABC（1）求△ABC 的面积和点C 的坐标；（2）如果在第二象限内有一点P （a ，21），试用含a 的代数式表示四边形ABPO 的面积。