物理化学-第一章 气体
pVm 0 p T , P 0
对比波义耳Boyle温度可以知 道实际气体压缩性的难易。
9
1.8 实际气体的状态方程 2.范德华方程
( p a2 )(Vm b) RT Vm
约翰尼斯· 迪德里 克· 范· 德· 瓦耳斯 （通常称为范德· 瓦耳斯或范德华， Johannes Diderik van der Waals， 1837－1923年）， 荷兰物理学家。 1910年诺贝尔物理 学奖
3
1.分子之间无相互作用力 2.分子本身不占有体积
状态方程 理想气体 分压及分体积定律 气体
P→0
T高温
液化及临界现象 对应状态原理及压缩因子图 状态方程
实际气体
如何变成理 想气体？
4
1.1 理想气体的状态方程
pV nRT pVm RT
Boyle-Marriotte定律
Charles-Gay-Lussac 定律
2
等离子体（电离的气体\电离子\电子及未经电离的中性粒 子所组成）叫做物质的第四态 存在于地球内部的超高温\超高压状态叫做物质的第五态 超导态 超流态
液晶态—结晶态和液态之间的一种形态，是一种在一定 温度范围内呈现既不同于固态、液态，又不同于气态的 特殊物质态，它既具有各向异性的晶体所特有的双折射 性，又具有液体的流动性。
临界参数 TC , pC, Vm,C 高于 TC 称为超临界流体
2018/1/4
TC 30C
超临界应用一：超临界流体萃取
二氧化碳为超临界溶剂
药物超临界流体萃取
18
超临界水氧化技术
超临界流体干燥
超临界流体染色 超临界流体制备超细微粒
超临界流体色谱
思考：
超临界应用的局限性？
19
应用二： 从临界参数求 a, b 值
Avogadro 定律
导出公式：
M mRT / pV
pM / RT
p, V, T, n的意义及单位 Vm：摩尔体积，m3· mol-1 R：摩尔气体常数，8.314 J· K-1· mol-1
5
1.1 理想气体混合物（5,6） 道尔顿分压定律:混合气体的总压力等于各组分 单独存在于混合气体的温度、体积条件下产生压
pVm ZRT
p / pC
对比参数：描述了气体所处 状态偏离临界点的程度。
对应状态原理: 若不同的气 体有两个对比状态参数相等, 则第三个对比状态参数大体 具有相同的值。
23
T / TC
V / Vm,C
Van der Waals’s equation of corresponding state（对比状态方程）
2018/1/4
Vm,C 3b 8a TC 27 Rb a pC 27b 2 8 pCVm,C R 3 TC
RTC 8 2.667 pCVm,C 3
27 R T a 64 pc R Tc b 8 pc
2
2 c
2018/1/4
临界参数应用三：求真实气体的压缩因子Z
真实气体的pVT关系： 对比参数： 对比压力: 对比温度: 对比体积:
(
应用:
3
2
)(3 1) 8
1、处于相同对比状态的不同气体具有相同的物 理性质，如粘滞性、折光率等。 2、处于相同对比状态的气体具有相同的Z和Zc。
2018/1/4
例：利用普遍化压缩因子图，求算N2、NH3在 30.3975MPa 和 723.15K时的压缩因子Z
已知：
N2
3.390 126.15
2018/1/4
应用二： 从临界参数求 a, b 值
van der Waals 方程改写为：
RT a p 2 Vm b Vm
p RTC 2a 3 0 2 Vm TC Vm,C b Vm,C
2 p 2 RTC 6a 4 0 2 3 Vm TC Vm,C b Vm,C
两周后，罗伯特·波义耳手持“U”形大玻璃管站在众会员面前。这个 “U”形玻璃管是不匀称的，一支又细又长，高出3英尺多，另一支又短 又粗，短的这支顶端密封，长的那只顶端开口。波义耳把水银倒进玻璃 管中，水银盖住了“U”形玻璃管的底部，两边稍有上升。在封闭的短管 中，水银堵住一小股空气。 波义耳解释，活塞就是任何压缩空气的装置，水银也可以看作“活塞”。 向法国实验所期望的那样，波义耳的做法不会因为摩擦而影响实验结果。 波义耳记录下水银重量，在水银和空气交界处刻了一条线。他向长玻璃 管中滴水银，一直把它滴满。这时，水银在短玻璃管中上升到一半的高 度。在水银的挤压下，堵住空气的体积变成不到原来的一半。在短玻璃 管上，波义耳刻下了第二条线，标示出里面水银的新高度和堵住空气的 压缩体积。然后，通过“U”形玻璃管底部的阀门，他把水银排出，直到 玻璃活塞和水银的重量与实验开始时的重量完全相等。水银柱又回到它 实验开始的高度，堵住的空气又回到它当初的位置。空气果真有弹性， 法国科学家的实验是错误的，波义耳是正确的。 罗伯特·波义耳用玻璃活塞继续实验，发现了很多值得注意的事情。 当他向堵住的空气施加双倍的压力时，空气的体积就会减半；施加 3倍的 压力时，体积就会变成原来的1/3。当受到挤压时，空气体积的变化与压 强的变化总是成比例。他创建了一个简单的数学等式来表示这一比例关 系，现在我们称之为“波义耳定律”。就认识大气、利用大气为人类服 务而言，这一定律是极为重要的。
van der Waals 方程改写为：
RT a p 2 Vm b Vm
p RTC 2a 3 0 2 Vm TC Vm,C b Vm,C
2 p 2 RTC 6a 4 0 2 3 Vm TC Vm,C b Vm,C
15
1.9 气体的液化及临界参数
饱和蒸气压：指定温度下，抽空的密闭系统中某 物质处于气液平衡共存时其蒸气的压力。
思考：温度与饱 和蒸气压关系？
临界参数：
TC 30C
Tc：临界温度
Vm.c：临界摩尔体积
pc：临界压力
16
临界温度 TC
在该温度之上无论 用多大压力,都无法 使气体液化 临界状态 气-液界面消失, 混为一体
10
11
b 4L r
4 3
3
a ab pVm RT bp 2 Vm Vm
符合范德华方程的气 体称为范德华气体
12
van der Waals 方程式
a ab pVm RT bp 2 Vm Vm
高温时，忽略分子间的引力 （忽略含a的项） pVm RT bp pVm > RT
a Vm b RTB b Vm
2
Vm b 1 Vm
a TB Rb
2.维里方程类型
B C D pVm RT (1 2 3 ) Vm Vm Vm
B：第二维里系数，表两个气体分子间的相互作用 对气体pVT关系的影响 C：第三维里系数，表三分子相互作用引起的偏差 D：第四维里系数……
pVm pVm p V T , p 0 m T Vm p T
RTVm a pVm Vm b Vm
RT RTVm a Vm 2 0 2 Vm b (Vm b) Vm p T
第一章 气体的pVT关系
1.了解理想气体的微观模型，能熟练使用理 想气体的状态方程 2.理解气体的液化和临界参数 3.理解真实气体的状态方程及对应状态原理 与压缩因子图 重点： 理想气体的状态方程、微观模型、 临界参数、压缩因。 难点：对应状态原理与压缩因子图。
1
问题： 1. 理想气体? 状态方程及应用？ 2. 理想气体混合物？在理想气体混合物中某 组分的分压是如何定义的？其物理意义如何， 如何计算？ 3. 纯液体的饱和蒸气压？它与哪些因素有关？
状态方程
实际气体
液化及临界现象
对应状态原理及压缩因子图
1.分子之间有相互作用力 2.分子本身占有体积
7
1.8 实际气体的状态方程
pV ZnRT
V V Z nRT / p V pg
(1) Z的意义：压缩因子，是温度与压力的函数， Z与1的差体的状态方程
力的总和。
pi yi p总
i i
p y p p y
i i i i
p
yi是摩尔分数
阿马加分体积定律:
Vi yiV总
*
Vi * ：纯气体i在混合物的温度和总压条件下所占有的体积
适合条件:理想气体或低压下的真实气体
6
1.分子之间无相互作用力 2.分子本身不占有体积
状态方程 理想气体 分压及分体积定律 气体
29
低温时，压力又比较低，忽略分子的体积(含b项) a pVm RT pVm < RT Vm
当压力增加到一定限度后，b的效应越来越显著， 又将出现 pVm > RT 的情况。这就是在Boyle温度以下 时， pVm 的值会随压力先降低，然后升高。
求Boyle 温度
( p a2 )(Vm b) RT Vm
NH3
11.313 405.48
Pc
（MPa）
Tc （K）
计算出：
N2
8.79 5.73
NH3
2.69 1.78
对比压力
对比温度
P/Pc T/Tc
pVm ZRT
26
27
罗伯特· 波义耳（Robert Boyle，1627年1月25日－1691年12
月30日），爱尔兰自然哲学家，在化学和物理学研究上都有杰 出贡献。波义耳生于伯爵之家，是英国科学协会的会员。在 1662年科学协会的会议上，罗伯特· 胡克（Robert Hooke）宣 读了一篇论文，论文描述法国关于“空气弹性”的实验。17世 纪，科学家对空气特征产生了浓厚兴趣。 法国科学家制造了一个黄铜气缸，中间装有活塞，安装得很 紧。几个人用力按下活塞，压缩缸里的空气。然后，他们松开 活塞，活塞弹回来，但是没有全部弹回来。不论他们隔多长时 间做一次实验，活塞总是不能全部弹回来。通过这项实验，法 国科学家声称空气根本不存在弹性，经过压缩，空气会保持轻 微的压缩状态。 波义耳宣称法国科学家的实验不能说明任何问题。他指出， 活塞之所以不能全部弹回来，是因为他们使用的活塞太紧。有 人反驳道，如果活塞稍松，四周就会漏气，影响实验。罗伯 特· 波义耳许诺要制造一个松紧适中的绝好活塞，证明上述实验 28 是错误的。
理想气体(物理化学)
即对于实际气体
lim pV nRT
p0
lim
p0
pVm
RT
看P10的图, 恒定温度下对几种气体pVm随压力的变化进行精确
测量，显然只有压力趋于零时，各种气体的pVm才具有相同的
数值 (pVm)p→0=RT
5000
4500 4000
N2 CH4
3500 3000
pVm / J mol 1 2500
2000 1500 1000
0
He
20 40 60 80 100 120 p/Mpa
而理想气体: pVm=RT(常数)， 水平线
注意：根据现在处理数据的统一标准要求，要用纯数作图、 列表。因此坐标轴上的标注应该为纯数，所以坐标轴上物理量的
表示应该为
物理量 单位
,如上图及下表:
列表时: p/MPa
…………
pVm/J . mol-1
…………
↑
↑
表头中物理量的表示: 物理量 表中均为纯数
单位
⑶ 低压气体可近似视作为理想气体。
即低压气体可近似使用理想气体状态方程计算p、T、V 关系。
二 理想气体的微观模型（p9）
按照分子运动论，理想气体微观模型应该是：
1. 分子间无作用力； 2. 分子本身没有体积 3. 分子不停顿地作无规则的热运动。
物质的量n确定时 f (p、V、T) =0 或四变量函数式 f (p、V、T、n) =0
固体、液体物质的体积V受压力p与温度T的影响很小,即它 们的可压缩性(p→ V)及热膨胀性(T→ V) 与气体物质相比小都
很小，在通常的物理化学讨论中常常忽略它们的体积随压力及
温度的变化。而气体物质p、V、T之间相互影响很大，所以这 一章我们先来讨论气体的p、V、T关系，并且气体体系是物理
理科物理化学章气体
对理想气体 VB= nB R T /P 对真实气体不适用。
§1.2 摩尔气体常数（R）
pVm / T J mol1 K1 R 8.3145
8
6
4
图1.4(a)
理想气体
T3 (531K) T2 (410K) T1(333K)
2
10
20
a Vm2
)(Vm
RT bp
b) RT
a ab Vm Vm2
高温时，忽略分子间的引力（忽略含a的项）
pVm RT bp
pVm > RT
低温时，压力又比较低，忽略分子的体积(含b项)
pVm
RT
a Vm
pVm < RT
当压力增加到一定限度后，b的效应越来越显著， 又将出现 pVm > RT 的情况。这就是在Boyle温度以下 时， pVm 的值会随压力先降低，然后升高。
p
3 pcVm2,c Vm2
Vm
Vm,c 3
8 3
pcVm,c Tc
T
p pc
3Vm2,c Vm2
Vm Vm,c
1 3
8T 3 Tc
对比状态和对比状态定律
p pc
3Vm2,c Vm2
Vm Vm,c
1 3
8 3
T Tc
定义： p
pc
Vm
Vm,c
T
Tc
代入上式，得van der Waals 对比状态方程
（2）当温度升到30.98℃时，等温线的水平部分缩 成一点，出现拐点，称为临界点。在这温度以上无 论加多大压力，气体均不能液化。
（3）在临界点以上，是气态的等温线，在高温或 低压下，气体接近于理想气体。
物理化学 第一章 绪论气体
物理化学讲课的内容
第一章 气体的pVT关系 第二章 热力学第一定律 第三章 热力学第二定律 第四章 多组分热力学 第五章 相平衡
3-10周 讲课 40 h
第六章 化学平衡 第七章 电化学 第八章 化学动力学 第九章 界面现象与
描述真实气体的 pVT 关系的方法： 1）引入压缩因子Z，修正理想气体状态方程 2）引入 p、V 修正项，修正理想气体状态方程 3）使用经验公式，如维里方程，描述压缩因子Z 它们的共同特点是在低压下均可还原为理想气体状态方程
1. 真实气体的 pVm - p 图及波义尔温度
T > TB
pVm - p曲线都有左图所示三种
c
T4
说明Vm(g) 与Vm(l)之差减小。
l2 l1
l
g2 g1
T3
Tc
TT12gg´´12 g
T = Tc时， l – g 线变为拐点c c：临界点 ；Tc 临界温度； pc 临界压力； Vm,c 临界体积
Vm
临界点处气、液两相摩尔体积及其它性质完全相同，界
面消失气态、液态无法区分，此时：
V p m Tc 0 ,
类型。
pVm
T = TB T < TB
(1) pVm 随 p增加而上升； (2) pVm 随 p增加，开始不变， 然后增加
p 图1.4.1 气体在不同温度下的 pVm－p 图
(3) pVm 随 p增加，先降后升。
T > TB T = TB
对任何气体都有一个特殊温度 -
波义尔温度 TB ，在该温度下，压
（密闭容器）
水
乙醇
苯
t / ºC 20 40 60 80 100 120
物理化学第五版_01章_气体
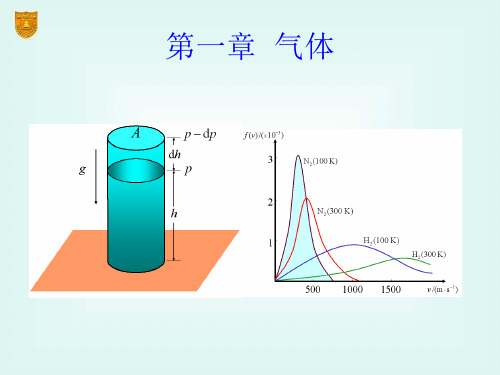
学平均速率与根均方速率
Maxwell 速率分布定律 设容器内有N个分子，速率在 v v dv 范围内的分子数为 d N v
则
d Nv Ndv
或
d Nv Nf (v)dv
f (v) 称为分子分布函数，
力却是一个定值，并且是一个宏观可测的物理量。
对于一定量的气体，当温度和体积一定时， 压力具有稳定的数值。 压力p是大量分子集合所产生的总效应，是 统计平均的结果。
压力和温度的统计概念
aa' , bb' 是两个半透膜
aa ' 只允许A分子出入
bb ' 只允许B分子出入
在中间交换能量，直至
双方分子的平均平动能相等
是摩尔气体常数，等于
是热力学温度，单位为 K
T (t /℃ 273.15)K
气体分子动理论的基本公式 气体分子的微观模型 (1)气体是大量分子的集合体 (2)气体分子不停地运动，呈均匀分布状态 (3)气体分子的碰撞是完全弹性的 设在体积为V的容器内，分子总数为N，单位体 积内的分子数为n（n = N/V），每个分子的质量为m。 令：在单位体积中各群的分子数分别是 n1 ，n2 ， … 等。则
n1 n2 ni ni n
i
气体分子动理论的基本公式 设其中第
i
群分子的速度为
u i ，它在 x, y, z
轴方向上的分速度为
2 ui 2 ui , x
ui, x , ui, y , ui, z ，则
2 ui , z
2 ui , y
在单位时间内，
在
物理化学 第一章 气 体
pV nRT
或
（1-1） (1-2)
pV
m RT M
其中的R称为摩尔气体常数，其值等于8.314J.K-1.mol-1，与气体种类无关。 理想气体状态方程只有理想气体完全遵守。 理想气体也可以定义为在任何温度、压强下都严格遵守理想气体状态方程的 气体。
实际气体处在温度较高、压力较低即气体十分稀薄时，能较好地符合这个关 系式。
图1.2 混合气体的分体积与总体积示意图
在压力很低的条件下，可得V=VA+VB，即混合气体的总体积等于所
有组分的分体积之和，称为阿马格分体积定律。通式为
V V i
式中 VB——组分B的分体积。 根据理想气体状态方程有
nB VB RT p
（1-5）
n总 V总 RT p
（1-
pV ZnRT
（1-16）
在压力较高或温度较低时，真实气体与理想气体的偏差较 大。定义“压缩因子（Z）”来衡量偏差的大小。
pV Z nRT
Z →
V V nRT / p V理想
等于同温、同压下，相同物质量的真实气体与理想气体的体
积之比。
理想气体的 pV=nRT ， Z =1。
对于真实气体，若Z＞1，则V＞ V(理想)，即真实气体的体积 大于理想气体的体积，说明真实气体比理想气体难于压缩；
（1-13）
称为截项维里方程，有较大的实用价值。 当压力达到几MPa时（5MPa左右），第三维里系数渐显重要，其近 似截断式为：
Z
pV B C 1 2 RT V V
（1-14）
第四节 对应态原理及普遍化压缩因子图 一.对应态原理 二.压缩因子法 三.普遍化压缩因子图
物理化学第一章气体
17
18
第一章 气体的pVT关系
1.了解理想气体的微观模型，能熟练使用理 想气体的状态方程 2.理解气体的液化和临界参数 3.了解真实气体的状态方程及对应状态原理 与压缩因子图 重点： 理想气体的状态方程、微观模型、 临界参数。 难点：对应状态原理与压缩因子图。
1
问题：1.理想气体的状态方程式主要有哪些 应用？ 2.何为理想气体混合物？在理想气体混合物中 某组分的分压是如何定义的？其物理意义如何，如 何计算？ 3.何为纯液体的饱和蒸气压？它与哪些因素
有关？
2
3
1.分子之间无相互作用力 2.分子本身不占有体积
状态方程 理想气体 分压及分体积定律 气体 液化及临界现象 实际气体 对应状态原理及压缩因子图 状态方程
如何变成理 想气体？
4
1.1 理想气体的状态方程
pV nRT
导出公式：
M mRT / pV
pM / RT
例：六氟化铀UF6是密度很大的一种气体，求在
适合条件:理想气体或低压下的真实气体
6
1.分子之间无相互作用力 2.分子本身不占有体积
状态方程 理想气体 分压及分体积定律 气体
液化及临界现象
实际气体 状态方程 对应状态原理及压缩因子图
7
1.3 气体的液化及临界参数
饱和蒸气压：指定温度下，密闭系统中某物质处 于气液平衡共存时其蒸气的压力。
临界参数：
9
b.求真实气体的压缩因子Z
真实气体的pVT关系： 对比参数： 对比压力: pr =p/pc
pVm ZRT
对比温度: Tr =T/Tc
对比体积: Vr =Vm/ Vm，c
物理化学第一章讲义
第一章气体的pVT 关系§1.1 理想气体状态方程§1.2 理想气体混合物§1.3 真实气体的液化及临界参数§1.4 真实气体状态方程§1.5 对应状态原理及普遍化压缩因子图教学重点及难点教学重点1.理解理想气体模型、摩尔气体常数,掌握理想气体状态方程。
2.理解混合物的组成、理想气体状态方程对理想气体混合物的应用,掌握理想气体的分压定律和分体积定律。
3.了解气体的临界状态和气体的液化,理解液体的饱和蒸汽压。
4.了解真实气体的pV m - p图、范德华方程以及压缩因子和对应状态原理。
教学难点:1.理想气体的分压定律和分体积定律。
前言宏观的物质可分成三种不同的聚集状态：气态:气体则最为简单，最易用分子模型进行研究。
液态:液体的结构最复杂，对其认识还很不充分。
固态:结构较复杂，但粒子排布的规律性较强，对其研究已有了较大的进展。
当物质的量n确定后，其pVT 性质不可能同时独立取值，即三者之间存在着下式所示的函数关系：f（p,V, T）= 0也可表示为包含n在内的四变量函数式，即f（p,V,T,n）= 0这种函数关系称作状态方程。
§1-1 理想气体的状态方程1.理想气体状态方程（1）气体的基本实验定律:波义尔定律:PV = 常数（n,T 恒定）盖·吕萨克定律:V／T = 常数（n,p恒定）阿伏加德罗定律:V／n＝常数（T,p恒定）( 2 ) 理想气体状态方程上述三经验定律相结合，可整理得理想气体状态方程:pV＝nRT(p: Pa（帕斯卡）V: m3(米3) T:K（开尔文）R（摩尔气体常数）: J·mol-1·K-1（焦·摩尔-1·开-1）)因为摩尔体积V m = V／n,气体的物质的量n=m /M理想气体状态方程又常采用下列两种形式：p V m＝RT、pV＝(m／M)RT2．理想气体模型(1)分子间力:分为相互吸引和相互排斥，按照兰纳德一琼斯的理论：E=E吸引+E排斥=-A r6+B r12由图可知:[1]当两个分子相距较远时，它们之间几乎没有相互作用。
《物理化学》第一章气体复习题.doc.docx
第一章练习题一、单选题1.理想气体状态方程pV=nRT 表明了气体的p、V、T、n、这几个参数之间的定量关系，与气体种类无关。
该方程实际上包括了三个气体定律，这三个气体定律是（ C）A 、波义尔定律、盖一吕萨克定律和分压定律B、波义尔定律、阿伏加德罗定律和分体积定律C、阿伏加德罗定律、盖一吕萨克定律和波义尔定律D、分压定律、分体积定律和波义尔定律2、在温度、容积恒定的容器中，含有A和 B 两种理想气体，这时A的分A A。
若在容器中再加入一定量的理想气体问P A 和A 的变化为：，分体积是 V C，V 是 P（C）A、P A和V A都变人B、P A和V A都变小C P A不变，V A变小D、P A变小， V A不变3、在温度 T、容积 V 都恒定的容器中，含有 A 和 B 两种理想气体，它的物质的量、分压和分体积分别为n A P A￥和1^ P B V B，容器中的总压为 P。
试判断&列公式屮哪个是正确的（ A ）A 、P A V= n A RTB、P A V= （ n A +n B）RT C、P A VA = n A RT D、P B V B= n B RT4、真实气体在如下哪个条件下，可以近似作为理想气体处理（ C ）A 、高温、高压B、低温、低压C、高温、低压D、低温、高压5、真实气体液化的必要条件是（ B ）A 、压力大于P cB、温度低于T cC、体积等于v c D、同时升高温度和压力6. 在 273 K，101.325 kPa时，CC14(1)的蒸气可以近似看作为理想气体。
已知CC14(1)的摩尔质量为isig.mor1的，则在该条件下，CC14(1)气体的密度为(A )A 、6.87 g.dm-3B、dm-3C、6.42 g.dm'D、3.44 g dm-34.52 g.37、理想气体模型的基本特征是( D ) A 、分子不断地作无规则运动、它们均匀分布在整个容器屮B、各种分子间的作用相等，各种分子的体积大小相等C、所有分子都可看作一个质点，并且它们具有相等的能量D、分子间无作用力，分子本身无体积8、理想气体的液化行为是：( A ) 。
物理化学第一章知识点
气体的pVT关系一、理想气体状态方程pV=nRT (R=8.314472Pa·m3·mol·K-1)根据V m=V/n,n=n/M可得pV m=RTpV m=(m/M)RT根据ρ=m/V和理想气态方程可以求出气体的ρ、V、T、n、M、ρ各种性质。
ρ=pM/RT、M=ρRT/p=RTM/Pv、m=Pvm/RT、n=Pv/RT二、理想气体模型(一)、分子间作用力：两个分子间的相互吸引势能与距离r的6次方成反比，相互排除势能与距离r的12次方成反比。
E=E吸引+E排斥=-A/r6+B/r12(二)、理想气体的微观上的两个特征1、分子间无相互作用力。
2、分子本身不占体积。
(三)、在任何温度和压力下均符合理想气体模型或服从理想气体状态方程的气体称为理想气体图一：兰纳德-琼斯势能曲线示意图(四)、摩尔气体常数当压力趋于零的极限条件下，各种气体pVT均服从pV m=RT的定量关系，R是一个对各种气体都适用的常数。
R=8.314472Pa·m3·mol·K-1三、真实气体状态方程(一)、范德华方程(p+a/V2m)(V m-b)=RT将V m=V/n带入可得(p+n2a/V2)(V-nb)=nRTa只与气体的种类有关，与温度条件无关。
（a/V m2）又称为内压力说明了分子间相互吸引力对压力的影响反比于分子间距离r的6次方。
一般分子间作用力越大，a越大。
a的单位是Pa·m6·mol-2b应该与气体的温度有关。
b是体积修正项，表示每摩尔真实气体分子本身占有体积儿时分子自由活动空间减少的数值。
b的单位是m3·mol-1。
范德华认为真实气体由于分子间的相互作用力会导致气体的压强比理想气体小即p=(p理+a/V2m),体积在考虑了分子本身占有的体积b之后自由活动空间应该是(V m-b)。
范德华方程是一种被简化了的真实气体的数学模型，在任何温度、压力条件下均符合范德华方程的气体叫范德华气体(二)、维里方程pV m=RT(1+Bp2+Cp3+Dp4+……)维里方程是纯经验方程，当压力p→0，摩尔体积V m→0时，维里方程还原为理想气态方程。
物理化学01气体
,
§1-1 理想气体的状态方程
气体理论的三位奠基者:
• 玻义尔 (1627 — 1691) Born in Ireland
00-7-22
•盖· 吕萨克 (1778 — 1850) Frenchman
• 阿伏加德罗 (1776 —1856) an Italian
3
1. 理想气体状态方程
波义尔定律 pV = 常数 (n, T 恒定)
pV (实际) nRT
Z def pV pVm (实) Vm (实) nRT RT Vm (理)
压缩因子Z:
Z 的大小描述了实际气体的关系偏离理想行为的情况:
Z 1, 理想气体; Z 1, Vm (实) Vm (理), 易压缩实际气体;
00-7-22
Z 1, Vm (实) Vm (理), 难压缩实际气体.
13
0.0323 y( Ar) 0.0094 3.452 2.694 y( N 2 ) 0.7804 3.452
00-7-22
（2）各组分气体的分压为
p( N 2 ) y( N 2 ) p 0.7804101.3 79.05kPa
p(O2 ) y(O2 ) p 0.2099101.3 21.26kPa
VB / V nB / n yB
而对非理想气体, 此二式不能成立. 应注意分压力和分体积的定义上的不同.
00-7-22 12
例：若有一空气样品，组成（质量%）如下：N275.47%，O223.19%， Ar1.29%，CO20.05%。（1）试用体积分数表示此空气的组成；（2） 计算25℃及101.325kPa下，此空气各组分气体的分压。设空气可看成理 想气体的混合物。 解：（1）体积分数即各气体的摩尔分数。设有100g空气，则