第三篇_电阻星形连接与三角形连接的等效变换
星形电阻三角形电阻等效变换

星形电阻三角形电阻等效变换形(△形)电阻网络。
星形电阻网络与三角形电阻网络可以根据需要进行等效变换。
(1)、由三角形电阻网络变为等效星形电阻网络星形网络中①、②两端间的端口等效电阻(③端开路)由与串联组成,三角形网络中①、②两端间的等效电阻(③端开路)由与串联后再与并联组成。
令此两等效电阻相等,即得(③端开路)(2-2-1)同理(①端开路)(2-2-2)(②端开路)(2-2-3)由式(2-2-1)至(2-2-3)联立得(2-2-4)(2-2-5)(2-2-6)以上三式是由三角形电阻网络变为等效星形电阻网络时计算星形网络电阻的公式。
这三个公式的结构规律可以概括为:星形网络中的一个电阻,等于三角形网络中联接到对应端点的两邻边电阻之积除以三边电阻之和。
(2)、由星形电阻网络变为等效三角形电阻网络可将式(2-2-4)、(2-2-5)、(2-2-6)对、和联立求解得(2-2-7)(2-2-8)(2-2-9)这是由星形电阻网络变换为等效三角形电阻网络时计算三角形网络电阻的公式。
这三个公式的结构规律可以概括为:三角形网络中一边的电阻,等于星形网络中联接到两个对应端点的电阻之和再加上这两个电阻之积除以另一电阻。
(3)、对称三端网络(symmetricalthree –terminal resistance network)三个电阻相等的三端网络称为对称三端网络。
对称三端电阻网络的等效变换:已知三角形网络电阻为变换为等效星形电阻网络的等效电阻为相反的变换是就是说:对称三角形电阻网络变换为等效星形电阻网络时,这个等效星形电阻网络也是对称的,其中每个电阻等于原对称三角形网络每边电阻的。
对称星形电阻网络变换为等效三角形电阻网络时,这个等效三角形电阻网络也是对称的,其中每边的电阻等于原对称星形网络每个电阻的3倍。
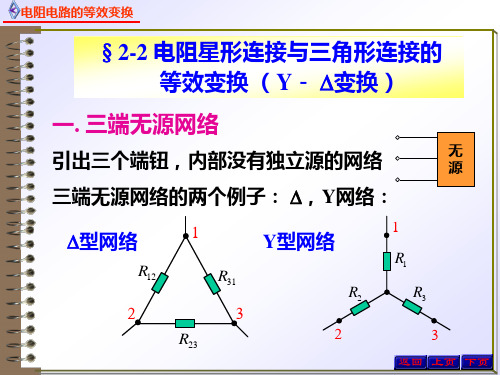
电阻星形连接与三角形连接的等效变换
i1
u12 R12
u31 R31
i2
u23 R23
u12 R12
(1)
i3
u31 R31
u23 R23
由等效条件,比较式(3)与式(1),得由Y接接的变换结果
R12
R1 R2
R2 R3 R3
R3 R1
R23
R1 R2
R2 R3 R1
R3
R1
或
R31
R1 R2
R2 R3 R2
R3
R1
d
h
b
f
a
e
c
g
b
f
返回 上页 下页
电阻电路的等效变换
d
将等电位点短接,
a
e
画出等效电路:
h
c
g
b
f
b de a
cf h
Rag
R 3
R 6
R 3
g
5
R
6
返回 上页 下页
电阻电路的等效变换
(2)求Rab
d
由电路对称性,
h
找出等电位点:
a c
b
a
e
d、e等电位
c、f等电位
g
7
f
Rab 12 R
hg
1.5 (0.6 1.4)(1 1) 2.5 0.6 1.4 1 1
求得: i 10 10 4 R 2.5
返回 上页 下页
电阻电路的等效变换
+
10V -
i1
3 2
2
1.4
3
图(a)
5 Y→△ +
4
10V
-
1
i1
3
2
三角形和星形电阻电路的等效变换

三角形和星形电阻电路的等效变换1. 引言大家好,今天我们聊聊电路中的那些事,特别是三角形和星形电阻电路的等效变换。
听起来是不是有点高大上?其实嘛,这就是把电阻放在不同的位置,让它们的工作变得更轻松而已。
电阻就像是电路里的小助手,有时候换个地方就能发挥出意想不到的效果,就像你换个角度看问题,顿时豁然开朗。
我们在这儿就像是在煮面,偶尔换点调料,味道也会大变样呢!2. 三角形电阻电路2.1 三角形电阻的特征首先,我们得认识一下三角形电阻。
想象一下,电阻排成一个三角形,三个边各自相连,就像三兄弟一起打拼。
这种连接方式让电流在不同的电阻之间穿梭,仿佛是在玩“你追我赶”的游戏。
而且,三角形的结构让我们能轻松计算出每个电阻的作用,真是聪明的设计!2.2 三角形电阻的用途那么,三角形电阻到底有什么用呢?比如,当我们需要调节电流或电压时,三角形电阻就派上了用场。
它能够将复杂的电路简化,让我们一目了然。
这就像是把一锅杂烩理顺成一碗清汤,简单明了,心里也舒服。
可是呢,三角形电阻有时候会让电流走得比较复杂,不容易理解。
3. 星形电阻电路3.1 星形电阻的特征说完了三角形,我们再来说说星形电阻。
这个星形可不是什么美丽的星空,而是电阻像星星一样,中心有个共同的节点,其他的电阻都从这个节点出发。
这就好比我们一家人围坐在一起,大家都有自己的事,但又紧紧联系在一起。
星形电阻的连接方式让电流分流更均匀,效率高得多,真是聪明绝顶!3.2 星形电阻的优势星形电阻的优势就在于它能有效降低电路的复杂度,简化计算。
想象一下,原本你得对着一大堆复杂的数学公式挠头,现在只需几笔,就能轻松搞定。
这样的电路就像是我们日常生活中的简约风格,虽然简单,却能达到很好的效果。
再说,星形电阻也能避免过大的电流,保护其他部件,就像是家里有个“大哥”,照顾着其他小弟弟们。
4. 三角形与星形的等效变换4.1 等效变换的原理好啦,说到这儿,咱们得聊聊怎么把三角形电阻变成星形电阻。
第三篇 电阻星形连接与三角形连接的等效变换

第三篇电阻星形连接与三角形连接的等效变
换
-CAL-FENGHAI.-(YICAI)-Company One1
第三篇电阻星形连接与三角形连接的等效变换
图 1 一 1 ( a )所示是一个桥式电路,显然用电阻串并联简化的办法求得端口 ab 处的等效电阻是极其困难的。
如果能将连接在 1 、 2 、 3 、三个端子间的 R12R23R31构成的三角形连接电路,等效变换为图 1 一 1 ( b )所示的由
R1R2R3构成的星形连接电路,则可方便地应用电阻串并联简化的办法求得端口ab 处的等效电阻,这就是工程实际中经常遇到的星形、三角形等效变换问题(简称 Y ―△变换)。
图1
在这里叙述 Y ―△变换并非要求同学们掌握此变换,而是通过讲解,了解变换的过程意义,为课程后续内容的学习(三相电路)先行建立一个感性认识,从而为更进一步的学习奠定基础。
等效要解决的问题是:图 1 一 2 ( a )所示三角形连接(连接)与图 1 一 2 ( b )星形连接( Y 连接),就其 1、 2 、 3 三个端子而言,要求对外等效。
要完成等效,应明确R1R2R3三个 Y 连接电阻与R12R23R31三个连接电阻应满足什麽关系。
一种推导等效变换的办法是两电路在一个对应端子悬空的同等条件下,分别测两电路剩余两端子间的电阻,并要求测得的电阻相等。
式 l 可方便地用来求三角形连接电阻等效的星形连接电阻。
若由星形连接求等效三角形连接的公式可将式!变换一下,即可得到。
电阻的星形连接与三角形连接的等效变换

Rc2 Rc2 Rd4
I
40 51A 4060
电子发烧友 电子技术论坛
第2章 直流电阻电路的分析计算
例 2.5(六)
为了求得R1、R3、R5的电流, 从图2.10(b)求得
U a cR a I R c I2 2 5 0 4 3 1V 1
回到图2.10(a)电路, 得
I1
Uac1122.8A R1 40
I2 R2
R5 I4
I
R3
R4
R0
+ Us -
R
a
I
I2
R c
R2
R
d
R0
I4 R4
+ Us -
(a)
(b)
图2.10例2.5图 电子发烧友 电子技术论坛
第2章 直流电阻电路的分析计算
例 2.5(三)
解 将△形连接的R1, R3, R5等效变换为Y形连接的 Ra, Rc、Rd, 如图2.10(b)所示, 代入式(2.8)求得
第2章 直流电阻电路的分析计算
⒉ 三角形、星形等效的条件
端口电压U12、U23、U31 和电流I1、I2 、I3都 分别相等,则三角形星形等效。
电子发烧友 电子技术论坛
第2章 直流电阻电路的分析计算
3.已知三角形连接电阻求星形连接电阻
R1
R 12
R 12 R 31 R 23
R 31
R2
R 12
⒈三角形连接和星形连接
三角形连接:三个电阻元件首尾相接构成一
个三角形。如下图a所示。 星形连接:三个电阻元件的一端连接在一起,
另一端分别连接到电路的三个节点。如上图b所 示。
I1
I1 1
1
I12
23电阻的星形和三角形连接的等效互换

例如要求出图2-10中a、b端的等效电阻,必须将 R12、 R23、 R31组成的三角形连接化为星形连接, 这样,运用电阻串、并联等效电阻公式可方便 地求出a、b端的等效电阻。
图2-10 电阻三角形连接等效变为Y形连接
1 连接的三个电阻的公式为:
2.3电阻的星形和三角形连接的等效互换
Y形连接,即三个电阻的一端连接在一个 公共节点上,而另一端分别接到三个不 同的端钮上。如下图中的R 同的端钮上。如下图中的R1R3 和R4 ( R2、 R3和R5)。 三角形连接,即三个 电阻分别接到每两个 端钮之间,使之本身 构成一个三角形。如 图2-9中的R1、 R2、 和 R3( R3、 R4和R5) 为三角形连接。
R1 = R
2
R 12 R 12 R 12
R 31 R 12 + R 23 + R R 12 R 23 + R 23 + R
31
=
31
R3 =
R 23 R 31 + R 23 + R
31
电工基础第二节3.2 电阻的星形与三角形连接的等效变换
1
作:习题二 2-6
返回本章开头
第二节电阻星形连接与返回本章开头 三角形连接的等效变换
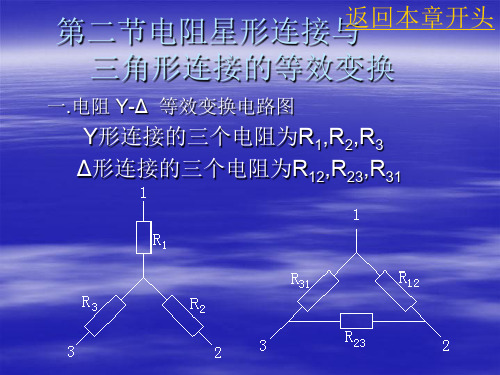
一.电阻 Y-Δ 等效变换电路图
Y形连接的三个电阻为R1,R2,R3 Δ形连接的三个电阻为R12,R23,R31
二.电阻星形联结 转换 三角形联结
R12
R1R2
R2 R3 R3
R3 R1
R23
R1R2
R2 R3 R1
R3 R1
R31
R1R2
R2 R3 R2
R3 R1
便于记忆公式形
形联结电阻
形联结电阻两两乘积之和 形联结不相邻电阻
三.电阻三角形联结 转 换 星形联结
R1
R12
R12 R31 R23
R31
R2
R12
R12 R23 R23
R31
R3
R12
R31R23 R23
R31
便于记忆公式
形联结
形联结相邻电阻乘积 形联结电阻之和
四. Y形联结成△形联结三个电阻
相等 Y 等效公式
R0 3R
R
1 3
R
例2.求图2-a所示电路a.b两端的电阻
解: 将3个1电阻组成的星形连接等效变换为三角形连接,
得到图(b),由此得
Rab
31.5 3 1.5
星形和三角形电阻网络的等效变换165页word文档

星形和三角形电阻网络的等效变换第 1 节等效及等效化简一、等效的概念等效在其端钮处具有相同端电压、端电流及其伏安关系( VAR )的两个网络,称为等效( equivalence )。
相互等效的网络在由它们组成的电路中可以相互替换。
注意:等效是仅对外电路而言,而对内部电路显然是不等效的。
图 2.1-1 中, N1 和 N 1' 是等效的,是指 N1 、 N 1' 对端钮以外部分是等效的,即对 N2 而言是等效的,而对 N1 和 N 1' 内部而言是绝对不会等效的。
二、等效化简等效化简的步骤1 、在电路中某两个关心的节点处作分解,把电路分解成两个或多个部分;2 、分别对各部分进行等效化简,求出其最简的等效电路;3 、用最简的等效电路替代原电路,求出端钮处的电压或电流;4 、若还需求电路中其他支路上的电压或电流,再回到原电路,根据已求得的端电压或端电流进行计算。
第 2 节二端电阻网络的等效一、电阻的串联( resistors in series )串联n 个电阻相串联的二端电阻网络可以用一个等效电阻来等效,其等效电阻 R 等于串联的各电阻之和。
分压关系对于串联的电阻网络,电阻上分得的电压与其电阻值成正比,即电阻值越大,其分得的电压也越大。
第 j 个电阻上分得的电压为两个电阻串联时的分压公式为例 2.2-1 电路如图 2.2-1 所示,,,,求各电阻两端的电压。
解:图中 R1 、 R2 、 R3 电阻相串联,其等效电阻为则 10A 电流源两端的电压由分压公式,得到二、电阻的并联( resistors in parallel )并联n 个电导相并联的二端网络可用一个等效电导来等效,其等效电导 G 等于相并联的各电导之和,即两个电阻并联时,其等效电阻为分流关系对于并联电阻网络,电阻上分得的电流与其电导值成正比,即与其电阻值成反比。
电阻值越大,其分得的电流越小。
第 j 个电导上分得的电流为两个电阻串联时的分流公式为三、电阻的混联方法对于二端混联电阻网络的等效,关键是要抓住二端网络的两个端钮,从一个端钮出发,逐个元件地缕到另一个端钮,分清每个部分的结构是串联还是并联,再利用串联和并联的等效公式,最终求得该二端混联网络的等效电路。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三篇电阻星形连接与三角形连接的等效变换
图1一1(a)所示是一个桥式电路,显然用电阻串并联简化的办法求得端口ab处的等效电阻是极其困难的。
如果能将连接在1、2、3、三个端子间的R12R23R31构成的三角形连接电路,等效变换为图1一1(b)所示的由R1R2R3构成的星形连接电路,则可方便地应用电阻串并联简化的办法求得
端口ab处的等效电阻,这就是工程实际中经常遇到的星形、三角形等效变换问题(简称Y―△变换)。
图1
在这里叙述Y―△变换并非要求同学们掌握此变换,而是通过讲解,了解变换的过程意义,为课程后续内容的学习(三相电路)先行建立一个感性认识,从而为更进一步的学习奠定基础。
等效要解决的问题是:图1一2(a)所示三角形连接(连接)与图1一2(b)星形连接(Y连接),就其1、2、3三个端子而言,要求对外等效。
要完成等效,应明确R1R2R3三个Y连接电阻与R12R23R31三个连接电阻应满足什麽关系。
一种推导等效变换的办法是两电路在一个对应端子悬空的同等条件下,分别测两电路剩余两端子间的电阻,并要求测得的电阻相等。
式l可方便地用来求三角形连接电阻等效的星形连接电阻。
若由星形连接求等效三角形连接的公式可将式!变换一下,即可得到。
