密勒定理
密勒电容与密勒效应

密勒电容与密勒效应 The manuscript was revised on the evening of 20211、密勒电容与密勒效应简单说来:对电子管,屏极与栅极之间的电容;对晶体管,集电极与基极之间的电容;对场效应管,漏极与栅极之间的电容。
这些管子作共阴极(共发射极、共源极)放大器时,输出端与输入端电压反相,使得该电容的充电放电电流增大,从输入端看进去,好像该电容增大了k 倍,k是放大倍数。
这种现象叫密勒效应。
也可以这样解释,在反相放大器中,输入极与输出极间的等效电容会扩大到1-Av倍反射到输入极的效应。
比如,考虑共源(或共射)的单管放大器,设C为GD (BC)电容,则有,i = (vi-vo) * jwC = vi * (1-Av) * jwC = vi * jw[(1-Av)*C]这里[(1-Av)*C]即可看作在GS(BE)处的等效电容。
详见维基百科()2、密勒效应密勒效应(Miller effect)是在中,反相放大电路中,输入与输出之间的分布或寄生电容由于的放大作用,其等效到输入端的电容值会扩大1+K倍,其中K是该级放大电路电压放大倍数。
虽然一般密勒效应指的是电容的放大,但是任何输入与其它高放大节之间的阻抗也能够通过密勒效应改变放大器的输入阻抗。
输入电容的增长值为A v是放大器的放大,C是反馈电容。
•密勒效应是米勒定理的一个特殊情况。
历史米勒效应是以命名的。
1919年或1920年密勒在研究三极管时发现了这个效应,但是这个效应也适用于现代的半导体。
引导假设一个放大率为A v的理想电压,其输入和输出点之间的阻抗为Z。
其输出电压因此为V o = A v V i,输入电流则为这个电流流过阻抗Z,上面的方程显示由于放大器的放大率实际上一个更大的电流流过Z,实际上Z就好像它小得多一样。
电路的输入阻抗为假如Z是电容的话,则由此导出的输入阻抗为因此密勒效应显示的电容C M为实际上的电容C乘以(1 A v)。
krein milman定理

krein milman定理Krein-Milman定理是数学中的一项重要定理,它描述了凸集的闭包与它的极大线性子空间的交集之间的关系。
这个定理最早由俄罗斯数学家格塔尔·科雷茨基和色尔盖·米尔曼在20世纪40年代提出,并在凸集理论和泛凸分析领域有广泛的应用。
本文将对Krein-Milman 定理进行详细介绍,并探讨它在数学和应用领域中的重要性。
首先,我们来定义一下什么是凸集。
一个集合被称为凸集,如果对于集合中的任意两个点,通过这两个点的线段上的所有点也在该集合中。
换句话说,凸集中的任意两个点之间的线段都完全包含在这个集合中。
凸集的闭包即为包含原始凸集以及所有极限点的集合。
Krein-Milman定理的表述如下:对于一个Hausdorff局部凸拓扑矢量空间V,任意一个凸紧函闭集C的闭包与它的极大线性子空间的交集非空。
这个定理的证明依赖于其他重要定理和定义,包括Hahn-Banach定理和超平面定理。
首先我们来介绍一下Hahn-Banach定理。
Hahn-Banach定理是泛凸分析中的一个基本定理,它陈述了对于给定的实线性赋范空间中的子空间和线性泛函,可以通过适当的约束条件,将这个线性泛函扩展为整个空间上的线性泛函。
这个定理为我们提供了在有限维线性空间上的线性函数在无限维线性空间上的推广。
超平面定理是Hahn-Banach定理的一个重要推论。
它说明了一个真紧集与外部点之间一定存在一个超平面。
一个超平面是一个线性子空间的补集,即由线性不等式定义的点的集合。
超平面定理说明了一个紧凸集在一个点的外部切实存在线性分割法。
利用Hahn-Banach定理和超平面定理,我们可以证明Krein-Milman定理。
首先,我们假设C是V中一个非空的凸紧函闭集。
考虑C在一个外部点x上的切实存在超平面P。
P将V分成了两个不交的部分:一个包含C的部分和另一个包含x的部分。
然后我们可以使用Hahn-Banach定理将超平面P扩展为一个线性泛函f,并满足f在C上为一个上界。
密勒定理及应用

图 1 中节点 1. 2 的节点电压方程是 :
图2 图1
( G + ……) U 1 - GU 2 + …… = is1
①
- GU 1 + ( G + ……) U 2 + …… = is2
②
其中 is1 , is2 分别为流向节点 1 ,节点 2 的电流源电流的代数和 。
将 U 2 = KU 1 带入方程 ①中 ,
一 、密勒定理 密勒定理是电路分析中的一个重要定理 ,它的内容如下 : 定理 :在电路中 ,若一个电导接在两个节点间 ,且节点 2 的节点电压是节点 1 的节点电压的 k 倍 。则可以在电路 中去掉此电导 ,并在节点 1 与地之间添加一个值为 (1 - K) G 的电导 , 在节点 2 与地之间添加一个值为 (1 - 1/ K) 的电 导 ,这样修改后的电路与原电路对于节点电压方程等效 。 证明 : 该定理的电路原理图如图 1 ,修改后的电路原理图如图 2 。
2020年深圳中考压轴题圆题型汇总(托勒密定理等圆中难题秘诀)

2020年深圳中考压轴题圆题型汇总(托勒密定理等圆中难题秘诀)中考专项练——圆一、圆中等积式证明(三角形相似)在圆中,我们常常需要证明一些等积式,其中一种常见的方法是利用三角形相似。
例如,我们可以证明在同一圆周上的两个弧所对应的圆心角相等,即 $\angle AOB = \angle COD$,其中 $AB$ 和 $CD$ 分别是这两个弧所对应的弦。
我们可以通过证明 $\triangle AOB \sim \triangle COD$ 来得到这个结论。
圆中的相似模型】在圆中,我们还可以利用相似模型来解决问题。
例如,我们可以利用相似模型证明切线与半径垂直,即 $\angle AOB = 90^\circ$,其中$OA$ 是圆的半径,$AB$ 是与圆相切的切线。
切线定理】切线定理是圆中一个重要的定理,用于描述切线与圆的关系。
根据切线定理,切线与圆的切点处的切线段长度相等。
例如,如果 $AB$ 和 $CD$ 是与圆相切的两条切线,它们的切点为 $P$,那么 $AP=PD$ 和 $BP=PC$。
中点弧模型】中点弧模型是圆中一个常见的模型,用于求解圆中线段的长度。
例如,如果 $AB$ 是圆中一条弦,$M$ 是 $AB$ 的中点,$OM$ 是圆的半径,那么 $AB=2OM$。
例题】例如,如果 $AB$ 是圆中一条直径,$C$ 是圆上一点,$CD$ 是过 $C$ 的切线,交直径 $AB$ 于 $E$,那么 $CE=DE$。
二、圆中线段和差比值问题利用三角形全等进行截长补短】在圆中,我们常常需要解决线段和差比值的问题。
例如,如果 $AB$ 和 $CD$ 是圆中两条相交的弦,交点为 $E$,那么$\dfrac{AE}{EB}=\dfrac{CD}{DB}$。
我们可以利用三角形全等来证明这个结论。
托密勒定理】托密勒定理是圆中一个重要的定理,用于描述线段和差的比值。
根据托密勒定理,如果 $AB$ 和 $CD$ 是圆中两条相交的弦,交点为 $E$,那么$\dfrac{AE}{EB}\cdot\dfrac{CD}{AD}=\dfrac{CE}{ED}$。
密勒效应的特性分析与应用

北京交通大学模拟电子技术研究论文密勒效应的特性分析与应用密勒效应的特性分析与应用摘要:本文通过研究密勒定理与密勒效应,分析了在高频电路中,密勒效应对共射、共集、共基电路频带的影响,并找到改善共射电路高频特性的方案。
分析了密勒效应在积分电路、多级放大电路和滤波器中的应用。
通过对密勒效应的研究,可利用其特点在不同的电路中取其利避其害。
关键字:密勒效应 高频 频带 密勒电容 一、 密勒定理与密勒效应密勒定理由M. Miller 于1920 年在研究真空电子三极管输入阻抗时提出的,但是这个效应也适用于现代半导体三极管。
在进行电路的分析过程中,利用密勒定理能够有效的简化电路,方便对电路分析。
在电路分析时,有时会如图1所示的网络结构:阻抗Z 接在输入输出端。
这样的接法增加了计算的复杂程度。
密勒定理则提供了一种简化分析的方法,把图1所示的电路转换为图2所示的电路,后者称为前者的密勒等效电路。
如果电路输出输入电压之比为K=U 2/U 1,则可以根据输入输出之间的电压电流的关系,得到KZZ -=11ZK K Z 12-=可以通过这个关系得到等效的阻抗值。
如果网络两端之间不是由阻抗连接,而是由电容连接,则可以得到C C K K C C K C ≈-=-=1)(121在分析高频电路的时候,三极管的结电容会对电路产生一定的影响,利用密勒定理等效分析这些问题时,会出现一些特殊的现象,影响电路的性能。
密勒效应是指在放大电路中,输入与输出之间图1π型网络图2密勒定理等效后的π型网络C bcC be C cebce图3三极管的高频模型的分布电容由于放大器的作用,等效到输入端的电容值扩大1+K 倍,其中K 为该级放大电路的电压放大倍数。
该效应在放大电路中可以影响到其工作频率。
二、 密勒效应的高频分析在高频分析的时候,三极管的扩散电容和势垒电容是不容忽视的。
图3是三极管的高频模型。
在高频分析时,需要考虑集电极和基极之间的势垒电容、发射极和基极的扩散电容。
密勒效应及其直观理解
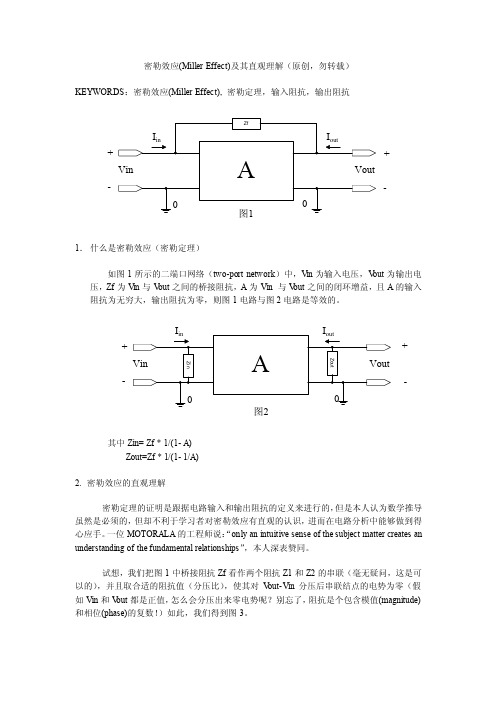
密勒效应(Miller Effect)及其直观理解(原创,勿转载)KEYWORDS:密勒效应(Miller Effect), 密勒定理,输入阻抗,输出阻抗+ -+ -1.什么是密勒效应(密勒定理)如图1所示的二端口网络(two-port network)中,V in为输入电压,V out为输出电压,Zf为V in与V out之间的桥接阻抗,A为Vin 与V out之间的闭环增益,且A的输入阻抗为无穷大,输出阻抗为零,则图1电路与图2电路是等效的。
+ -+ -其中Zin= Zf * 1/(1- A)Zout=Zf * 1/(1- 1/A)2. 密勒效应的直观理解密勒定理的证明是跟据电路输入和输出阻抗的定义来进行的,但是本人认为数学推导虽然是必须的,但却不利于学习者对密勒效应有直观的认识,进而在电路分析中能够做到得心应手。
一位MOTORALA的工程师说:“only an intuitive sense of the subject matter creates an understanding of the fundamental relationships”,本人深表赞同。
试想,我们把图1中桥接阻抗Zf看作两个阻抗Z1和Z2的串联(毫无疑问,这是可以的),并且取合适的阻抗值(分压比),使其对V out-Vin分压后串联结点的电势为零(假如Vin和V out都是正值,怎么会分压出来零电势呢?别忘了,阻抗是个包含模值(magnitude)和相位(phase)的复数!)如此,我们得到图3。
-+-+仔细比较图3和图2,是不是发现这两个图是一样的?只是Z1和Z2换了个地方,再分别改成Zin 和Zout 就完全一样了。
至此,我们只需跟据上面假设的两个条件,列两个方程: Z1+Z2 = Zf(V out-Vin)*Z1/(Z1+Z2) + V in=0就可求得Z1和Z2的值,事实上: Z1=Zin= Zf * 1/(1- A) Z2=Zout= Zf * 1/(1- 1/A)为免麻烦,其实我们可以直接把Zin 和Zout 的值代入方程,以证明是不是Z1=Zin, Z2=Zout 。
密克尔点定理

密克尔点定理
"密克尔点定理"(Michelson Point Theorem)是一个与微分拓扑学和微分几何学相关的数学定理,由法国数学家亨利·密克尔(Henri Poincaré)于19世纪末提出。
这个定理涉及了流形的拓扑性质,特别是关于奇点(Singularities)的性质。
在拓扑学中,流形(Manifold)是一种具有局部欧几里德空间性质的空间,可以近似于欧几里德空间。
密克尔点定理的一个版本表述如下:
定理:在三维欧几里德空间中,任何光滑闭曲面上的连续向量场至少有一个奇点。
换句话说,对于一个在三维空间中的光滑闭曲面(例如球面),无论如何分布连续的向量场,必然会存在至少一个点,这个点上向量场变为零,即出现奇点。
这个定理在数学和物理学中都有应用,特别是在研究流体力学、电磁场、场论等领域。
它揭示了流形上连续向量场的一些重要性质,对于理解奇点、稳定性以及流体的运动等问题具有重要意义。
托米勒定理

托米勒定理托勒密定理(依八谷)【1】(*^__^*) 嘻嘻定理的内容托勒密(Ptolemy)定理指出,圆的内接凸四边形两对对边乘积的和等于两条对角线的乘积。
原文:圆的内接四边形中,两对角线所包矩形的面积等于一组对边所包矩形的面积与另一组对边所包矩形的面积之和。
从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.(见托米勒1)【2 】(*^__^*) 嘻嘻从这个定理可以推出正弦、余弦的和差公式及一系列的三角恒等式,托勒密定理实质上是关于共圆性的基本性质.定理内容指圆内接凸四边形两对对边乘积的和等于两条对角线的乘积。
【3】【】(*^__^*) 嘻嘻证明一、(以下是推论的证明,托勒密定理可视作特殊情况。
)在任意凸四边形ABCD中(如右图),作△ABE使∠BAE=∠CAD ∠ABE=∠ACD,连接DE. 则△ABE∽△ACD 所以BE/CD=AB/AC,即BE·AC=AB·CD (1)由△ABE∽△ACD得AD/AC=AE/AB,又∠BAC=∠EAD, 所以△ABC∽△AED. BC/ED=AC/AD,即ED·AC=BC·AD (2) (1)+(2),得AC(BE+ED)=AB·CD+AD·BC 又因为BE+ED≥BD (仅在四边形ABCD 是某圆的内接四边形时,等号成立,即“托勒密定理”)【3.2 】复数证明用a、b、c、d分别表示四边形顶点A、B、C、D 的复数,则AB、CD、AD、BC、AC、BD的长度分别是:(a-b)、(c-d)、(a-d)、(b-c)、(a-c)、(b-d)。
首先注意到复数恒等式:(a ? b)(c ? d) + (a ? d)(b ? c) = (a ? c)(b ? d) ,两边取模,运用三角不等式得。
等号成立的条件是(a-b)(c-d)与(a-d)(b-c)的辐角相等,这与A、B、C、D四点共圆等价。
