第五章(频率响应)

合集下载

自动控制原理简明教程第五章频率响应法

这时，求扰动输入下的误差传递函数 en(s) ，
先求 E(s) 0 C(s) 1GG（（s）s） N（s）
而
e（n s）
NE（（ss））
1
G（s） G（s）
则 ess（2 t） An e（n j）sin(t en( j))
幅频特性
相频特性
二.频率特性的物理意义及求解方法
R
ur
C uc
RC网络微分方程为:
优点:
(1).可以根据系统的开环频率特性判断闭环系统的稳定性,而不必求解特征方程。
(2).很容易研究系统的结构,参数变化对系统性能的影响,并可指出改善系统性能的途径,便于
对系统进行校正。
(3).提供了一种通过实验建立元件或系统数学模型的方法。
(4).可以方便地设计出使系统噪声小到规定程度的系统。
一.比例环节
传递函数为G(s)=k
频率特性为 G( jw) ke j 0
幅频特性为 A(w)=k
相频特性为 (w) 0
极坐标图和伯德图为：
L(w)(dB)
20lgk
(w)(度) 0.1 1 10 100
w
0
w
-30
Bode图
j
w=0
w
0k
w
极坐标图
二.积分环节和微分环节
积分环节: G(s) C(s) R(s) 1/ s
w? ?
450 W=1/T
1 W=0 w
对数幅频特性：L(w) 20lg 1 T 2w2 1
20lg T 2w2 1
当wT≥1时,L(w)≈-20lgwT
当wT≥1时,L(w)可用一条斜率为-20dB/dec的渐近直线来表示。
当wT≤1时,L(w)≈0,是一条与0分贝线重合的直线。两直线交于横坐标w=1/T的地方。

第五章放大电路的频率响应-new

放大电路中有电容,电感等电抗元件放大电路中有电容电感等电抗元件, 电感等电抗元件阻抗随f 阻抗随变化而变化
1 ZC = jωC
C1
& Ib I& c
& Ib
V&O
前面分析, 前面分析隔直电容处理为:直流开路交流短路处理为直流开路,交流短路直流开路
f 1Hz 10Hz 100Hz 1kHz 10kHz
60 40
带宽 20 0 2
2. 频率响应的分析任务
20 fL
2× 102
2× 103
2× 104 fH
f/Hz
（1）频率响应表达式 AV = AV (ω )∠ϕ (ω ) ）频率响应表达式: & 下限频率f （2）带宽）带宽BW、上限频率 f H、下限频率 L 、
继续
3. AV随 f 变化的原因
继续
（1）高通电路：频率响应）高通电路：
fL
& Uo jωRC & = Au = & U i 1 + jωRC
1 & = j f fL 令f L = ，则Au 2 πRC 1 + j f fL
f>>fL时放大倍数约为1 倍数约为
f fL & Au = 1 + ( f f L )2 ϕ = 90° − arctan( f f L )
由于放大电路中耦合电容、旁路电容、由于放大电路中耦合电容、旁路电容、半导体器耦合电容极间电容的存在使放大倍数为频率的函数。的存在，件极间电容的存在，使放大倍数为频率的函数。
继续
5.1 频率响应概述
频率响应——放大器的电压放大倍数放大器的电压放大倍数频率响应与频率的关系

自动控制原理第五章-频率响应法

Im
（K，0°）
0
Re
图5.5 比例环节乃氏图
南京工业职业技术学机械学院——自动控制原理
L( )
0
( )
dB K>1
K=1 K<1
lg
0
lg
图5.6 比例环节的Bode图
作用：比例环节只改变原系统的幅值（K＜1，降低；K ＞ 1，抬高），不改变原系统的相位。
南京工业职业技术学机械学院——自动控制原理
➢ 乃氏图的绘制—— “三点法”
G(jω)= A(ω)ejφ(ω) →
A(ω)：起止位置 φ(ω) ：起止方向
起点：ω→0，[A(0),φ(0)] 终点： ω→∞，[A(∞),φ(∞)] 与负实轴的交点：令φ(ω) =-180°→ ωx
相位截止频率或相位剪
切频率
则交点为[A(ωg)，-180°]
注意：由φ(0) → φ(∞)的变化范围可判断乃氏图所在的象限。
2 ( )
1 ( )
图5.8 积分、微分环节Bode图
南京工业职业技术学机械学院——自动控制原理
3. 纯微分环节
G(s) s
G( j) j e j90
传递函数与积分环节互为倒数
Im
A()
（1）乃氏图 ( ) 90
起点：[0, 90°]；终点： [∞, 90°]
0
Re
图5.9 微分环节乃氏图
I ( )
T 1 2T
2
联立消去ω可以得到实部和虚部的关系式：
[R( ) 0.5]2 [I( )]2 0.52
故，惯性环节的乃氏图是圆心为点（0.5，j0）上，半径为 0.5的半园（ω=0~∞）。
（2）Bode图

第五章放大电路的频率响应

1 fH 2 RC
1 fL 2 RC
当信号频率等于上（下）限频率时，放大电路的增益下降3dB，且产生±45°相移
近似分析时，可用折线化的波特图表示电路的频率特性
一个电容对应的渐进线斜率为20dB/十倍频
简单 RC 电路的频率特性
Ui
•
R C
Uo
•
Ui
•
C R
Uo
•
RC 低通电路
RC 高通电路
Au
• |Au |
1 0.707
1 f 1 j fH
1 0.707
Au
1 fL 1 j f
|Au |
fL
f
•
O

fH f
f
O
O –45° –90°
90° 45° O
f
研究频率响应的方法 (1) 三个频段的划分 1) 中频区(段) 特点:Aus与f无关
与f无关
5.4 单管放大电路的频率响应
本节以单管共射电路为例，介绍频率响应的一般分析方法。
5.4.1 单管共射放大电路的频率响应
1、画出全频段的微变等效电路
+VCC RB C1 + . Ui VT RL . Uo RC C2 + + . Ui _ RB rb′e
C1
rbb′ . gmUb'e Cπ′
C2 + RC . RL U o _
R
fL
L 1 1 下限截止频率 2 2 2 RC
Au பைடு நூலகம்
1
L 1 j

1 fL 1 jf

f j fL f 1 j fL
1、RC高通电路的频率响应

自动控制原理(第三版)第五章频率响应法

频段的两条直线组成的折线近似表示, 如图5-18的渐近线所
示。这两条线相交处的交接频率ω=1/T, 称为振荡环节的无阻尼
自然振荡频率。在交接频率附近, 对数幅频特性与渐近线存在
一定的误差, 其值取决于阻尼比ζ的值, 阻尼比越小, 则误差越大, 如表5-4所示。当ζ＜0.707时, 在对数幅频特性上出现峰值。根
一个单位长度。设对数分度中的单位长度为L, ω0为参考点, 则当ω以ω0为起点, 在10倍频程内变化时, 坐标点相对于ω0的距离
为表5-1中的第二行数值乘以L。
第五章频率响应法
图 5-4 对数分度和线性分度
第五章频率响应法
表 5-1 10倍频程内的对数分度
第五章频率响应法
第五章频率响应法
图 5-7 比例环节的伯德图
第五章频率响应法
2. 积分环节积分环节的频率特性为
其幅频特性和相频特性为
(5.18)
(5.19)
由式(5.19)可见,它的幅频特性与角频率ω成反比, 而相频特性恒
为-90°。对数幅频特性和相频特性为
(5.20)
第五章频率响应法
T), 则有
因此有
这表明φ(ω)是关于ω=1/T, φ(ω)=-45°这一点中心对称的。用
MATLAB画出的惯性环节的伯德图如图5-14所示(T=1)。
第五章频率响应法
图 5-14 MATLAB绘制的惯性环节的伯德图
第五章频率响应法
5. 一阶微分环节一阶微分环节的频率特性为幅频特性和相频特性为
即所以, 惯性环节的奈氏图是圆心在(0.5, 0), 半径为0.5的半圆 (
见图5-12)。对数幅频特性和相频特性为

控制系统--第五章系统频率响应分析

第五章系统频率响应分析 5.1.2 频率特性的特点和作用 1. 频率特性可通过频率响应试验求取
根据频率特性的定义，首先改变输入正弦信号 Xie jt 的频率并测出与此相应的输出幅值Xo ()与相移 ()。然后作出幅值比 Xo () / Xi 对频率的函数曲线，此即幅频特性曲线；作出相移 () 对频率的函数曲线，此即相频特性曲线。
Im
[G(jω)] 0
ω=∞
Re -90°
定的相位滞后。
ω
3. 微分环节
图5.7 积分环节的Nyquist图
传递函数频率特性
G(s) Xo (s) Ts Xi (s)
G( j) = jT
第五章系统频率响应分析
实频特性恒为0，虚频特性则为；
幅频特性|G(j)| = ，相频特性∠ G(j) = 90°。
G(s)Xi (s)
bmsm ansn
bm1sm-1 b1s bo a n1sn1 a1s a o
Xi s2 2
(5.5) (5.6)
第五章系统频率响应分析
若系统无重极点，则上式可写为
Xo (s)
n i1
Ai s si
( B s j
B* ) s j
(5.7)
其中，si为系统特征方程的根；Ai、B、B* (B*为B 的共轭负数)
(5.12)
式中 u()是频率特性的实部，称为实频特性；
v()是频率特性的虚部，称为虚频特性。
综上所述，一个系统可以用微分
微分方程 dtd
sபைடு நூலகம்
dt d
jω
方程或传递函数来描述，也可以用频
系统
率特性来描述。他们之间的相互关系如图5.3所示。

自动控制原理第五章频率响应法

智能化和自适应频率响应分析方法
随着人工智能和机器学习技术的发展，将人工智能和机器学习技术应用于频率响应分析中，可以大大提高分析的准确性和效率，是未来研究的一个重要方向。
06
参考文献
参考文献
01
《现代控制系统分析与设计（第八版）》作者： Richard C. Dorf and Robert H. Bishop
01
频率响应法的起源可以追溯到20世纪30年代，当时研究者开始使用频率响应法来分析电气系统的稳定性。
02
随着计算机技术和信号处理技术的发展，频率响应法的应用范
围不断扩大，分析精度和计算效率也不断提高。
目前，频率响应法已经成为自动控制原理中最重要的分析方法
03
之一，广泛应用于控制系统的分析和设计。
02
非线性系统的频率响应分析
非线性系统的频率响应分析是研究非线性系统对不同频率输入信号的响应特性。由于非线性系统的输出与输入之间不存在明确的函数关系，因此需要采用特殊的方法进行分析。
在实际应用中，非线性系统的频率响应分析广泛应用于音频处理、图像处理、通信等领域。通过分析非线性系统的频率响应特性，可以揭示系统的内在规律，为系统设计和优化提供依据。
02
《自动控制原理（第五版）》作者：孙亮
03
《控制系统设计指南（第二版）》作者：王树青
感谢您的观看
THANKS
对数坐标图分析法
对数坐标图分析法也称为伯德图，通过将系统的频率响应以对数坐标的形式表示出来，可以方便地观察系统在不同频率下的性能变化。
在对数坐标图中，幅值响应和相位响应分别以对数形式表示，这样可以更好地展示系统在不同频率下的变化趋势。
对数坐标图分析法适用于分析各种类型的系统和多输入多输出系统，对于非线性系统也可以进行一定的分析。

第五章频率响应.ppt

-90
-180 -270
fL1 fL2
fH
f
-45/十倍频
5.4 多级放大器的频率特性
1、幅频特性 A u n A ui i 1
20lg Au 20lg Au1 20lg Au2 20lg Aun
n
20lg Aui i 1 n
2、相频特性 1 2 n i i 1
ui
ui
uo
uo
结论：是低频角频率 Au缩小是中频角频率Au较大是高频角频率 Au缩小
实验表明：增益A = A(j)
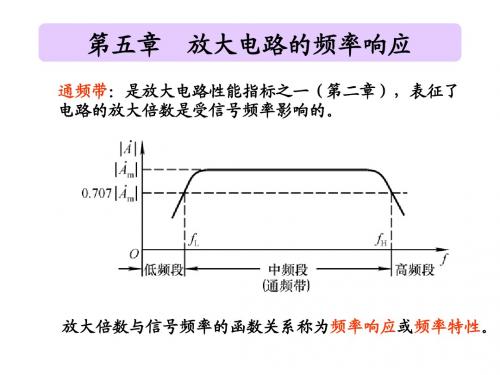
一、频率响应与通频带
1、频率响应幅频特性
相频特性
Au Au ( jf ) Au ( f ) e j ( f )
后果：若通频带不够宽，输入信号中不同频率的成分得不到同样的放大，输出信号就会失真。
u

U o U i
1
1 j( fL /
f
)
幅频特性表达式为：Au ( f )
1 1 ( fL / f )2
相频特性表达式为： ( f ) arctan( fL / f )
２０lgA·u(f)/dB
０
Au ( f )
3dB fL
1 1 ( fL / f )2
f
fL即为转折频率
)

180

arctan(
fL1 f
)

arctan(
fL2 f
)

arctan(
f fH
)
．
20lgAus(f)/dB
+20dB/十倍频
．
3dB
20lgA usm

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

第五章（频率响应）
5.1一个放大电路的传输函数为：，
请画出的幅度和相位波特图。

解：
5.2已知某共射放大电路的波特图如图P5.2所示，试写出的表达式。

图P5.2图P5.3
解：观察波特图可知，中频电压增益为40dB ，即中频放大倍数为−100 ; 下限截止频率为1Hz
4
24510()(1)(1)1010T s s s =++()T
s u
A
和10Hz ，上限截止频率为250kHz 。

故电路u
A 的表达式为： 25510010110(1)(1)(1)(1)(1)(1)2.5101010u f A f f f j jf j j jf jf -+==++++++⨯
5.3已知某电路的幅频特性如图P5.3所示，试问：(1)该电路的耦合方式；(2)该电路由几级
放大电路组成；(3)当f =104H Z 时，附加相移为多少？当f =105H Z 时，附加相移又约为多
少？（4）该电路的上限频率为多少？
解：(1)因为下限截止频率为0 , 所以电路为直接耦合电路；
(2)因为在高频段幅频特性为−60dB ／十倍频，所以电路为三级放大电路；
(3)当f =104Hz 时，'00
453135φ=-⨯=-；
当f =105Hz 时，'903270o o φ=-⨯=-。

（4）该电路的33410(1)10
u A f j ±=+
；上限频率为' 5.2H f kHz ≈≈
5.4一个工作在I C = 2mA 的BJT 有，，。

则和为多少？
5.5在一个FET 放大器中，例如图P5.5所示的电路，源电阻R=100K ，放大器输入电阻
，C gs ＝1Pf ，C gd ＝0.1pF ，现g m ＝3mA/V ，r 0＝50K ，R D ＝8K 以
及RL ＝10K 。

确定期望的3dB 截止频率f H 和中频增益。

要使f H 增大一倍，设计者可
以考虑改变R out 或者R in 。

那么为了使f H 增大一倍，单独改变R out 或者R in 时要求它们如
何变化？在每种情况下得到的中频增益为多少？
图P5.5
5.6一个分立MOSFET 共源放大器有R in ＝2M ，g m ＝4mA/V ，r 0＝100K ，R D ＝8K ，C gs ＝2pF ，C gd ＝0.5Pf 。

该放大器由内阻为500K 的电压源激励，并连接到一个10K 的负载。

求：
H f pF C 1=μpF C 10=π150=βT f βf ΩΩ==K R R G G 10021ΩΩ
ΩΩΩΩΩΩ
（1）总中频增益A M。

（2）上限3dB频率f H。