内压薄壁容器的设计
合集下载
8 内压薄壁容器设计基础
储存液体的回转薄壳
圆筒形壳体 球形壳体
21
8 内压薄壁容器设计基础（续）
1、 受内压的圆筒形壳体 已知圆筒平均直径为 D，厚度为δ，试求圆筒上
任一点 A 处的经向应力和环向应力。
22
8 内压薄壁容器设计基础（续）
薄壁圆筒中各点的第一曲率半径和第二曲率半径
分别为 R1=∞；R2=R
将R1、R2代入薄膜应力理论计算公式得经向应力 与环向应力：
a/b＜2 时，σθ＞0 a/b ＝2 时，σθ＝0 a/b ＞2 时，σθ＜0 σθ<0，表明σθ为压应力；a/b值越大，即封头成型越浅，x=a 处的压应力越大。
31
8 内压薄壁容器设计基础（续）
32
8 内压薄壁容器设计基础（续）
（4）当a/b=2时，为标准型式的椭圆形封头。
在x=0处，
m
pa
椭圆曲线方程
x2 a2
y2 b2
1
27
8 内压薄壁容器设计基础（续）
推导思路：
椭圆曲线方程
式（8-1）（8-2）
R1和R2
, m
m
pR2
2
p
2
a4
x2 (a2
b2 )
1 2
b
（8-9）
（8-10）
p
2
a4
x2 (a2 b
b2 )
1 2
2
a4
a4 x2 (a2
b2
)
又称胡金伯格方程
② 壳体的边界处不受横向剪力、弯矩和转矩作用。
③ 壳体的边界处的约束沿经线的切线方向，不得限制边界处 的转角与挠度。
对很多实际问题：无力矩理论求解 ╬ 有力矩理论修正
20
内压薄壁容器设计
不被加热或冷却，筒内介质最高或最低温度。
用蒸汽、热水或其它载热体加热或冷却，载体最高温度或最低温度。
㈡设计温度
㈢许用应力系数
焊接削弱而降低设计许用应力的系数。 根据接头型式及无损检测长度比例确定。
焊接接头形式
无损检测的长度比例
100%
局部
1.0
0.85
小位移假设
各点位移都远小于厚度。可用变形前尺寸代替变形后尺寸。变形分析中高阶微量可忽略。
2．基本假设
02
直线法假设
变形前垂直于中面直线段，变形后仍是直线并垂直于变形后的中面。变形前后法向线段长度不变。沿厚度各点法向位移相同，厚度不变。
不挤压假设
各层纤维变形前后互不挤压。
01
2．基本假设
2．球形壳体
直径与内压相同，球壳内应力仅是圆筒形壳体环向应力的一半，即球形壳体的厚度仅需圆筒容器厚度的一半。 当容器容积相同时，球表面积最小，故大型贮罐制成球形较为经济。 制造 球壳R1＝R2=D/2，得：
3．圆锥形壳体
圆锥形壳半锥角为a，A点处半径为r，厚度为d，则在A点处： 代入（4-3）、（4-4）可得A点处的应力：
㈡受液体静压的圆筒形壳体的受力分析 筒壁上任一点的压力值（不考虑气体压力）为： 根据式（4-3） （4-4）可得：
上部支承圆筒（b），液体重量使得圆筒壁受轴向力作用，在圆筒壁上产生经向应力：
底部支承的圆筒（a），液体重量由支承传递给基础，筒壁不受液体轴向力作用，则s1=0。
[s]t-设计温度t℃下材料许用应力，MPa。
㈠焊接接头系数
钢板卷焊。夹渣、气孔、未焊透等缺陷，导致焊缝及其附近区域强度可能低于钢材本体的强度。 钢板 [s]t乘以焊接接头系数f，f≤1
用蒸汽、热水或其它载热体加热或冷却，载体最高温度或最低温度。
㈡设计温度
㈢许用应力系数
焊接削弱而降低设计许用应力的系数。 根据接头型式及无损检测长度比例确定。
焊接接头形式
无损检测的长度比例
100%
局部
1.0
0.85
小位移假设
各点位移都远小于厚度。可用变形前尺寸代替变形后尺寸。变形分析中高阶微量可忽略。
2．基本假设
02
直线法假设
变形前垂直于中面直线段，变形后仍是直线并垂直于变形后的中面。变形前后法向线段长度不变。沿厚度各点法向位移相同，厚度不变。
不挤压假设
各层纤维变形前后互不挤压。
01
2．基本假设
2．球形壳体
直径与内压相同，球壳内应力仅是圆筒形壳体环向应力的一半，即球形壳体的厚度仅需圆筒容器厚度的一半。 当容器容积相同时，球表面积最小，故大型贮罐制成球形较为经济。 制造 球壳R1＝R2=D/2，得：
3．圆锥形壳体
圆锥形壳半锥角为a，A点处半径为r，厚度为d，则在A点处： 代入（4-3）、（4-4）可得A点处的应力：
㈡受液体静压的圆筒形壳体的受力分析 筒壁上任一点的压力值（不考虑气体压力）为： 根据式（4-3） （4-4）可得：
上部支承圆筒（b），液体重量使得圆筒壁受轴向力作用，在圆筒壁上产生经向应力：
底部支承的圆筒（a），液体重量由支承传递给基础，筒壁不受液体轴向力作用，则s1=0。
[s]t-设计温度t℃下材料许用应力，MPa。
㈠焊接接头系数
钢板卷焊。夹渣、气孔、未焊透等缺陷，导致焊缝及其附近区域强度可能低于钢材本体的强度。 钢板 [s]t乘以焊接接头系数f，f≤1
第3章 内压薄壁容器
径。无缝钢管的公称直径、外径及无缝钢管制作筒体时的公称直径见表3-15。
第3章 内压薄壁容器
3.3 压力试验
3.3.1 压力试验的对象、目的及方法 压力试验包括液压试验和气压试验。从安全考虑，多数情况下尽可能采用液压试
验。但对不允许有微量残留液体或容积过大及结构复杂的容器；严寒下易发生冰胀而 不适宜作液压试验的容器均须进行气压试验。对剧毒介质容器和高压易燃介质等不允 许有微量介质泄漏的容器，在液压试验合格后还要做气密性试验。对需要进行热处理 的容器，应在热处理后再做压力试验。
第3章 内压薄壁容器
3.2 设计参数的确定
3.2.3 许用应力 许用应力是容器壳体、封头等受压元件的材料许用强度，它是根据材料各项强
度性能指标分别除以相应的标准中所规定的安全系数来确定的。 钢制压力容器用材料（除螺栓材料外）许用应力的取值方法见表3-6。
第3章 内压薄壁容器
3.2 设计参数的确定
（3）
设计压力p
指设定的容器顶部的最高压力，与相应的设计温度一起作为设计载荷条件，其值不得低 于工作压力。
第3章 内压薄壁容器
3.2 设计参数的确定
3.2.2 设计温度t 设计温度是指容器在正常工作情况下，在相应设计压力下，设定的受压元件的
金属温度
元件的金属温度可用传热计算求得，或在已使用的同类容器上测定，或按内部 介质温度测定。当不可能通过传热计算或测试结果确定时，可按以下方法确定。
3.1.4 各类厚度的关系 各类厚度之间的关系如图3-1和表3-1所示。
第3章 内压薄壁容器
3.2 设计参数的确定
3.2.1 压力参数
（1）
工作压力pw
指在正常工作情况下，容器顶部可能达到的最高压力，也称为最高工作压力。
第3章 内压薄壁容器
3.3 压力试验
3.3.1 压力试验的对象、目的及方法 压力试验包括液压试验和气压试验。从安全考虑，多数情况下尽可能采用液压试
验。但对不允许有微量残留液体或容积过大及结构复杂的容器；严寒下易发生冰胀而 不适宜作液压试验的容器均须进行气压试验。对剧毒介质容器和高压易燃介质等不允 许有微量介质泄漏的容器，在液压试验合格后还要做气密性试验。对需要进行热处理 的容器，应在热处理后再做压力试验。
第3章 内压薄壁容器
3.2 设计参数的确定
3.2.3 许用应力 许用应力是容器壳体、封头等受压元件的材料许用强度，它是根据材料各项强
度性能指标分别除以相应的标准中所规定的安全系数来确定的。 钢制压力容器用材料（除螺栓材料外）许用应力的取值方法见表3-6。
第3章 内压薄壁容器
3.2 设计参数的确定
（3）
设计压力p
指设定的容器顶部的最高压力，与相应的设计温度一起作为设计载荷条件，其值不得低 于工作压力。
第3章 内压薄壁容器
3.2 设计参数的确定
3.2.2 设计温度t 设计温度是指容器在正常工作情况下，在相应设计压力下，设定的受压元件的
金属温度
元件的金属温度可用传热计算求得，或在已使用的同类容器上测定，或按内部 介质温度测定。当不可能通过传热计算或测试结果确定时，可按以下方法确定。
3.1.4 各类厚度的关系 各类厚度之间的关系如图3-1和表3-1所示。
第3章 内压薄壁容器
3.2 设计参数的确定
3.2.1 压力参数
（1）
工作压力pw
指在正常工作情况下，容器顶部可能达到的最高压力，也称为最高工作压力。
内压薄壁容器的设计计算
1
2、容器的分类 （1）按受力情况：内部介质的压力大于外界压力，称为内
压容器。反之称为外压容器。 常压容器：压力p<0.07MPa
内压容器：
0.07<p<1.6MPa；低压容器 1.6<p<10MPa；中压容器 p>10MPa；高压容器
外压容器
2
（2）按壁厚分为薄壁容器、厚壁容器 按照容器的外径（Do）和内径（Di）的比值K= Do/ Di
－设计温度下材料的蠕变极限，MPa
nb、ns、nD、nn－安全系数，可从有关手册中查到。
16
4. 焊缝系数
设计计算中所取焊缝系数的大小，主要是根据压力容器受 压部分的焊缝位置、焊接接头和焊缝的无损探伤检验要求 而定的。
焊接接头型式
双面焊或相当于双面焊的全焊透对接焊缝 单面焊的对接焊缝，在焊接过程中，沿焊逢根 部全长有紧贴基本金属的垫板 无法进行探伤的单面焊环向对接焊缝，无垫板
薄壁容器：K<1.2 厚壁容器： K>1.2 厚壁容器多用于高温、高压条件，制浆造纸应用较多的是 薄壁容器。
3
（3）按照容器的形状 方形或矩形：由平板焊接而成，制造简单，但承压能力低，
用于小型常压贮槽。
球形：节省材料，承压能力强，但制造困难，设备内件安 装不方便，一般用作贮罐。
圆筒形：主体为圆柱形筒体，加各种形式的封头（半球形、 椭圆形、锥形、碟形、平盖板）。制造容易，设备内件安 装方便，承压能力强，应用广泛。
PDi
SC 2[ ] P C
（7-5）
式中 Di－圆筒体内径，mm Sc－考虑了腐蚀裕度时圆筒体设计壁厚，mm
－焊缝系数
C－壁厚附加量，mm 其他符号意义同式（7-2）。
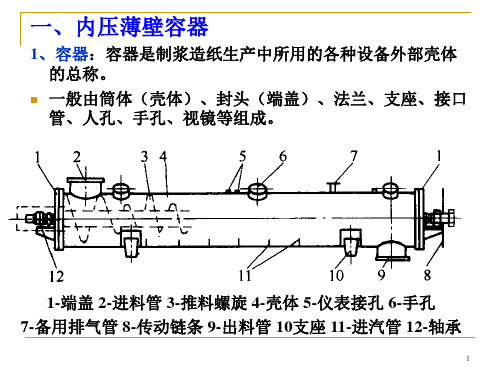
2、容器的分类 （1）按受力情况：内部介质的压力大于外界压力，称为内
压容器。反之称为外压容器。 常压容器：压力p<0.07MPa
内压容器：
0.07<p<1.6MPa；低压容器 1.6<p<10MPa；中压容器 p>10MPa；高压容器
外压容器
2
（2）按壁厚分为薄壁容器、厚壁容器 按照容器的外径（Do）和内径（Di）的比值K= Do/ Di
－设计温度下材料的蠕变极限，MPa
nb、ns、nD、nn－安全系数，可从有关手册中查到。
16
4. 焊缝系数
设计计算中所取焊缝系数的大小，主要是根据压力容器受 压部分的焊缝位置、焊接接头和焊缝的无损探伤检验要求 而定的。
焊接接头型式
双面焊或相当于双面焊的全焊透对接焊缝 单面焊的对接焊缝，在焊接过程中，沿焊逢根 部全长有紧贴基本金属的垫板 无法进行探伤的单面焊环向对接焊缝，无垫板
薄壁容器：K<1.2 厚壁容器： K>1.2 厚壁容器多用于高温、高压条件，制浆造纸应用较多的是 薄壁容器。
3
（3）按照容器的形状 方形或矩形：由平板焊接而成，制造简单，但承压能力低，
用于小型常压贮槽。
球形：节省材料，承压能力强，但制造困难，设备内件安 装不方便，一般用作贮罐。
圆筒形：主体为圆柱形筒体，加各种形式的封头（半球形、 椭圆形、锥形、碟形、平盖板）。制造容易，设备内件安 装方便，承压能力强，应用广泛。
PDi
SC 2[ ] P C
（7-5）
式中 Di－圆筒体内径，mm Sc－考虑了腐蚀裕度时圆筒体设计壁厚，mm
－焊缝系数
C－壁厚附加量，mm 其他符号意义同式（7-2）。
化工机械基础-第08章 内压薄壁容器设计基础
化工设备机械 基础
例8-2回转壳体薄膜应力分析例题
例：有一圆筒形容器，两端为椭圆形封头， 已知圆筒的平均直径为D=2000mm厚度为 20mm,设计压力为2MPa，试确定：
(1)筒身上的经向应力和环向应力？ (2)如果椭圆封头的a/b分别为2、1.414和3， 封头厚度为20mm，分别确定封头的最大经向 应力和最大环向应力所在的位置。
d1
2
2 dl1
d2
2
0
pdl1dl2
m dl1dl2
1 R1
dl1dl2
1 R2
0
m p R1 R2
化工设备机械 基础
经推导，可得环向应力计算公式为：
m p R1 R2
R1: 该点的第一曲率半径，m
：环向应力，MPa
Page16
化工设备机械 基础
薄膜理论适用范围
• 除了要求壳体较薄，还要满足如下条件： • 回转体轴对称，壁面厚度无突变。曲率半径连
n
锥截面
中间面
M
横截面
壁厚在那个截面量取？
Page5
化工设备机械 基础
➢ 三个曲率半径
1) 第一曲率半径：中间面上任一点经线 的曲率半径。R1=MK1(K1点在法线上)
2) 第二曲率半径：通过经线上M点的法 线作垂直于经线的平面，其与中间面相 交得到一平面曲线EM，此曲线在M点 处的曲率半径.R2=MK2(K2点是法线与 回转轴的交点)
1) 直法线假设：壳体在变形前垂直于中间面的直 线段，在变形后仍保持直线段并垂直于变形后的 中间面，且直线段长度不变。
2) 互不挤压假设：壳体各层纤维变形后均互不挤 压。
忽略弯矩作用，对于薄壁壳体，计算结果足够精 确。（无力矩理论）
第三章-内压薄壁容器设计
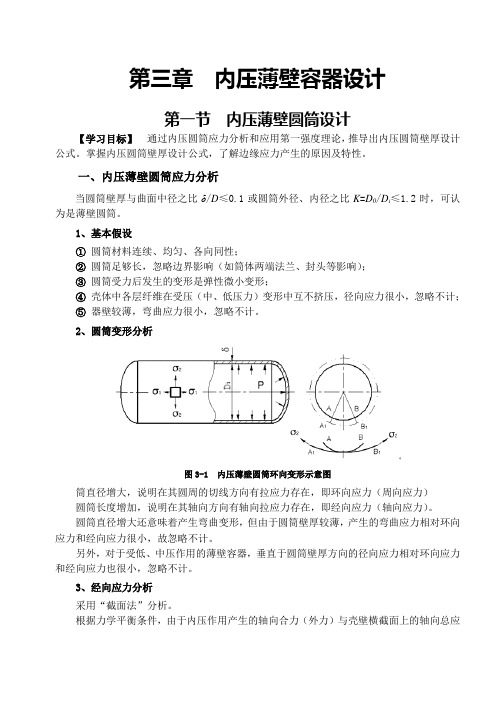
第三章内压薄壁容器设计第一节内压薄壁圆筒设计【学习目标】通过内压圆筒应力分析和应用第一强度理论，推导出内压圆筒壁厚设计公式。
掌握内压圆筒壁厚设计公式，了解边缘应力产生的原因及特性。
一、内压薄壁圆筒应力分析当圆筒壁厚与曲面中径之比δ/D≤0.1或圆筒外径、内径之比K=D0/D i≤1.2时，可认为是薄壁圆筒。
1、基本假设①圆筒材料连续、均匀、各向同性；②圆筒足够长，忽略边界影响（如筒体两端法兰、封头等影响）；③圆筒受力后发生的变形是弹性微小变形；④壳体中各层纤维在受压（中、低压力）变形中互不挤压，径向应力很小，忽略不计；⑤器壁较薄，弯曲应力很小，忽略不计。
2、圆筒变形分析图3-1 内压薄壁圆筒环向变形示意图筒直径增大，说明在其圆周的切线方向有拉应力存在，即环向应力（周向应力）圆筒长度增加，说明在其轴向方向有轴向拉应力存在，即经向应力（轴向应力）。
圆筒直径增大还意味着产生弯曲变形，但由于圆筒壁厚较薄，产生的弯曲应力相对环向应力和经向应力很小，故忽略不计。
另外，对于受低、中压作用的薄壁容器，垂直于圆筒壁厚方向的径向应力相对环向应力和经向应力也很小，忽略不计。
3、经向应力分析采用“截面法”分析。
根据力学平衡条件，由于内压作用产生的轴向合力（外力）与壳壁横截面上的轴向总应力（内力）相等，即：124δσππD p D =由此可得经向应力： δσ41pD=图3-2 圆筒体横向截面受力分析4、环向应力分析 采用“截面法”分析。
图3-3 圆筒体纵向截面受力分析根据力学平衡条件，由于内压作用产生的环向合力（外力）与壳壁纵向截面上的环向总应力（内力）相等，即：22δσL LDp = （3-3）由此可得环向应力： δσ22pD= （3-4） 5、结论通过以上分析可以得到结论：122σσ=，即环向应力是经向应力的2倍。
因此，对于圆筒形内压容器，纵向焊接接头要比环向焊接接头危险程度高。
在圆筒体上开设椭圆形人孔或手孔时，应当将短轴设计在纵向，长轴设计在环向，以减少开孔对壳体强度的影响。
第二章第三节内压薄壁容器的设计计算
液 压 试 验
试验 方法 夹 套 容 器 试 验温 度 t 试 验 压 力 按 表 试 液 一 用 水 需 时 用 会 致 生 险 其 液 验 体 般 ， 要 可 不 导 发 危 的 它 体
充 液时 将 容 器 内 空气 排尽 缓 慢 升 压 至 PT 保 压 30 分 钟 以 上 降 压 至 80% P T
考虑容器内部介质或周围大气腐蚀
td = pc Di + C2 t 2[σ ] ϕ − pc
式中： 设计厚度， 式中：td ——设计厚度，mm； 设计厚度 ； C2——腐蚀裕量，mm。 腐蚀裕量， 腐蚀裕量 。
名义厚度： 名义厚度：tn≥td+C1 厚度附加量 C = C1 + C2
td=t+C2
tn=td+C1+圆整值 圆整值
缓慢升压至 10%PT 且≤ 0.05MPa
保压 5 分钟 修
渗漏
合 格 合 格
缓慢升压至 50%PT
按 10% PT 的级差 逐级增压至 PT
渗漏
降压至 87%PT
必须用两只量程相同，经校正压力表 1.5PT≤量程≤4 PT
空压机
试压前通入 0.4~0.5Mpa 压缩空气检查焊接接头
介质的毒性程度为极高或高度的容器， 在压力试验合格后进行气密性试验
直立容器卧置试压时，此压力应计入容器立置时的液柱静压力。 直立容器卧置试压时，此压力应计入容器立置时的液柱静压力。
气压试验
pT ( Di + te ) σT = ≤ 0.8σ s (σ 0.2 ) 2teϕ
压力试验
按图样规定
气压试验
水压试验
优先选用 当不适合做液压试验的容器，如容器内不允许有微量残 留液体，或由于结构原因不能充满液体的容器，可采用 气压试验。
第三章内压薄壁容器的设计与计算(3)_化工设备
c i t c
计算值中的较大值。 K-系数，查表3-20；f-系数,
1 f 2r 1 cos Di 2 cos
t 0.5 pc
fpc Di
,其值列于表3-21。
—— 折边锥形封头小端厚度计算
当锥形封头半顶角
45
时，若采用小端无折边，其小端厚度与无折边锥形封
e n C n C1 C2
凸形封头强度计算和校核 半球形封头：
d
4 pc
t
pc Di
C2
适用范围： pc 0.6 t
椭圆和碟形封头：
Kp c Di 2 t 0 .5 pc
2 t e pw KDi 0.5 e
t
dc
p c Dc 1 C2 t 2 pc cos
（3-20）
充分考虑边缘应力的影响和自限性的特点，采用局部加强结构，并引
入与半顶角 、p / 的影响的应力增强系数Q，计算壁厚：
c
—— 封头大端与圆筒连接，确定连接处锥壳大端的厚度：
① 根据半顶角 及 缘处的加强；
径不等的圆筒，使气流均匀，如图3-6所示 。
结构与特点 锥形封头有两种结构形式，进行结构设计时需要分别考虑： 当锥形封头半顶角 30 ，可以选用无折边结构，如图3-7（a）所示； 当 30 ,应采用带有过渡段的折边结构，如图3-7（b）（c）所示。 —— 大端:若折边,过渡段的转角半径r应不小于封头大端内直径Di的10%，且 不小于该过渡段厚度的3倍； —— 小端：当半顶角 45 时，可以采用无折边结构；
pc /
t
，按图3-8（P75）判定是否需要在封头大端连接边
计算值中的较大值。 K-系数，查表3-20；f-系数,
1 f 2r 1 cos Di 2 cos
t 0.5 pc
fpc Di
,其值列于表3-21。
—— 折边锥形封头小端厚度计算
当锥形封头半顶角
45
时，若采用小端无折边，其小端厚度与无折边锥形封
e n C n C1 C2
凸形封头强度计算和校核 半球形封头：
d
4 pc
t
pc Di
C2
适用范围： pc 0.6 t
椭圆和碟形封头：
Kp c Di 2 t 0 .5 pc
2 t e pw KDi 0.5 e
t
dc
p c Dc 1 C2 t 2 pc cos
（3-20）
充分考虑边缘应力的影响和自限性的特点，采用局部加强结构，并引
入与半顶角 、p / 的影响的应力增强系数Q，计算壁厚：
c
—— 封头大端与圆筒连接，确定连接处锥壳大端的厚度：
① 根据半顶角 及 缘处的加强；
径不等的圆筒，使气流均匀，如图3-6所示 。
结构与特点 锥形封头有两种结构形式，进行结构设计时需要分别考虑： 当锥形封头半顶角 30 ，可以选用无折边结构，如图3-7（a）所示； 当 30 ,应采用带有过渡段的折边结构，如图3-7（b）（c）所示。 —— 大端:若折边,过渡段的转角半径r应不小于封头大端内直径Di的10%，且 不小于该过渡段厚度的3倍； —— 小端：当半顶角 45 时，可以采用无折边结构；
pc /
t
，按图3-8（P75）判定是否需要在封头大端连接边
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
2. 径向（轴向）应力： 圆筒形容器，当 起承受内压力作用后，筒体的“纵向纤 维”也要伸长，在筒体的横向截面内必 定也有应力产生，此应力称为径向应力 以表示σm。
二、内压圆筒的应力计算
1. 环向应力的计算公式 采用截面法，用一通过
圆筒轴线的假想截面B-B 将圆筒刨开,移走上半部， 再从下半个圆筒上截取 长度为L的一段筒体作为 脱离体，合力为Py。 建立静力平衡方程。 外力在y轴方向上投影的
m
PD 4S
(3-2)
P---内压，Mpa；
D---圆筒平均直径，亦称中径，mm;
S---壁厚，mm；
σm---轴向应力，Mpa。
对比（3-1）和（3-2)式，可 以看出：薄壁圆筒承受内压 时，其环向应力是轴向应力 的两倍。因此在设计过程中， 必须注意：如果需要在圆筒 上开设椭筒形孔时，应使椭 圆孔之短轴平行于筒体的轴 线（图3-5),以尽量减小纵截 面的削弱程度，从而使环向 应力增加少一些。
与介质内压合力Py相平衡的是作用在单 元体筒壁纵截面上的内力的合力Ny
显然
Ny=2Siσθ
Py=Ny
即
DiLP=2Siσθ
由此得
PD 2S
(3-1)
式中的DL是承压曲面在假想纵截面上的投影面 积。由此可得如下结论：作用在任一曲面上的 介质压力，其合力等于压办P与该曲面沿合力 方向所得投影面积的乘积，而与曲面形状无 关．由于承压不同的圆筒其壁厚与直径相比很 小，对于这类圆筒的受力分析均以中径（即平
（2）联接边缘区的变形与应力。所谓联 接边缘是指壳体与法兰、封头或不同厚 度、不同材料的筒节、群式支座与壳体 相联接的边缘等。圆筒形容器受内压时， 由于联接边缘区的刚性不同，连接处二 者的变形大小亦不同，如图所示。
二、边缘应力的特点
如图所示是一内径为Di=1000 mm，壁厚 S=10 mm的钢制内压圆筒，其一端为平 板封头，且封头厚度远远大于筒体壁厚。 内压为P＝1MPa。经理论计算和实测其 内、外壁轴向应力（薄膜应力与边缘弯 曲应力的叠加值）分布情况。
这个容器上的各部分应力分布是不相 同的，对于离开封头和平底盖稍远的圆 筒中段①处，受压前后经线仍近似保持 直线（图中虚线），故这部分只承受拉 应力，没有显著的弯曲应力；这里可以 忽略薄壁圆筒变形前后圆周方向曲率半 径变大所引起的弯曲应力。
在凸形封头、平底盖与筒体连接处② 和③，则因封头与平底盖的变形小于筒 体部分的变形，边缘连接处由于变形谐 调形成一种机械约束，从而导致在边缘 附近产生附加的弯曲应力。
均直径）为准，故上式可以写成：
1. 径向应力的计算公式 同样采用截面法，用一假想截面B-B
将圆筒刨开,移走右半部。 建立静力平衡方程。
外力作用在圆筒环形截面上的应力的合 力为：Nz
NPxz==πDSσDm2 P
4
由平衡条件得
Px-Nx=0
或
Px=Nx
即
D2P
4
=πDSσm
由此得：
三、对边缘应力的处理
由于边缘应力具有局部性，在设计中可以 在结构上只作局部处理。例如改变连接边缘的 结构，在边缘应力区进行局部加强；保证边缘 区内焊缝质量；降低边缘区的残余应力（进行 消除应力的热处理）；避免边缘区附加局部应 力或应力集中，如不在连接边缘区开孔等。
大多数塑性较好的材料制成的容器，除结 构上作某些处理外，一般并不对边缘应力作特 别处理。
由上述例子可以看到，边缘应力具有以 下两个特点：
尽管边缘应力有时相当大，但其作 用的范围是很小的。随着离开边缘处的 距离的增大，边缘应力则迅速衰减。且 壳壁越薄，衰减的越快，这一特征称为 边缘应力的局部性。
边缘应力的另一特性是自限性。发 生边缘弯曲的原因是由于薄膜变形不连 续而引起的。但是当边缘处的局部材料 发生屈服进人塑性变形阶段时，上述这 种弹性约束就开始缓解，因而原来不同 的薄膜变形便趋于谐调，结果边缘应力 就自动限制。边缘应力的这一特性决定 了它的危害性没有薄膜应力大。
m
P 2S
D
m
P 4S
D
同时从（3-1）和（3-2)式还可以看出， 筒体承受内压时，器壁内所产生的应力 是与圆筒的S/D成反比的，即 S/D越大， 应力越小。
例题3-1有一外径为D0=206 mm的压力 容器最小壁厚为S=6.0，材质为20Mn。 工作压力为10MPa，试求容器筒身壁内 的应力是多少？
在任何一个压力容器中，总是存在 这样两类不同性质的应力。前者称为薄 膜应力，可用简单的无力矩理论来计算； 后者称为边缘应力，要用比较复杂的有 力矩理论及变形谐调条件才能计算。
薄壁容器及其应力分析
1. 环向应力：圆筒形容器，当起承受内 压力作用后，其直径要稍微增大，故筒 壁内的“环向纤维”要伸长，因此在筒 体的纵截面上必定有应力产生，此应力 称为环向应力以表示σθ。
解：容器筒身平均直径为：
D=D0-S=206-6.0=200mm
m
PD 2S
= 10 200 4 6.0
=83.3 MPa
PD 2S
= 10 200 2 6.0
=166.6 MPa
第二节 内压圆筒边缘应力及其处理
一、边缘应力的概念
上述对典型圆筒壳体的应力分析是在将薄 壁内压圆筒简化成薄膜，忽略了两种变形与应 力，圆筒受内压作用直径要增大，而且它的曲 率半径由原来的R变到R+△R，根据力学可知， 有曲率变化就有弯曲应力。所以在内压圆筒壁 的纵向截面上，除作用有环向应力外，还存在 着弯曲应力。但由于这一应力数值相对很小， 可以忽略不计。
第三章 内压薄壁容器的设计
第一节 内压薄壁圆筒的应力分析
一、薄壁容器及其应力特点 压力容器按壁厚可分为薄壁容器和厚壁容器。
通常K=D0/Di ≤1.2的称为薄壁容器，超过这一 范围的为厚壁容器。D0为外径,Di为内径。 化工与石油化学工业中，应用最多的是薄壁 容器。对压力容器各部分进行应力分析，是强 度设计中首先需要解决的问题。