14.3.2 第2课时 运用完全平方公式因式分解.pptx
合集下载
运用完全平方公式因式分解 优秀课件

化为非负数的和的形式,然后利用非负数性 质解答问题.
例6 已知a,b,c分别是△ABC三边的长,且 a2+2b2+c2-2b(a+c)=0,请判断△ABC的形 状,并说明理由. 解:由a2+2b2+c2-2b(a+c)=0,得
a2-2ab+b2+b2-2bc+c2=0,
即(a-b)2+(b-c)2=0, ∴a-b=0,b-c=0, ∴a=b=c, ∴△ABC是等边三角形.
a a² a
ab a ab a b²b
b
b
b
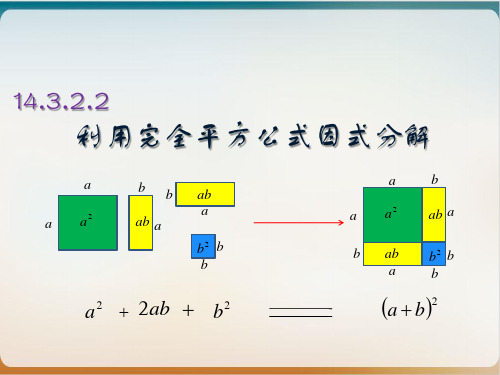
拼出图形为:
b ab b² 大正方形的面积可以怎么求?
(a+b)2 = a2+2ab+b2
a a² ab
上面的等式反过来看,能
a
b 得到:
a2+2ab+b2 = (a+b)2
我们把a²+2ab+b²和a²-2ab+b²这样的式子叫
作完全平方式.
观察这两个式子:
简记口诀:
首平方,尾平方,首尾两倍在中央.
凡具备这些特点的三项式,就是完全平方式, 将它写成完全平方形式,便实现了因式分解.
a2 ±2ab
首2 ±2× 首×尾
+b2
两个数的平方和加 =(a ± b)² 上(或减去)这两个
+尾2 (首±尾)2 数的积的2倍,等 于这两个数的和(或
差)的平方.
对照 a²±2ab+b²=(a±b)²,填空:
当堂练习
1.下列四个多项式中,能因式分解的是( )
A.a2+1
B.a2-6a+9
C.x2+5y D.x2-5y
2.多项式4x2y-4xy2-x3分解因式的结果是( ) A.4xy(x-y)-x3 B.-x(x-2y)2 C.x(4xy-4y2-x2) D.-x(-4xy+4y2+x2)
例6 已知a,b,c分别是△ABC三边的长,且 a2+2b2+c2-2b(a+c)=0,请判断△ABC的形 状,并说明理由. 解:由a2+2b2+c2-2b(a+c)=0,得
a2-2ab+b2+b2-2bc+c2=0,
即(a-b)2+(b-c)2=0, ∴a-b=0,b-c=0, ∴a=b=c, ∴△ABC是等边三角形.
a a² a
ab a ab a b²b
b
b
b
拼出图形为:
b ab b² 大正方形的面积可以怎么求?
(a+b)2 = a2+2ab+b2
a a² ab
上面的等式反过来看,能
a
b 得到:
a2+2ab+b2 = (a+b)2
我们把a²+2ab+b²和a²-2ab+b²这样的式子叫
作完全平方式.
观察这两个式子:
简记口诀:
首平方,尾平方,首尾两倍在中央.
凡具备这些特点的三项式,就是完全平方式, 将它写成完全平方形式,便实现了因式分解.
a2 ±2ab
首2 ±2× 首×尾
+b2
两个数的平方和加 =(a ± b)² 上(或减去)这两个
+尾2 (首±尾)2 数的积的2倍,等 于这两个数的和(或
差)的平方.
对照 a²±2ab+b²=(a±b)²,填空:
当堂练习
1.下列四个多项式中,能因式分解的是( )
A.a2+1
B.a2-6a+9
C.x2+5y D.x2-5y
2.多项式4x2y-4xy2-x3分解因式的结果是( ) A.4xy(x-y)-x3 B.-x(x-2y)2 C.x(4xy-4y2-x2) D.-x(-4xy+4y2+x2)
初中数学《完全平方公式》优秀课件北师大版2
a2 2• a •bb2
(1)、解:16x2 24x 9
方法:当一个式子满足完全
(4x)2 2 4x 3 32
平方式的所有特征时,可直 接分解因式。结果为这两平
4x 32
方项底数和或差的平方,是
和是差看中间项的符号
分析:- x2 4xy 4 y2 - x2 2 • x • 2 y 2 y2
• 学习重点:
运用完全平方公式分解因式.
学习难点:综合运用提公因式和公式法分解
因式
复习引入
问题一:大家还记得什么是因式分解吗?
因式分解就是将一个多项式化成几个整式的 积的形式
即: 和
积
问题二:我们已经学习了分解因式的哪
些方法?
1、提公因式法 2、公式法
平方差公式 a2 b2 a ba b
即:两个数的平方差等于 这两个数的和与差的积
方法:若式子有整体满足完全平方 式可直接进行因式分解,需注意中 间项的符号
练习2 将下列多项式分解因式:
1 25a3 ax2 10a2x
2 12x3 12x2 2 y 1- 3x2y -12
答案:
1 a5a x2
a b2 b a2
2 - 3x2 y 1 2x2
或 - 32x 2 y 12
你对因式分解的方法有什么新的发现?请尝试概括 你的发现.
把整式的乘法公式——完全平方公式 倒过来 就得到因式分解的完全平 方公式:
a2 2ab+b2 =(a b)2
首2 2 首 尾 尾2 首 尾2
即两个数的平方和加上(或减去)这两个 数的积的2倍,等于这两个数的和(或差) 的平方
1、在下面括号ቤተ መጻሕፍቲ ባይዱ填空
14.3.2.2 利用完全平方公式因式分解
14.3.2公式法-完全平方公式法 课件人教版数学八年级上册

5.如果x2+mxy+9y2是一个完全平方式,那么m的值为( B ) A.6 B.±6 C.3 D.±3
6.已知a、b、c是三角形的三边,请你判断a2-b2-c2-2bc的值的正负.
7.说明无论a、b为何值,代数(a+b)²+2(a+b)+5 的值均为正值.
8.若a+b=1,a+c=2,b+c=3,利用因式分解求值: a2+b2+c2+ab+ac+bc.
自 学 检 查
1.下列各式是不是完全平方式?
(1)a2-ab+b2 × (2)a2-4a+4 =a2 -4a +22 √ (3)x2+4xy+4y2=x2+4xy + (2y)2√ (4)x2-6x-9 =x2-6x-32 ×
2.按照完全平方公式填空:
(1)a2-10a+( 25 )=( a-5 )2
(4)原式=(2x +y-3) 2
总结:①因式分解的一般思路: 一提(提公因式法) 二套(套用公式法)
②整体思想,例如:把 2x+y 看做一个整体。
巩固练习
1.(1)若x2+2kx+9是一个完全平方式,则k= ___±___3__ (2)若x2+8x+k2是一个完全平方式,则k= __±___4___.
( (23))1(a2-y2()+r2s)a+yr+21s2==((
ay+1)2
½ - rs)2
4
自 3.把下列各式因式分解 1 x2 12x 36 2 2xy x2 y2
学 (3) 3ax2﹢6axy﹢3ay2
检 查
人教版八年级数学上册课件:14.3.2因式分解(公式法-平方差公式)

--因式分解的平方差公式
你学了什么方法进行分解因式?
把下列各式因式分解:
(1) ax - ay = a( x – y ) (2) 9a2 - 6ab+3a =3a(a-2b+1) (3) 3a(a+b)-5(a+b) =(a+b)(3a - 5) (4) ax2 - a3 =a(x2-a2) =a(x+a)(x-a) (5) 2xy2 - 50x =2x(y2-25) =2x(y+5)(y - 5)
个整体,加括号
熟记公式 a2 b2 (a b)(a b)
把下列式子分解因式
(x p)2 (x q)2
a² - b²= ( a + b)( a - b )
(1)a2-1
=( a )2-( 1 )2
(2)x4y2-4
=( x2y )2-( 2 )2
(3) 9 x2-0.01y2
49
=( 3
=(x+2)(x-2) =(3+y)(3-y)
(3) 1-a2
(4) 4x2-y2
=(1+a)(1-a) =(2x+y)(2x-y)
把下列各式分解因式
(1) 1-25x2
解: 1-25x2
=12-(5x)2
把两项写成平方的形式,
=(1+5x)(1-5x) 找出a和b。底数既有数
字还有字母,需要看成一
7
x )2-( 0.1y )2
(4)0.0001-121x2源自=( 0.01 )2-( 11x )2
因式分解:
1、 – a4 + 16 2、 4(a+2)2 - 9(a - 1)2 3、 (x+y+z)2 - (x-y-z)2
你学了什么方法进行分解因式?
把下列各式因式分解:
(1) ax - ay = a( x – y ) (2) 9a2 - 6ab+3a =3a(a-2b+1) (3) 3a(a+b)-5(a+b) =(a+b)(3a - 5) (4) ax2 - a3 =a(x2-a2) =a(x+a)(x-a) (5) 2xy2 - 50x =2x(y2-25) =2x(y+5)(y - 5)
个整体,加括号
熟记公式 a2 b2 (a b)(a b)
把下列式子分解因式
(x p)2 (x q)2
a² - b²= ( a + b)( a - b )
(1)a2-1
=( a )2-( 1 )2
(2)x4y2-4
=( x2y )2-( 2 )2
(3) 9 x2-0.01y2
49
=( 3
=(x+2)(x-2) =(3+y)(3-y)
(3) 1-a2
(4) 4x2-y2
=(1+a)(1-a) =(2x+y)(2x-y)
把下列各式分解因式
(1) 1-25x2
解: 1-25x2
=12-(5x)2
把两项写成平方的形式,
=(1+5x)(1-5x) 找出a和b。底数既有数
字还有字母,需要看成一
7
x )2-( 0.1y )2
(4)0.0001-121x2源自=( 0.01 )2-( 11x )2
因式分解:
1、 – a4 + 16 2、 4(a+2)2 - 9(a - 1)2 3、 (x+y+z)2 - (x-y-z)2
利用完全平方公式进行因式分解ppt课件

④ 4x2 – 8xy + 4y2 = 4 (x2–2xy+y2) = 4 (x–y)2
例3 把下列完全平方式因式分解。
(1)x2+14x+49; (2)(m+n)2-6(m+n)+9.
例4 把下列各式因式分解。
(1)3ax2+6axy+3ay2; (2)-x2-4y2+4xy。
补例 把9x2 3x 1 因式分解
试计算:9992 + 2×1999998×1 + 1 = (999+1)2 = 106
就像平方差公式一样,完全平方公式也可 以逆用,从而进行一些简便计算与因式分解。 即:
a 2 2 a b b 2 a b 2
a 2 2 a b b 2 a b 2
这个公式可以用文字表述为:
两个数的平方和加上(或减去)这两个数的 积的两倍,等于这两个数的和(或差)的平方。
a 2 2 a b b 2 a b 2
牛刀小试(对下列各式因式分解):
① a2+6a+9 = _______(a_+__3)_2______ ② n2–10n+25 = ____(n_–_5_)_2_______ ③ 4t2–8t+4 = _____4_(t_–_1_)_2 _______ ④ 4x2–12xy+9y2 = _(_2_x_–_3_y_)2______
形如a2±2ab+b2的式子称为完全平方式。
① 16x2 + 24x + 9
② – 4x2 + 4xy – y2 ③ x2 + 2x – 1
完全平方式
④ 4x2 – 8xy + 4y2 ⑤ 1 – 2a2 + a4 ⑥ (p+q)2 – 12(p+q) + 36
14.3.2因式分解完全平方公式课件八年级数学人教版上册

a
b
探究新知 理解新知 经典例题 归纳总结 巩固提升 小结回顾
利用公式把某些具有特殊 形式(如平方差式,完全平 方式等)的多项式分解因式, 这种分解因式的方法叫做 公式法因式分解.
探究新知 理解新知 经典例题 归纳总结 巩固提升 小结回顾
判断下列各式是完全平方式吗?
a2 4a 22 (a 2)2
探究新知 理解新知 经典例题 归纳总结 巩固提升 小结回顾
例4 计算:
(1) 1002–2×100×99+99²;
解:(1)原式=(100–99)² =1.
(2) 342+34×32+162.
(2)原式=(34+16)2 =2500.
利用完全平方 公式分解因式, 可以简化计算.
探究新知 理解新知 经典例题 归纳总结 巩固提升 小结回顾
2a(x y)2
先纳总结 巩固提升 小结回顾
例2 因式分解
(2) 16a4 8a2b2 b4 解:原式 (4a2 )2 2 4a2 b2 (b2 )2
(4a2 b2 )2 [(2a b)(2a b)]2 (2a b)2 (2a b)2
因式分解 步骤方法
先提公因式→一提 再用公式→二用 继续分解→三查
例2 因式分解
(5) ( p 1)( p 4) p 解:原式 p2 4 p p 4 p
p2 4p 4 ( p 2)2
无提无公式, 展开合并 再观察。
探究新知 理解新知 经典例题 归纳总结 巩固提升 小结回顾
例3 已知: a2+b2+2a–4b+5=0,求 2a2+4b–3的值.
解:∵a2+b2+2a–4b+5=0
∴ 2a2+4b–3
14.3.2公式法 课件 2024—2025学年人教版数学八年级上册
13.在括号内填上适当的数,使之能用完全平方公式进行因式分解.
(1)x2 ( )xy+25y2; (2) 9a2 36ab ( ) .
14.已知a,b,c为三角形的三边,且a2 b2 c2 ab bc ac 0
判断此三角形的形状.
15.证明:无论a,b为何值,a2 b2 6a 10b 40 的值都大于0.
(1)a2b2 10ab 25;
(2) 16m2 40mn 25n2 ;
(3) x2 y2 8xy3 16 y4;
(4) x4 6x2 y2 9 y4 ;
(5) (m n)2 8(m n) 16 ; (6) (x y)2 4xy ;
(7) x2 4x 4;
(8) m2 12m 36 ;
16.若x 2z 3y,求 x2 9 y2 4z2 4xz 的值.
(3) x2 2x 1 ;
(6) 1 x2 x 1; 4
(9) a2 1 ab 1 b2 ; 24
(12) a2b2 6ab 9
2.把下列各式分解因式:
(1)a2 12a 36; (3) 9x2 12xy 4 y2 ; (5) 3x2 6xy 3y2; (7)(a b)2 6(a b) 9; (9) x4 2x2 1 ;
把(a-b)看作一个整体,这个多项式恰好是
(a-b)与5的平方,及(a-b)与5的乘积的2
倍,这样就可以利用完全平方公式分解因式了.
解:(1)m2 10mn 25n2 (m)2 2 (m)(5n) (5n)2 (m 5n)2
(3)(a b)2 1(0 a b) 25 (a b)2 2 5(a b) 52 (a b 5)2
(4)
x2 4x
2
8
x2 4x
(1)x2 ( )xy+25y2; (2) 9a2 36ab ( ) .
14.已知a,b,c为三角形的三边,且a2 b2 c2 ab bc ac 0
判断此三角形的形状.
15.证明:无论a,b为何值,a2 b2 6a 10b 40 的值都大于0.
(1)a2b2 10ab 25;
(2) 16m2 40mn 25n2 ;
(3) x2 y2 8xy3 16 y4;
(4) x4 6x2 y2 9 y4 ;
(5) (m n)2 8(m n) 16 ; (6) (x y)2 4xy ;
(7) x2 4x 4;
(8) m2 12m 36 ;
16.若x 2z 3y,求 x2 9 y2 4z2 4xz 的值.
(3) x2 2x 1 ;
(6) 1 x2 x 1; 4
(9) a2 1 ab 1 b2 ; 24
(12) a2b2 6ab 9
2.把下列各式分解因式:
(1)a2 12a 36; (3) 9x2 12xy 4 y2 ; (5) 3x2 6xy 3y2; (7)(a b)2 6(a b) 9; (9) x4 2x2 1 ;
把(a-b)看作一个整体,这个多项式恰好是
(a-b)与5的平方,及(a-b)与5的乘积的2
倍,这样就可以利用完全平方公式分解因式了.
解:(1)m2 10mn 25n2 (m)2 2 (m)(5n) (5n)2 (m 5n)2
(3)(a b)2 1(0 a b) 25 (a b)2 2 5(a b) 52 (a b 5)2
(4)
x2 4x
2
8
x2 4x
运用完全平方公式分解因式精选教学PPT课件
=(x+2)2+(y-1)2=0得
x+2=0,y-1=0
∴x=-2,y=1
∴x-y=(-2)-1= 1 2
分解因式:
1. x2 8x 16 =-(x+4)2
2. 4x2 x y2 4xx y =(3x+y)2
3. ax2 2a2 x a3 =a(x+a)2
3(a b) 2(a b)2
(5a b)2
因式分解:
(y2 + x2 )2 - 4x2y2
解: 原式 ( y2 x2 2xy)(y2 x2 2xy)
=(y+x)2(y-x)2
简便计算: 562 68 56 342
解:原式=(56+34)2=902=8100
= 3 2(a b)2
=(3-2a+2b)2
分解因式:
(1)x2-12xy+36y2 =(x-6y)2 (2)16a4+24a2b2+9b4 =(4a2+3b2)2 (3)-2xy-x2-y2 =-(x+y)2 (4)4-12(x-y)+9(x-y)2=(2-3x+3y)2
总结与反思:
课前复习:1、分解因式学了哪些方法
提取公因式法:ma+mb+mc=m(a+b+c) 运用公式法: ① a2-b2=(a+b)(a-b)
练习 把下列各式分解因式
① ax4 ax2
② x4-16
解:原式=ax2(x2-1)
解:原式=(x2+4)(x2-4)
=ax2(x+1)(x-1)
=(x2 +4)(x+2)(x-2)
x+2=0,y-1=0
∴x=-2,y=1
∴x-y=(-2)-1= 1 2
分解因式:
1. x2 8x 16 =-(x+4)2
2. 4x2 x y2 4xx y =(3x+y)2
3. ax2 2a2 x a3 =a(x+a)2
3(a b) 2(a b)2
(5a b)2
因式分解:
(y2 + x2 )2 - 4x2y2
解: 原式 ( y2 x2 2xy)(y2 x2 2xy)
=(y+x)2(y-x)2
简便计算: 562 68 56 342
解:原式=(56+34)2=902=8100
= 3 2(a b)2
=(3-2a+2b)2
分解因式:
(1)x2-12xy+36y2 =(x-6y)2 (2)16a4+24a2b2+9b4 =(4a2+3b2)2 (3)-2xy-x2-y2 =-(x+y)2 (4)4-12(x-y)+9(x-y)2=(2-3x+3y)2
总结与反思:
课前复习:1、分解因式学了哪些方法
提取公因式法:ma+mb+mc=m(a+b+c) 运用公式法: ① a2-b2=(a+b)(a-b)
练习 把下列各式分解因式
① ax4 ax2
② x4-16
解:原式=ax2(x2-1)
解:原式=(x2+4)(x2-4)
=ax2(x+1)(x-1)
=(x2 +4)(x+2)(x-2)
14.3.2公式法_因式分解(完全平方公式)
a 2ab b a 2ab b
2 2
2
2
完全平方式的特点: 1、必须是三项式 2、有两个“项”的平方 3、有这两“项”的2倍或-2倍
2 2 首 2首尾 尾
判别下列各式是不是完全平方式
1x 2 xy y 2 2 2A 2 AB B 2 2 3甲 2 甲乙 乙 2 2 4 2
a 2ab b a b
2 2
2
a 2ab b a b
2 2
2
这两个多项式有什么特征?
2 2 2 2 a +2ab+b 与a -2ab+b
这两个多项式是两个数的平方和加上(或 减去)这两个数的积的2倍,这恰是两个 数和或差的平方。
我们把 2 2 和 2 2 a +2ab+b a -2ab+b 这样的式子叫做完全平方式。
1. 因式分解:9x2-y2-4y-4=_____. 2 2 【解析】9x -y -4y-4
= 9x2-(y2+4y+4) = 答案: 2. 分解因式:2a2–4a+2 2 【解析】 2a – 4a+2 = 2(a 2 – 2a +1) = 2(a – 1) 2
需要我们掌握: 1:如何用符号表示完全平方公式?
(1) (2) 1 6 a 4 + 2 4 a 2 b 2 + 9 b 4 2 2 解:(1)x - 12xy+36y 2 2 = x -2· x· 6y+ ( 6y ) = ( x - 6y ) 2 ( 2 ) 16a 4 +24a 2 b 2 +9b 4
2. 因式分解.
2 2 x - 12xy+36y
运用完全平方公式因式分解课件.ppt
a2 2ab b.2
探究新知 完全平方式与完全平方公式 (1)完全平方式: 乘法公式(a+b)2和(a-b)2结果 a2+2ab+b2 ,a2-2ab+b2 把a2+2ab+b2和a2-2ab+b2这样的式子叫做完全平方式.
a2+2ab+b2 =(a+b)2, a2-2ab+b2=(a-b)2
=(m2+n2)(m2-n2) =(m2+n2)(m+n)(m-n) (4)ab(x-y)3+ab3(y-x) = ab(x-y)3-ab3(x-y) = ab(x-y)[(x-y)2-b2]
= ab(x-y)(x-y+b)(x-y-b)
3.填空: (1)(a+b)2=
a2
2ab b;2 (2)(a-b)2=
14.3 因式分解
第2课时 运用完全平方公式因式分解
1.理解完全平方公式的特点. 2.会应用完全平方公式进行因式分解,发展学生的推 理能力 . 3.能灵活应用提公因式、完全平方公式分解因式。
重点 用完全平方公式分解因式. 难点 领会因式分解的解题步骤和分解因式的彻底性.
1.叙述平方差公式,并写出公式.
-(a+2b)2
-(5x+3y)2
例 2 分解因式: (1)3ax2+6axy+3ay2;(2)(a+b)2-12(a+b)+36.
解:(1)3ax2+6axy+3ay2; =3a(x2+2xy+y2) =3a(x+y)2
(2)(a+b)2-12(a+b)+36. =(a+b)2-2×(a+b)×6+62 =(a+b-6)2
(2) m4-16;
(m2+4)(m+2)(m-2)
(3)(x+2)(x+4)+x2-4.
