天津大学2007年硕士研究生运筹学入学考试试题答案
2007天大录取
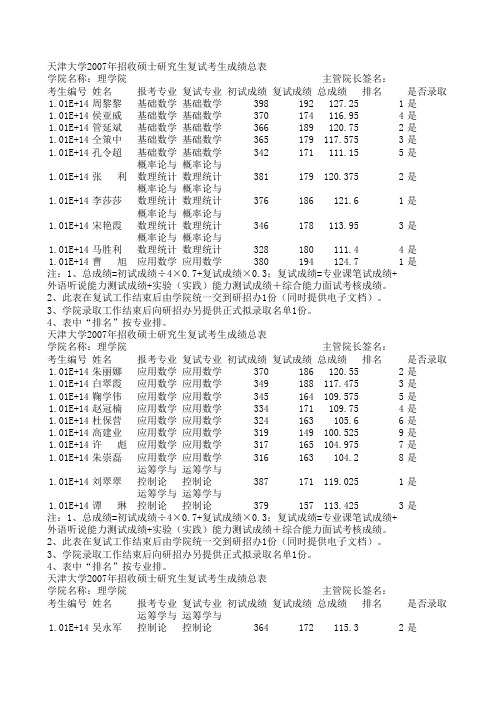
考生编号姓名报考专业复试专业初试成绩复试成绩总成绩排名是否录取1.01E+14周黎黎基础数学基础数学398192127.251是1.01E+14侯亚威基础数学基础数学370174116.954是1.01E+14管延斌基础数学基础数学366189120.752是1.01E+14仝策中基础数学基础数学365179117.5753是1.01E+14孔令超基础数学基础数学342171111.155是1.01E+14张 利概率论与数理统计概率论与数理统计381179120.3752是1.01E+14李莎莎概率论与数理统计概率论与数理统计376186121.61是1.01E+14宋艳霞概率论与数理统计概率论与数理统计346178113.953是1.01E+14马胜利概率论与数理统计概率论与数理统计328180111.44是1.01E+14曹 旭应用数学应用数学380194124.71是考生编号姓名报考专业复试专业初试成绩复试成绩总成绩排名是否录取1.01E+14朱丽娜应用数学应用数学370186120.552是1.01E+14白翠霞应用数学应用数学349188117.4753是1.01E+14鞠学伟应用数学应用数学345164109.5755是1.01E+14赵冠楠应用数学应用数学334171109.754是1.01E+14杜保营应用数学应用数学324163105.66是1.01E+14高建业应用数学应用数学319149100.5259是1.01E+14许 彪应用数学应用数学317165104.9757是1.01E+14朱崇磊应用数学应用数学316163104.28是1.01E+14刘翠翠运筹学与控制论运筹学与控制论387171119.0251是1.01E+14谭 琳运筹学与控制论运筹学与控制论379157113.4253是考生编号姓名报考专业复试专业初试成绩复试成绩总成绩排名是否录取1.01E+14吴永军运筹学与控制论运筹学与控制论364172115.32是3、学院录取工作结束后向研招办另提供正式拟录取名单1份。
天大运筹学考研历年试题分类

(一)选择填空题型):(1)初表的出基变量为,进基变量为。
[]=-1*)2(B 最优基逆(3)填完终表。
=*)4(X 最优解=*)5(y 对偶问题最优解(6)若原问题增加一个新的非负变量,则对偶问题的最优目标值将(变大、不变、变小)。
(2007) 1.用图解法解线性规划时,以下几种情况中不可能出现的是( )。
A .可行域(约束集合)有界,无有限最优解(或称无解界)B .可行域(约束集合)无界,有唯一最优解C .可行域(约束集合)是空集,无可行解D .可行域(约束集合)有界,有多重最优解 (2006)2.根据线性规划的互补松弛定理,安排生产的产品机会成本一定( )利润。
A . 小于 B . 等于 C . 大于 D . 大于等于 (2006)1.用大M 法求解Max 型线形规划时,人工变量在目标函数中的系数均为____________,若最优解的_______________中含有人工变量,则原问题无解。
(2005)1. 设线性规划问题}{0max ≥=bx Ax cx 有最优解*x 和影子价格*y ,则线性规划问题}{02max ≥=bx Ax cx 的最优解= ,影子价格=。
(2004)3. 某工程公司拟从1、2、3、4四个项目中选择若干项目。
若令4101⋯⋯=⎩⎨⎧=,,个项目未选中,第个项目被选中,第i i i x i请用i x 的线性表达式表示下列要求:(1)若项目2被选中,则项目4不能被选中: (2)只有项目1被选中,项目3才能被选中:。
(2004)一、简答(18%)(1)请简述影子价格的定义。
(2)在使用单纯型表求解型线性规划时,资源的影子价格在单纯型表的什么位置上? (3)写出影子价格的数学表达式并用其定义加以验证 (4)试述运输问题中检验数的经济意义(2003)线性规划原问题中约束的个数与其对偶问题中的个数相等。
若原问题第j 个约束为等式,则对偶问题第j 个自由。
(2002)1. 设线性规划问题max:{cx|Ax ≤bx ≥0}有最优解,且最优解值z>0;如果c 和b 分别被v>1所乘,则改变后的问题(也有、不一定有)最优解;若有最优解,其最优解(大于、小于、等于)z 。
运筹学考试练习题(天津大学)

07级工管运筹学期末习题课一、考虑线性规划问题〔P max 0z CXAX bX ==⎧⎨≥⎩(1) 若12,X X 均为〔P 的可行解,[0,1]λ∈,证明12(1)X X λλ+-也是〔P 的可行解;(2) 写出〔P 的对偶模型〔仍用矩阵式表示。
二、有三个线性规划:<Ⅰ> [Min] z =CX <Ⅱ> [Min] z '=C 'X <Ⅲ> [Min] z =CX 约束条件AX =b 约束条件AX =b 约束条件AX =b X ≥0 X ≥0 X ≥0已知X *是<Ⅰ>的最优解,X '*是<Ⅱ>的最优解,X *是<Ⅲ>的最优解,Y *是<Ⅰ>的对偶问题的最优解,试证:〔1()()'-'-≤**C C X X 0; <2> C X X Y b b ()()***-≤-。
三、已知线性规划问题当1t =2t =0时,用单纯形法求得最终表如下:要求:1. 确定23222113*********,,,,,,,,,,a a a a a a b b c c c 的值;2. 当2t =0时,1t 在什么围变化上述最优解不变;3. 当1t =0时,2t 在什么围变化上述最优基不变。
四、某公司准备以甲、乙、丙三种原料生产A 、B 、C 、D 四种型号的产品,每一单位产品对各原料的消耗系数、价格系数及原料成本等已知条件如下表:1x 2x 3x 4x 5x3x 5/20 1/2 1 1/2 0 1x 5/2 1 -1/2 0 -1/6 1/3 j j z c --4-4-21.为解决"在现有原料量限制下,如何安排A、B、C、D四种产品的产量,使总利润〔这里利润简化为销售收入与原料成本之差最大"这一问题,可建立一线性规划模型,令x1、x2、x3、x4依次表示各型号产品的计划产量,试列出这个模型,并记该模型为模型1;2.利用一解线性规划的程序解上述问题〔模型1,得到的部分结果如下:OBJECTIVE FUNCTION V ALUE1> 19923.08V ARIABLEV ALUE REDUCED COSTX1 230.769226 0.000000X2 100.000000 0.000000X3 1238.461548 0.000000X4 0.000000 4.384615ROW SLACK OR SURPLUSDUAL PRICES2> 0.000000 1.3846153> 0.000000 1.2307694> 0.000000 4.000000RANGES IN WHICH THE BASIS IS UNCHANGEDRIGHTHANDSIDERANGESROW CURRENT ALLOWABLE ALLOWABLERHS INCREASEDECREASE2 5500.000000 1499.999878 4025.0000003 3500.000000 500.000000 749.9999394 2000.000000 6192.307617 250.000000根据以上计算结果,分析并回答以下问题:〔1最优生产方案和最大总利润是什么?按此方案生产,现有的原料是否还有剩余?哪一种有剩余?余多少?〔2如果市场上甲原料的价格为4.5〔百元/公斤,那么从市场上购得1000公斤的甲原料扩大生产是否合算〔即总利润是否增加?为什么?〔3若D产品的价格系数增大到34〔百元/公斤,原最优解会否发生变化?为什么?〔4在原考虑的A、B、C、D四种型号产品基础上,如果又提出产品E,它对甲、乙、丙的消耗系数分别为5、6、2,价格系数为74〔百元/公斤,那么原最优方案是否要改变,为什么?〔5若在本题已有已知条件基础上,还要考虑各产品的生产准备费用〔视为固定成本,其中A产品的生产准备费为1000〔百元,B产品的生产准备费为800〔百元,C产品的生产准备费为950〔百元,D产品的生产准备费为750〔百元,而且由于某些原因,A、B、C三种产品至多生产其中的两种。
天大2000年运筹学硕士研究生入学考试试题答案

天津大学研究生院2000年招收硕士生入学试题答案考试科目:运筹学基础 一、 填空(36%)1. 线性规划单纯形算法的基本步骤是:(1) (2)(3) 每次迭代保持解的 ,改善解值的 。
对偶单纯形法每次迭代保持解的 ,改善解值的 。
解:确定一个初始基可行解;检验一个基可行解是否为最优解;寻找一个更好基可行解;可行性;最优性。
2. 设有线性规划问题[]{}0,|,min ≥==∈=X b AX X R X CX f ,有一可行基B (为A中的前m 列),记相应基变量为πX ,价格系数为C B ,相应于非基变量为X N ,价格系数为C N ,则相应于B 的基本可行解为X= ;用非基变量来表示基变量的表达式为X B = ;用非基变量表示目标函数的表达式为f= ,B 为最优基的条件是 。
解:111111,,(),00N B N B N N B B b B b B NX C B b C C B N X C C B N ------⎛⎫-+--≥ ⎪⎝⎭3. 线性规划(Min 型)问题有多重最优解时,其最优单纯形表上的特征为: 解:0,0.j k j x σσ≥=所有检验数而某一个非基变量检验数4. 用表上作业法求解m 个发点和n 个收点的平衡运输问题,其方案表上有数格的个数为 ,空格的个数为 ;若从检验数为-2的某空格调整,调量为2,则调后可使总运费下降 。
解:m+n-1, (m-1)(n-1), 4.5. 目标规划模型的特点是引入了 变量,模型的目标函数是这些变量的极(大还是小)化,模型的约束中也含有用这种变量表示的 约束。
解:偏差变量;极小;目标(软).6. 某足球队要从1,2,3,4,5号五名队员中挑选若干名上场。
令⎩⎨⎧=54321i i 0i 1,,,,=号不上场,第号上场第i x请用x i 的线性表达式表示下列要求:(1)从1,2,3中至多选2名: (2)如果2号和3号都上场,则5号不上场: (3)只有4号上场,1号才上场: 解:12345142,0, 1.x x x x x x x ++≥-≥+≤7. 请在下图所示的最短路问题求解过程中进行一步:下一步给 节点标号,标号为 。
天大离线《运筹学》五组全答案

运筹学
要求:
一、独立完成,下面已将五组题目列出,请按照学院平台指定
..的做题组数作答,
每人只答一组题目
....,满分100分;
........,多答无效
平台查看做题组数操作:学生登录学院平台→系统登录→学生登录→课程考试→离线考核→离线考核课程查看→做题组数,显示的数字为此次离线考核所应做哪一组题的标识;
例如:“做题组数”标为1,代表学生应作答“第一组”试题;
二、答题步骤:
1.使用A4纸打印学院指定答题纸(答题纸请详见附件);
2.在答题纸上使用黑色水笔
..作答;答题纸上全部信息要求手
....按题目要求手写
写,包括学号、姓名等基本信息和答题内容,请写明题型、题号;
三、提交方式:请将作答完成后的整页答题纸以图片形式依次粘贴在一个
....
.......Word
文档中
...上传(只粘贴部分内容的图片不给分),图片请保持正向、清晰;
1.上传文件命名为“中心-学号-姓名-科目.doc”
2.文件容量大小:不得超过20MB。
提示:未按要求作答题目的作业及雷同作业,成绩以
..!
....................0.分记
题目如下:
第一组:
计算题(每小题25分,共100分)
1、某企业生产三种产品A1、A
2、A3。
每种产品在销售时可能出现销路好(S1),销路一般(S2)
和销路差(S3)三种状态,每种产品在不同销售状态的获利情况(效益值)如表1所示,请按乐观法则进行决策,选取生产哪种产品最为合适。
天津大学研究生运筹学B试题

天津大学研究生运筹学B 试题学院年级_________________ 姓名____________ 学号_____________ 成绩__________一、填空(25%)1. 无约束优化方法中下降类算法的一般步骤为__________________________________ ________________________________________________________________________________________________________________________。
无约束极值问题的DFP 法中每次的搜索方向P k =_____________________________________。
2. 一维搜索中黄金分割(0.618)法的基本思想是逐次缩小含_____________的区间,每次缩小所得区间长与上次区间长之比是_____________。
3.二次规划模型的一般形式(矩阵式)是__________________________________;它可用K -T 条件求解的条件是_____________________________________;可用K -T 条件求解时相应的线性规划模型(矩阵式)是:__________________________________________。
4. 多目标优化问题有效解(非劣解)的定义是:______________________________________________________________________________________。
))(,),((min 1x f x f V p Dx ∈−5.记多目标优化问题绝对最优解集为,有效解集为,弱有效解集为,单目标的最优解集为,若≠))(,),((min 1x f x f V p Dx ∈−*abR*paR*wpRif *iR*abRΦ,则上述4种解之间的关系是:_________________________________________________________________________。
天大2002年运筹学硕士研究生入学考试试题
天津大学研究生院2002年招收硕士生入学试题考试科目:运筹学基础 一、填空(20%)1. 线性规划原问题中约束的个数与其对偶问题中的 变量 个数相等。
若原问题第j 个约束为等式,则对偶问题第j 个 变量 自由。
2. 设线性规划问题max:{cx|Ax ≤bx ≥0}有最优解,且最优解值z>0;如果c 和b 分别被v>1所乘,则改变后的问题 也有 (也有、不一定有)最优解;若有最优解,其最优解 大于 (大于、小于、等于)z 。
3. 目标规划模型的一个主要特点是引入了偏差变量,模型的目标就是这些变量的极 小(大还是小化),模型的约束中也要包括用这些变量表示的目标约束。
4. 无权的连通图称为树。
求出右图网络的最小部分树(用粗线在图上标出),最小权和为 16 。
5. 网络计划方法中关键路径法的实质是求网络图中耗时最 长 (长、短)的路径。
6. 货船按泊松流到达某港口,平均到达率为每天50条,平均卸货率为μ。
又知船在港口停泊一天的费用为1货币单位,平均卸货费为2μ货币单位,则使总费用最少的平均卸货率μ*= 条/天。
7. 矩阵对策的研究对象是 对策问题。
它在纯策略意义下有解的充要条件是:该解是 点;如果它在纯策略意义下无解,则它在 意义下必有解。
二、(17%)已知线性规划问题max z = (c 1+t 1) x 1 + c 2x 2 + c 3x 3 + 0x 4 + 0x 5⎪⎩⎪⎨⎧⋯=≥+=++++=+++)51(03..225323222112214313212111,,j x t b x x a x a x a t b x x a x a x a t s j当t 1=t 2=0时,用单纯形法求得最终表如下:X 1 X 2 X 3 X 4 X 5 X 3 5/2 01/2 1 1/2 0 X 1 5/2 1 -1/2 0 -1/6 1/3 C j -Z j442要求:1.确定c 1,c 2,c 3,b 1,b 2,a 11,a 12,a 13,a 21,a 22,a 23的值;2.当t 2=0时,t 1在什么范围内变化上述最优解不变; 3.当t 1=0时,t 2在什么范围内变化上述最优基不变。
运筹学天津大学作业答案
运筹学复习题第一阶段练习题 一、填空题1.某足球队要从1、2、3、4号五名队员中挑选若干名上场,令⎩⎨⎧=号不上场第号上场第i i x i 014,,1 =i ,请用x i 的线性表达式表示下列要求:(1)若2号被选中,则4号不能被选中:_________________;(2)只有1名队员被选中,3号才被选中:___________________。
2.线性规划的对偶问题约束的个数与原问题____________的个数相等。
因此,当原问题增加一个变量时,对偶问题就增加一个____________。
这时,对偶问题的可行域将变_______________(大、小还是不变?),从而对偶目标值将可能变____________(好还是坏?)。
3.将非平衡运输问题化为平衡运输问题,在表上相当于增加一个虚设的 ,在模型中相当于增加若干个 变量。
二、某厂生产Ⅰ,Ⅱ,Ⅲ三种产品。
产品Ⅰ依次经A 、B 设备加工,产品Ⅱ经A 、C 设备加工,产品Ⅲ经C 、B 设备加工。
已知有关数据如下表所示,请为该厂制定一个(4)如劳动力数量不变,材料不足时可从市场购买,每单位0.4元,问该厂要不要购进原材料扩大生产,购多少为宜?四、某彩色电视机组装工厂,生产A 、B 、C 三种规格电视机。
装配工作在同一生产线上完成,三种产品装配时的工时消耗分别为6小时,8小时和10小时。
生产线每月正常工作时间为200小时;三种规格电视机销售后,每台可获利分别为500元,650元和800元。
每月销量预计为12台、10台、6台。
该厂经营目标如下:1p :利润指标定为每月4106.1⨯元; 2p :充分利用生产能力; 3p :加班时间不超过24小时;4p :产量以预计销量为标准;为确定生产计划,试建立该问题的目标规划模型。
第一阶段练习题答案一、填空题1.0;13142≥-≤+x x x x2.变量个数,约束条件,小,坏 3.产地或销地,松弛(或剩余)二、答:用j x 表示第j 种产品的生产数量,使该厂获利最大的线性规划模型为: 三、答:(1)建立线性规划模型,模型中321,,x x x ,分别代表A 、B 、C 产品的产量,用单纯形法求解得最优计划的单纯形表如下:(2)产品A 利润在(544,522)范围内变化时,最优计划不变。
天津大学832运筹学基础考研真题及解析
【内部资料】
天津大学考研历年真题解析
——832 运筹学基础
主编:弘毅考研 编者:裴家老大
弘毅教育出品
1
完整版资料请查看来源网站:/thread-1119585-1-1.html
历年真题解析
【内部资料】
【资料说明】
制规则
计算题 选择、填空
时间参数计算、关键路线的确定
计算题
15%-20%
缩短工程工期问题、工程的时间费 用分析、工程完工期的概率分析
计算题
决策问题的基本概念及决策分类 选择、填空
先验分析(期望值准则、效用期望 值准则、完全信息期望值、决策
树)、后验分析、预后分析 悲观法、乐观法、最小后悔值法、
等可能性法
法、随机性动态规划问题 对策问题的组成
纯策略对策问题的解、优超原理
选择、填空 计算题
填空、计算题
混合策略对策的基本概念、混合对 策的解、混合策略对策解得存在性 基本概念、排队模型的表示、排队
问题的求解
系统运行的指标、里特公式
计算题
选择、填空、计 算题
15%-20% 5%-10% 5%-10%
3
完整版资料请查看来源网站:/thread-1119585-1-1.html
免有不妥之处,尚需考生谅解,并恳切希望不吝赐教。
本套资料的整理,得到了老师的指导,广大考生的支持,在此深表感谢。
4
完整版资料请查看来源网站:/thread-1119585-1-1.html
历年真题解析
【内部资料】
目录
2013 年天津大学运筹学基础考研真题 ................................................................................................ 6 2012 年天津大学运筹学基础考研真题 .................................................................错误!未定义书签。 2011 年天津大学运筹学基础考研真题 .................................................................错误!未定义书签。 2010 年天津大学运筹学基础考研真题 .................................................................错误!未定义书签。 2009 年天津大学运筹学基础考研真题 .................................................................错误!未定义书签。 2008 年天津大学运筹学基础考研真题 .................................................................错误!未定义书签。 2007 年天津大学运筹学基础考研真题.................................................................错误!未定义书签。 2006 年天津大学运筹学基础考研真题.................................................................错误!未定义书签。 2005 年天津大学运筹学基础考研真题 .................................................................错误!未定义书签。 2004 年天津大学运筹学基础考研真题 .................................................................错误!未定义书签。 2003 年天津大学运筹学基础考研真题.................................................................错误!未定义书签。 2013 年运筹学专业课试题解析 .............................................................................错误!未定义书签。 2012 年运筹学专业课试题解析 .............................................................................错误!未定义书签。 2011 年运筹学专业课试题解析 .............................................................................错误!未定义书签。 2010 年运筹学专业课试题解析 .............................................................................错误!未定义书签。 2009 年运筹学专业课试题解析 .............................................................................错误!未定义书签。 2008 年运筹学专业课试题解析 .............................................................................错误!未定义书签。 2007 年运筹学专业课试题解析 .............................................................................错误!未定义书签。 2006 年运筹学专业课试题解析 .............................................................................错误!未定义书签。 2005 年运筹学专业课试题解析 .............................................................................错误!未定义书签。 2004 年运筹学专业课试题解析 .............................................................................错误!未定义书签。 2003 年运筹学专业课试题解析.............................................................................错误!未定义书签。
2015年天津大学考研2008年运筹学基础考研真题参考书考研经验专业课重点
活动 A B C D
最乐观时间 3 5 2 4
最可能时间 4 8 4 5
最悲观时间 8 11 6 12
5
育明教育中国考研专业课辅导第一品牌 育明教育官方网站: 育明教育天津分校 赵老师预祝大家考研成功!
杰森估计修理车身需要的零件将花费 3000 美元,修理引擎需要的零件将花费 5000 美元。目前她指出的劳动力需用为 400 美元/天。 (1) 画出该项目的网络图,基于三时估计法,求出其期望完成时间; (2) 假定总的修理费用是劳动力的费用加上零件费用,如果杰森是通过投标拿到这 份工作,并且投标的报价是期望完成时间相应的费用,那么他会亏本的可能性是多少? (3) 如果杰森是花了 16800 美元拿到的这份工作,他亏本的可能性是多少?
1
育明教育中国考研专业课辅导第一品牌 育明教育官方网站: 育明教育天津分校 赵老师预祝大家考研成功!
4、下图中 1 号节点表示某有线电视台,2-7 号节点表示几个居民小区,虚线表示有线 台与小区之间或不同小区间可以架设传输电视信号的电缆,虚线旁的数字为架设这段电 缆的费用,现需确定一使各居民小区都能收到电视信号且总费用最少的架设电缆的方案。 该问题可以看作一个( ) 。 A、最小费用流问题 B、最小支撑树问题 ② 9 9 ① 5 ③ 7 3 4 8 4 ⑥ 2 3 ⑦ 6 ⑤ C、最大流问题 D、最短路问题
0 1 2 3 4 5
0.88 0.90 0.92 0.93 0.94 0.95
0.82 0.85 0.90 0.93 0.94 0.96
0.90 0.92 0.95 0.97 0.98 0.99
若同一工作日内只能对一个部件进行调试, 那么如何分配这 5 个工作日于各部件的调试,
天津大学招收 2008 年硕士学位研究生入学考试试题
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
天津大学招收2007年硕士学位研究生入学考试试题参考答案
考试科目名称:运筹学基础考试科目编号:832 一、
1.(1)出基变量为x4;进基变量为x3。
(2)*121
0 510
13
0 510
1
11
2
B-
⎡⎤
⎢⎥
⎢⎥
⎢⎥
=
⎢⎥
⎢⎥
⎢⎥
-
⎢⎥
⎣⎦。
(3)
(4) *(4511)T
X=
(5) *
14
55
T
Y
⎛⎫
=--
⎪
⎝⎭
(6) 变小
2.产地或销地;松弛。
3..≥
4.P N;λ(1- P N)
二、
1.
1
11112211
21122222
1122
12
m in
..
,,0
n
j j
j
n n
n n
m m m n n m
n
z c x
a x a x a x b
a x a x a x
b s t
a x a x a x b
x x x
=
=∑
++⋯+≥
⎧
⎪
++⋯+≥
⎪
⎪
⋯⋯
⎨
⎪++⋯+≥
⎪
⋯≥
⎪⎩,
2.
1
1112121112122222112212m ax ..
,,0
m
i i
i m m m m n n m n m n
m z y b a y a y a y c a y a y a y c s t a y a y a y c
y y y ==∑++⋯+≤⎧⎪
++⋯+≤⎪⎪
⋯⋯
⎨⎪++⋯+≤⎪⋯≥⎪⎩, 经济意义:i y 为第i 种有害副产品不经处理直接废弃的费用。
三、 *
*
**
*
*
*
*
*
*
'
(')0
(1)
''''(')0
(2)
(2)(1)(')(')0
C X C X C X X C X C X C X X C C X X ≤-≥≤-≤---≤因为所以
又因为所以得
四、 解: 1.
11(1) ()10000; 50000k k AK k k BK s x i s x i s +=⋅+-⋅+=
)
04.01)(()06.01()(),()
04.01)(()
60.01(),( )2(5555555555566+-+++⋅-+⋅=+-++=--x s x i x s i x x s v x s x x s v B A k
k k k
k k k k 阶段指标函数
{}{}
10000
)()
4,3,2,1()()
04.01)(()
60.01(max
)()()04.01)(()06.01()(max
)(0)()3(1116606655555555055665
5+⋅-+⋅==++-++=++-+++⋅-+⋅==+++--≤≤≤≤BK k k AK k k k k k
k k k
k
s x k k B A s x i x s i x s k s f x s x
s f s f x s x i x s i x s f s f k
k 递推方程
2.
{}
{}
{}
{}
{}
{}
{}
{}
10950
1521.1)(10950
0212.01309.1max ]10000)(045.0026.0[095.1)(0816.11236.1max ]
10000)([095.1)04.1)(()60.1(max
095.1)04.01)(()60.01(max )
()
04.01)(()
60.01(max )(095.1)(0005.0095.1max 0)04.01)(()06.01()(055.00.03max )()04.01)(()06.01()(max
)(4444*
44404444440444442
442
4
052
442
4
0554
6444
64
0445
55*
5550555555066555555550554
44
44
44
44
45
55
55
5+==++=+-++-+=+⋅-+⋅+-+=++-++=++-++===-=++-+++-+=++-+++⋅-+⋅=≤≤≤≤≤≤≤≤--≤≤≤≤≤≤≤≤s s f s x x s x s x x s x i x s i x x s x
s x s x s f x s x s f s s f x x s x s x x s x s f x s x i x s i x s f s x s x B A s x s x s x s x s x B A s x 时,取得最大值,
当时,取得最大值,当五、 解:
1.
关键线路如图中双线标出,A,C,E,H 工期为18天
2.增加M 后的网络计划如图
关键线路如图中双线标出,A,M,E,H 工期为22天
C
3.
第一步 调整E 为5天
第二步 调整E 为4天,调整G 为7天 第三步 调整A 为3天
第四步 调整A 为2天,调整B 为2天 最后方案的网络计划如图所示 关键线路如双线所示,工期为18天 A ,M ,E ,H B ,M ,E ,H A ,M ,G B ,M ,G
六、设A 表示大批生产销售成功,B 表示试销成功。
由题设可知(|)0.84,(|)0.36P B A P B A ==,可计算得
()()(|)()(|)
110.840.360.6
22
()(|)
0.42(|)0.7
()
0.6
(|)0.3()(|)
0.08(|)0.2
()
0.4
(|)0.8
P B P A P B A P A P B A P A P B A P A B P B P A B P A P B A P A B P B P A B =+=⨯+
⨯==
====
===
根据EMV 准则对决策树计算,应在大量销售前先进行试销。
在试销成功条件下进行大量销售;在试销失败时,应取消销售计划。
所以甲的损益矩阵⎥⎥⎥
⎦
⎤------⎢⎢⎢⎣⎡--310121121013。
