第3章：粘性流体运动
合集下载
第3章-流体力学连续性方程微分形式
• 符号说明
物理意义
z 单位重流体的位能（比位能）
p
单位重流体的压能（比压能）
u 2 单位重流体的动能（比动能）
2g
z
p
单位重流体总势能（比势能）
z
p
u2 2g
总比能
第四节 欧拉运动微分方程的积分
几何意义
位置水头 压强水头 流速水头 测压管水头 总水头
( Xdx Ydy
Zdz)
1
(
p x
0
物理意义：不可压缩流体单位时间内流入单位空间的流体体积（质量） ，
与流出的流体体积（质量）之差等于零。
适用范围：理想、实际、恒定流或非恒定流的不可压缩流体流动。
第三节 流体动力学基本方程式
6
二、理想流体运动微分方程
理想流体的动水压强特性与静水压强的特性相同：
px py pz p
从理想流体中任取一(x,y,z)为 中心的微元六面体为控制体，边 长为dx,dy,dz，中心点压强为 p(x,y,z) 。
u2
( )dx ( )dy ( )dz
z x x 2
y 2
z 2
u2 d( )
2
由以上得：
gdz
d
(
p
)
d
u2 (
)
2
积分得：
z
p
u2 2g
C
第四节 欧拉运动微分方程的积分
• 理想势流伯努里方程
17
z
p
u2 2g
C
或
z1
p 1
u2 1
2g
z2
p2
u22 2g
物理意义：在同一恒定不可压缩流体重力势流中 ，理想流体各点的总比能 相等即在整个势流场中，伯努里常数C均相等。（应用条件：“——”所示）
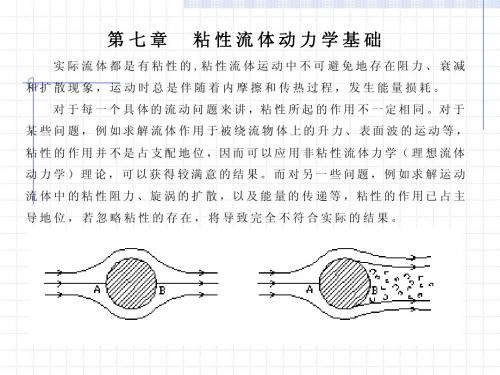
粘性流体动力学基础
f 1 p = dv dt
ρ
1 p dvx fx = ρ x dt 1 p dv y fy = ρ y dt 1 p dvz fz = ρ z dt
方程中， f ：作用在单位质量流体上的质量力
1
ρ
p ：作用在单位质量流体上的表面力
dv ：作用在单位质量流体上的惯性力 dt
这一方程就是以应力形式表示的运动微分方程。
在这一方程中，通常质量力 f x 、 f y 、 f z 是已知的，对不可压缩流体 ρ
τ 也是已知的。方程组中的未知量有：三个法向应力 pii ，六个切向应力 ij ，
三个速度分量vi 。 运动微分方程加上连续性方程共四个， 无法求解 12 个未 知量，下面寻求补充方程。 三 、 切应力分量之间的关系 切应力分量之间存在着一定的联系， 应用力矩平衡原理可以证明切应 力具有对称性。 τ xy = τ yx τ yz = τ zy
τ yz dz τ zy dz τ yz dxdydz τ zy dxdydz + dxdydz dxdydz = 0 y 2 z 2
略去高阶无穷小，可得：
τ yz = τ zy
同理可得：
τ xy = τ yx
τ xz = τ zx
可见应力分量中的切应力是两两对称的。 四 、 切应力与变形速度的关系 牛顿内摩擦定律（平面流动） dv dα τ = x =
M ，六面体为 ABCD, A 点的应力为：
pxx τ yx τ zx
τ xy
p yy
τ zy
τ xz τ yz
pzz
其方向确定为：法向应力以内法线方向为正，切向应力（正） ，过 A 点 的三个面上切向应力与坐标方向相反，其它三个面则相同。 采用泰勒级数展开并取前二项可写出其它三个面上的应力分量。
ρ
1 p dvx fx = ρ x dt 1 p dv y fy = ρ y dt 1 p dvz fz = ρ z dt
方程中， f ：作用在单位质量流体上的质量力
1
ρ
p ：作用在单位质量流体上的表面力
dv ：作用在单位质量流体上的惯性力 dt
这一方程就是以应力形式表示的运动微分方程。
在这一方程中，通常质量力 f x 、 f y 、 f z 是已知的，对不可压缩流体 ρ
τ 也是已知的。方程组中的未知量有：三个法向应力 pii ，六个切向应力 ij ，
三个速度分量vi 。 运动微分方程加上连续性方程共四个， 无法求解 12 个未 知量，下面寻求补充方程。 三 、 切应力分量之间的关系 切应力分量之间存在着一定的联系， 应用力矩平衡原理可以证明切应 力具有对称性。 τ xy = τ yx τ yz = τ zy
τ yz dz τ zy dz τ yz dxdydz τ zy dxdydz + dxdydz dxdydz = 0 y 2 z 2
略去高阶无穷小，可得：
τ yz = τ zy
同理可得：
τ xy = τ yx
τ xz = τ zx
可见应力分量中的切应力是两两对称的。 四 、 切应力与变形速度的关系 牛顿内摩擦定律（平面流动） dv dα τ = x =
M ，六面体为 ABCD, A 点的应力为：
pxx τ yx τ zx
τ xy
p yy
τ zy
τ xz τ yz
pzz
其方向确定为：法向应力以内法线方向为正，切向应力（正） ，过 A 点 的三个面上切向应力与坐标方向相反，其它三个面则相同。 采用泰勒级数展开并取前二项可写出其它三个面上的应力分量。
《工程流体力学》第三章 流体运动研究方法及一维定常流基本方程
截面1-1和2-2：垂直于流动方向，为什么? 侧面1-2：平行于流动方向，为什么？
控制体：1-1-2-2，用I+III表示 在空间上：固定的
t时体系：1-1-2-2，t时刻占据控制体I+III的流体
t+dt时体系：1’-1’-2’-2’ dt时间后： t时体系沿流线运动到III+II
由质量守恒定律： t时体系内质量＝t+dt时体系内质量
定常流：空间中任一点参数随不随时间变化？ 不随
物理意义？
A1, r1, V1 —— 控制面1-1上的横截面积、气流密度、速度
物理意义？
A2, r2, V2 —— 控制面2-2上的横截面积、气流密度、速度
物理意义？
一维定常流连续方程：在一维定常流中，通过同一流管任 意截面上的流体质量流量、重量流量保持不变。
例1：已知平面非定常流中的流速分量为：ux=x+t, uy= -y+t, 求：流线方程和迹线方程。 解：流线微分方程：
其中t为常数 积分后：
最后得：
迹线微分方程：
其中t为变量
结论：非定常流中迹线与流线不同
—— 迹线方程 ——流线方程
例2：已知平面定常流中的流速分量为：ux=x, uy= -y, 求：流线方程和迹线方程。 解：由流线微分方程：
体系动量对时间变化率：
控制体 = t时体系 环境对控制体内流体作用力 = 环境对t时体系内流体作用力
牛顿第二定律： 某瞬时作用在体系上全部外力合力 =该瞬时体系动量对时间的变化率
分量形式：
作用在控制体内流体上的外力： 1)表面力：控制体外流体或固体壁面作用在控制面上力
作用在进口截面上切向力：0 作用在出口截面上切向力：0
控制体：1-1-2-2，用I+III表示 在空间上：固定的
t时体系：1-1-2-2，t时刻占据控制体I+III的流体
t+dt时体系：1’-1’-2’-2’ dt时间后： t时体系沿流线运动到III+II
由质量守恒定律： t时体系内质量＝t+dt时体系内质量
定常流：空间中任一点参数随不随时间变化？ 不随
物理意义？
A1, r1, V1 —— 控制面1-1上的横截面积、气流密度、速度
物理意义？
A2, r2, V2 —— 控制面2-2上的横截面积、气流密度、速度
物理意义？
一维定常流连续方程：在一维定常流中，通过同一流管任 意截面上的流体质量流量、重量流量保持不变。
例1：已知平面非定常流中的流速分量为：ux=x+t, uy= -y+t, 求：流线方程和迹线方程。 解：流线微分方程：
其中t为常数 积分后：
最后得：
迹线微分方程：
其中t为变量
结论：非定常流中迹线与流线不同
—— 迹线方程 ——流线方程
例2：已知平面定常流中的流速分量为：ux=x, uy= -y, 求：流线方程和迹线方程。 解：由流线微分方程：
体系动量对时间变化率：
控制体 = t时体系 环境对控制体内流体作用力 = 环境对t时体系内流体作用力
牛顿第二定律： 某瞬时作用在体系上全部外力合力 =该瞬时体系动量对时间的变化率
分量形式：
作用在控制体内流体上的外力： 1)表面力：控制体外流体或固体壁面作用在控制面上力
作用在进口截面上切向力：0 作用在出口截面上切向力：0
空气动力学粘性流体力学
D=
2 R
∫ (τ π
0
sin θ − ps cos θ )ds ≠ 0
4.1、流体的粘性及其对流动的影响 4.1、
总的结论如下： 总的结论如下： （1）粘性摩擦切应力与物面的粘附条件（无滑移条件）是粘性流体运动 ）粘性摩擦切应力与物面的粘附条件（无滑移条件） 有别与理想流体运动的主要标志。 有别与理想流体运动的主要标志。 （2）粘性的存在是产生阻力的主要原因。 ）粘性的存在是产生阻力的主要原因。 （3）边界层的分离必要条件是，流体的粘性和逆压梯度。 ）边界层的分离必要条件是，流体的粘性和逆压梯度。 （4）粘性对于研究阻力、边界层及其分离、旋涡的扩散等问题起主导作 ）粘性对于研究阻力、边界层及其分离、 用，不能忽略。 不能忽略。
F=µAU/h
（U
h
F） ）
4.1、流体的粘性及其对流动的影响 4.1、
流层之间的内摩擦力与接触面上的压力无关。 流层之间的内摩擦力与接触面上的压力无关。 设τ表示单位面积上的内摩擦力（粘性切应力），则 表示单位面积上的内摩擦力（粘性切应力），则 ），
F U τ = =µ A h
µ-----流体的动力粘性系数。（量纲、单位）： 流体的动力粘性系数。（量纲、单位）：[µ]=M/L/T kg/m/s 流体的动力粘性系数。（量纲 ）： Ns/m2=Pa.s；ν =µ/ρ---流体的运动粘性系数。量纲、单位： 流体的运动粘性系数。 ； ρ 流体的运动粘性系数 量纲、单位： [ν ]=L2/T ν m2/s。 。 空气： 空气： 1.461×10-5 × 水： 1.139×10-6 ×
u ( x, y , z , t ) v ( x, y , z , t ) w( x, y, z , t )
点处， 在 M 1 ( x + ∆x, y + ∆y, z + ∆z, t ) 点处，速度为
第三章 粘性流体的流动
h1 =h2 ; v1 = v2 P1 —P2 = W 能量损失表现为： 压强降低
V
V
牛顿流体：遵循牛顿黏滞定律的流体，水，血浆
非牛顿流体：染料，混浊液
三、 雷诺数（Reynolds number） Re：→ 判断层流与湍流 ⚫Re < 1000 层流； ⚫Re > 1500 湍流； ⚫1000 < Re <1500 过渡流
例：在主动脉内,求血液进行层流的最大速度
四、黏性流体的伯努利方程
S1 S1’
S2 S2’
W为单位体积的流体从S1S2运动到S1 ’ S2 ’过程中 因存在粘性力而引起的能量损耗。
ห้องสมุดไป่ตู้
如果黏性流体沿着粗细均匀的管道作稳定流动
p1 + gh1 = p2 + gh2 + w
或
( p1 − p2 ) + g(h1 − h2 ) = w
可见，由于黏性力的存在, 要流体在管道中作稳 定流动，管道两端要有压强差或者高度差 (h1−h2) 或者两者兼而有之。
第二节 黏性流体的流动
一、层流和湍流 1、层流
特点： ①分层流动，各层流速不
同； ②流速方向与层面相切； ③层间无质量交换。
2、湍流：流速超过一定值（临界速度vC），各液层 相互混合
特点：非稳定流动、产生声响、消耗能量大。 二、牛顿粘滞定律
切应力
切应变
切变率
= = F/S d / dx
牛顿粘滞定律
F = S d
dx
物理含意：单位速度梯度下单位接触面积受到的内
摩擦力。
（1）速度梯度
lim = d
x→0 x dx
（2）S，层与层之间的接触面积
第3章流体流动特性
z)
cos(,
z)
第三章 流体流动特性
3.2流体流动的速度场
三、迹线和流线
流线微分方程
即：
ud,x d,y dz
v ds v ds v ds
或写成：
d sd,x vu
d v sd ,y
d v sd z
得： u(x,d y,zx ,t)(x,d y,zy ,t)(x,d y,zz,t) （3-10**）
3.2流体流动的速度场
例3-1： u x t
已知：
y
t
0
求：t＝0 时，A（－1，1）点流线的方程。
解：将已知条件代入流线微分方程式（3-10）
u(x,d y,zx ,t)(x,d y,zy ,t)(x,d y,zz,t)
得： dx dy xt yt
第三章 流体流动特性
了解流动特性是研究流体运动规律的第一步
本章内容：
关于流场 流体流动的速度场 粘性流体的运动形态 流体流动的分类
3.1流场及其描述方式
一、流场 由流体流动所占据的全部空间称为流场。
二、流场研究的两种方法
拉格朗日（Larange）法－跟随质点法
研究对象为流体质点。着眼于流体各质 点的运动情况，研究各质点的运动历程，通 过综合所有被研究流体质点的运动情况来获 得整个流体运动的规律。
3.4粘性流体的流动形态
水箱A注满水，利用溢水管H 保持水箱中的水位恒定。微 微打开调节阀C，水流以很小 速度沿玻璃管流出。再打开 颜色水瓶D上的小阀K，使颜 色水沿细管E流入玻璃管B中。 观察管中颜色水的流动形状。
3.4粘性流体的流动形态
粘性流体的流型对流体流动的能量损 失有很大关系。
《流变学》 第三章 PART1~2
6.弹性模量随温度上升而增大：当温度升高时，分子链的热 运动加强，回缩力逐渐变大，弹性形变的能力变小，因而表 现为弹性模量随温度的上升而增大。
橡胶弹性的唯象理论 唯象理论：钱学森称唯象理论是知其然不知其所以然的科 学理论 。杨振宁把物理学分为实验、唯象理论和理论架 构三个路径，唯象理论是实验现象更概括的总结和提炼， 但是无法用已有的科学理论体系作出解释，唯象理论被称 作前科学，因为它们也能被实践所证实。而理论架构是比 唯象理论更基础的，它可以用数学和已有的科学体系进行 解释。
4.小应变时符合线性弹性：小应变时符合线性弹性，但它的 模量很低，为0.1-1MPa数量级，比玻璃态聚合物的模量低3-4 个数量级。它的体积模量则仍为103-104MPa,即K＞＞G,泊松比 ν=（3K-2G）/(6K+2G)=0.5。 5.变形时有热效应:当把橡胶试样急速拉伸（绝热拉伸）时， 试样温度升高。这种热效应虽然不很强烈，但随伸长程度的 增加而增大。
1.变形的时间依赖性：流体的变形随时间不断发展，即 时间依赖性。 γ=σ/η=dγ/dt 考虑变形则：γ=(σ/η)t 2.流体变形的不可回复性：永久形变，当外力移除后， 变形保持不变（完全不回复）。聚合物熔体发生流动， 涉及到分子链之间的相对滑移，当然这种变形是不能回 复的。 3.能量散失：外力对流体所作的功在流动中转为热能而 散失，这一点与弹性过程中的贮能完全相反。 4.正比性：应力与应变速率成正比，粘度与应变速率无 关。
3.时间依赖性：橡胶受到外力时，应变是随时间发展的，但是 不会无限制增大而是趋近一个平衡值，即平衡应变εe。橡胶变 形是靠分子链段运动来实现的，整个分子链从一种平衡状态过 渡到与外力相适应的平衡状态，这个过程需要一定的时间。 强调：在非线性弹性这一流变学模式中讨论的是平衡时的应力应 变关系，他们已无时间依赖性。橡胶变形的时间依赖性不在非线 性弹性中考虑，而将在线性弹性这一模式中讨论。
粘性流体的流动
雷诺提出了一个无量纲的数，作 为决定流体从层流向湍流转变的判 据，即流动的雷诺数 Re ：
r Re
试验表明：
Re<1000Re<1500时，流动状态不稳定，为过渡流。5
细管子的地方不易出现湍流，但在弯管处，在较
低的 Re 值也可发生湍流，且弯曲的程度愈大，Re 的
分速度，因而各流层将混淆起来，
并有可能形成漩涡，整个流动显得
杂乱而不稳定，这样的流动状态成
为湍流。
介于层流和湍流之间的流动状态称为过渡流，这种
流动很不稳定。
3
第三节 粘性流体的流动
一、粘性流体的流动状态 二、雷诺数 三、牛顿黏滞定律
4
二、雷诺数
粘性流体的流动状态怎样，决定与流动速度 ， 流体的密度 ，粘度 以及管子的半径r。
第二章 流体的流动
医学物理学 仇惠 余大昆主编 科学出版社
1
第三节 粘性流体的流动
一、粘性流体的流动状态 二、雷诺数 三、牛顿黏滞定律
2
一、粘性流体的流动状态
粘性流体的流动状态有：层流、湍流和过渡流
层流：指流体的分层流动状态。
特点：相邻两层之间只做相对滑
动，层流间没有横向混杂。
湍流：在垂直于层流的方向上有
lim v d v x0 x dx
8
3. 牛顿粘性定律：粘性力F的大小两流层的接触 面积S成正比，与该处的速度梯度成正比，即：
F S d
dx
叫粘度系数或粘度
值的大小决定于流体的性质，并和温度有关。 通常液体的 值随温度升高而减小，气体则相反。
9
F S d
dx
f dv
S dx
f
精修水力学发展简史精选全文
其中，v是速度； k是转换常数，国际单位制中值为1； n是糙率；
是水力半径； S指明渠的坡度。
十八世纪末，1783年，拉格朗日
（Lagrangge，1736-1813）在总结前人工作
十 的基础上，提出了一种新的描述流体运动的 方法—拉格朗日法。
九
拉格朗日法又称随体法：跟随流体质点
世 运动，记录该质点在运动过程中物理量随时 间变化规律。
阿基米德(Archimedes，前 287—前212)
1.2 水力学发展简史
公元1世纪前后，劳动人民基于水流的动力，制成了水碓、水磨和 水排等水
力器具。
水碓：一种借水力舂米的工具。是脚踏碓机 械化的结果。水碓的动力机械是一个大的立 式水轮，轮上装有若干板叶，转轴上装有一 些彼此错开的拨板，拨板是用来拨动碓杆的。 每个碓用柱子架起一根木杆，杆的一端装一 块圆锥形石头。下面的石臼里放上准备加工 的稻谷。流水冲击水轮使它转动，轴上的拨 板臼拨动碓杆的梢，使碓头一起一落地进行 舂米。值得注意的是，立式水轮在这里得到 最恰当最经济的应用，正如在水磨中常常应 用卧式水轮一样。利用水碓，可以日夜加工 粮食。
蓬 用于粘度可以忽略、不可被压缩的理想流体。 使用伯努利定律必须符合以下假设，方可使用；如没完全符合以下假
勃 设，所求的解也是近似值。
发 定常流：在流动系统中，流体在任何一点之性质不随时间改变。 不可压缩流：密度为常数，在流体为气体适用于马赫数(Ma)<0.3。
展 无摩擦流：摩擦效应可忽略，忽略黏滞性效应。
纪
拉格朗日法是以研究单个流体质点运动 拉格朗日（Lagrangge，1736-1813）
水 过程作为基础，综合所有质点的运动，构成 整个流体的运动。
力 学 1847年英国物理学家、生理学家亥姆霍
是水力半径； S指明渠的坡度。
十八世纪末，1783年，拉格朗日
（Lagrangge，1736-1813）在总结前人工作
十 的基础上，提出了一种新的描述流体运动的 方法—拉格朗日法。
九
拉格朗日法又称随体法：跟随流体质点
世 运动，记录该质点在运动过程中物理量随时 间变化规律。
阿基米德(Archimedes，前 287—前212)
1.2 水力学发展简史
公元1世纪前后，劳动人民基于水流的动力，制成了水碓、水磨和 水排等水
力器具。
水碓：一种借水力舂米的工具。是脚踏碓机 械化的结果。水碓的动力机械是一个大的立 式水轮，轮上装有若干板叶，转轴上装有一 些彼此错开的拨板，拨板是用来拨动碓杆的。 每个碓用柱子架起一根木杆，杆的一端装一 块圆锥形石头。下面的石臼里放上准备加工 的稻谷。流水冲击水轮使它转动，轴上的拨 板臼拨动碓杆的梢，使碓头一起一落地进行 舂米。值得注意的是，立式水轮在这里得到 最恰当最经济的应用，正如在水磨中常常应 用卧式水轮一样。利用水碓，可以日夜加工 粮食。
蓬 用于粘度可以忽略、不可被压缩的理想流体。 使用伯努利定律必须符合以下假设，方可使用；如没完全符合以下假
勃 设，所求的解也是近似值。
发 定常流：在流动系统中，流体在任何一点之性质不随时间改变。 不可压缩流：密度为常数，在流体为气体适用于马赫数(Ma)<0.3。
展 无摩擦流：摩擦效应可忽略，忽略黏滞性效应。
纪
拉格朗日法是以研究单个流体质点运动 拉格朗日（Lagrangge，1736-1813）
水 过程作为基础，综合所有质点的运动，构成 整个流体的运动。
力 学 1847年英国物理学家、生理学家亥姆霍
第3章-流体力学连续性方程微分形式
欧拉运动微分方程组各式分别乘以dx，dy，dz（流场任意相邻两点间距ds 的坐标分量），然而相加得：
( Xdx
Ydy
Zdz)
1
( px
dx
p y
dy
p z
dz)
dux dt
dx
duy d;
<II>
<III>
一、在势流条件下的积分
考虑条件 1、恒定流
当为恒定流时
t
0
(ux
x
)
(uy
y
)
(uz
z
)
0
适用范围：理想、实际、可压缩、不可压缩的恒定流。
（2）不可压缩流体的连续性微分方程
当为不可压缩流时 Const
u x x
u y y
u z z
0
物理意义：不可压缩流体单位时间内流入单位空间的流体体积（质量） ，
dt
p'xx 'xz 'xy
x
第三节 流体动力学基本方程式
考虑条件：
13
1）
不可压缩流体的连续性微分方程：uxx
uy y
uz z
0
2）切应力与主应力的关系表达式
• 不可压缩粘性流体运动微分方程：纳维埃-斯托克斯方程（Navier-
Stokes，N-S)方程：
X
1
p x
1
第三章 流体动力学基础
第三节 流体动力学基本方程式
一、连续性微分方程 二、理想流体运动微分方程 三、粘性流体的运动微分方程
3粘性流体的流动及规律
———粘滞流体作稳定流动时的伯努利方程
若h1 h2 , v1 v2，则上式变为 P 1 P 2 w
P1＞p2，在水平细管的两端，必须维持一定的压 强差，才能使粘性流体作匀速流动。
2—3 黏性流体的流动及规律
第二章 流体的运动
1 1 2 2 v1 gh1 p1 v2 gh2 p2 w 2 2
2—3 黏性流体的流动及规律
Hale Waihona Puke 第二章 流体的运动定义：
说明：（5点）
vr Re
雷诺数没有量纲
在几何形状相似的管道中流动的流体，不论它们的v(液体的平 均流速）、r、 、（液体密度）如何，只要Re相同，它们的
流动类型就相同。
Re<1000时，流体流动为层流； Re>1500时，流体流动为湍流；
2—3 黏性流体的流动及规律
第二章 流体的运动
第三节 黏性流体的流动
2—3 黏性流体的流动及规律 一、层流、湍流
（laminar flow 、turbulent flow)
第二章 流体的运动
2—3 黏性流体的流动及规律
层流
第二章 流体的运动
流动的液体，实际
分成许多平行与管
壁的薄圆桶状薄层
，各层之间有相对
流体的黏度愈小,密度愈大,流速愈大,管半径愈大,愈
容易发生湍流.
2—3 黏性流体的流动及规律 第二章 流体的运动 三、牛顿黏滞定律(Newtonian viscosity law) 1.速度梯度(velocity gradient)
黏性流体作层流时，速度的逐层变化可以用速度梯度 来定量表示。
则泊肃叶公式为
p Q Rf
2—3 黏性流体的流动及规律 关于流阻：
若h1 h2 , v1 v2，则上式变为 P 1 P 2 w
P1＞p2，在水平细管的两端，必须维持一定的压 强差，才能使粘性流体作匀速流动。
2—3 黏性流体的流动及规律
第二章 流体的运动
1 1 2 2 v1 gh1 p1 v2 gh2 p2 w 2 2
2—3 黏性流体的流动及规律
Hale Waihona Puke 第二章 流体的运动定义：
说明：（5点）
vr Re
雷诺数没有量纲
在几何形状相似的管道中流动的流体，不论它们的v(液体的平 均流速）、r、 、（液体密度）如何，只要Re相同，它们的
流动类型就相同。
Re<1000时，流体流动为层流； Re>1500时，流体流动为湍流；
2—3 黏性流体的流动及规律
第二章 流体的运动
第三节 黏性流体的流动
2—3 黏性流体的流动及规律 一、层流、湍流
（laminar flow 、turbulent flow)
第二章 流体的运动
2—3 黏性流体的流动及规律
层流
第二章 流体的运动
流动的液体，实际
分成许多平行与管
壁的薄圆桶状薄层
，各层之间有相对
流体的黏度愈小,密度愈大,流速愈大,管半径愈大,愈
容易发生湍流.
2—3 黏性流体的流动及规律 第二章 流体的运动 三、牛顿黏滞定律(Newtonian viscosity law) 1.速度梯度(velocity gradient)
黏性流体作层流时，速度的逐层变化可以用速度梯度 来定量表示。
则泊肃叶公式为
p Q Rf
2—3 黏性流体的流动及规律 关于流阻：
第三章流体的运动
（2）流体动力学 —— 研究流体运动规律以及 运动着的流体与流体中的物体之间的相互作用 的学科。
2
第一节 理想流体的定常流动
一、理想流体
实际流体 ——具有粘性和可压缩的流体。
理想流体 —— 绝对不可压缩、完全没有粘 性的流体。
二、 定常流动
研究流体的运动的两种方法： (1)拉格朗日法 —— 以流体的各个质元为研 究对象，根据牛顿定律研究每个流体质元的 运动状态随时间的变化。
1
2 gh
25
26
图(b)是测量气体的流速，设液体的密度为 ，压强计中两液面的高度差为ｈ， 则 P2 P 1 gh ，因此
1 2 1 gh 2
故
1
2 gh
27
４、虹吸管
虹吸管是用来从不能倾斜的 容器中排出液体的装置。
（1）流体流速
视液体为理想流体，且排水管均匀，对容器内 液面A和管口D，应用伯努利方程得：
d F d F S 也可以写成： S dx dx
令τ=F/S，它表示作用在单位面积上与流体层 相切的内摩擦力，叫做切应力。
35
位移bb 与垂距ab之比叫做切应变， bb td 用来表示，即： ab tg d 。 切应变对时间的变化率叫做切变率，
表示，即 以 因此
5
流体做定常流动时流线的特点：由于空间各点 的流速不随时间变化，则流线的形状保持不变， 此时流线与流体粒子的运动轨迹相重合。
流管——在稳定流动的流体中划出一个小截面 S1，并且通过它的周边各点作出许多流线，由 这些流线所组成的管状体就称为流管。
6
三、 连续性方程
流量——单位时间内通过某一流管内任意横 截面的流体的体积。 流量用Q来表示,其单位为（m3· s-1）。
2
第一节 理想流体的定常流动
一、理想流体
实际流体 ——具有粘性和可压缩的流体。
理想流体 —— 绝对不可压缩、完全没有粘 性的流体。
二、 定常流动
研究流体的运动的两种方法： (1)拉格朗日法 —— 以流体的各个质元为研 究对象，根据牛顿定律研究每个流体质元的 运动状态随时间的变化。
1
2 gh
25
26
图(b)是测量气体的流速，设液体的密度为 ，压强计中两液面的高度差为ｈ， 则 P2 P 1 gh ，因此
1 2 1 gh 2
故
1
2 gh
27
４、虹吸管
虹吸管是用来从不能倾斜的 容器中排出液体的装置。
（1）流体流速
视液体为理想流体，且排水管均匀，对容器内 液面A和管口D，应用伯努利方程得：
d F d F S 也可以写成： S dx dx
令τ=F/S，它表示作用在单位面积上与流体层 相切的内摩擦力，叫做切应力。
35
位移bb 与垂距ab之比叫做切应变， bb td 用来表示，即： ab tg d 。 切应变对时间的变化率叫做切变率，
表示，即 以 因此
5
流体做定常流动时流线的特点：由于空间各点 的流速不随时间变化，则流线的形状保持不变， 此时流线与流体粒子的运动轨迹相重合。
流管——在稳定流动的流体中划出一个小截面 S1，并且通过它的周边各点作出许多流线，由 这些流线所组成的管状体就称为流管。
6
三、 连续性方程
流量——单位时间内通过某一流管内任意横 截面的流体的体积。 流量用Q来表示,其单位为（m3· s-1）。
第3章流体运动学上PPT课件
3.2 描述流体运动的两种方法
3.2.1 Lagrange法
1.基本思想：跟踪每个流体质点的运动全过程，记录 它们在运动过程中的各物理量及其变化
2.拉格朗日变数：（a,b,c,t）——区分流体 质点的标志
3.质点物理量：B(a,b,c,t)， 如：
pp(a,b,c,t) (a,b,c,t)
3.2 描述流体运动的两种方法
3.2 描述流体运动的两种方法
3.2.0 流体质点和空间点
•流体质点：是个物理点，它是在 两者相互关系：流场
连续介质中取出的，在几何尺寸 中空间某一点，先后由 上无限小，可以看作一点，但包 不 同 的 流 体 质 点 所 占 含许多分子，具有一定物理量。 据；流体质点物理量会
发生变化，而空间点是
•空间点：几何点，表示空间位置 不动的。
Reynolds数的物理意义：
惯性力 Re 粘性力
惯性使扰动放大，导致湍流，粘性抑制扰动使流动保持稳定。 当 Re 时，流动趋于理想流体运动。
2. 机翼绕流风洞试验
机翼绕流流场的特点：
流线(streamline)： 上翼面：流线密 下翼面：流线稀
(a) Re~1
3. 卡门涡街(Karman vortex street)
第3章 流体运动学
(Fluid Kinematics)
第3章 流体运动学
从几何的观点研究流体的运动，不 讨论运动产生的动力学原因。
ma F
rrx,y,z,t vvx,y,z,t aax,y,z,t
3.1 流动图形观察 (flow visualization)
观察几个典型流动，感受实际流动现象和特征。 圆管流动——流动状态 机翼绕流——升力、阻力 圆柱绕流——涡激振荡
流体力学中的流体的黏滞流动特性
流体力学中的流体的黏滞流动特性在流体力学中，黏性是指由于流体分子内部间的摩擦而产生的一种阻碍流体流动的现象。
黏性可以影响流体的流动速度、流体层间的相对运动以及流体中的剪切力等因素。
本文将探讨流体的黏滞流动特性，并介绍一些经典的黏滞流动模型。
黏性是指流体分子之间的内部摩擦力，也可以说是流体流动的内部阻力。
在流体的黏滞流动中，流体分子之间的摩擦力会导致流体内部各层间存在相对滑动。
黏滞系数是流体黏滞性的度量，常用符号为η。
流体的黏滞性取决于流体的物理性质，如温度、压力和组成等，通常是温度的函数。
黏滞流动可以分为层流和湍流两种模式。
层流是指流体在管道或流动通道中呈现的流线型流动，其中各个流体层之间不存在明显的相互干扰。
在黏滞流动的层流中，黏性力主导着流体的运动，使得流体的速度沿流动方向逐渐减小。
湍流是指流体在管道或流动通道中呈现的混乱和不规则的流动模式，其中各个流体层之间存在剧烈的相对运动。
在湍流中，黏性力无法抑制流体的变动和混乱，形成了涡旋和湍旋等流体结构。
黏滞流动的特性可以用流体黏滞系数来描述。
对于层流，流体的黏滞系数η可以用斯托克斯公式进行计算。
斯托克斯公式是一种经验公式，适用于小尺度和低速流动条件下的层流情况。
斯托克斯公式表明，流体的黏滞系数与流体的密度、流体粘度以及流体粒径等因素相关。
对于湍流，黏滞系数的计算较为复杂，需要考虑流体中的湍流结构、湍流强度以及涡旋等因素。
在工程应用中，黏滞流动的特性对于流体的传输、输运以及搅拌等过程具有重要的影响。
例如，在石油工业中，黏滞流动的特性对于油井生产、管道输送以及油品精炼等环节具有重要的作用。
在飞行器设计中，黏滞流动的特性影响着飞机、火箭等载具的气动性能，对于提高飞行器的飞行效率和稳定性有着关键的作用。
除了层流和湍流外，黏滞流动还可以分为准层流和过渡流动等模式。
准层流是介于层流和湍流之间的一种流动状态，具有一定的流体混合和层状流动的特性。
过渡流动是从层流到湍流的过渡过程，其中流体的黏滞力开始失去控制，流动呈现出不规则和混乱的特性。
黏性流体运动规律
黏性流体运动规律引言黏性流体是一种具有粘性的流体，其运动规律受到黏性力的影响。
黏性流体的运动规律在科学技术领域有着广泛的应用，例如在物理学、化学工程、地球科学以及工业生产等方面。
本文将探讨黏性流体的运动规律，包括黏性流体的类型、黏性力的作用机制以及黏性流体运动的相关方程。
黏性流体的类型黏性流体主要分为牛顿型流体和非牛顿型流体两种类型。
牛顿型流体牛顿型流体是指满足牛顿流动定律的流体，即黏性力正比于流体速度梯度。
牛顿型流体的黏滞性不随时间和剪切速率的变化而改变，常见的牛顿型流体包括水、空气等。
非牛顿型流体非牛顿型流体是指不满足牛顿流动定律的流体，其黏滞性随时间和剪切速率的变化而改变。
非牛顿型流体的行为复杂多样，常见的非牛顿型流体包括胶体、溶胶、凝胶等。
非牛顿型流体的黏滞性可以通过应力-应变关系来描述，其中包括剪切应力、剪切应变率等参数。
黏性力的作用机制黏性力是黏性流体中的一种力，它使流体分子间相互摩擦，阻碍流体分子的运动。
黏性力的作用机制主要有两方面：分子间相互作用力和分子内作用力。
分子间相互作用力分子间相互作用力主要包括范德华力、静电作用力等。
这些力会使流体分子间发生吸引或斥力，并限制流体分子间的运动。
分子间相互作用力的强弱直接影响着黏性力的大小。
分子内作用力分子内作用力是指流体分子内部的力，如化学键等。
这些作用力使得分子具有一定的刚度和结构，从而影响流体分子的运动方式。
分子内作用力对黏性力的大小有一定的影响。
黏性流体运动的相关方程黏性流体运动的相关方程是描述黏性流体运动规律的数学方程，其中包括连续性方程、动量方程和能量方程。
连续性方程连续性方程描述了黏性流体的质量守恒定律。
它表达了单位时间内通过流体某一截面的质量流量和该截面的流体密度和速度之间的关系。
连续性方程可用以下公式表示：$$\\frac{{\\partial \\rho}}{{\\partial t}} + \ abla \\cdot (\\rho \\mathbf{V}) = 0$$其中，$\\rho$表示流体的密度，$\\mathbf{V}$表示流体的速度矢量，abla表示梯度运算符，$\\cdot$表示矢量的点乘运算符。
第3章流体力学连续性方程微分形式
第三章 流体动力学基础
第三节 流体动力学基本方程式
一、连续性微分方程 二、理想流体运动微分方程
三、粘性流体的运动微分方程
第四节 欧拉运动微分方程的积分
一、在势流条件下的积分
二、沿流线的积分
第三节 流体动力学基本方程式
一、连续性微分方程
在流场内取一微元六面体（如图），边长为dx,dy,dz，中心点O流速为 （ ux,uy,uz ） D' z C' ux dx ux dx A' dz u B' u ux x 2 z x x 2 o’ M uy ux N 以x轴方向为例： C D u 1 x dx dy u u dx 左表面流速 M A x x 2 B o u x x 1 右表面流速 u u dx N x 2 x y ∴ 单位时间内x方向流出流进的质量流量差： ( u ) ( u ) x x 1 1 M M [ u dx ] dydz [ u dx ] dydz x 右 左 x 2 x 2 x
u u u u pdu x x x x x 1 X u u u x dt t x x y y z z
•
理想流体的运动微分方程（欧拉运动微分方程）
du ux ux ux p ux x 1 X ux uy uz z x dt t x y du uy uy uy uy p y 1 Y ux uy uz y dt t x y z du uz uz uz uz p 1 z Z ux uy uz z dt t x y z
质量力 x向受力
'zy xy xz
dz
p'zzx
第三节 流体动力学基本方程式
一、连续性微分方程 二、理想流体运动微分方程
三、粘性流体的运动微分方程
第四节 欧拉运动微分方程的积分
一、在势流条件下的积分
二、沿流线的积分
第三节 流体动力学基本方程式
一、连续性微分方程
在流场内取一微元六面体（如图），边长为dx,dy,dz，中心点O流速为 （ ux,uy,uz ） D' z C' ux dx ux dx A' dz u B' u ux x 2 z x x 2 o’ M uy ux N 以x轴方向为例： C D u 1 x dx dy u u dx 左表面流速 M A x x 2 B o u x x 1 右表面流速 u u dx N x 2 x y ∴ 单位时间内x方向流出流进的质量流量差： ( u ) ( u ) x x 1 1 M M [ u dx ] dydz [ u dx ] dydz x 右 左 x 2 x 2 x
u u u u pdu x x x x x 1 X u u u x dt t x x y y z z
•
理想流体的运动微分方程（欧拉运动微分方程）
du ux ux ux p ux x 1 X ux uy uz z x dt t x y du uy uy uy uy p y 1 Y ux uy uz y dt t x y z du uz uz uz uz p 1 z Z ux uy uz z dt t x y z
质量力 x向受力
'zy xy xz
dz
p'zzx
水力学 第3章 流体力学基本方程
V V V V a u v w t x y z
V V V V dV a u v w t x y z dt
加速度的投影值：
u u u u du ax u v w t x y z dt
v v v v dv ay u v w t x y z dt
速度：
x y z u ,v ,w t t t
加速度：
u 2 x ax 2, t t v 2 y ay 2, t t w 2 z az 2 t t
这里：
V ui v j wk
a ax i a y j az k
此方程称为积分形式的连续性方程。
d dM d dt t d vn dA (1) dt A
方程（1）对于任一物理量φ（比如：动量等）亦成立。
d d t d vn dA dt A
式中：φ——流体单位体积的某物理量。
2.渐变流与急变流：
在非均匀流中，各流线是接近于平行直线的流动称为渐 变流（或称缓变流）；否之，则为急变流。
七.一元流动、二元流动、三元流动：
若流体的流动参数是空间三个坐标和时间的函数，这种 流动称为三元流动；若流动参数是两个坐标和时间的函数， 这种流动称为二元流动；若流动参数是一个坐标和时间的 函数，这种流动称为一元流动。
若用粗体字母表示矢量，则：
加速度：
v1 v 0 a lim ( t o ) t
V V V V V1 V0 t x y z t x y z
而：
注意到： 因此：
x lim u, t 0 t
y lim v, t 0 t
z lim w t 0 t
高等流体力学 第三章 流体力学基本方程组-3
p xx P p yx p zx p xy p yy p zy
P pI P
p xz p p yz 0 p zz 0
0 p 0
xx 0 0 yx p zx
xy
(3) 固壁处：
当固壁与流体一起运动时：
v f vs
Tm1 Tm 2
T T k k n m1 n m 2 T T k k n m1 n m 2
16
当固壁静止时：
v f vs 0
Tm1 Tm 2
第七节 初始条件和边界条件
(b) 边界条件：流体运动边界上方程组的解应该满足的条件：
(4) 自由边界处，对理想流体：
p p0
17
随堂作业
(1) 粘性不可压缩均质流体定常运动（绝热过程）方程组在 二维直角坐标系中的形式 (2) P200 (3) P202 (4) P140 第9题（1）；P201 第22题 第二题1（2）； P141 第三题1（3）； 第13题（1）
1 u v 2 y x
1 v w 2 z y
1 P pI 2 S I v 3
1，i=j
Ⅰ= 0，i≠j
i,j=1,2,3
5
1 P pI 2 S I v 3
1 u w 2 z x u x 1 v w 1 u 2 z y 2 y 1 u 0 2 z 1 u v 2 y x v x w x v y 1 v w 2 z y 1 u w 2 z x 1 v w 2 z y w z
P pI P
p xz p p yz 0 p zz 0
0 p 0
xx 0 0 yx p zx
xy
(3) 固壁处：
当固壁与流体一起运动时：
v f vs
Tm1 Tm 2
T T k k n m1 n m 2 T T k k n m1 n m 2
16
当固壁静止时：
v f vs 0
Tm1 Tm 2
第七节 初始条件和边界条件
(b) 边界条件：流体运动边界上方程组的解应该满足的条件：
(4) 自由边界处，对理想流体：
p p0
17
随堂作业
(1) 粘性不可压缩均质流体定常运动（绝热过程）方程组在 二维直角坐标系中的形式 (2) P200 (3) P202 (4) P140 第9题（1）；P201 第22题 第二题1（2）； P141 第三题1（3）； 第13题（1）
1 u v 2 y x
1 v w 2 z y
1 P pI 2 S I v 3
1，i=j
Ⅰ= 0，i≠j
i,j=1,2,3
5
1 P pI 2 S I v 3
1 u w 2 z x u x 1 v w 1 u 2 z y 2 y 1 u 0 2 z 1 u v 2 y x v x w x v y 1 v w 2 z y 1 u w 2 z x 1 v w 2 z y w z
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
p x dp dx L
1 h h 2 p v x vx dy h 0 12 L
Wh 3 p 流量 Q 12 L
(a)情形的流量是(b)情形和(c)情形的流量之和
圆管内的一维稳态流动分析。
不可压缩流体在水平 圆管内作一 维稳态层流流动。试写出该条件下的连 续性方程和运动微分方程。并证明管道 截面上任一点的总势能和轴向压力梯度 为常数。
(即:线变形率)，同固体力学中的虎 克定律。
线变形率与流体流动： 从流体流动角度看，线变形率的正负
反映了流体的流动是加速还是减速； 体变形率的正负反映了流动过程中流 体体积是增加还是减少。
正应力中的粘性应力：
xx
x 2 vx v y vz p 2 x 3 x y z
vx v y vx vz y x x y z z
适用于牛顿流体 常见条件下N－S方程的表达形式：
常粘度条件下N－S方程：
2
const
N-S方程
牛顿流体的本构方程
引入的基本假设：
为了寻求流体应力与变形速率之间的关系，Stokes提出三个 基本假设：
应力与变形速率成线性关系; 应力与变形速率之间的关系各向同性；
静止流场中，切应力为零，各正应力均等于静压力
xx yy zz p
牛顿流体的本构方程：
xx
例题
1．圆管内的稳定层流
y
v v v 分量： t v r r r 1 1 rv r r r r
v v r v v f z p z z vz r z 2 2 1 v 2 v r v 2 2 2 2 r r z
连续方程和N－S方程是粘性流体流动应遵循的质量守恒和 动量守恒的数学表达式。
N-S方程应用概述
封闭条件：理论上方程是封闭的，但若要考虑到物性参数 的变化，应将物性变化的关系作为补充方程。
应用条件：只适用于牛顿流体 方程求解：N－S方程无普遍解；特殊条件下，有可能获得 准确或近似的分析解；通常通过数值计算获得离散解。
流动微分方程的应用求解步骤
(1)根据问题特点对一般形式的运动方程进行简化，获 得针对具体问题的微分方程或方程组。
(2)提出相关的初始条件和边界条件。
初始条件：非稳态问题 流体具有粘性，在与壁面接 固壁－流体边界： 触处流体速度为零。 边界条件 对非高速流，气液界面上， 液体－气体边界： 液相速度梯度为零。 液体－液体边界： 液液界面两侧的速度或切应 力相等。
矢量形式：v
非定常项 定常流动为0 静止流场为0
Dt
1 2 ( ) f p
扩散项（粘性力项） 对静止或理想流体为0 高速非边界层问题≈0 单位质量流体 的压力差
对流项 静止流场为0 蠕变流时≈ 0
单位质量流体 的体积力
流体流动微分方程的应用
Dv y
2 y 2 y 2 y 1 p fy 2 2 2 Dt y x y z
2 z 2 z 2 z Dvz 1 p fz 2 2 2 Dt z x y z
zz
xy yx
vx v y x y
yz
v y vz zy z y
vz vx zx xz x z
本构方程的讨论： 正应力与线变形速率： 流体正应力与三个速度偏导数有关
2 2
x x x 1 Dvx 1 p fx 2 2 2 Dt x x y z 3 x 2 2 2 Dv y y y y 1 p 1 fy 2 2 2 x Dt y y y z 3 2 2 2 z z z 1 Dvz 1 p fz 2 2 2 Dt z z y z 3 x
矢量形式：
1 Dv 2 f p Dt
适用于牛顿流体 const 常粘度条件下不可压缩流体的N－S方程： const
2 x 2 x 2 x vx vx vx vx 1 p vx vy vz fx 2 2 2 t x y z x x y z
r x 1 rvr 1 v v z 连： 0 r r r z v z v v z v z v z o z z分量： t v r r r v z z 流向 2 2 1 v z 1 v z v z 化简条件： r 2 2 2 z z 流动稳定 /t=0， r r r r 2 一维流动 vr=v=0， v r v v v v v r r分量： vr r v z r 轴向对称，/=0 t r r r z 2 2 v z 1 v 1 v 2 v r r 0 rv r r 2 2 r 2 r r r r z 2
矢量形式：
1 1 Dv 2 f p ( ) Dt 3
适用于牛顿流体 不可压缩流体的N－S方程： const
2 x 2 x 2 x Dvx 1 p fx 2 2 2 Dt x x y z
yy
x 2 vx v y vz p 2 x 3 x y z 2 vx v y vz p 2 y 3 x y z z 2 vx v y vz p 2 z 3 x y z y
2. 层流，流速x 方向
vy vz 0
v x v x 0 y z
3. 连续性方程 （不可压缩）
v x v y v z 0 x y z
v x 0 x
4. 设板平行于地面，质量力gx=gz=0,gy=－g(忽略质量力时，gy=0)
5. 平板沿z向相对于二板距离为无限宽，忽略此方向上边界面影响。
第三章
粘性流体运动
粘性流体运动微分方程
Navier－Stokes方程
以应力表示的运动方程，需补充方程才能求解。
对一维流动问题： 补充方程：牛顿剪切定律
对粘性流体流动问题： 补充方程：广义的牛顿剪切定律
即：牛顿流体本构方程
目的
关键：寻
求流体应 力与变形 速率之间 的关系
将应力从运动方程中消去，得到 由速度分量和压力表示的粘性流 体运动微分方程，即N-S方程。
xx p xx
xx
附加粘性正应力
附加粘性正应力的产生是速度沿流动方向的变化所导致的。
正应力与压力：
由于粘性正应力的存在，流动流体的压力在数值上一般不等 于正应力值。但有：
p
xx
yy zz 3
这说明：三个正压力在数值上一般不等于压力，但它们的平 均值却总是与压力大小相等。
v v max
vdA u A 1 R 2
r 1 R
2
R
0
v 2rdr
2 v max 1 R r 2v max 1 rdr 2 0 2 R R
v max
2 R 4 L
引入：阻力系数（又称范宁因子）
f
v v max
w
u2 2
r 1 R
2
而由牛顿粘性定律可知，圆管内层流时： dv 2 4 w v max u rR dr R R
8 16 16 f uR ud Re
引入：摩擦因数
64 4f Re
速度势和流函数
h 2
2
(3-68)
对(c)情形： v0=0，流体两端压力差 p = px－px+L
vx 1 p y (h y ) 2 L
h 2 p vx,max 2 L
(3-69)
(3-70) (3-71) (3-72)
1 dp vx y ( y h) 2 dx
h y 时, 2
将以上条件代入N-S方程，得
2v x p 2 x x (1)
p 0 y (2)
p 0 z
(3)
1 dp 2 解(1)式，得 v x 2 dx y C1y C2
边界条件——对(a) (b)情形： y=0时，vx=0; y=h时，vx=v0 得（3-64）式： v0 y 1 dp vx y( y h) 2 dx h 特别对(b)情形： v0 y v (3-65) (3-66) x y h 时 , v v dp x , max 0 h 0 dx 1 h 1 1 v x v x dy v0 (3-67) 流量 Q v v0Wh xWh 0
一 速度势函数
V 0 ，由矢量分析知，任一标 对于无旋流场，处处满足：
量函数梯度的旋度恒为零，所以速度 数 的梯度，即: V
切应力与角边形率：
流体切应力与角变形率相关。
牛顿流体本构方程反映了流体应力与变形速率之间的关系， 是流体力学的虎克定律（反映应力和应变的关系）。
适用于牛顿流体 流体运动微分方程——Navier－Stokes方程
Dvx p 2 x fx 2 Dt x 3 x x x
两平行平板间的层流流动
(a) (a) (a) 压力梯度＋上板速 v 压力梯度＋上板速 v0 0 压力梯度＋上板速 v