C1四面四面体网格生成V10
Ls-Dyna_负体积问题

LS-DYNA FAQ 中英文版-Negative Volume 负体积2007年09月13日星期四下午 10:26泡沫材料的负体积(或其它软的材料)对于承受很大变形的材料,比如说泡沫,一个单元可能变得非常扭曲以至于单元的体积计算得到一个负值。
这可能发生在材料还没有达到失效标准前。
对一个拉格朗日(Lagrangian)网格在没有采取网格光滑(mesh smoothing)或者重划分(remeshing)时能适应多大变形有个内在的限制。
LS-DYNA中计算得到负体积(negative volume)会导致计算终止,除非在*control_timestep卡里面设置ERODE选项为1,而且在*control_termination里设置DTMIN项为任何非零的值,在这种情况下,出现负体积的单元会被删掉而且计算继续进行(大多数情况)。
有时即使ERODE和DTMIN换上面说的设置了,负体积可能还是会导致因错误终止。
有助于克服负体积的一些方法如下:* 简单的把材料应力-应变曲线在大应变时硬化。
这种方法会非常有效。
* 有时候修改初始网格来适应特定的变形场将阻止负体积的形成。
此外,负体积通常只对非常严重的变形情况是个问题,而且特别是仅发生在像泡沫这样的软的材料上面。
* 减小时间步缩放系数(timestep scale factor)。
缺省的0.9可能不足以防止数值不稳定。
* 避免用全积分的体单元(单元类型2和3),它们在包含大变形和扭曲的仿真中往往不是很稳定。
全积分单元在大变形的时候鲁棒性不如单点积分单元,因为单元的一个积分点可能出现负的Jacobian而整个单元还维持正的体积。
在计算中用全积分单元因计算出现负的Jacobian而终止会比单元积分单元来得快。
* 用缺省的单元方程(单点积分体单元)和类型4或者5的沙漏(hourglass)控制(将会刚化响应)。
对泡沫材料首先的沙漏方程是:如果低速冲击type 6,系数1.0; 高速冲击type 2或者3。
TetGen用户手册中文版

一款优良的四面体格网生成和 3D Delaunay 三角剖分器
版本 1.5 用户手册 2012 年 11 月 5 日
Hang Si si@wias-berlin.de http://www.tetgen.osg c 2002 – 2012
周顺 陈强译 E_mail:shunzhou@ 2014 年 1 月
3 使用 TetGen.................................................................................................18
3.1 命令行语法..............................................................................................................18 3.2 命令行开关...............................................................................................................18 3.2.1 四面体格网化一个点集(-w, -v)...................................................................19 3.2.2 分段线性复合体(PLC)四面体格网化(-p, -Y).............................................21 3.2.3 生成优良格网 (-q).......................................................................................23 3.2.4 分配范围属性(-A)........................................................................................24 3.2.5 体积约束(-a).................................................................................................25 3.2.6 应用格网尺寸函数(-m)................................................................................25 3.2.7 重建四面体格网(-r) .....................................................................................25 3.2.8 插入附加点列表(-i)......................................................................................26 3.2.9 格网优化(-O)................................................................................................26 3.2.10 设置容差(-T) ..............................................................................................26 3.2.11 格网统计(-V)..............................................................................................27 3.2.12 其他选项.....................................................................................................27
ICEM自动体网格生成

Training Manual
Min size limit
Refinement = 12
1/10/2007 © 2006 ANSYS, Inc. All rights reserved.
11.0 New Features ANSYS, Inc. Proprietary
Inventory #002382 1-14
11.0 New Features
自动体网格划分
1/10/2007 © 2006 ANSYS, Inc. All rights reserved.
11.0 New Features ANSYS, Inc. Proprietary
Inventory #002382 1-1
ANSYS v11.0
体网格划分
• 自动创建三维网格单元填充空间
– 一般为 “非结构”
• 主要为 四面体网格
– 全三维分析
• 二维分析不能真实模拟
– 内/外流动模拟 – 结构化实体建模 – 热应力 – 更多内容!
• 标准流程
– 从几何开始 • Octree tetra(八叉树四面体–)从已存在的网格开始
– Robust(鲁棒性) – Walk over features
• 八叉树四面体网格对几何的需求
Training Manual
需要封闭的几何模型
Build Diagnostic Topology
几何修复工具能快速 找到问题并予以解决
查找丢失的面
查找洞和缝隙
四面体能忽略小于当地网格尺寸的缝隙
推荐捕捉几何的特征线和点
推荐定义区域的材料点
对于简单的几何,四面体网格生成器能够自动生成
• 加密
– 沿圆上布置的网格数量 – 避免网格细分达到global
四面体网格生成方法的与实现

四面体网格生成方法的研究与实现
田素垒 , 张志毅 , 陈 敏 , 张 娴
( ) 西北农林科技大学 信息工程学院 ,陕西 杨凌 7 1 2 1 0 0
摘 要 : 针对四面体网格生成过程中需 要 人 工 构 造 背 景 网 格 和 指 定 尺 寸 信 息 的 问 题 , 提 出 了 一 种 自 动 计 算 网 格 尺 寸 的 方 法 。 该方法通过按层次推进产生四面体网格 , 根据周围前沿面的尺寸 和 法 线 信 息 , 计 算 新 生 成 四 面 体 的 尺 寸 , 使 四 面 体 网 格在尺寸上能够均匀分布 。 在网格生成过程中 , 无需人工指定相关信 息 , 并 能 保 证 新 生 成 四 面 体 的 质 量 。 联 立 直 线 和 平 面 的参数方程 , 根据方程组解的情况判断线段和三角形是否相交 , 并对相交 的 条 件 作 了 详 细 的 分 析 。 使 用 空 间 八 叉 树 管 理 前 沿面 , 降低与前沿面相关操作的复杂度 。 数值算例表明 , 该方法能够生成较高质量的四面体网格 。 关键词 : 四面体网格 ; 层次推进 ; 尺寸计算 ; 相交测试 ; 八叉树 )1 中图法分类号 : T P 3 9 1 . 4 1 文献标识号 :A 文章编号 : 1 0 0 0 7 0 2 4( 2 0 1 2 1 4 4 1 6 0 6 - - -
( ,N ,Y ) C o l l e e o f I n f o r m a t i o n E n i n e e r i n o r t h w e s t A r i c u l t u r e a n d F o r e s t U n i v e r s i t a n l i n 7 1 2 1 0 0, C h i n a g g g g y g g
三维约束Delaunay四面体网格生成算法及实现-精选文档

三维约束Delaunay四面体网格生成算法及实现一、引言网格生成是工程科学与计算科学相交叉的一个重要研究领域,是有限元前置处理的关键技术。
从总体上讲,网格生成技术分为结构化网格和非结构化网格两大类,其中,非结构网格能适应复杂外形且自动性高,逐渐成为数值求解偏微分方程的有效方法之一,它在有限元分析、科学计算可视化、生物医学和机器人等学科领域具有重要的应用价值。
当前,典型的非结构四面体网格生成算法主要有八叉树法(Octree)、前沿推进法(AFT)和Delauay法等。
较其它方法而言,Delauay法具有成熟的理论基础和判断准则,更适用于三维实体的网格生成。
Delaunay法最早由Delaunay于1934年提出,在此基础上,Chew、Ruppert、Miller和等学者在算法改良方面开展了大量研究。
目前,二维Delaunay法的研究已趋成熟,但三维Delaunay法在处理复杂实体的边界一致性问题仍是学者研究的热点。
本文在前人研究的基础上,采用约束Delaunay四面体(Constrained Delaunay Tetrahedralization ,CDT)法来处理指定区域的边界一致性问题,编制了基于CDT的三维自适应四面体网格生成程序,并对工程实例进行了分析。
二、CDT定义及算法(一)CDT定义在三维区域的四面体网格生成中,四面体的外接球内部不包含任何网格顶点的四面体称为符合Delaunay准则的四面体,如果一个点集的四面体生成中每个四面体都符合Delaunay准则,则此四面体生成是点集的Delaunay四面体生成。
在一定条件限定之下以Delaunay准则为标准将空间分解成许多四面体称为约束Delaunay四面体生成。
通常情况下,将约束Delaunay三角(二维)/四面体(三维)生成的问题记为CDT。
(二)CDT存在性由于三维空间存在不能划分为四面体集合的多面体(如多面体),故给定一个用分段线性复合体(piecewise linear complexes,PLCs)描述的三维区域,的CDT可能不存在。
四面体网格生成方法的与实现

一种全四边形有限元网格生成方法——堆砌法

一种全四边形有限元网格生成方法——堆砌法一种全四边形有限元网格生成方法——堆砌法第36卷第l0期2000年10月机械工程CHINESEJOURNALOFMECHANICALENGINEERING V36No10Oct.2000一种全四边形有限元网格生成方法——堆砌法王世军(西安理工夫学机械与张广鹏院西安710048)7一7仡1))中围j2_-一——,0《ul1..0前言有限元方法是一种在工程上非常重要的数值分析方法,尤其是在复杂结构的分析中得到广泛应用随着计算机技术的快速发展,分析问题的规模越来越大,从印,70年代的几十至几百个结点到目前的几十万至几百万个结点.用人工进行网格划分已经不能满足需要.另一方面,自适应分析与设计技术的出现与发展,也迫切要求网格划分自动化.有限元网格的自动生成算法有着潜在的,巨大的价值,在这个领域一直有着广泛的研究.这些研究多数都使用三角形网格,三角形单元的精度较四边形低,在分析过程中并不推荐使用.也有部分算法可以实现部分的或完全的四边形网格划分,但是这些算法往往存在这样或那样的问题,不能获得广泛使用.铺路法(Pavingmethod)_】是目前较好的一种全四边形网格生成算法_2"J,生成的网格质量较高.缺点是算法复杂,计算时问长,对复杂形状的划分区域适应性差,因此,难以将其推广到三维区域.本文针对铺路法的这些特点,提出了一种改进算法一堆砌法,较好地克服了铺路法存在的缺点.1堆砌法的原理铺路技术是将单元一层一层从边界铺到区域的内部,如图1所示,这些单元最终会填满整个划分区域.一般说,在区域内部铺设单元时,肯定会产生交叠.在一层单元铺设完毕后,要对交叉的部分进行特殊处理——边的缝合和单元湮灭,使得生成的单*西安理工大学青年科技基盎资助项目,20000228收到初稿2o~o4i5收到修改祷元之间保持相容性.之后进行光顺处理.交叉部分的处理,是铺路技术的难点.区域形状越复杂,产生的交叉越多,处理起来越麻烦,处理时间也越长.口口(b)日醒噩(c)图1铺路法原理堆砌技术的基本思想是沿着网格划分区域内的一条直线铺设单元,铺完一层单元以后,平移这条直线,在新的平行线上继续铺设新一层单元.直到整个区域铺满单元.如图2所示,在铺设每一层单元时,都是从区域的一个边界开始向另一个边界铺设.(B)图2螓砌浩原理图口加∞年1O月王世军等:一种全四边形有限元网格生成方法——堆砌法铺完一层后,再开始铺设另一层,直到铺满整个区域.可以看出,与铺路法明显不同的是,这里每一个单元层都是不封闭的,一般情况下只有2个端点在固定边界上,单元层不会产生交叉,避免了复杂的单元缝合处理.下面说明堆砌法的几个主要步骤.1.1单元的生成单元的生成是堆砌法的核心,涉及多方面的内容.首先是选择背景线的起点,问距和推进方向,其次是单元组中单元的生成,最后是单元的光顺处理.在任何一个单元生成之前,必须首先定义单元的大小(单元的尺度).单元的尺度是以单元的边长来表示的,它是单元边长的期望值.单元尺度是在划分区域的背景上,以尺度场的方式定义的.1.2背景线的确定背景线(也称为水面线)是一条指示单元层铺设位置和方向的线.背景线的起点可以是任意的边界位置,方向也可以随机选定.在铺出第1层单元以后,根据第2层单元中的最大的基本尺寸确定第2条背景线的位置.通常,背景线的方向可以选择几何区域最大尺寸的方向,这样生成的单元层数比较少,相应地,不规则结点的数目也比较少.如图3所示,由于背景线的控制,不会发生铺路法中必然产生的单元层的交叠.(日)多十浮动边界的生成(b)多十浮动边界的台井图3浮动边界的生成与合并1.3根结点的选定与单元层的生成网格划分之前,首先要将区域的边界按指定的单元数目或大小进行离散,形成离散边界.选择背景线以下与离散边界结点最近的结点作为第1层单元的根结点.第1层单元的铺设是从根结点开始,沿着固定边界向第2个根结点单向铺设.浮动边界与固定边界的交点作为单元层的生长结点从第2 层开始,以新旧浮动边界的交点作为单元的生长结点.单元层的第1个生长结点总是浮动边界与固定边界的交点.这样,可以避免铺路法中单元铺设位置的复杂判断.通常情况下,根结点是成对的.而且可以有多对.在单元的生成过程中,可以产生新的根结点,原有的根结点也可能湮灭.如图3所示.1.4单元组中单元的生成单元的生成分两步,第1步是预测,第2步是校正. 图4显示了预测步骤的过程.构造1个矢量厶c-,矢量的方向根据结点A剩余角度大小相应地取1/2,1/3剩余角度,保证新生成单元A点内角尽图4新结点位置的搜索可能接近90~.类似地可以构造另一个矢量k,.两个矢量的交点就是新结点的试探位置C.找到初始的试探位置后,还需进一步的校正,以改善新单元的质量.以基本边长为半径,以A,B结点为圆心,构造2个圆.求2个圆的交点.交点可能有2个,1个,或者没有.对于存在2个交点的情况.取内角为正的结点为.可以证明,对于有一个交点和没有交点的情况,只要保证前面生成单元的内角均接近90~,就不会发生这2种情况.得到2个新结点的位置以后,以这两个结点联线的中点作为新单元的最终结点位置C.这样获得的单元,兼顾边长和角度的要求,单元生成的速度比较快.在试探新结点位置之前,要先作一下检查,防止生成单元交叠或与边界不相容.如图4所示.检查的方法是以为半径,以当前结点为圆心,构造一个圆=kl^r一l+N (I)k是1个系数.一和+是2个矢量,起点都是结点^r,末端点分别是结点—I和^r…,如图4所74机械工程第36卷第lO期示.较快.在这个圆内,可能存在固定边界上的结点或多于1个的旧浮动边界上的结点.如果存在这两种情况,就不能按照前面的步骤生成单元.第1种情况,圆内存在固定边界结点,说明浮动边界已经接近固定边界.如果固定结点在半径为R:√21的同心圆内,则以固定比边界上的结点作为新结点位置.l为基本边长.固定边界和浮动边界因为有公共结点而被分为2个部分.新生成的固定边界和浮动边界两两构成的封闭区域,其边界结点数应保持为偶数,否则不应以这个固定结点作新结点,而位取另1个相邻的固定结点作边界结点.如果在圆内存在另外1个与之相邻的固定边界结点,就选择另1个.否则,按前述方法生成新结点.第2种情况,圆内存在第二个浮动边界上的结点,新结点的位置应该取在圆心与浮动边界的结点联线的中心上.为保持浮动边界的平直性,新单元生成以后,应当结束单元层的生成,从新的根结点开始生成新一层单元.由上述单元生成过程可以看出,新方法与铺路法相比,有几个优点.第一,不会产生铺路法特有的单元交叠,从而避免了包含复杂的拓扑形状判断的单元缝合过程.第二,铺路法中楔单元的插入和角结点单元的形成在这里都是单元生成过程中自然形成的,不需要特殊处理,程序结构得到简化.第三,单元的生成过程已经考虑到相邻的未生成单元的形状,不会生成质量越来越差的单元.避免了铺路法中每生成一个单元都要进行的局部光顺处理.2单元的光顺处理在区域内充满单元以后,对整体单元的质量进行一次检查,如果单元角度或边长比有超过允许值的,需要对整体单元进行光顺处理,以进一步提高整体单元的质量.这里使用修正的加权长度的拉普拉斯光顺算法j.这种算法是用一系列矢量从一个内部结点指向这个结点所有相邻结点.用一个贡献矢量作为这个内部结点相邻结点的贡献量.如图5所示,结点位置的修正量为互IcJIcj△=号置'cJIc是与内部结点i相邻结点的贡献矢量,是与结点i相邻结点的个数.这个算法使得边界单元的边趋向垂直于边界,边长则趋于均化,而且收敛速度3算例N.图5单元的光顺处理图6是在一个内部含有空洞的区域上获得的网图6古有复杂内部边界的区域剖分效果格.背景线方向沿水平方向,自下而上推进.网格的基本尺寸定义得比较大,生成网格在边界上仍然有较好的形状和尺寸一致性最大偏差角△=29.1..图7是一个具有复杂边界形状的陕西省地图的固7具有复杂外边界的区域剖分效果2OOO年10月王世军等:一种全四边形有限元网格生成方法——堆砌法轮廓.网格密度定义为上疏下密.背景线方向沿水平方向,推进方向也是自下而上.图示结果表明,算法对复杂边界的适应性是比较强的,疏密过渡也较为平滑.最大偏差角A:3O.7..4结论由于网格划分过程的复杂性,精确地评价一个算法的优劣是困难的.新算法避免了单元层之间的交叠,从而避免了网格生成过程中复杂的拓扑结构的判断和单元形状校正所需的迭代计算.因而可以定性地说,这-t-~t法与铺路法相比是一个好的算法.圈8是实测的网格结点数与划分时间的关系.在60∞个结点以下,结点数与时间基本保持线性关系之*匠蕾晶同格结点数/个数图8网格结点数与时间的关系参考文献TedDIll~ker,Micl~lBsIpIler咖Paving:ar?e8pn日chL0automatedq【md_咖meshm帆IntJ.Numberie~9inbginl1g,1991,32:811—847752SabinM.Criteriaforc0ⅢD日m0fal1l0mcmeshge~aon m由A.EI】gs0盘ware,1991,13(5/6):2213—2253Hc-LeKFimteelementmesh珊0I|meLl:areviewarIdcl~itlcationC~uter-Aided咄,1988,加(1):27—384M哪S.NoelF,LeonJC.r唧劬0n0fquadrilateralmesl1s 0nfree-ferm目u1b∞C∞1a-,d~ures,1999,71:505—524HEA]PlNG:ANEWM咽1l10DmRALLQ10~DIlILA/~_,SttGE既10NWang蜘皿ⅫY~2eiZhangGuo,~,peng(_衄妇ofwf0)Atr毗Ametl~a—b嘲pil】gmeIIl0d,Ⅶl1icI1岬b曰oulld htodetenffmer日∞e_吐ofquadrilateralelements presentedThemd-l0disn∞陀simplelpavingIT_et}-0din ~turearld_细inu目eitavoidsa∞8esimelcrIslⅥe目lelemellnt~laye~-Inthisp日per,II'e0fyofl|pn,tetl~is缸irred.Secondly,tw.忸amplesaregiven.AIl86t.;tsl~erfol'lnanceiBevuaKey,r凼:Finiteele~enlMee~hQI1ad同日-eIalH嘲ping作者荷彳r王世军,男,1967年出生,讲师.博士生.主要从事机械结掏的有限元分析爰同格捌分算{击的研究.(上接第71页)REC暇E圈睡:ED00N0FAMaI】.I℃H'sE】GAGEMENTGeAn//nGao咖.肺删(同of西)Ab喇AI1ewccmetl~ofhydrauliceyli~risput.ItcontroltI.ecydir?d盱speedbdiscretepr黜ise也pIcem咖.Theperformi~itufionAjIfr(A岫舢a0edmeclmi~tI】蛐日mis吕i0I.)vehicle'sclutchalwaysadop饵hya~alcylindBr.But mt~iollpIeE艘1bedbe血gectedl0manyfaete~inreBIily,has血ec0f胡'svi州arIdtI.ete帅force0fIIg,eIc.Itbr;di伍to.1heperimen出thattI.epmf~edmethodcanetI.eclutcher日IaHy~--eeisepeedarld删atv0ffaulttoler~.脚:Hy~ulieeyli~rHiglIswitchdec舡啊rmrcvalveSpeed∞rIⅡ0l作者苘彳r葛安林.男,1936年出生.吉林工业大学穰力机艟传动研究所所长,教授,博士生导师,主要从事自动变速理论与控制技术的研究.先后获国家,省部毅奖励lO余璃.发明专利6项,发表论文6o余篇。
Ansys 第七节 ICEM实例-棱柱体网格自动生成
– 确认 part定义正确
– 检查是否存在应属于一个part一些单元,却分散到其他part – 避免一些孤立单元的拉伸(会临近单元很可能破坏) – 修改不合适单元的par分配
9/9/05
ANSYS ICEMCFD V10
Inventory #002277 C4-4
金子塔型单元覆盖或替换
Ortho weight 正交权因子
– 节点移动权因子(0为提高三角形质量 ,1为提高棱柱正交性)
Fillet ratio 圆角比率
见下一页
9/9/05
ANSYS ICEMCFD V10
Inventory #002277 C4-8
高级选项 – 圆角比率Fillet Ratio
Fillet Ratio = 1.0
Inventory #002277 C4-9
高级选项 –最大棱柱角 Max Prism Angle
Max prism angle 最大棱柱角 – 控制弯曲附近或到邻近曲面棱柱层的生成 – 在棱柱网格停止的位置用金字塔连接形网格 – 通常设置为120º 到180º 范围内 – 这些需要经验. 如果只从一个 part拉伸而临近的part不执行拉伸操作, 并
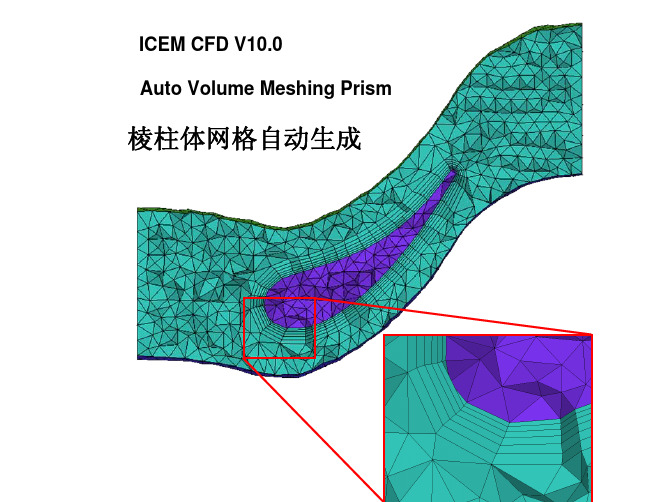
ICEM CFD V10.0 Auto Volume Meshing Prism
棱柱体网格自动生成
棱柱网格划分
对于CFD应用来说,完全的四面体网格并不理想.
– 边界层条件需要几层棱柱单元 – 两种方式生成棱柱体网格 – Mesh -> Prism
• 邻近壁面几何生长棱柱层. 定义局部初始高度(如果必要)initial height, growth ratio
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
设置表面/曲线网格参数
– Maximum element size/Element size • 基于边的长度 • 在表面或曲线上 • 需要乘以 Scale Factor
– Number of Nodes • 仅仅曲线时的参数 • 沿曲线的节点数
– Height • 面上体网格的高 • 仅适用于六面体/三棱柱
ANSYS ICEMCFD V10
Inventory #002277
C1-6
全局网格参数
9/9/05
全局网格参数
– Mesh -> Set Global Mesh Size -> General Parameters
– Scale Factor • 乘以其他参数得到实际网格参数 • 例子: – 输入 Maximum size set to 4 units – Scale factor 设为 3.5 – 实际 max element size; 4 x 3.5 = 14.0 units • 改变了全局的网格尺寸(体、表面、线)
• Centroid of 2 points – 选用两点中间点定义 – 首选的
• At specified point – 用指定点定义材料点区域
– By Topology • 通过封闭表面定义体区域 • 首先必须创建拓扑结构
• Entire model – 自动定义所有封闭区域
• Selected surfaces – 用户选择能封闭的表面
ICEM CFD V10.0
自动四面体网格划分 Tetra
Octree 方法
大多数四面体网格生成器 – 首先生成三角形网格
• 面到面处理
– 需要处理每一个表面
• 困难
– 细长表面, – 缺陷表面的参数化 – 缝隙
– 完成表面网格后
• 基于面网格生成体网格
网格细节
面网格
几何
9/9/05
ANSYS ICEMCFD V10
9/9/05
ANSYS ICEMCFD V10
Inventory #002277
C1-8
局部网格控制
用Parts设置网格参数
– “所有Part列在表中Spreadsheet” – 能快速方便设置Part的网格参数 – 网格参数位于列中 – Part 列于行中 – 所有 Part 中的对象都能获得该参数值
ANSYS ICEMCFD V10
长条几何忽略
Inventory #002277
C1-3
使用点和线
引入几何模型
• 曲线和点包括 • 网格参数在面和线上设置
捕捉了网格细节
• •
9/9/05
不包括点和线 仅在表面设定网格大小
粗化的网格忽略了几何细节
• 曲线和点影响网格捕 捉几何的能力!
• 创建拓扑 能容易地 捕捉几何的特征线与 点
ANSYS ICEMCFD V10
Inventory #002277
C1-10
Octree 四面体网格划分
9/9/05
Mesh -> Mesh Volume -> Tetra -> From Geometry
– 能自动划分网格
– Smooth mesh
• 完成初始网格后自动光滑网格以提高质量
– 粗化网格Coarsen mesh
• 设置全局、表面和线段的网格参数
– 注意网格数量信息
几何修复工具能快速 找到问题并予以解决
9/9/05
丢失入口面
高亮黄边显示洞的存在
ANSYS ICEMCFD V10
Inventory #002277
C1-5
体/材料点
9/9/05
体区域 – 选项
• 复杂几何推荐使用 – Geometry -> Create Body – 两种材料点定义方法
– 要单独设定面或线的参数,
– 可先选Surface 或 Curve Mesh Size,再使用Part选择
9/9/05
ANSYS ICEMCFD V10
Inventory #002277
C1-9
设置网格尺寸
9/9/05
Create Mesh Density – 用一定大小的网格填充体区域,例如. 在机翼尾迹设定这样 的区域 – 无实际几何!(例如圆柱)
Inventory #002277
C1-2
Octree 方法
ICEM Tetra 使用 独立于几何小面的 Octree 方法 – 体网格
• 首先生成独立的几何模型 • 网格调整、映射到表面、线和点上 • 产生表面网格
– 网格与几何表面的不关联
• 不是表面上所有的边需要捕捉
网格细节
几何
9/9/05
网格
– Smooth transition
• 用 Delauney 算法重新填充体网格 – 同 Mesh Tet -> From Surface Mesh
ANSYS ICEMCFD V10
Inventory #002277
C1-4
Octree 划分对几何的要求
• 需要封闭的几何模型
– 实体方式显示几何表面
• 查找丢失的面 • 查找洞和缝隙
– 四面体能容忍小于当地网格尺寸的缝 隙
• 推荐捕捉几何的特征线和点
• 推荐定义区域的材料点
– 对于简单的几何,四面体网格生成器 能够自动生成物质点
–பைடு நூலகம்Global Element Seed Size
• 与 Scale factor相乘
• 模型中最大可能的网格大小
• 可以设置任意大的值
– 实际网格很可能达不到那么大
MAX
– 复选Display
• 显示体网格的大小示意
ANSYS ICEMCFD V10
Inventory #002277
C1-7
局部网格控制
– Height Ratio • 六面体/三棱柱层的增长率
– Number of layers • 均匀的四面体增长层数或三棱柱增长层数 • 大小由表面参数确定
– Tetra Size Ratio • 四面体平均生长率
– Minimum Size • 表面最小的四面体 • 自动细分的限制
– Maximum Deviation • 表面 三角形中心到表面的距离小于设定值,就停止细分
• 网格节点不限制在密度盒表面 • 可以与几何表面相交
– 在密度盒内创建密度盒 – 设置Size
• 需要乘以比例因子Scale Factor • Ratio 网格生长比率 • Width 密度盒内填充网格的层数
– 类型Type
• Points – 用2-8个 位置的点(2点为圆柱状)
• Entity bounds – 用选择对象的边界作密度盒
