信号与系统-14-冲激偶取样性证明
《信号与系统引论》郑君里版第一章课后答案解析
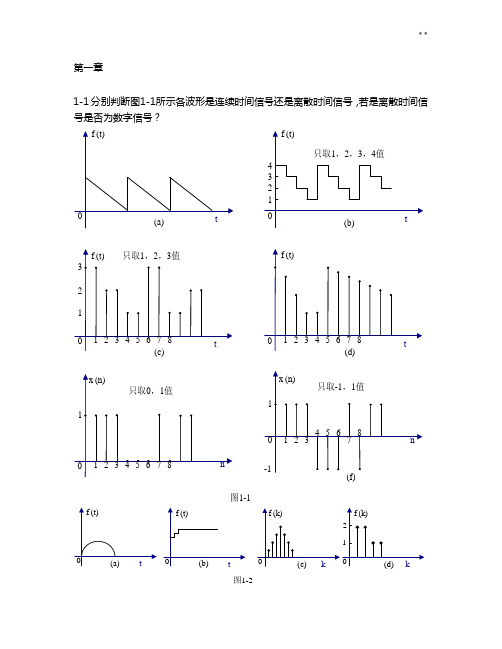
第一章1-1 分别判断图1-1所示各波形是连续时间信号还是离散时间信号,若是离散时间信号是否为数字信号?图1-1图1-2解 信号分类如下:⎪⎪⎩⎪⎪⎨⎧⎩⎨⎧--⎩⎨⎧--))(散(例见图数字:幅值、时间均离))(连续(例见图抽样:时间离散,幅值离散))(连续(例见图量化:幅值离散,时间))(续(例见图模拟:幅值、时间均连连续信号d 21c 21b 21a 21图1-1所示信号分别为 (a )连续信号(模拟信号); (b )连续(量化)信号; (c )离散信号,数字信号; (d )离散信号;(e )离散信号,数字信号; (f )离散信号,数字信号。
1-2 分别判断下列各函数式属于何种信号?(重复1-1题所示问) (1))sin(t e at ω-; (2)nT e -; (3))cos(πn ;(4)为任意值)(00)sin(ωωn ;(5)221⎪⎭⎫⎝⎛。
解由1-1题的分析可知: (1)连续信号; (2)离散信号;(3)离散信号,数字信号; (4)离散信号; (5)离散信号。
1-3 分别求下列各周期信号的周期T : (1))30t (cos )10t (cos -;(2)j10t e ; (3)2)]8t (5sin [;(4)[]为整数)(n )T nT t (u )nT t (u )1(0n n ∑∞=-----。
解 判断一个包含有多个不同频率分量的复合信号是否为一个周期信号,需要考察各分量信号的周期是否存在公倍数,若存在,则该复合信号的周期极为此公倍数;若不存在,则该复合信号为非周期信号。
(1)对于分量cos (10t )其周期5T 1π=;对于分量cos (30t ),其周期15T 2π=。
由于5π为21T T 、的最小公倍数,所以此信号的周期5T π=。
(2)由欧拉公式)t (jsin )t (cos e t j ωωω+=即)10t (jsin )10t (cos e j10t +=得周期5102T ππ==。
《信号与系统》30道思考参考答案

13、试说明傅里叶变换、拉普拉斯变换和 Z 变换在信号分析中的作用、各自的 局限性及他们之间的联系。
答:傅里叶变换将系统的激励和响应关系从时域变换到频域来研究,从解微分方 程转化为解代数方程;拉普拉斯变换则将信号从时域变换到了复频域,同样也是 从解微分方程转化为解代数方程;z 变换是将时域离散时间序列变换成为 z 域的 连续函数,将离散问题转化成了连续问题。
对信号能够完成某种变换或运算功能的集合体称为系统。系统在哲学上有着 更为广泛的涵义:一般是指由若干相互作用和相互依赖的事物组合而成的具有某 种特定功能的整体。
系统分析与信号分析密不可分,对信号进行传输和加工处理,必须借助于系 统;离开了信号,系统将失去意义,分析系统就是分析某一个特定的信号,分析 信号与信号的相互作用,信号分析是系统分析的基础。所以信号与系统之间的关 系是相辅相成的,离开了信号谈论系统是毫无意义的,系统只能依靠信号的作用 才能显示出特性及用途,信号离开了系统,也就不能发挥其应有的作用。
方法是根据题意列出微分方程,然后求解微分方程。步骤是:(1)求解通解: 由方程左边部分得到的特征方程所得到的特征频率解得的系统的自然响应(或自 由响应);(2)求特解:由激励得到系统的受迫响应;(3)代入初始条件,确定 通解和特解中的待定系数。
卷积法:将响应分成两个部分:(1)零输入响应:系统在没有输入激励的情
Step4:乘积,把变换后的两信号相乘; 例如: x(τ )h(t −τ )
Step5:积分,根据位移不同导致的信号乘积的不同结果,在非零区间进行积分
∫ 运算; 即 t2 x(τ )h(t −τ )dτ 。 t1
奥本海姆《信号与系统》配套题库【课后习题】(周期信号的傅里叶级数表示)

第3章周期信号的傅里叶级数表示基本题3.1 有一实值连续时间周期信号x(t),其基波周期了T=8,x(t)的非零傅里叶级数系数为a1=a-1=2,a3=a-3=4j。
试将x(t)表示成:解:3.2 有一实值离散时间周期信号x[n],其基波周期N=5,x[n]的非零傅里叶级数系数为,试将x[n]表示成:解:3.3 对下面连续时间周期信号求基波频率ω0和傅里叶级数系数a k,以表示成解:即非零的傅里叶级数系数为3.4 利用傅里叶级数分析式计算下连续时间周期信号(基波频率ω0=π)的系数a k:解:因ω0=π,故3.5 设x1(t)是一连续时间周期信号,其基波频率为叫ω1,傅里叶系数为a k,已知x2(t)=x1(1-t)十x1(t-1),问x2(t)的基波频率ω2与ω1是什么关系?求x2(t)的傅里叶级数系数b k与系数a k之间的关系。
解:x1(1-t)和x1(t-1)的基波频率都是ω1,则它们的基波周期都是T1=2π/π。
因为x2(t)是x1(1-t)和x1(t-1)的线性组合,所以x2(t)的基波周期,即ω2=ω1。
又故即3.6 有三个连续时间周期信号,其傅里叶级数表示如下:利用傅里叶级数性质回答下列问题:(a)三个信号中哪些是实值的?(b)哪些又是偶函数?解:(a)与式对照可知,对于x1(t),有由共轭对称性可知,若x1(t)为实信号,则有显然故x1(t)不是实信号。
同理,对于x2(t),对于x3(t),由于故可知x2(t)和x3(t)都是实信号。
(b)由于偶函数的傅里叶级数是偶函数,由上可知,只有x2(t)的a k是偶函数,故只有x2(t)是偶信号。
3.7 假定周期信号x(t)有基波周期为T,傅里叶系数为,的傅里叶级数系数为b k。
已知,试利用傅里叶级数的性质求a k用b k和T表达的表达式。
解:当k=0时,故3.8 现对一信号给出如下信息:(1)x(t)是实的且为奇函数;(2)x(t)是周期的,周期T=2,傅里叶级数为a k;(3)对|k|>1,a k=0;(4)试确定两个不同的信号都满足这些条件。
信号与系统 冲激函数

4
4
4
2
1
f (t) (t 2 4)dt 0
1
第1章 信号与系统的基本概念
1.6 基本离散时间信号
单位阶跃序列 单位抽样序列 复指数序列
第1章 信号与系统的基本概念
单位阶跃序列
0 n 1,2,...... u[n] 1 n 0,1,2,......
f '(ti )
第1章 信号与系统的基本概念
例6 计算下列函数的值
f (t ) (t 2 4)dt
1
f (t ) (t 2 4)dt 1
解: (t 2 4) 0 t 2
f
' (t1 )
d dt
(t 2
4)
t 2
2t
4
f
' (t2 )
d dt
(t 2
4)
t 2
2t
4
(t第21章信4号)与系统的1基本概念(t 2) 1 (t 2)
4
4
1 [ (t 2) (t 2)]
4
(t 2 4)dt
[ 1 (t 2) 1 (t 2)]dt 1 2 1
f (t) ' (t)dt f ' (0)
t
'( )d (t)
第1章 信号与系统的基本概念
-
x(t )
(t
t0 )dt
x(t0 )
x(t) (t
例5:计算下列积-分(性质的应用)
(完整版)《信号与系统》期末试卷与答案

《信号与系统》期末试卷A 卷班级: 学号:__________ 姓名:________ _ 成绩:_____________一. 选择题(共10题,20分) 1、n j n j een x )34()32(][ππ+=,该序列是 D 。
A.非周期序列B.周期3=NC.周期8/3=ND. 周期24=N2、一连续时间系统y(t)= x(sint),该系统是 C 。
A.因果时不变B.因果时变C.非因果时不变D. 非因果时变3、一连续时间LTI 系统的单位冲激响应)2()(4-=-t u et h t,该系统是 A 。
A.因果稳定B.因果不稳定C.非因果稳定D. 非因果不稳定4、若周期信号x[n]是实信号和奇信号,则其傅立叶级数系数a k 是 D 。
A.实且偶B.实且为奇C.纯虚且偶D. 纯虚且奇5、一信号x(t)的傅立叶变换⎩⎨⎧><=2||02||1)(ωωω,,j X ,则x(t)为 B 。
A.tt22sin B.t t π2sin C. t t 44sin D. ttπ4sin 6、一周期信号∑∞-∞=-=n n t t x )5()(δ,其傅立叶变换)(ωj X 为 A 。
A.∑∞-∞=-k k )52(52πωδπB. ∑∞-∞=-k k)52(25πωδπ C. ∑∞-∞=-k k )10(10πωδπD.∑∞-∞=-k k)10(101πωδπ7、一实信号x[n]的傅立叶变换为)(ωj e X ,则x[n]奇部的傅立叶变换为C 。
A. )}(Re{ωj eX j B. )}(Re{ωj e X C. )}(Im{ωj e X j D. )}(Im{ωj e X8、一信号x(t)的最高频率为500Hz ,则利用冲激串采样得到的采样信号x(nT)能唯一表示出原信号的最大采样周期为 D 。
A. 500 B. 1000 C. 0.05D. 0.0019、一信号x(t)的有理拉普拉斯共有两个极点s=-3和s=-5,若)()(4t x e t g t=,其傅立叶变换)(ωj G 收敛,则x(t)是 C 。
信号与系统

1 CR ht e u t t CR
1
2-9
基于基尔霍夫电压回路、电流定理列出系统方程:
diL t t xt iL t uc t C d uc t L uc dt R dt 2 d u t L duc t uc t xt 代入系统元件值 整理,得 LC 2 dt R dt du t d 2u t 3 c 2uc t 2 xt 整理得 dt 2 dt 2 2 2 根据特征方程: 3 2 0 求到特征根:1 1
(5)信号的微分
df (t ) f t f ' t dt
(6)信号的积分 将信号f(t)在区间(-∞,t)内求一次积分,成为对信号f(t)的积分运算, t 所得信号y(t)= f d 称为f(t)积分信号。
8、正交函数集的判断
t2
t1
0 g i (t ) g j (t )dt Ki
再进一步对式子进行降阶,可得
1 r t tut 2
平衡
可以看出,r(t)在起始点无跳变,即r(0+)- r(0-)=0 所以, r(0+)=r(0-)=1
2-5 (1)首先求取零输入响应rzi(t) 特征方程为:
特征根为:
rzi t C1 C2t e t
t
由(1)中求解可知h(t)的形式为: ht k1 k 2t e t
求取冲激响应h(t)的导数,可得
d ht k1 t k 2 k1 k 2t e t u t dt d2 ht k1 ' t k 2 k1 t k1 2k 2 k 2t e t u t dt 2
信号与系统题库(完整版)

信号与系统题目部分,(卷面共有200题,0。
0分,各大题标有题量和总分) 一、选择题(7小题,共0.0分)[1]题图中,若h '(0)=1,且该系统为稳定的因果系统,则该系统的冲激响应()h t 为。
A 、231()(3)()5tt h t e e t ε-=+- B 、32()()()tt h t e e t ε--=+C 、3232()()55tt e t e t εε--+D 、3232()()55tt e t e t εε--+-[2]已知信号x [n]如下图所示,则x [n]的偶分量[]e x n 是。
[3]波形如图示,通过一截止角频率为50rad sπ,通带内传输值为1,相移为零的理想低通滤波器,则输出的频率分量为() A 、012cos 20cos 40C C t C t ππ++ B 、012sin 20sin 40C C t C t ππ++ C 、01cos 20C C t π+ D 、01sin 20C C t π+[4]已知周期性冲激序列()()T k t t kT δδ+∞=-∞=-∑的傅里叶变换为()δωΩΩ,其中2TπΩ=;又知111()2(),()()2T T f t t f t f t f t δ⎛⎫==++⎪⎝⎭;则()f t 的傅里叶变换为________。
A 、2()δωΩΩ B 、24()δωΩΩ C 、2()δωΩΩ D 、22()δωΩΩ[5]某线性时不变离散时间系统的单位函数响应为()3(1)2()kkh k k k εε-=--+,则该系统是________系统。
A 、因果稳定B 、因果不稳定C 、非因果稳定D 、非因果不稳定 [6]一线性系统的零输入响应为(23kk --+)u(k), 零状态响应为(1)2()k k u k -+,则该系统的阶数A 、肯定是二阶B 、肯定是三阶C 、至少是二阶D 、至少是三阶 [7]已知某系统的冲激响应如图所示则当系统的阶跃响应为。
智慧树答案信号与系统(西安交通大学)知到课后答案章节测试2022年

绪论1.图像增强属于系统综合。
答案:对2.这门课程中研究的信号是确定性信号。
答案:对第一章1.ω0越大,离散时间序列sin(ω0n)的频率越高。
答案:错2.离散时间信号在n1≦n≦n2区间的平均功率为答案:错3.一切物理可实现的连续时间系统都是因果的。
答案:错4.对任意的线性系统,当输入为零时输出也一定为零。
答案:对5.已知信号x当n<—2或n>4时等于零,则x当()时一定等于零。
答案:n<-7和n>-16.某系统的输入输出关系为y=,则该系统是一个()系统。
答案:因果不稳定7.离散时间信号的基波频率是()。
答案:8.在信号与系统这门课程中,信号和系统的主要研究对象分别是()。
答案:一维确定性信号,线性时不变系统9.关于单位冲激函数的取样性质,表达正确的是()。
答案:10.下面关于和的表达式中,正确的有()。
答案:;第二章1.由两个因果的LTI系统的级联构成的系统一定是因果系统。
答案:对2.一切连续时间线性系统都可以用它的单位脉冲响应来表征。
答案:错3.具有零附加条件的线性常系数微分方程所描述的系统是线性的。
答案:对4.两个单位冲激响应分别为,的LTI系统级联构成的系统,其总的单位冲激响应是。
答案:错5.若和,则。
答案:对6.线性时不变系统的单位脉冲响应为,该系统稳定的充要条件为()。
答案:7.由离散时间差分方程所描述的系统为()。
答案:FIR(有限长脉冲响应)系统8.LTI系统的单位脉冲响应为,输入为,求时系统的输出时,输入的加权系数是()。
答案:9.信号通过单位冲激响应为的LTI系统,输出等于()。
答案:10.离散时间LTI系统的单位脉冲响应,则该系统是。
答案:因果稳定系统第三章1.对一个信号进行尺度变换,其傅里叶级数系数及傅里叶级数表示均不会改变。
答案:错2.令是一个基波周期为T、傅里叶级数系数为的周期信号,则的傅里叶级数系数是:()答案:3.令是一个基波周期为T、傅里叶级数系数为的实值周期信号,则下列说法正确的是:()答案:若是偶信号,则它的傅里叶级数系数一定为实偶函数4.对于一个周期信号,如果一次谐波分量相移了,为了使合成后的波形只是原始信号的一个简单的时移,那么k次谐波应该相移。
