自动控制原理 第4章 线性系统的根轨迹法:根轨迹法的基本概念 绘制的基本法则
自动控制原理 第四章根轨迹

第四章根轨迹法4-1 根轨迹法的基本概念4-2 常规根轨迹的绘制法则4-3 广义根轨迹4-1 根轨迹法的基本概念一、根轨迹的概念根轨迹:系统中某个参数从零到无穷变化时,系统闭环特征根在s平面上移动的轨迹。
根指的是闭环特征根(闭环极点)。
根轨迹法是根据开环传递函数与闭环传递函数的关系,通过开环传递函数直接分析闭环特征根及系统性能的图解法。
K =0 s 1=0 s 2=-40 < K <1s 1 s 2为不等的负实根K =1s 1=-2 s 2=-21 < K < ∞s 1s2 实部均为-2由根轨迹可知:1)当K =0时,s 1=0,s 2=-1,这两点恰是开环传递函数的极点,同时也是闭环特征方程的极点.2)当0<K < 1 时,s 1,2都是负实根,随着k 的增长,s 1从s 平面的原点向左移,s 2从-1点向右移。
3) 当K = 1时, s 1,2= -2,两根重合在一起,此时系统恰好处在临界阻尼状态。
4) 1 <K <∞,s 1,2为共轭复根,它们的实部恒等于-2,虚部随着K 的增大而增大,系统此时为欠阻尼状态。
★在s平面上,用箭头标明K增大时,闭环特征根移动的方向,以数值表明某极点处的增益大小。
有了根轨迹图就可以分析系统的各种性能:(1)稳定性:根轨迹均在s的左半平面,则系统对所有K>0都是稳定的。
(2)稳态性能:如图有一个开环极点(也是闭环极点)s=0。
说明属于I型系统,阶跃作用下的稳态误差为0。
在速度信号V0t作用下,稳态误差为V0/K,在加速度信号作用下,稳态误差为∞。
(3)动态性能:过阻尼临界阻尼欠阻尼K越大,阻尼比ξ越小,超调量σ%越大。
由此可知:1、利用根轨迹可以直观的分析K的变化对系统性能的影响。
2、根据性能指标的要求可以很快确定出系统闭环特征根的位置;从而确定出可变参数的大小,便于对系统进行设计。
由以上分析知:根轨迹与系统性能之间有着密切的联系,但是,高阶方程很难求解,用直接解闭环特征根的办法来绘制根轨迹是很麻烦的。
第四章 线性系统的根轨迹法-4-2——【南航 自动控制原理】

根轨迹起于开环极点,终于开环零点。
由根轨迹方程,有
m
n
K (s zi )+ (s pi )=0
i 1
i 1
根轨迹起点 K =0 s pi , i 1, , n n个开环有限极点
由根轨迹方程,又有
m
n
(s zi )+(K )1 (s pi )=0
i 1
i 1
根轨迹终点 K s zi , i 1, , m m个开环有限零点
a
(2k 1)
nm
, k 0, 1,
ቤተ መጻሕፍቲ ባይዱ
a
=
(a1 n
b1 m
)
由多项式的根与系数关系
n
n
a1 pi b1 zi
i 1
i 1
n
m
pi z j
a
i 1
j 1
nm
例4.2-1 已知单位反馈系统的开环传递函数为
K G(s)
s(s 3) (s )2 2
0, 0
试分析开环极点参数变化时渐近线。
1
n
1
j1 d z j i1 d pi
分离点处相邻两条根 轨分迹离分点支处切一线共之有间多的少
夹条角根等轨于迹分支/?l
分离点处根轨迹的分离角d 为
d (2k 1) / l k 0,1,
分离点处,根轨迹进
侧的开环实有限零极点数为奇数。
系统的开环零极点分为 两类:实数零极点和复数 零极点,且复数零点或复 数极点必共轭成对。
系统开环零极点的分布为
图示,取实轴任一点 s=s1
·对复共轭开环极点
p4 j, p5 p4 j,
(s1 j)+(s1 +j)=2
自动控制原理第第四章 线性系统的根轨迹法

2
自动控制原理
§4.1 根轨迹的基本概念
例:开环传递函数
Gs
k1
ss
a
开环系统两个极点为:P1 0, P2 a R(s)
闭环传递函数为:
GB s
s2
k1 as
k1
-
k1
C(s)
ss a
闭环特征方程: s2 as k1 0
闭环特征根:s1,2
a 2
a 2
2
k1
(闭环极点)
3
自动控制原理
在p5附近取一实验点sd, 则∠sd-p5可以认为是p5点的出射角 Sd Z Sd P1 Sd P2 Sd P3 Sd P4 Sd P5 1800
近似为 P5 Z P5 P1 P5 P2 P5 P3 P5 P4 p 1800
p Sd P5 1800
法则4 实轴上存在根轨迹的条件——
这些段右边开环零极点个数之和为奇
数。
m
n
证明:根据相角条件 S Z j S Pi 18002q 1
j 1
i 1
p4
j s平面
例:sd为实验点
p3
z2 sd
p2 z1 p1
p5
① 实验点sd右侧实 轴上零极点提供 1800相角
③ 共轭复零点,复极点提供的相角和为 3600。
2
s1=-1.172,s2=-6.828
33
自动控制原理
法则6 开环复数极点处根轨迹出射角为
p 1800
开环复数零点处根轨迹入射角为:
Z 1800
其中 z p(不包括本点)
34
自动控制原理
j p5
p5
p3 p3
p2
根轨迹法(自动控制原理)ppt课件精选全文完整版

课程:自动控制原理
第4章 根轨迹法
➢ 以K为参变量的根轨迹上的每一点都必须满足以上方程, 相应地,称之为‘典型根轨迹方程’。
也可以写成
m
n
(s zl ) K (s pi ) 0
可见,根轨迹可以清晰地描绘闭环极点与开环增益K之间的 关系。
课程:自动控制原理
第4章 根轨迹法
2.根轨迹的基本条件
❖ 考察图示系统,其闭环传递函数为:
Y(s) G(s) R(s) 1 G(s)H(s)
闭环特征方程为:
1 G(s)H(s) 0
➢ 因为根轨迹上的每一点s都是闭环特征方程的根,所以根轨 迹上的每一点都应满足:
l 1
i 1
对应的幅值条件为:
相角条件为:
n
( s pi ) K i1
m
(s zl )
l 1
m
n
(s zl ) (s pi ) (2k 1)180
k 1,2,
l 1
i 1
课程:自动控制原理
第4章 根轨迹法
❖ 上述相角条件,即为绘制根轨迹图的依据。具体绘制方法 是:在复平面上选足够多的试验点,对每一个试验点检查 它是否满足相角条件,如果是则该点在根轨迹上,如果不 是则该点不在根轨迹上,最后将在根轨迹上的试验点连接 就得到根轨迹图。
显然,位于实轴上的两个相邻的开环极点之间一定有分离 点,因为任何一条根轨迹不可能开始于一个开环极点终止 于另一个开环极点。同理,位于实轴上的两个相邻的开环 零点之间也一定有分离点。
课程:自动控制原理
第4章 根轨迹法
自动控制原理第四章根轨迹法.

(s z j ) pi )
m
lim
sm s
n
s
lim
1
s s nm
0
即其余的 n-m 条根轨迹终止于无穷远处,即终止于系 统的n-m个无穷大零点。
回章首 回节首
18
4-2-5 实轴上的根轨迹 实轴上根轨迹的判别方法。 在实轴上选取实验点si, 如果实验点 si 的右方实轴上的开环 零点数和极点数的总和为奇数,则 实验点 si 所在的实验段是根轨迹, 否则该实验段不是根轨迹。 图中, [-1,0]段和[-∞,-5]段是根轨迹。 而(-5,-1)段和(0,+∞)段不是根轨迹。
第四章 根轨迹法
§4-1 根轨迹法的基本概念 §4-2 绘制根轨迹图的基本法则 §4-3 控制系统根轨迹的绘制
§4-4 控制系统的根轨迹法分析
退出
.R.Evans)提出了一种在复平面上由系 统的开环极、零点来确定闭环系统极、零点的图 解方法,称为根轨迹法。 意义:可以分析系统的性能,确定系统应有的结 构和参数,也可用于校正装置的综合。
回章首 回节首
22
分离点或会合点位置的计算
(1) 重根法 数条根轨迹在复平面上某点相遇又分开,该点 必为特征方程的重根。 如两条根轨迹相遇又分开,该点为二重根。 三条根轨迹相遇又分开,该点为三重根等等。 重根的确定可以借助于代数重根法则。
回章首
回节首
23
代数重根法则
已知n次代数方程为
f ( x) x n an1x n1 ... a1x a0 0
根轨迹法是一种简便的图解方法,在控制工 程上得到了广泛的应用。
回章首
2
§4-1 根轨迹法的基本概念
自动控制原理 第四章 根轨迹法
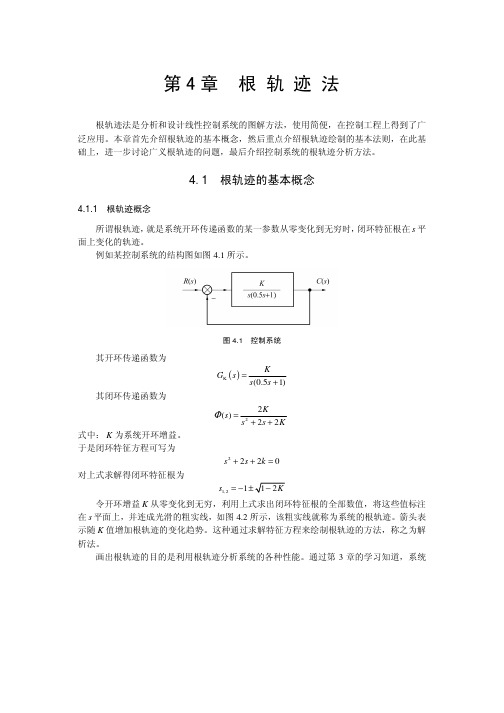
第4章 根 轨 迹 法根轨迹法是分析和设计线性控制系统的图解方法,使用简便,在控制工程上得到了广泛应用。
本章首先介绍根轨迹的基本概念,然后重点介绍根轨迹绘制的基本法则,在此基础上,进一步讨论广义根轨迹的问题,最后介绍控制系统的根轨迹分析方法。
4.1 根轨迹的基本概念4.1.1 根轨迹概念所谓根轨迹,就是系统开环传递函数的某一参数从零变化到无穷时,闭环特征根在s 平面上变化的轨迹。
例如某控制系统的结构图如图4.1所示。
图4.1 控制系统其开环传递函数为()K (0.51)KG s s s =+其闭环传递函数为22()22Ks s s KΦ=++式中:K 为系统开环增益。
于是闭环特征方程可写为2220s s k ++=对上式求解得闭环特征根为1,21s =−令开环增益K 从零变化到无穷,利用上式求出闭环特征根的全部数值,将这些值标注在s 平面上,并连成光滑的粗实线,如图4.2所示,该粗实线就称为系统的根轨迹。
箭头表示随K 值增加根轨迹的变化趋势。
这种通过求解特征方程来绘制根轨迹的方法,称之为解析法。
画出根轨迹的目的是利用根轨迹分析系统的各种性能。
通过第3章的学习知道,系统第4章 根轨迹法·101··101·特征根的分布与系统的稳定性、暂态性能密切相关,而根轨迹正是直观反应了特征根在复平面的位置以及变化情况,所以利用根轨迹很容易了解系统的稳定性和暂态性能。
又因为根轨迹上的任何一点都有与之对应的开环增益值,而开环增益与稳态误差成反比,因而通过根轨迹也可以确定出系统的稳态精度。
可以看出,根轨迹与系统性能之间有着比较密切的联系。
图4.2 控制系统根轨迹4.1.2 根轨迹方程对于高阶系统,求解特征方程是很困难的,因此采用解析法绘制根轨迹只适用于较简单的低阶系统。
而高阶系统根轨迹的绘制是根据已知的开环零、极点位置,采用图解的方法来实现的。
下面给出图解法绘制根轨迹的根轨迹方程。
自动控制原理根轨迹法
21
二、根轨迹绘制的基本法则(4)
法则2
根轨迹的分支数和对称性 根轨迹的分支数与开环极点数n相等(n>m),或与开
环有限零点数m相等(n<m)。 根轨迹连续:根轨迹增益是连续变化导致特征根也连
续变化。 实轴对称:特征方程的系数为实数,特征根必为实数
或共轭复数。
22
二、根轨迹绘制的基本法则(5)
法则3
s(s 2.5)( s 0.5 j1.5)( s 0.5 j1.5)
试绘制该系统概略根轨迹。
解:将开环零、极点画在后面图中。按如下典型步骤
1)确定实轴上的根轨迹。本例实轴上区域
和
为轨迹。
0,-1.5
2)确定-根2.轨5,迹-的渐 近线。本例n=4,m=3,故只有
一条 的渐近线。 180
36
K均* 有关。
15
一、 根轨迹法的基本概念(13)
4 -1- 4 根轨迹方程
1、系统闭环特征方程
由闭环传函可得系统闭环特征方程为:
(s)
G(s)
1 G(s)H(s)
1 G(s)H (s) 0
2 、根轨迹方程
当系统有m个开环零点和n个开环极点时,下式称为
根轨迹方程
m
(s z j )
K * j1 n
i 1
j 1
n
n
n
(s si ) sn ( si )sn1 ... (si ) 0
i 1
i 1
i 1
式中,s i 为闭环特征根。
31
二、根轨迹绘制的基本法则(14)
当n m 2 时,特征方程第二项系数与K * 无关,无
论 K * 取何值,开环n个极点之和总是等于闭环特征方程n
自动控制原理 第四章.
s1.2 1 1 K1 1 1 2 K
第 4章
根轨迹
根轨迹的基本概念(续)
s1 0 ① K 0 s 2 2
j
2
② K 0.5 s1 s2 1 ③ K 1 s1 , 2 1 j ④ K 2.5 s1 , 2 1 j 2 p2
由于实际控制系统闭环特征方程的系数或为已知
实数,或为根轨迹增益Kg 的函数,所以当Kg 由0→∞
连续变化时,闭环特征根的变化必然也是连续的,所
以根轨迹具有连续性。 系统闭环特征方程的系数仅与系统的参数有关。
对于实际控制系统而言,这些参数都是实数。具有实
系数的闭环特征方程的根为共轭复数的形式,必然对
称于实轴。因而,根轨迹也必然பைடு நூலகம்于实轴对称。
s pi s zj
j 1
n
而 ( s z j ) ( s pi ) ( 2 K 1) ——相角方程
j 1 i 1
m
n
第 4章
根轨迹
根轨迹的基本概念(续)
若s平面上的点是闭环极点,则它与zj 、pi所组成
的相量必定满足上述两方程,而且模值方程与Kg有
第四章 根轨迹法
§4-1 根轨迹的基本概念 §4-2 绘制根轨迹的基本法则 §4-3 广义根轨迹
主要内容
1.根轨迹基本概念和根轨迹方程
2.绘制常规根轨迹的九大法则
3.参量根轨迹与零度根轨迹
第 4章
根轨迹
重点与难点
重 点
1、绘制常规根轨迹的九大法则 2、参量根轨迹与零度根轨迹 3、控制系统根轨迹法分析
§4—2 绘制根轨迹的基本法则
绘制根轨迹的基本法则(续)
《自动控制原理》第4章 线性系统的根轨迹法
68
4.5 广义根轨迹
根轨迹部分是个半圆,半径是 k *
证明:根轨迹上一点S满足相角条件
s (s j2) (s j2)
代入s j
( j) ( j( 2)) ( j( 2))
arctan arctan 2 arctan 2
K* G(s)
s(s 2)(s 1)
26
法则五:根轨迹的分离点与分离角
分离点:几条根轨迹在[s]某一点相遇后又分开 的点。
说明有重根
27
实轴上的分离点(常见)
如果根轨迹位于实轴上相邻的两个开环极点之间, 其中一个可以是无限极点,则在这两个极点之间至 少存在一个分离点;
如果根轨迹位于实轴上相邻的两个开环零点之间, 其中一个可以是无限零点,则在这两个零点之间至 少存在一个分离点;
开环极点:
p1 0 p2 0 p3 2 p4 5
(2)实轴上的根轨迹 (3)根轨迹分支数
4
59
G0 ( s)
s2(s
k* 2)(s
5)
(4)渐近线
4条
渐近线与实轴的夹角
a
4
3
4
3
4
4
渐近线与实轴的交点(σa , 0)
4
pi
a
i 1
4
1.75
60
G0 ( s)
s2(s
k* 2)(s
法则二:根轨迹的分支数,对称性和 连续性
• 根轨迹的分支数与开环有限零点数m和有限 极点数n中的大者相等,它们是连续的并且 对称于实轴。
22
法则三:根轨迹的渐近线(n>m)
• 当开环有限零点数m小于有限极点数n时, 有n-m条根轨迹分支沿着与实轴交点 ,
根轨迹法的基本概念
K*
s1,2 1
1 K*
令K*(由0到∞ )变动,s1、s2在s平面的移动轨 迹即为根轨迹。
K* 0, s1 0, s2 2 K* 1, s1 1, s2 1 K* 2, s1 1 j, s2 1 j K* 5, s1 1 2 j, s2 1 2 j
特征方程的根 运动模态 性、系统性能)
1
1
1 ,d 4
m
(s zi )
1 G(s)H(s) 0
G(s)H(s) K*
i1 n
m
(s pj )
(s zi )
j 1
K * i1 n
1
(s pj )
j 1
m
n
模值条件: (s zi ) (s pj ) (2k 1)
i1
j1
n
s pj
相角条件: K *
j 1 m
s zi
i 1
相角条件是确定根轨迹的充分必要条件。相角条件满足(2k 1) 称为180º根轨迹。
4-2 绘制根轨迹的基本法则
一、基本法则
1、 根轨迹的起点和终点:
根轨迹起始于开环极点,终止于开环零点;如果开环零点个数少于 开环极点个数,则有(n-m)条根轨迹终止于无穷远处。
起点: K* 0 s pi
K* s p1 s z1
i 1, 2, n
s pn s zm
终点: K* s zi j 1, 2, m
例题:单位反馈系统的开环传递函数为:G(s)H (s) K *(s 1)
s(s 2)(s 3)
试绘制闭环系统的根轨迹
解: 1、开环零点z1=-1,开环极点p1=0,p2=-2,p3=-3, 根轨迹分支数为3条,有两个无穷远的零点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
(2)渐近线与实轴的交点
a
p
i 1
n
i
zj
j 1
m
nm
a
渐近线的交点总在实轴上,即
必为实数。在计算时,
考虑到共轭复数极点、零点的虚部总是相互抵消,只须把 开环零、极点的实部代入即可。
2019/2/17
n-m=1,有一条渐进线
A
2019/2/17
n-m=2,有两条渐进线
例4-1
* K G ( S ) H ( S ) S ( S 1 )( S 2 )
求根轨迹
jω
j 2
解:①在S平面中确定开环零、极点的位置。
② 确定实轴上的根轨迹。
③ n=3,m=0,应有三个分支,
K1=6
并且都趋向无穷远处。
④ 确定渐近线的位置。 p1 p 2 p 3 0 1 2 a 1 nm 30 ( 2 k 1)180 ( 2 k 1)180 a nm 3
j
-2
-1
0
综上所述: (1)k*从0 ~ ∞ 时,系统的根轨迹是连续变化。可见:
系统的参量变化对系统闭环极点分布的影响。
(2)由根轨迹图,可得系统动、静态性能的信息: 1)稳定性 无论k*值如何变化( k*>0),闭环极点不出现
在s的右半平面,所以系统是稳定的。
2)稳态误差
I型系统,K为静态速度误差系数。
j
z1
0
终止角(入射角): 根轨迹进入复平面上开环零点处的切线与实轴的夹角。
2019/2/17
在根轨迹上任取一点s,无限接近极点 - p
切线与实轴的夹角
m n o zi 180 zjzi pjzi 1 j 1 j j i
2019/2/17
zi
。
j
p 3
3 2.3
1
0
起始角(出射角): 根轨迹离开复平面上开环极点处的切线与实轴的夹角 。
2019/2/17
规则6:根轨迹的起始角(出射角)和终止角 (入射角)
起始角(出射角):根轨迹离开复平面上开环极点处的
切线与实轴的夹角
pi
。
m n o pi 1 8 0 zj p p p i j i 1 j 1 j j i
终止角(入射角):根轨迹进入复平面上开环零点处的
n
i 1
j 1
m
4. 根轨迹方程(P139)
特征方程 1+GH = 0 Z 开环零点“○”,是常数! j m
* 1+K
∏ ( s - zj )
j=1
∏ ( s -pi)
i=1
n
=0
pi开环极点“× ”,也是常数 根轨迹增益k * 不是定数,从 0变化到 ! !
这种形式的特征方程就是根轨迹方程 1+k*P(s)=0
2019/2/17
实轴上的根轨迹
设系统开环零、极点分布如 图所示。为在实轴上确定属 于根轨迹的线段,首先在 z 1 和 p 3 之间任选一个试验 点 s1 。
jω ×
p1
s1
z1
o
*
×
p3
σ
p
×
2
2019/2/17
1.共轭复数极点到 s 1 的幅角之 和为0°,相互抵消,因此开 环共轭复数极点、零点对实轴 上根轨迹的位置没有影响,仅 取决于实轴上的开环零、极点。 2.若实轴上的某一段是根轨迹, 一定满足相角条件。试验点左 s 1 侧的开环零、极点提供的相角 为0°,而右侧的相角为180°。 点满足相角条件,所以z 1 ~ p 3 之间是根轨迹。
2019/2/17
幅值条件改写为:
∞ K*
jω
m
(s z j ) (s pi )
j 1 n
1 K*
K*=0 × -2 K* ∞
K*=0.5 ×K*=0 σ
i 1
在控制系统中,总有n>m,所以根轨迹从n个开环极点
处起始,到m个开环零点处终止,剩下的n-m条根轨迹将趋 于无穷远处。
例:
K G( S) S( S 2)
*
起点:0,-2 零极点:n=2,m=0
有两条根轨迹(n-m=2)→∞
规则2:根轨迹的分支数、对称性和连续性
根轨迹的分支数: 与开环极点数n相等(n>m) 根轨迹连续性:
根轨迹增益是连续变化导致特征根也连续变化。
根轨迹对称于实轴: 特征方程的系数为实数,特征根必为实数 或共轭复数。
第四章
线性系统的根轨迹法
根轨迹法的基本概念
根轨迹绘制的基本法则
广义根轨迹 系统性能的分析
2019/2/17
4-1 根轨迹的基本概念
特征方程的根
运动模态
系统动态响应
(稳定性、系统性能) 1. 根轨迹概念 开环传递函数中的某一个参数从零变化到 无穷时,闭环系统特征方程根在 s 平面上的轨 迹称为根轨迹。
2019/2/17
3)动态性能 ① 0<k<0.5 时,系统为过阻尼状态,阶跃响应为
非周期过程。 ② k=0.5 时,系统为临界阻尼状态,阶跃响应为非 周期过程。 ③ k>0.5 时,系统为欠阻尼状态,阶跃响应为阻尼
震荡过程。
(3)结论: 根轨迹与系统性能之间有着直接联系。
2019/2/17
2. 根轨迹与系统性能
2019/2/17
规则3: 根轨迹的渐近线
(1)根轨迹中(n-m)条趋向无穷远处的分支的渐近线 的倾角为
( 2 k 1 ) 180 k 1 , 2 , , ( n m 1 ) a n m
当 k 0时,求得的渐近线倾角最小; K增大,倾角值将重复出现,而独立的渐近线只有 (n-m)条。
( s z) ( s p ) ( 2 k 1 ) 180
j 1 j i 1 i
m
n
k 0 , 1 , 2 ,
2019/2/17
规则5:根轨迹分离点与会合点
① 两条以上根轨迹分支的交点称为根轨迹的分离点或会合点。 ② 当根轨迹分支在实轴上相交后走向复平面时,该相交点 称为根轨迹的分离点。 ③ 当根轨迹分支出由复平面走向实轴时,它们在实抽上的 交点称为会合点。 分离点(会合点)的坐标 d 由下列方程所决定: K Bs () 0 1 G ( sHs ) ( ) 1 0 A ( s )
D ( s ) A ( s ) K Bs ( ) 0 0 ' ' ( 1 ) ' A ( s ) B ( s ) A ( sBs ) ( ) 0 ' ' Ds ( ) As ( ) K Bs ( ) 0 0 或
m n ' ' 1 1 d K A () s B ( s ) A () s B () s 0 (3) , ( 2 ) 0 sd 2 d s B () s j 1 d z j i 1 d pi
i=1 j=1 i=1
k n m时 k * f l 1 k * *
*
* G
j=1
n=q+h m=f+l
k k *
* * k G H
(s ) =
k (s z i ) ( s p j )
* G
f
h
(s p i ) k * (s z j )
i 1
j 1
根轨迹的模值条件与相角条件 没有零点的相角条件和模值条件你会推吗? 相角条件: (P140) n m
∑ ∠ (s-z ) - ∑ ∠ (s-p ) = (2k+1) π j i j=1 i=1
m 绘制根轨迹的充要条件
k=0, ±1, ±2, …
模值条件:
1+K Kn =
i=1
) ∏︱ ( s - zn ︱ j p s ︱ ︱ ∏ j=1 i * *
A
2019/2/17
, 或 , 2 2 2 2
3
n-m=3,有三条渐进线
A
5 , , 或, ,
2019/2/17
3
3
3 3
n-m=4,有四条渐进线
A
3 7 3 5 , 或 , , , 4 4 4 44 4
4-2 根轨迹绘制的基本法则 1. 绘制根轨迹的基本法则 规则1:根轨迹的起点和终点
根轨迹起始于开环极点(K*=0),终止于开环零点。
简要证明:
( s p ) K ( s z ) 0
* i j i 1 j 1 n m
当 K*
0
,必有S= p i ,即终点是开环零点。
当 K* ,必有S= z j ,即起点是开环极点。
m n j 1 j i 1 i
jω ×1
p
1 0
z1
o
s1
*
1
×
p3
σ
p
×
2
( s z) ( s p ) ( 2 k 1 ) 180
2019/2/17
规则4:实轴上的根轨迹
若实轴上某段右边的 开环实数零点数+开环实数极点数=奇数 则该段是根轨迹的一部分。 这个结论可以用相角条件证明:
稳定性:考察根轨迹是否进入右半 s 平面。
稳态性能:开环传函在坐标原点有一个极点,系统为
1型系统,根轨迹上的K值就是静态速度误差系数。
注意:根轨迹图上的参数是根轨迹增益,根轨迹增益与 开环增益之间有一个转换关系。
