第四章 线性系统的根轨迹法(下)
夏德钤《自动控制原理》(第4版)章节题库-第4章线性系统的根轨迹分析【圣才出品】

夏德钤《⾃动控制原理》(第4版)章节题库-第4章线性系统的根轨迹分析【圣才出品】第4章 线性系统的根轨迹分析1.系统的开环传递函数试证明:点在根轨迹上,并求出相应的和系统开环增益K。
证明:根据系统的开环传递函数可知,系统的开环极点为由闭环根轨迹的相⾓条件可得:当时,故点在根轨迹上。
由闭环根轨迹的幅值条件可知,此时即相应的根轨迹增益和系统开环增益仿真曲线如图4-1所⽰。
MATLAB程序:exe402.m2.设单位反馈控制系统的开环传递函数为试⽤解析法绘出K*从零变到⽆穷时的闭环根轨迹图,并判断下列点是否在根轨迹上:(﹣2+j0),(0+j1),(﹣3+j2)解:闭环传递函数为则闭环特征⽅程为闭环特征根为当。
可逐个描点得闭环根轨迹如图4-2所⽰,从图4-2中明显可见,只有(-2,j0)在根轨迹上。
图4-23.设单位反馈控制系统的开环传递函数如下,试概略绘制闭环根轨迹图。
解:(1)系统的开环传递函数令为根轨迹增益。
①实轴上的根轨迹:[0,-2],[-5,-∞)。
②根轨迹的渐近线:③根轨迹的分离点:根轨迹的分离点坐标满⾜解得④根轨迹与虚轴的交点:由系统的开环传递函数可知系统的闭环特征⽅程令s=jω,将其代⼊上式可得即由于ω≠0,故可解得则根轨迹与虚轴的交点为±j3.16。
根据以上⼏点,可以画出概略根轨迹如图4-3所⽰。
图4-3 系统(1)概略根轨迹图(2)系统的开环传递函数①实轴上的根轨迹[0,-2],[-3,-5]。
③根轨迹的分离点:根轨迹的分离点坐标满⾜通过试凑可得d=-0.89。
根据以上⼏点,可以画出概略根轨迹如图4-4所⽰。
图4-4 系统(2)概略根轨迹图(3)系统的开环传递函数①实轴上的根轨迹:[-1,-3],[-10,-5]。
②根轨迹的渐近线:③根轨迹的分离点:根轨迹的分离点坐标满⾜通过试凑可得d=-7.27。
根据以上⼏点,可以画出概略根轨迹如图4-5所⽰。
图4-5 系统(3)概略根轨迹图(4)系统的开环传递函数实轴上的根轨迹为[-2,-1],系统概略根轨迹如图4-6所⽰。
自动控制原理第第四章 线性系统的根轨迹法

2
自动控制原理
§4.1 根轨迹的基本概念
例:开环传递函数
Gs
k1
ss
a
开环系统两个极点为:P1 0, P2 a R(s)
闭环传递函数为:
GB s
s2
k1 as
k1
-
k1
C(s)
ss a
闭环特征方程: s2 as k1 0
闭环特征根:s1,2
a 2
a 2
2
k1
(闭环极点)
3
自动控制原理
在p5附近取一实验点sd, 则∠sd-p5可以认为是p5点的出射角 Sd Z Sd P1 Sd P2 Sd P3 Sd P4 Sd P5 1800
近似为 P5 Z P5 P1 P5 P2 P5 P3 P5 P4 p 1800
p Sd P5 1800
法则4 实轴上存在根轨迹的条件——
这些段右边开环零极点个数之和为奇
数。
m
n
证明:根据相角条件 S Z j S Pi 18002q 1
j 1
i 1
p4
j s平面
例:sd为实验点
p3
z2 sd
p2 z1 p1
p5
① 实验点sd右侧实 轴上零极点提供 1800相角
③ 共轭复零点,复极点提供的相角和为 3600。
2
s1=-1.172,s2=-6.828
33
自动控制原理
法则6 开环复数极点处根轨迹出射角为
p 1800
开环复数零点处根轨迹入射角为:
Z 1800
其中 z p(不包括本点)
34
自动控制原理
j p5
p5
p3 p3
p2
自动控制原理第四章-根轨迹分析法

×
p4 z 2
×
p3
×
×
p 2 z1 p1
σ
规则4:根轨迹的分会点(分离点和会合点)d。 (1)定义:分会点是指根轨迹离开实轴进入复平面的点(分 离点)或由复平面进入实轴的点(汇合点),位于相邻两极点 或两零点之间。
(2)位置:大部分的分会点在实轴上,若出现在复平面内时,则 成对出现。
(3)特点:分会点对应于闭环特征方程有重根的点;根轨迹离开
(4)与虚轴的交点:
方法1:闭环特征方程为s3 + 6s2 + 8s + K*= 0 令s = jω得:-jω3 -6ω2 + j8ω + K* = 0
-6ω2 + K* = 0 即
-ω3 + 8ω= 0
K* = 48 ω= 2.8 s-1
方法2:闭环特征方程为 s3 + 6s2 + 8s + K*= 0 列劳斯表如下:
规则1:根轨迹的起点和终点。 根轨迹起始于开环极点,终止开环零点或无穷远。
m
i 1
s
zi
n
s
l 1
pl
1 K
K
K
0 s pl
s s
zi , m条 (, n
m)条
规则2: 根轨迹的条数和对称性。 n阶系统有n条根轨迹。根轨迹关于实轴对称。
规则3: 实轴上的根轨迹分布。
由实数开环零、极点将实轴分为若干段,如某段右边 开环零、极点(包括该段的端点)数之和为奇数,则该段就 是根轨迹,否则不是。如下图所示。
又因为开环传函的零极点表达式为:
m
GK (s)
G(s)H(s)
K
n
(s
自动控制原理第四章根轨迹法

第四章 根轨迹法
第一节 根轨迹与根轨迹方程 根轨迹 系统的某个参数(如开环增益K)由0到∞变化时, 闭环特征根在S平面上运动的轨迹。
例: GK(S)= K/[S(0.5S+1)] = 2K/[S(S+2)] GB(S)= 2K/(S2+2S+2K) 特征方程:S2+2S+2K = 0
-P1)(S-P2)…(S-Pn)
单击此处可添加副标题
当n>m时,只有m条根轨迹趋向于开环零点,还有(n-m)条? m,S→∞,有: (S-Z1)(S-Z2)…(S-Zm) -1 -1 ———————-— = —— = —— P1)(S-P2)…(S-Pn) K* AK 可写成:左边 = 1/Sn-m = 0 当K=∞时,右边 = 0 K=∞(终点)对应于S→∞(趋向无穷远). 即:有(n-m)条根轨迹终止于无穷远。
分解为:
03
例:GK(S)= K/[S(0.05S+1)(0.05S2+0.2S+1)] 试绘制根轨迹。 解: 化成标准形式: GK(S)= 400K/[S(S+20)(S2+4S+20)] = K*/[S(S+20)(S+2+j4)(S+2-j4)] K*=400K——根迹增益 P1=0,P2=-20,P3=-2+j4,P4=-2-j4 n=4,m=0
一点σa。
σa= Zi= Pi
ΣPi-ΣZi = (n-m)σa
σa= (ΣPi-ΣZi)/(n-m)
绘制根轨迹的基本法则
K*(S-Z1)(S-Z2)…(S-Zm)
—————————— = -1 (S-P1)(S-P2)…(S-Pn)
《自动控制原理》第4章 线性系统的根轨迹法

68
4.5 广义根轨迹
根轨迹部分是个半圆,半径是 k *
证明:根轨迹上一点S满足相角条件
s (s j2) (s j2)
代入s j
( j) ( j( 2)) ( j( 2))
arctan arctan 2 arctan 2
K* G(s)
s(s 2)(s 1)
26
法则五:根轨迹的分离点与分离角
分离点:几条根轨迹在[s]某一点相遇后又分开 的点。
说明有重根
27
实轴上的分离点(常见)
如果根轨迹位于实轴上相邻的两个开环极点之间, 其中一个可以是无限极点,则在这两个极点之间至 少存在一个分离点;
如果根轨迹位于实轴上相邻的两个开环零点之间, 其中一个可以是无限零点,则在这两个零点之间至 少存在一个分离点;
开环极点:
p1 0 p2 0 p3 2 p4 5
(2)实轴上的根轨迹 (3)根轨迹分支数
4
59
G0 ( s)
s2(s
k* 2)(s
5)
(4)渐近线
4条
渐近线与实轴的夹角
a
4
3
4
3
4
4
渐近线与实轴的交点(σa , 0)
4
pi
a
i 1
4
1.75
60
G0 ( s)
s2(s
k* 2)(s
法则二:根轨迹的分支数,对称性和 连续性
• 根轨迹的分支数与开环有限零点数m和有限 极点数n中的大者相等,它们是连续的并且 对称于实轴。
22
法则三:根轨迹的渐近线(n>m)
• 当开环有限零点数m小于有限极点数n时, 有n-m条根轨迹分支沿着与实轴交点 ,
第四章 线性系统的根轨迹法(下)
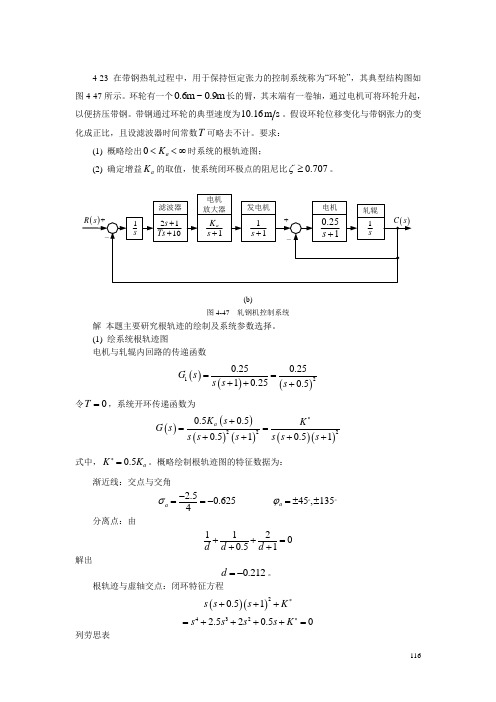
1164-23 在带钢热轧过程中,用于保持恒定张力的控制系统称为“环轮”,其典型结构图如图4-47所示。
环轮有一个0.6m ~0.9m 长的臂,其末端有一卷轴,通过电机可将环轮升起,以便挤压带钢。
带钢通过环轮的典型速度为10.16m s 。
假设环轮位移变化与带钢张力的变化成正比,且设滤波器时间常数T 可略去不计。
要求:(1) 概略绘出0a K <<∞时系统的根轨迹图;(2) 确定增益a K 的取值,使系统闭环极点的阻尼比0.707ζ≥。
(b)图4-47 轧钢机控制系统解 本题主要研究根轨迹的绘制及系统参数选择。
(1) 绘系统根轨迹图电机与轧辊内回路的传递函数()()()120.250.2510.250.5G s s s s ==+++ 令0T =,系统开环传递函数为()()()()()()2220.50.50.510.51a K s K G s s s s s s s *+==++++式中,0.5a K K *=。
概略绘制根轨迹图的特征数据为:渐近线:交点与交角2.50.6254a σ-==- 45,135a ϕ=±± 分离点:由11200.51d d d ++=++ 解出0.212d =-。
根轨迹与虚轴交点:闭环特征方程()()20.51s s s K *+++4322.520.50s s s s K *=++++=列劳思表1174s 1 2 K * 3s 2.50.52s 1.8 K *1s 0.9 2.51.8K *-0s K *令0.9 2.50K *-=,得0.36K *=。
令21.80s K *+=代入s j ω=及0.36K *=,解出0.447ω=。
交点处20.72a K K *==系统概略根轨迹图如图(a)所示。
图(a) 概略根轨迹图(2) 确定使系统0.707ζ≥的a K在根轨迹图上,作0.707ζ=阻尼比线,得系统主导极点1,20.1550.155s j =-±利用模值条件,得1s 处的0.0612K *=;分离点d 处的0.0387K *=。
第4章 线性系统的根轨迹法

m
s p
i 1
n
0
或写成
* s p K i s zi 0 i 1 i 1
m
它是直接利用开环传递函数分析闭环特征根及其性能的图解法。
『例』已知单位反馈系统开环传递函数 G s
讨论系统闭环极点的分布情况(0<K<∞)。
开环增益 K K * i bd
j
z
ac
i
p
j
四、根轨迹方程
(1) 根轨迹方程
1 Gs H s 0 或 Gs H s 1
假设开环传递函数中有m个零点和n个极点
1
K * s zi
i 1
m
s p
i i 1
n
0,
j z2
p3
S1
p2 z3
z1
p4
p1
4. 根轨迹的渐近线
当开环极点数n大于开环零点数m,有n-m条根轨迹 分支沿着与实轴夹角为 a 和交点为 的一组渐进线 a 趋向无穷远处。
(2k 1) a , a nm
p z
i 1 i i 1
n
m
i
nm
『例』指出单位反馈系统根轨迹的条数、根轨迹渐近线与 实轴的夹角和交点。 K* G(s) s( s 1)(s 2) 60 (2k 1) 0 1 2 解:有3条根轨迹, a 180 , a 1 30 3 60
『问题』开环传递函数的3个极点和2个零点如下图,
判断s1是否根轨迹上的点?
s1
5 4
z1 z2
× p3
3
2
× p2
线性系统的根轨迹法

法则7. 根轨迹与虚轴的交点
交点和临界根轨迹增益的求法:
解: 方法一
例8.
,试求根轨迹与虚轴的交点。
K*=0 w =0 舍去(根轨迹的起点)
与虚轴的交点:
闭环系统的特征方程为:
s=jw
劳斯表:
01
s2的辅助方程:
02
K* =30
03
当s1行等于0时,特征方程可能出现纯虚根。
04
等效的开环传递函数为:
参数根轨迹簇
二、附加开环零、极点的作用
试验点s1点
例1.设系统的开环传递函数为: 试求实轴上的根轨迹。
解:
零极点分布如下:
p1=0,p2=-3,p3=-4,z1=-1,z2=-2
实轴上根轨迹为:[-1,0]、[-3,-2]和 (- ∞ ,-4]
jw
-2
-1
1
2
-1
-2
s
.
.
.
.
.
.
.
.
三、闭环零极点与开环零极点的关系
反馈通路传函:
前向通路传函:
典型闭环系统结构图
KG*--前向通路根轨迹增益 KH*--反馈通路根轨迹增益
K*--开环系统根轨迹增益
1
闭环传递函数:
2
开环传递函数:
01
04
02
03
闭环系统根轨迹增益,等于开环系统前向通路根轨迹增益。 对于单位反馈系统,闭环系统根轨迹增益等于开环系统根轨迹益。
(5)用(s-s1)去除Q(s),得到余数R2 ;
(6)计算s2 =s1-R1/R2 ;
(7)将s2 作为新的试探点重复步骤(4)~(6)。
例4.试用牛顿余数定理法确定例3的分离点。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
1164-23 在带钢热轧过程中,用于保持恒定张力的控制系统称为“环轮”,其典型结构图如图4-47所示。
环轮有一个0.6m ~0.9m 长的臂,其末端有一卷轴,通过电机可将环轮升起,以便挤压带钢。
带钢通过环轮的典型速度为10.16m s 。
假设环轮位移变化与带钢张力的变化成正比,且设滤波器时间常数T 可略去不计。
要求:(1) 概略绘出0a K <<∞时系统的根轨迹图;(2) 确定增益a K 的取值,使系统闭环极点的阻尼比0.707ζ≥。
(b)图4-47 轧钢机控制系统解 本题主要研究根轨迹的绘制及系统参数选择。
(1) 绘系统根轨迹图电机与轧辊内回路的传递函数()()()120.250.2510.250.5G s s s s ==+++ 令0T =,系统开环传递函数为()()()()()()2220.50.50.510.51a K s K G s s s s s s s *+==++++式中,0.5a K K *=。
概略绘制根轨迹图的特征数据为:渐近线:交点与交角2.50.6254a σ-==- 45,135a ϕ=±± 分离点:由11200.51d d d ++=++ 解出0.212d =-。
根轨迹与虚轴交点:闭环特征方程()()20.51s s s K *+++4322.520.50s s s s K *=++++=列劳思表1174s 1 2 K * 3s 2.50.52s 1.8 K *1s 0.9 2.51.8K *-0s K *令0.9 2.50K *-=,得0.36K *=。
令21.80s K *+=代入s j ω=及0.36K *=,解出0.447ω=。
交点处20.72a K K *==系统概略根轨迹图如图(a)所示。
图(a) 概略根轨迹图(2) 确定使系统0.707ζ≥的a K在根轨迹图上,作0.707ζ=阻尼比线,得系统主导极点1,20.1550.155s j =-±利用模值条件,得1s 处的0.0612K *=;分离点d 处的0.0387K *=。
由于2a K K *=,故取0.07740.1224a K <≤,可使0.7071ζ≤<;取0.0774a K ≤,可使1ζ≥。
()()20.51010.5aK s s s +=++118(3) MATLAB 验证0.707ζ=时,系统主导极点及增益和根轨迹分离点处系统增益如图(b)所示;系统根轨迹图如图(c)所示。
分别令a K 为0.05,0.11,0.4和0.8,系统的单位阶跃响应如图(d)所示。
0.11a K =时,系统动态性能 % 2.17%,σ= 27.6s s t = ()=2%∆0.4a K =时, 系统动态性能 %53.2%,σ= 57.9s s t = ()=2%∆MATLAB 程序:exe423.m% 建立等效开环传递函数模型 G=zpk([], [-0 -0.5 -1 -1], 1); z=0.707;% 绘制相应系统的根轨迹 figure (1)rlocus(G); sgrid(z,'new') % 取阻尼比为 0.707axis([-0.5 0.1 -0.3 0.3]) figure (2)K=0.0612; % 最佳阻尼比对应的根轨迹增益 hold on; rlocus(G ,K) % 阻尼比为 0.707时, 系统的闭环特征根 axis([-1.5 0.5 -1 1])rlocus(G); % Ka=0.05,0.11,0.4,0.8时的阶跃响应 Ka=0.05;% Ka 可相应设置 numc=[0.5*Ka]; denc=[1 2.5 2 0.5 0]; [num, den]=cloop(numc, denc);% 系统闭环传递函数 roots(den);% 系统闭环极点sys=tf(num, den); t=0:0.01:120; figure(3)step(sys,t); grid on;图(b) 确定0.707ζ=以及分离点处的a K (MA TLAB)119图(c) 轧钢机系统根轨迹图 (MA TLAB)(1) 0.05a K = (2) 0.11a K =(3) 0.4a K = (4) 0.8a K =图(d) 轧钢机系统时间响应 (MA TLAB)4-24 图4-48(a)是22V -鱼鹰型倾斜旋翼飞机示意图。
22V -既是一种普通飞机,又是一种直升机。
当飞机起飞和着陆时,其发动机位置可以如图示那样,使22V -像直升机那样垂直起降;而在起飞后,它又可以将发动机旋转90,切换到水平位置,像普通飞机一120样飞行。
在直升机模式下,飞机的高度控制系统如图4-48(b)所示。
要求:(1) 概略绘出当控制器增益1K 变化时的系统根轨迹图,确定使系统稳定的1K 值范围; (2) 当去1280K =时,求系统对单位阶跃输入()()1r t t =的实际输出()h t ,并确定系统的超调量和调节时间()2%∆=;(3) 当1280K =,()0r t =时,求系统对单位阶跃扰动()1N s s =的输出()n h t ; (4) 若在()R s 和第一个比较点之间增加一个前置滤波器()20.51.50.5p G s s s =++试重作问题(2)。
(b) 控制系统图4-48 V -22旋翼机的高度控制系统解 本题属于应用根轨迹法设计系统参数的综合性问题,其中包括引入前置滤波器,以抵消闭环零点的不利影响,改善系统性能。
(1) 绘制系统的根轨迹图由图4-48(b),系统开环传递函数()()()()()21 1.50.52011010.51K s s G s s s s s ++=+++()()()()()0.510.050.12K s s s s s s *++=+++ 式中10.01K K *=渐近线:交点与交角0.325a σ=- 90a ϕ=±分离点:1111110.050.120.51d d d d d d +++=++++++ 0.022d =-根轨迹与虚轴交点:闭环特征方程(R s121()()()()()0.050.120.510s s s s K s s *++++++=整理得()()4322.150.3050.01 1.50.50s s K s K s K ***++++++=列劳思表4s 1 0.305K *+ 0.5K * 3s 2.15 0.01 1.5K *+ 2s 0.30.302K *+ 0.5K *1s 20.0030.6220.4530.30.302K K K***-++ 0s 0.5K *令()20.4530.6220.0030KK **-+=,解得10.005K *=, 2 1.368K *=令()20.30.3020.50K s K **++=,代入s j ω=、1K *及2K *,解得10.09ω=, 20.977ω=绘出系统概略根轨迹图,如图(a)所示。
0.325as 0.022d图(a) 概略根轨迹图()()()21 1.50.5102011010.51s s K s s s s +++=+++122由于1100K K *=,因此使系统稳定的1K 值范围为:100.5K <<以及1136.8K >。
应用MATLAB 软件包,得到系统根轨迹图如图(b)所示。
图(b) 根轨迹图 (MA TLAB)(2) 当1280K =时,确定系统单位阶跃输入响应应用MA TLAB 软件包,得到单位阶跃输入时系统的输出响应曲线,如图(c)-(1)中虚线所示。
由图可得%92.1%σ=, 43.9s s t = ()2%∆=显然,系统动态性能不佳。
(3) 当1280K =时,确定系统单位阶跃扰动响应应用MA TLAB 软件包,得到单位阶跃扰动输入下系统的输出响应曲线,如图(c)-(2)所示。
由图可见,扰动响应是振荡的,但最大振幅约为0.003,故可略去不计。
(1) 单位阶跃输入响应 (2) 单位阶跃扰动响应图(c) V -22旋翼机的高度时间响应 (MA TLAB)(4) 有前置滤波器时,系统的单位阶跃输入响应(1280K =)()()()21 1.50.5102011010.51s s K s s s s +++=+++123无前置滤波器时,闭环传递函数()()()14322.80.512.15 3.105 4.21 1.4s s s s s s s Φ++=++++有前置滤波器()20.51.50.5p G s s s =++时,闭环传递函数 ()()()21p s G s s ΦΦ=⋅4321.42.153.1054.21 1.4s s s s =++++ 可见,()1s Φ与()2s Φ有相同的极点,但()1s Φ有0.5-和1-两个闭环零点,虽可加快响应速度,但却极大增加了振荡幅度,使超调量过大;而()2s Φ的闭环零点被前置滤波器完全对消,因而最终改善了系统动态性能。
应用MATLAB 软件包,得有前置滤波器时系统的单位阶跃响应如图(c)-(1)中实线所示,其%7.08%σ=, 25.8s s t = ()2%∆=MATLAB 程序:exe424.m% 建立等效开环传递函数模型 G=zpk([-0.5 -1], [0 -0.05 -0.1 -2], 1); % 绘制相应系统的根轨迹figure rlocus(G); axis( [-1.5,1.5,-1.5,1.5] ); % 系统输入时间响应 % 原系统 K=280;num1=[K 1.5*K 0.5*K]; den1=[0 0 1 0]; num2=[1]; den2=[100 215 30.5 1]; [numc, denc]=series(num1,den1,num2,den2); [numr, denr]=cloop(numc,denc);sysr=tf(numr, denr) ; t=0: 0.01:80; figurestep(sysr,t); hold on; % 添加前置滤波器numf=[0.5]; denf=[1 1.5 0.5]; [num, den]=series(numr,denr,numf,denf);sys=tf(num, den) ; step(sys,t); grid % 系统扰动时间响应 K=280;numh=[K 1.5*K 0.5*K]; denh=[0 0 1 0]; numg=[1]; deng=[100 215 30.5 1];124[numn,denn]=feedback(numg,deng,numh,denh); sysn=tf(numn, denn) figurestep(sysn,t); grid4-25 在未来的智能汽车-高速公路系统中,汇集了各种电子设备,可以提供事故、堵塞、路径规划、路边服务和交通控制等实时信息。
