均匀平面电磁波的特性与特征参量
合集下载
电磁场理论-05 均匀平面电磁波

5、解的物理意义
ˆ E1e jkz x ˆ E2 e jkz x ˆ E r E x z x ˆ Em 2 cost kz 2 x ˆ E r , t Em1 cost kz 1 x
• 波动方程的解的物理意义是:两个向相反方向传 播的行波的迭加。
传播方向的电磁波。
E H
某一瞬间的 空间场分布图
传播 方向
H
电场、磁场、 传播方向三者成 右手螺旋关系。
传播 方向
3、电场与磁场同相变化 ˆ E r , t E m cost kz x k ˆ H r , t Em cost kz y
• 不失一般性,可作一些假设,使求解更方便: ˆ; (1)设 E 只有x方向的分量,即 E r E x x ˆ ; x (2)设 E 只随z 坐标变化,即 E r E x z x • E x z 满足的常微分方程:
2 Er k Er 0 2 2 H r k H r 0
8、平面波传播方向的判断方法:
• 从平均Poynting矢量判断:若已知电场、磁场,则 平均Poynting矢量的方向就是电磁波的传播方向。
ˆ E z, t Em cost kzx ˆ E z, t Em cost kzx
即:在某一固定时刻,相位连续 减小的方向就是传播方向。
y
vp
6、从行波角度理解电磁波各参数的物理意义: 相速度 ( vp ):等相位面在一秒钟之内前进的距离 波长(λ):等相位面在一个周期 T 之内前进的距离 2 2 v pT k k 周期(T ):等相位面前进一个波长所需的时间
ch7(3)导电媒质中的均匀平面波

E x ( z) E x0 e
jkc z
E x0 e
jkc z
Ex Ex
Ex
E x0
Hy
H y0
kc c
Ex Hy
E x0 H y0
c
c c c e j c (1 j ) (1 j )
7.3 导电媒质中的均匀平面波的特性
波在理想介质中传播的最大特点是 没有损耗,所以理想介质又叫无耗媒 质。 实际的媒质都是有耗媒质。当 媒质的电导率σ ≠0,在媒质中存在 传导电流,形成焦耳损耗。
无源导电媒质中的麦氏第一方程
D H J c E j E j j E t
E x 0 e jkc z
z j z
kc
E x 0 e jkc z
c
E x0 e
e
1
c
E x 0 e z e j z
Hy Hy
入射波瞬时值:
Ex ( z, t ) 2Ex0 e
H y ( z, t ) 2 Ex 0
z
2
je z j z
e
c
)
( E x 0 ) 2z ( E x 0 ) 2 2z j az e az e e j ( c e ) c
则能流密度平均值为:
Sav
平面电磁波的性质

uv E
'
积分并取积分常数为0
v k
×
uv E
=
uv kv B
v k
×
uv B
=
−με
uv kv E
结论:E、B、k三个矢量互相垂直,并顺序组成右手坐标系。 电场波E和磁场波B都是横波
回
顾
1.3.2 电磁波的矢量性质
分析:电磁波是由高频振荡的电场E和磁场B按一定的规 律随空间坐标r和时间t传播而形成的。电磁波的波函数描 述了E、 B随r、t的变化规律。在一般情况下,E、B的大 小和方向均随r、t的变化而变化,总是发生在垂直波传播 方向的平面内(横波)。
由于 : k × E = kν B
Qk ⊥ E
且 k = k ⇒ E =νB = 1 B = c B με n
E和B之间的数值关系
r E Qr= B
1 =v
εμ
两波振幅之比是一个正实数, ∴ Er、Br两矢量位相相同。
回 顾
• 平面电磁波的能量传播特性
1.能流密度矢量(各向同性)
电场:u E
=
1 2
•光波在折反射过程中振动分量的状态不变。入射波为s分量时,反射 波和折射波也是s分量,不会出现p分量,反之亦然
这种方向只是一种人为的规定,改变这种规定,并不影响结果的 普遍适用性。
③非铁磁性媒质: μ1 = μ2 = μ0
④
uv E
的正方向的规定:S分量
为正, 为负;P分量:在界面的投影向
右为正,左为负
• 在光学中,常常要处理光波从一种介质到另 一种介质的传播问题,由于两种介质的物理 性质不同(分别以ε1、μ1 和ε2、μ2 表征), 在两种介质的分界面上,电磁场将不连续,
第七章 均匀平面电磁波

4 107 120 1 109 36
第七章 均匀平面电磁波
四.传播特性 5.波印廷矢量
E0 cos(t kz ) S E H a x E0 cos(t kz ) a y 2 E0 az cos2 (t kz )
②等相位面:任一固定时刻,相位相同的点组成的面.
③等相位面方程:
t kz x 常数
④显然随t增加,等相位面必向Z增加方向移动,也即某 一定的E x 值向Z增加的方向移动,也即整个波形向Z增 加方向移动,即向+Z方向传播的简谐波.
第七章 均匀平面电磁波
二.所以波动方程及解:
⑤等相位面上各点相位相等,随时间推移和位置变化始终=常数 等相位面垂直于传播方向(+Z). 小结:
大小上是波阻抗的倍数关系。
(3)瞬时值形式: 将此式乘 e jt取实部可得时域关系式(略)
第七章 均匀平面电磁波
四.传播特性
根据波动方程的解及电磁场关系式不妨设: E a x E 0 cos(t kz ) E0 H a y cos(t kz ) a y H 0 cos(t kz )
2 2 1 T T f
第七章 均匀平面电磁波
四.传播特性
4.波阻抗 电场与磁场复振幅之比,称平面波的波阻抗
E0 k k H0
一般为复数,在理想媒质中,η为实数,即此时 E和H 的相位相同,
如果是真空/空气,则为
0
0 0
第七章 均匀平面电磁波
三.电磁场的关系
E x E x0 cos(t kz x ) Re[Ex e ] 其中 E E e jkz
均匀平面电磁波

E1 Em1e j1 , E2 Em2e j2 , Em1、Em2 0, 1、2为 实 数
即:E
r
Em1e j1 e jkz xˆ Em2e j2 e jkz xˆ
2、解的瞬时表示式:
E r,
t
Re
[E
r
e
jt
]
Em1 cost kz 1 xˆ Em2 cost kz 2 xˆ
• 两个行波幅度不一定相同,且不一定同时存在。存 在一个还是两个行波、存在哪个方向的行波,由具体 问题决定。
• 两行波性质相同,研究其中之一即可,取第一项。
四、均匀平面波(uniform plane wave):
1、等相位面:
在任意固定时刻,电磁波的相位相同的点所构成 的空间曲面。
2、• E平 r面, t波 Em cost kz xˆ 的等相位面:
第四章 均匀平面电磁波
主要内容:
1、无界均匀理想介质中的时谐场波动方程的均匀平面 电磁波解 2、均匀平面电磁波传播的特点 3、平面电磁波在导电媒质中的传播特性 4、电磁波的极化
4.1 无界均匀理想介质中的均匀平面波
一、无耗2介E质r中时 谐k 2电E磁r场的频0域无源波动方程
2
H
r
k
2
H
r
0
k 为 实 数
传播方向
z
• 解的第二项 Em2 cost kz 2 是向 zˆ 方向传播
的正弦行波。
传播方向
t4 t3 t2 t1
z
5、解的物理意义
EE• rr波,t动 方EE程xm1的zc解xoˆsEt 1ekz
jkz xˆ
1 xˆ
E2e jkz xˆ
Em2 cost
平面波特性
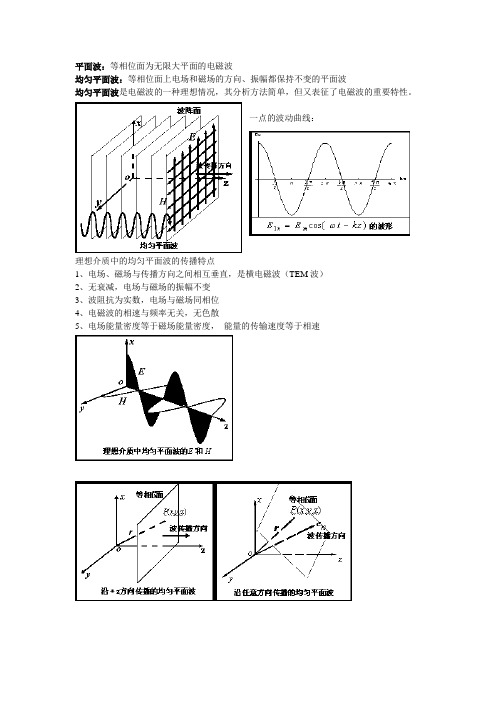
平面波:等相位面为无限大平面的电磁波
均匀平面波:等相位面上电场和磁场的方向、振幅都保持不变的平面波
均匀平面波是电磁波的一种理想情况,其分析方法简单,但又表征了电磁波的重要特性。
一点的波动曲线:
理想介质中的均匀平面波的传播特点
1、电场、磁场与传播方向之间相互垂直,是横电磁波(TEM波)
2、无衰减,电场与磁场的振幅不变
3、波阻抗为实数,电场与磁场同相位
4、电磁波的相速与频率无关,无色散
5、电场能量密度等于磁场能量密度,能量的传输速度等于相速。
6 均匀平面电磁波

数,称为波矢量或传播矢量。
第6章 均匀平面电磁波
由于常矢量
Em
并不会因为坐标的旋转而改变,只是在
不同坐标系中的表达式有所不同,在坐标系 xyz 中,仍用
符号
Em
表示,则沿任意方向传播的电磁波可表示为
E
Em
e
jkr
,
H
1
ek
E
, ek
E
ek
H
0
ek 为传播方向的单位矢量。
第6章 均匀平面电磁波
2、均匀平面波的传播参数
只考虑电场的 x 分量,瞬时值: Ex (z,t) Exm cost k z x
时间变化特性(固定位置):
角频率 ω:单位时间内的相位变化,单位为 rad /s
在固定位置:z=常数,Ex 随时 Ex 间 t 作正弦周期性变化,如图。
周期与频率:相位改变 2 对
t
应的时间为周期,由T 2 得
Ey Eym cos(t kz y )
由于 Ex 、Ey 的振幅和相位可能不同,因此在空间任意固定
点上,合成电场强度矢量的大小和方向都可能随时间变
化,其端点随时间变化将描绘出不同的轨迹。
第6章 均匀平面电磁波
波的极化是指空间任一固定点上电场矢量的指向随
时间变化的方式,一般用电场矢量
E
的矢端轨迹来描述。
101
0.4
3
rad/m
第6章 均匀平面电磁波
∴
Ex
4 cos(t k z )
3
4 cos(2
107 t 0.4
3
z)
3
mV/m
E
ex 4 cos(2
107 t
0.4
第07讲 媒质中的均匀平面电磁波

Ex = Eme e e Em −αz − jβz jφ0 Hy = e e e ηc
µε
2
−αz − jβz jφ0
σ α =ω 1+ −1 2 ωε
2 µε σ β =ω 1+ +1 2 ωε
电磁场理论>>均匀平面电磁波
均匀平面电磁波 波阵面上各点的振幅相同
轴为电场E的方 以x轴为电场 的方 轴为电场 轴为磁场H的方向 向,y轴为磁场 的方向, 轴为磁场 的方向, 电磁波传播方向为z轴建 电磁波传播方向为 轴建 立直角坐标系
电磁场理论>>均匀平面电磁波
一、平面波的概念 v 2v 2 ∇ E+k E =0
∇ Ex + k Ex = 0 ∇2Ey + k 2Ey = 0 ∇2Ez + k 2Ez = 0
电磁场理论>>均匀平面电磁波
三、导电媒质中的均匀平面电磁波
沿z方向平面波的复数形式
Ex = Eme e k = ω µε γ = jω µεc σ = jω µε − j ω = α + jβ
α 称为衰减常数 β 称为相移常数
jφ0 − jkz
Ex = Eme e Em jφ0 −γz Hy = e e ηc
电磁场理论>>正弦电磁场
回顾
v v v ∇× H = J + jωD v v ∇× E = − jωB v ∇⋅ B = 0 v ∇⋅ D = ρ v v D = εE v v B = µH v v J = σE
麦克斯韦方程的 复数形式 时变电磁场的波动方程
v 2 v ∂E 2 ∇ E − µε 2 = 0 ∂t v v ∂2 H ∇2 H − µε 2 = 0 ∂t ∂t
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
理想介质中的均匀平面电磁波
的特性与特征参量
11:43
引
言
在无源空间中,时变电磁场相互激励,电磁场以波动的形式存在, 并且在空间中传播,形成电磁波。
电磁波传播的媒介环境:
无界:无障碍的自由空间(理想情况) 半无界:介质表面反、折射问题 有界:波导、传输线 等 媒介性质: 无耗(非导电)
有耗(导电)
11:43
11:43
( E0为电场振幅)
11:43
相位速度(波速)
相速v:电磁波的等相位面在空间中的 移动速度
波形中任意一点处的相位为
t kz 0 令 t kz 0=const
dz dz 1 两边对时间t去导数,得: k 0 vp dt dt k 关于波的相速的说明
1 H 2 (ez ) E2
同理,可以推得:
磁场与电场相互 垂直,且同相位
1 H H1 H 2 (ez E1 ez E2 )
结论:在理想介质中,均匀平面波的电场强度与磁场强度相互垂
直,且同相位。
11:43
波动方程解的物理意义
电磁波传播的相位速度仅与媒质特性相关。 真空中电磁波的相位速度: p 0 v
1
=
11:43
1 f
vp f
0 0
3 108 (m / s) c(光速)
vp f
如果以 e n为表示波传播方向的单位矢量
对于均匀平面电磁波,有: H
同理可以推得: 重要结论:
0 0 0
4 107 120 377() 1 109 36
在自由空间中传播的电磁波,电场幅度与磁场幅度之比为377。
11:43
能量密度和能流密度
实数表达形式
1 2 电场能量密度: we E 2 磁场能量密度: w 1 H 2 1 ( E )2 1 E 2 m 2 2 2 we wm
首先考察
均匀平面波函数
。其实数形式为: cos(t kz) E e jkz E
t 0
Ex
t
4
t
2π
2
kz
0
π
3π
从图可知,随时间t增加,波形向+z方向平移。
不同时刻 E x 的波形
e jkz为表示向+z方向传播的均匀平面波函数; e jkz 表示向-z方向传播的均匀平面波波函数;
在实际应用中,理想的均匀平面波并 不存在。但某些实际存在的波型,在远离 波源的一小部分波阵面,仍可近似看作均 匀平面波。
11:43
o
y
H
均匀平面波
z
1.1 一维波动方程的平面波解
电场强度矢量的解 在正弦稳态下,在均匀、各向同性理想媒质的无源区域中,电 场场量满足亥姆霍兹方程,即:
2
2 2 E E E 2 2 2 2 k E 0 x y z 2 Ex 2 Ex 2 Ex 2 2 k 2 Ex 0 2 y z x 2 Ey 2 Ey 2 Ey 2 2 k 2 Ey 0 x y 2 z 2 2 2 Ez Ez Ez 2 2 k 2 Ez 0 x 2 y z
11:43
(s)
t
波长与相位常数
波长λ :空间相位差为2π 的两个波阵面的间距,即
k 2π
2π 1 k f
(m)
相位常数 k :表示波传播单位距离的相位变化
k
2π
(rad/m)
o
Ex
k 的大小等于空间距离2π内所 包含的波长数目,因此也称为波数。
z
Ex ( z,0) Emcoskz 的曲线
11:43
相伴的磁场
令
jkz jkz E E1 E2 ex E e ex E e ,由 E j H 得 j ( E e jkz ) j H1 E1 ey z 1 jkz e E k jkz z 1 ey E e ez ex E e
2
11:43
2 E k E 0 (k 2 2 )
考虑一种简单情况:
性质,知 E 只随z坐标变化。则方程可以简化为: 2 Ex k 2 Ex 0 z 2
解一元二次微分方程,可得上方程通解为:
均匀平面波电场矢量沿x方向,波沿z方向传播,则由均匀平面波
Ex E e jkz E e jkz
H e E 、 、 n三者相互垂直,且满足右手螺旋关系
11:43
媒质本征阻抗(波阻抗)
从公式可知:均匀平面电磁波中电场幅度和磁场幅度之比为一定值。 定义电场幅度和磁场幅度比为媒质本征阻抗,用 表示,即:
E H
——媒质本征波阻抗
特殊地:真空(空气)的本振阻抗为:
式中: E 、 为待定常数(由边界条件确定),表征场的幅度. E
上式为一维波动方程通解的复数表达形式,其实数表达形式为:
Ex Re[( E e jkz E e jkz )e jt ] Em cos(t kz 1 ) Em cos(t kz 2 )
一维波动方程解的物理意义:沿+z,-z方向传播的均匀平面波的 合成波。
11:43
1.2 无界理想媒质中均匀平面波的传播特性
在无界媒质中,若均匀平面波向+z向传播,且电场方向指向 e 方 x 向,则其电场场量表达式为:
E ex E0e jkz e j (场量的复数形式) 或E ex E0 cos(t kz ) (场量的实数形式)
jkz 当 E e E e 时,其相伴的磁场为 H x 当 E e E e jkz 时,其相伴的磁场为 H x
en E
场量 E , 的关系 H
ez E ( e z ) E
E H en
1 理想介质中的均匀平面波
均匀平面波的几个概念
波阵面:空间相位相同的点构成的曲面,即等相位面
平面波:等相位面为无限大平面的电磁波 均匀平面波:等相位面上电场和磁场的方向、振幅都保持不 变的平面波
均匀平面波的特点:在与波传播方向 垂直的无限大平面内,电、磁场的振幅、 方向和相位保持不变。
波阵面
x
E
波传播方向
结论:理想媒质中均匀平面波的电场能量等于磁场能量。 电磁波的能量密度:w we wm E 2 H 2
电磁波的能流密度:
1 1 2 S E H E en E E en 1 1 2 Sav Re[ E H ] E0 en 2 2
由电磁波的场量表达式可总结出波的传播特性 均匀平面波的传播参数
角频率、频率和周期 角频率ω :表示单位时间内的相位变化,单位为rad /s
周期T :时间相位变化 2π的时间间隔,即
Ex
o
T
Ex (0, t ) Emcost 的曲线
T 2π
T
2π
1 (Hz) 频率f : f T 2π
的特性与特征参量
11:43
引
言
在无源空间中,时变电磁场相互激励,电磁场以波动的形式存在, 并且在空间中传播,形成电磁波。
电磁波传播的媒介环境:
无界:无障碍的自由空间(理想情况) 半无界:介质表面反、折射问题 有界:波导、传输线 等 媒介性质: 无耗(非导电)
有耗(导电)
11:43
11:43
( E0为电场振幅)
11:43
相位速度(波速)
相速v:电磁波的等相位面在空间中的 移动速度
波形中任意一点处的相位为
t kz 0 令 t kz 0=const
dz dz 1 两边对时间t去导数,得: k 0 vp dt dt k 关于波的相速的说明
1 H 2 (ez ) E2
同理,可以推得:
磁场与电场相互 垂直,且同相位
1 H H1 H 2 (ez E1 ez E2 )
结论:在理想介质中,均匀平面波的电场强度与磁场强度相互垂
直,且同相位。
11:43
波动方程解的物理意义
电磁波传播的相位速度仅与媒质特性相关。 真空中电磁波的相位速度: p 0 v
1
=
11:43
1 f
vp f
0 0
3 108 (m / s) c(光速)
vp f
如果以 e n为表示波传播方向的单位矢量
对于均匀平面电磁波,有: H
同理可以推得: 重要结论:
0 0 0
4 107 120 377() 1 109 36
在自由空间中传播的电磁波,电场幅度与磁场幅度之比为377。
11:43
能量密度和能流密度
实数表达形式
1 2 电场能量密度: we E 2 磁场能量密度: w 1 H 2 1 ( E )2 1 E 2 m 2 2 2 we wm
首先考察
均匀平面波函数
。其实数形式为: cos(t kz) E e jkz E
t 0
Ex
t
4
t
2π
2
kz
0
π
3π
从图可知,随时间t增加,波形向+z方向平移。
不同时刻 E x 的波形
e jkz为表示向+z方向传播的均匀平面波函数; e jkz 表示向-z方向传播的均匀平面波波函数;
在实际应用中,理想的均匀平面波并 不存在。但某些实际存在的波型,在远离 波源的一小部分波阵面,仍可近似看作均 匀平面波。
11:43
o
y
H
均匀平面波
z
1.1 一维波动方程的平面波解
电场强度矢量的解 在正弦稳态下,在均匀、各向同性理想媒质的无源区域中,电 场场量满足亥姆霍兹方程,即:
2
2 2 E E E 2 2 2 2 k E 0 x y z 2 Ex 2 Ex 2 Ex 2 2 k 2 Ex 0 2 y z x 2 Ey 2 Ey 2 Ey 2 2 k 2 Ey 0 x y 2 z 2 2 2 Ez Ez Ez 2 2 k 2 Ez 0 x 2 y z
11:43
(s)
t
波长与相位常数
波长λ :空间相位差为2π 的两个波阵面的间距,即
k 2π
2π 1 k f
(m)
相位常数 k :表示波传播单位距离的相位变化
k
2π
(rad/m)
o
Ex
k 的大小等于空间距离2π内所 包含的波长数目,因此也称为波数。
z
Ex ( z,0) Emcoskz 的曲线
11:43
相伴的磁场
令
jkz jkz E E1 E2 ex E e ex E e ,由 E j H 得 j ( E e jkz ) j H1 E1 ey z 1 jkz e E k jkz z 1 ey E e ez ex E e
2
11:43
2 E k E 0 (k 2 2 )
考虑一种简单情况:
性质,知 E 只随z坐标变化。则方程可以简化为: 2 Ex k 2 Ex 0 z 2
解一元二次微分方程,可得上方程通解为:
均匀平面波电场矢量沿x方向,波沿z方向传播,则由均匀平面波
Ex E e jkz E e jkz
H e E 、 、 n三者相互垂直,且满足右手螺旋关系
11:43
媒质本征阻抗(波阻抗)
从公式可知:均匀平面电磁波中电场幅度和磁场幅度之比为一定值。 定义电场幅度和磁场幅度比为媒质本征阻抗,用 表示,即:
E H
——媒质本征波阻抗
特殊地:真空(空气)的本振阻抗为:
式中: E 、 为待定常数(由边界条件确定),表征场的幅度. E
上式为一维波动方程通解的复数表达形式,其实数表达形式为:
Ex Re[( E e jkz E e jkz )e jt ] Em cos(t kz 1 ) Em cos(t kz 2 )
一维波动方程解的物理意义:沿+z,-z方向传播的均匀平面波的 合成波。
11:43
1.2 无界理想媒质中均匀平面波的传播特性
在无界媒质中,若均匀平面波向+z向传播,且电场方向指向 e 方 x 向,则其电场场量表达式为:
E ex E0e jkz e j (场量的复数形式) 或E ex E0 cos(t kz ) (场量的实数形式)
jkz 当 E e E e 时,其相伴的磁场为 H x 当 E e E e jkz 时,其相伴的磁场为 H x
en E
场量 E , 的关系 H
ez E ( e z ) E
E H en
1 理想介质中的均匀平面波
均匀平面波的几个概念
波阵面:空间相位相同的点构成的曲面,即等相位面
平面波:等相位面为无限大平面的电磁波 均匀平面波:等相位面上电场和磁场的方向、振幅都保持不 变的平面波
均匀平面波的特点:在与波传播方向 垂直的无限大平面内,电、磁场的振幅、 方向和相位保持不变。
波阵面
x
E
波传播方向
结论:理想媒质中均匀平面波的电场能量等于磁场能量。 电磁波的能量密度:w we wm E 2 H 2
电磁波的能流密度:
1 1 2 S E H E en E E en 1 1 2 Sav Re[ E H ] E0 en 2 2
由电磁波的场量表达式可总结出波的传播特性 均匀平面波的传播参数
角频率、频率和周期 角频率ω :表示单位时间内的相位变化,单位为rad /s
周期T :时间相位变化 2π的时间间隔,即
Ex
o
T
Ex (0, t ) Emcost 的曲线
T 2π
T
2π
1 (Hz) 频率f : f T 2π
