正切函数、余切函数的图象和性质·典型例题分析
三角函数的图像和性质知识点及例题讲解

三角函数的图像和性质1、用五点法作正弦函数和余弦函数的简图(描点法):正弦函数y=sinx ,x ∈[0,2π]的图象中,五个关键点是:(0,0) (2π,1) (π,0) (23π,-1) (2π,0) 余弦函数y=cosx x ∈[0,2π]的图像中,五个关键点是:(0,1) (2π,0) (π,-1) (23π,0) (2π,1) 2 sin y x = cos y x = tan y x =图象定义域 R R,2x x k k ππ⎧⎫≠+∈Z ⎨⎬⎩⎭值域[]1,1-[]1,1-R最值 当22x k ππ=+时,max 1y =;当22x k ππ=- 时,min 1y =-.当2x k π=时,max 1y =;当2x k ππ=+时,min1y =-.既无最大值也无最小值周期性 2π 2ππ奇偶性奇函数 偶函数 奇函数单调性 在2,222k k ππππ⎡⎤-+⎢⎥⎣⎦上是增函数; 在32,222k k ππππ⎡⎤++⎢⎥⎣⎦上是减函数. 在[]2,2k k πππ-上是增函数; 在[]2,2k k πππ+上是减函数.在,22k k ππππ⎛⎫-+⎪⎝⎭上是增函数.对称性 对称中心(),0k π 对称轴2x k ππ=+对称中心,02k ππ⎛⎫+ ⎪⎝⎭对称轴x k π=对称中心,02k π⎛⎫⎪⎝⎭无对称轴函数 性质例作下列函数的简图(1)y=|sinx|,x ∈[0,2π], (2)y=-cosx ,x ∈[0,2π]例利用正弦函数和余弦函数的图象,求满足下列条件的x 的集合:21sin )1(≥x 21cos )2(≤x3、周期函数定义:对于函数()y f x =,如果存在一个非零常数T ,使得当x 取定义域内的每一个值时,都有:()()f x T f x +=,那么函数()y f x =就叫做周期函数,非零常数T 叫做这个函数的周期。
注意: 周期T 往往是多值的(如sin y x = 2π,4π,…,-2π,-4π,…都是周期)周期T 中最小的正数叫做()y f x =的最小正周期(有些周期函数没有最小正周期)sin y x =, cos y x =的最小正周期为2π (一般称为周期)正弦函数、余弦函数:ωπ=2T 。
正切、余切函数的图象和性质

正切、余切函数的图象和性质正切、余切函数的图象和性质张思明教学目的:〔略〕教学过程择录:一、引题:师:比照上一节的习题,请同学们看一看自己的作业本,对正弦和余弦函数,在作业中,我们已涉及了多少类型的问题?生众:P159〔11〕正弦,余弦函数的定义域:P158〔3〕正弦,余弦函数的最值〔值域〕:P158〔6〕正弦,余弦函数的奇偶性P159〔8〕正弦,余弦函数的单调性P159〔7〕正弦,余弦函数的应用一-----比大小P158〔4〕正弦,余弦函数的周期〔最小正周期〕P159〔12〕正弦,余弦函数的图象P160〔16、17〕正弦,余弦函数性质的应用教师在黑板上书写:〔1〕定义域〔2〕值域〔3〕奇偶性〔4〕单调性〔5〕比大小〔6〕求最小正周期〔7〕作图〔8〕应用教师:今天我们来学习正切、余切函数的图象和性质,可以想一想,我们要觖决什么问题?生众:不就是上面这几点问题吗?教师:说的不错,我们就是要来解决把“正弦、余弦函数〞换成“正切、余切函数〞后〔1〕~〔7〕后面加一个“是什么?〞这样一些问题。
请同学们带的这些问题看书5分钟〔P153~P157〕。
[评述]:这里是通过作业小结的方式引入问题。
学生常常是很肓目的做作业,很少观察作业所涉及的问题类型和范围。
教师有意识地引导学生作这种观察,既培养了学生看课本的习惯,又自然引出了今天的课题和要探索解决的问题。
二、学生自己回忆性设问,〔自问自答〕5分钟以后:学生阅读完毕,教师指导第一组学生〔7人〕为相邻的同桌的同学〔第二组学生〕就前面七个方向提一个有关正、余切函数性质的问题,要求是后面的同学不要提前面已经提到过的问题,并请同桌同学〔起立〕对着大家答复。
做完后,问、答的两组学生角色交换。
其它组的同学一边听,一边作判断,对的放过,不对时请同一行的同学予以更正:生1:正切函数的定义域是什么?邻生答:除了,k∈Z外的全体实数。
生2:正切函数的值域是整个y轴吗?邻生改正:应说成是全体实数生3:………生10:学过四种三角函数都是奇数吗?都是增函数吗?邻生答:不对,反例是余弦函数〕生11:正切函数是它定义域上的增函数吗?〔好问题!〕邻生答:是,其它学生更正:不是。
三角函数的正切与余切关系解析

三角函数的正切与余切关系解析三角函数是数学中重要的概念之一,其中正切和余切是相互关联的两个函数。
在本文中,我们将详细解析正切和余切的关系及其相关性质。
一、正切与余切的定义正切函数(tangent function)和余切函数(cotangent function)是三角函数中的两个重要函数。
在单位圆上,这两个函数与正弦和余弦函数之间存在一定的关系。
正切函数定义如下:tan(x) = sin(x) / cos(x)余切函数定义如下:cot(x) = 1 / tan(x) = cos(x) / sin(x)其中,x为角度值或弧度值,sin(x)代表正弦函数值,cos(x)代表余弦函数值。
二、正切与余切的性质1. 定义域和值域:正切函数和余切函数的定义域为x ≠ (2k + 1)π/2 (k为整数),即除去所有以π/2为倍数的点。
正切函数的值域为R,即所有实数。
余切函数的值域也为R,即所有实数。
2. 奇偶性:正切函数是奇函数,即tan(-x) = -tan(x)。
余切函数是奇函数,即cot(-x) = -cot(x)。
3. 周期性:正切函数和余切函数的周期都是π,即tan(x + π) = tan(x),cot(x + π) = cot(x)。
4. 正切和余切的关系:由正弦和余弦函数定义可得,tan(x) = sin(x) / cos(x),cot(x) = cos(x) / sin(x)。
这意味着正切和余切是正弦和余弦的倒数关系。
5. 正切和余切的图像:正切函数和余切函数的图像都是无界的,并且在定义域内具有周期性。
三、正切与余切的应用正切与余切在数学和科学中有广泛的应用,以下是其中一些重要应用:1. 三角方程的求解:在解三角方程时,正切和余切的性质可以用来简化等式,从而求解方程。
2. 函数图像的分析:正切和余切函数的图像特点可以用于分析函数的性质,如最值、增减性、极值点等。
3. 三角恒等式的证明:在证明三角恒等式时,正切和余切的关系可以用来推导等式的两边,从而证明恒等式的成立。
高一数学正切函数和余切函数的图像与性质1(学生版)

(2)
例2、求函数 的定义域、值域,并指出它的周期性、奇偶性、单调性。
变式练习1:讨论函数 的性质
变式练习2: 的单调区间怎么求?
例3、观察正切曲线写出满足tanx>0的x的值的范围:
变式练习:方法同上,求出分别满足下列条件的x的值的范围
(1)
(2)
例4、求下列函数的定义域
(1)y=tan2x
例5、求学下列函数的最小正周期和单调区间
(1) ;
(2)
【课堂小练】
1、函数y=tan(ax+ )(a≠0)的最小正周期为( )
2、以下函数中,不是奇函数的是( )
A y=sinx+tanxB.y=xtanx-1C.y= D.y=lg
3、下列命题中正确的是( )
A.y=cosx在第二象限是减函数B.y=tanx在定义域内是增函数
C.y=|cos(2x+ )|的周期是 D.y=sin|x|是周期为2π的偶函数
4、函数y= + 的定义域是( )
A (2k+1)π≤x≤(2k+1)π+ ,k∈Z
B (2k+1)π<x<(2k+1)π+ ,k∈Z
C (2k+1)π≤x<(2k+1)π+ ,k∈Z
D (2k+1)π<x<(2k+1)π+ 或x=kπ,k∈Z
5、已知y=tan2x-2tanx+3,求它的最小值
6、求适合下列条件的 的集合:
6.单调性:在开区间 内,函数单调递增
余切函数y=cotx的图象及其性质(要求学生了解):
——即将 的图象,向左平移 个单位,
再以x轴为对称轴上下翻折,即得 的图象
定义域:
值域:R,
当 时 ,当 时
周期:
奇偶性:奇函数
单调性:在区间 上函数单调递减
讲义21:正切函数的图像与性质
精锐教育学科教师辅导讲义讲义编号_学员编号: 年 级:高一 课 时 数:3 学员姓名: 辅导科目:数学 学科教师:课 题 正、余切函数的图像和性质授课日期及时段教学目的熟练掌握正、余切函数的图像及其性质(单调性、奇偶性、周期性);能灵活利用他们的性质解题。
教学内容一、知识梳理1、正切函数的图像2、正切函数的性质 (1)定义域:⎭⎬⎫⎩⎨⎧∈+≠z k k x x ,2|ππ, (2)值域:R ,当z k k k x ∈⎪⎭⎫⎝⎛+∈2,πππ时0>y ,当z k k k x ∈⎪⎭⎫⎝⎛-∈πππ,2时0<y(3)周期性:π=T说明:函数()()tan 0,0y A x A ωϕω=+≠≠的周期T πω=求三角函数式的最小正周期时,要尽可能地化为只含一个三角函数,且三角函数的次数为1的形式,否则很容易出现错误。
(4)奇偶性:()x x tan tan -=-奇函数,对称中心是,02k π⎛⎫⎪⎝⎭()k Z ∈ 特别提醒:正(余)切型函数的对称中心有两类:一类是图像与x 轴的交点,另一类是渐近线与x 轴的交点,但无对称轴,这是与正弦、余弦函数的不同之处。
(5)单调性:在开区间z k k k ∈⎪⎭⎫⎝⎛+-2,2ππππ内,函数单调递增。
但要注意在整个定义域上不具有单调性。
余切函数的图像和性质:二、例题解析例1 函数y =x tan log 21的定义域是( )A {x |0<x ≤4π) B {x |2k π<x ≤2k π+4π,k ∈Z }C {x |k π<x ≤k π+4π,k ∈Z }D {x |k π-2π<x ≤k π+4π,k ∈Z }巩固训练1、函数1tan y x =-的定义域是_______2、函数)1(cot log 2-x 的定义域是________2、函数tan 2()tan xf x x=的定义域为( ) A .{|x x R ∈ 且,4k x k Z π⎫≠∈⎬⎭B .{|x x R ∈ 且,2x k k Z ππ⎫≠+∈⎬⎭C .{|x x R ∈ 且,4x k k Z ππ⎫≠+∈⎬⎭D .{|x x R ∈ 且,4k x k k Z ππ⎫≠-∈⎬⎭4、函数tan()4y x π=-的定义域是( )A .|,4x x x R π⎧⎫≠∈⎨⎬⎩⎭ B .|,4x x x R π⎧⎫≠-∈⎨⎬⎩⎭C .|,,4x x k k R x R ππ⎧⎫≠+∈∈⎨⎬⎩⎭ D .3|,,4x x k k Z x R ππ⎧⎫≠+∈∈⎨⎬⎩⎭例2 函数tan()(0)6y ax a π=+≠的周期为( ).A .2a π B .2aπ C .a π D .a π 例3 比较大小:(1)125tan 与137tan ; (2)⎪⎭⎫ ⎝⎛-34tan π与⎪⎭⎫⎝⎛-511tan π。
正切函数和余切函数的图像和性质
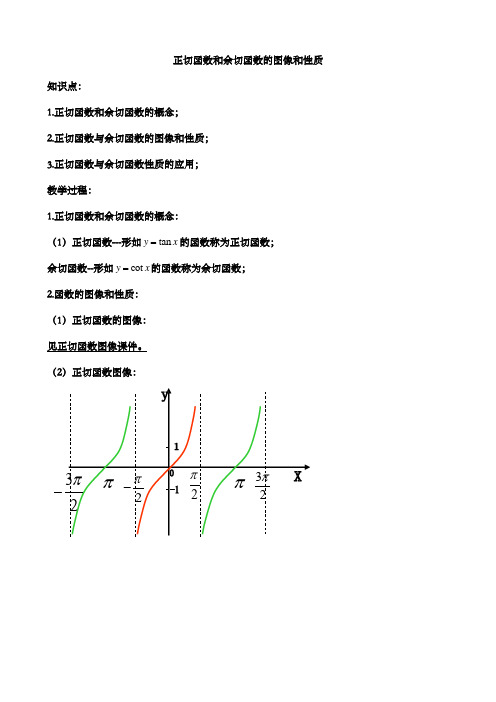
正切函数和余切函数的图像和性质知识点:1.正切函数和余切函数的概念;2.正切函数与余切函数的图像和性质;3.正切函数与余切函数性质的应用;教学过程:1.正切函数和余切函数的概念:(1)正切函数---形如tan=的函数称为正切函数;y x余切函数--形如cot=的函数称为余切函数;y x2.函数的图像和性质:(1)正切函数的图像:见正切函数图像课件。
(2)正切函数图像:-(3)与切函数的图像:归纳填表格:例1.求下列函数的周期: (1)tan(3)3y x π=-+;(2)221tgxy tg x=+;(3)cot tan y x x =-;(4)22tan21tan 2xy x=-; (5)sin 1tan tan 2x y x x ⎛⎫=+ ⎪⎝⎭例2.求下列函数的单调区间: (1)tan(2)24y x π=++;(2)tan()123x y π=-+-;(3)12log cot y x ⎛= ⎝⎭ 例3.求下列函数的定义域:(1)tan 4y x π⎛⎫=- ⎪⎝⎭;(2)y =(3)y = 例4.(1)求函数21)tan tan ]y x x =-的定义域; (2)解不等式:23tan (2)(3tan(2)044x x ππ+-+≤例5.已知2tan tan y x a x =-,当1[0,],[0,]34x a π∈∈时,函数max y =a 的值;例6.已知函数tan ,(0,)2y x x π=∈,若1212,(0,),2x x x x π∈≠。
求证:1212()()()22f x f x x xf ++>。
正切、余切函数的图象和性质

正切、余切函数的图象和性质
正切、余切函数的图象和性质
正切、余切函数的图象和性质
张思明
教学目的:(略)
教学过程择录:
一、引题:
师:对比上一节的习题,请同学们看一看自己的作业本,对正弦和余弦函数,在作业中,我们已涉及了多少类型的问题?
生众:P159(11)正弦,余弦函数的定义域:
P158(3)正弦,余弦函数的最值(值域):
P158(6)正弦,余弦函数的奇偶性
P159(8)正弦,余弦函数的单调性
P159(7)正弦,余弦函数的应用一-----比大小
P158(4)正弦,余弦函数的周期(最小正周期)
P159(12)正弦,余弦函数的图象
P160(16、17)正弦,余弦函数性质的应用
教师在黑板上书写:(1)定义域(2)值域(3)奇偶性(4)单调性(5)比大小(6)求最小正周期(7)作图(8)应用教师:今天我们来学习正切、余切函数的图象和性质,可以想一想,我们要觖决什么问题?
生众:不就是上面这几点问题吗?
教师:说的不错,我们就是要来解决把“正弦、余弦函数”换成“正切、余切函数”后(1)~(7)后面加一个“是什么?”这样一些问题。
请同学们带的这些问题看书5分钟(P153~P157)。
[评述]:这里是通过作业小结的方式引入问题。
学生常常是很肓目的做作业,很少观察作业所涉及的问题类型和范围。
教师有意识地引导学生作这种观察,既培养了学生看课本的习惯,又自然引出了今天的课题和要探索解决的问题。
二、学生自己回顾
[1] [2] [3] [4] [5]。
三角函数的图象与性质

三角函数的图象与性质教学目标1.熟练掌握正弦函数、余弦函数、正切函数、余切函数的性质,并能用它研究复合函数的性质.2.熟练掌握正弦函数、余弦函数、正切函数、余切函数图象的形状、态度,并会用“五点法”画出函数y=sin(ωx+φ)的图象。
3.理解图象平移变换、伸缩变换的意义,并会用这两种变换研究函数图象的变化.重点难点重点是通过复习,能运用四种三角函数的性质研究复合三角函数的性质及图象的特点,特别是三角函数的周期性,是需要重点明确的问题.难点是,在研究复合函数性质时,有些需要先进行三角变换,把问题转化到四种三角函数上,才能进行研究,这就增加了问题的综合性和难度.教学过程三角函数的图象与性质是三角函数的核心问题,要熟练、准确地掌握.特别是三角函数的周期性,反映了三角函数的特点,在复习“三角函数的性质与图象”时,要牢牢抓住“三角函数周期性”这一内容,认真体会周期性在三角函数所有性质中的地位和作用.这样才能把性质理解透彻.【要点复习】一.y=sinx的图象和性质:1.图象:列表后描点,用平滑曲线相连得到y=sinx,x∈[0,2π]的图象y=sinx,x∈R时的完整的图象.由此可见,画出y=sinx 的图象关键是首先要画出y=sinx 在[0,2π]内的图象.而y=sinx 在[0,2π]的图象有这样五个点很重要:(0,0),(2π,1),(π,0),(32π,-1),(2π,0);其中(0,0), (π,0),(2π,0)是轴上的点,(2π,1), (32π,-1)分别是函数图象的最高、最低点.所以这五个点是确定y=sinx 图象的基本点.因此,代数描点法也可简称为“五点法”,以后再画y=sinx 图象时,就可直接使用五点法了.2.性质:(1)定义域:x ∈R .(2)值域:y ∈[-1,1], ∴y=sinx 是有界函数。
(3)周期性:正弦函数y=sinx 是周期函数.2π是它的最小正周期,2k π(k ∈Z ,k =0)都是它的周期.(4)单调性:从图象上可以看出正弦函数在整个实数域上不是增函数,也不是减函数,但具有增减区间。
