学而思奥数2016秋季班提高班第5讲讲义
三年级学而思奥数讲义精编版

目录第一讲加减法的巧算(一) (2)第二讲加减法的巧算(二) (7)第三讲乘法的巧算 (12)第四讲配对求和 (16)第五讲找简单的数列规律 (17)第六讲图形的排列规律 (19)第七讲数图形 (23)第八讲分类枚举 (26)能力测试(一) (26)第九讲填符号组算式 (28)第十讲填数游戏 (31)第十一讲算式谜(一) (35)第十二讲算式谜(二) (37)第十三讲火柴棒游戏(一) (39)第十四讲火柴棒游戏(二) (40)第十五讲从数量的变化中找规律 (45)第十六讲数阵中的规律 (45)第17讲时间与日期……………第18讲推理……………能力测试(二) (63)第19讲循环………………第20讲最大和最小…………………………第21讲最短路线…………………………第22讲图形的分与合…………………第23讲格点与面积……………………第24讲一笔画………………………阶段测试(三)……………………第25讲移多补少与求平均数………………第26讲上楼梯与植树………………第27讲简单的倍数问题……………………第28讲年龄问题……………………………第29讲鸡兔同笼问题……………………第30讲盈亏问题…………………第31讲还原问题……………………第32讲周长的计算……………………第33讲等量代换……………………第34讲一题多解……………………能力测试(四)………………………………第一讲加减法的巧算森林王国的歌舞比赛进行得既紧张又激烈。
选手们为争夺冠军,都在舞台上发挥着自己的最好水平。
台下的工作人员小熊和小白兔正在统计着最后的得分。
由于他们对每个选手分数的及时通报,台下的观众频频为选手取得的好成绩而热烈鼓掌,同时,观众也带着更浓厚的兴趣边看边猜测谁能拿到冠军。
观众的情绪也影响着两位分数统计者。
只见分数一到小白兔手中,就像变魔术般地得出了答案。
等小熊满头大汗地算出来时,小白兔已欣赏了一阵比赛,结果每次小熊算得结果和小白兔是一样的。
学而思小学奥数个精彩讲座总汇全

第1讲计算综合(一)繁分数的运算,涉及分数与小数的定义新运算问题,综合性较强的计算问题.1.繁分数的运算必须注意多级分数的处理,如下所示:甚至可以简单地说:“先算短分数线的,后算长分数线的”.找到最长的分数线,将其上视为分子,其下视为分母.2.一般情况下进行分数的乘、除运算使用真分数或假分数,而不使用带分数.所以需将带分数化为假分数.3.某些时候将分数线视为除号,可使繁分数的运算更加直观.4.对于定义新运算,我们只需按题中的定义进行运算即可.5.本讲要求大家对分数运算有很好的掌握,可参阅《思维导引详解》五年级[第1讲循环小数与分数].1.计算:71147 18262 13581333416⨯+⨯-÷【分析与解】原式=7123723174612241488128131233+⨯=⨯=-2.计算:【分析与解】注意,作为被除数的这个繁分数的分子、分母均含有5199.于是,我们想到改变运算顺序,如果分子与分母在5199后的两个数字的运算结果一致,那么作为被除数的这个繁分数的值为1;如果不一致,也不会增加我们的计算量.所以我们决定改变作为被除数的繁分数的运算顺序.而作为除数的繁分数,我们注意两个加数的分母相似,于是统一通分为1995×.具体过程如下:原式=5919(3 5.22)19930.41.6910()52719950.5199519(6 5.22)950+-⨯÷+⨯-+=5191.3219930.440.40.59()519950.419950.5191.329-⨯⨯⨯÷+⨯⨯-=199320.41()19950.5+÷⨯=0.410.5÷=1143.计算:1111111987-+-【分析与解】原式=11198711986-+=198613973-=198739734.计算:已知=181111+12+1x+4=,则x等于多少【分析与解】方法一:1118x68114x112x7111+11148x62+214x1x+4+====+++++++交叉相乘有88x+66=96x+56,x=1.25.方法二:有11131118821x4+==+++,所以18222133x4+==++;所以13x42+=,那么x=.5.求944,43,443,...,44 (43)个这10个数的和.【分析与解】方法一:944+43+443...44 (43)++个=1044(441)(4441)...(44...41)+-+-++-个=104444444...44 (49)++++-个=1094(999999...999...9)99⨯++++-个=1004[(101)(1001)(10001)...(1000...01)]99⨯-+-+-++--个=914111.1009=49382715919⨯-个.方法二:先计算这10个数的个位数字和为39+4=31⨯;再计算这10个数的十位数字和为4×9=36,加上个位的进位的3,为36339+=;再计算这10个数的百位数字和为4×8=32,加上十位的进位的3,为32335+=;再计算这10个数的千位数字和为4×7=28,加上百位的进位的3,为28331+=;再计算这10个数的万位数字和为4×6=24,加上千位的进位的3,为24327+=;再计算这10个数的十万位数字和为4×5=20,加上万位的进位的2,为20222+=;再计算这10个数的百万位数字和为4×4=16,加上十万位的进位的2,为16218+=;再计算这10个数的千万位数字和为4×3=12,加上百万位的进位的1,为12113+=;再计算这10个数的亿位数字和为4×2=8,加上千万位的进位的1,为819+=;最后计算这10个数的十亿位数字和为4×1=4,加上亿位上没有进位,即为4.所以,这10个数的和为91.6.如图1-1,每一线段的端点上两数之和算作线段的长度,那么图中6条线段的长度之和是多少【分析与解】因为每个端点均有三条线段通过,所以这6条线段的长度之和为:1173(0.60.875)1+0.75+1.8+2.625=6.175=63440⨯+++=7.我们规定,符号“○”表示选择两数中较大数的运算,例如:3.5○=○=.符号“△”表示选择两数中较小数的运算,例如:△=△=.请计算:23155 (0.625)(0.4)33384 1235(0.3)( 2.25) 3104⨯+【分析与解】原式1550.6255155725384218384122562.253⨯=⨯÷=+8.规定(3)=2×3×4,(4)=3×4×5,(5)=4×5×6,(10)=9×10×11,….如果111(16)(17)(17)-=⨯,那么方框内应填的数是多少【分析与解】111(17)()1(16)(17)(17)(16)=-÷=-=161718111516175⨯⨯-=⨯⨯.9.从和式11111124681012+++++中必须去掉哪两个分数,才能使得余下的分数之和等于1【分析与解】因为1116124+=,所以12,14,16,112的和为l,因此应去掉18与110.10.如图1-2排列在一个圆圈上10个数按顺时针次序可以组成许多个整数部分是一位的循环小数,例如.那么在所有这种数中。
学而思奥数2016寒假班提高班第5讲讲义

位数、三位数.请你将其中的质数都 写出来. 【答案】 5 个:2,3,13,31,23 【分析】 (第二届华杯赛复赛第 2 题)一位数: 2,3;两位数:13、31、23,共 5 个.
37 38 39 40 41 42 聚 起 华 夏 中 兴 力,同 唱 移 山 壮 丽 歌. 43 44 45 46 47 48 49 50 51 52 53 54 55 56 将质数对应的汉字依次写出就是:少 年朋友亲切联欢;一九九七相聚中山.
2.某质数加 6 或减 6 得到的数仍是质 数,在 50 以内你能找出几个这样的质 数?把它们写出来. 【答案】 有六个这样的数,分别是 11,13,17,
(3)已知 A、B 都是质数,且 35A +12B = 130 ,求 A、B 各是多少. 【答案】 (1)2 和 89; (2)36 = 2 + 3 + 31 = 2 + 5 + 29 = 2 +11+ 23 = 2 +17 +17; (3)A=2,B=5
2. (1)已知两个质数和为 30,这两 个质数分别是多少? (2)已知三个互不相同的质数和为 25,这三个质数的积可能是多少?
拓展 3 哥德巴赫猜想是说:“每个大于 2 的偶 数都可以表示成两个质数之和”. 问:
168 是哪两个两位数的质数之和,并且 其中一个的个位数字是 1? 【答案】 97 和 71 【分析】 两个数是两位数,最小数至少为 69, 比 69 大的个位为 1 的质数只有 71,此 时另外一个数为168 - 71 = 97所以这两 个数分别为 71、97.
学而思奥数2016秋季班提高班第6讲讲义
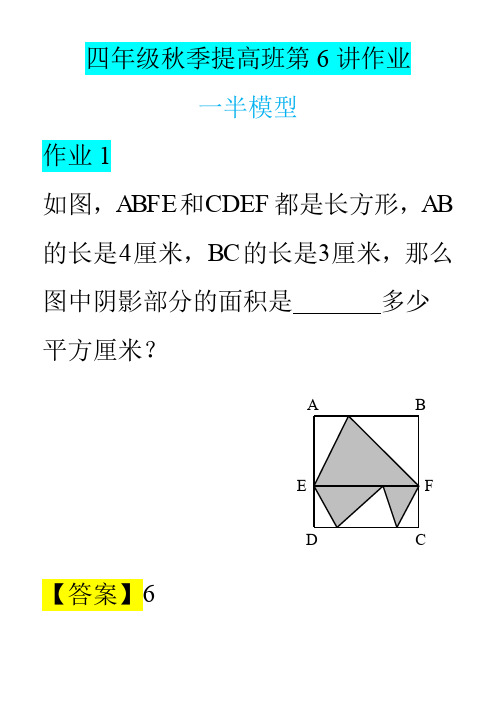
BC 边上靠近 B 点的三等分点,那么阴
影部分的面积为
.
A
B
F E
D
C
【答案】30 平方厘米 【分析】△BEC 的面积是梯形的一半, S△BEC 180 2 90(cm2),阴影面积 是90 3 30(cm2).
拓展 4
如图,在梯形 ABCD中,E 、F 分别是
AB、CD 的中点,S1和S2的面积分别是 5 和 15,求梯形 ABCD 的面积.
为面积相等的两部分,且每个三角形
中的两部分都分属于S1 S4、S2 S3这
两个不同的组合,所以S1 S4 S2 S3.
C G D
S1
S2 F
H
O
S3 S4
A
E
B
8.56 因为 ABFD 是平行四边形,所以 AD BF ,那么FC 22 14 8cm.又 CDEF 是正方形,所以
EF FC 8cm.三角形 ABF 的面积是 14 8 2 56cm2.因为三角形 ABF 在 平行四边形 ABFD,长方形 AGHF 中 都是一半,因此阴影部分面积为 56cm2.
四年级秋季提高班第 6 讲 一半模型
例1 (1)如图所示,一个长方形分成 4 个 不同的三角形,其中红色部分的面积 和为 50 平方厘米,黄色三角形面积是 21 平方厘米,则绿色三角形的面积是 ________平方厘米;
黄
红
红
绿
(2)如图所示,长方形的面积均为 20, 则下面两个图形中阴影部分的面积依
4.连 DC,S BDC 6S BDE 6, S ABC 2S BDC 12
5.如图,连接 CF,那么 CF 平行 BD ,所以,阴影面积 三角形 BDF 的面积 三角形 BCD 的面积=0.72(平 方厘米).
学而思小学奥数知识点梳理(大纲视图)资料讲解

⑷三视图与展开图
最短线路与展开图形状问题
⑸染色问题
几面染色的块数与“芯”、棱长、顶点、面数的关系。
四、
1
①开放型与封闭型
②间隔与株数的关系
2
外层边长数-2=内层边长数
(外层边长数-1)×4=外周长数
外层边长数2-中空边长数2=实面积数
3
①车长+桥长=速度×时间
②车长甲+车长乙=速度和×相遇时间
学而思小学奥数知识点梳理
学而思教材编写组侍春雷
前言
小学奥数知识点梳理,对于学而思的小学奥数大纲建设尤其必要,不过,对于知识点的概括很可能出现以偏概全挂一漏万的现象,为此,本人参考了单尊主编的《小学数学奥林匹克》、中国少年报社主编的《华杯赛教材》、《华杯赛集训指南》以及学而思的《寒假班系列教材》和华罗庚学校的教材共五套教材,力图打破原有体系,重新整合划分,构建十七块体系(其第十七为解题方法汇集,可补充相应杂题),原则上简明扼要,努力刻画小学奥数知识的主树干。
③车长甲+车长乙=速度差×追及时间
列车与人或骑车人或另一列车上的司机的相遇及追及问题
车长=速度和×相遇时间
车长=速度差×追及时间
4
差不变原理
5
假设法的解题思想
6
原有草量=(牛吃速度-草长速度)×时间
7
8
分析差量关系
9
10
11
12
还原法,从结果入手
13
列表消元法
等价条件代换
五、
1
路程和=速度和×相遇时间
n的约数个数:d(n)=(a1+1)(a2+1)....(ak+1)
二年级学而思秋季数学超常班讲义第五讲
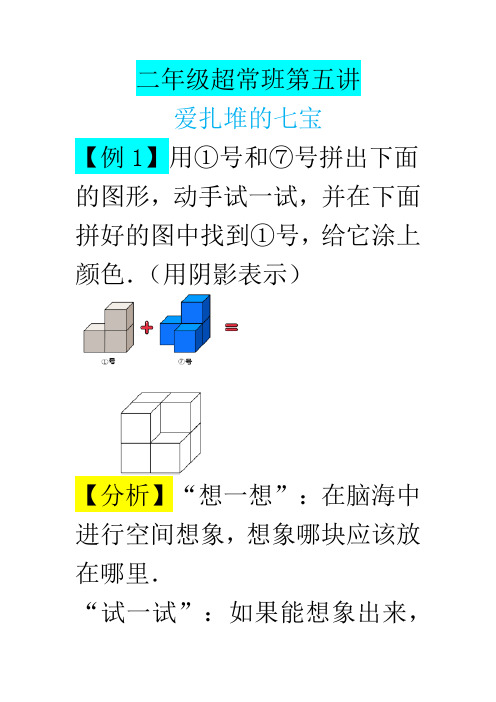
二年级超常班第五讲爱扎堆的七宝【例1】用①号和⑦号拼出下面的图形,动手试一试,并在下面拼好的图中找到①号,给它涂上颜色.(用阴影表示)【分析】“想一想”:在脑海中进行空间想象,想象哪块应该放在哪里.“试一试”:如果能想象出来,可以实际动手操作验证一下.当无法想象出来的时候,可以进行动手操作.我们已经学习了“知道位置两拼”和“知道粘贴面两拼”,本活动是知道拼好的样子去两拼,和前面的方法一样,可以先将其中的一个摆在桌子上,比如先将⑦号放在桌子上,再将①号和⑦号拼在一起,观察拼成的图形是什么样子,是否和题中所给图形相同,或者拼好的图形经过旋转、翻转以后,是否和题中所给图形相同.“记一记”:把我们尝试出来的结果记录下来,并总结方法.可以利用“找图形法”帮助分析图形,在题目所给的图形中,找到①号,标注出来,如果①号在上面一层,那么剩下的不可能是⑦号;如果①号在下面一层,那么剩下的可能是⑦号;如果①号在左面一层,那么剩下的可能是⑦号;如果①号在右面一层,那么剩下的不可能是⑦号;如果①号在前面一层,那么剩下的不可能是⑦号;如果①号在后面一层,那么剩下的可能是⑦号.再在所有可能的情况里确定①号和⑦号的具体位置,将①号画出来.要求学生至少能找到一种可能,并画出来,程度好的班,可以要求学生找出尽可能多的情况.通过尝试,答案如下:【例2】用①号和⑥号拼出下面的图形,动手试一试,并在下面拼好的图中找到①号,给它涂上颜色.(用阴影表示)【分析】用①号和⑥号拼出下面的图形,动手试一试,并在下面拼好的图中找到①号,给它涂上颜色.(用阴影表示)“想一想”:在脑海中进行空间想象,想象哪块应该放在哪里.“试一试”:如果能想象出来,可以实际动手操作验证一下.当无法想象出来的时候,可以进行动手操作.我们已经学习了“知道位置两拼”和“知道粘贴面两拼”,本例题是知道拼好的样子去两拼,和前面的方法一样,可以先将其中的一个摆在桌子上,比如先将⑥号放在桌子上,再将①号和⑥号拼在一起,观察拼成的图形是什么样子,是否和题中所给图形相同,或者拼好的图形经过旋转、翻转以后,是否和题中所给图形相同.“记一记”:把我们尝试出来的结果记录下来,并总结方法.可以利用“找图形法”帮助分析图形,在题目所给的图形中,找到①号,标注出来,如果①号在上面一层,那么剩下的不可能是⑥号;如果①号在下面一层,那么剩下的可能是⑥号;如果①号在左面一层,那么剩下的不可能是⑥号;如果①号在右面一层,那么剩下的可能是⑥号;如果①号在前面一层,那么剩下的不可能是⑥号;如果①号在后面一层,那么剩下的可能是⑥号.再在所有可能的情况里确定①号和⑥号的具体位置,将①号画出来.要求学生至少能找到一种可能,并画出来,程度好的班,可以要求学生找出尽可能多的情况.通过尝试,答案如下:(答案不唯一)【例3】①号和③号拼在一起会变成什么样的图形呢?请你动手试一试.下面的A、B、C、D 都是由①号和③号拼成的,请你把它们的①号都涂上颜色.(用阴影表示)【分析】“想一想”:在脑海中进行空间想象,想象①号和③号拼在一起,会变成什么样子.“试一试”:如果能想象出来,可以实际动手操作验证一下.当无法想象出来的时候,可以进行动手操作.和前面的方法一样,可以先将其中的一个摆在桌子上,比如先将③号放在桌子上,再将①号和③号拼在一起,观察拼成的图形是什么样子,是否和选项中所给图形相同,或者拼好的图形经过旋转、翻转以后,是否和选项中所给图形相同.“记一记”:把我们尝试出来的结果记录下来,并总结方法.可以利用“找图形法”帮助排除选项,在选项中,找到③号,本题可以从和①号相比特殊的③号入手,③号要在能放下3块的地方,那么A选项中,③号可以在右面横着,剩下的部分正好是①号,A选项正确,在选项中画出①号;B选项中,③号可以在下面横着,剩下的部分正好是①号,B选项正确,在选项中画出①号;C选项中,③号可以在前面横着,剩下的部分正好是①号,C选项正确,在选项中画出①号;D选项中,③号可以在后面横着,剩下的部分正好是①号,D选项正确,在选项中画出①号.要求学生至少可以判断出选项是否符合题意,程度好的班,可以要求学生自己动手操作,尽量多的拼出和选项不同的情况.通过尝试,答案如下:(答案不唯一)【例4】④号和⑦号拼在一起会变成什么样的图形呢?请你动手试一试.下面的A、B、C、D都是由④号和⑦号拼成的,请你把它们的④号都涂上颜色.(用阴影表示)【分析】“想一想”:在脑海中进行空间想象,想象⑦号和④号拼在一起,会变成什么样子.“试一试”:如果能想象出来,可以实际动手操作验证一下.当无法想象出来的时候,可以进行动手操作.和前面的方法一样,可以先将其中的一个摆在桌子上,比如先将④号放在桌子上,再将⑦号和④号拼在一起,观察拼成的图形是什么样子,是否和选项中所给图形相同,或者拼好的图形经过旋转、翻转以后,是否和选项中所给图形相同.“记一记”:把我们尝试出来的结果记录下来,并总结方法.可以利用“找图形法”帮助排除选项,在选项中,找到④号,本题可以从和⑦号相比特殊的④号入手,④号要在能放下3块的地方,那么A选项中,④号可以在后面横着,剩下的部分正好是⑦号,A选项正确,在选项中画出④号;B选项中,④号可以在后面竖着,剩下的部分正好是⑦号,B选项正确,在选项中画出④号;C选项中,④号可以在后面竖着,剩下的部分正好是⑦号,C选项正确,在选项中画出④号;D选项中,④号可以在后面横着,剩下的部分正好是⑦号,D选项正确,在选项中画出④号.要求学生至少可以判断出选项是否符合题意,程度好的班,可以要求学生自己动手操作,尽量多的拼出和选项不同的情况.通过尝试,答案如下:(答案不唯一)【例5】用③号、⑤号和⑦号拼出下面的床,动手试一试,并在下面拼好的床中找到⑦号,给它涂上颜色.(用阴影表示)【分析】“想一想”:在脑海中进行空间想象,想象哪块应该放在哪里.⑤号和⑦号无论从哪个方向都是两层,只有③号可以平铺在一层,而床头是两层,床板是一层,可以推测③号平铺在床板上,⑤号和⑦号拼出床头.“试一试”:如果能想象出来,可以实际动手操作验证一下.当无法想象出来的时候,可以进行动手操作.可以先将其中的一个摆在桌子上,比如先将③号放在桌子上,再将⑤号和⑦号拼在一起,观察拼成的图形是什么样子,是否和题中所给图形相同,或者拼好的图形经过旋转、翻转以后,是否和题中所给图形相同.“记一记”:把我们尝试出来的结果记录下来,并总结方法.可以利用“找图形法”帮助从结果入手分析图形,在题目所给的图形中,找到⑤号和⑦号,本题中⑤号和⑦号比较特殊,它们不能平铺在一层,总要高出一块,那么可以知道⑤号和⑦号要拼出床头,剩下的用③号补充完整.要求学生一定要动手操作.通过尝试,答案如下:【超常挑战】1.用①号、②号、③号和④号拼出下面的墙角,动手试一试,并在下面拼好的墙角中找到②号,给它涂上颜色.(用阴影表示)2.用②号、④号、⑤号和⑦号拼出下面的楼梯,动手试一试,并在下面拼好的楼梯中找到⑦号,给它涂上颜色.(用阴影表示)3.用①号、②号、④号和⑤号拼出下面的坦克,动手试一试,并在下面拼好的坦克中找到④号,给它涂上颜色.(用阴影表示)4.有3个和图1相同的图形.把3个图形组合到一起,可以组成各种形状.从①到⑥的6个图形中,找出能够用3个图1的图形组合起来构成的图形,并用○表示,不能组成的,请用×表示.(2009年第1届日本算术奥林匹克预赛试题)【分析】1.用①号、②号、③号和④号拼出下面的墙角,动手试一试,并在下面拼好的墙角中找到②号,给它涂上颜色.(用阴影表示)答案如下:(答案不唯一)2.“想一想”:在脑海中进行空间想象,想象哪块应该放在哪里.“试一试”:如果能想象出来,可以实际动手操作验证一下.当无法想象出来的时候,可以进行动手操作.可以先将其中的一个摆在桌子上,比如先将②号放在桌子上,再将④号、⑤号和⑦号拼在一起,观察拼成的图形是什么样子,是否和题中所给图形相同,或者拼好的图形经过旋转、翻转以后,是否和题中所给图形相同.“记一记”:把我们尝试出来的结果记录下来,并总结方法.可以利用“找图形法”帮助从结果入手分析图形,可以从楼梯的顶端开始拼,能放在顶端的只有④号或⑦号,如果将⑦号放在顶端,那么剩下的三块不能拼出剩下的楼梯.那么顶端就是④号竖着放,剩下的用②号、⑤号和⑦号补充完整.要求学生一定要动手操作.通过尝试,答案如下:3.答案如下:(答案不唯一)4.①○;②○;③○;④×;⑤×;⑥×.显而易见,①、②、③都可以分成3个图1的图形,④、⑤、⑥最多可以分出两个图1的图形.在④中,面前的两个小正方体都只能和中间的小正方体组合,所以不行;在⑤中,高出去的两个小正方体无法组成图①的图形,所以不行;在⑥中,最左和最右的两个小正方体都只有一种组合方法,这样剩下中间一列三个小正方体,所以不行.。
学而思三年级秋季班第五讲(多笔画).pdf
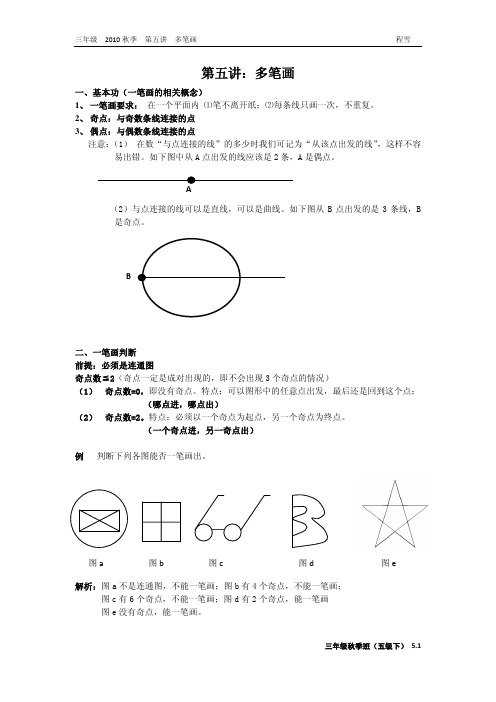
第五讲:多笔画一、基本功(一笔画的相关概念)1、 一笔画要求: 在一个平面内 ⑴笔不离开纸;⑵每条线只画一次,不重复。
2、 奇点:与奇数条线连接的点3、 偶点:与偶数条线连接的点注意:(1) 在数“与点连接的线”的多少时我们可记为“从该点出发的线”,这样不容易出错。
如下图中从A 点出发的线应该是2条,A 是偶点。
(2)与点连接的线可以是直线,可以是曲线。
如下图从B 点出发的是3条线,B是奇点。
二、一笔画判断前提:必须是连通图奇点数≦2(奇点一定是成对出现的,即不会出现3个奇点的情况)(1) 奇点数=0,即没有奇点。
特点:可以图形中的任意点出发,最后还是回到这个点;(哪点进,哪点出)(2) 奇点数=2。
特点:必须以一个奇点为起点,另一个奇点为终点。
(一个奇点进,另一奇点出)例 判断下列各图能否一笔画出。
解析:图a 不是连通图,不能一笔画;图b 有4个奇点,不能一笔画; 图c 有6个奇点,不能一笔画;图d 有2个奇点,能一笔画 图e 没有奇点,能一笔画。
图a图b图c图d图e三、多笔画概念:不能一笔画的点线图,即为多笔画。
最少笔画数: 奇点个数÷2例1 看图填写下表解析:图 ① ② ③ ④ ⑤ ⑥ 奇点数 4 4 6 6 88 笔画数 2 2 3 3 4 4四、多笔画转化为一笔画宗旨:减少奇点数方法:(1)添线(2)去线例2 加一条线或去一条线,一笔画出这个图形(以一幅图为例讲解)解析:本图有4个奇点,不能一笔画。
想要一笔画成,就要将其奇点数减少到2个或者0个,可以去线,如下图或也可以添线,如下图① ② ③ ④ ⑤ ⑥一条线能改变其连接的2个点的奇偶性,故添/去一条线最多能将2个奇点转化为偶点去掉连接2个奇点的线,这两个点就成为偶点五、一笔画的实际应用1、判断能否一次不重复走完某路线方法:转化为点线图,观察奇点的数量,即可判断 关键:如何将题目转化为点线图窍门:线——路线,题目中要求一次不重复走的东西,比如,一次不重复经过所有的门,那一道门就是一条线。
第5讲.和倍问题.例题+拓展练习

第5讲和倍问题一、讲义例题例1. 学而思三年级奥数基础班和提高班共有图书160本。
基础班的图书本数是提高班的3倍,基础班和提高班各有图书多少本?例2. 甲仓库存粮108吨,乙仓库存粮140吨,要是甲仓库存粮是已仓库的3倍,必须从乙仓库运出多少吨放入甲仓库?例3.甲、乙两船原有乘客共561人,到某地后,从甲船下去40人,乙船上来10人,这时甲船人数正好是乙船人数的2倍。
问甲、乙两船原来各有乘客多少人?例4.新华书店去年和今年共售书380万册,今年售书量比去年售书量的2倍还多20万册,问去年和今年各售书多少万册?例5. 小猴子聪聪和明明共有28个香蕉,聪聪的香蕉比明明的2倍少2个。
聪聪和明明各有几个香蕉?例6. 一筐苹果、一筐梨、一筐香蕉共重112千克。
一直苹果的重量是梨的3倍,香蕉的重量比梨少3千克。
一筐苹果、一筐梨、一筐香蕉各重多少千克?二、拓展练习1、小王家养了公鸡和母鸡,一共35只,公鸡的只数是母鸡的4倍,王刚家养的公鸡和母鸡各有多少只?2、某学校五、六年级共有学生150人,五年级的学生人数是六年级学生人数的2倍,五、六年级各有学生多少人?3、某厂生产一批零件,原计划由甲车间生产510件,乙车间生产505件,后因情况变化,要求乙车间完成的数量是甲车间的4倍,那么应从甲车间的任务中拨给乙车间多少件?4、弟弟有课外书20本,哥哥有课外书25本,哥哥给弟弟过少本后,弟弟的书是哥哥的2倍?5、小小图书室有故事书和童话书共54本,其中童话的本数比故事书的2倍少6本。
童话书和故事书各有多少本?6、少先队员栽苹果树和梨树共134棵,苹果树比梨树棵树的3倍少10棵,这两种树各栽了多少棵?7、果园里共有梨树、苹果树和桃树410棵,一直苹果树的棵树是梨树的3倍,桃树的棵树比梨树的2倍还多20棵,分别求出桃树、梨树、苹果树各多少棵?。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
AA EE
C C 3.18(平方B 厘B 米). D D C C
拓展 2 如图,正方形 ABCD 的边长为 12cm, 正方形 CEFG 的边长为 5cm,求阴影 部分的面积.
G
F
D
M CN
E
G
F
D
MC N
E
A
B
A
B
【答案】60 平方厘米
【分析】阴影部分可等积变形为两个
直角三角形 DCG 与 BCE,面积为
D
C
【分析】如下图,连接 AD,可以看
出, AD∥BC,所以
S△ABC 例3
S△BCD
44
2 8cm2
(1)如图,BD 长 12 厘米,DC 长 4
厘米,B、C 和 D 在同一条直线上.三
角形 ABD 的面积是三角形 ADC 面积
的多少倍?三角形 ABC 的面积是三角
形 ADC 面积的多少倍?
A
B
三角形 AEF 的面积是 40 平方厘米.
深化练习 7.31 连接 DE、EC,根据等积变形可知,阴 影部分的面积等于三角形 CDE 的面 积,即直角梯形减去两个直角三角形 的面积.梯形面积:(5 7) (6 4) 2 60, 三角形 ADE 面积:5 6 2 15,三角 形 CEB 面积:7 4 2 14,所以阴影 部分的面积为:60 15 14 31.
ห้องสมุดไป่ตู้
复习巩固 作业 1 四年级九个班进行拔河单循环赛,每 个班要进行几场比赛?一共要进行几 场比赛? 【答案】8;36 【分析】每个班要进行 8 场,一共要 进行8 9 2 36场比赛.
作业 2 数一数,下面的图形中有多少个包含 “★”的长方形?
★
【答案】36 【分析】左上方的点有 4 个,右下方 的点有 9 个,4 9 36个.
3.6 平方厘米,求三角形 CDE 的面积.
【答案】三角形 ABE、ADC、ADE; 14.4 平方厘米 例4 (1)如图,三角形 ABC 中,DC 2BD, CE 3AE,三角形 ADE 的面积是 20, 三角形 ABC的面积是多少?
A E
BD
C
(2)如图,在三角形 ABC 中,E 是 BC 中点,D、F 是 AB 边上的三等分点, 已知三角形 BEF 的面积是 2,求三角 形 ABC 的面积是多少?
A
D
G
F
B
C
E
第一题的图
E
F
A
D
H
B
C
G
【随堂练】
1. ABCD和CEFG均为正方形, AB=6cm,CE=2.5cm,则阴影部分面积 是多少
A
D
G
F
B
C
E
【答案】2.5 6 2 7.5(cm2)
2. ABCD和CEFG均为正方形, AB=10cm,CE=4cm,求阴影部分面积。
A
D
G F
B
C
E
例2 (1) 如图,正方形 ABCD 与正方形 CEFG 并排放置,B、C 、E 在同一条 直线上,且正方形 ABCD 边长为 10 厘 米,则图中阴影面积为多少平方厘
米?
A
D
G
F
B
C
E
(2) 如图,正方形 ABCD 和正方形
ECGF 并排放置,BF 与 CD 相交于点
H,已知 AB 6厘米,则阴影部分的面
【随堂练】
CD=4BD,则三角形 ADC 是三角形 ABD 的几倍?三角形 ABC 是三角形 ABD 的几倍?
A
B D
C
【答案】4 倍,5 倍
练一练 如图,在三角形 CDE 中,B 是 EC 中 点,A 是 BD 中点,连接 AE、AC,那 么与三角形 ABC 面积相等的三角形一 共有哪几个?若三角形 ABC 的面积是
D
C
F
A
E
B
4.6 因为F 是 AC的中点,所以 S△ABC 2S△ABF ,同理S△ABF 2S△BEF ,
故S△BEF S△ABC 4 8 6 2 4 6(平方 厘米).
5.54 S△BFD 12 2 3 18, S△ABD 18 2 3 27, S△ABC 27 2 54.
6.40 平方厘米 △ABD与△ABC等高,BD DC ,有 S△ABD 180 2 90(平方厘米).同理 有S△ABE 90 3 2 60(平方厘米), S△AFE 60 3 2 40 (平方厘米).即
作业 3 计算:9999 1111 【答案】11108889 【分析】原式=(10000 1) 1111
11110000 1111 11108889
四年级秋季提高班第 5 讲练习册答案 等积变形
同步练习 1.3.18 如图,连接 AE,BD.因为 AD∥BC,则: S△PDC S△PDB,又 AB∥ED,则: S△EAD S△EBD,所以, S阴影 S△EPD S△PDC
四年级秋季提高班第 5 讲作业 等积变形
作业 1
如图,大小两个正方形摞在一起,已
知大正方形的边长为 20 厘米,小正方
形的边长为 16 厘米,求阴影三角形的
面积.
A
D
B C
E
G
F
【答案】连接 BD ,发现 BD∥GE ,由
平行线同的等积变形知,S△GDE , S△GBE
所以阴影部分面积等于大正方形的一 半,即20 20 2=200(平方厘米).
45 3 4 60.
作业 5 如图,三角形 ABC 的面积是 45,BC 是CD的 5 倍, AE是CE的 2 倍,那么 三角形CDE 的面积是多少?
A
A
E
E
B
CD
B
CD
【答案】3 【分析】如右图,连接BE.BC 5CD, 所以S△BCE 5S△CDE,又 AC 3CE,所 以S△ABC 3S△BCE 15S△CDE , S△CDE 45 15 3.
实战练习 10. 连接 BF,根据等高模型,S△EFB 8, S△CFB 8,所求面积是 (8 8 8) 2 48.
D
C
F
A
E
B
四年级秋季提高班第 5 讲 等积变形
例1 (1)已知长方形 ABCD 中, AB 8, BC 5,求三角形 ABE 的面积.
D
C
E
A
B
(2)如图,正方形 ABCD 的边长为 18, BE 8,求三角形 AEF 的面积.
D
C
F
A
BE
(3)如图,正方形 ABCD 的边长为 18, AE 4,求阴影部分的总面积.
D
C
AEF B
【答案】(1)20; (2)72; (3)126
【分析】(1)可以过 E 作三角形的高, 高与 BC 等长;也可以利用等积变形将 E 点移动至 C 点;
(2) AD∥BC,所以S△ABF S△DBF , 此时S△AEF S△DBE ,面积为 8 18 2 72(如果想更直观一些,可 以将三角形 DBE 再次等积变形为直角 三角形 CBE). (3)(18 4) 18 2 126.
练一练 如图,三角形 ABC 中,DC 3BD, AE 1.5BE,三角形 ABC 的面积是 60, 三角形 BDE 的面积是多少?
A
E
BD
C
【答案】6 【分析】S△ABD 60 (1 3) 15, S△BED 15 (1 1.5) 6.
例5
(1)如图,已知三角形 ABC 的面积为 8 平方厘米,BD 3BC, AB 2AE, 求三角形 BDE 的面积.
DC
(2)如图,D、E 在 BC 上,DC 2BD,
EC 3DE.求三角形 ABC 的面积是三
角形 ADE 面积的几倍?
A
B
DE
C
【答案】
(1)3 倍;4 倍; (2)6 倍
【分析】 (1)等高模型,两个三角形高相等, 底是几倍,面积就是几倍. (2)EC 3DE ,则S△AEC 3S△ADE , 可设三角形 ADE 的面积为 1 份,则三 角形 AEC 的面积为 3 份;DC 2BD, 则S△ADC 2S△ABD,所以三角形 ABD 是 2 份;则三角形 ABC 的面积为 6 份, 所以面积 是三角形 ADE 的 6 倍. 方法二:通过边的关系导出BC 6DE, 所以是 6 倍.
积是多少平方厘米?
E
F
A
D
H
B
C
G
【答案】50 平方厘米;18 平方厘米
【分析】(1)连接 CF,那么 CF 平行
BD ,所以,阴影面积等于三角形
BCD的面积,即10 10 2=50平方厘
米.
(2)连接 DF、FC,根据平行线间的
等积变形,S△DHG S△DHF ,同理 S△BDF S△BDC ,阴影的面积为 6 6 2 18平方厘米.
【答案】10 10 2 50(cm2)
3. ABCD和CEFG均为正方形,
AB=10cm,CE=4cm,求阴影部分面积。
D
A
F
G
H
E
C
B
【答案】4 4 2 8(cm2)
练一练 此图是由大、小两个正方形组成的, 小正方形的边长是4厘米,求三角形 ABC 的面积是多少?
A
A
B
B
4
4
C
【答案】8 平方厘米
E A
【随堂练】
如图,平行四边形 ABCD,底为 10, 高为 6。则阴影部分面积是多少?
A
D
A
D
B
C
B
C
A
B
C
A
D
A
D
B C
D
B
C
【答案】10 6 2 30
