2020—2021年新高考总复习数学《立体几何》高考考点专项复习及答案解析.docx

合集下载

2023届高考数学总复习《立体几何》附答案解析

（2）若点 N 为 BC 的中点，求四面体 A'MNB 的体积．
【解答】证明：（1）连接 BD，设 BD∩EC＝F，连接 MF，
由题意可得四边形 BCDE 为正方形，则 F 为 BD 的中点，
∴MF 为△A′BD 的中位线，可得 MF∥A′B，
又 A′B⊄平面 EMC，MF⊂平面 EMC，
∴A'B∥平面 EMC；
2023 年高考：立体几何复习题及答案
1．如图，已知直角梯形 ABCD，BC∥AD，BC＝CD＝2，AD＝4，∠BCD＝90°，点 E 为 AD 的中点，现将三角形 ABE 沿 BE 折叠，得到四棱锥 A'﹣BCDE，其中∠A'ED＝120°，点 M 为 A'D 的中点．
（1）求证：A'B∥平面 EMC；
第2页共3页
∵BE⊂平面 BEF，∴平面 BEF⊥平面 AMD，结合题意分析知，点 F 在线段 AD 上，连接 MF，过 A 作 AH⊥MF，交 MF 的延长线于点 H，
则结合已知条件得
，解得 AH ，
设 Dt ，
第3页共3页
【解答】解：（1）证明：由题意知 PC2+AC2＝PA2，∴PC⊥AC，同理，PC⊥BC，又 AC∩BC＝C，∴PC⊥平面 ABC， ∵D，E 分别是 AC，PA 的中点，∴DE∥PC， ∴DE⊥平面 ABC，又 DE⊂平面 BDE，∴平面 BDE⊥平面 ABC．（2）在△BDE 中，DE⊥BD，BD＝2 ，DE＝2，∴BE＝4，如图，过 A 作 AM⊥BE 于 M，连接 MD，在△ABE 中，AB＝BE＝4，AE＝2 ，解得 AM ，ME＝1， ∵DM⊂平面 BDE，∴AC⊥DM，在 Rt△ADM 中，AM ，AD＝2，∴DM ， ∴DM2+EM2＝DE2，∴MD⊥BE， ∵AM∩MD＝M，∴BE⊥平面 AMD，

2023年高考数学总复习《立体几何》附答案解析

．
所以 z1＝0，
，故可取
，，，
于是＜，＞
，
设所成锐二面角为θ，所以 sinθ
，
所以平面 PAD 和平面 PBE 所成锐二面角的正弦值为．
第3页共3页
第1页共3页
∴CF CC1 AA1 ， ∵∠BAC＝90°，
∴CD
，
在 Rt△FCD 中，tan∠FDC 맨
，
故直线 DF 与平面 ABC 所成角的正切值为．
2．如图所示，四棱锥 P﹣ABCD 的底面 ABCD 是边长为 1 的菱形，∠BCD＝60°，E 是 CD 的中点，PA⊥底面 ABCD，PA＝2．（1）证明：平面 PBE⊥平面 PAB；（2）求平面 PAD 和平面 PBE 所成二面角（锐角）的正弦值．
【解答】（1）证明：如图所示，连接 BD，由 ABCD 是菱形且∠BCD＝60°，知△ABC 是等边三角形． ∵E 是 CD 的中点， ∴BE⊥CD，又 AB∥CD， ∴AB⊥BE，∴BE⊥平面 PAB，又 BE⊂平面 PBE， ∴平面 PBE⊥平面 PAB．（2）解：在平面 ABCD 内，过点 A 作 AB 的垂线，如图所示，以 A 为原点建立空间直角
【解答】（1）证明：连接 DG、FG，由直三棱柱的性质知，BB1∥CC1，且 BB1＝CC1， ∵B1E＝2EB，C1F＝2FC， ∴EB∥FC，且 EB＝FC， ∴四边形 BCFE 为平行四边形， ∴EF∥BC，EF＝BC， ∵BD＝2DA，CG＝2GA， ∴GD∥BC，且 GD BC， ∴EF∥GD，且 GD EF， ∴四边形 DEFG 为梯形，即 D、E、F、G 四点共面， ∴点 G 在平面 EFD 内．（2）解：由直三棱柱的性质知，CC1⊥平面 ABC， ∵F 为 CC1 上一点， ∴点 F 在平面 ABC 上的投影为点 C，连接 CD，则∠FDC 即为直线 DF 与平面 ABC 所成角． ∵点 D 在棱 AB 上，且 BD＝2DA， ∴AD AB ， ∵C1F＝2FC，

高考数学压轴专题2020-2021备战高考《空间向量与立体几何》单元汇编含答案解析

【最新】高中数学《空间向量与立体几何》专题解析一、选择题1．如图，在正三棱柱111ABC A B C -中，2AB =,123AA =，D ，F 分别是棱AB ，1AA 的中点，E 为棱AC 上的动点，则DEF ∆的周长的最小值为()A ．222+B ．232+C ．62+D ．72+【答案】D 【解析】【分析】根据正三棱柱的特征可知ABC ∆为等边三角形且1AA ⊥平面ABC ，根据1AA AD ⊥可利用勾股定理求得2DF =；把底面ABC 与侧面11ACC A 在同一平面展开，可知当,,D E F 三点共线时，DE EF +取得最小值；在ADF ∆中利用余弦定理可求得最小值，加和得到结果. 【详解】Q 三棱柱111ABC A B C -为正三棱柱 ABC ∆∴为等边三角形且1AA ⊥平面ABCAD ⊂Q 平面ABC 1AA AD ∴⊥ 132DF ∴=+=把底面ABC 与侧面11ACC A 在同一平面展开，如下图所示：当,,D E F 三点共线时，DE EF +取得最小值又150FAD ∠=o ，3AF =1AD =()22min32cos 42372DE EF AF AD AF AD FAD ⎛⎫∴+=+-⋅∠=-⨯-= ⎪ ⎪⎝⎭DEF ∴∆周长的最小值为：72+本题正确选项：D 【点睛】本题考查立体几何中三角形周长最值的求解问题，关键是能够将问题转化为侧面上两点间最短距离的求解问题，利用侧面展开图可知三点共线时距离最短.2．一个几何体的三视图如图所示，其中正视图和俯视图中的四边形是边长为2的正方形，则该几何体的表面积为( )A ．132πB ．7πC ．152πD ．8π【答案】B 【解析】【分析】画出几何体的直观图，利用三视图的数据求解表面积即可．【详解】由题意可知：几何体是一个圆柱与一个14的球的组合体，球的半径为：1，圆柱的高为2，可得：该几何体的表面积为：22141212274ππππ⨯⨯+⨯⨯+⨯=．故选：B ．【点睛】思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽.由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整.3．已知四棱锥S ABCD -的底面是正方形，侧棱长均相等，E 是线段AB 上的点（不含端点）．设SE 与BC 所成的角为α，SE 与平面ABC D 所成的角为β，二面角S-AB-C 的平面角为γ，则（）A ．αβγ≤≤B ．βαγ≤≤C ．a βγ≤≤D ．γβα≤≤【答案】C 【解析】【分析】根据题意，分别求出SE 与BC 所成的角α、SE 与平面ABC D 所成的角β、二面角S-AB-C 的平面角γ的正切值，由正四棱锥的线段大小关系即可比较大小. 【详解】四棱锥S ABCD -的底面是正方形，侧棱长均相等，所以四棱锥为正四棱锥，（1）过E 作//EF BC ，交CD 于F ，过底面中心O 作ON EF ⊥交EF 于N ，连接SN ，取AB 中点M ，连接OM ，如下图（1）所示：则tan SN SN NE OMα==；（2）连接,OE 如下图（2）所示，则tan SO OEβ=;（3）连接OM ，则tan SOOMγ=，如下图（3）所示：因为,,SN SO OE OM ≥≥ 所以tan tan tan αγβ≥≥，而,,αβγ均为锐角，所以,αγβ≥≥ 故选：C. 【点睛】本题考查了异面直线夹角、直线与平面夹角、平面与平面夹角的求法，属于中档题.4．如图，正三棱柱（底面是正三角形的直棱柱）111ABC A B C -的底面边长为a ，侧棱长2a ，则1AC 与侧面11ABB A 所成的角是( )A ．30°B ．45︒C ．60︒D ．90︒【答案】A 【解析】【分析】以C 为原点，在平面ABC 中，过点C 作BC 的垂线为x 轴，CB 为y 轴，1CC 为z 轴，建立空间直角坐标系，利用向量法能求出1AC 与侧面11ABB A 所成的角．【详解】解：以C 为原点，在平面ABC 中，过点C 作BC 的垂线为x 轴，CB 为y 轴，1CC 为z 轴，建立空间直角坐标系，则3(a A ，2a ，0)，1(0C ，02)a ，13(a A 2a 2)a ，(0B ，a ，0)， 13(a AC =u u u u r ，2a -2)a ，3(a AB =u u u r ，2a ，0)，1(0AA =u u u r ，02)a ，设平面11ABB A 的法向量(n x =r，y ，)z ，则13·022·20a an AB x y n AA az ⎧=-+=⎪⎨⎪==⎩u u u v v u u u v v ，取1x =，得(1n =r 3，0)，设1AC 与侧面11ABB A 所成的角为θ，则111||31sin |cos ,|2||||23n AC a n AC n AC a θ=<>===r u u u u rr u u u u r g r u u u ur g ， 30θ∴=︒，1AC ∴与侧面11ABB A 所成的角为30°．故选：A ．【点睛】本题考查线面角的求法，考查空间中线线、线面、面面间的位置关系等基础知识，考查运算求解能力，属于中档题．5．若底面是菱形的棱柱其侧棱垂直于底面，且侧棱长为5，它的对角线的长分别是9和15，则这个棱柱的侧面积是( )． A ．130 B ．140C ．150D ．160【答案】D 【解析】设直四棱柱1111ABCD A B C D -中，对角线119,15AC BD ==，因为1A A ⊥平面,ABCD AC Ì,平面ABCD ，所以1A A AC ⊥，在1Rt A AC ∆中，15A A =，可得221156AC AC A A =-= 同理可得2211200102BD D B D D =-==，因为四边形ABCD 为菱形，可得,AC BD 互相垂直平分，所以2211()()1450822AB AC BD =+=+=，即菱形ABCD 的边长为8，因此，这个棱柱的侧面积为1()485160S AB BC CD DA AA =+++⨯=⨯⨯=，故选D.点睛：本题考查了四棱锥的侧面积的计算问题，解答中通过给出的直四棱柱满足的条件，求得底面菱形的边长，进而得出底面菱形的底面周长，即可代入侧面积公式求得侧面积，着重考查了学生分析问题和解答问题的能力，以及空间想象能力，其中正确认识空间几何体的结构特征和线面位置关系是解答的关键.6．以下说法正确的有几个（）①四边形确定一个平面；②如果一条直线在平面外，那么这条直线与该平面没有公共点；③过直线外一点有且只有一条直线与已知直线平行；④如果两条直线垂直于同一条直线，那么这两条直线平行； A ．0个 B ．1个C ．2个D ．3个【答案】B 【解析】【分析】对四个说法逐一分析，由此得出正确的个数. 【详解】①错误，如空间四边形确定一个三棱锥. ②错误，直线可能和平面相交. ③正确，根据公理二可判断③正确. ④错误，在空间中，垂直于同一条直线的两条直线可能相交，也可能异面，也可能平行.综上所述，正确的说法有1个，故选B. 【点睛】本小题主要考查空间有关命题真假性的判断，属于基础题.7．如图，直三棱柱ABC A B C '''-的侧棱长为3，AB BC ⊥，3AB BC ==，点E ，F 分别是棱AB ，BC 上的动点，且AE BF =，当三棱锥B EBF '-的体积取得最大值时，则异面直线A F '与AC 所成的角为（）A ．2π B ．3π C ．4π D ．6π 【答案】C 【解析】【分析】设AE BF a ==，13B EBF EBF V S B B '-'=⨯⨯V ，利用基本不等式，确定点 E ，F 的位置，然后根据//EF AC ，得到A FE '∠即为异面直线A F '与AC 所成的角，再利用余弦定理求解. 【详解】设AE BF a ==，则()()23119333288B EBFa a V a a '-+-⎡⎤=⨯⨯⨯-⨯≤=⎢⎥⎣⎦，当且仅当3a a =-，即32a =时等号成立，即当三棱锥B EBF '-的体积取得最大值时，点E ，F 分别是棱AB ，BC 的中点，方法一：连接A E '，AF ，则352A E '=，352AF =，2292A F AA AF ''=+=，13222EF AC ==，因为//EF AC ，所以A FE '∠即为异面直线A F '与AC 所成的角，由余弦定理得222819452424cos 93222222A F EF A E A FE A F EF +-''+-'∠==='⋅⋅⨯⨯， ∴4A FE π'∠=．方法二：以B 为坐标原点，以BC 、BA 、BB '分别为x 轴、y 轴、z 轴建立空间直角坐标系，则()0,3,0A ，()3,0,0C ，()0,3,3A '，3,0,02F ⎛⎫⎪⎝⎭， ∴3,3,32A F ⎛⎫'=-- ⎪⎝⎭u u u u r ，()3,3,0AC =-u u u r ，所以9922cos ,92322A F AC A F AC A F AC +'⋅'==='⋅⨯u u u u r u u u r u u u u r u u u r u u u u r u u u r ，所以异面直线A F '与AC 所成的角为4π．故选：C【点睛】本题主要考查异面直线所成的角，余弦定理，基本不等式以及向量法求角，还考查了推理论证运算求解的能力，属于中档题.8．如图，在正方体1111ABCD A B C D -，点P 在线段1BC 上运动，则下列判断正确的是（）①平面1PB D ⊥平面1ACD ②1//A P 平面1ACD③异面直线1A P 与1AD 所成角的取值范围是0,3π⎛⎤⎥⎝⎦④三棱锥1D APC -的体积不变 A ．①② B ．①②④C ．③④D ．①④【答案】B 【解析】【分析】由面面垂直的判定定理判断①，由面面平行的性质定理判断②，求出P 在特殊位置处时异面直线所成的角，判断③，由换底求体积法判断④．【详解】正方体中易证直线AC ⊥平面11BDD B ，从而有1AC B D ⊥，同理有11B D AD ^，证得1B D ⊥平面1ACD ，由面面垂直判定定理得平面1PB D ⊥平面1ACD ，①正确；正方体中11//A B CD ，11//BC AD ，从而可得线面平行，然后可得面面平行，即平面11A BC //平面1ACD ，而1A P ⊂平面11A BC ，从而得1//A P 平面1ACD ，②正确；当P 是1BC 中点时，1A P 在平面11A B CD 内，正方体中仿照上面可证1AD ⊥平面11A B CD ，从而11AD A P ⊥，1A P 与1AD 所成角为90︒．③错；∵11D APC P AD C V V --=，由1//BC 平面1ACD ，知P 在线段1BC 上移动时，P 到平面1ACD 距离相等，因此1P AD C V -不变，④正确．故选：B ．【点睛】本题考查面面垂直的判定定理、面面平行的性质定理、异面直线所成的角、棱锥的体积等知识，考查学生的空间想象能力，属于中档题．9．在四面体ABCD 中，AB ，BC ，BD 两两垂直，4AB BC BD ===，E 、F 分别为棱BC 、AD 的中点，则直线EF 与平面ACD 所成角的余弦值（） A ．13B．3 C ．223D ．6 【答案】C 【解析】【分析】因为AB ，BC ，BD 两两垂直，以BA 为X 轴，以BD 为Y 轴，以BC 为Z 轴建立空间直角坐标系，求出向量EF u u u r 与平面ACD 的法向量n r ，再根据cos ,||||EF nEF n EF n ⋅〈〉=u u u r ru u u r r u u ur r ，即可得出答案. 【详解】因为在四面体ABCD 中，AB ，BC ，BD 两两垂直，以BA 为X 轴，以BD 为Y 轴，以BC 为Z 轴建立空间直角坐标系，又因为4AB BC BD ===；()4,0,0,(0,0,0),(0,4,0),(0,0,4)A B D C ，又因为E 、F 分别为棱BC 、AD 的中点所以(0,0,2),(2,2,0)E F故()2,2,2EF =-u u u r ，(4,4,0)AD =-u u u r ，(4,0,4)AC =-u u u r.设平面ACD 的法向量为(,,)n x y z =r，则00n AD n AC ⎧⋅=⎨⋅=⎩u u u v v u u u v v 令1,x = 则1y z ==；所以(1,1,1)n =r 1cos ,3||||332EF n EF n EF n ⋅〈〉===⨯u u u r r u u u r r u u u r r 设直线EF 与平面ACD 所成角为θ ，则sin θ= cos ,EF n 〈〉u u u r r所以222cos 1sin 3θθ=-=故选：C【点睛】本题主要考查线面角，通过向量法即可求出，属于中档题目.10．已知平面α⊥平面β，l αβ=I ，a α⊂，b β⊂，则“a l ⊥”是“a b ⊥r r ”的（）A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件【答案】A【解析】【分析】根据面面垂直的性质定理，以及充要条件的判定方法，即可作出判定，得到答案.【详解】由题意知，平面α⊥平面β，,,l a b αβαβ⋂=⊂⊂，当a l ⊥时，利用面面垂直的性质定理，可得a b ⊥r r 成立，反之当a b ⊥r r时，此时a 与l 不一定是垂直的，所以a l ⊥是a b ⊥r r 的充分不必要条件，故选A.【点睛】本题主要考查了充要条件的判定，其中解答中熟记线面位置关系的判定定理与性质定理，以及充要条件的判定方法是解答的关键，着重考查了推理与论证能力，属于基础题.11．已知某几何体的三视图如图所示，则该几何体的体积为A．273B．276C．274D．272【答案】D【解析】【分析】先还原几何体，再根据锥体体积公式求结果.【详解】几何体为一个三棱锥，高为33，底为一个直角三角形，直角边分别为333，，所以体积为1127=33333=322V⨯⨯⨯⨯，选D.【点睛】(1)解决本类题目的关键是准确理解几何体的定义，真正把握几何体的结构特征，可以根据条件构建几何模型，在几何模型中进行判断；(2)解决本类题目的技巧：三棱柱、四棱柱、三棱锥、四棱锥是常用的几何模型，有些问题可以利用它们举特例解决或者学会利用反例对概念类的命题进行辨析．12．一个几何体的三视图如图所示，则该几何体的体积为A．238B．823+C．283D．10【答案】A【解析】【分析】根据三视图可知该几何体为一组合体，是一个棱长为2的正方体与三棱锥的组合体，根据体积公式分别计算即可.【详解】几何体为正方体与三棱锥的组合体，由正视图、俯视图可得该几何体的体积为311232+232832V=⨯⨯=,故选A.【点睛】本题主要考查了三视图，正方体与三棱锥的体积公式，属于中档题.13．设α为平面，a ，b 为两条不同的直线，则下列叙述正确的是( )A ．若//a α，//b α，则//a bB ．若a α⊥，//a b ，则b α⊥C ．若a α⊥，a b ⊥r r ，则//b αD ．若//a α，a b ⊥r r ，则b α⊥【答案】B【解析】【分析】利用空间线线、线面、面面间的关系对每一个选项逐一分析判断得解．【详解】若//a α，//b α，则a 与b 相交、平行或异面，故A 错误；若a α⊥，//a b ，则由直线与平面垂直的判定定理知b α⊥，故B 正确；若a α⊥，a b ⊥r r ，则//b α或b α⊂，故C 错误；若//a α，a b ⊥r r ，则//b α，或b α⊂，或b 与α相交，故D 错误．故选：B ．【点睛】本题考查命题的真假的判断，是基础题，解题时要认真审题，注意空间思维能力的培养．14．等腰三角形ABC 的腰5AB AC ==，6BC =，将它沿高AD 翻折，使二面角B AD C --成60︒，此时四面体ABCD 外接球的体积为（）A ．7πB ．28πCD 【答案】D【解析】分析：详解：由题意，设BCD ∆所在的小圆为1O ，半径为r ，又因为二面角B AD C --为060，即060BDC ∠=，所以BCD ∆为边长为3的等边三角形，又正弦定理可得，032sin 60r ==BE = 设球的半径为R ，且4=AD ，在直角ADE ∆中，()2222224428R AD DE R =+⇒=+=，所以R =，所以球的体积为3344333V R ππ==⨯=，故选D ．点睛：本题考查了有关球的组合体问题，以及三棱锥的体积的求法，解答时要认真审题，注意球的性质的合理运用，求解球的组合体问题常用方法有（1）三条棱两两互相垂直时，可恢复为长方体，利用长方体的体对角线为外接球的直径，求出球的半径；（2）直棱柱的外接球可利用棱柱的上下底面平行，借助球的对称性，球心为上下底面外接圆的圆心连线的中点，再根据勾股定理求球的半径.15．在空间中，下列命题正确的是A ．如果一个角的两边和另一角的两边分别平行,那么这两个角相等B ．两条异面直线所成的有的范围是0,2π⎡⎤⎢⎥⎣⎦C ．如果两个平行平面同时与第三个平面相交，那么它们的交线平行D ．如果一条直线和平面内的一条直线平行,那么这条直线和这个平面平行【答案】C【解析】【分析】根据两个角可能互补判断A ；根据两条异面直线所成的角不能是零度,判断B ；根据根据两个平面平行的性质定理知判断C ；利用直线与这个平面平行或在这个平面内判断D.【详解】如果一个角的两边和另一个角的两边分别平行,这两个角相等或互补,故A 不正确；两条异面直线所成的角不能是零度,故B 不正确；根据两个平面平行的性质定理知C 正确；如果一条直线和一个平面内的一条直线平行,那么这条直线与这个平面平行或在这个平面内,故D 不正确,综上可知只有C 的说法是正确的,故选C.【点睛】本题考查平面的基本性质及推论,考查等角定理,考查两个平面平行的性质定理,考查异面直线所成的角的取值范围,考查直线与平面平行的判断定理,意在考查对基础知识的掌握情况，本题是一个概念辨析问题.16．已知直线和不同的平面，下列命题中正确的是A ．//m m αβαβ⊥⎫⇒⎬⊥⎭B ．m m αββα⊥⎫⇒⊥⎬⊂⎭C ．//////m m ααββ⎫⇒⎬⎭D ．////m m αββα⎫⇒⎬⊂⎭【答案】D【解析】【分析】对各个选项逐一进行分析即可【详解】 A ，若αβ⊥，m β⊥，则有可能m α⊂，故A 错误B ，若αβ⊥，m α⊂，则m 与β不一定垂直，可能相交或平行，故B 错误C ，若//m α，//m β则推不出//αβ，面面平行需要在一个面内找出两条相交线与另一个平面平行，故C 错误D ，若//αβ，m α⊂，则有//m β，故D 正确故选D【点睛】本题考查了线面平行与面面平行的判断和性质，在对其判定时需要运用其平行的判定定理或者性质定理，所以要对课本知识掌握牢固，从而判断结果17．已知某几何体的三视图如图所示，其中正视图与侧视图是全等的直角三角形，则该几何体的各个面中，最大面的面积为（）A ．2B ．5C 13D 22【答案】D【解析】【分析】根据三视图还原出几何体，找到最大面，再求面积.【详解】由三视图可知，该几何体是一个三棱锥，如图所示，将其放在一个长方体中，并记为三棱锥P ABC -.13PAC PAB S S ∆∆=22PAC S ∆=，2ABC S ∆=22.选D.【点睛】本题主要考查三视图的识别，复杂的三视图还原为几何体时，一般借助长方体来实现.18．如图1，已知正方体ABCD-A 1B 1C 1D 1的棱长为2，M ，N ，Q 分别是线段AD 1，B 1C ，C 1D 1上的动点，当三棱锥Q-BMN 的正视图如图2所示时，三棱锥俯视图的面积为A ．2B ．1C ．32D ．52【答案】C【解析】【分析】判断俯视图的形状，利用三视图数据求解俯视图的面积即可．【详解】由正视图可知：M 是1AD 的中点，N 在1B 处，Q 在11C D 的中点，俯视图如图所示：可得其面积为：1113222111122222⨯-⨯⨯-⨯⨯-⨯⨯=，故选C ．【点睛】本题主要考查三视图求解几何体的面积与体积，判断它的形状是解题的关键，属于中档题.19．设,αβ是两个不同的平面，,l m 是两条不同的直线，且l α⊂，m β⊂，则（）A ．若//αβ，则//l mB ．若//m a ，则//αβC ．若m α⊥，则αβ⊥D ．若αβ⊥，则//l m【答案】C【解析】【分析】根据空间线线、线面、面面的位置关系，对选项进行逐一判断可得答案.【详解】A. 若//αβ，则l 与m 可能平行，可能异面，所以A 不正确.B. 若//m a ，则α与β可能平行，可能相交，所以B 不正确.C. 若m α⊥，由m β⊂，根据面面垂直的判定定理可得αβ⊥，所以C 正确. D 若αβ⊥，且l α⊂，m β⊂，则l 与m 可能平行，可能异面，可能相交, 所以D 不正确.【点睛】本题考查空间线线、线面、面面的位置判断定理和性质定理，考查空间想象能力，属于基础题.20．一个各面均为直角三角形的四面体有三条棱长为2，则该四面体外接球的表面积为（）A ．6πB ．12πC ．32πD ．48π【答案】B【解析】【分析】先作出几何图形，确定四个直角和边长，再找到外接球的球心和半径，再计算外接球的表面积.【详解】由题得几何体原图如图所示，其中SA⊥平面ABC,BC⊥平面SAB,SA=AB=BC=2,所以2,3SC=设SC中点为O,则在直角三角形SAC中，3,在直角三角形SBC中，OB=13 2SC=所以3所以点O3所以四面体外接球的表面积为43=12ππ.故选：B【点睛】本题主要考查四面体的外接球的表面积的计算，意在考查学生对这些知识的理解掌握水平和分析推理的能力.。

高考数学压轴专题2020-2021备战高考《空间向量与立体几何》分类汇编附答案解析

新数学《空间向量与立体几何》试卷含答案一、选择题1．如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的体积为（）6483C．2882A．B．163D．1633【答案】 B【分析】【剖析】联合三视图，复原直观图，获得一个圆锥和一个圆柱，计算体积，即可．【详解】联合三视图，复原直观图，获得故体积V r 2h1r 2 l22 412223 168 3，应选 B．333【点睛】本道题考察了三视图复原直观图，考察了组合体体积计算方法，难度中等．2．如图，在长方体ABCD A1B1C1D1中，AB AD3, AA 1 ,而对角线A1B上存1在一点 P ，使得AP D1P 获得最小值，则此最小值为（）A．7B．3C．1+ 3D．2【答案】 A【分析】【剖析】把面 AA1 B 绕 A1B 旋转至面BA1M使其与对角面A1BCD1在同一平面上，连结MD 1并求出，就是最小值．【详解】把面 AA1 B 绕 A1B 旋转至面BA1M使其与对角面A1BCD1在同一平面上，连结MD1． MD1就是|AP|| D1 P | 的最小值，Q |AB| |AD|3，|AA1| 1 ， tan AA1 B33,AA1B600 ．1因此 MA1D1=90 o +60o =150oMD1A D2 A M 22A D1A M cos MA D1 3 22 3 ( 3 )711111112应选 A．【点睛】此题考察棱柱的构造特点，考察计算能力，空间想象能力，解决此类问题常经过转变，转变为在同一平面内两点之间的距离问题，是中档题．3．在以下命题中：r r r r rr①三个非零向量 a ， b ，c不可以组成空间的一个基底，则 a ，b，c共面；r r r r② 若两个非零向量 a ，b与任何一个向量都不可以组成空间的一个基底，则 a ，b共线；uuur uuur uuuur uuuur③ 对空间随意一点O和不共线的三点 A，B，C，若OP2OA2OB2OC，则P，A，B，C四点共面r r r r r r r r,④ 若a，b是两个不共线的向量，且c a b(R, ,0) ，则 { a,b, c} 组成空间的一个基底r r r r r r r r r⑤若 a, b, c 为空间的一个基底，则a b,b c,c a组成空间的另一个基底；此中真命题的个数是（）A．0B． 1C． 2D． 3【答案】 D【分析】【剖析】依据空间向量的运算法例，逐个判断即可获得结论.【详解】r r r r r①由空间基底的定义知，三个非零向量 a ，b，c不可以组成空间的一个基底，则 a ， b ，rc 共面，故①正确；r r②由空间基底的定义知，若两个非零向量 a ，b与任何一个向量都不可以组成空间的一个基r r底，则a，b共线，故② 正确；③由 2 2 221，依据共面向量定理知P, A, B, C 四点不共面，故③错误；r r r r r r r r r④由c a b ，当 1 时，向量c与向量a，b组成的平面共面，则a,b,c不能组成空间的一个基底，故④ 错误；r r r r r r⑤利用反证法：若a b,b c, c a不组成空间的一个基底，r r r r1x r r r r r r r r设 a b x b c c a，整理得c xa 1 x b ，即a,b,c共面，又因r r r r r r r r ra,b,c为空间的一个基底，因此a b, b c, c a能组成空间的一个基底，故⑤正确.综上：①②⑤正确.应选： D.【点睛】此题考察空间向量基本运算，向量共面，向量共线等基础知识，以及空间基底的定义，共面向量的定义，属于基础题．4．已知平面α∩β=l， m 是α内不一样于A．若 m∥ β，则 m∥l l 的直线，那么以下命题中错误的选项是（B．若 m∥l ，则 m∥ β）C．若 m⊥ β，则Dm⊥ l D．若m⊥l ，则m⊥ β【分析】【剖析】A由线面平行的性质定理判断 .B 依据两个平面订交，一个面中平行于它们交线的直线必平行于另一个平面判断 .C 依据线面垂直的定义判断 .D 依据线面垂直的判判定理判断 .【详解】A选项是正确命题，由线面平行的性质定理知，能够证出线线平行；B选项是正确命题，因为两个平面订交，一个面中平行于它们交线的直线必平行于另一个平面；C选项是正确命题，因为一个线垂直于一个面，则必垂直于这个面中的直线；D选项是错误命题，因为一条直线垂直于一个平面中的一条直线，不可以推出它垂直于这个平面；应选： D.【点睛】此题主要考察线线关系和面面关系，还考察了推理论证的能力，属于中档题.5．《九章算术》卷五商功中有以下问题：今有刍甍（音meng，底面为矩形的屋脊状的几何体），下广三丈，袤四丈，上袤二丈，无广，高一丈，问积几何.已知该刍甍的三视图如图所示，则此刍甍的体积等于( )A．3B．5C．6D．12【答案】 B【分析】【剖析】第一由三视图复原几何体，再将刍甍分为三部分求解体积，最后计算求得刍甍的体积.【详解】由三视图换元为以下图的几何体，该几何体分为三部分，中间一部分是直棱柱，双侧是同样的三棱锥，而且三棱锥的体积11 31 1，3中间棱柱的体积 V 112 3 ,32因此该刍甍的体积是 1 23 5 .应选： B【点睛】此题考察组合体的体积，要点考察空间想象能力和计算能力，属于中档题型.6．如图，棱长为 1 的正方体ABCD A1 B1C1D1，O 是底面 A B C D 的中心，则O到平1111面 ABC1 D1的距离是（）A．1223B．4C．D．222【答案】 B【分析】【剖析】如图成立空间直角坐标系，可证明A1 D平面ABC1D1，故平面ABC1 D1的一个法向量uuuur为：DA1，利用点到平面距离的向量公式即得解.【详解】如图成立空间直角坐标系，则：11O( ,,1), D1 (0,0,1), A(1,0,0), B(1,1,0),C1 (0,1,1)22 uuuur( 1,1,0)OD122因为 AB平面 ADD1 A1 , AD1平面 ADD 1A1 AB A1 D ，又 AD1A1D ， AB I AD1A1D平面ABC1D1uuuur故平面 ABC1 D1的一个法向量为：DA1(1,0,1) O到平面 ABC1D1的距离为：uuuur uuuur1d | OD1DA1 |22 uuuur4 |DA1|2应选： B【点睛】此题考察了点到平面距离的向量表示，考察了学生空间想象，观点理解，数学运算的能力，属于中档题 .7．三棱柱ABC A1B1C1中，底面边长和侧棱长都相等，BAA1CAA1 60 ，则异面直线 AB1与 BC1所成角的余弦值为（）A．3B．63D．3 3C．664【答案】 B【分析】【剖析】uuuv v uuuv v uuuv v uuuv uuuuv设 AA1 c ， AB a， AC b ，依据向量线性运算法例可表示出AB1和 BC1；分别求解uuuv uuuuv uuuv uuuuv uuuv uuuuv出 AB1BC1和 AB1， BC1，依据向量夹角的求解方法求得 cos AB1, BC1，即可得所求角的余弦值 .【详解】uuuv uuuv uuuvv v v设棱长为 1 ，AA1c ，AB a，AC b由题意得： v v 1 v v 1 v v1a b ， b c ， a c 22 2 uuuv v v uuuuv uuuv uuuv v v vQ AB 1 a c ， BC 1 BC BB 1 b a cuuuv uuuuv v v v v v v v v 2 v vvv v v v 21 1 AB 1 BC 1a cb ac a b aa cbc a c c11 1uuuv22v v 2 v 2v vv23又AB 1a ca 2a c cuuuuv v v v 2 v 2 v 2 BC 1b a cb auuuv uuuuvuuuv uuuuvcosAB 1 BC 1AB 1 , BC 1uuuv uuuuvAB 1 BC 1v 2 v vv v v v 2c 2a b2b c 2a c1 6666 即异面直线 AB 1 与 BC 1 所成角的余弦值为：6此题正确选项： B【点睛】此题考察异面直线所成角的求解，要点是能够经过向量的线性运算、数目积运算将问题转变为向量夹角的求解问题 .8．如图，在正方体ABCD A 1B 1C 1D 1 中， M ， N 分别为棱 C 1D 1 ,CC 1 的中点，以下四个结论： ① 直线 DM 与 CC 1 是订交直线； ② 直线 AM 与 NB 是平行直线；③ 直线 BN 与MB 1 是异面直线； ④ 直线 AM 与 DD 1 是异面直线．此中正确的个数为（）A ．1B ．2C ．3D ．4【答案】 C【分析】【剖析】依据正方体的几何特点，可经过判断每个选项中的两条直线字母表示的点能否共面；假如共面，则可能是订交或许平行；若不共面，则是异面.【详解】① ： CC 1 与DM 是共面的，且不平行，因此必然订交，故正确；② ：若 AM 、 BN 平行，又 AD 、BC 平行且AMADA, BNBCB，因此平面BNC P 平面 ADM ，显然不正确，故错误；③ ： BN 、MB 不共面，因此是异面直线，故正确；1④ ： AM 、DD 1 不共面，因此是异面直线，故正确；应选 C.【点睛】异面直线的判断方法：一条直线上两点与此外一条直线上两点不共面，那么两条直线异面；反之则为共面直线，可能是平行也可能是订交.9．在四周体 ABCD 中， AB ， BC ， BD 两两垂直， AB BC BD 4，E 、F 分别为棱 BC 、 AD 的中点，则直线 EF 与平面 ACD 所成角的余弦值（）A ．1B ．3 C ．2 2D ．6 3333【答案】 C【分析】【剖析】因为 AB ， BC ， BD 两两垂直，以 BA 为 X 轴，以 BD 为 Y 轴，以 BC 为 Z 轴成立空间直 uuurr uuur ruuur rEF n角坐标系，求出向量EF 与平面 ACD 的法向量 n ，再依据 cos EF , nuuur r ，即可 | EF || n |得出答案 .【详解】因为在四周体ABCD 中， AB ， BC ， BD 两两垂直，以 BA 为 X 轴，以 BD 为 Y 轴，以 BC 为 Z 轴成立空间直角坐标系，又因为 AB BC BD 4；A 4,0,0 , B(0,0,0), D(0,4,0), C(0,0,4) ，又因为 E 、 F 分别为棱 BC 、 AD 的中点因此 E(0,0,2),F (2,2,0)uuur 2,2,uuur uuur故 EF2 ，AD ( 4,4,0) ， AC ( 4,0, 4) .rv uuuvn AD设平面 ACD 的法向量为 n( x, y, z) ，则 v uuuvn AC令 x 1, 则 yz 1；r(1,1,1) 因此 nuuur r uuur r2 1 EF ncos EF , nuuur r323 3| EF || n |设直线 EF 与平面 ACD 所成角为 uuur r，则 sin cos EF , n因此cos1 sin 22 23应选： C【点睛】此题主要考察线面角，经过向量法即可求出，属于中档题目.10．三棱锥 D ABC 中， CD 底面 ABC,ABC 为正三角形，若AE / /CD, ABCDAE2，则三棱锥 DABC 与三棱锥 E ABC 的公共部分组成的几何体的体积为（）A ．3 B ．31 D ． 393C ．3【答案】 B【分析】依据题意画出以下图的几何体：∴三棱锥 D ABC 与三棱锥 E ABC 的公共部分组成的几何体为三棱锥 F ABC∵ ABC 为正三角形， AB 21 2 23 ∴S ABC322∵ CD 底面 ABC ， AE/ /CD ，CD AE 2∴四边形 AEDC 为矩形，则 F 为 EC 与 AD 的中点 ∴三棱锥 FABC 的高为 1CD12∴三棱锥 FABC 的体积为 V1 3 3 133应选 B.11．已知平面，和直线 l 1 ， l 2 ，且 αI “P l 2 ”是 “l 1∥ 且 l 1 ∥ β”的β l 2 ，则 l 1 （）A ．充足不用要条件B ．必需不充足条件C．充要条件D．既不充足也不用要条件【答案】 B【分析】【剖析】将“P l 2”与“l1∥且 l1∥ β”相互推导，依据可否推导的状况判断充足、必需条件.l1【详解】当“P l 2”时， l1可能在或内，不可以推出“且 l1∥ β”当.“l1∥且 l1∥ β”时，l1l1∥因为αI β l2，故“l1 P l2”所.以“l1 P l2”是“l1∥且 l1∥ β”的必需不充足条件.应选： B.【点睛】本小题主要考察充足、必需条件的判断，考察空间直线、平面的地点关系，属于基础题.12．设，为两条不一样的直线，，为两个不一样的平面，以下命题中，正确的选项是（）A．若，与所成的角相等，则B．若，，则C．若，，则D．若，，则【答案】 C【分析】试题剖析：若，与所成的角相等，则或，订交或，异面； A错.若，，则或，B错.若，，则正确 . D．若，，则，订交或，异面， D错考点：直线与平面，平面与平面的地点关系13．在正四周体A BCD 中，P是 AB 的中点，Q是直线 BD 上的动点，则直线PQ与AC 所成角可能为（）A．B．C．5D．121242【答案】 C【分析】【剖析】依据题意，取 BC 的中点 M ，连结 MQ ，则AC / / MQ，因此QPM 为异面直线 PQ 与AC 所成角，在利用余弦定理可得MQ4x2 2 x，易知 PQ MQ ，因此在等腰三角形 PMQ 中 cos QPM1，0x 4，即可求出x242xcos QPM 3 ， 3，从而求出结果 .123【详解】取 BC的中点M，连结 MQ，则AC / /MQ，因此QPM 为异面直线 PQ 与AC所成角，以以下图所示：设正四周体 A BCD 的棱长为 4 ，BQ x，0x4，在 BMQ 中，MQ2BM 2BQ 22BM BQ cos604x22x，在正四周体 A BCD 中，易知PQ MQ ，因此在等腰三角形 PMQ 中， cos QPM1，0x44x22x因此 cos QPM3，3，PQ 与AC所成角可能为5123因此异面直线.12应选： C.【点睛】此题主要考察了异面直线成角，余弦定理的应用，考察了空间几何中的动向问题，考察学生的应用能力和空间想象能力，属于中档题.14．以下说法正确的有几个（）① 四边形确立一个平面；② 假如一条直线在平面外，那么这条直线与该平面没有公共点；③ 过直线外一点有且只有一条直线与已知直线平行；④ 假如两条直线垂直于同一条直线，那么这两条直线平行；A．0个B．1 个C．2 个D．3 个【答案】B【分析】【剖析】对四个说法逐个剖析，由此得出正确的个数.【详解】①错误，如空间四边形确立一个三棱锥.②错误，直线可能和平面订交.③正确，依据公理二可判断 ③ 正确 . ④错误，在空间中，垂直于同一条直线的两条直线可能订交，也可能异面，也可能平行 .综上所述，正确的说法有 1个，应选 B.【点睛】本小题主要考察空间相关命题真假性的判断，属于基础题.15 ．等腰三角形ABC 的腰 AB AC 5， BC 6 ，将它沿高 AD 翻折，使二面角BAD C 成 60 ，此时四周体 ABCD 外接球的体积为（）A ． 7B ． 28C ． 19 19D ．28 763【答案】 D 【分析】剖析：详解：由题意，设 BCD 所在的小圆为 O 1 ，半径为 r ，又因为二面角 B AD C 为 600，即BDC600 ，因此 BCD 为边长为 3 的等边三角形，3又正弦定理可得，2rsin 6002 3，即BE 2 3 ，设球的半径为 R ，且 AD 4 ，22 DE 2 4R 42 (2 3) 2 28在直角 ADE 中， 2RAD ，因此 R7 ，因此球的体积为 V4 R 3 4 ( 7) 328 7 ，应选 D ．333点睛：此题考察了相关球的组合体问题，以及三棱锥的体积的求法，解答时要仔细审题，注意球的性质的合理运用，求解球的组合体问题常用方法有（1）三条棱两两相互垂直时，可恢复为长方体，利用长方体的体对角线为外接球的直径，求出球的半径；（2）直棱柱的外接球可利用棱柱的上下底面平行，借助球的对称性，球心为上下底面外接圆的圆心连线的中点，再依据勾股定理求球的半径.16．已知空间四边形OABC ，其对角线为 OB ， AC ， M ， N 分别是边 OA ， CB 的中点，点 G 在线段 MN 上，且使 MGuuuv uuuv uuuv uuuv2GN ，用向量 OA ， OB ， OC 表示向量 OG 是（）uuuv uuuv 2 uuuv 2 uuuvuuuv1 uuuv2 uuuv 2 uuuvA ． OGOAOBOCB ． OGOAOBOC3 32 3 3uuuv1 uuuv 1 uuuv 1 uuuvuuuv1 uuuv 1 uuuv2 uuuvC ． OGOAOBOCD ． OGOAOBOC633633【答案】 C【分析】【剖析】依据所给的图形和一组基底，从起点 O 出发，把不是基底中的向量，用是基底的向量来表示，就能够获得结论．【详解】uuur uuuur uuuur uuuur 2 uuuur Q OG OM MG OM 3MN ,uuuur 2 uuuur uuur uuur 1 uuuur2 uuuruuur uuur1 uuur 1 uuur 1 uuur1 OMMOOCCNOMOC3OBOCOA OB OC333633uuur 1 uuur 1 uuur1 uuurOGOAOBOC ,63 3应选： C ．【点睛】此题考察向量的基本定理及其意义，解题时注意方法，即从要表示的向量的起点出发，沿着空间图形的棱走到终点，若出现不是基底中的向量的状况，再重复这个过程．17．设 ,是两个不一样的平面， l , m 是两条不一样的直线，且 l， m，则（）A ．若/ / ，则 l // mB ．若 m / /a ，则 / /C ．若 m ，则D ．若，则 l // m【答案】 C【分析】【剖析】依据空间线线、线面、面面的地点关系，对选项进行逐个判断可得答案 .【详解】A.若 //，则 l 与 m 可能平行，可能异面，因此A 不正确. B. 若 m / /a ，则与可能平行，可能订交，因此B 不正确 .C. 若 m ，由 D 若，且确.m ，依据面面垂直的判判定理可得，因此 C 正确 .l ， m，则 l 与 m 可能平行，可能异面，可能订交 , 因此 D 不正【点睛】此题考察空间线线、线面、面面的地点判判定理和性质定理，考察空间想象能力，属于基础题 .18．已知,是不一样的两个平面，直线a，直线 b，条件 p : a 与 b 没有公共点，条件 q :/ /，则p是 q的（）A．充足不用要条件B．必需不充足条件C．充要条件D．既不充足又不用要条件【答案】 B【分析】∵ a 与b没有公共点时， a 与b所在的平面可能平行，也可能订交（交点不在直线b 上）∴命题p： a 与b没有公共点?命题q：∥ ，为假命题又∵ ∥时， a 与b平行或异面，即 a 与b没有公共点∴命题 q：∥? 命题p：a与b没有公共点，为真命题；故 p 是q的必需不充足条件应选 B19．已知直三棱柱ABC A1B1C1的全部棱长都相等，M 为A1C1的中点，则AM与BC1所成角的余弦值为 ( )A．15B．5C．6D．10 3344【答案】 D【分析】【剖析】取 AC 的中点 N ，连结C1N，则AM / /C1N,因此异面直线AM与 BC1所成角就是直线AM与 C1N 所成角，在BNC1中，利用余弦定理，即可求解．【详解】由题意，取 AC 的中点 N ，连结C1N，则AM / /C1N,因此异面直线AM与 BC1所成角就是直线AM与 C1N 所成角，设正三棱柱的各棱长为 2 ,则 C1N5, BC122, BN 3 ，设直线 AM与C1N所成角为，在 BNC1中，由余弦定理可得cos(5) 2(22) 2(3) 210 ，2522410，应选D．即异面直线 AM与BC1所成角的余弦值为4【点睛】此题主要考察了异面直线所成角的求解，此中解答中把异面直线所成的角转变为订交直线所成的角是解答的要点，侧重考察了推理与运算能力，属于基础题．20．一个各面均为直角三角形的四周体有三条棱长为2，则该四周体外接球的表面积为（）A．6πB． 12πC． 32πD． 48π【答案】 B【分析】【剖析】先作出几何图形，确立四个直角和边长，再找到外接球的球心和半径，再计算外接球的表面积 .【详解】由题得几何体原图以下图，此中 SA⊥平面 ABC,BC⊥平面 SAB,SA=AB=BC=2,因此 AC=2 2 ,SC 2 3,设 SC中点为 O,则在直角三角形 SAC中， OA=OC=OS= 3 ,在直角三角形1SBC中， OB= SC3 ,2因此 OA=OC=OS=OB= 3 ,因此点 O 是四周体的外接球球心，且球的半径为 3 .因此四周体外接球的表面积为243=12.应选： B【点睛】此题主要考察四周体的外接球的表面积的计算，意在考察学生对这些知识的理解掌握水平易剖析推理的能力 .。

高考数学压轴专题2020-2021备战高考《空间向量与立体几何》知识点总复习含答案解析

【最新】高考数学《空间向量与立体几何》专题分析一、选择题1．如图，在正方体ABCD A 1B 1C 1D 1 中， M ， N 分别为棱 C 1D 1 ,CC 1 的中点，以下四个结论： ① 直线 DM 与 CC 1 是订交直线； ② 直线 AM 与 NB 是平行直线；③ 直线 BN 与MB 1 是异面直线； ④ 直线 AM 与 DD 1 是异面直线．此中正确的个数为（）A ．1B ．2C ．3D ．4【答案】 C【分析】【剖析】依据正方体的几何特点，可经过判断每个选项中的两条直线字母表示的点能否共面；假如共面，则可能是订交或许平行；若不共面，则是异面 .【详解】① ： CC 1 与DM 是共面的，且不平行，因此必然订交，故正确；② ：若 AM 、 BN 平行，又 AD 、BC 平行且AMAD A, BNBCB，因此平面BNC P 平面 ADM ，明显不正确，故错误；③ ： BN 、MB 不共面，因此是异面直线，故正确；1④ ： AM 、DD 1 不共面，因此是异面直线，故正确；应选 C. 【点睛】异面直线的判断方法：一条直线上两点与此外一条直线上两点不共面，那么两条直线异面；反之则为共面直线，可能是平行也可能是订交.2．设 α、 β是两个不一样的平面， m 、 n 是两条不一样的直线，以下说法正确的选项是（A ．若 α⊥ β， α∩β＝ m ， m ⊥n ，则 n ⊥ βB ．若 α⊥ β，n ∥α，则 n ⊥βC ．若 m ∥ α，m ∥ β，则 α∥ βD ．若 m ⊥ α， m ⊥ β， n ⊥ α，则 n ⊥ β）【答案】 D【分析】【剖析】依据直线、平面平行垂直的关系进行判断．【详解】由α、β是两个不一样的平面，m、n 是两条不一样的直线，知：在A中，若α β α∩β m，m n，则n与βnβA错误；⊥ ，＝⊥订交、平行或?，故在 B中，若α⊥ β， n∥ α，则 n 与β订交、平行或 n? β，故 B 错误；在 C 中，若 m∥ α， m∥ β，则α与β订交或平行，故 C 错误；在 D 中，若 m⊥ α， m⊥ β，则α∥ β，∴若 n⊥ α，则 n⊥ β，故 D 正确 .应选： D.【点睛】此题考察命题真假的判断，考察空间中线线、线面、面面间的益关系等基础知识，考察运算求解能力，是中档题 .3．已知正方体ABCD A1 B1C1D1中，M，N分别为AB， AA1的中点，则异面直线C1M 与BN所成角的大小为（）A． 30°B．45C．60D．90【答案】 D【分析】【剖析】依据题意画出图形，可将异面直线转变共面的订交直线，再进行求解【详解】如图：作 AN 的中点 N '，连结N 'M，C1N '由题设可知N 'M P BN，则异面直线C1M与BN所成角为 N ' MC1或其补角，设正方体的边长为4，由几何关系可得，N 'M 5 ，C1M 6，CN'222N'MC19041，得 CN'N'M C M，即111应选 D【点睛】此题考察异面直线的求法，属于基础题4．四周体ABCD的四个极点都在球O 的表面上，AB平面BCD，VBCD是边长为3的等边三角形，若AB2，则球 O 的表面积为()A．1632C． 12D．32 B．3【答案】 A【分析】【剖析】先求底面外接圆直径,再求球的直径 ,再利用表面积S D2求解即可 .【详解】dCD3 VBCD 外接圆直径sin CBD2 3, 32故球的直径平方D2AB2 d 222(2 3)216 ,故外接球表面积 SD 216应选： A【点睛】此题主要考察侧棱垂直底面的锥体外接球表面积问题,先利用正弦定理求得底面直径 d ,再利用锥体高 h ,依据球直径D d2h2求解即可.属于中等题型.5．一个几何体的三视图如下图，则该几何体的体积为23C．28A．8B．823D． 1033【答案】 A【分析】【剖析】依据三视图可知该几何体为一组合体，是一个棱长为 2 的正方体与三棱锥的组合体，依据体积公式分别计算即可.【详解】几何体为正方体与三棱锥的组合体，由正视图、俯视图可得该几何体的体积为V 23+11 2 328 2 3 , 323应选 A.【点睛】此题主要考察了三视图，正方体与三棱锥的体积公式，属于中档题.6．如下图是一个组合几何体的三视图，则该几何体的体积为（）A ．16B ．64C ．163 64 D ． 16 6433【答案】 C【分析】由三视图可知，该几何体是有一个四棱锥与一个圆锥的四分之一构成，此中四棱锥的底面是边长为 4 的正方形，高为 4 ，圆锥的底面半径为 4 ，高为 4 ，该几何体的体积为， V1 42 4 1424 1664，应选 C.3337．已知某几何体的三视图如下图，则该几何体的外接球的表面积为（）A ．3 C ． 3D ． 12B ．2【答案】 C【分析】【剖析】该几何体是一个三棱锥，且同一个极点处的三条棱两两垂直而且相等，把这个三棱锥放到正方体中，即可求出其外接球的表面积.【详解】由三视图可知，该几何体是一个三棱锥，且同一个极点处的三条棱两两垂直而且相等，如下图该几何体是棱长为 1 的正方体中的三棱锥A BCD ，AB BC BD 1.因此该三棱锥的外接球即为此正方体的外接球，球的直径 2r 为正方体体对角线的长 .即2r1212 123.因此外接球的表面积为 4 r 23 .应选： C .【点睛】此题考察几何体的三视图，考察学生的空间想象能力，属于基础题 .8．如图，在棱长为 2 的正方体 ABCD A 1B 1C 1D 1 中，点 M 是 AD 的中点，动点 P 在底面 ABCD 内（不包含界限），若B 1P P平面A 1BM，则C 1P的最小值是（）A ．30 B ．23055 C ．27 D ．4755【答案】 B【分析】【剖析】在 A 1 D 1 上取中点 Q ，在 BC 上取中点 N ，连结 DN , NB 1 , B 1Q, QD ，依据面面平行的判断定理可知平面 B 1QDN / / 平面 A 1BM ，进而可得 P 的轨迹是 DN （不含 D, N 两点）；由垂直关系可知当CPDN 时， C 1 P 获得最小值；利用面积桥和勾股定理可求得最小值.【详解】如图，在 A 1D 1 上取中点 Q ，在 BC 上取中点 N ，连结 DN , NB 1 , B 1Q,QDQ DN //BM ，DQ//A1M且DN I DQ D，BMI A1M M平面 B1QDN / / 平面 A1BM ，则动点P的轨迹是DN（不含D, N两点）又 CC1平面ABCD，则当CP DN 时，C1P获得最小值212222302此时， CP22C1P212555此题正确选项：B【点睛】此题考察立体几何中动点轨迹及最值的求解问题，重点是能够经过面面平行关系获得动点的轨迹，进而找到最值获得的点 .9．如图是由圆柱与圆锥组合而成的几何体的三视图，则该几何体的体积为（）6483C．2882A．B．163D．1633【答案】 B【分析】【剖析】联合三视图，复原直观图，获得一个圆锥和一个圆柱，计算体积，即可．【详解】联合三视图，复原直观图，获得故体积V r 2h1r 2 l22 412223 168 3，应选 B．333【点睛】本道题考察了三视图复原直观图，考察了组合体体积计算方法，难度中等．10．已知 m, l 是两条不一样的直线，, 是两个不一样的平面，则以下能够推出的是（）． m l , m, l．l ,l , mA B mC．m / /l , m,l D．l, m / /l , m / /【答案】 D【分析】【剖析】A，有可能出现，平行这类状况 .B，会出现平面，订交但不垂直的状况.C，依据面面平行的性质定理判断.D，依据面面垂直的判断定理判断.【详解】关于 A，m l ，m，若 l，则// ，故A错误；关于 B，会出现平面，订交但不垂直的状况，故 B 错误；关于 C，由于m//l，m，则 l，又由于 l∥，故 C错误；关于 D，l， m ∥ l m，又由 m∥，故 D正确.应选： D【点睛】此题考察空间中的平行、垂直关系的判断，还考察学生的空间想象能力和逻辑推理能力，属于中档题 .11．设，是两个不一样的平面，m 是直线且 m．“m P”是“ P”的（）A ．充足而不用要条件B ．必需而不充足条件C ．充足必需条件D ．既不充足也不用要条件【答案】 B 【分析】试题剖析：，得不到，由于可能订交，只需和的交线平行即可获得；，，∴和没有公共点，∴，即能获得；∴ “”是“”的必需不充足条件．应选B ．考点：必需条件、充足条件与充要条件的判断.【方法点晴】考察线面平行的定义，线面平行的判断定理，面面平行的定义，面面平行的判断定理，以及充足条件、必需条件，及必需不充足条件的观点，属于基础题；并得不到，依据面面平行的判断定理，只有内的两订交直线都平行于，而，而且，明显能获得，这样即可找出正确选项.12．设 A ， B ， C ， D 是同一个球面上四点， ABC 是斜边长为 6 的等腰直角三角形，若三棱锥 D ABC 体积的最大值为 27，则该球的表面积为（）A ． 36B ． 64πC ． 100D ． 144【答案】 C【分析】【剖析】由题意画出图形，求出三棱锥 D ABC 的外接球的半径，代入表面积公式求解．【详解】解：如图，ABC 是斜边 BC 长为 6 的等腰直角三角形，则当 D 位于直径的端点时，三棱锥D ABC 体积取最大值为 27，由 AB AC ， ABAC ， BC 6 ，可得斜边 BC 上的高 AE3， AB AC 32，由11 323 2 DE 27 ，解得 DE 9，3 2 则 EF AE 2 1．DE∴球 O 的直径为 DE EF 10，则球 O 的半径为 110 5．2∴该球的表面积为S 452100．应选 C ．【点睛】此题考察多面体外接球表面积的求法，考察数形联合的解题思想方法，是中档题．13．已知底面是等腰直角三角形的三棱锥 P-ABC 的三视图如下图，俯视图中的两个小三角形全等，则（）A ． PA ， PB ， PC 两两垂直8B ．三棱锥 P-ABC 的体积为3C ．|PA| |PB| |PC|6D ．三棱锥 P-ABC 的侧面积为 3 5【答案】 C 【分析】【剖析】依据三视图，可得三棱锥 P-ABC 的直观图，而后再计算可得 .【详解】解：依据三视图，可得三棱锥P-ABC 的直观图如下图，此中 D 为 AB 的中点， PD 底面 ABC.因此三棱锥 P-ABC 的体积为11 2 2 2 4 ，32 3AC BC PD 2 ，AB 2BC 22 ，AC2|DA | |DB | |DC |2， |PA| |PB| |PC|22226,222Q PA PB AB ， PA 、 PB 不行能垂直，即 PA, PB , PC 不行能两两垂直，11 2QS PBA2 2 2 2 2，QS PBC S PAC 6 122 5 .22三棱锥 P-ABC 的侧面积为 2 5 2 2 .故正确的为 C.应选： C.【点睛】此题考察三视图复原直观图，以及三棱锥的表面积、体积的计算问题，属于中档题.14．在四周体 ABCD 中， AB ， BC ， BD 两两垂直， AB BC BD 4，E 、F 分别为棱 BC 、 AD 的中点，则直线 EF 与平面 ACD 所成角的余弦值（）A ．1B ．3 C ．2 2D ．6 3333【答案】 C【分析】【剖析】由于 AB ， BC ， BD 两两垂直，以 BA 为 X 轴，以 BD 为 Y 轴，以 BC 为 Z 轴成立空间直uuurr uuur ruuur rEF n角坐标系，求出向量EF 与平面 ACD 的法向量 n ，再依据 cos EF , nuuur r ，即可 | EF || n |得出答案 .【详解】由于在四周体ABCD 中， AB ， BC ， BD 两两垂直，以 BA 为 X 轴，以 BD 为 Y 轴，以 BC 为 Z 轴成立空间直角坐标系，又由于 AB BC BD 4；A 4,0,0 , B(0,0,0), D(0,4,0), C(0,0,4) ，又由于 E 、 F 分别为棱 BC 、 AD 的中点因此 E(0,0,2),F (2,2,0)uuur 2,2, uuur uuur 4,0, 4) . 故 EF 2 ，AD ( 4,4,0) ， AC ( r v uuuvn AD设平面 ACD 的法向量为 n( x, y, z) ，则 v uuuvn AC令 x 1, 则 y z1；r(1,1,1)因此 nuuur r uuur r2 1 EF ncos EF , nuuur r323 3| EF || n |设直线 EF 与平面 ACD 所成角为 uuur r，则 sin cos EF , n因此cos1 sin 22 23应选： C【点睛】此题主要考察线面角，经过向量法即可求出，属于中档题目.15．已知直三棱柱 ABC A 1 B 1C 1 的底面为直角三角形，且两直角边长分别为 1 和 3 ，此三棱柱的高为2 3 ，则该三棱柱的外接球的体积为32168D ．64A ．B ．C ．3333【答案】 A【分析】【剖析】求得该直三棱柱的底面外接圆直径为 2r12 ( 3) 22 ，再依据球的性质，求得外接球的直径 R 2 ，利用球的体积公式，即可求解 .【详解】由题意可得该直三棱柱的底面外接圆直径为 2r 12 ( 3)2 2r1，依据球的性质，可得外接球的直径为2R(2r ) 2h 222 (2 3) 24 ，解得R 2 ，因此该三棱柱的外接球的体积为 V4 R 3 32 ，应选 A.3 3【点睛】此题主要考察了球的体积的计算，以及组合体的性质的应用，此中解答中找出适合的模型，合理利用球的性质求得外接球的半径是解答的重点，侧重考察了剖析问题和解答问题的能力，属于中档试题 .16．等腰三角形ABC 的腰 AB AC 5 ， BC 6 ，将它沿高 AD 翻折，使二面角BADC 成 60 ，此时四周体 ABCD 外接球的体积为（）A ． 7B ． 28C ． 19 19D ．28 763【答案】 D【分析】剖析：详解：由题意，设BCD 所在的小圆为 O1，半径为 r ，又由于二面角 B AD C 为600，即BDC600，因此BCD 为边长为 3 的等边三角形，又正弦定理可得，2r323，即 BE2 3 ，sin 600设球的半径为 R ，且AD 4，ADE 中，2R22DE 24R42(23) 228在直角AD，因此 R7 ，因此球的体积为V 4 R34(7) 3287，应选 D．333点睛：此题考察了相关球的组合体问题，以及三棱锥的体积的求法，解答时要仔细审题，注意球的性质的合理运用，求解球的组合体问题常用方法有（1）三条棱两两相互垂直时，可恢复为长方体，利用长方体的体对角线为外接球的直径，求出球的半径；（2）直棱柱的外接球可利用棱柱的上下底面平行，借助球的对称性，球心为上下底面外接圆的圆心连线的中点，再依据勾股定理求球的半径.17．已知某几何体的三视图如下图，此中正视图与侧视图是全等的直角三角形，则该几何体的各个面中，最大面的面积为（）A．2B． 5C．13D．22【答案】 D【分析】【剖析】依据三视图复原出几何体，找到最大面，再求面积.【详解】由三视图可知，该几何体是一个三棱锥，如下图，将其放在一个长方体中，并记为三棱锥P ABC .S PAC S PAB13 ， S PAC 22 ， S ABC 2 ，故最大面的面积为 22 .选 D.【点睛】此题主要考察三视图的辨别，复杂的三视图复原为几何体时，一般借滋长方体来实现.18．由两个 1圆柱组合而成的几何体的三视图如下图，则该几何体的体积为（）4A ．π π D ． 2πB ．C ． π32【答案】 C【分析】【剖析】依据题意可知，圆柱的底面半径为 1，高为 2，利用圆柱的体积公式即可求出结果。

2020—2021年高考总复习数学《立体几何》高考考点专项复习及参考答案(精品试题).docx

届高三第二次模拟数学理试题分类汇编：立体几何一、填空、选择题1、（崇明县2016届高三二模）已知圆锥的母线长为5cm ，侧面积为15πcm2，则此圆锥的体积为cm 2．2、（奉贤区2016届高三二模）在棱长为1的正方体ABCD A B C D ''''-中，若点P 是棱上一点，则满足2PA PC '+=的点P 的个数_______．3、（虹口区2016届高三二模）已知A 、B 是球O 的球面上两点，90AOB ∠=o ，C 为该球面上的动点，若三棱锥ABC O -体积的最大值为323，则球O 的表面积为__________4、（黄浦区2016届高三二模）已知一个凸多边形的平面展开图由两个正六边形和六个正方形构成，如右上图所示，若该凸多面体所有棱长均为1，则其体积V =5、（静安区2016届高三二模）如图，正四棱锥P ABCD -的底面边长为23cm ，侧面积为 283cm ，则它的体积为.6、（闵行区2016届高三二模）若一个圆锥的母线长是底面半径的3倍，则该圆锥的侧面积是底面积的倍.7、（浦东新区2016届高三二模）已知四面体ABCD 中，2==CD AB ，E ，F分别为BC ，AD 的中点，且异面直线AB 与CD 所成的角为3π，则EF =________．8、（普陀区2016届高三二模）若a 、b 表示两条直线，α表示平面，下列命题中的真命题为（）（A ）若α⊥a ，b a ⊥，则α//b （B ）若α//a ，b a ⊥，则α⊥b （C ）若α⊥a ，α⊆b ，则b a ⊥ （D ）若α//a ，α//b ，则b a // 9、（徐汇、金山、松江区2016届高三二模）．如图，圆锥形容器的高为,h 圆锥内水面的高为1,h 且11,3h h =若将圆锥倒置，水面高为2,h 则2h 等于------------------------------------------------（）（A ）23h （B ）1927h （C ）363h （D ）3193h10、（杨浦区2016届高三二模）已知命题：“若a,b 为异面直线，平面α过直线a 且与直线b 平行，则直线b 与平面α的距离等于异面直线a,b 之间的距离”为真命题.根据上述命题，若a,b 为异面直线，且它们之间的距离为d ，则空间中与a,b 均异面且距离也均为d 的直线c 的条数为（）A0条 B.1条 C.多于1条，但为有限条 D.无数多条11、（闸北区2016届高三二模）已知,,,S A B C 是球O 表面上的点，SA ⊥平面ABC ，AB BC ⊥，1SA AB == 2BC =，则球O 的表面积等于（）A ．π4 B ．π3 C ．π2 D ．π12、（长宁、青浦、宝山、嘉定四区2016届高三二模）下列命题正确的是（）．（A ）若直线1l ∥平面α，直线2l ∥平面α，则1l ∥2l ；（B ）若直线l 上有两个点到平面α的距离相等，则l ∥α；（C ）直线l 与平面α所成角的取值范围是⎪⎭⎫⎝⎛2,0π；（D ）若直线1l ⊥平面α，直线2l ⊥平面α，则1l ∥2l .13、（闵行区2016届高三二模）如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点，P 为底面ABCD 内一动点，设1PD PE 、与底面ABCD 所成的角分别为12θθ、（12θθ、均不为0)．若12θθ=，则动点P 的轨迹为哪种曲线的一部分（）.(A)直线 (B)圆 (C) 椭圆 (D) 抛物线14、（浦东新区2016届高三二模）给出下列命题，其中正确的命题为( )（A ）若直线a 和b 共面，直线b 和c 共面，则a 和c 共面；（B ）直线a 与平面α不垂直，则a 与平面α内的所有直线都不垂直；（C ）直线a 与平面α不平行，则a 与平面α内的所有直线都不平行；（D ）异面直线a 、b 不垂直，则过a 的任何平面与b 都不垂直. 二、解答题1、（崇明县2016届高三二模）如图，在棱长为1的正方体1111ABCD A B C D -中，点E 是棱BC 的中点，点F 是棱CD 的中点．（1）求证：11EF B D ∥；（2）求二面角1C EF A --的大小（结果用反三角函数值表示）．AC BC 1A 1B 1（第19题图）D 1D FE2、（奉贤区2016届高三二模）面ABC 外的一点P ，,,AP AB AC 两两互相垂直，过AC 的中点D 作ED ⊥面ABC ，且1ED =，2PA =，2AC =，连,BP BE ，多面体B PADE -的体积是33． (1)画出面PBE 与面ABC 的交线，说明理由；（2）求面PBE 与面ABC 所成的锐二面角的大小．ADBCPEQ A DCBP （第20题图）3、（虹口区2016届高三二模）如图，在四棱锥ABCD P -中，已知⊥PA 平面ABCD ，且四边形ABCD 为直角梯形，90ABC BAD ∠=∠=︒，2AB AD AP ===，1BC =.(1) 求点A 到平面PCD 的距离； (2) 若点Q 为线段BP 的中点，求直线CQ 与平面ADQ 所成角的大小.4、（黄浦区2016届高三二模）如图，小凳的凳面为圆形，凳脚为三根细钢管，考虑到钢管的受力等因素，设计的小凳应满足：三根细钢管相交处的节点P 与凳面圆形的圆心O 的连线垂直于凳面和地面，且P 分两钢管上下两段的比值为0.618，三只凳脚与地面所成的角均为60°，若A 、B 、C 是凳面圆周的三等分点，18AB =厘米，求凳面的高度h 及三根细钢管的总长度（精确到0.01）；5、（静安区2016届高三二模）设点,E F 分别是棱长为2的正方体1111ABCD A B C D -的棱1,AB AA 的中点．如图，以C 为坐标原点，射线CD 、CB 、1CC 分别是x 轴、y 轴、z 轴的正半轴，建立空间直角坐标系．（1）求向量1D E u u u u r与1C F u u u u r 的数量积；（2）若点,M N 分别是线段1D E 与线段1C F 上的点，问是否存在直线MN ，MN ⊥平面ABCD ？若存在，求点,M N 的坐标；若不存在，请说明理由E FB 1A 1C 1D 1BC DA6、（闵行区2016届高三二模）如图，在直角梯形PBCD中，//PB DC，DC BC⊥，22PB BC CD===，点A是PB的中点，现沿AD将平面PAD折起，设PABθ∠=．（1）当θ为直角时，求异面直线PC与BD所成角的大小；（2）当θ为多少时，三棱锥P ABD-的体积为26．7、（浦东新区2016届高三二模）如图，在圆锥SO中，AB为底面圆O 的直径，点C为»AB的中点，SO AB=.（1）证明：AB⊥平面SOC；（2）若点D为母线SC的中点，求AD与平面SOC所成的角.（结果用反三角函数表示）8、（普陀区2016届高三二模）在正四棱柱1111D C B A ABCD -中，底面边长为1，B C 1与底面ABCD 所成的角的大小为2arctan ，如果平面11C BD 与底面ABCD 所成的二面角是锐角，求出此二面角的大小（结果用反三角函数值）9、（徐汇、金山、松江区2016届高三二模）在直三棱柱111C B A ABC -中，1==AC AB ，90=∠BAC ，且异面直线BA 1与11CB 所成的角等于060，设a AA =1. （1）求a 的值；（2）求三棱锥BC A B 11-的体积．1A 1B 1CA BCD.A 1CEA BCDB 110、（杨浦区2016届高三二模）如图，底面是直角三角形的直三棱柱111ABC A B C -中，1112AC BC AA ===，D 是棱1AA 上的动点.(1)证明：1DC BC ⊥； (2)求三棱锥1C BDC -的体积.11、（闸北区2016届高三二模）在长方体1111ABCD A B C D -中，2AB =，1AD =，11AA =，点E 在棱AB 上移动．（1）探求AE 多长时，直线1D E 与平面11AA D D成45o 角；（2）点E 移动为棱AB 中点时，求点E 到平面11A DC 的距离．12、（长宁、青浦、宝山、嘉定四区2016届高三二模）如图，在直三棱柱111C B A ABC -中，底面△ABC 是等腰直角三角形，21===AA BC AC ，D 为侧棱1AA 的中点．（1）求证：⊥BC 平面11A ACC ；（2）求二面角11C CD B --的大小（结果用反三角函数值表示）．参考答案一、填空、选择题ABCA 1B 1C 1D1、12π2、23、64π4、3325、4106、37、1 或3 8、C 9、D 10、D 11、A 12、D13、B 14、D二、解答题1、可得有关点的坐标为11111(0,0,1),(1,1,1),(,1,0),(0,,0),(0,1,1)22D BEF C 11(,,0)22EF =--u u u r ，11(1,1,0)B D =--u u u u r (4)分所以112B D EF =u u u u r u u u r...............................5分所以11EF B D ∥...............................6分（2）设1(,,)n u v w =u r是平面1C EF 的一个法向量.因为111,n EF n FC ⊥⊥u r u u u u r u r u u u u r所以1111110,0222n EF u v n FC v w ⋅=--=⋅=+=u r u u u ru r u u u u r解得,2u v v w =-=- .取1w = ，得1(2,2,1)n =-u r.............................9分因为1DD ABCD ⊥平面，所以平面ABCD 的一个法向量是2(0,0,1)n =u u r (10)分设1n u r 与2n u u r 的夹角为α ，则12121cos 3||||n n n n α⋅==⋅u r u u ru r uu r .......................11分结合图形，可判别得二面角1C EF A --是钝角，其大小为1arccos 3π- (12)分2、(1)根据条件知:PE 与AD 交点恰好是C 1分ACBC 1A 1B 1（第19题图）D 1 D FE x yz,C PE C ∈∴∈面PBE ,,C AC C ∈∴∈面ABC 2分B ∈面PBE ,B ∈面ABC3分面PBE与面ABC的交线BC5分 (2)(理) ,,AP AB AC 两两互相垂直,BA ⊥面EDAP 7分多面体B PADE -的体积是()113323PA DE AD BA ⨯+⨯⨯=9分233BA ∴=10分建立空间直角坐标系,设平面的法向量是()1,,n x y z u r23,0,03B ⎛⎫ ⎪ ⎪⎝⎭，()0,2,0C ()0,1,0D ()0,1,1E ()0,0,2P23,0,23BP ⎛⎫=- ⎪ ⎪⎝⎭u u u r ，23,1,13BE ⎛⎫=- ⎪ ⎪⎝⎭u u u r123203n BP x z ⋅=-+=u r u u u r12303n BE x y z ⋅=-++=u r u u u r()13,1,1n ∴=u r11分面ABC 的法向量()20,0,1n =u u rADBC PE zxyQA D CBP（第20题解答图）z yx 1212cos n nn n θ⋅==⋅u r u u ru r u u r 1555= 12分所以面PBE 与面ABC 所成的锐二面角大小5arccos 513分注：若作出二面角得2分，计算再3分 (2)(文),,AP AB AC 两两互相垂直,BA ⊥面EDAP7分多面体B PADE -的体积是()113323PA DE AD BA ⨯+⨯⨯=9分233BA ∴=10分连接AEAE 是BE 在面EDAP 的射影BEA ∠是BE 与面PADE 所成的线面角． 11分计算2AE =,2363tan 32BAE ∠==12分BEA ∠是BE 与面PADE 所成的线面角6arctan 3． 13分3、（理）解：(1)以},,{AP AD AB 为正交基底建立空间直角坐标系xyz A -，则相关点的坐标为B （2,0,0），(2,1,0),(0,2,0),(0,0,2).C D P ……2分设平面PCD 的法向量为(,,),n x y z =r由(2,1,0),DC =-uuu r (0,2,2),DP =-u u u r (0,2,0).DA =-u u u r则ADBCPE202,2.220n DC x y y x z x n DPy z r u u u r r u u u r ìïì?-==ïïïÞ眄镲=?-+=ïîïî 令1x =，则(1,2,2)n =r.……5分所以点A 到平面PCD 的距离为：(0,2,0)(1,2,2)4.(1,2,2)3DA n d nu u u r r r×-?=== ……7分(2) 由条件，得(1,0,1),Q =(0,2,0),(1,0,1),AD AQ ==u u u r u u u r 且(1,1,1).CQ u u u r=--设平面ADQ 的法向量为0000(,,),n x y z =r 则00000000200,.0n AD y y z x n AQx z r u u u r r u u u r ìïì?==ïï镲Þ眄镲=-?+=ïïîî令01x =，则0(1,0,1)n =-r.……10分设直线CQ 与平面ADQ 所成角为,θ则00026sin cos ,.332CQ n CQ n CQ n θ⋅=<>===⋅u u u r u u r u u u r u u ru u u r u u r故直线CQ 与平面ADQ 所成角的大小为6sin.3arc ……14分注：第（1）小题也可用等积法来做.4、[解] 联结PO ，AO ，由题意，PO ⊥平面ABC ，因为凳面与地面平行，所以PAO ∠就是PA 与平面ABC 所成的角，即60PAO ∠=︒．（2分）在等边三角形ABC 中，18AB =，得63AO =，（4分）在直角三角形PAO 中，318OP AO ==，（6分）由0.618OPh OP=-，解得47.13h ≈厘米．（9分）三根细钢管的总长度3163.25sin 60h≈︒厘米．（12分）5、（1）在给定空间直角坐标系中，相关点及向量坐标为11(2,0,2),(1,2,0),(1,2,2)D E D E =--u u u u r (2)分PA BCD xy z PA BCD 11(0,0,2),(2,2,1),(2,2,1)C F C F =-u u u u r (4)分所以111222(2)(1)4D E C F ⋅=-⨯+⨯+-⨯-=u u u u r u u u u r。

2021年高中数学立体几何多选题专题复习附答案

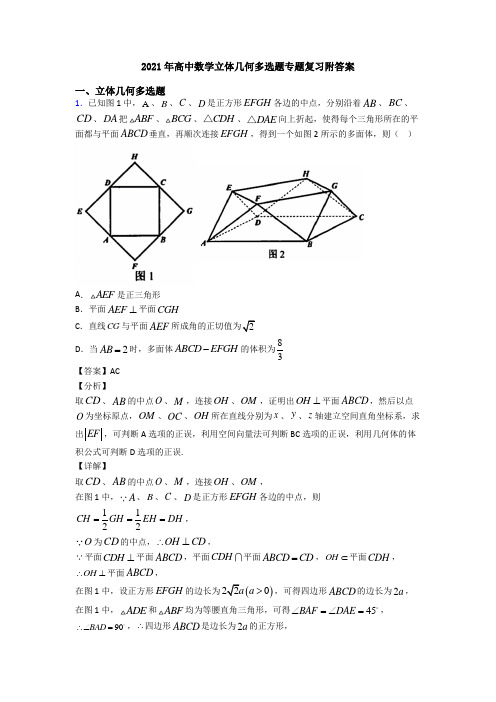
2021年高中数学立体几何多选题专题复习附答案一、立体几何多选题1．已知图1中，A 、B 、C 、D 是正方形EFGH 各边的中点，分别沿着AB 、BC 、CD 、DA 把ABF 、BCG 、CDH △、DAE △向上折起，使得每个三角形所在的平面都与平面ABCD 垂直，再顺次连接EFGH ，得到一个如图2所示的多面体，则（）A ．AEF 是正三角形B ．平面AEF ⊥平面CGHC ．直线CG 与平面AEF 2D ．当2AB =时，多面体ABCD EFGH -的体积为83【答案】AC 【分析】取CD 、AB 的中点O 、M ，连接OH 、OM ，证明出OH ⊥平面ABCD ，然后以点O 为坐标原点，OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系，求出EF ，可判断A 选项的正误，利用空间向量法可判断BC 选项的正误，利用几何体的体积公式可判断D 选项的正误. 【详解】取CD 、AB 的中点O 、M ，连接OH 、OM ，在图1中，A 、B 、C 、D 是正方形EFGH 各边的中点，则1122CH GH EH DH ===，O 为CD 的中点，OH CD ∴⊥，平面CDH ⊥平面ABCD ，平面CDH 平面ABCD CD =，OH ⊂平面CDH ，OH ∴⊥平面ABCD ，在图1中，设正方形EFGH 的边长为()220a a >，可得四边形ABCD 的边长为2a ，在图1中，ADE 和ABF 均为等腰直角三角形，可得45BAF DAE ∠=∠=， 90BAD ∴∠=，∴四边形ABCD 是边长为2a 的正方形，O 、M 分别为CD 、AB 的中点，则//OC BM 且OC BM =，且90OCB ∠=，所以，四边形OCBM 为矩形，所以，OM CD ⊥，以点O 为坐标原点，OM 、OC 、OH 所在直线分别为x 、y 、z 轴建立空间直角坐标系，则()2,,0A a a -、()2,,0B a a 、()0,,0C a 、()0,,0D a -、(),,E a a a -、()2,0,F a a 、(),,G a a a 、()0,0,H a .对于A 选项，由空间中两点间的距离公式可得2AE AF EF a ===，所以，AEF 是正三角形，A 选项正确；对于B 选项，设平面AEF 的法向量为()111,,m x y z =，(),0,AE a a =-，()0,,AF a a =，由11110m AE ax az m AF ay az ⎧⋅=-+=⎪⎨⋅=+=⎪⎩，取11z =，则11x =，11y =-，则()1,1,1m =-，设平面CGH 的法向量为()222,,n x y z =，(),0,CG a a =，()0,,CH a a =-，由222200n CG ax az n CH ay az ⎧⋅=+=⎪⎨⋅=-+=⎪⎩，取21z =-，可得21x =，21y =-，则()1,1,1n =--，()22111110m n ⋅=+--⨯=≠，所以，平面AEF 与平面CGH 不垂直，B 选项错误；对于C 选项，6cos ,23CG m CG m a CG m⋅<>===⨯⋅，设直线CG 与平面AEF 所成角为θ，则sin 6θ=，23cos 1sin θθ=-=，所以，sin tan 2cos θθθ==，C 选项正确；对于D 选项，以ABCD 为底面，以OH 为高将几何体ABCD EFGH -补成长方体1111ABCD A B C D -，则E 、F 、G 、H 分别为11A D 、11A B 、11B C 、11C D 的中点，因为2AB =，即1a =，则1OH =，长方体1111ABCD A B C D -的体积为2214V =⨯=，11211111113326A A EF A EF V S AA -=⋅=⨯⨯⨯=△，因此，多面体ABCD EFGH -的体积为111044463ABCD EFGH A A EF V V V --=-=-⨯=， D 选项错误. 故选：AC. 【点睛】方法点睛：计算线面角，一般有如下几种方法：（1）利用面面垂直的性质定理，得到线面垂直，进而确定线面角的垂足，明确斜线在平面内的射影，即可确定线面角；（2）在构成线面角的直角三角形中，可利用等体积法求解垂线段的长度h ，从而不必作出线面角，则线面角θ满足sin hlθ=（l 为斜线段长），进而可求得线面角；（3）建立空间直角坐标系，利用向量法求解，设a 为直线l 的方向向量，n 为平面的法向量，则线面角θ的正弦值为sin cos ,a n θ=<>.2．已知球O 为正方体1111ABCD A B C D -的内切球，平面11A C B 截球O 的面积为24π，下列命题中正确的有（）A ．异面直线AC 与1BC 所成的角为60°B ．1BD ⊥平面11AC B C ．球O 的表面积为36πD ．三棱锥111B AC B -的体积为288 【答案】AD 【分析】连接11A C ，1A B ，通过平移将AC 与1BC 所成角转化为11A C 与1BC 所成角可判断A ；通过反证法证明B ；由已知平面11A C B 截球O 的面积为24π求出正方体棱长，进而求出内切球的表面积可判断C ；利用等体积法可求得三棱锥111B AC B -的体积可判断D. 【详解】对于A ，连接11A C ，1A B ，由正方体1111ABCD A B C D -，可知11//A C AC ，11AC B ∴∠为异面直线AC 与1BC 所成的角，设正方体边长为a ，则1111AC A B BC ==，由等边三角形知1160A C B ∠=，即异面直线AC 与1BC 所成的角为60，故A 正确；对于B ，假设1BD ⊥平面11A C B ，又1A B ⊂平面11A C B ，则11BD B A ⊥，设正方体边长为a ，则11A D a =，1A B =，1BD =，由勾股定理知111A D B A ⊥，与假设矛盾，假设不成立，故1BD 不垂直于平面11A C B ，故B 错误；对于C ，设正方体边长为a ，则112AC a =，内切球半径为2a，设内切球的球心O 在面11A C B 上的投影为O '，由等边三角形性质可知O '为等边11A C B △的重心，则111623332332O A AC a a =⨯'=⨯=，又132OA a =，∴球心O 到面11A C B 的距离为121222326336a a a OA O A ⎛⎫⎛⎫ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭=-='-，又球心与截面圆心的连线垂直于截面，∴截面圆的半径为2236626a a a ⎛⎫⎛⎫ ⎪ ⎪ ⎪⎝⎭⎝⎭-=，又截面圆的面积26246S a ππ⎛⎫= ⎪ ⎪⎝⎭=，解得12a =，则内切球半径为6，内切球表面积214644S ππ==⨯，故C 错误；对于D ，由等体积法知111111111111212122812383B A C B B A C B A C B V V S a --==⨯⨯=⨯⨯=，故D 正确；故选：AD【点睛】关键点点睛：本题考查了正方体和它的内切球的几何结构特征，关键是想象出截面图的形状，从而求出正方体的棱长，进而求出内切球的表面积及三棱锥的体积，考查了空间想象能力，数形结合的思想，属于较难题.3．在棱长为1的正方体1111ABCD A B C D -中，P 为底面ABCD 内（含边界）一点．（） A ．若13A P P 点有且只有一个 B ．若12A P ，则点P 的轨迹是一段圆弧 C ．若1//A P 平面11B D C ，则1A P 2D ．若12A P =且1//A P 平面11B DC ，则平面11A PC 截正方体外接球所得截面的面积为23π【答案】ABD 【分析】选项A ，B 可利用球的截面小圆的半径来判断；由平面1//A BD 平面11B D C ，知满足1//A P 平面11B D C 的点P 在BD 上，1A P 长的最大值为2；结合以上条件点P 与B 或D 重合，利用12sin 60A P r =︒，求出63r =，进而求出面积. 【详解】对A 选项，如下图：由13A P =，知点P 在以1A 为球心，半径为3的球上，又因为P 在底面ABCD 内（含边界），底面截球可得一个小圆，由1A A ⊥底面ABCD ，知点P 的轨迹是在底面上以A 为圆心的小圆圆弧，半径为22112r A P A A =-=，则只有唯一一点C满足，故A 正确；对B 选项，同理可得点P 在以A 为圆心，半径为22111r A P A A =-=的小圆圆弧上，在底面ABCD 内（含边界）中，可得点P 轨迹为四分之一圆弧BD .故B 正确；对C 选项，移动点P 可得两相交的动直线与平面11B D C 平行，则点P 必在过1A 且与平面11B D C 平行的平面内，由平面1//A BD 平面11B D C ，知满足1//A P 平面11B D C 的点P 在BD上，则1A P 长的最大值为12A B C 不正确；对选项D ，由以上推理可知，点P 既在以A 为圆心，半径为1的小圆圆弧上，又在线段BD 上，即与B 或D 重合，不妨取点B ，则平面11A PC 截正方体外接球所得截面为11A BC 的外接圆，利用2126622,,sin 603A B r r S r ππ==∴=∴==︒.故D 正确.故选：ABD 【点睛】（1）平面截球所得截面为圆面，且满足222=R r d +（其中R 为球半径，r 为小圆半径，d 为球心到小圆距离）；（2）过定点A 的动直线平行一平面α，则这些动直线都在过A 且与α平行的平面内.4．正方体1111ABCD A B C D -中，E 是棱1DD 的中点，F 在侧面11CDD C 上运动，且满足1//B F 平面1A BE .以下命题正确的有（）A ．侧面11CDD C 上存在点F ，使得11B F CD ⊥ B ．直线1B F 与直线BC 所成角可能为30︒C ．平面1A BE 与平面11CDD C 所成锐二面角的正切值为2D ．设正方体棱长为1，则过点E ，F ，A 5【答案】AC 【分析】取11C D 中点M ，1CC 中点N ，连接11,,B M B N MN ，易证得平面1//B MN 平面1A BE ，可得点F 的运动轨迹为线段MN ．取MN 的中点F ，根据等腰三角形的性质得1B F MN ⊥，即有11B F CD ⊥，A 正确；当点F 与点M 或点N 重合时，直线1B F 与直线BC 所成角最大，可判断B 错误；根据平面1//B MN 平面1A BE ，11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角，计算可知C 正确；取11C D 中点M ，1CC 中点N ，连接11,,B M B N MN ，则易证得11//B N A E ，1//MN A B ，从而平面1//B MN 平面1A BE ，所以点F 的运动轨迹为线段MN ．取MN 的中点F ，因为1B MN △是等腰三角形，所以1B F MN ⊥，又因为1//MN CD ，所以11B F CD ⊥，故A 正确；设正方体的棱长为a ，当点F 与点M 或点N 重合时，直线1B F 与直线BC 所成角最大，此时11tan C B F ∠=1tan 3023︒<=，所以B 错误；平面1//B MN 平面1A BE ，取F 为MN 的中点，则1MN C F ⊥，1MN B F ⊥，∴11B FC ∠即为平面1B MN 与平面11CDD C 所成的锐二面角，11111tan B C B FC C F∠==22，所以C 正确；因为当F 为1C E 与MN 的交点时，截面为菱形1AGC E （G 为1BB 的交点），面积为6，故D 错误. 故选：AC.【点睛】本题主要考查线面角，二面角，截面面积的求解，空间几何中的轨迹问题，意在考查学生的直观想象能力和数学运算能力，综合性较强，属于较难题．5．在长方体1111ABCD A B C D -中，23AB =12AD AA ==，,,P Q R 分别是11,,AB BB AC 上的动点，下列结论正确的是（） A ．对于任意给定的点P ，存在点Q 使得1D P CQ ⊥ B ．对于任意给定的点Q ，存在点R 使得1D R CQ ⊥ C ．当1AR A C ⊥时，1AR D R ⊥D ．当113AC A R =时，1//D R 平面1BDC 【答案】ABD如图所示建立空间直角坐标系，计算142D P CQ b ⋅=-，()12222D R CQ b λλ⋅=--，134AR D R ⋅=-，10D R n ⋅=，得到答案.【详解】如图所示，建立空间直角坐标系，设()2,,0P a，a ⎡∈⎣，()Q b ，[]0,2b ∈，设11A R AC λ=，得到()22,22R λλ--，[]0,1λ∈. ()12,,2P a D -=，()2,0,CQ b =，142D P CQ b ⋅=-，当2b =时，1D P CQ ⊥，A 正确；()122,2D R λλ=--，()12222D R CQ b λλ⋅=--，取22bλ=+时，1D R CQ ⊥，B 正确； 1AR A C ⊥，则()()12,222212440AR AC λλλλλ⋅=--⋅--=-+-+=， 14λ=，此时113313,,02222224AR D R ⎛⎫⎛⎫⋅=-⋅-=-≠ ⎪ ⎪ ⎪ ⎪⎝⎭⎝⎭，C 错误； 113AC A R =，则4433R ⎛⎫ ⎪ ⎪⎝⎭，14233D R ⎛⎫=- ⎪ ⎪⎝⎭，设平面1BDC 的法向量为(),,n x y z =，则100n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩，解得(3,n =-，故10D R n ⋅=，故1//D R 平面1BDC ，D 正确. 故选：ABD .【点睛】本题考查了空间中的线线垂直，线面平行，意在考查学生的计算能力和空间想象能力，推断能力.6．已知棱长为1的正方体1111ABCD A B C D -，过对角线1BD 作平面α交棱1AA 于点E ，交棱1CC 于点F ，以下结论正确的是（） A ．四边形1BFD E 不一定是平行四边形 B ．平面α分正方体所得两部分的体积相等 C ．平面α与平面1DBB 不可能垂直 D ．四边形1BFD E 面积的最大值为2 【答案】BD 【分析】由平行平面的性质可判断A 错误;利用正方体的对称性可判断B 正确;当E ､F 为棱中点时,通过线面垂直可得面面垂直,可判断C 错误;当E 与A 重合,F 与1C 重合时,四边形1BFD E 的面积最大,且最大值为2,可判断D 正确. 【详解】如图所示,对于选项A,因为平面1111//ABB A CC D D ,平面1BFD E 平面11ABB A BE =,平面1BFD E平面111CC D D D F =,所以1//BE D F ,同理可证1//D E BF ,所以四边形1BFD E 是平行四边形,故A 错误; 对于选项B,由正方体的对称性可知,平面α分正方体所得两部分的体积相等,故B 正确; 对于选项C,在正方体1111ABCD A B C D -中,有1,AC BD AC BB ⊥⊥, 又1BD BB B ⋂=,所以AC ⊥平面1BB D , 当E ､F 分别为棱11,AA CC 的中点时, 有//AC EF ,则EF ⊥平面1BB D , 又因为EF ⊂平面1BFD E ,所以平面1BFD E ⊥平面1BB D ,故C 错误;对于选项D,四边形1BFD E 在平面ABCD 内的投影是正方形ABCD , 当E 与A 重合,F 与1C 重合时,四边形1BFD E 的面积有最大值, 此时1212S D E BE =⋅=⋅=,故D 正确; 故选:BD. 【点睛】本题考查了正方体的几何性质与应用问题,也考查了点线面的位置关系应用问题,属于中档题.7．在正方体1111ABCD A B C D -中，如图，,M N 分别是正方形ABCD ，11BCC B 的中心.则下列结论正确的是（）A ．平面1D MN 与11BC 的交点是11B C 的中点 B ．平面1D MN 与BC 的交点是BC 的三点分点 C ．平面1D MN 与AD 的交点是AD 的三等分点 D ．平面1D MN 将正方体分成两部分的体积比为1∶1 【答案】BC 【分析】取BC 的中点E ，延长DE ，1D N ，并交于点F ，连FM 并延长分别交,BC AD 于,P Q ，连1,D Q PN 并延长交11B C 与H ，平面四边形1D HPQ 为所求的截面，进而求出,,P Q H 在各边的位置，利用割补法求出多面体11QPHD C CD 的体积，即可求出结论.【详解】如图，取BC 的中点E ，延长DE ，1D N ，并交于点F ，连接FM 并延长，设FM BC P ⋂=，FM AD Q ⋂=，连接PN 并延长交11B C 于点H .连接1D Q ，1D H ，则平面四边形1D HPQ 就是平面1D MN 与正方体的截面，如图所示.111111////,22NE CC DD NE CC DD ==，NE ∴为1DD F ∆的中位线，E ∴为DF 中点，连BF ， ,,90DCE FBE BF DC AB FBE DCE ∴∆≅∆==∠=∠=︒， ,,A B F ∴三点共线，取AB 中点S ，连MS ，则12//,,23BP FB MS BP MS BC MS FS =∴==， 22111,33236BP MS BC BC PE BC ∴==⨯=∴=， E 为DF 中点，11//,233PE DQ DQ PE BC AD ∴===N 分别是正方形11BCC B 的中心，11113C H BP C B ∴==所以点P 是线段BC 靠近点B 的三等分点，点Q 是线段AD 靠近点D 的三等分点，点H 是线段11B C 靠近点1C 的三等分点. 做出线段BC 的另一个三等分点P '，做出线段11A D 靠近1D 的三等分点G ，连接QP '，HP '，QG ，GH ，1H QPP Q GHD V V '--=，所以111113QPHD C CD QPHQ DCC D V V V -==多面体长方体正方体从而平面1D MN 将正方体分成两部分体积比为2∶1. 故选:BC.【点睛】本题考查直线与平面的交点及多面体的体积，确定出平面与正方体的交线是解题的关键，考查直观想象、逻辑推理能力，属于较难题.8．如果一个棱锥的底面是正方形，且顶点在底面内的射影是底面的中心，那么这样的棱锥叫正四棱锥．若一正四棱锥的体积为18，则该正四棱锥的侧面积最小时，以下结论正确的是（）．A ．棱的高与底边长的比为22B ．侧棱与底面所成的角为4π C ．棱锥的高与底面边长的比为2 D ．侧棱与底面所成的角为3π 【答案】AB 【分析】设四棱锥S ABCD -的高为h ，底面边长为a ，由21183V a h ==得254h a=，然后可得侧面积为242108a a+，运用导数可求出当32a =时侧面积取得最小值，此时3h =，然后求出棱锥的高与底面边长的比和SAO ∠即可选出答案. 【详解】设四棱锥S ABCD -的高为h ，底面边长为a 可得21183V a h ==，即254h a=所以其侧面积为2222244215410842244a a a h a a a a⋅⋅+=+=+ 令()242108f a a a =+，则()23321084f a a a⨯'=- 令()233210840f a a a⨯'=-=得32a = 当()0,32a ∈时()0f a '<，()f a 单调递减当()32,a ∈+∞时()0f a '>，()f a 单调递增所以当32a =时()f a 取得最小值，即四棱锥的侧面积最小此时3h =所以棱锥的高与底面边长的比为22，故A 正确，C 错误侧棱与底面所成的角为SAO ∠，由3h =，32a =可得3AO = 所以4SAO π∠=，故B 正确，D 错误故选：AB 【点睛】本题考查的知识点有空间几何体的体积和表面积、线面角及利用导数求最值，属于综合题.9．如图，正三棱柱11ABC A B C -中，11BC AB ⊥、点D 为AC 中点，点E 为四边形11BCC B 内（包含边界）的动点则以下结论正确的是（）A ．()1112DA A A B A BC =-+ B ．若//DE 平面11ABB A ，则动点E 2AC C ．异面直线AD 与1BC ，所成角的余弦值为66D ．若点E 到平面11ACC A 3EB ，则动点E 的轨迹为抛物线的一部分【答案】BCD 【分析】根据空间向量的加减法运算以及通过建立空间直角坐标系求解，逐项判断，进而可得到本题答案. 【详解】解析：对于选项A ，()1112AD A A B A BC =-+，选项A 错误；对于选项B ，过点D 作1AA 的平行线交11A C 于点1D ．以D 为坐标原点，1DA DB DD ,,分别为,,x y z 轴的正方向建立空间直角坐标系Oxyz ．设棱柱底面边长为a ，侧棱长为b ，则002a A ⎛⎫⎪⎝⎭,,，00B ⎛⎫ ⎪ ⎪⎝⎭,，10B b ⎛⎫ ⎪ ⎪⎝⎭,，102a C b ⎛⎫- ⎪⎝⎭,,，所以122a BC a b ⎛⎫=-- ⎪ ⎪⎝⎭,,，122a AB a b ⎛⎫=- ⎪ ⎪⎝⎭,,． ∵11BC AB ⊥，∴110BC AB ⋅=，即222022a a b ⎛⎫⎛⎫--+= ⎪ ⎪ ⎪⎝⎭⎝⎭，解得2b a =．因为//DE 平面11ABB A ，则动点E的轨迹的长度等于1BB =．选项B 正确．对于选项C ，在选项A 的基础上，002a A ⎛⎫⎪⎝⎭,,，00B ⎛⎫ ⎪ ⎪⎝⎭,，()0,0,0D ，1022a C a ⎛⎫- ⎪ ⎪⎝⎭,,，所以002a DA ⎛⎫= ⎪⎝⎭,,，1222a BC a ⎛⎫=- ⎪ ⎪⎝⎭,-,，因为2111cos ,||||aBC DA BC DA BC DA a ⎛⎫- ⎪⋅<>===1,BC DA 所成角C 正确．对于选项D，设点E 在底面ABC 的射影为1E ，作1E F 垂直于AC ，垂足为F ，若点E 到平面11ACC A 的距离等于2EB ，即有12E F EB =，又因为在1CE F ∆中，11E F C =，得1EB E C =，其中1E C 等于点E 到直线1CC 的距离，故点E 满足抛物线的定义，另外点E 为四边形11BCC B 内（包含边界）的动点，所以动点E 的轨迹为抛物线的一部分,故D 正确.故选：BCD 【点睛】本题主要考查立体几何与空间向量的综合应用问题，其中涉及到抛物线定义的应用.10．如图，1111ABCD A B C D -为正方体，下列结论中正确的是（）A ．11A C ⊥平面11BB D D B ．1BD ⊥平面1ACBC ．1BD 与底面11BCC B 2 D ．过点1A 与异面直线AD 与1CB 成60角的直线有2条【答案】ABD 【分析】由直线与平面垂直的判定判断A 与B ；求解1BD 与底面11BCC B 所成角的正切值判断C ；利用空间向量法可判断D ．【详解】对于A 选项，如图，在正方体1111ABCD A B C D -中，1BB ⊥平面1111D C B A ，11A C ⊂平面1111D C B A ，则111BB A C ⊥，由于四边形1111D C B A 为正方形，则1111AC B D ⊥， 1111BB B D B =，因此，11A C ⊥平面11BB D D ，故A 正确；对于B 选项，在正方体1111ABCD A B C D -中，1DD ⊥平面ABCD ，AC ⊂平面ABCD ，1AC DD ∴⊥，因为四边形ABCD 为正方形，所以，AC BD ⊥，1D DD BD =，AC ∴⊥平面11BB D D ， 1BD ⊂平面11BB D D ，1AC BD ∴⊥，同理可得11BD B C ⊥，1ACB C C =，1BD ∴⊥平面1ACB ，故B 正确；对于C 选项，由11C D ⊥平面11BCC B ，得11C BD ∠为1BD 与平面11BCC B 所成角，且111112tan 2C D C BD BC ∠==，故C 错误；对于D 选项，以点D 为坐标原点，DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系，设正方体的棱长为1，则()1,0,0A 、()0,0,0D 、()0,1,0C 、()11,1,1B ，()1,0,0DA =，()11,0,1CB =，设过点1A 且与直线DA 、1CB 所成角的直线的方向向量为()1,,m y z =，则221cos ,21DA m DA m DA my z ⋅<>===⋅++， 1122111cos ,221CB m zCB m CB my z ⋅+<>===⋅⋅++，整理可得2222341y z y z z ⎧+=⎨=++⎩，消去y 并整理得2210z z +-=，解得12z =-12z =-由已知可得3z ≤，所以，12z =-+22y =± 因此，过点1A 与异面直线AD 与1CB 成60角的直线有2条，D 选项正确. 故选：ABD. 【点睛】方法点睛：证明线面垂直的方法：一是线面垂直的判定定理；二是利用面面垂直的性质定理；三是平行线法（若两条平行线中一条垂直于这个平面，则另一条也垂直于这个平面），解题时，注意线线、线面与面面关系的相互转化；另外，在证明线线垂直时，要注意题中隐含的垂直关系，如等腰三角形的底边上的高、中线和顶角的角平分线三线合一、矩形的内角、直径所对的圆周角、菱形的对角线互相垂直、直角三角形（或给出线段长度，经计算满足勾股定理）、直角梯形等等．。

2023年高考数学总复习：立体几何及答案解析

又∵已知 E 为 PB 的中点，∴OE∥PD．
∵PD⊄平面 AEC，OE⊂平面 AEC，
∴PD∥平面 AEC．
解：（2）∵
⺁，
⺁，∴
⺁⺁．
又∵PD⊥底面 ABCD，∴ 三棱锥 െ
∵E 是 PB 的中点，∴ 三棱锥 െ
⺁三棱锥 െ
⺁⺁⺁⺁⺁
⺁．
⺁三棱锥 െ
⺁⺁．
2．如图，在四棱锥 P﹣ABCD 中，PA⊥平面 ABC，AD∥BC，∠ABC＝90°，AD＝2，⺁， BC＝6．（1）求证：平面 PBD⊥平面 PAC；（2）PA 长为何值时，直线 PC 与平面 PBD 所成角最大？并求此时该角的正弦值．
第1页共3页
【解答】（1）证明：∵PA⊥平面 ABCD，BD⊂平面 ABCD，∴BD⊥PA，
又㋨๗
，㋨๗
，
∴∠ABD＝30°，∠BAC＝60°，∴∠AEB＝90°，即 BD⊥AC（E 为 AC 与 BD 交点）．
又 PA∩AC，∴BD⊥平面 PAC
又因为 BD⊂平面 PBD，所以平面 PBD⊥平面 PAC．
则๗ ๗
，即 െ ⺁㌳⺁ െ⺁㌳ ൅
，取 x＝1，
⺁得平面 PBD 的一个法向量为๗ （1，，），
所以 cos＜，๗＞
๗
，
๗
쳌㌳⺁
㌳
⺁⺁
㌳⺁㌳⺁
因为㌳⺁㌳⺁
㌳⺁⺁⺁
，当且仅当 t＝2 时等号成立，
所以 cos＜，๗＞
，记直线 PC 与平面 PBD 所成角为θ，
则 sinθ＝|cos＜，๗＞|，故 t๗ ，
即⺁时，直线 PC 与平面 PBD 所成角最大，此时该角的正弦值为．

立体几何高考考点梳理及真题分类解析

第九章立体几何（2021年文科数学高考备考版）第一节空间几何体的三视图和直观图一、高考考点梳理（一）、空间几何体的结构特征1．多面体①棱柱：两个面互相平行，其余各面都是四边形，并且每相邻两个四边形的公共边都互相平行，这些面围成（一）、简单几何体的结构特征的几何体叫作棱柱．②棱锥：有一个面是多边形，其余各面是有一个公共顶点的三角形，这些面围成的几何体叫作棱锥．③棱台：用一个平行于棱锥底面的平面去截棱锥，底面与截面之间的部分叫作棱台．2．旋转体①圆锥可以由直角三角形绕其任一直角边旋转得到．②圆台可以由直角梯形绕直角腰或等腰梯形绕上下底中点连线旋转得到，也可由平行于圆锥底面的平面截圆锥得到．③球可以由半圆或圆绕直径旋转得到．（二）、三视图1．三视图的名称：几何体的三视图包括主视图、左视图、俯视图．2．三视图的画法①画三视图时，重叠的线只画一条，挡住的线要画成虚线．②三视图的主视图、左视图、俯视图分别是从几何体的正前方、正左方、正上方观察几何体得到的正投影图．③观察简单组合体是由哪几个简单几何体组成的，并注意它们的组成方式，特别是它们的交线位置．（三）、直观图简单几何体的直观图常用斜二测画法来画，其规则是：1．在已知图形中建立直角坐标系xOy.画直观图时，它们分别对应x′轴和y′轴，两轴交于点O′，使∠x′O′y′＝45°，它们确定的平面表示水平平面；2．已知图形中平行于x轴或y轴的线段，在直观图中分别画成平行于x′轴和y′轴的线段；3．已知图形中平行于x轴的线段，在直观图中保持原长度不变；平行于y轴的线段，长度为原来的1 2.二、历年高考真题题型分类突破题型一空间几何体的三视图【例1】（2020全国Ⅲ卷）右图为某几何体的三视图，则该几何体的表面积是（）A.B.C.D. D.解析：由三视图可知几何体的直观图如图：几何体是正方体的一个角，，、、两两垂直，故，几何体的表面积为：，故选：C．【例2】（2018全国Ⅰ卷）某圆柱的高为2，底面周长为16，其三视图如图．圆柱表面上的点M在正视图上的对应点为A，圆柱表面上的点N在左视图上的对应点为B，则在此圆柱侧面上，从M到N的路径中，最短路径的长度为（）A．217 B．2 5C．3 D．2解析：所求最短路径MN为四份之一圆柱侧面展开图对角线的长.故选B.【例3】（2017全国Ⅱ卷）如图,网格纸上小正方形的边长为1,粗实线画出的是某几何体的三视图,该几何体由一平面将一圆柱截去一部分后所得,则该几何体的体积为( )A .90πB .63πC .42πD .36π解析：由题意,该几何体是一个组合体,下半部分是一个底面半径为3,高为4的圆柱,其体积V 1＝π×32×4＝36π,上半部分是一个底面半径为3,高为6的圆柱的一半,其体积V 2＝12×(π×32×6)＝27π,∴该组合体的体积V ＝V 1＋V 2＝63π.故选B .题型二与球有关的几何体【例4】（2020全国Ⅰ卷）已知A ,B ,C 为球O 的球面上的三个点，⊙O 1为∆ABC 的外接圆，若⊙O 1的面积为4π，AB=BC=AC=OO 1，则球O 的表面积为( ) A ．64πB ．48πC ．36πD ．32π解析：设球O 半径为R ，⊙O 1的半径为r ，依题πr 2=4π，∴r =2。

2021年高考数学立体几何多选题之知识梳理与训练及解析

2021年高考数学立体几何多选题之知识梳理与训练及解析一、立体几何多选题1.如图，在棱长为2的正方体ABCD-A!B f C f D f中，M为边的中点，下列结论正确的有（）A. AM与所成角的余弦值为迈10B. 过三点A、M、D的正方体ABCD-A!B f C f D f的截而而积为乂2C. 四而体ACBD的内切球的表而积为冬3D. 正方体ABCD—A'B'C'D'中，点P在底而A'B'CQ'（所在的平而）上运动并且使ZMAC = APAC,那么点P的轨迹是椭圆【答案】AB【分析】由异而直线方向向量的夹角cos< AM.D f B r >=构建空间直角坐标系,AM与所成角的余弦值判断A的正误：同样设P（x,”0）结合向量夹角的坐标表示，>Jly + 2皿且由等角的余弦值相等可得~~；—厂=W，进而判断P的轨迹知D的正误；yjx~ + y + 4 X V3 、由立方体的截而为梯形，分别求MN,AD'、AMQN ,进而得到梯形的髙即可求面积，判断B的正误：由四面体的体枳与内切球半径及侧面而积的关系求内切球半径r,进而求内切球表而积，判断C的正误.【详解】A：构建如下图所示的空间直角坐标系：则有：A(0,0,2),M(122)&(020),D(2,0,0),・•・血=(12 0),血=(-2,2,0),； AM ・D'B' 2 y/10 .,.A ZDI AM II D f B f I V5x>/8 10B：若/V为CC‘的中点，连接M/V,则有MN//AD\如下图示,.・・梯形AMND^为过三点A、A/、D的正方体ABCD-AEC Q的截而，而MN = ^、AD = 2^、AM=D'N = £,可得梯形的髙为玄，2梯形的而积为S=lx3>/2x^=-,故正确.2 2 2c：如下图知：四而体ACBD的体积为正方体体积减去四个直棱锥的体积,I I Q _v =8-4x-x-x8 = -,而四而体的棱长都为2y/2 >有表面积为3 2 3S =4x —x2>/2 x2>/2 xsin — = 8>/3 ,2 3i o /T・•・若英内切圆半径为厂，则有-x8V3-r = -.即r =宜,所以内切球的表而积为3 3 3Arr4^r2 =—.故错误.D：正方体ABCD-A'B'CD'中，点P在底面AB'CD1 (所在的平而)上运动且ZMAC = APAC.即P的轨迹为而A'B'CQ截以AM. AP为母线，为轴的圆锥体侧而所得曲线，如下图曲线GPK,—,2),C f(O,2^.O),若P(x」,0),则构建如下空间直角坐标系，A(0,0,2),M(-2 2丽=(—拿芈0), AC； = (0,2>/2, -2), AP = (x, ” -2),刁一… 丽疋6 V15/. coszMAC =. ― = —— = ------ ,I AM II AC I V5xV12 5 cosZPACJ兰竺=I APII AC'I(y +10^)2 -9x 2 = 216(y > 0),即轨迹为双曲线的一支，故错误.故选：AB 【点睛］关键点点睛：应用向量的坐标表示求异而直线的夹角，并结合等角的余弦值相等及向疑数虽:积的坐标表示求动点的轨迹，综合立方体的性质求截而而积，分割几何体应用等体积法求内切球半径，进而求内切球的表面积.2・已知正方体ABCD-A^C }D }的棱长为2,点E ，F 在平面AdG 。

2020—2021年新高考总复习数学(理)二轮复习精选《空间几何体》试题及答案解析.docx

高三数学二轮复习精选专题练（理科，有解析）空间几何体1、已知某个几何体的三视图如图(主视图中的弧线是半圆),根据图中标出的尺寸,可得这个几何体的体积是 ( )A.8π+B.283π+C.12π+D.2123π+【答案】A2、在直角坐标系xOy 中，设(2,2),(2,3)A B --，沿y 轴把坐标平面折成120o的二面角后，AB 的长是（）37 B. 6 C. 35 53 【答案】A【解析】做AC 垂直y 轴于点C,BD 垂直y 轴于点D ，BM 平行于y 轴，且NC 垂直Y 轴，则0=120ACM ∠，又AC=MC=2，所以由余弦定理得AM=23,在ABM ∆，0=9023,537BMA AM BM AB ∠===，，所以.即AB 的长是37.3、已知某个几何体的三视图如下,根据图中标出的尺寸（单位：cm ）.可得这个几何体的体积是（）A.133cmB.233cmC.433cmD.833cm【答案】C4、已知某几何体的三视图如图所示，其中正视图中半圆的直径为2，则该几何体的体积为（）A.243π- B.242π- C.3242π- D.24π-【答案】C5、如图,某几何体的正视图和俯视图都是矩形,侧视图是等腰直角三角形,则该几何体的体积为()A.163B.8C.16D. 83【答案】B6、平面四边形ABCD 中,1===CD AD AB ,CD BD BD ⊥=,2,将其沿对角线BD 折成四面体BCD A -',使平面⊥BD A '平面BCD ,若四面体BCD A -'顶点在同一个球面上,则该球的体积为( ) A. π23 B. π3 C. π32 D. π2【答案】ABD 所在的圆直径就是BD,BDC 所在的圆直径是BC,由题意两个圆面垂直,且ABD 所在的圆面被BDC 所在的圆平分,所以BDC 所在的圆就是大圆;球的直径就是BC 3,所以正确的选项是A.7、设集合P={直四棱柱}，Q={正四棱柱}，S={长方体}，则（）A ．()S Q P =UB ．()P Q S ⊆IC ．()P S Q⊆I D ．()P Q S ⊆U 【答案】B【解析】底面为正方形的直四棱柱是长方体的一种，所以正确选项为B.8、半径为R 的半圆卷成一个圆锥，则它的体积为（） 3324R πB 338R πC 3524R πD 358R π【答案】A设圆锥底面圆的半径为r ，高为h ，则2πr=πR ，∴r=2R ∵R 2=r 2+h 2，∴h=32R ，∴V=213()322R R π=3324R π，故选A 。

专题05 立体几何专项高考真题总汇(带答案与解析)

专题05立体几何（选择题、填空题）1．【2021·浙江高考真题】某几何体的三视图如图所示，则该几何体的体积是（）A ．32B ．3C．2D．【答案】A【分析】根据三视图可得如图所示的几何体，根据棱柱的体积公式可求其体积.【解析】几何体为如图所示的四棱柱1111ABCD A B C D -，其高为1，底面为等腰梯形ABCD ，，下底为12=，故1111131222ABCD A B C D V -=⨯+⨯⨯=，故选：A.2．【2021·北京高考真题】某四面体的三视图如图所示，该四面体的表面积为（）A ．332+B ．4C ．33D ．2【答案】A【分析】根据三视图可得如图所示的几何体（三棱锥），根据三视图中的数据可计算该几何体的表面积.【解析】根据三视图可得如图所示的几何体-正三棱锥O ABC -，其侧面为等腰直角三角形，底面等边三角形，由三视图可得该正三棱锥的侧棱长为1，故其表面积为213333112242+⨯⨯⨯+⨯=，故选：A.3．【2021·浙江高考真题】如图已知正方体1111ABCD A B C D -，M ，N 分别是1A D ，1D B 的中点，则（）A ．直线1A D 与直线1DB 垂直，直线//MN 平面ABCD B ．直线1A D 与直线1D B 平行，直线MN ⊥平面11BDD BC ．直线1AD 与直线1D B 相交，直线//MN 平面ABCD D ．直线1A D 与直线1D B 异面，直线MN ⊥平面11BDD B 【答案】A【分析】由正方体间的垂直、平行关系，可证1//,MN AB A D ⊥平面1ABD ，即可得出结论.【解析】连1AD ，在正方体1111ABCD A B C D -中，M 是1A D 的中点，所以M 为1AD 中点，又N 是1D B 的中点，所以//MN AB ，MN ⊄平面,ABCD AB ⊂平面ABCD ，所以//MN 平面ABCD .因为AB 不垂直BD ，所以MN 不垂直BD 则MN 不垂直平面11BDD B ，所以选项B,D 不正确；在正方体1111ABCD A B C D -中，11AD A D ⊥，AB ⊥平面11AA D D ，所以1AB A D ⊥，1AD AB A ⋂=，所以1A D ⊥平面1ABD ，1D B ⊂平面1ABD ，所以11A D D B ⊥，且直线11,A D D B 是异面直线，所以选项B 错误，选项A 正确.故选：A.【点睛】关键点点睛：熟练掌握正方体中的垂直、平行关系是解题的关键，如两条棱平行或垂直，同一个面对角线互相垂直，正方体的对角线与面的对角线是相交但不垂直或异面垂直关系.4．【2021·全国高考真题（理）】已如A ，B ，C 是半径为1的球O 的球面上的三个点，且,1AC BC AC BC ⊥==，则三棱锥O ABC -的体积为（）A ．212B ．312C ．24D ．34【答案】A【分析】由题可得ABC 为等腰直角三角形，得出ABC 外接圆的半径，则可求得O 到平面ABC 的距离，进而求得体积.【解析】,1AC BC AC BC ⊥== ，ABC ∴ 为等腰直角三角形，AB ∴=，则ABC 外接圆的半径为22，又球的半径为1，设O 到平面ABC 的距离为d ，则2d ==，所以1112211332212O ABC ABC V S d -=⋅=⨯⨯⨯⨯=.故选：A.【点睛】关键点睛：本题考查球内几何体问题，解题的关键是正确利用截面圆半径、球半径、球心到截面距离的勾股关系求解.5．【2021·全国高考真题（理）】在正方体1111ABCD A B C D -中，P 为11B D 的中点，则直线PB 与1AD 所成的角为（）A ．π2B ．π3C ．π4D ．π6【答案】D【分析】平移直线1AD 至1BC ，将直线PB 与1AD 所成的角转化为PB 与1BC 所成的角，解三角形即可.【解析】如图，连接11,,BC PC PB ，因为1AD ∥1BC ，所以1PBC ∠或其补角为直线PB 与1AD 所成的角，因为1BB ⊥平面1111D C B A ，所以11BB PC ⊥，又111PC B D ⊥，1111BB B D B ⋂=，所以1PC ⊥平面1P B B ，所以1PC PB ⊥，设正方体棱长为2，则111112BC PC D B ===1111sin 2PC PBC BC ∠==，所以16PBC π∠=.故选：D6．【2021·全国高考真题】已知圆锥的底面半径为，其侧面展开图为一个半圆，则该圆锥的母线长为（）A ．2B．C ．4D．【答案】B【分析】设圆锥的母线长为l ，根据圆锥底面圆的周长等于扇形的弧长可求得l 的值，即为所求.【解析】设圆锥的母线长为l，由于圆锥底面圆的周长等于扇形的弧长，则2l ππ=解得l =.故选：B.7．【2021·北京高考真题】定义：24小时内降水在平地上积水厚度（mm ）来判断降雨程度．其中小雨（10mm <），中雨（10mm 25mm -），大雨（25mm 50mm -），暴雨（50mm 100mm -），小明用一个圆锥形容器接了24小时的雨水，如图，则这天降雨属于哪个等级（）A ．小雨B ．中雨C ．大雨D ．暴雨【答案】B【分析】计算出圆锥体积，除以圆面的面积即可得降雨量，即可得解.【解析】由题意，一个半径为()200100mm 2=的圆面内的降雨充满一个底面半径为()20015050mm 2300⨯=，高为()150mm 的圆锥，所以积水厚度()22150150312.5mm 100d ππ⨯⨯==⨯，属于中雨.故选：B.8．【2021·全国高考真题】在正三棱柱111ABC A B C -中，11AB AA ==，点P 满足1BP BC BB λμ=+，其中[]0,1λ∈，[]0,1μ∈，则（）A ．当1λ=时，1AB P △的周长为定值B ．当1μ=时，三棱锥1P A BC -的体积为定值C ．当12λ=时，有且仅有一个点P ，使得1A P BP ⊥D ．当12μ=时，有且仅有一个点P ，使得1A B ⊥平面1AB P 【答案】BD【分析】对于A ，由于等价向量关系，联系到一个三角形内，进而确定点的坐标；对于B ，将P 点的运动轨迹考虑到一个三角形内，确定路线，进而考虑体积是否为定值；对于C ，考虑借助向量的平移将P 点轨迹确定，进而考虑建立合适的直角坐标系来求解P 点的个数；对于D ，考虑借助向量的平移将P 点轨迹确定，进而考虑建立合适的直角坐标系来求解P 点的个数．【解析】易知，点P 在矩形11BCC B 内部（含边界）．对于A ，当1λ=时，11=BP BC BB BC CC μμ=++，即此时P ∈线段1CC ，1AB P △周长不是定值，故A 错误；对于B ，当1μ=时，1111=BP BC BB BB B C λλ=++，故此时P 点轨迹为线段11B C ，而11//B C BC ，11//B C 平面1A BC ，则有P 到平面1A BC 的距离为定值，所以其体积为定值，故B 正确．对于C ，当12λ=时，112BP BC BB μ=+，取BC ，11B C 中点分别为Q ，H ，则BP BQ QH μ=+，所以P 点轨迹为线段QH ，不妨建系解决，建立空间直角坐标系如图，13,0,12A ⎛⎫ ⎪ ⎪⎝⎭，()0,0P μ,，10,,02B ⎛⎫⎪⎝⎭，则13,0,12A P μ⎛⎫=-- ⎪ ⎪⎝⎭，10,,2BP μ⎛⎫=- ⎪⎝⎭ ，()110A P BP μμ⋅=-=，所以0μ=或1μ=．故,H Q 均满足，故C 错误；对于D ，当12μ=时，112BP BC BB λ=+ ，取1BB ，1CC 中点为,M N ．BP BM MN λ=+ ，所以P 点轨迹为线段MN ．设010,,2P y ⎛⎫ ⎪⎝⎭，因为0,02A ⎛⎫ ⎪ ⎪⎝⎭，所以01,22AP y ⎛⎫= ⎪ ⎪⎝⎭，11,,122A B ⎛⎫=-- ⎪ ⎪⎝⎭，所以00311104222y y +-=⇒=-，此时P 与N 重合，故D 正确．故选：BD ．【点睛】本题主要考查向量的等价替换，关键之处在于所求点的坐标放在三角形内．9．【2021·全国高考真题（理）】以图①为正视图，在图②③④⑤中选两个分别作为侧视图和俯视图，组成某三棱锥的三视图，则所选侧视图和俯视图的编号依次为_________（写出符合要求的一组答案即可）．【答案】③④（答案不唯一）【分析】由题意结合所给的图形确定一组三视图的组合即可.【解析】选择侧视图为③，俯视图为④，如图所示，长方体1111ABCD A B C D -中，12,1AB BC BB ===，,E F 分别为棱11,BC BC 的中点，则正视图①，侧视图③，俯视图④对应的几何体为三棱锥E ADF -.故答案为：③④.【点睛】三视图问题解决的关键之处是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系.10．【2020年高考全国Ⅰ卷理数】埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥.以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为A ．514-B ．512-C ．514D ．512+【答案】C【解析】如图，设,CD a PE b ==，则22224a PO PE OEb =-=-由题意得212PO ab =，即22142a b ab-=，化简得24()210b b a a -⋅-=，解得14b a +=（负值舍去）.故选C ．【点晴】本题主要考查正四棱锥的概念及其有关计算，考查学生的数学计算能力，是一道容易题.11．【2020年高考全国Ⅱ卷理数】如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M ，在俯视图中对应的点为N ，则该端点在侧视图中对应的点为A ．EB ．FC ．GD ．H【答案】A【解析】根据三视图，画出多面体立体图形，14D D 上的点在正视图中都对应点M ,直线34B C 上的点在俯视图中对应的点为N,∴在正视图中对应M ,在俯视图中对应N 的点是4D ,线段34D D ,上的所有点在侧试图中都对应E ,∴点4D 在侧视图中对应的点为E .故选A.【点睛】本题主要考查了根据三视图判断点的位置，解题关键是掌握三视图的基础知识和根据三视图能还原立体图形的方法，考查了分析能力和空间想象，属于基础题.12．【2020年高考全国II 卷理数】已知△ABC 是面积为934O 的球面上.若球O 的表面积为16π，则O 到平面ABC 的距离为A 3B ．32C ．1D ．32【答案】C【解析】设球O 的半径为R ，则2416R π=π，解得：2R =.设ABC △外接圆半径为r ，边长为a ，ABC △是面积为934的等边三角形，21393224a ∴⨯=，解得：3a =，22229933434a r a ∴=-=⨯-，∴球心O 到平面ABC 的距离22431d R r =-=-=.故选：C ．【点睛】本题考查球的相关问题的求解，涉及到球的表面积公式和三角形面积公式的应用；解题关键是明确球的性质，即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.13．【2020年高考全国Ⅲ卷理数】如图为某几何体的三视图，则该几何体的表面积是A ．2B ．4+42C ．3D ．4+23【答案】C 【解析】根据三视图特征，在正方体中截取出符合题意的立体图形根据立体图形可得：12222ABC ADC CDB S S S ===⨯⨯=△△△根据勾股定理可得：22AB AD DB ===∴ADB △是边长为的等边三角形根据三角形面积公式可得：2113sin 60222ADB S AB AD =⋅⋅︒=⋅=△∴该几何体的表面积是：632=⨯++.故选：C ．【点睛】本题主要考查了根据三视图求立体图形的表面积问题，解题关键是掌握根据三视图画出立体图形，考查了分析能力和空间想象能力，属于基础题.14．【2020年高考全国Ⅰ卷理数】已知,,A B C 为球O 的球面上的三个点，⊙1O 为ABC △的外接圆，若⊙1O 的面积为4π，1AB BC AC OO ===，则球O 的表面积为A ．64πB ．48πC ．36πD ．32π【答案】A【解析】设圆1O 半径为r ，球的半径为R ，依题意，得24,2r r π=π=∴， ABC 为等边三角形，由正弦定理可得2sin 60AB r =︒=，1OO AB ∴==，根据球的截面性质1OO ⊥平面ABC ，11,4OO O A R OA ∴⊥====，∴球O 的表面积2464S R ππ==.故选：A.【点睛】本题考查球的表面积，应用球的截面性质是解题的关键，考查计算求解能力，属于基础题.15．【2020年高考天津】若棱长为为A ．12πB ．24πC ．36πD ．144π【答案】C【解析】这个球是正方体的外接球，其半径等于正方体的体对角线的一半，即3R ==，所以，这个球的表面积为2244336S R πππ==⨯=.故选：C ．【点睛】本题考查正方体的外接球的表面积的求法，求出外接球的半径是本题的解题关键，属于基础题.求多面体的外接球的面积和体积问题，常用方法有：（1）三条棱两两互相垂直时，可恢复为长方体，利用长方体的体对角线为外接球的直径，求出球的半径；（2）直棱柱的外接球可利用棱柱的上下底面平行，借助球的对称性，球心为上下底面外接圆的圆心连线的中点，再根据勾股定理求球的半径；（3）如果设计几何体有两个面相交，可过两个面的外心分别作两个面的垂线，垂线的交点为几何体的球心.16．【2020年高考北京】某三棱柱的底面为正三角形，其三视图如图所示，该三棱柱的表面积为A ．6+B ．6+C ．12+D ．12+【答案】D 【解析】由题意可得，三棱柱的上下底面为边长为2的等边三角形，侧面为三个边长为2的正方形，则其表面积为：()1322222sin 60122S ⎛⎫=⨯⨯+⨯⨯⨯⨯︒=+⎪⎝⎭故选：D ．【点睛】(1)以三视图为载体考查几何体的表面积，关键是能够对给出的三视图进行恰当的分析，从三视图中发现几何体中各元素间的位置关系及数量关系．(2)多面体的表面积是各个面的面积之和；组合体的表面积应注意重合部分的处理．(3)圆柱、圆锥、圆台的侧面是曲面，计算侧面积时需要将这个曲面展为平面图形计算，而表面积是侧面积与底面圆的面积之和．17．【2020年高考浙江】某几何体的三视图（单位：cm ）如图所示，则该几何体的体积（单位：cm 3）是A ．73B ．143C ．3D ．6【答案】A 【解析】由三视图可知，该几何体是上半部分是三棱锥，下半部分是三棱柱，且三棱锥的一个侧面垂直于底面，且棱锥的高为1，棱柱的底面为等腰直角三角形，棱柱的高为2，所以几何体的体积为11117211212232233⎛⎫⎛⎫⨯⨯⨯⨯+⨯⨯⨯=+=⎪ ⎪⎝⎭⎝⎭.故选：A【点睛】本小题主要考查根据三视图计算几何体的体积，属于基础题.18．【2020年高考浙江】已知空间中不过同一点的三条直线l ，m ，n ．“l ，m ，n 共面”是“l ，m ，n 两两相交”的A ．充分不必要条件B ．必要不充分条件C ．充分必要条件D ．既不充分也不必要条件【答案】B【解析】依题意,,m n l 是空间不过同一点的三条直线，当,,m n l 在同一平面时，可能////m n l ，故不能得出,,m n l 两两相交.当,,m n l 两两相交时，设,,m n A m l B n l C ⋂=⋂=⋂=，根据公理2可知,m n 确定一个平面α，而,B m C n αα∈⊂∈⊂，根据公理1可知，直线BC 即l α⊂，所以,,m n l 在同一平面.综上所述，“,,m n l 在同一平面”是“,,m n l 两两相交”的必要不充分条件.故选：B【点睛】本小题主要考查充分、必要条件的判断，考查公理1和公理2的运用，属于中档题.19．【2020年新高考全国Ⅰ卷】日晷是中国古代用来测定时间的仪器，利用与晷面垂直的晷针投射到晷面的影子来测定时间．把地球看成一个球(球心记为O )，地球上一点A 的纬度是指OA 与地球赤道所在平面所成角，点A 处的水平面是指过点A 且与OA 垂直的平面.在点A 处放置一个日晷，若晷面与赤道所在平面平行，点A 处的纬度为北纬40°，则晷针与点A 处的水平面所成角为A ．20°B ．40°C ．50°D ．90°【答案】B 【解析】画出截面图如下图所示，其中CD 是赤道所在平面的截线；l 是点A 处的水平面的截线，依题意可知OA l ⊥；AB 是晷针所在直线.m 是晷面的截线，依题意依题意,晷面和赤道平面平行，晷针与晷面垂直，根据平面平行的性质定理可得可知//m CD 、根据线面垂直的定义可得AB m ⊥..由于40,//AOC m CD ∠=︒，所以40OAG AOC ∠=∠=︒，由于90OAG GAE BAE GAE ∠+∠=∠+∠=︒，所以40BAE OAG ∠=∠=︒，也即晷针与点A 处的水平面所成角为40BAE ∠=︒.故选：B.【点睛】本小题主要考查中国古代数学文化，考查球体有关计算，涉及平面平行，线面垂直的性质，属于中档题.20．【2019年高考全国Ⅰ卷理数】已知三棱锥P −ABC 的四个顶点在球O 的球面上，PA =PB =PC ，△ABC 是边长为2的正三角形，E ，F 分别是PA ，AB 的中点，∠CEF =90°，则球O 的体积为A ．B ．C ．D 【答案】D【解析】解法一：,PA PB PC ABC == △为边长为2的等边三角形，P ABC ∴-为正三棱锥，PB AC ∴⊥，又E ，F 分别为PA ，AB 的中点，EF PB ∴∥，EF AC ∴⊥，又EF CE ⊥，,CE AC C EF =∴⊥ 平面PAC ，∴PB ⊥平面PAC ，APB PA PB PC ∴∠=90︒,∴===，P ABC ∴-为正方体的一部分，2R ==364466,π2338R V R =∴=π=⨯=，故选D ．解法二：设2PA PB PC x ===，,E F 分别为,PA AB 的中点，EF PB ∴∥，且12EF PB x ==，ABC △为边长为2的等边三角形，CF ∴=又90CEF ∠=︒，12CE AE PA x ∴===，AEC △中，由余弦定理可得()2243cos 22x x EAC x +--∠=⨯⨯，作PD AC ⊥于D ，PA PC = ，D \为AC 的中点，1cos 2AD EAC PA x ∠==，2243142x x x x+-+∴=，221221222x x x ∴+=∴==，，，PA PB PC ∴===，又===2AB BC AC ，,,PA PB PC ∴两两垂直，2R ∴==，62R ∴=，34466338V R ∴=π=π⨯=，故选D.【名师点睛】本题主要考查学生的空间想象能力，补体法解决外接球问题．可通过线面垂直定理，得到三棱两两互相垂直关系，快速得到侧棱长，进而补体成正方体解决．21．【2019年高考全国Ⅱ卷理数】设α，β为两个平面，则α∥β的充要条件是A ．α内有无数条直线与β平行B ．α内有两条相交直线与β平行C ．α，β平行于同一条直线D ．α，β垂直于同一平面【答案】B【解析】由面面平行的判定定理知：α内两条相交直线都与β平行是αβ∥的充分条件，由面面平行性质定理知，若αβ∥，则α内任意一条直线都与β平行，所以α内两条相交直线都与β平行是αβ∥的必要条件，故选B ．【名师点睛】本题考查了空间两个平面的判定与性质及充要条件，渗透直观想象、逻辑推理素养，利用面面平行的判定定理与性质定理即可作出判断．面面平行的判定问题要紧扣面面平行判定定理，最容易犯的错误为定理记不住，凭主观臆断，如：“若,,a b a b αβ⊂⊂∥，则αβ∥”此类的错误．22．【2019年高考全国Ⅲ卷理数】如图，点N 为正方形ABCD 的中心，△ECD 为正三角形，平面ECD ⊥平面ABCD ，M 是线段ED 的中点，则A ．BM =EN ，且直线BM ，EN 是相交直线B ．BM ≠EN ，且直线BM ，EN 是相交直线C ．BM =EN ，且直线BM ，EN 是异面直线D ．BM ≠EN ，且直线BM ，EN 是异面直线【答案】B【解析】如图所示，作EO CD ⊥于O ，连接ON ，BD ，易得直线BM ，EN 是三角形EBD 的中线，是相交直线.过M 作MF OD ⊥于F ，连接BF ，平面CDE ⊥平面ABCD ，,EO CD EO ⊥⊂平面CDE ，EO ∴⊥平面ABCD ，MF ⊥平面ABCD ，MFB ∴△与EON △均为直角三角形．设正方形边长为2，易知12EO ON EN ===,，5,,22MF BF BM ==∴=BM EN ∴≠，故选B ．【名师点睛】本题考查空间想象能力和计算能力，解答本题的关键是构造直角三角形.解答本题时，先利用垂直关系，再结合勾股定理进而解决问题．23．【2019年高考浙江卷】祖暅是我国南北朝时代的伟大科学家，他提出的“幂势既同，则积不容异”称为祖暅原理，利用该原理可以得到柱体的体积公式V柱体=Sh，其中S是柱体的底面积，h是柱体的高．若某柱体的三视图如图所示（单位：cm），则该柱体的体积（单位：cm3）是A．158B．162C．182D．324【答案】B【解析】由三视图得该棱柱的高为6，底面可以看作是由两个直角梯形组合而成的，其中一个上底为4，下底为6，高为3，另一个的上底为2，下底为6，高为3，则该棱柱的体积为2646336162 22++⎛⎫⨯+⨯⨯=⎪⎝⎭.故选B.【名师点睛】本题首先根据三视图，还原得到几何体——棱柱，根据题目给定的数据，计算几何体的体积，常规题目.难度不大，注重了基础知识、视图用图能力、基本计算能力的考查.易错点有二，一是不能正确还原几何体；二是计算体积有误.为避免出错，应注重多观察、细心算.24．【2019年高考浙江卷】设三棱锥V–ABC的底面是正三角形，侧棱长均相等，P是棱VA 上的点（不含端点）．记直线PB与直线AC所成的角为α，直线PB与平面ABC所成的角为β，二面角P–AC–B的平面角为γ，则A．β<γ，α<γB．β<α，β<γC．β<α，γ<αD．α<β，γ<β【答案】B【解析】如图，G 为AC 中点，连接VG ，V 在底面ABC 的投影为O ，则P 在底面的投影D 在线段AO 上，过D 作DE 垂直于AC 于E ，连接PE ，BD ，易得PE VG ∥，过P 作PF AC ∥交VG 于F ，连接BF ，过D 作DH AC ∥，交BG 于H ，则,,BPF PBD PED αβγ=∠=∠=∠，结合△PFB ，△BDH ，△PDB 均为直角三角形，可得cos cos PF EG DH BD PB PB PB PB αβ===<=，即αβ>；在Rt △PED 中，tan tan PD PD ED BD γβ=>=，即γβ>，综上所述，答案为B.【名师点睛】本题以三棱锥为载体，综合考查异面直线所成的角、直线与平面所成的角、二面角的概念，以及各种角的计算.解答的基本方法是通过明确各种角，应用三角函数知识求解，而后比较大小.而充分利用图形特征，则可事倍功半.常规解法下易出现的错误有，不能正确作图得出各种角，未能想到利用“特殊位置法”，寻求简便解法.25．【2020年高考全国Ⅱ卷理数】设有下列四个命题：p 1：两两相交且不过同一点的三条直线必在同一平面内．p 2：过空间中任意三点有且仅有一个平面．p 3：若空间两条直线不相交，则这两条直线平行．p 4：若直线l ⊂平面α，直线m ⊥平面α，则m ⊥l ．则下述命题中所有真命题的序号是__________．①14p p ∧②12p p ∧③23p p ⌝∨④34p p ⌝∨⌝【答案】①③④【解析】对于命题1p ，可设1l 与2l 相交，这两条直线确定的平面为α；若3l 与1l 相交，则交点A 在平面α内，同理，3l 与2l 的交点B 也在平面α内，所以，AB α⊂，即3l α⊂，命题1p 为真命题；对于命题2p ，若三点共线，则过这三个点的平面有无数个，命题2p 为假命题；对于命题3p ，空间中两条直线相交、平行或异面，命题3p 为假命题；对于命题4p ，若直线m ⊥平面α，则m 垂直于平面α内所有直线，直线l ⊂平面α，∴直线m ⊥直线l ，命题4p 为真命题.综上可知，，为真命题，，为假命题，14p p ∧为真命题，12p p ∧为假命题，23p p ⌝∨为真命题，34p p ⌝∨⌝为真命题.故答案为：①③④.【点睛】本题考查复合命题的真假，同时也考查了空间中线面关系有关命题真假的判断，考查推理能力，属于中等题.26．【2020年高考全国Ⅲ卷理数】已知圆锥的底面半径为1，母线长为3，则该圆锥内半径最大的球的体积为_________．【答案】23【解析】易知半径最大球为圆锥的内切球，球与圆锥内切时的轴截面如图所示，其中2,3BC AB AC ===，且点M 为BC 边上的中点，设内切圆的圆心为O ，由于223122AM =-=，故1222222S =⨯⨯=△ABC 设内切圆半径为r ，则：ABC AOB BOC AOC S S S S =++△△△△111222AB r BC r AC r =⨯⨯+⨯⨯+⨯⨯()1332222r =⨯++⨯=解得：22r =，其体积：34233V r =π=π.故答案为：23π.【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.27．【2020年高考浙江】已知圆锥的侧面积（单位：cm 2）为2π，且它的侧面展开图是一个半圆，则这个圆锥的底面半径（单位：cm ）是_______．【答案】1【解析】设圆锥底面半径为r ，母线长为l ，则21222r l r l ππππ⨯⨯=⎧⎪⎨⨯⨯=⨯⨯⨯⎪⎩，解得1,2r l ==.故答案为：1【点睛】本小题主要考查圆锥侧面展开图有关计算，属于基础题.28．【2020年高考江苏】如图，六角螺帽毛坯是由一个正六棱柱挖去一个圆柱所构成的．已知螺帽的底面正六边形边长为2cm ，高为2cm ，内孔半轻为0.5cm ，则此六角螺帽毛坯的体积是▲cm.【答案】2π【解析】正六棱柱体积为2624⨯⨯⨯，圆柱体积为21()222ππ⋅=，所求几何体体积为2π.故答案为：2π-【点睛】本题考查正六棱柱体积、圆柱体积，考查基本分析求解能力，属基础题.29．【2020年新高考全国Ⅰ卷】已知直四棱柱ABCD –A 1B 1C 1D 1的棱长均为2，∠BAD =60°．以1D 为球心，为半径的球面与侧面BCC 1B 1的交线长为________．【答案】22π.【解析】如图：取11B C 的中点为E ，1BB 的中点为F ，1CC 的中点为G ，因为BAD ∠=60°，直四棱柱1111ABCD A B C D -的棱长均为2，所以△111D B C 为等边三角形，所以1D E =111D E B C ⊥，又四棱柱1111ABCD A B C D -为直四棱柱，所以1BB ⊥平面1111D C B A ，所以111BB B C ⊥，因为1111BB B C B = ，所以1D E ⊥侧面11B C CB ，设P 为侧面11B C CB 与球面的交线上的点，则1D E EP ⊥，，1D E =，所以||EP ===，所以侧面11B C CB 与球面的交线上的点到E ，因为||||EF EG ==11B C CB 与球面的交线是扇形EFG 的弧 FG ，因为114B EF C EG π∠=∠=，所以2FEG π∠=，所以根据弧长公式可得 22FGπ==.故答案为：22π.【点睛】本题考查了直棱柱的结构特征，考查了直线与平面垂直的判定，考查了立体几何中的轨迹问题，考查了扇形中的弧长公式，属于中档题.30．【2019年高考全国Ⅲ卷理数】学生到工厂劳动实践，利用3D 打印技术制作模型.如图，该模型为长方体1111ABCD A B C D -挖去四棱锥O —EFGH 后所得的几何体，其中O 为长方体的中心，E ，F ，G ，H 分别为所在棱的中点，16cm 4cm AB =BC =, AA =，3D 打印所用原料密度为0.9g/cm 3，不考虑打印损耗，制作该模型所需原料的质量为___________g.【答案】118.8【解析】由题意得，214642312cm 2EFGH S =⨯-⨯⨯⨯=四边形，∵四棱锥O −EFGH 的高为3cm ，∴3112312cm 3O EFGH V -=⨯⨯=．又长方体1111ABCD A B C D -的体积为32466144cm V =⨯⨯=，所以该模型体积为3214412132cm O EFGH V V V -=-=-=，其质量为0.9132118.8g ⨯=．【名师点睛】本题考查几何体的体积问题，理解题中信息联系几何体的体积和质量关系，从而利用公式求解．根据题意可知模型的体积为长方体体积与四棱锥体积之差进而求得模型的体积，再求出模型的质量即可.31．【2019年高考北京卷理数】某几何体是由一个正方体去掉一个四棱柱所得，其三视图如图所示．如果网格纸上小正方形的边长为1，那么该几何体的体积为__________．【答案】40【解析】如图所示，在棱长为4的正方体中，三视图对应的几何体为正方体去掉棱柱1111MPD A NQC B -之后余下的几何体，则几何体的体积()3142424402V =-⨯+⨯⨯=.【名师点睛】本题首先根据三视图，还原得到几何体，再根据题目给定的数据，计算几何体的体积.属于中等题.(1)求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解；(2)若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解．32．【2019年高考北京卷理数】已知l ，m 是平面α外的两条不同直线．给出下列三个论断：①l ⊥m ；②m ∥α；③l ⊥α．以其中的两个论断作为条件，余下的一个论断作为结论，写出一个正确的命题：__________．【答案】如果l ⊥α，m ∥α，则l ⊥m .【解析】将所给论断，分别作为条件、结论，得到如下三个命题：（1）如果l ⊥α，m ∥α，则l ⊥m ，正确；（2）如果l ⊥α，l ⊥m ，则m ∥α，不正确，有可能m 在平面α内；（3）如果l ⊥m ，m ∥α，则l ⊥α，不正确，有可能l 与α斜交、l ∥α.故答案为：如果l ⊥α，m ∥α，则l ⊥m.【名师点睛】本题主要考查空间线面的位置关系、命题、逻辑推理能力及空间想象能力.将所给论断，分别作为条件、结论加以分析即可.33．【2019年高考天津卷理数】2的正方形，5若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，另一个底面的圆心为四棱锥底面的中心，则该圆柱的体积为_____________．【答案】π4【解析】由题意，的正方形，借助勾股定理，2=.若圆柱的一个底面的圆周经过四棱锥四条侧棱的中点，一个底面的圆心为四棱锥底面的中心，故圆柱的高为1，圆柱的底面半径为12，故圆柱的体积为21ππ124⎛⎫⨯⨯= ⎪⎝⎭.【名师点睛】根据棱锥的结构特点，确定所求的圆柱的高和底面半径.注意本题中圆柱的底面半径是棱锥底面对角线长度的一半、不是底边棱长的一半.34．【2019年高考江苏卷】如图，长方体1111ABCD A B C D -的体积是120，E 为1CC 的中点，则三棱锥E −BCD 的体积是▲.【答案】10【解析】因为长方体1111ABCD A B C D -的体积为120，所以1120AB BC CC ⋅⋅=，因为E 为1CC 的中点，所以112CE CC =，由长方体的性质知1CC ⊥底面ABCD ，所以CE 是三棱锥E BCD -的底面BCD 上的高，所以三棱锥E BCD -的体积1132V AB BC CE =⨯⋅⋅=111111201032212AB BC CC =⨯⋅⋅=⨯=.【名师点睛】本题蕴含“整体和局部”的对立统一规律.在几何体面积或体积的计算问题中，往往需要注意理清整体和局部的关系，灵活利用“割”与“补”的方法解题.由题意结合几何体的特征和所给几何体的性质可得三棱锥的体积.35．【2019年高考全国Ⅱ卷理数】中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图1）.半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美．图2是一个棱数为48的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为1．则该半正多面体共有________个面，其棱长为_________．（本题第一空2分，第二空3分．）【答案】261【解析】由图可知第一层（包括上底面）与第三层（包括下底面）各有9个面，计18个面，第二层共有8个面，所以该半正多面体共有18826+=个面．如图，设该半正多面体的棱长为x ，则AB BE x ==，延长CB 与FE 的延长线交于点G ，延长BC 交正方体的棱于H ，由半正多面体对称性可知，BGE △为等腰直角三角形，22,21)122BG GE CH x GH x x x ∴===∴=⨯+=+=，1x ∴=1．。

2021年高考数学立体几何多选题专项练习及解析

2021年高考数学立体几何多选题专项练习及解析一、立体几何多选题1．已知正方体1111 ABCD A B C D -的棱长为2，M 为1DD 的中点，N 为正方形ABCD 所在平面内一动点，则下列命题正确的有（）A ．若2MN =，则MN 的中点的轨迹所围成图形的面积为πB ．若N 到直线1BB 与直线DC 的距离相等，则N 的轨迹为抛物线C ．若1D N 与AB 所成的角为3π，则N 的轨迹为双曲线 D ．若MN 与平面ABCD 所成的角为3π，则N 的轨迹为椭圆【答案】BC 【分析】对于A ，连接MN ，ND ，DP ，得到直角MDN △，且P 为斜边MN 的中点，所以1PD =，进而得到P 点的轨迹为球面的一部分，即可判断选项A 错误；对于B ，可知1NB BB ⊥，即NB 是点N 到直线1BB 的距离，在平面ABCD 中，点N 到定点B 的距离与到定直线DC 的距离相等，利用抛物线定义知B 正确；对于C ，建立空间直角坐标系，设(,,0)N x y ，利用空间向量求夹角知122121cos3224D N AB y x y D N ABπ⋅===⨯++⋅，化简可知N 的轨迹为双曲线；对于D ，MN 与平面ABCD 所成的角为3MND π∠=，3ND =，可知N 的轨迹是以D 为圆心，33为半径的圆周；【详解】对于A ，如图所示，设P 为MN 的中点，连接MN ，ND ，DP ，由正方体性质知MDN △为直角三角形，且P 为MN 的中点，2MN =，根据直角三角形斜边上的中线为斜边的一半，知MDN △不管怎么变化，始终有1PD =，即P 点的轨迹与正方体的面围城的几何体是一个以D 为球心，1为半径的球的18，其面积214182S ππ=⨯⨯=，故A 错误；对于B ，由正方体性质知，1BB ⊥平面ABCD 由线面垂直的性质定理知1NB BB ⊥，即NB 是点N 到直线1BB 的距离，在平面ABCD 中，点N 到定点B 的距离与到定直线DC 的距离相等，所以点N 的轨迹是以点B 为焦点，直线DC 为准线的抛物线，故B 正确；对于C ，如图以D 为直角坐标系原点，建立空间直角坐标系，(,,0)N x y ，1(0,0,2)D ，(0,2,0)A ，(2,2,0)B ，则1(,,2)D N x y =-，(0,2,0)AB =，利用空间向量求夹角知122121cos3224D N AB y x y D N ABπ⋅===⨯++⋅，化简整理得：2234y x -=，即221443y x -=，所以N 的轨迹为双曲线，故C 正确；对于D ，由正方体性质知，MN 与平面ABCD 所成的角为MND ∠，即3MND π∠=，在直角MDN △中，3ND =，即N 的轨迹是以D 3D 错误；故选：BC 【点睛】关键点睛：本题考查立体几何与解析几何的综合，解题的关键是抓住解析几何几种特殊曲线的定义，考查学生的逻辑推理能力，转化与划归能力与运算求解能力，属于难题.2．如图，正方体1111ABCD A B C D -中的正四面体11A BDC -的棱长为2，则下列说法正确的是（）A ．异面直线1AB 与1AD 所成的角是3πB ．1BD ⊥平面11AC DC ．平面1ACB 截正四面体11A BDC -所得截面面积为3D ．正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23【答案】ABD 【分析】选项A ，利用正方体的结构特征找到异面直线所成的角；选项B ，根据正方体和正四面体的结构特征以及线面垂直的判定定理容易得证；选项C ，由图得平面1ACB 截正四面体11A BDC -所得截面面积为1ACB 面积的四分之一；选项D ，分别求出正方体的体对角线长和正四面体11A BDC -的高，然后判断数量关系即可得解. 【详解】A ：正方体1111ABCD ABCD -中，易知11//AD BC ，异面直线1A B 与1AD 所成的角即直线1A B 与1BC 所成的角，即11A BC ∠，11A BC 为等边三角形，113A BC π∠=，正确；B ：连接11B D ，1B B ⊥平面1111DC B A ，11A C ⊂平面1111D C B A ，即111AC B B ⊥，又1111AC B D ⊥，1111B B B D B ⋂=，有11A C ⊥平面11BDD B ，1BD ⊂平面11BDD B ，所以111BD AC ⊥，同理可证：11BD A D ⊥，1111AC A D A ⋂=，所以1BD ⊥平面11AC D ，正确；C ：易知平面1ACB 截正四面体11A BDC -所得截面面积为134ACB S=，错误；D ：易得正方体1111ABCD A B C D -()()()2222226++=2的正四面体11A BDC -22222262213⎛⎫--⨯ ⎪⎝⎭，故正四面体11A BDC -的高等于正方体1111ABCD A B C D -体对角线长的23，正确. 故选：ABD. 【点睛】关键点点睛：利用正方体的性质，找异面直线所成角的平面角求其大小，根据线面垂直的判定证明1BD ⊥平面11AC D ，由正四面体的性质，结合几何图形确定截面的面积，并求高，即可判断C 、D 的正误.3．在三棱柱111ABC A B C -中，ABC ∆是边长为23的等边三角形，侧棱长为43，则（）A ．直线1A C 与直线1BB 之间距离的最大值为3B ．若1A 在底面ABC 上的投影恰为ABC ∆的中心，则直线1AA 与底面所成角为60︒ C ．若三棱柱的侧棱垂直于底面，则异面直线AB 与1A C 所成的角为30D ．若三棱柱的侧棱垂直于底面，则其外接球表面积为64π 【答案】AD 【分析】建立空间直角坐标系，用向量法求解. 【详解】如图示，以A 为原点，AC 为y 轴正方向，Ax 为x 轴正方向，过A 点垂直于面ABC 的向上方向为z 轴正方向建系，则()()()0,0,0,3,0,0,23,0,A B C 设()()()100010001000,,,3,3,,,23,,A x y z B x y z C x y z ++所以()()()1000100011,23,,,,,3,3,0,AC x y z BB x y z A B =---== 对于A:设n 为直线1A C 与直线1BB 的公垂线的方向向量，则有：11·0·0AC n BB n ⎧=⎪⎨=⎪⎩，即()()000000230x x y y zzx x y y zz⎧-+--=⎪⎨++=⎪⎩解得：()00,0n z x=-设直线1A C与直线1BB之间距离为d，则220011222200009||||zA B nd dx zn x z==∴=++2209x d≥∴≤，即3d≤，故A正确；对于B：若1A在底面ABC上的投影恰为ABC∆的中心，则()11,3,211A底面法向量()()10,0,1,1,3,211m AA==，设直线1AA与底面所成角为θ，则：121133sin|cos,|6143AA nθ===⨯，故B错误；对于C：三棱柱的侧棱垂直于底面时，则()()()1110,0,43,3,3,43,0,23,43,A B C则()()13,3,0,0,23,43,AB AC==-设异面直线AB与1A C所成的角为θ，则1115cos|cos,|||||||23215AB ACAB ACAB ACθ====⨯,故C错误；对于D：若三棱柱的侧棱垂直于底面时，外接球的球心O为上下底面中心DD1连线的中点,所以外接球的半径()222324R=+=，所以2464S Rππ==.故D正确故选：AD【点睛】向量法解决立体几何问题的关键：(1)建立合适的坐标系；(2)把要用到的向量正确表示；(3)利用向量法证明或计算.4．如图，在棱长为2的正方体ABCD A B C D ''''-中，M 为BC 边的中点，下列结论正确的有（）A ．AM 与DB ''10 B ．过三点A 、M 、D 的正方体ABCD A BCD ''''-的截面面积为92C ．四面体A C BD ''的内切球的表面积为3π D ．正方体ABCD A B C D ''''-中，点P 在底面A B C D ''''（所在的平面）上运动并且使MAC PAC ''∠=∠，那么点P 的轨迹是椭圆【答案】AB 【分析】构建空间直角坐标系，由异面直线方向向量的夹角cos ,||||AM D B AM D B AM D B ''⋅''<>=''为AM 与D B ''所成角的余弦值判断A 的正误；同样设(,,0)P x y 结合向量夹角的坐标表示，22215543x y =++⨯P 的轨迹知D 的正误；由立方体的截面为梯形，分别求,,,MN AD AM D N ''，进而得到梯形的高即可求面积，判断B 的正误；由四面体的体积与内切球半径及侧面面积的关系求内切球半径r ，进而求内切球表面积，判断C 的正误. 【详解】A ：构建如下图所示的空间直角坐标系：则有：(0,0,2),(1,2,2),(0,2,0),(2,0,0)A M B D ''， ∴(1,2,0),(2,2,0)AM D B ''==-，10cos ,10||||58AM D B AM D B AM D B ''⋅''<>===''⨯，故正确.B ：若N 为CC '的中点，连接MN ，则有//MN AD '，如下图示，∴梯形AMND’为过三点A 、M 、D 的正方体ABCD A B C D ''''-的截面，而2,2,5MN AD AM D N ''====322， ∴梯形的面积为132932222S =⨯=，故正确. C ：如下图知：四面体A C BD ''的体积为正方体体积减去四个直棱锥的体积，∴118848323V =-⨯⨯⨯=，而四面体的棱长都为22，有表面积为142222sin 8323S π=⨯⨯⨯⨯=，∴若其内切圆半径为r ，则有188333r ⨯⋅=，即33r =，所以内切球的表面积为2443r ππ=.故错误. D ：正方体ABCD A B C D ''''-中，点P 在底面A B C D ''''（所在的平面）上运动且MAC PAC ''∠=∠，即P 的轨迹为面A B C D ''''截以AM 、AP 为母线，AC’为轴的圆锥体侧面所得曲线，如下图曲线GPK ，构建如下空间直角坐标系，232(0,0,2),(2),(0,22,0)22A M C '-，若(,,0)P x y ，则232(,,0),(0,22,2),(,,2)22AM AC AP x y '=-=-=-，∴15cos ||||512AMAC MAC AM AC '⋅'∠==='⨯，2222cos ||||43AP AC y PAC AP AC x y '⋅+'∠=='++⨯，即222215543y x y +=++⨯，整理得22(102)9216(0)y x y +-=>，即轨迹为双曲线的一支，故错误.故选：AB 【点睛】关键点点睛：应用向量的坐标表示求异面直线的夹角，并结合等角的余弦值相等及向量数量积的坐标表示求动点的轨迹，综合立方体的性质求截面面积，分割几何体应用等体积法求内切球半径，进而求内切球的表面积.5．如图，已知正方体1ABCD ABC D -的棱长为a ，E 是棱CD 上的动点.则下列结论中正确的有（）A ．11EB AD ⊥B ．二面角11E A B A --的大小为4π C ．三棱锥11A B D E -体积的最小值为313a D ．1//D E 平面11A B BA【答案】ABD 【分析】连接1A D 、1B C ，则易证1AD ⊥平面11A DCB ，1EB ⊂平面11A DCB ，则由线面垂直的性质定理可以判断选项A 正确；二面角11E A B A --的平面角为1DA A ∠，易知14DA A π∠=，则可判断选项B 正确；用等体积法，将求三棱锥11A B D E -的体积转化为求三棱锥11E AB D -的体积，当点E 与D 重合时，三棱锥11E AB D -的体积最小，此时的值为316a ，则选项C 错误；易知平面11//D DCC 平面11A B BA ，而1D E ⊂平面11D DCC ，则根据面面平行的性质定理可得1//D E 平面11A B BA ，可判断选项D 正确. 【详解】选项A ，连接1A D 、1B C ，则由正方体1ABCD ABC D -可知，11A D AD ⊥，111A B AD ⊥，1111A DA B A =，则1AD ⊥平面11A DCB ，又因为1EB ⊂平面11A DCB ，所以11EB AD ⊥，选项A 正确；选项B ，因为11//DE A B ，则二面角11E A B A --即为二面角11D A B A --，由正方体1ABCD ABC D -可知，11A B ⊥平面1DA A ，则1DA A ∠为二面角11D A B A --的平面角，且14DA A π∠=，所以选项B 正确；选项C ，设点E 到平面11AB D 的距离为d ，则11111113A B D E E AB D AB D V V S d --==⋅，连接1C D 、1C B ，易证平面1//BDC 平面11AB D ，则在棱CD 上，点D 到平面11AB D 的距离最短，即点E 与D 重合时，三棱锥11A B D E -的体积最小，由正方体1ABCD ABC D -知11A B ⊥平面1ADD ，所以1111123111113326D AB D B ADDADD a V V S A B a a --==⋅=⋅⋅=，则选项C 错误；选项D ，由正方体1ABCD ABC D -知，平面11//CC D D 平面11A B BA ，且1D E ⊂平面11CC D D ，则由面面平行的性质定理可知1//D E 平面11A B BA ，则选项D 正确. 故选：ABD. 【点睛】关键点点睛：本题对于选项C 的判断中，利用等体积法求三棱锥的体积是解题的关键.6．如图，正方体1111ABCD A B C D -的棱长为3，点E ，F 分别在1CC ，1BB 上，12C E EC →→=，12BF FB →→=.动点M 在侧面11ADD A 内(包含边界)运动，且满足直线//BM 平面1D EF ，则（）A ．过1D ，E ，F 的平面截正方体所得截面为等腰梯形B ．三棱锥1D EFM -的体积为定值C ．动点M 10D ．过B ，E ，M 的平面截正方体所得截面面积的最小值为10【答案】BCD 【分析】由题做出过1D ，E ，F 的平面截正方体所得截面为梯形1D EFN ，进而计算即可排除A 选项；根据//BM平面1D EF ，由等体积转化法得1111D EFM M D EF B D EF D BEFV V V V ----===即可得B 选项正确；取1AA 靠近1A 点的三等分点H ， 1DD 靠近D 点的三等分点I ，易知M 的轨迹为线段HI ，故C 选项正确；过M 点做BE 的平行线交1AA 于P ，交1DD 于O ，连接,BP OE ，易知过B ，E ，M 的平面截正方体所得截面即为平行四边形BPOE ，进而得当H 位于点I 时，截面面积最小，为四边形ABEI 的面积，且面积为S AB BE =⋅= 【详解】解：对于A 选项，如图，取BF 中点G ，连接1A G ，由点E ，F 分别在1CC ，1BB 上，12C E EC →→=，12BF FB →→=，故四边形11A D EG 为平行四边形，故11//AGD E ，由于在11A B G △，F 为1B G 中点，当N 为11A B 中点时，有11////NF A G D E ，故过1D ，E ，F 的平面截正方体所得截面为梯形1D EFN ，此时1D N ==，EF ==1D EFN 不是等腰梯形，故A 选项错误；对于B 选项，三棱锥1D EFM -的体积等于三棱锥1M D EF -的体积，由于//BM平面1D EF ，故三棱锥1M D EF -的体积等于三棱锥1B D EF -的体积，三棱锥1B D EF -的体积等于三棱锥1D BEF -的体积，而三棱锥1D BEF -的体积为定值，故B 选项正确；对于C 选项，取1AA 靠近1A 点的三等分点H ， 1DD 靠近D 点的三等分点I ，易知1////HB AG NF ，1//BI D F ，由于1,HI BI I NFD F F ==，故平面//BHI 平面1D EF ，故M 的轨迹为线段HI ，故C 选项正确；对于D 选项，过M 点做BE 的平行线交1AA 于P ，交1DD 于O ，连接,BP OE ，则过B ，E ，M 的平面截正方体所得截面即为平行四边形BPOE ，易知当H 位于点I 时，平行四边形BPOE 边BP 最小，且为AB ，此时截面平行四边形BPOE 的面积最小，为四边形ABEI 的面积，且面积为S AB BE =⋅=D 选项正确；故选：BCD【点睛】本题解题的关键在于根据题意，依次做出过1D ，E ，F 的平面截正方体所得截面为梯形1D EFN ，过B ，E ，M 的平面截正方体所得截面即为平行四边形BPOE ，进而讨论AD选项，通过//BM平面1D EF ，并结合等体积转化法得1111D EFM M D EF B D EF D BEF V V V V ----===知B 选项正确，通过构造面面平行得M 的轨迹为线段HI ，进而讨论C 选项，考查回归转化思想和空间思维能力，是中档题.7．在三棱锥M ABC -中，下列命题正确的是（）A ．若1233AD AB AC =+，则3BC BD = B ．若G 为ABC 的重心，则111333MG MA MB MC =++C ．若0MA BC ⋅=，0MC AB ⋅=，则0MB AC ⋅=D ．若三棱锥M ABC -的棱长都为2，P ，Q 分别为MA ，BC 中点，则2PQ = 【答案】BC 【分析】作出三棱锥M ABC -直观图，在每个三角形中利用向量的线性运算可得. 【详解】对于A ，由已知12322233AD AB AC AD AC AB AD AC AB AD =+⇒=+⇒-=-，即2CD DB =，则32BD BD DC BC =+=，故A 错误；对于B ，由G 为ABC 的重心，得0GA GB GC ++=，又MG MA AG =+，MG MB BG =+，MG MC CG =+，3MA MB MC MG ∴++=，即111333MG MA MB MC =++，故B 正确；对于C ，若0MA BC ⋅=，0MC AB ⋅=，则0MC MA BC AB ⋅+⋅=，即()00MA BC AC CB MA BC AC C MC C M B M C ⋅++=⇒⋅++⋅⋅=⋅()00MA BC A MC MC MC MC C BC MA BC AC ⋅⋅⋅⇒⋅+-=⇒-+=⋅()000MC M CA BC AC AC CB AC CB AC C MC ⇒+=⇒+=⇒+=⋅⋅⋅⋅⋅，即0MB AC ⋅=，故C 正确；对于D ，111()()222PQ MQ MP MB MC MA MB MC MA ∴=-=+-=+- ()21122PQ MB MC MA MB MC MA ∴=+-=+-，又()2222222MB MC MA MB MC MA MB MC MB MA MC MA+-=+++⋅-⋅-⋅2221112222222222228222=+++⨯⨯⨯-⨯⨯⨯-⨯⨯⨯=，1822PQ ∴==，故D 错误. 故选：BC 【点睛】关键点睛：本题考查向量的运算，用已知向量表示某一向量的三个关键点： (1)用已知向量来表示某一向量，一定要结合图形，以图形为指导是解题的关键．(2)要正确理解向量加法、减法与数乘运算的几何意义，如首尾相接的若干向量之和，等于由起始向量的始点指向末尾向量的终点的向量． (3)在立体几何中三角形法则、平行四边形法则仍然成立．8．在长方体1111ABCD A B C D -中，AB =12AD AA ==，P 、Q 、R 分别是AB 、1BB 、1A C 上的动点，下列结论正确的是（）A ．对于任意给定的点P ，存在点Q 使得1D P CQ ⊥B ．对于任意给定的点Q ，存在点R 使得1D R CQ ⊥C ．当1AR A C ⊥时，1ARD R ⊥D ．当113AC A R =时，1//D R 平面1BDC 【答案】ABCD 【分析】本题先建立空间直角坐标系，再运用空间向量在立体几何中的应用逐一判断即可. 【详解】如图所示，建立空间直角坐标系，设(2,,0)P a，0a ⎡∈⎣，(2,)Q b ，[]0,2b ∈，设11A R AC λ=，得到(22,,22)R λλ--，[]0,1λ∈. 1(2,,2)D P a =-，(2,0,)CQ b =，142D P CQ b ⋅=-，当2b =时，1D P CQ ⊥，A 正确；1(22,2)D R λλ=--，12(22)2D R CQ b λλ⋅=--，取22bλ=+时，1D R CQ ⊥，B 正确；1AR A C ⊥，则1(2,22)(2)412440AR AC λλλλλ⋅=--⋅--=+-+=，解得：15λ=，此时12282(,)(,)0555555AR D R ---⋅=⋅=，1AR D R ⊥，C 正确；113AC A R =，则44(,)333R，142(,)333D R =-，设平面1BDC 的法向量为(,,)n x y z =，则100n BD n DC ⎧⋅=⎪⎨⋅=⎪⎩，解得(3,n =-，故10n D R ⋅=，故1//D R 平面1BDC ，D 正确.故选：ABCD.【点睛】本题考查了空间向量在立体几何中的应用，是偏难题.9．已知正方体1111ABCD A B C D -棱长为2，如图，M 为1CC 上的动点，AM ⊥平面α.下面说法正确的是（）A ．直线AB 与平面α所成角的正弦值范围为32⎣⎦B ．点M 与点1C 重合时，平面α截正方体所得的截面，其面积越大，周长就越大 C ．点M 为1CC 的中点时，若平面α经过点B ，则平面α截正方体所得截面图形是等腰梯形D ．已知N 为1DD 中点，当AM MN +的和最小时，M 为1CC 的中点【答案】AC 【分析】以点D 为坐标原点，DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系D xyz -，利用空间向量法可判断A 选项的正误；证明出1AC ⊥平面1A BD ，分别取棱11A D 、11A B 、1BB 、BC 、CD 、1DD 的中点E 、F 、Q 、N 、G 、H ，比较1A BD 和六边形EFQNGH 的周长和面积的大小，可判断B 选项的正误；利用空间向量法找出平面α与棱11A D 、11A B 的交点E 、F ，判断四边形BDEF 的形状可判断C 选项的正误；将矩形11ACC A 与矩形11CC D D 延展为一个平面，利用A 、M 、N 三点共线得知AM MN +最短，利用平行线分线段成比例定理求得MC ，可判断D 选项的正误.【详解】对于A 选项，以点D 为坐标原点，DA 、DC 、1DD 所在直线分别为x 、y 、z 轴建立空间直角坐标系D xyz -，则点()2,0,0A 、()2,2,0B 、设点()()0,2,02M a a ≤≤，AM ⊥平面α，则AM 为平面α的一个法向量，且()2,2,AM a =-，()0,2,0AB =，2232cos ,288AB AMAB AM AB AM a a ⋅⎡<>===⎢⋅⨯++⎣⎦，所以，直线AB 与平面α所成角的正弦值范围为322⎣⎦，A 选项正确；对于B 选项，当M 与1CC 重合时，连接1A D 、BD 、1A B 、AC ，在正方体1111ABCD A B C D -中，1CC ⊥平面ABCD ，BD ⊂平面ABCD ，1BD CC ∴⊥，四边形ABCD 是正方形，则BD AC ⊥，1CC AC C =，BD ∴⊥平面1ACC ，1AC ⊂平面1ACC ，1AC BD ∴⊥，同理可证11AC A D ⊥， 1A D BD D ⋂=，1AC ∴⊥平面1A BD ，易知1A BD 是边长为22(12322234A BD S =⨯=△为22362=.设E 、F 、Q 、N 、G 、H 分别为棱11A D 、11A B 、1BB 、BC 、CD 、1DD 的中点，易知六边形EFQNGH 是边长为2的正六边形，且平面//EFQNGH 平面1A BD ，正六边形EFQNGH 的周长为62，面积为()236233⨯⨯=，则1A BD 的面积小于正六边形EFQNGH 的面积，它们的周长相等，B 选项错误；对于C 选项，设平面α交棱11A D 于点(),0,2E b ，点()0,2,1M ，()2,2,1AM =-，AM ⊥平面α，DE ⊂平面α，AM DE ∴⊥，即220AM DE b ⋅=-+=，得1b =，()1,0,2E ∴，所以，点E 为棱11A D 的中点，同理可知，点F 为棱11A B 的中点，则()2,1,2F ，()1,1,0EF =，而()2,2,0DB =，12EF DB ∴=，//EF DB ∴且EF DB ≠，由空间中两点间的距离公式可得2222015DE =++=()()()2222212205BF =-+-+-=，DE BF ∴=，所以，四边形BDEF 为等腰梯形，C 选项正确；对于D 选项，将矩形11ACC A 与矩形11CC D D 延展为一个平面，如下图所示：若AM MN +最短，则A 、M 、N 三点共线，11//CC DD ，2222222MC AC DN AD ∴===+， 11222MC CC =≠，所以，点M 不是棱1CC 的中点，D 选项错误.故选：AC. 【点睛】本题考查线面角正弦值的取值范围，同时也考查了平面截正方体的截面问题以及折线段长的最小值问题，考查空间想象能力与计算能力，属于难题.10．如果一个棱锥的底面是正方形，且顶点在底面内的射影是底面的中心，那么这样的棱锥叫正四棱锥．若一正四棱锥的体积为18，则该正四棱锥的侧面积最小时，以下结论正确的是（）．A ．棱的高与底边长的比为22B ．侧棱与底面所成的角为4π C 2 D ．侧棱与底面所成的角为3π 【答案】AB 【分析】设四棱锥S ABCD -的高为h ，底面边长为a ，由21183V a h ==得254h a=，然后可得侧242108a a+32a =时侧面积取得最小值，此时3h =，然后求出棱锥的高与底面边长的比和SAO ∠即可选出答案. 【详解】设四棱锥S ABCD -的高为h ，底面边长为a 可得21183V a h ==，即254h a= 所以其侧面积为2222244215410842244a a a h a a a⋅⋅+=+=+令()242108f a a a =+，则()23321084f a a a ⨯'=- 令()233210840f a a a ⨯'=-=得32a = 当(0,32a ∈时()0f a '<，()f a 单调递减当()32,a ∈+∞时()0f a '>，()f a 单调递增所以当32a =时()f a 取得最小值，即四棱锥的侧面积最小此时3h = 所以棱锥的高与底面边长的比为22，故A 正确，C 错误侧棱与底面所成的角为SAO ∠，由3h =，32a =可得3AO = 所以4SAO π∠=，故B 正确，D 错误故选：AB【点睛】本题考查的知识点有空间几何体的体积和表面积、线面角及利用导数求最值，属于综合题.。

2020年高考理科数学《立体几何》题型归纳与训练及答案解析

12020年高考理科数学《立体几何》题型归纳与训练【题型归纳】题型一线面平行的证明1例1如图，高为1的等腰梯形 ABCD 中，AM = CD = 3AB = 1•现将△AMD 沿MD 折起，使平面 AMD 丄平面 MBCD ，连接 AB , AC.试判断：在AB 边上是否存在点【解析】线面平行，可以线线平行或者面面平行推出。

此类题的难点就是如何构造辅助线。

构造完辅助线,证明过程只须注意规范的符号语言描述即可。

本题用到的是线线平行推出面面平行。

【易错点】不能正确地分析DN 与BN 的比例关系，导致结果错误。

【思维点拨】此类题有两大类方法: 1.构造线线平行，然后推出线面平行。

此类方法的辅助线的构造须要学生理解线面平行的判定定理与线面平行的性质之间的矛盾转化关系。

在此，我们需要借助倒推法进行分析。

首先，此类型题目大部分为证明题，结论必定是正确的，我们以此为前提可以得到线面平行。

再次由线面平行的性质可知，过已知直线的平面与已知平面的交线必定平行于该直线，而交线就是我们要找的线，从而做出辅助线。

从这个角度上看我们可以看出线线平行推线面平行的本质就是过已知直线做一个平面与已知平面相交即可。

如本题中即是过AD 做了一个平面ADB与平面MPC 相交于线PN 。

最后我们只须严格使用正确的符号语言将证明过程反向写一遍即可。

即先证1【答案】当AP = 3AB 时，有AD //平面MPC. 理由如下：连接BD 交MC 于点N ，连接NP.在梯形 MBCD 中，DC // MB ,DN NB DC MB 12,Ap 1在△ADB 中，pp 二」AD 〃 PN . •/ AD?平面 MPC , PN?平面 MPC , ••• AD //平面 MPC.P ,使AD //平面 MPC?并说明理由AD平行于PN，最后得到结论。

构造交线的方法我们可总结为如下三个图形。

PP上一方法二方法三2.构造面面平行，然后推出线面平行。

专题06 立体几何专项高考真题总汇(带答案与解析)

专题06立体几何（解答题）1．【2021·全国高考真题】如图，在三棱锥A BCD -中，平面ABD ⊥平面BCD ，AB AD =，O 为BD 的中点.（1）证明：OA CD ⊥；（2）若OCD 是边长为1的等边三角形，点E 在棱AD 上，2DE EA =，且二面角E BC D --的大小为45︒，求三棱锥A BCD -的体积.【答案】(1)详见解析(2)6【分析】（1）根据面面垂直性质定理得AO ⊥平面BCD ，即可证得结果；（2）先作出二面角平面角，再求得高，最后根据体积公式得结果.【解析】（1）因为AB=AD,O 为BD 中点，所以AO ⊥BD因为平面ABD 平面BCD =BD ,平面ABD ⊥平面BCD ，AO ⊂平面ABD ，因此AO ⊥平面BCD ，因为CD ⊂平面BCD ，所以AO ⊥CD (2)作EF ⊥BD 于F,作FM ⊥BC 于M,连FM 因为AO ⊥平面BCD ，所以AO ⊥BD,AO ⊥CD所以EF ⊥BD,EF ⊥CD,BD CD D ⋂=,因此EF ⊥平面BCD ，即EF ⊥BC 因为FM ⊥BC ，FM EF F =I ,所以BC ⊥平面EFM ，即BC ⊥ME 则EMF ∠为二面角E-BC-D 的平面角,4EMF π∠=因为BO OD =,OCD 为正三角形,所以BCD 为直角三角形因为2DE EA =,1112(1)2233FM BF ∴==+=从而EF=FM=213AO ∴=AO ⊥Q 平面BCD,所以11131133326BCD V AO S ∆=⋅=⨯⨯⨯⨯=【点睛】二面角的求法：一是定义法，二是三垂线定理法，三是垂面法，四是投影法.2．【2021·浙江高考真题】如图，在四棱锥P ABCD -中，底面ABCD 是平行四边形，120,1,4,15ABC AB BC PA ∠=︒===M ，N 分别为,BC PC 的中点，,PD DC PM MD ⊥⊥.（1）证明：AB PM ⊥；（2）求直线AN 与平面PDM 所成角的正弦值.【答案】（1）证明见解析；（2）156．【分析】（1）要证AB PM ⊥，可证DC PM ⊥，由题意可得，PD DC ⊥，易证DM DC ⊥，从而DC ⊥平面PDM ，即有DC PM ⊥，从而得证；（2）取AD 中点E ，根据题意可知，,,ME DM PM 两两垂直，所以以点M 为坐标原点，建立空间直角坐标系，再分别求出向量AN和平面PDM 的一个法向量，即可根据线面角的向量公式求出．【解析】（1）在DCM △中，1DC =，2CM =，60DCM ∠= ，由余弦定理可得DM =，所以222DM DC CM +=，∴DM DC ⊥．由题意DC PD ⊥且PD DMD ⋂=，DC ∴⊥平面PDM ，而PM ⊂平面PDM ，所以DC PM ⊥，又//AB DC ，所以AB PM ⊥．（2）由PM MD ⊥，AB PM ⊥，而AB 与DM 相交，所以PM ⊥平面ABCD，因为AM =，所以PM =，取AD 中点E ，连接ME ，则,,ME DM PM 两两垂直，以点M 为坐标原点，如图所示，建立空间直角坐标系,则(2,0),(0,0,A P D,(0,0,0),1,0)M C -又N 为PC中点，所以31335,,,2222N AN ⎛⎛-=- ⎝⎝ .由（1）得CD ⊥平面PDM ，所以平面PDM 的一个法向量(0,1,0)n =从而直线AN 与平面PDM所成角的正弦值为5||2sin 6||AN n AN n θ⋅===‖．【点睛】本题第一问主要考查线面垂直的相互转化，要证明AB PM ⊥，可以考虑DC PM ⊥，题中与DC 有垂直关系的直线较多，易证DC ⊥平面PDM ，从而使问题得以解决；第二问思路直接，由第一问的垂直关系可以建立空间直角坐标系，根据线面角的向量公式即可计算得出．3．【2021·全国高考真题（理）】已知直三棱柱111ABC A B C -中，侧面11AA B B 为正方形，2AB BC ==，E ，F 分别为AC 和1CC 的中点，D 为棱11A B 上的点．11BF A B ⊥（1）证明：BF DE ⊥；（2）当1B D 为何值时，面11BB C C 与面DFE 所成的二面角的正弦值最小?【答案】（1）见解析；（2）112B D =【分析】通过已知条件，确定三条互相垂直的直线，建立合适的空间直角坐标系，借助空间向量证明线线垂直和求出二面角的平面角的余弦值最大，进而可以确定出答案．【解析】因为三棱柱111ABC A B C -是直三棱柱，所以1BB ⊥底面ABC ，所以1BB AB ⊥因为11//A B AB ，11BF A B ⊥，所以BF AB ⊥，又1BB BF B ⋂=，所以AB ⊥平面11BCC B ．所以1,,BA BC BB 两两垂直．以B 为坐标原点，分别以1,,BA BC BB 所在直线为,,x y z 轴建立空间直角坐标系，如图．所以()()()()()()1110,0,0,2,0,0,0,2,0,0,0,2,2,0,2,0,2,2B A C B A C ，()()1,1,0,0,2,1E F ．由题设(),0,2D a （02a ≤≤）．（1）因为()()0,2,1,1,1,2BF DE a ==--，所以()()0121120BF DE a ⋅=⨯-+⨯+⨯-= ，所以BF DE ⊥．（2）设平面DFE 的法向量为(),,m x y z =，因为()()1,1,1,1,1,2EF DE a =-=--，所以00m EF m DE ⎧⋅=⎨⋅=⎩，即()0120x y z a x y z -++=⎧⎨-+-=⎩．令2z a =-，则()3,1,2m a a =+-因为平面11BCC B 的法向量为()2,0,0BA =，设平面11BCC B 与平面DEF 的二面角的平面角为θ，则cos m BA m BA θ⋅===⋅ ．当12a =时，2224a a -+取最小值为272，此时cos θ63=．所以()min3sin 3θ==，此时112B D =．【点睛】本题考查空间向量的相关计算，能够根据题意设出(),0,2D a （02a ≤≤），在第二问中通过余弦值最大，找到正弦值最小是关键一步．4．【2021·全国高考真题（理）】如图，四棱锥P ABCD -的底面是矩形，PD ⊥底面ABCD ，1PD DC ==，M 为BC 的中点，且PB AM ⊥．（1）求BC ；（2）求二面角A PM B --的正弦值．【答案】（12；（2）7014【分析】（1）以点D 为坐标原点，DA 、DC 、DP 所在直线分别为x 、y 、z 轴建立空间直角坐标系，设2BC a =，由已知条件得出0PB AM ⋅=，求出a 的值，即可得出BC 的长；（2）求出平面PAM 、PBM 的法向量，利用空间向量法结合同角三角函数的基本关系可求得结果.【解析】（1）PD ⊥ 平面ABCD ，四边形ABCD 为矩形，不妨以点D 为坐标原点，DA 、DC 、DP 所在直线分别为x 、y 、z 轴建立如下图所示的空间直角坐标系D xyz -，设2BC a =，则()0,0,0D 、()0,0,1P 、()2,1,0B a 、(),1,0M a 、()2,0,0A a ，则()2,1,1PB a =- ，(),1,0AM a =-，PB AM ⊥ ，则2210PB AM a ⋅=-+= ，解得22a =，故2BC a ==；（2）设平面PAM 的法向量为()111,,m x y z = ，则2,1,02AM ⎛⎫=- ⎪ ⎪⎝⎭，()AP = ，由111102m AM x y mAP z ⎧⋅=-+=⎪⎨⎪⋅=+=⎩，取1x =，可得)2m = ，设平面PBM 的法向量为()222,,n x y z = ，2,0,02BM ⎛⎫=- ⎪ ⎪⎝⎭，()1,1BP =- ，由2222202n BM x nBP y z ⎧⋅=-=⎪⎨⎪⋅=-+=⎩ ，取21y =，可得()0,1,1n =r，314cos ,14m n m n m n⋅<>==⋅，所以，70sin ,14m n <>==，因此，二面角A PM B --的正弦值为14.【点睛】思路点睛：利用空间向量法求解二面角的步骤如下：（1）建立合适的空间直角坐标系，写出二面角对应的两个半平面中对应的点的坐标；（2）设出法向量，根据法向量垂直于平面内两条直线的方向向量，求解出平面的法向量（注：若半平面为坐标平面，直接取法向量即可）；（3）计算（2）中两个法向量的余弦值，结合立体图形中二面角的实际情况，判断二面角是锐角还是钝角，从而得到二面角的余弦值.5．【2021·北京高考真题】已知正方体1111ABCD A B C D -，点E 为11A D 中点，直线11B C 交平面CDE 于点F ．（1）证明：点F 为11B C 的中点；（2）若点M 为棱11A B 上一点，且二面角M CF E --的余弦值为53，求111A M A B 的值．【答案】（1）证明见解析；（2）11112A M AB =．【分析】(1)首先将平面CDE 进行扩展，然后结合所得的平面与直线11BC 的交点即可证得题中的结论；(2)建立空间直角坐标系，利用空间直角坐标系求得相应平面的法向量，然后解方程即可求得实数λ的值.【解析】(1)如图所示，取11B C 的中点'F ，连结,','DE EF F C ，由于1111ABCD A B C D -为正方体，,'E F 为中点，故'EF CD ，从而,',,E F C D 四点共面，即平面CDE 即平面'CDEF ，据此可得：直线11B C 交平面CDE 于点'F ，当直线与平面相交时只有唯一的交点，故点F 与点'F 重合，即点F 为11B C 中点.(2)以点D 为坐标原点，1,,DA DC DD 方向分别为x 轴，y 轴，z 轴正方形，建立空间直角坐标系D xyz -，不妨设正方体的棱长为2，设()11101A MA B λλ=≤≤，则：()()()()2,2,2,0,2,0,1,2,2,1,0,2M C F E λ，从而：()()()2,22,2,1,0,2,0,2,0MC CF FE λ=---==-，设平面MCF 的法向量为：()111,,m x y z =，则：()111112222020m MC x y z m CF x z λ⎧⋅=-+--=⎪⎨⋅=+=⎪⎩，令11z =-可得：12,,11m λ⎛⎫=- ⎪-⎝⎭，设平面CFE 的法向量为：()222,,n x y z =，则：2222020n FE y n CF x z ⎧⋅=-=⎪⎨⋅=+=⎪⎩，令11z =-可得：()2,0,1n =-，从而：5,m n m n ⋅===则：,5cos 3m n m n m n ⋅===⨯ ，整理可得：()2114λ-=，故12λ=（32λ=舍去）.【点睛】本题考查了立体几何中的线面关系和二面角的求解问题，意在考查学生的空间想象能力和逻辑推理能力，对于立体几何中角的计算问题，往往可以利用空间向量法，通过求解平面的法向量，利用向量的夹角公式求解.6．【2020年高考全国Ⅰ卷理数】如图，D 为圆锥的顶点，O 是圆锥底面的圆心，AE 为底面直径，AE AD =．ABC △是底面的内接正三角形，P 为DO 上一点，66PO DO =．（1）证明：PA ⊥平面PBC ；（2）求二面角B PC E --的余弦值．【解析】（1）设DO a =，由题设可得63,,63PO a AO a AB a ===，22PA PB PC a ===.因此222PA PB AB +=，从而PA PB ⊥.又222PA PC AC +=，故PA PC ⊥.所以PA ⊥平面PBC .（2）以O 为坐标原点，OE 的方向为y 轴正方向，||OE为单位长，建立如图所示的空间直角坐标系O xyz -.由题设可得312(0,1,0),(0,1,0),(,,0),(0,0,222E A C P --.所以312(,,0),(0,1,222EC EP =--=- .设(,,)x y z =m 是平面PCE 的法向量，则00EP EC ⎧⋅=⎪⎨⋅=⎪⎩m m，即021022y z x y ⎧-+=⎪⎪⎨⎪--=⎪⎩，可取3(3=-m .由（1）知2(0,1,2AP = 是平面PCB 的一个法向量，记AP = n ，则25cos ,|||5⋅==n m n m n m |.所以二面角B PC E --的余弦值为255.【点晴】本题主要考查线面垂直的证明以及利用向量求二面角的大小，考查学生空间想象能力，数学运算能力，是一道容易题.7．【2020年高考全国Ⅱ卷理数】如图，已知三棱柱ABC -A 1B 1C 1的底面是正三角形，侧面BB 1C 1C 是矩形，M ，N 分别为BC ，B 1C 1的中点，P 为AM 上一点，过B 1C 1和P 的平面交AB 于E ，交AC 于F ．（1）证明：AA 1∥MN ，且平面A 1AMN ⊥平面EB 1C 1F ；（2）设O 为△A 1B 1C 1的中心，若AO ∥平面EB 1C 1F ，且AO =AB ，求直线B 1E 与平面A 1AMN 所成角的正弦值．【解析】（1）因为M ，N 分别为BC ，B 1C 1的中点，所以1MN CC ∥．又由已知得AA 1∥CC 1，故AA 1∥MN ．因为△A 1B 1C 1是正三角形，所以B 1C 1⊥A 1N ．又B 1C 1⊥MN ，故B 1C 1⊥平面A 1AMN ．所以平面A 1AMN ⊥平面11EB C F ．（2）由已知得AM ⊥BC ．以M 为坐标原点，MA的方向为x 轴正方向， MB 为单位长，建立如图所示的空间直角坐标系M -xyz ，则AB =2，AM 3连接NP ，则四边形AONP 为平行四边形，故23231(,0)333PM E =．由（1）知平面A 1AMN ⊥平面ABC ，作NQ ⊥AM ，垂足为Q ，则NQ ⊥平面ABC ．设(,0,0)Q a ，则22123234()(4())33NQ a B a a =----，故21123223210(,,4()|3333B E a a B E =-----=．又(0,1,0)=-n 是平面A 1AMN 的法向量，故1111π10sin(,)cos ,210||B E B E B E B E ⋅-===⋅ n n |n |所以直线B 1E 与平面A 1AMN 所成角的正弦值为1010．8．【2020年高考全国Ⅱ卷理数】如图，在长方体1111ABCD A B C D -中，点,E F 分别在棱11,DD BB 上，且12DE ED =，12BF FB =．（1）证明：点1C 在平面AEF 内；（2）若2AB =，1AD =，13AA =，求二面角1A EF A --的正弦值．【解析】设AB a =，AD b =，1AA c =，如图，以1C 为坐标原点，11C D的方向为x 轴正方向，建立空间直角坐标系1C xyz -．（1）连结1C F ，则1(0,0,0)C ，(,,)A a b c ，2(,0,)3E a c ，1(0,,)3F b c ，1(0,,)3EA b c = ，11(0,,)3C F b c = ，得1EA C F = ．因此1EA C F ∥，即1,,,A E F C 四点共面，所以点1C 在平面AEF 内．（2）由已知得(2,1,3)A ，(2,0,2)E ，(0,1,1)F ，1(2,1,0)A ，(0,1,1)AE =--，(2,0,2)AF =-- ，1(0,1,2)A E =- ，1(2,0,1)A F =-．设1(,,)x y z =n 为平面AEF 的法向量，则110,0,AE AF ⎧⋅=⎪⎨⋅=⎪⎩ n n 即0,220,y z x z --=⎧⎨--=⎩可取1(1,1,1)=--n ．设2n 为平面1A EF 的法向量，则22110,0,A E A F ⎧⋅=⎪⎨⋅=⎪⎩n n 同理可取21(,2,1)2=n ．因为121212cos ,||||⋅〈〉==⋅n n n n n n ，所以二面角1A EF A --的正弦值为427．9．【2020年高考江苏】在三棱柱ABC －A 1B 1C 1中，AB ⊥AC ，B 1C ⊥平面ABC ，E ，F 分别是AC ，B 1C 的中点．（1）求证：EF ∥平面AB 1C 1；（2）求证：平面AB 1C ⊥平面ABB 1．【解析】因为,E F 分别是1,AC B C 的中点，所以1EF AB ∥.又/EF ⊂平面11AB C ，1AB ⊂平面11AB C ，所以EF ∥平面11AB C .（2）因为1B C ⊥平面ABC ，AB ⊂平面ABC ,所以1B C AB ⊥.又AB AC ⊥,1B C ⊂平面11AB C ,AC ⊂平面1AB C ,1,B C AC C = 所以AB ⊥平面1AB C .又因为AB ⊂平面1ABB ,所以平面1AB C ⊥平面1ABB .【点睛】本小题主要考查线面平行的证明，考查面面垂直的证明，属于中档题.10．【2020年高考浙江】如图，在三棱台ABC —DEF 中，平面ACFD ⊥平面ABC ，∠ACB =∠ACD =45°，DC =2BC ．（Ⅰ）证明：EF ⊥DB ；（Ⅱ）求直线DF 与平面DBC 所成角的正弦值．【解析】（Ⅰ）如图，过点D 作DO AC ⊥，交直线AC 于点O ，连结OB ．由45ACD ∠=︒，DO AC ⊥得2CD CO =，由平面ACFD ⊥平面ABC 得DO ⊥平面ABC ，所以DO BC ⊥.由45ACB ∠=︒，1222BC CD ==得BO BC ⊥.所以BC ⊥平面BDO ，故BC ⊥DB ．由三棱台ABC DEF -得BC EF ∥，所以EF DB ⊥.（Ⅱ）方法一：过点O 作OH BD ⊥，交直线BD 于点H ，连结CH .由三棱台ABC DEF -得DF CO ∥，所以直线DF 与平面DBC 所成角等于直线CO 与平面DBC 所成角.由BC ⊥平面BDO 得OH BC ⊥，故OH ⊥平面BCD ，所以OCH ∠为直线CO 与平面DBC 所成角.设CD =.由2,DO OC BO BC ====BD OH ==所以sin OH OCH OC ∠==，因此，直线DF 与平面DBC 所成角的正弦值为33.方法二：由三棱台ABC DEF -得DF CO ∥，所以直线DF 与平面DBC 所成角等于直线CO 与平面DBC 所成角，记为θ.如图，以O 为原点，分别以射线OC ，OD 为y ，z 轴的正半轴，建立空间直角坐标系O xyz -.设CD =.由题意知各点坐标如下：(0,0,0),(1,1,0),(0,2,0),(0,0,2)O B C D .因此(0,2,0),(1,1,0),(0,2,2)OC BC CD ==-=-.设平面BCD 的法向量(,,z)x y =n .由0,0,BC CD ⎧⋅=⎪⎨⋅=⎪⎩ n n 即0220x y y z -+=⎧⎨-+=⎩，可取(1,1,1)=n .所以|3sin |cos ,|3|||OC OC OC θ⋅===⋅n |n n |.因此，直线DF 与平面DBC【点睛】本题主要考查空间点、线、面位置关系，线面垂直的判定定理的应用，直线与平面所成的角的求法，意在考查学生的直观想象能力和数学运算能力，属于基础题．11．【2020年高考天津】如图，在三棱柱111ABC A B C -中，1CC ⊥平面,,2ABC AC BC AC BC ⊥==，13CC =，点,D E 分别在棱1AA 和棱1CC 上，且2,1,AD CE M ==为棱11A B的中点．（Ⅰ）求证：11C M B D ⊥；（Ⅱ）求二面角1B B E D --的正弦值；（Ⅲ）求直线AB 与平面1DB E 所成角的正弦值．【解析】依题意，以C 为原点，分别以1,,CA CB CC的方向为x 轴，y 轴，z 轴的正方向建立空间直角坐标系（如图），可得1(0,0,0),(2,0,0),(0,2,0),(0,0,3)C A B C ，11(2,0,3),(0,2,3),(2,0,1),(0,0,2)A B D E ，(1,1,3)M ．（Ⅰ）证明：依题意，1(1,1,0)C M = ，1(2,2,2)B D =--，从而112200C M B D ⋅=-+=，所以11C M B D ⊥．（Ⅱ）解：依题意，(2,0,0)CA = 是平面1BB E 的一个法向量，1(0,2,1)EB =，(2,0,1)ED =- ．设(,,)x y z =n 为平面1DB E 的法向量，则10,0,EB ED ⎧⋅=⎪⎨⋅=⎪⎩n n 即20,20.y z x z +=⎧⎨-=⎩不妨设1x =，可得(1,1,2)=-n ．因此有|||6cos ,6|A CA C CA ⋅〈〉==n n n ，于是30sin ,6CA 〈〉= n ．所以，二面角1B B E D --的正弦值为306．（Ⅲ）解：依题意，(2,2,0)AB =-．由（Ⅱ）知(1,1,2)=-n 为平面1DB E 的一个法向量，于是3cos ,3||||AB AB AB ⋅==-n n n ．所以，直线AB 与平面1DB E 所成角的正弦值为33．12．【2019年高考全国Ⅰ卷理数】如图，直四棱柱ABCD–A 1B 1C 1D 1的底面是菱形，AA 1=4，AB =2，∠BAD =60°，E ，M ，N 分别是BC ，BB 1，A 1D 的中点．（1）证明：MN ∥平面C 1DE ；（2）求二面角A−MA 1−N 的正弦值．【答案】（1）见解析；（2）105.【解析】（1）连结B 1C ，ME ．因为M ，E 分别为BB 1，BC 的中点，所以ME ∥B 1C ，且ME =12B 1C ．又因为N 为A 1D 的中点，所以ND =12A 1D ．由题设知A 1B 1= DC ，可得B 1C = A 1D ，故ME =ND ，因此四边形MNDE 为平行四边形，MN ∥ED ．又MN ⊄平面EDC 1，所以MN ∥平面C 1DE ．（2）由已知可得DE ⊥DA ．以D 为坐标原点，DA的方向为x 轴正方向，建立如图所示的空间直角坐标系D −xyz ，则(2,0,0)A ，A 1(2，0，4)，3,2)M ，(1,0,2)N ，1(0,0,4)A A =- ，1(3,2)A M =--，1(1,0,2)A N =-- ，(0,3,0)MN =-．设(,,)x y z =m 为平面A 1MA 的法向量，则1100A M A A ⎧⋅=⎪⎨⋅=⎪⎩m m ，所以32040x z z ⎧-+-=⎪⎨-=⎪⎩，．可取(3,1,0)=m ．设(,,)p q r =n 为平面A 1MN 的法向量，则100MN A N ⎧⋅=⎪⎨⋅=⎪⎩，．n n 所以3020q p r ⎧-=⎪⎨--=⎪⎩，．可取(2,0,1)=-n ．于是2315cos ,||525⋅〈〉==⨯‖m n m n m n ，所以二面角1A MA N --的正弦值为105．【名师点睛】本题考查线面平行关系的证明、空间向量法求解二面角的问题.求解二面角的关键是能够利用垂直关系建立空间直角坐标系，从而通过求解法向量夹角的余弦值来得到二面角的正弦值，属于常规题型.13．【2019年高考全国Ⅱ卷理数】如图，长方体ABCD –A 1B 1C 1D 1的底面ABCD 是正方形，点E 在棱AA 1上，BE ⊥EC 1．（1）证明：BE ⊥平面EB 1C 1；（2）若AE =A 1E ，求二面角B –EC –C 1的正弦值．【答案】（1）证明见解析；（2）32.【解析】（1）由已知得，11B C ⊥平面11ABB A ，BE ⊂平面11ABB A ，故11B C ⊥BE ．又1BE EC ⊥，所以BE ⊥平面11EB C ．（2）由（1）知190BEB ∠=︒．由题设知Rt ABE △≌11Rt A B E △，所以45AEB ∠=︒，故AE AB =，12AA AB =．以D 为坐标原点，DA的方向为x 轴正方向，||DA 为单位长，建立如图所示的空间直角坐标系D –xyz ，则C （0，1，0），B （1，1，0），1C （0，1，2），E （1，0，1），(1,0,0)CB = ，(1,1,1)CE =-，1(0,0,2)CC =．设平面EBC 的法向量为n =（x ，y ，x ），则0,0,CB CE ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,0,x x y z =⎧⎨-+=⎩所以可取n =(0,1,1)--.设平面1ECC 的法向量为m =（x ，y ，z ），则10,0,CC CE ⎧⋅=⎪⎨⋅=⎪⎩m m 即20,0.z x y z =⎧⎨-+=⎩所以可取m =（1，1，0）．于是1cos ,||||2⋅<>==-n m n m n m ．所以，二面角1B EC C --的正弦值为2．【名师点睛】本题考查了利用线面垂直的性质定理证明线线垂直以及线面垂直的判定，考查了利用空间向量求二角角的余弦值，以及同角的三角函数关系，考查了数学运算能力.14．【2019年高考全国Ⅲ卷理数】图1是由矩形ADEB ，Rt △ABC 和菱形BFGC 组成的一个平面图形，其中AB =1，BE =BF =2，∠FBC =60°，将其沿AB ，BC 折起使得BE 与BF 重合，连结DG ，如图2.（1）证明：图2中的A ，C ，G ，D 四点共面，且平面ABC ⊥平面BCGE ；（2）求图2中的二面角B−CG−A 的大小.【答案】（1）见解析；（2）30 .【解析】（1）由已知得AD BE ，CG BE ，所以AD CG ，故AD ，CG 确定一个平面，从而A ，C ，G ，D 四点共面．由已知得AB ⊥BE ，AB ⊥BC ，故AB ⊥平面BCGE ．又因为AB ⊂平面ABC ，所以平面ABC ⊥平面BCGE ．（2）作EH ⊥BC ，垂足为H ．因为EH ⊂平面BCGE ，平面BCGE ⊥平面ABC ，所以EH ⊥平面ABC ．由已知，菱形BCGE 的边长为2，∠EBC =60°，可求得BH =1，EH以H 为坐标原点，HC的方向为x 轴的正方向，建立如图所示的空间直角坐标系H –xyz，则A （–1，1，0），C （1，0，0），G （2，0），CG =（1，0AC=（2，–1，0）．设平面ACGD 的法向量为n =（x ，y ，z ），则0,0,CG AC ⎧⋅=⎪⎨⋅=⎪⎩n n即0,20.x x y ⎧+=⎪⎨-=⎪⎩所以可取n =（3，6，）．又平面BCGE 的法向量可取为m =（0，1，0），所以3cos ,||||2⋅〈〉==n m n m n m ．因此二面角B –CG –A 的大小为30°．【名师点睛】本题是很新颖的立体几何考题，首先是多面体折叠问题，考查考生在折叠过程中哪些量是不变的，再者折叠后的多面体不是直棱柱，最后通过建系的向量解法将求二面角转化为求二面角的平面角问题，突出考查考生的空间想象能力.15．【2019年高考北京卷理数】如图，在四棱锥P –ABCD 中，PA ⊥平面ABCD ，AD ⊥CD ，AD∥BC，PA=AD=CD=2，BC=3．E为PD的中点，点F在PC上，且13 PFPC=．（1）求证：CD⊥平面PAD；（2）求二面角F–AE–P的余弦值；（3）设点G在PB上，且23PGPB=．判断直线AG是否在平面AEF内，说明理由．【答案】（1）见解析；（2）33；（3）见解析.【解析】（1）因为PA⊥平面ABCD，所以PA⊥CD．又因为AD⊥CD，所以CD⊥平面PAD．（2）过A作AD的垂线交BC于点M．因为PA⊥平面ABCD，所以PA⊥AM，PA⊥AD．如图建立空间直角坐标系A−xyz，则A（0，0，0），B（2，-1，0），C（2，2，0），D（0，2，0），P（0，0，2）．因为E为PD的中点，所以E（0，1，1）．所以(0,1,1),(2,2,2),(0,0,2)AE PC AP==-=．所以1222224,,,,,3333333PF PC AF AP PF⎛⎫⎛⎫==-=+=⎪ ⎪⎝⎭⎝⎭.设平面AEF的法向量为n=（x，y，z），则0,0,AEAF⎧⋅=⎪⎨⋅=⎪⎩nn即0,2240.333y zx y z+=⎧⎪⎨++=⎪⎩令z=1，则1,1y x=-=-．于是=(1,1,1)--n．又因为平面PAD的法向量为p=（1，0，0），所以3cos ,||3⋅〈〉==-‖n p n p n p .由题知，二面角F −AE −P为锐角，所以其余弦值为3．（3）直线AG 在平面AEF 内．因为点G 在PB 上，且2,(2,1,2)3PG PB PB ==--，所以2424422,,,,,3333333PG PB AG AP PG ⎛⎫⎛⎫==--=+=- ⎪ ⎪⎝⎭⎝⎭.由（2）知，平面AEF 的法向量=(1,1,1)--n .所以4220333AG ⋅=-++= n .所以直线AG 在平面AEF 内.【名师点睛】（1）由题意利用线面垂直的判定定理即可证得题中的结论；（2）建立空间直角坐标系，结合两个半平面的法向量即可求得二面角F −AE −P 的余弦值；（3）首先求得点G 的坐标，然后结合平面AEF 的法向量和直线AG 的方向向量即可判断直线是否在平面内.16．【2019年高考天津卷理数】如图，AE ⊥平面ABCD ，,CF AE AD BC ∥∥，,AD AB ⊥1,2AB AD AE BC ====．（1）求证：BF ∥平面ADE ；（2）求直线CE 与平面BDE 所成角的正弦值；（3）若二面角E BD F --的余弦值为13，求线段CF 的长．【答案】（1）见解析；（2）49；（3）87．【解析】依题意，可以建立以A 为原点，分别以AB AD AE，，的方向为x 轴，y 轴，z轴正方向的空间直角坐标系（如图），可得(0,0,0),(1,0,0),(1,2,0),(0,1,0)A B C D ，(0,0,2)E ．设(0)CF h h =>>，则()1,2,F h ．（1）依题意，(1,0,0)AB = 是平面ADE 的法向量，又(0,2,)BF h =，可得0BF AB ⋅=，又因为直线BF ⊄平面ADE ，所以BF ∥平面ADE ．（2）依题意，(1,1,0),(1,0,2),(1,2,2)BD BE CE =-=-=--．设(,,)x y z =n 为平面BDE 的法向量，则0,0,BD BE ⎧⋅=⎪⎨⋅=⎪⎩n n 即0,20,x y x z -+=⎧⎨-+=⎩不妨令1z =，可得(2,2,1)=n ．因此有4cos ,9||||CE CE CE ⋅==-n n n ．所以，直线CE 与平面BDE 所成角的正弦值为49．（3）设(,,)x y z =m 为平面BDF 的法向量，则0,0,BD BF ⎧⋅=⎪⎨⋅=⎪⎩m m 即0,20,x y y hz -+=⎧⎨+=⎩不妨令1y =，可得21,1,h ⎛⎫=-⎪⎝⎭m ．由题意，有224||1cos ,||||3432h h -⋅〈〉==+m n m n m n ，解得87h =．经检验，符合题意．所以，线段CF的长为8 7．【名师点睛】本小题主要考查直线与平面平行、二面角、直线与平面所成的角等基础知识．考查用空间向量解决立体几何问题的方法．考查空间想象能力、运算求解能力和推理论证能力．17．【2019年高考江苏卷】如图，在直三棱柱ABC－A1B1C1中，D，E分别为BC，AC的中点，AB=BC．求证：（1）A1B1∥平面DEC1；（2）BE⊥C1E．【答案】（1）见解析；（2）见解析.【解析】（1）因为D，E分别为BC，AC的中点，所以ED∥AB.在直三棱柱ABC−A1B1C1中，AB∥A1B1，所以A1B1∥ED.又因为ED⊂平面DEC1，A1B1 平面DEC1，所以A1B1∥平面DEC1.（2）因为AB =BC ，E 为AC 的中点，所以BE ⊥AC .因为三棱柱ABC−A 1B 1C 1是直棱柱，所以CC 1⊥平面ABC .又因为BE ⊂平面ABC ，所以CC 1⊥BE .因为C 1C ⊂平面A 1ACC 1，AC ⊂平面A 1ACC 1，C 1C ∩AC =C ，所以BE ⊥平面A 1ACC 1.因为C 1E ⊂平面A 1ACC 1，所以BE ⊥C 1E .【名师点睛】本小题主要考查直线与直线、直线与平面、平面与平面的位置关系等基础知识，考查空间想象能力和推理论证能力.18．【2019年高考浙江卷】如图，已知三棱柱111ABC A B C -，平面11A ACC ⊥平面ABC ,90ABC ∠=︒，1130,,,BAC A A A C AC E F ∠=︒==分别是AC ，A 1B 1的中点.（1）证明：EF BC ⊥；（2）求直线EF 与平面A 1BC 所成角的余弦值.【答案】（1）见解析；（2）35．【解析】方法一：（1）连接A 1E ，因为A 1A =A 1C ，E 是AC 的中点，所以A 1E ⊥AC ．又平面A 1ACC 1⊥平面ABC ，A 1E ⊂平面A 1ACC 1，平面A 1ACC 1∩平面ABC =AC ，所以，A 1E ⊥平面ABC ，则A 1E ⊥BC ．又因为A 1F ∥AB ，∠ABC =90°，故BC ⊥A 1F ．所以BC ⊥平面A 1EF ．因此EF ⊥BC ．（2）取BC 中点G ，连接EG ，GF ，则EGFA 1是平行四边形．由于A 1E ⊥平面ABC ，故A 1E ⊥EG ，所以平行四边形EGFA 1为矩形．由（1）得BC ⊥平面EGFA 1，则平面A 1BC ⊥平面EGFA 1，所以EF 在平面A 1BC 上的射影在直线A 1G 上．连接A 1G 交EF 于O ，则∠EOG 是直线EF 与平面A 1BC 所成的角（或其补角）．不妨设AC =4，则在Rt △A 1EG 中，A 1E 3EG 3由于O 为A 1G 的中点，故11522A G EO OG ===，所以2223cos 25EO OG EG EOG EO OG +-∠==⋅．因此，直线EF 与平面A 1BC 所成角的余弦值是35．方法二：（1）连接A 1E ，因为A 1A =A 1C ，E 是AC 的中点，所以A 1E ⊥AC .又平面A 1ACC 1⊥平面ABC ，A 1E ⊂平面A 1ACC 1，平面A 1ACC 1∩平面ABC =AC ，所以，A 1E ⊥平面ABC ．如图，以点E 为原点，分别以射线EC ，EA 1为y ，z 轴的正半轴，建立空间直角坐标系E –xyz ．不妨设AC =4，则A 1（0，0，），B，1，0），1B，33,,22F ，C (0，2，0)．因此，33(,,22EF =，(BC = ．由0EF BC ⋅=得EF BC ⊥．（2）设直线EF 与平面A 1BC 所成角为θ．由（1）可得1=(10)=(02BC A C -，，，．设平面A 1BC 的法向量为n ()x y z =，，，由100BC A C ⎧⋅=⎪⎨⋅=⎪⎩n n，得0y y ⎧+=⎪⎨=⎪⎩，取n (11)=，故||4sin |cos |=5|||EF EF EF θ⋅==⋅，n n n |，因此，直线EF 与平面A 1BC 所成的角的余弦值为35．【名师点睛】本题主要考查空间点、线、面位置关系，直线与平面所成的角等基础知识，同时考查空间想象能力和运算求解能力.。

高考数学复习总结专题05 立体几何(选择题、填空题) (解析版)

立体几何（选择题、填空题）1.【2020年高考全国Ⅰ卷理数】埃及胡夫金字塔是古代世界建筑奇迹之一，它的形状可视为一个正四棱锥，以该四棱锥的高为边长的正方形面积等于该四棱锥一个侧面三角形的面积，则其侧面三角形底边上的高与底面正方形的边长的比值为（）515 1 5 1 5 1A. B. C. D.4 2 4 2【答案】C【解析】【分析】1设C D a,PE b，利用P O2 CD PE 得到关于a,b的方程，解方程即可得到答案.22a【详解】如图，设C D a,PE b，则P O PE 2 2 2 ，OE b41 a2 1 b b由题意P O2 ab，即b 2 ab，化简得4() 2 210，2 4 2 a ab1 5解得（负值舍去）.a 4故选：C.【点晴】本题主要考查正四棱锥的概念及其有关计算，考查学生的数学计算能力，是一道容易题.2.【2020年高考全国I I卷理数】如图是一个多面体的三视图，这个多面体某条棱的一个端点在正视图中对应的点为M ，在俯视图中对应的点为N ，则该端点在侧视图中对应的点为（）A. EB. FC.GD.H【答案】A【解析】【分析】根据三视图，画出多面体立体图形，即可求得M 点在侧视图中对应的点.【详解】根据三视图，画出多面体立体图形，D D B C上的点在俯视图中对应的点为N,3 4上的点在正视图中都对应点M,直线1 4∴在正视图中对应M ,在俯视图中对应N 的点是D4,线段D D,上的所有点在侧试图中都对应E ,∴点3 4D4在侧视图中对应的点为E .故选：A【点睛】本题主要考查了根据三视图判断点的位置，解题关键是掌握三视图的基础知识和根据三视图能还原立体图形的方法，考查了分析能力和空间想象，属于基础题.A, B,C 为球O 的球面上的三个点，⊙O为 A B C的外接圆，若⊙O3. 【2020 年高考全国Ⅰ卷理数】已知11的面积为 4π ， AB BC AC OO ，则球O的表面积为（）1A. 64πB. 48πC. 36πD. 32π【答案】A 【解析】【分析】由已知可得等边 AB C 的外接圆半径，进而求出其边长，得出O O的值，根据球的截面性质，求出球的半 1径，即可得出结论. 【详解】设圆O半径为，球的半径为 R ，依题意， r 14,r 2 ， A B C为等边三角形，得r2由正弦定理可得 AB 2rsin 60 2 3 ，O O AB 2 3 ，根据球的截面性质O O 平面 ABC ， 11 O O O A ,R OA O O2 O A 2 OO 1 2 r 4 ， 21 1 1 1 O 球2 的表面积 S 4R 64 .故选：A【点睛】本题考查球的表面积，应用球的截面性质是解题的关键，考查计算求解能力，属于基础题. 4. 【2020 年高考全国Ⅲ理数】下图为某几何体的三视图，则该几何体的的表面积是（）A.6+4 2B.4+4 2C.6+2 3D.4+2 3【答案】C【解析】【分析】根据三视图特征，在正方体中截取出符合题意的立体图形，求出每个面的面积，即可求得其表面积.【详解】根据三视图特征，在正方体中截取出符合题意的立体图形1根据立体图形可得：S△ABC S△AD C S△C DB 22 22根据勾股定理可得：AB A D DB 2 2△A DB是边长为22的等边三角形根据三角形面积公式可得：1 1 3S △A D B AB AD s in60(22) 2 2 32 2 2该几何体的表面积是：3223623.故选：C.【点睛】本题主要考查了根据三视图求立体图形的表面积问题，解题关键是掌握根据三视图画出立体图形，考查了分析能力和空间想象能力，属于基础题. 5. 【2020 年高考全国 I I 卷理数】已知△ABC 是面积为若球 O 的表面积为 16π，则 O 到平面 ABC 的距离为（ 3 9 34的等边三角形，且其顶点都在球 O 的球面上. ）3 A. 3 B.C. 1D.22【答案】C 【解析】【分析】根据球O 的表面积和 ABC 的面积可求得球O 的半径 R 和 AB C 外接圆半径，由球的性质可知所求距r 离 2 2 .d R r 【详解】设球O 的半径为 R ，则 4 R 16 ，解得： R 2 . 2 设 AB C 外接圆半径为，边长为 a，r 9 3ABC是面积为的等边三角形， 41 3 9 32 a 22 9 a 2 ，解得： a 3，r a 2 93 ， 2 24 3 4 3 4球心 O 到平面 ABC 2 2 的距离d R r 43 1.故选：C.【点睛】本题考查球的相关问题的求解，涉及到球的表面积公式和三角形面积公式的应用；解题关键是明确球的性质，即球心和三角形外接圆圆心的连线必垂直于三角形所在平面.6. 【2019 年高考全国Ⅰ卷理数】已知三棱锥 P −AB C 的四个顶点在球 O 的球面上，PA=PB=P C ，△ABC 是边长为 2 的正三角形，E ，F 分别是 PA ，AB 的中点，∠CEF =90°，则球 O 的体积为A ．8 6B ． 4 6 D ． 6C ． 2 6 【答案】D【解析】解法一： PA P B PC, ABC 为边长为 2 的等边三角形，P ABC为正三棱锥，△ PB AC ，又 E ， F 分别为 PA ， AB 的中点，EF ∥PB ，EF AC ，又 EF CE ，C E AC C,EF 平面 PAC ，∴ PB 平面 PAC ，APB PA PB PC 2 ，P ABC 为正方体的一部分， 2R 2 2 2 6 ，即6 4 4 6 68 R, V R 3 π 6，故选 D ． P A, AB 2 3 3解法二：设 PA PB PC 2x ，E, F 分别为的中点， 1EF ∥PB ，且 EF PB x ，△ABC 为边长为 2 的等边三角形，C F 3 ，21 又 CEF 90，CE 3 x 2, AE PA x ， 2 x 243 x 22 x2△AEC 中，由余弦定理可得 cos EAC作 PD AC 于 D ，，A D 1 x 2 4 3 x 4x 21PA PC \ D AC cos EAC ，，为的中点，，PA 2x 2x1 2 2x 2 1 2，x 2，x ，PA PB PC 2 ，2 2又 AB=B C=A C=2 ， PA , PB , PC 两两垂直，6 2R 2 2 2 6 ，R，24 4 6 68 V R 3 6 ，故选 D. 3 3【名师点睛】本题主要考查学生的空间想象能力，补体法解决外接球问题．可通过线面垂直定理，得到三棱两两互相垂直关系，快速得到侧棱长，进而补体成正方体解决．7. 【2019 年高考全国Ⅱ卷理数】设α，β为两个平面，则α∥β的充要条件是 A ．α内有无数条直线与β平行 C ．α，β平行于同一条直线【答案】BB ．α内有两条相交直线与β平行 D ．α，β垂直于同一平面【解析】由面面平行的判定定理知：内两条相交直线都与平行是∥的充分条件，由面面平行性质定理知，若∥，则必要条件，故选 B ．内任意一条直线都与平行，所以平行是∥内两条相交直线都与的【名师点睛】本题考查了空间两个平面的判定与性质及充要条件，渗透直观想象、逻辑推理素养，利用面面平行的判定定理与性质定理即可作出判断．面面平行的判定问题要紧扣面面平行判定定理，最容易犯的错误为定理记不住，凭主观臆断，如：“若 a ,b ,a b ，则 ∥ ∥”此类的错误．8. 【2019 年高考全国Ⅲ卷理数】如图，点 N 为正方形 AB C D 的中心，△EC D 为正三角形，平面 EC D ⊥平面 ABC D ，M 是线段 E D 的中点，则A ．B M =E N ，且直线 B M ，EN 是相交直线 B ．B M ≠EN ，且直线 B M ，E N 是相交直线C ．B M =E N ，且直线 B M ，E N 是异面直线D ．B M ≠EN ，且直线 B M ，EN 是异面直线【答案】B【解析】如图所示，作 EO C D 于O ，连接O N ，B D ，易得直线 B M ，E N 是三角形 EB D 的中线，是相交直线.过 M 作 MF OD 于 F ，连接 BF ，AB C D ，E O C D, E O 平面C DE ，EO平面C D E 平面平面 ABC D ， M F 平面 AB C D ，△MFB 与△EO N 均为直角三角形．设正方形边长为 2 ，易知 E O 3,ON 1,EN 2 ，3 5M F,BF ,BM 7 ，B M EN ，故选 B ．2 2【名师点睛】本题考查空间想象能力和计算能力，解答本题的关键是构造直角三角形.解答本题时，先利用垂直关系，再结合勾股定理进而解决问题．9. 【2018 年高考全国Ⅰ卷理数】某圆柱的高为 2，底面周长为 16，其三视图如图．圆柱表面上的点 M 在正视图上的对应点为 A ，圆柱表面上的点 N 在左视图上的对应点为 B ，则在此圆柱侧面上，从 M 到 N 的路径中，最短路径的长度为A ． 2 17B ． 2 5 D ．2C ．3 【答案】B【解析】根据圆柱的三视图以及其本身的特征，知点 M 在上底面上，点 N 在下底面上，且可以确定点 M 和点 N 分别在以圆柱的高为长方形的宽，圆柱底面圆周长的四分之一为长的长方形的对角线的端点处，所以所求的最短路径的长度为，故选 B ．【名师点睛】该题考查的是有关几何体的表面上两点之间的最短距离的求解问题，在解题的过程中，需要明确两个点在几何体上所处的位置，再利用平面上两点间直线段最短，所以处理方法就是将面切开平铺，利用平面图形的相关特征求得结果.10. 【2018 年高考全国Ⅰ卷理数】已知正方体的棱长为 1，每条棱所在直线与平面所成的角都相等，则截此正方体所得截面面积的最大值为3 342 3 3 A ．C ．B ．D ．3 2 43 2【答案】A【解析】根据相互平行的直线与平面所成的角是相等的，AB C D A B C D 中，1所以在正方体 1 1 1AB D AA , A B , A D 所成的角是相等的，11 11 1平面与线 1 1AB D 所以平面与正方体的每条棱所在的直线所成角都是相等的，11 C BD 1同理，平面也满足与正方体的每条棱所在的直线所成角都是相等的，AB D C BD要求截面面积最大，则截面的位置为夹在两个面与1中间，且过棱的中点的正六边形，且1 12边长为，223 2 3 34所以其面积为S 6，故选A.4 2【名师点睛】该题考查的是有关平面被正方体所截得的截面多边形的面积问题，首要任务是需要先确定截面的位置，之后需要从题的条件中找寻相关的字眼，从而得到其为过六条棱的中点的正六边形，利用六边形的面积的求法，应用相关的公式求得结果.即首先利用正方体的棱是3组每组有互相平行的4条棱，所以与12条棱所成角相等，只需与从同一个顶点出发的三条棱所成角相等即可，从而判断出面的位置，截正方体所得的截面为一个正六边形，且边长是面的对角线的一半，应用面积公式求得结果.11.【2018年高考全国Ⅲ卷理数】中国古建筑借助榫卯将木构件连接起来，构件的凸出部分叫榫头，凹进部分叫卯眼，图中木构件右边的小长方体是榫头．若如图摆放的木构件与某一带卯眼的木构件咬合成长方体，则咬合时带卯眼的木构件的俯视图可以是【答案】A【解析】本题主要考查空间几何体的三视图.由题意知，俯视图中应有一不可见的长方形，且俯视图应为对称图形.故选A．12.【2018年高考全国Ⅲ卷理数】设A ，，，是同一个半径为的球的球面上四点，△A B C 为等边三B C D 4角形且其面积为A．12 3，则三棱锥D ABC 体积的最大值为9 3B．18 3D．54 3C．24 3【答案】B【解析】如图所示，设点 M 为三角形 ABC 的重心，E 为 AC 中点，当点 D 在平面 ABC 上的射影为 M 时，三棱锥 D ABC 的体积最大，此时，O D OB R 4，3 S △AB CAB 9 3 ，AB 6 ,点 M 为三角形 ABC 的重心，2 4 2B M BE 2 3 ，3 Rt △OB M 中，有O M OB 2 2 2，D M O D O M 4 2 6，B M1V DABCm ax9 36 18 3 ，故选 B. 3【名师点睛】本题主要考查三棱锥的外接球，考查了勾股定理，三角形的面积公式和三棱锥的体积公式，判断出当点 D 在平面 ABC 上的射影为三角形 AB C 的重心时，三棱锥 DABC 体积最大很关键，2由 M 为三角形 ABC 的重心，计算得到 B M BE 2 3 ，再由勾股定理得到 O M ，进而得到结果， 3属于较难题型.13. 【2018 年高考全国Ⅱ卷理数】在长方体 AB C D A B C D 中，AB BC 1，AA 3 ，则异面直线 A D 与 1 1 1 1 11 D B 所成角的余弦值为1 1 A ．5 5 B ． D ．6 5 2 C ．52【答案】C【解析】方法一：用一个与原长方体相同的长方体拼到原长方体的前面，B P ∥A D D B DP= 5B P 2，，则11如图，则 1，连接 DP ，易求得 1 DB P A D DB与所成的角，11是异面直线1 D B2 1 B P 2 DP 25 4 5 5 由余弦定理可得cos DB P 1. 12DB PB 4 5 5 1 1故选 C.方法二：以 D 为坐标原点，DA,D C,D D 所在直线分别为 x ,y ,z 轴建立空间直角坐标系， 1D 0, 0, 0, A 1, 0, 0,B 1, 1, 3,D 0, 0, 3A D1, 0, 3 ,DB 1, 1, 3 ,则 ,所以 1 1 1 1cos AD , DB A D DB A D DB 1 3 2 5 5 1 1因为， 1 15 1 15 A D DB 所以异面直线与所成角的余弦值为 1，故选 C. 15【名师点睛】先建立空间直角坐标系，设立各点坐标，利用向量数量积求向量夹角，再根据向量夹角与线线角相等或互补关系求结果.利用法向量求解空间线面角的关键在于“四破”：第一，破“建系关”，构建恰当的空间直角坐标系；第二，破“求坐标关”，准确求解相关点的坐标；第三，破“求法向量关”，求出直线的方向向量或平面的法向量；第四，破“应用公式关”. ABC A B C 中， ABC 120 BC CC 1，AB 2 ，，113. 【2017 年高考全国Ⅱ卷理数】已知直三棱柱1 1 1 AB BC 所成角的余弦值为1则异面直线与 13 15 5 A ．B ．D ．2 103 C ． 53【答案】CAB C D A B C D ，1【解析】如图所示，补成直四棱柱 1 1 1则所求角为 BC D,BC 2, BD 2 21 221cos 60 3,C D AB 5 ，11 1 1 BC12 5105 易得 C D 12 BD 2BC 12 ，因此cos BC D，故选 C ． 1C D1【名师点睛】平移法是求异面直线所成角的常用方法，其基本思路是通过平移直线，把异面问题化归为共面问题来解决，具体步骤如下：①平移：平移异面直线中的一条或两条，作出异面直线所成的角； ②认定：证明作出的角就是所求异面直线所成的角； ③计算：求该角的值，常利用解三角形；④取舍：由异面直线所成的角的取值范围是(0,]，当所作的角为钝角时，应取它的补角作为两条异面2直线所成的角．求异面直线所成的角要特别注意异面直线之间所成角的范围．14.【2017年高考全国Ⅰ卷理数】某多面体的三视图如图所示，其中正视图和左视图都由正方形和等腰直角三角形组成，正方形的边长为2，俯视图为等腰直角三角形.该多面体的各个面中有若干个是梯形，这些梯形的面积之和为A．10 B．12D．16C．14【答案】B【解析】由题意该几何体的直观图是由一个三棱锥和三棱柱构成，如下图，则该几何体各面内只有两个相同的梯形，则这些梯形的面积之和为12(24)212，故选．B2【名师点睛】三视图往往与几何体的体积、表面积以及空间线面关系、角、距离等问题相结合，解决此类问题的关键是由三视图准确确定空间几何体的形状及其结构特征并且熟悉常见几何体的三视图.15.【2017年高考全国Ⅱ卷理数】如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，该几何体由一平面将一圆柱截去一部分后所得，则该几何体的体积为A．90 C．42B．63 D．36【答案】B【解析】由题意，该几何体是一个组合体，下半部分是一个底面半径为3，高为4的圆柱，其体积V 32 436，上半部分是一个底面半径为，高为的圆柱的一半，其体积3 611 V (3 26) 27，故该组合体的体积V V V36 27 63．21 2 2故选 B ．【名师点睛】在由三视图还原为空间几何体的实际形状时，要从三个视图综合考虑，根据三视图的规则，空间几何体的可见轮廓线在三视图中为实线，不可见轮廓线在三视图中为虚线．在还原空间几何体实际形状时，一般是以正视图和俯视图为主，结合侧视图进行综合考虑．求解以三视图为载体的空间几何体的体积的关键是由三视图确定直观图的形状以及直观图中线面的位置关系和数量关系，利用相应体积公式求解．16. 【2017 年高考全国Ⅲ卷理数】已知圆柱的高为 1，它的两个底面的圆周在直径为 2 的同一个球的球面上，则该圆柱的体积为3π π A ．C ．B ．D ．4 π π24【答案】B【解析】绘制圆柱的轴截面如图所示：21 1 3 由题意可得： AC 1, AB ，结合勾股定理，底面半径 r 1 2，2 2 223 3由圆柱的体积公式，可得圆柱的体积是V πr 2h π 1 π ，故选 B.2 4【名师点睛】（1）求解空间几何体体积的关键是确定几何体的元素以及线面的位置关系和数量关系，利用相应体积公式求解；（2）若所给几何体的体积不能直接利用公式得出，则常用等积法、分割法、补形法等方法进行求解.17. 【2020 年高考全国 I I 卷理数】设有下列四个命题： p ：两两相交且不过同一点的三条直线必在同一平面内.1p ：过空间中任意三点有且仅有一个平面.2p ：若空间两条直线不相交，则这两条直线平行.3p ：若直线 l 平面α，直线 m ⊥平面α，则 m ⊥l . 4则下述命题中所有真命题的序号是__________.p p p p p ppp③④122334① ② 1 4【答案】①③④【解析】【分析】p p2利用两交线直线确定一个平面可判断命题的真假；利用三点共线可判断命题的真假；利用异面直线可1p p4判断命题的真假，利用线面垂直的定义可判断命题的真假.再利用复合命题的真假可得出结论.3p1l1l2【详解】对于命题，可设与相交，这两条直线确定的平面为；l l若与相交，则交点A 在平面内，3 1l l同理，与的交点B 也在平面内，3 2所以，AB ，即l3，命题为真命题；p1p2对于命题，若三点共线，则过这三个点的平面有无数个，p命题为假命题；2p对于命题，空间中两条直线相交、平行或异面，3p命题为假命题；3p4，若直线m 平面，对于命题m 垂直于平面则内所有直线，直线l 平面，直线m 直线，lp命题为真命题.4综上可知，，为真命题，，为假命题，p p p p为假命题，1 2为真命题，1 4p p p p为真命题.3 4为真命题，2 3故答案为：①③④.【点睛】本题考查复合命题的真假，同时也考查了空间中线面关系有关命题真假的判断，考查推理能力，属于中等题.18. 【2020 年高考全国Ⅲ理数】已知圆锥的底面半径为 1，母线长为 3，则该圆锥内半径最大的球的体积为_________． 2 【答案】 3【解析】【分析】将原问题转化为求解圆锥内切球的问题，然后结合截面确定其半径即可确定体积的值. 【详解】易知半径最大球为圆锥的内切球，球与圆锥内切时的轴截面如图所示，B C 2, AB AC 3 其中，且点 M 为 BC 边上的中点，设内切圆的圆心为O ，1由于A M 3 2 1 22 2 ，故 S △ABC2 2 2 2 2 ， 2r设内切圆半径为，则：1 1 1 S △AB C S △A O B S △BO C S △A O C AB r BC r AC r2 2 21 3 3 2r2 2 ，22 4 2解得： r =，其体积：V r 3 . 2 3 32故答案为：. 3【点睛】与球有关的组合体问题，一种是内切，一种是外接．解题时要认真分析图形，明确切点和接点的位置，确定有关元素间的数量关系，并作出合适的截面图，如球内切于正方体，切点为正方体各个面的中心，正方体的棱长等于球的直径；球外接于正方体，正方体的顶点均在球面上，正方体的体对角线长等于球的直径.19. 【2019 年高考全国Ⅲ卷理数】学生到工厂劳动实践，利用 3D 打印技术制作模型.如图，该模型为长方体AB C D A B C D 挖去四棱锥 O —EF G H 后所得的几何体，其中 O 为长方体的中心，E ，F ，G ，H 分11 1 1AB = BC = 6 cm, AA = 4 cm 别为所在棱的中点，，3D 打印所用原料密度为 0.9 g/cm 3，不考虑打印 1损耗，制作该模型所需原料的质量为___________g .【答案】118.81【解析】由题意得， S 46 4 23 12cm 2 ，四边形EF G H2 1∵四棱锥 O −EF G H 的高为 3cm ， ∴V O EF G H 123 12cm 3 ．3AB C D A B C D V 466 144cm，3又长方体的体积为 1 1 1 1 2 所以该模型体积为 VV V144 12 132cm 3 ，其质量为 0.9132 118.8g ．OEF G H2 【名师点睛】本题考查几何体的体积问题，理解题中信息联系几何体的体积和质量关系，从而利用公式求解．根据题意可知模型的体积为长方体体积与四棱锥体积之差进而求得模型的体积，再求出模型的质量即可.20. 【2019 年高考全国Ⅱ卷理数】中国有悠久的金石文化，印信是金石文化的代表之一．印信的形状多为长方体、正方体或圆柱体，但南北朝时期的官员独孤信的印信形状是“半正多面体”（图 1）.半正多面体是由两种或两种以上的正多边形围成的多面体．半正多面体体现了数学的对称美．图 2 是一个棱数为 48 的半正多面体，它的所有顶点都在同一个正方体的表面上，且此正方体的棱长为 1．则该半正多面体共有________个面，其棱长为_________．（本题第一空 2 分，第二空 3 分．）【答案】26，21【解析】由图可知第一层（包括上底面）与第三层（包括下底面）各有9个面，计18个面，第二层共有8个面，所以该半正多面体共有18826个面．x如图，设该半正多面体的棱长为，则AB BE x，延长CB与FE 的延长线交于点G，延长BC交正方体的棱于H ，由半正多面体对称性可知，△BG E 为等腰直角三角形，2 2BG GE C H x,G H 2x x(21)x1，2 21x21，21即该半正多面体的棱长为21．【名师点睛】本题立意新颖，空间想象能力要求高，物体位置还原是关键，遇到新题别慌乱，题目其实很简单，稳中求胜是关键．立体几何平面化，无论多难都不怕，强大空间想象能力，快速还原图形．721.【2018年高考全国I I卷理数】已知圆锥的顶点为S，母线SA，SB 所成角的余弦值为，SA与圆锥8 底面所成角为45°，若△SAB 的面积为515，则该圆锥的侧面积为__________．【答案】402π7 15 8【解析】因为母线 SA ， SB 所成角的余弦值为，所以母线 SA ， SB 所成角的正弦值为，因为 81 15 8 △SAB 的面积为5 15 ，设母线长为l ,所以l 2 25 15 ,l80 ， 2π 2因为 SA 与圆锥底面所成角为 45°，所以底面半径为 r l cosl , 4 22 因此圆锥的侧面积为 πr lπl 40 2π. 22【名师点睛】本题考查线面角、圆锥的侧面积、三角形面积等知识点，考查学生空间想象与运算能力. 先根据三角形面积公式求出母线长，再根据母线与底面所成角得底面半径，最后根据圆锥侧面积公式求结果.22. 【2017 年高考全国 I 卷理数】如图，圆形纸片的圆心为 O ，半径为 5 c m ，该纸片上的等边三角形 ABC 的中心为 O.D ，E ，F 为圆 O 上的点，△DB C ，△ECA ，△FA B 分别是以 BC ，CA ，AB 为底边的等腰三角形.沿虚线剪开后，分别以 BC ，CA ，AB 为折痕折起△DB C ，△ECA ，△FAB ，使得 D ，E ，F 重合，得到三棱锥.当△ABC 的边长变化时，所得三棱锥体积（单位：cm 3）的最大值为【答案】 4 15.【解析】如下图，连接 DO 交 BC 于点 G ，设 D ，E ，F 重合于 S 点，正三角形的边长为 x(x>0)，则 1 3 3O G x x. 3 2 63FG SG 5x ， 6223 3x3x， SO h SG2GO2 5 x 556 631 1 3 3 15 3 三棱锥的体积V S △ABC h x2 5 5 x 4 x 5 . 5x3 34 3 1233 5 3 设 n x 5x 4x 5 ，x>0，则 n x 20x 3 x 4， 3 3x 4 n x 0 ，即 4x 30，得，易知 n x 在令处取得最大值. x 4 3x 4 3 3 15∴V max 48 5 4 4 15 .12【名师点睛】对于三棱锥最值问题，需要用到函数思想进行解决，本题解决的关键是设好未知量，利用图形特征表示出三棱锥体积.当体积中的变量最高次是2次时可以利用二次函数的性质进行解决，当变量是高次时需要用到求导的方式进行解决.。

2020年高考数学立体几何专题复习(后附答案)

2020年高考数学立体几何专题复习（后附答案）教学目的1. 复习《立体几何初步》的相关知识及基本应用2. 掌握典型题型及其处理方法教学重点、难点《立体几何初步》的知识梳理和题型归类以及重点题型的处理方法知识分析1. 多面体的结构特征对于多面体的结构要从其反应的几何体的本质去把握，棱柱、棱锥、棱台是不同的多面体，但它们也有联系，棱柱可以看成是上、下底面全等的棱台；棱锥又可以看作是一底面缩为一点的棱台，因此它们的侧面积和体积公式可分别统一为一个公式。

2. 旋转体的结构特征旋转体是一个平面封闭图形绕一个轴旋转生成的，一定要弄清圆柱、圆锥、圆台、球分别是由哪一种平面图形旋转生成的，从而可掌握旋转体中各元素的关系，也就掌握了它们各自的性质。

3. 表面积与体积的计算有关柱、锥、台、球的面积和体积的计算，应以公式法为基础，充分利用几何体中的直角三角形、直角梯形求有关的几何元素。

4. 三视图与直观图的画法三视图和直观图是空间几何体的不同的表现形式，空间几何体的三视图可以使我们很好地把握空间几何体的性质．由空间几何体可以画出它的三视图，同样由三视图可以想象出空间几何体的形状，两者之间可以相互转化。

5. 线线平行的判定方法（1）定义：同一平面内没有公共点的两条直线是平行直线；（2）公理4：a b b c a c //////，，⇒；（3）平面几何中判定两直线平行的方法；（4）线面平行的性质：a a b a b ////αβαβ，，⊂=⇒ ；（5）线面垂直的性质：a b a b ⊥⊥⇒αα，//；（6）面面平行的性质：αβαγβγ////，， ==a a b 。

6. 直线和平面平行的判定方法（1）定义：a a αα=∅⇒//；（2）判定定理：a b a b a ////，，⊄⊂⇒ααα；（3）线面垂直的性质：b a b a a ⊥⊥⊄，，，ααα//；（4）面面平行的性质：αβαβ////，a a ⊂⇒。

7. 判定两个平面平行的方法（1）依定义采用反证法；（2）利用判定定理：αββαααβ//////，，，，b a b a b A ⊂⊂=⇒ ；（3）垂直于同一条直线的两个平面平行； a a ⊥⊥⇒αβαβ，//；（4）平行于同一平面的两个平面平行；αγβγαβ////，/⇒/。

高考数学压轴专题2020-2021备战高考《空间向量与立体几何》分类汇编附答案

新数学《空间向量与立体几何》高考知识点一、选择题1．如图，在正方体1111ABCD A B C D -中，M ， N 分别为棱111,C D CC 的中点，以下四个结论：①直线DM 与1CC 是相交直线；②直线AM 与NB 是平行直线；③直线BN 与1MB 是异面直线；④直线AM 与1DD 是异面直线．其中正确的个数为（）A ．1B ．2C ．3D ．4【答案】C【解析】【分析】根据正方体的几何特征，可通过判断每个选项中的两条直线字母表示的点是否共面；如果共面，则可能是相交或者平行；若不共面，则是异面.【详解】①：1CC 与DM 是共面的，且不平行，所以必定相交，故正确；②：若AM BN 、平行，又AD BC 、平行且,AM AD A BN BC B ⋂=⋂=，所以平面BNC P 平面ADM ，明显不正确，故错误；③：1BN MB 、不共面，所以是异面直线，故正确；④：1AM DD 、不共面，所以是异面直线，故正确；故选C.【点睛】异面直线的判断方法：一条直线上两点与另外一条直线上两点不共面，那么两条直线异面；反之则为共面直线，可能是平行也可能是相交.2．某四面体的三视图如图所示，正视图，俯视图都是腰长为2的等腰直角三角形，侧视图是边长为2的正方形，则此四面体的四个面中面积最大的为（）A．22B．23C．4 D．26【答案】B【解析】解：如图所示，该几何体是棱长为2的正方体中的三棱锥P ABC-，其中面积最大的面为：1232232PACSV=⨯⨯= .本题选择B选项.点睛：三视图的长度特征：“长对正、宽相等，高平齐”，即正视图和侧视图一样高、正视图和俯视图一样长，侧视图和俯视图一样宽．若相邻两物体的表面相交，表面的交线是它们的分界线，在三视图中，要注意实、虚线的画法．3．在正四面体A BCD-中，P是AB的中点，Q是直线BD上的动点，则直线PQ与AC所成角可能为（）A ．12πB ．4πC ．512πD ．2π 【答案】C【解析】【分析】根据题意，取BC 的中点M ，连接MQ ，则//AC MQ ，所以QPM ∠为异面直线PQ 与AC 所成角，在利用余弦定理可得242MQ x x =+-，易知PQ MQ =，所以在等腰三角形PMQ 中()2cos 0442QPM x x x ∠=≤≤+-，，即可求出33cos 123QPM ⎡⎤∠∈⎢⎥⎣⎦，，进而求出结果. 【详解】取BC 的中点M ，连接MQ ，则//AC MQ ，所以QPM ∠为异面直线PQ 与AC 所成角，如下图所示：设正四面体A BCD -的棱长为4，()04BQ x x =≤≤，，在BMQ ∆中，22222cos 6042MQ BM BQ BM BQ x x =+-⋅︒=+-，在正四面体A BCD -中，易知PQ MQ =，所以在等腰三角形PMQ 中，()2cos 0442QPM x x x ∠=≤≤+-所以33cos QPM ∠∈⎣⎦，，所以异面直线PQ 与AC 所成角可能为512π. 故选：C.【点睛】本题主要考查了异面直线成角，余弦定理的应用，考查了空间几何中的动态问题，考查学生的应用能力和空间想象能力，属于中档题.4．已知底面是等腰直角三角形的三棱锥P -ABC 的三视图如图所示，俯视图中的两个小三角形全等，则（）A ．PA ，PB ，PC 两两垂直B ．三棱锥P -ABC 的体积为83 C ．||||||6PA PB PC ===D ．三棱锥P -ABC 的侧面积为35【答案】C 【解析】【分析】根据三视图，可得三棱锥P -ABC 的直观图，然后再计算可得.【详解】解：根据三视图，可得三棱锥P -ABC 的直观图如图所示，其中D 为AB 的中点，PD ⊥底面ABC .所以三棱锥P -ABC 的体积为114222323⨯⨯⨯⨯=， 2AC BC PD ∴===，2222AB AC BC ∴=+=，||||||2DA DB DC ∴===()22||||||226,PA PB PC ∴===+=222PA PB AB +≠Q ，PA ∴、PB 不可能垂直，即,PA ,PB PC 不可能两两垂直， 1222222PBA S ∆=⨯=Q ()22161252PBC PAC S S ∆∆==-=Q ∴三棱锥P -ABC 的侧面积为2522故正确的为C.故选：C.【点睛】本题考查三视图还原直观图，以及三棱锥的表面积、体积的计算问题，属于中档题.5．如图所示是一个组合几何体的三视图，则该几何体的体积为（）A ．163πB ．643C ．16643π+ D ．1664π+ 【答案】C 【解析】由三视图可知，该几何体是有一个四棱锥与一个圆锥的四分之一组成，其中四棱锥的底面是边长为4 的正方形，高为4 ，圆锥的底面半径为4 ，高为4，该几何体的体积为， 221116644444333V ππ+=⨯⨯+⨯⨯⨯=，故选C. 6．鲁班锁（也称孔明锁、难人木、六子联方）起源于古代中国建筑的榫卯结构.这种三维的拼插器具内部的凹凸部分（即榫卯结构）啮合，十分巧妙.鲁班锁类玩具比较多，形状和内部的构造各不相同，一般都是易拆难装.如图1，这是一种常见的鲁班锁玩具，图2是该鲁班锁玩具的直观图，每条棱的长均为2，则该鲁班锁的表面积为（）A ．8(6623)+B ．6(8823)+C ．8(632)+D ．6(8832)+【答案】A【解析】【分析】该鲁班锁玩具可以看成是一个正方体截去了8个正三棱锥所余下来的几何体，然后按照表面积公式计算即可.【详解】由题图可知，该鲁班锁玩具可以看成是一个棱长为222+的正方体截去了8个正三棱锥所余下来的几何体，且被截去的正三棱锥的底面边长为22，则该几何体的2116(222)42282322S ⎡⎤=⨯+-⨯⨯⨯+⨯⨯⨯⎢⎥⎣⎦8(6623)=++. 故选：A.【点睛】本题考查数学文化与简单几何体的表面积，考查空间想象能力和运算求解能力.7．已知,m l 是两条不同的直线，,αβ是两个不同的平面，则下列可以推出αβ⊥的是（）A ．,,m l m l βα⊥⊂⊥B ．,,m l l m αβα⊥⋂=⊂C ．//,,m l m l αβ⊥⊥D ．,//,//l m l m αβ⊥【答案】D【解析】【分析】A ，有可能出现α，β平行这种情况.B ，会出现平面α，β相交但不垂直的情况.C ，根据面面平行的性质定理判断.D ，根据面面垂直的判定定理判断.【详解】对于A ，m l ⊥，m β⊂，若l β⊥，则//αβ，故A 错误；对于B ，会出现平面α，β相交但不垂直的情况，故B 错误；对于C ，因为//m l ，m α⊥，则l α⊥，又因为l βαβ⊥⇒∥，故C 错误；对于D ，l α⊥，m l m α⇒⊥∥，又由m βαβ⇒⊥∥，故D 正确.故选：D【点睛】本题考查空间中的平行、垂直关系的判定，还考查学生的空间想象能力和逻辑推理能力，属于中档题.8．如图，正方形网格纸中的实线图形是一个多面体的三视图，则该多面体各表面所在平面互相垂直的有（）A ．2对B ．3对C ．4对D ．5对【答案】C【分析】画出该几何体的直观图P ABCD -，易证平面PAD ⊥平面ABCD ，平面PCD ⊥平面PAD ，平面PAB ⊥平面PAD ，平面PAB ⊥平面PCD ，从而可选出答案．【详解】该几何体是一个四棱锥，直观图如下图所示，易知平面PAD ⊥平面ABCD ，作PO ⊥AD 于O ，则有PO ⊥平面ABCD ，PO ⊥CD ，又AD ⊥CD ，所以，CD ⊥平面PAD ，所以平面PCD ⊥平面PAD ，同理可证：平面PAB ⊥平面PAD ，由三视图可知：PO ＝AO ＝OD ，所以，AP ⊥PD ，又AP ⊥CD ，所以，AP ⊥平面PCD ，所以，平面PAB ⊥平面PCD ，所以该多面体各表面所在平面互相垂直的有4对．【点睛】本题考查了空间几何体的三视图，考查了四棱锥的结构特征，考查了面面垂直的证明，属于中档题．9．在四面体ABCD 中，AB ，BC ，BD 两两垂直，4AB BC BD ===，E 、F 分别为棱BC 、AD 的中点，则直线EF 与平面ACD 所成角的余弦值（）A ．13B ．33C ．23D ．63【答案】C【解析】【分析】因为AB ，BC ，BD 两两垂直，以BA 为X 轴，以BD 为Y 轴，以BC 为Z 轴建立空间直角坐标系，求出向量EF u u u r 与平面ACD 的法向量n r ，再根据cos ,||||EF n EF n EF n ⋅〈〉=u u u r r u u u r r u u u r r ，即可得出答案.【详解】因为在四面体ABCD 中，AB ，BC ，BD 两两垂直，以BA 为X 轴，以BD 为Y 轴，以BC 为Z 轴建立空间直角坐标系，又因为4AB BC BD ===；()4,0,0,(0,0,0),(0,4,0),(0,0,4)A B D C ，又因为E 、F 分别为棱BC 、AD 的中点所以(0,0,2),(2,2,0)E F 故()2,2,2EF =-u u u r ，(4,4,0)AD =-u u u r ，(4,0,4)AC =-u u u r .设平面ACD 的法向量为(,,)n x y z =r ，则00n AD n AC ⎧⋅=⎨⋅=⎩u u u v v u u uv v 令1,x = 则1y z ==；所以(1,1,1)n =r 1cos ,3||||332EF n EF n EF n ⋅〈〉===⨯u u u r r u u u r r u u u r r 设直线EF 与平面ACD 所成角为θ ，则sin θ= cos ,EF n 〈〉u u u r r 所以222cos 1sin θθ=-=故选：C【点睛】本题主要考查线面角，通过向量法即可求出，属于中档题目.10．在以下命题中： ①三个非零向量a r ，b r ，c r 不能构成空间的一个基底，则a r ，b r ，c r 共面； ②若两个非零向量a r ，b r 与任何一个向量都不能构成空间的一个基底，则a r ，b r 共线； ③对空间任意一点O 和不共线的三点A ，B ，C ，若222OP OA OB OC =--u u u r u u u r u u u u r u u u u r ，则P ，A ，B ，C 四点共面 ④若a r ，b r 是两个不共线的向量，且(,,,0)c a b R λμλμλμ=+∈≠r r r ，则{},,a b c r r r 构成空间的一个基底 ⑤若{},,a b c r r r 为空间的一个基底，则{},,a b b c c a +++r r r r r r 构成空间的另一个基底；其中真命题的个数是（）A ．0B ．1C ．2D ．3【答案】D【解析】【分析】根据空间向量的运算法则，逐一判断即可得到结论.【详解】①由空间基底的定义知，三个非零向量a r ，b r ，c r 不能构成空间的一个基底，则a r ，b r ，c r 共面，故①正确；②由空间基底的定义知，若两个非零向量a r ，b r与任何一个向量都不能构成空间的一个基底，则a r ，b r 共线，故②正确；③由22221--=-≠，根据共面向量定理知,,,P A B C 四点不共面，故③错误； ④由c a b λμ=+r r r ，当1λμ+=时，向量c r 与向量a r ，b r 构成的平面共面，则{},,a b c r r r 不能构成空间的一个基底，故④错误； ⑤利用反证法：若{},,a b b c c a +++r r r r r r 不构成空间的一个基底，设()()()1a b x b c x c a +=++-+r r r r r r ，整理得()1c xa x b =+-r r r ，即,,a b c r r r 共面，又因{},,a b c r r r 为空间的一个基底，所以{},,a b b c c a +++r r r r r r 能构成空间的一个基底，故⑤正确. 综上：①②⑤正确.故选：D.【点睛】本题考查空间向量基本运算，向量共面，向量共线等基础知识，以及空间基底的定义，共面向量的定义，属于基础题．11．如图，在直三棱柱111ABC A B C -中，4AC BC ==，AC BC ⊥，15CC =，D 、E 分别是AB 、11B C 的中点，则异面直线BE 与CD 所成的角的余弦值为（）A ．3B ．13C ．58D ．387 【答案】C【解析】【分析】取11A C 的中点F ，连接DF 、EF 、CF ，推导出四边形BDFE 为平行四边形，可得出//BE DF ，可得出异面直线BE 与CD 所成的角为CDF ∠，通过解CDF V ，利用余弦定理可求得异面直线BE 与CD 所成的角的余弦值.【详解】取11A C 的中点F ，连接DF 、EF 、CF .易知EF 是111A B C △的中位线，所以11//EF A B 且1112EF A B =. 又11//AB A B 且11AB A B =，D 为AB 的中点，所以11//BD A B 且1112BD A B =，所以//EF BD 且EF BD =.所以四边形BDFE 是平行四边形，所以//DF BE ，所以CDF ∠就是异面直线BE 与CD 所成的角.因为4AC BC ==，AC BC ⊥，15CC =，D 、E 、F 分别是AB 、11B C 、11A C 的中点，所以111122C F AC ==，111122B E BC ==且CD AB ⊥.由勾股定理得AB ==AC BC CD AB ⋅===由勾股定理得CF ===DF BE ====.在CDF V 中，由余弦定理得222cosCDF +-∠==. 故选：C.【点睛】本题考查异面直线所成角的余弦值的计算，一般利用平移直线法找出异面直线所成的角，考查计算能力，属于中等题.12．在棱长为1的正方体1111ABCD A B C D -中,点12,P P 分别是线段1,AB BD （不包括端点）上的动点,且线段12PP 平行于平面11AADD ,则四面体121PP AB 的体积的最大值是 A ．124 B ．112 C ．16 D ．12【答案】A【解析】由题意在棱长为1的正方体1111ABCD A B C D -中，点12,P P 分别是线段1,AB BD 上的动点，且线段12PP 平行于平面11121,AADD PP B AD B ∆~∆，设1,(0,1)PB x x =∈，即122,PP P =到平面11AA B B 的距离为x ，所以四棱锥121PP AB 的体积为2111(1)1()326V x x x x =⨯⨯-⨯⨯=-，当12x=时，体积取得最大值124，故选A．点睛：本题考查了空间几何体的结构特征，及几何体的体积的计算，其中解答中找出所求四面体的底面面积和四面体的高是解答的关键，着重考查了分析问题和解答问题的能力，对于空间几何体的体积与表面积的计算时，要正确把握几何体的结构特征和线面位置关系在解答中的应用．13．一个几何体的三视图如图所示，则该几何体的体积为A．383+B．823+C．283D．10【答案】A【解析】【分析】根据三视图可知该几何体为一组合体，是一个棱长为2的正方体与三棱锥的组合体，根据体积公式分别计算即可.【详解】几何体为正方体与三棱锥的组合体，由正视图、俯视图可得该几何体的体积为311232+2328323V=⨯⨯=+,故选A.【点睛】本题主要考查了三视图，正方体与三棱锥的体积公式，属于中档题.14．已知正方体1111ABCD A B C D -中，M ，N 分别为AB ，1AA 的中点，则异面直线1C M 与BN 所成角的大小为（）A ．30°B ．45︒C ．60︒D ．90︒【答案】D【解析】【分析】根据题意画出图形，可将异面直线转化共面的相交直线，再进行求解【详解】如图：作AN 的中点'N ，连接'N M ，1'C N 由题设可知'N M BN P ，则异面直线1C M 与BN 所成角为1'N MC ∠或其补角，设正方体的边长为4，由几何关系可得，'5N M =，16C M =，1'41C N =21122''N M M C N C =+，即1'90N MC ∠=︒ 故选D【点睛】本题考查异面直线的求法，属于基础题15．已知圆柱的上、下底面的中心分别为1O ，2O ，过直线12O O 的平面截该圆柱所得的截面是面积为8的正方形，则该圆柱的表面积为A ．122πB ．12πC ．82πD ．10π【答案】B【解析】分析：首先根据正方形的面积求得正方形的边长，从而进一步确定圆柱的底面圆半径与圆柱的高，从而利用相关公式求得圆柱的表面积. 详解：根据题意，可得截面是边长为2 2的圆，且高为2，所以其表面积为222)22212S πππ=+=，故选B.点睛：该题考查的是有关圆柱的表面积的求解问题，在解题的过程中，需要利用题的条件确定圆柱的相关量，即圆柱的底面圆的半径以及圆柱的高，在求圆柱的表面积的时候，一定要注意是两个底面圆与侧面积的和.16．已知直线和不同的平面，下列命题中正确的是A ．//m m αβαβ⊥⎫⇒⎬⊥⎭B ．m m αββα⊥⎫⇒⊥⎬⊂⎭C ．//////m m ααββ⎫⇒⎬⎭D ．////m m αββα⎫⇒⎬⊂⎭【答案】D【解析】【分析】对各个选项逐一进行分析即可【详解】 A ，若αβ⊥，m β⊥，则有可能m α⊂，故A 错误B ，若αβ⊥，m α⊂，则m 与β不一定垂直，可能相交或平行，故B 错误C ，若//m α，//m β则推不出//αβ，面面平行需要在一个面内找出两条相交线与另一个平面平行，故C 错误D ，若//αβ，m α⊂，则有//m β，故D 正确故选D【点睛】本题考查了线面平行与面面平行的判断和性质，在对其判定时需要运用其平行的判定定理或者性质定理，所以要对课本知识掌握牢固，从而判断结果17．已知某几何体的三视图如图所示，其中正视图与侧视图是全等的直角三角形，则该几何体的各个面中，最大面的面积为（）A ．2B ．5C 13D 22【答案】D【解析】【分析】根据三视图还原出几何体，找到最大面，再求面积.【详解】由三视图可知，该几何体是一个三棱锥，如图所示，将其放在一个长方体中，并记为三棱锥P ABC -.13PAC PAB S S ∆∆==，22PAC S ∆=，2ABC S ∆=，故最大面的面积为22.选D.【点睛】本题主要考查三视图的识别，复杂的三视图还原为几何体时，一般借助长方体来实现.18．如图1，已知正方体ABCD-A 1B 1C 1D 1的棱长为2，M ，N ，Q 分别是线段AD 1，B 1C ，C 1D 1上的动点，当三棱锥Q-BMN 的正视图如图2所示时，三棱锥俯视图的面积为A ．2B ．1C ．32D ．52【答案】C【解析】【分析】判断俯视图的形状，利用三视图数据求解俯视图的面积即可．【详解】由正视图可知：M 是1AD 的中点，N 在1B 处，Q 在11C D 的中点，俯视图如图所示：可得其面积为：1113222111122222⨯-⨯⨯-⨯⨯-⨯⨯=，故选C ．【点睛】本题主要考查三视图求解几何体的面积与体积，判断它的形状是解题的关键，属于中档题.19．设,αβ是两个不同的平面，,l m 是两条不同的直线，且l α⊂，m β⊂，则（） A ．若//αβ，则//l mB ．若//m a ，则//αβC ．若m α⊥，则αβ⊥D ．若αβ⊥，则//l m【答案】C【解析】【分析】根据空间线线、线面、面面的位置关系，对选项进行逐一判断可得答案.【详解】A. 若//αβ，则l 与m 可能平行，可能异面，所以A 不正确.B. 若//m a ，则α与β可能平行，可能相交，所以B 不正确.C. 若m α⊥，由m β⊂，根据面面垂直的判定定理可得αβ⊥，所以C 正确. D 若αβ⊥，且l α⊂，m β⊂，则l 与m 可能平行，可能异面，可能相交, 所以D 不正确.【点睛】本题考查空间线线、线面、面面的位置判断定理和性质定理，考查空间想象能力，属于基础题.20．一个各面均为直角三角形的四面体有三条棱长为2，则该四面体外接球的表面积为（）A ．6πB ．12πC ．32πD ．48π【答案】B【解析】【分析】先作出几何图形，确定四个直角和边长，再找到外接球的球心和半径，再计算外接球的表面积.【详解】由题得几何体原图如图所示，其中SA⊥平面ABC,BC⊥平面SAB,SA=AB=BC=2,所以2,3SC=设SC中点为O,则在直角三角形SAC中，3,在直角三角形SBC中，OB=13 2SC=所以3所以点O3所以四面体外接球的表面积为43=12ππ.故选：B【点睛】本题主要考查四面体的外接球的表面积的计算，意在考查学生对这些知识的理解掌握水平和分析推理的能力.。

高考数学压轴专题2020-2021备战高考《空间向量与立体几何》基础测试题含答案解析

高考数学《空间向量与立体几何》课后练习一、选择题1．如图，平面四边形ABCD 中，1AB AD CD ===，2BD =，BD CD ⊥，将其沿对角线BD 折成四面体A BCD '-，使平面A BD '⊥平面BCD ，若四面体A BCD '-的顶点在同一个球面上，则该球的表面积为（）A ．3πB 3C ．4πD 3 【答案】A【解析】【分析】设BC 的中点是E ，连接DE ，由四面体A′BCD 的特征可知，DE 即为球体的半径.【详解】设BC 的中点是E ，连接DE ，A′E ，因为AB ＝AD ＝1，BD 2由勾股定理得：BA ⊥AD又因为BD ⊥CD ，即三角形BCD 为直角三角形所以DE 为球体的半径3DE = 2343S ππ== 故选A【点睛】求解球体的表面积、体积的问题，其实质是求球体的半径，解题的关键是构造关于球体半径R 的方程式，构造常用的方法是构造直角三角形，再利用勾股定理建立关于半径R 的方程.2．若四面体的三视图如图所示，则该四面体的四个面中，直角三角形的面积和为（）A ．2B ．25+C ．425+D ．4【答案】B【解析】【分析】根据四面体的三视图可知：一侧面垂直于底面，且底面是以该侧面与底面的交线为直角边的直角三角形，然后根据面面垂直的性质定理，得到与底面的另一直角边为交线的侧面为直角三角形求解.【详解】由四面体的三视图可知：平面PAB ⊥平面ABC ，BC AB ⊥，所以BC ⊥平面PAB ，所以BC PB ⊥，所以,ABC PBC V V 是直角三角形，如图所示：所以直角三角形的面积和为:11112252252222ABC PBC S S AB BC PB BC +=⨯⨯+⨯⨯=⨯⨯+=+V V 故选：B【点睛】本题主要考查三视图的应用以及线面垂直，面面垂直的关系，还考查了运算求解的能力，属于中档题.3．如图，棱长为1的正方体1111ABCD A B C D -，O 是底面1111D C B A 的中心，则O 到平面11ABC D 的距离是（）A ．12B ．24C ．22D ．32【答案】B【解析】【分析】如图建立空间直角坐标系，可证明1A D ⊥平面11ABC D ，故平面11ABC D 的一个法向量为：1DA u u u u r ，利用点到平面距离的向量公式即得解.【详解】如图建立空间直角坐标系，则：1111(,,1),(0,0,1),(1,0,0),(1,1,0),(0,1,1)22O D A B C 111(,,0)22OD ∴=--u u u u r 由于AB ⊥平面111,ADD A AD ⊂平面11ADD A1AB A D ∴⊥，又11AD A D ⊥，1AB AD I1A D ∴⊥平面11ABC D 故平面11ABC D 的一个法向量为：1(1,0,1)DA =u u u u rO ∴到平面11ABC D 的距离为： 1111||224||2OD DA d DA ⋅===u u u u r u u u u r u u u u r 故选：B【点睛】本题考查了点到平面距离的向量表示，考查了学生空间想象，概念理解，数学运算的能力，属于中档题.4．如图，网格纸是由边长为1的小正方形构成，若粗实线画出的是某几何体的三视图，则该几何体的表面积为（）A ．920π+B ．926π+C ．520π+D ．526π+【答案】C【解析】【分析】根据三视图还原为几何体，结合组合体的结构特征求解表面积.【详解】由三视图可知，该几何体可看作是半个圆柱和一个长方体的组合体，其中半圆柱的底面半圆半径为1，高为4，长方体的底面四边形相邻边长分别为1，2，高为4，所以该几何体的表面积2112141222S ππ=⨯+⨯⨯⨯+⨯⨯14224520π+⨯⨯+⨯=+，故选C. 【点睛】本题主要考查三视图的识别，利用三视图还原成几何体是求解关键，侧重考查直观想象和数学运算的核心素养.5．已知某几何体的三视图如图所示，则该几何体的外接球的表面积为（）A ．3πB ．πC ．3πD ．12π【答案】C【解析】【分析】该几何体是一个三棱锥，且同一个顶点处的三条棱两两垂直并且相等，把这个三棱锥放到正方体中，即可求出其外接球的表面积.【详解】由三视图可知，该几何体是一个三棱锥，且同一个顶点处的三条棱两两垂直并且相等，如图所示该几何体是棱长为1的正方体中的三棱锥1A BCD AB BC BD -===，.所以该三棱锥的外接球即为此正方体的外接球，球的直径2r 为正方体体对角线的长. 即22221113r =++=.所以外接球的表面积为243r ππ=.故选：C .【点睛】本题考查几何体的三视图，考查学生的空间想象能力，属于基础题.6．三棱柱111ABC A B C -中，底面边长和侧棱长都相等，1160BAA CAA ︒∠=∠=，则异面直线1AB 与1BC 所成角的余弦值为（）A 3B 6C 3D ．36【答案】B【解析】【分析】设1AA c=u u u v v ，AB a =u u u v v ，AC b =u u u v v ，根据向量线性运算法则可表示出1AB u u u v 和1BC u u u u v ；分别求解出11AB BC ⋅u u u v u u u u v 和1AB u u u v ，1BC u u u u v ，根据向量夹角的求解方法求得11cos ,AB BC <>u u u v u u u u v ，即可得所求角的余弦值.【详解】设棱长为1，1AA c =u u u v v ，AB a =u u u v v ，AC b =u u u v v 由题意得：12a b ⋅=v v ，12b c ⋅=v v ，12a c ⋅=v v 1AB a c =+u u u v v v Q ，11BC BC BB b a c =+=-+u u u u v u u u v u u u v v v v()()22111111122AB BC a c b a c a b a a c b c a c c ∴⋅=+⋅-+=⋅-+⋅+⋅-⋅+=-++=u u u v u u u u v v v v v v v v v v v v v v v v 又()222123AB a c a a c c =+=+⋅+=u u u v v v v v v v ()222212222BC b a c b a c a b b c a c =-+=++-⋅+⋅-⋅=u u u u v v v v v v v v v v v v v 1111116cos ,6AB BC AB BC AB BC ⋅∴<>===⋅u u u v u u u u v u u u v u u u u v u u u v u u u u v 即异面直线1AB 与1BC 所成角的余弦值为：66本题正确选项：B【点睛】本题考查异面直线所成角的求解，关键是能够通过向量的线性运算、数量积运算将问题转化为向量夹角的求解问题.7．如图，在底面边长为4，侧棱长为6的正四棱锥P ABCD -中，E 为侧棱PD 的中点，则异面直线PB 与CE 所成角的余弦值是（）A ．34B ．234C ．517D ．317 【答案】D【解析】【分析】首先通过作平行的辅助线确定异面直线PB 与CE 所成角的平面角，在PCD ∆中利用余弦定理求出cos DPC ∠进而求出CE ，再在GFH ∆中利用余弦定理即可得解.【详解】如图，取PA 的中点F ，AB 的中点G ，BC 的中点H ，连接FG ，FH ，GH ，EF ，则//EF CH ，EF CH =，从而四边形EFHC 是平行四边形，则//EC FH ，且EC FH =.因为F 是PA 的中点，G 是AB 的中点，所以FG 为ABP ∆的中位线，所以//FG PB ，则GFH ∠是异面直线PB 与CE 所成的角.由题意可得3FG =，1222HG AC ==. 在PCD ∆中，由余弦定理可得2223636167cos 22669PD PC CD DPC PD PC +-+-∠===⋅⨯⨯，则2222cos 17CE PC PE PC PE DPC =+-⋅∠=，即17CE =在GFH ∆中，由余弦定理可得222cos 2FG FH GH GFH FG FH +-∠=⋅317172317==⨯⨯. 故选：D【点睛】本题考查异面直线所成的角，余弦定理解三角形，属于中档题.8．《九章算术》是中国古代的数学瑰宝，其第五卷商功中有如下问题：“今有羡除，下广六尺，上广一丈，深三尺，末广八尺，无深，袤七尺，问积几何？”翻译成现代汉语就是：今有三面皆为等腰梯形，其他两侧面为直角三角形的五面体的隧道，前端下宽6尺，上宽一丈，深3尺，末端宽8尺，无深，长7尺（注：一丈=十尺）．则该五面体的体积为（）A ．66立方尺B ．78立方尺C ．84立方尺D ．92立方尺【答案】C【解析】【分析】如图，在DC ，EF 上取G ，H ，使得DG EH AB ==，连接BG ，BH ，GH ，CH ，ADE BGH B CGHF V V V --=+，计算得到答案.【详解】如图，在DC ，EF 上取G ，H ，使得DG EH AB ==，连接BG ，BH ，GH ，CH ，故多面体的体积11()7332ADE BGH B CGHF V V V S AB CG HF --=+=⋅+⨯+⨯⨯直截面 111736(42)7384232=⨯⨯⨯+⨯⨯⨯⨯=，故选：C ．【点睛】本题考查了几何体体积的计算，意在考查学生的计算能力和空间想象能力.9．若圆锥的高等于底面直径，则它的底面积与侧面积之比为A ．1∶2B ．13C ．15D 32【答案】C【解析】【分析】由已知，求出圆锥的母线长，进而求出圆锥的底面面积和侧面积，可得答案【详解】设圆锥底面半径为r ，则高h ＝2r ，∴其母线长l ＝r ．∴S 侧＝πrl ＝πr 2，S 底＝πr 故选C ．【点睛】本题考查的知识点是旋转体，圆锥的表面积公式，属于基础题．10．如图，在正方体1111ABCD A B C D -中，M ， N 分别为棱111,C D CC 的中点，以下四个结论：①直线DM 与1CC 是相交直线；②直线AM 与NB 是平行直线；③直线BN 与1MB 是异面直线；④直线AM 与1DD 是异面直线．其中正确的个数为（）A ．1B ．2C ．3D ．4【答案】C【解析】【分析】根据正方体的几何特征，可通过判断每个选项中的两条直线字母表示的点是否共面；如果共面，则可能是相交或者平行；若不共面，则是异面.【详解】①：1CC 与DM 是共面的，且不平行，所以必定相交，故正确；②：若AM BN 、平行，又AD BC 、平行且,AM AD A BN BC B ⋂=⋂=，所以平面BNC P 平面ADM ，明显不正确，故错误；③：1BN MB 、不共面，所以是异面直线，故正确；④：1AM DD 、不共面，所以是异面直线，故正确；故选C.【点睛】异面直线的判断方法：一条直线上两点与另外一条直线上两点不共面，那么两条直线异面；反之则为共面直线，可能是平行也可能是相交.11．我国南北朝时期数学家祖暅，提出了著名的祖暅原理：“缘幂势既同，则积不容异也”．“幂”是截面积，“势”是几何体的高，意思是两等高几何体，若在每一等高处的截面积都相等，则两几何体体积相等．已知某不规则几何体与右侧三视图所对应的几何体满足“幂势既同”，其中俯视图中的圆弧为14圆周，则该不规则几何体的体积为（）A ．12π+B ．136π+C ．12π+D ．1233π+ 【答案】B【解析】【分析】根据三视图知该几何体是三棱锥与14圆锥体的所得组合体，结合图中数据计算该组合体的体积即可．【详解】解：根据三视图知，该几何体是三棱锥与14圆锥体的组合体，如图所示；则该组合体的体积为21111111212323436V ππ=⨯⨯⨯⨯+⨯⨯⨯=+；所以对应不规则几何体的体积为136π+．故选B ．【点睛】本题考查了简单组合体的体积计算问题，也考查了三视图转化为几何体直观图的应用问题，是基础题．12．一个几何体的三视图如图所示，其中正视图和俯视图中的四边形是边长为2的正方形，则该几何体的表面积为( )A ．132πB ．7πC ．152πD ．8π【答案】B【解析】【分析】画出几何体的直观图，利用三视图的数据求解表面积即可．【详解】由题意可知：几何体是一个圆柱与一个14的球的组合体，球的半径为：1，圆柱的高为2，可得：该几何体的表面积为：22141212274ππππ⨯⨯+⨯⨯+⨯=．故选：B ．【点睛】思考三视图还原空间几何体首先应深刻理解三视图之间的关系，遵循“长对正，高平齐，宽相等”的基本原则，其内涵为正视图的高是几何体的高，长是几何体的长；俯视图的长是几何体的长，宽是几何体的宽；侧视图的高是几何体的高，宽是几何体的宽.由三视图画出直观图的步骤和思考方法：1、首先看俯视图，根据俯视图画出几何体地面的直观图；2、观察正视图和侧视图找到几何体前、后、左、右的高度；3、画出整体，然后再根据三视图进行调整.13．古代数学名著《张丘建算经》中有如下问题：“今有仓，东西袤一丈二尺，南北广七尺，南壁高九尺，北壁高八尺，问受粟几何？”.题目的意思是：“有一粮仓的三视图如图所示（单位：尺），问能储存多少粟米？”已知1斛米的体积约为1.62立方尺，估算粮仓可以储存的粟米约有（取整数）（）A ．441斛B ．431斛C ．426斛D ．412斛【答案】A【解析】【分析】由三视图可知：上面是一个横放的三棱柱，下面是一个长方体．由体积计算公式即可得出．【详解】解：由三视图可知：上面是一个横放的三棱柱，下面是一个长方体．∴体积1171278127142V =⨯⨯⨯+⨯⨯=，∴粮仓可以储存的粟米7144411.62=≈斛．故选：A ．14．已知正三棱柱111ABC A B C -的所有棱长都相等，D 是11A B 的中点，则AD 与平面11BCC B 所成角的正弦值为（） A 5B 25 C 10D 15 【答案】D【解析】【分析】先找出直线AD 与平面11BCC B 所成角，然后在1B EF V 中，求出1sin EB F ∠，即可得到本题答案.【详解】如图，取AB 中点E ，作EF BC ⊥于F ，连接11,B E B F ，则1EB F ∠即为AD 与平面11BCC B 所成角.不妨设棱长为4，则1,2BF BE ==，13,25EF B E ∴==1315sin 1025EB F ∴∠==. 故选：D【点睛】本题主要考查直线与平面所成角的求法，找出线面所成角是解决此类题目的关键.15．某四面体的三视图如图所示，正视图，俯视图都是腰长为2的等腰直角三角形，侧视图是边长为2的正方形，则此四面体的四个面中面积最大的为（）A ．2B ．3C ．4D ．26【答案】B【解析】解：如图所示，该几何体是棱长为2的正方体中的三棱锥P ABC - ，其中面积最大的面为：1232232PAC S V =⨯= 本题选择B 选项.点睛：三视图的长度特征：“长对正、宽相等，高平齐”，即正视图和侧视图一样高、正视图和俯视图一样长，侧视图和俯视图一样宽．若相邻两物体的表面相交，表面的交线是它们的分界线，在三视图中，要注意实、虚线的画法．16．已知四面体P ABC -的外接球的球心O 在AB 上，且PO ⊥平面ABC ，23AC AB =，若四面体P ABC -的体积为32，求球的表面积( ) A ．8πB ．12πC ．83πD ．3π 【答案】B【解析】【分析】依据题意作出图形，设四面体P ABC -的外接球的半径为R ，由题可得：AB 为球的直径，即可求得：2AB R =，3AC R =， BC R =，利用四面体P ABC -的体积为32列方程即可求得3R =【详解】依据题意作出图形如下：设四面体P ABC -的外接球的半径为R ，因为球心O 在AB 上，所以AB 为球的直径，所以2AB R =，且AC BC ⊥ 由23AC =可得：3AC R =， BC R =所以四面体P ABC -的体积为111333322ABC V S PO R R R ∆=⋅=⨯⨯⨯= 解得：3R =所以球的表面积2412S R ππ==故选：B【点睛】本题主要考查了锥体体积公式及方程思想，还考查了球的表面积公式及计算能力，考查了空间思维能力，属于中档题。

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

2019届高三第二次模拟数学理试题分类汇编：立体几何一、填空、选择题1、（崇明县2016届高三二模）已知圆锥的母线长为5cm ，侧面积为15πcm 2，则此圆锥的体积为cm 2．2、（奉贤区2016届高三二模）在棱长为1的正方体ABCD A B C D ''''-中，若点P 是棱上一点，则满足2PA PC '+=的点P 的个数_______．3、（虹口区2016届高三二模）已知A 、B 是球O 的球面上两点，90AOB ∠=o，C 为该球面上的动点，若三棱锥ABC O -体积的最大值为323，则球O 的表面积为__________4、（黄浦区2016届高三二模）已知一个凸多边形的平面展开图由两个正六边形和六个正方形构成，如右上图所示，若该凸多面体所有棱长均为1，则其体积V =5、（静安区2016届高三二模）如图，正四棱锥P ABCD -的底面边长为23cm ，侧面积为 283cm ，则它的体积为.6、（闵行区2016届高三二模）若一个圆锥的母线长是底面半径的3倍，则该圆锥的侧面积是底面积的倍.7、（浦东新区2016届高三二模）已知四面体ABCD 中，2==CD AB ，E ，F分别为BC ，AD 的中点，且异面直线AB 与CD 所成的角为3π，则EF =________．8、（普陀区2016届高三二模）若a 、b 表示两条直线，α表示平面，下列命题中的真命题为（）（A ）若α⊥a ，b a ⊥，则α//b （B ）若α//a ，b a ⊥，则α⊥b （C ）若α⊥a ，α⊆b ，则b a ⊥ （D ）若α//a ，α//b ，则b a // 9、（徐汇、金山、松江区2016届高三二模）．如图，圆锥形容器的高为,h 圆锥内水面的高为1,h 且11,3h h =若将圆锥倒置，水面高为2,h 则2h 等于------------------------------------------------（）（A ）23h （B ）1927h（C ）363h （D ）10、（杨浦区2016届高三二模）已知命题：“若a,b 为异面直线，平面α过直线a 且与直线b 平行，则直线b 与平面α的距离等于异面直线a,b 之间的距离”为真命题.根据上述命题，若a,b 为异面直线，且它们之间的距离为d ，则空间中与a,b 均异面且距离也均为d 的直线c 的条数为（）A0条 B.1条 C.多于1条，但为有限条 D.无数多条11、（闸北区2016届高三二模）已知,,,S A B C 是球O 表面上的点，SA ⊥平面ABC ，AB BC ⊥，1SA AB == BC =O 的表面积等于（）A ．π4 B ．π3 C ．π2 D ．π12、（长宁、青浦、宝山、嘉定四区2016届高三二模）下列命题正确的是（）．（A ）若直线1l ∥平面α，直线2l ∥平面α，则1l ∥2l ；（B ）若直线l 上有两个点到平面α的距离相等，则l ∥α；（C ）直线l 与平面α所成角的取值范围是⎪⎭⎫ ⎝⎛2,0π；（D ）若直线1l ⊥平面α，直线2l ⊥平面α，则1l ∥2l .13、（闵行区2016届高三二模）如图，在正方体1111ABCD A B C D -中，E 是1AA 的中点，P 为底面ABCD 内一动点，设1PD PE 、与底面ABCD 所成的角分别为12θθ、（12θθ、均不为0)．若12θθ=，则动点P 的轨迹为哪种曲线的一部分（）.(A)直线 (B)圆 (C) 椭圆 (D) 抛物线14、（浦东新区2016届高三二模）给出下列命题，其中正确的命题为( )（A ）若直线a 和b 共面，直线b 和c 共面，则a 和c 共面；（B ）直线a 与平面α不垂直，则a 与平面α内的所有直线都不垂直；（C ）直线a 与平面α不平行，则a 与平面α内的所有直线都不平行；（D ）异面直线a 、b 不垂直，则过a 的任何平面与b 都不垂直. 二、解答题1、（崇明县2016届高三二模）如图，在棱长为1的正方体1111ABCD A B C D -中，点E 是棱BC 的中点，点F 是棱CD 的中点．（1）求证：11EF B D ∥；（2）求二面角1C EF A --的大小C C 1A 1B 1D 1DFE（结果用反三角函数值表示）．2、（奉贤区2016届高三二模）面ABC 外的一点P ，,,AP AB AC 两两互相垂直，过AC 的中点D 作ED ⊥面ABC ，且1ED =，2PA =，2AC =，连,BP BE ，多面体B PADE -的体积是3．(1)画出面PBE 与面ABC 的交线，说明理由；（2）求面PBE 与面ABC 所成的锐二面角的大小．ADBCPEQ A DCBP （第20题图）3、（虹口区2016届高三二模）如图，在四棱锥ABCD P -中，已知⊥PA 平面ABCD ，且四边形ABCD 为直角梯形，90ABC BAD ∠=∠=︒，2AB AD AP ===，1BC =.(1) 求点A 到平面PCD 的距离； (2) 若点Q 为线段BP 的中点，求直线CQ 与平面ADQ 所成角的大小.4、（黄浦区2016届高三二模）如图，小凳的凳面为圆形，凳脚为三根细钢管，考虑到钢管的受力等因素，设计的小凳应满足：三根细钢管相交处的节点P 与凳面圆形的圆心O 的连线垂直于凳面和地面，且P 分两钢管上下两段的比值为0.618，三只凳脚与地面所成的角均为60°，若A 、B 、C 是凳面圆周的三等分点，18AB =厘米，求凳面的高度h 及三根细钢管的总长度（精确到0.01）；5、（静安区2016届高三二模）设点,E F 分别是棱长为2的正方体1111ABCD A B C D -的棱1,AB AA 的中点．如图，以C 为坐标原点，射线CD 、CB 、1CC 分别是x 轴、y 轴、z 轴的正半轴，建立空间直角坐标系．（1）求向量1D E u u u u r与1C F u u u u r 的数量积；（2）若点,M N 分别是线段1D E 与线段1C F 上的点，问是否存在直线MN ，MN ⊥平面ABCD ？若存在，求点,M N 的坐标；若不存在，请说明理由E FB 1A 1C 1D 1BC DA6、（闵行区2016届高三二模）如图，在直角梯形PBCD 中，//PB DC ，DC BC ⊥，22PB BC CD ===，点A 是PB 的中点，现沿AD 将平面PAD 折起，设PAB θ∠=．（1）当θ为直角时，求异面直线PC 与BD 所成角的大小；（2）当θ为多少时，三棱锥P ABD -的体积为26．7、（浦东新区2016届高三二模）如图，在圆锥SO 中，AB 为底面圆O的直径，点C 为»AB 的中点，SO AB =. （1）证明：AB ⊥平面SOC ；（2）若点D 为母线SC 的中点，求AD 与平面SOC 所成的角.（结果用反三角函数表示）8、（普陀区2016届高三二模）在正四棱柱1111D C B A ABCD -中，底面边长为1，B C 1与底面ABCD 所成的角的大小为2arctan ，如果平面11C BD 与底面ABCD 所成的二面角是锐角，求出此二面角的大小（结果用反三角函数值）9、（徐汇、金山、松江区2016届高三二模）在直三棱柱111C B A ABC -中，1==AC AB ，090=∠BAC ，且异面直线BA 1与11CB 所成的角等于060，设a AA =1.1A 1B 1CACD.A 1CEABC D B 1（1）求a 的值；（2）求三棱锥BC A B 11-的体积．10、（杨浦区2016届高三二模）如图，底面是直角三角形的直三棱柱111ABC A B C -中，1112AC BC AA ===，D是棱1AA 上的动点.(1)证明：1DC BC ⊥； (2)求三棱锥1C BDC -的体积.11、（闸北区2016届高三二模）在长方体1111ABCD A B C D -中，2AB =，1AD =，11AA =，点E 在棱AB 上移动．（1）探求AE 多长时，直线1D E 与平面11AA D D成45o角；（2）点E 移动为棱AB 中点时，求点E 到平面11A DC 的距离．12、（长宁、青浦、宝山、嘉定四区2016届高三二模）如图，在直三棱柱111C B A ABC -中，底面△ABC 是等腰直角三角形，21===AA BC AC ，D 为侧棱1AA 的中点．（1）求证：⊥BC 平面11A ACC ；（2）求二面角11C CD B --的大小（结果用反三角函数值表示）．A BC A 1 B 1C 1D参考答案一、填空、选择题1、12π2、23、64π 45、4106、37、1 或38、C 9、D 10、D 11、A 12、D13、B 14、D二、解答题1、可得有关点的坐标为11111(0,0,1),(1,1,1),(,1,0),(0,,0),(0,1,1)22D B E F C11(,,0)22EF =--u u u r ，11(1,1,0)B D =--u u u u r (4)分所以112B D EF =u u u u r u u u r (5)分所以11EF B D ∥...............................6分（2）设1(,,)n u v w =u r是平面1C EF因为111,n EF n FC ⊥⊥u r u u u u r u r u u u u r所以1111110,222n EF u v n FC v w ⋅=--=⋅=+=u r u u u r u r u u u u r解得,2u v v w =-=- .取1w = ，得1(2,2,1)n =-u r (9)分因为1DD ABCD ⊥平面，所以平面ABCD 的一个法向量是2(0,0,1)n =u u r (10)分设1n u r 与2n u u r 的夹角为α ，则12121cos 3||||n n n n α⋅==⋅u r u u r u r uu r .......................11分结合图形，可判别得二面角1C EF A --是钝角，其大小为1arccos3π- (12)分2、(1)根据条件知:PE 与AD 交点恰好是C 1分,C PE C ∈∴∈面PBE ,,C AC C ∈∴∈面ABC2分B ∈面PBE ,B ∈面ABC3分面PBE与面ABC的交线BC5分 (2)(理) ,,AP AB AC 两两互相垂直,BA ⊥面EDAP7分多面体B PADE -的体积是()11323PA DE AD BA ⨯+⨯⨯=9分BA ∴=10分建立空间直角坐标系,设平面的法向量是()1,,n x y z u r,0,03B ⎛⎫ ⎪⎪⎝⎭ ，()0,2,0C()0,1,0D ()0,1,1E ()0,0,2P ,0,23BP ⎛⎫=- ⎪ ⎪⎝⎭u u u r ，,1,13BE ⎛⎫=- ⎪ ⎪⎝⎭u u u r120n BP x z ⋅=+=u r u u u r 103n BE x y z ⋅=-++=u r u u u r)1n ∴=u r11分面ABC 的法向量()20,0,1n =u u r1212cos n nn n θ⋅==⋅u r u u r u r u u r 5= 12分所以面PBE 与面ABC 所成的锐二面角大小arccos13分注：若作出二面角得2分，计算再3分 (2)(文),,AP AB AC 两两互相垂直,BA ⊥面EDAP7分多面体B PADE -的体积是()1132PA DE AD BA ⨯+⨯⨯=9分BA ∴=10分连接AEAE 是BE 在面EDAP 的射影ADCPE（第20题解答图）BEA ∠是BE 与面PADE 所成的线面角． 11分计算AE =tan BAE ∠==12分BEA ∠是BE 与面PADE所成的线面角arctan． 13分3、（理）解：(1)以},,{直角坐标系xyz A -，则相关点的坐标为(2,1,0),(0,2,0),(0,0,2).C D P ……2设平面PCD 的法向量为(,,),n x y z =r由(2,1,0),DC =-uuu r (0,2,2),DP =-u u u r (0,2,0).DA =-u u u r则202,2.220n DC x y y x z x n DP y z r u u u r r u u u r ìïì?-==ïïïÞ眄镲=?-+=ïîïî令1x =，则(1,2,2)n =r.……5分所以点A 到平面PCD 的距离为：(0,2,0)(1,2,2)4.(1,2,2)3DA n d nu u u r r r×-?=== ……7分(2)由条件，得(1,0,1),Q =(0,2,0),(1,0,1),AD AQ ==u u u r u u u r 且(1,1,1).CQ u u u r=--设平面ADQ 的法向量为0000(,,),n x y z =r则00000000200,.0n AD y y z x n AQ x z r u u u r r u u u r ìïì?==ïï镲Þ眄镲=-?+=ïîïî令01x =，则0(1,0,1)n =-r.……10分设直线CQ 与平面ADQ 所成角为,θ则000sin cos ,CQ n CQ n CQ n θ⋅=<>===u u u r u u r u u u r u u ru u u r u u r故直线CQ 与平面ADQ 所成角的大小为arc……14分注：第（1）小题也可用等积法来做.4、[解] 联结PO ，AO ，由题意，PO ⊥平面ABC ，因为凳面与地面平行，所以PAO ∠就是PA 与平面ABC 所成的角，即60PAO ∠=︒．（2分）在等边三角形ABC 中，18AB =，得AO =4分）在直角三角形PAO 中，18OP ==，（6分）由0.618OPh OP =-，解得47.13h ≈厘米．（9分）三根细钢管的总长度3163.25sin 60h≈︒厘米．（12分）5、（1）在给定空间直角坐标系中，相关点及向量坐标为11(2,0,2),(1,2,0),(1,2,2)D E D E =--u u u u r…………2分11(0,0,2),(2,2,1),(2,2,1)C F C F =-u u u u r (4)分所以111222(2)(1)4D E C F ⋅=-⨯+⨯+-⨯-=u u u u r u u u u r。