高中数学 第二章2.3.3-4直线、平面垂直的性质课件 新人教A版必修2
合集下载
人教A版高中数学必修二2.3.3 直线与平面垂直的性质课件

符号表示:
a ,b a // b
a
b
线面垂直性质定理的应用
1、判断下列命题的正误。
√ (1)平行于同一直线的两条直线互相平行( )
(2)垂直于同一直线的两条直线互相平行(×) (3)平行于同一平面的两条直线互相平行(×)
√ (4)垂直于同一平面的两条直线互相平行( )
2.如果直线l 平面, (1)若直线m ,则m / /l. (2)若直线m ,则l m. (3)若直线m / /,则m l. (4)若直线m l,则m / /.
因为a ,b ,所以a c,b c,
a
b b'
又因为b' // a,所以b' c.
这样在平面 内,经过 c上同一
c o.
点O就有两条直线 b,b'与c垂直,
显然不可能,因此假设不成立,
β
所以a // b.
思考:通过上题的证明你能得出什么结论?
4、归纳: 直线与平面垂直的性质定理 :
垂直于同一个平面的两条直线平行.
证明:m n o
直线m、n确定一个平面
又l1 m,l1 n, m , n l1 l2 m,l2 n, m , n l2
故 l1 // l2 (线面垂直性质定理)
l1、l2都与l相交
1 2
l1 1
o
l 2 2 l
m n
2.如图,已知平面,,且 =l,CA ,
CB ,A,B是垂足,a , a AB C
⑦ 点O c.
⑧ 这样在平面 内,经过 c上同一
b'
a
b
o·c
β
点O就有两条直线 b,b'与c垂直, ⑨ 与定理矛盾,及假设不成立.
高中数学人教A版必修第二册《空间直线、平面的垂直---直线与平面、平面与平面垂直的性质》名师课件

掌握平面与平面垂直的性质定理.
核心素养
逻辑推理
逻辑推理
学习目标
课程目标
1.理解直线和平面、平面和平面垂直的性质定理并能运用其解决相关问题.
2.通过对性质定理的理解和应用,培养学生的空间转化能力和逻辑推理能力.
数学学科素养
1.逻辑推理:探究归纳直线和平面、平面和平面垂直的性质定理,线线垂直、线面垂直、
变式训练
3.如图所示,在四棱锥PABCD中,底面ABCD是边长为a的菱形,且∠DAB=60°,G为AD边
的中点,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.
(1)求证:BG⊥平面PAD;(2)求证:AD⊥PB.
证明
(1)因为在菱形ABCD中,G为AD的中点, ∠DAB=60° ,所以BG⊥AD.
复习引入
直线与平面垂直的定义:
如果直线与平面内的任意一条直线都垂直,我们说直
线与平面互相垂直,记作 ⊥ .
直线与平面垂直的判定定理:
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平
面垂直.
复习引入
平面与平面垂直的定义
一般地,两个平面相交,如果它们所成的二面角是直二面角,就说
这两个平面互相垂直.
求证:(1)DE=DA;(2)平面BDM⊥平面ECA;(3)平面DEA⊥平面ECA.
证明
(1)如图,取EC的中点F,连接DF.
因为EC⊥平面ABC,BC⊂平面ABC,所以EC⊥BC.
易知DF//BC,所以DF⊥EC.
在Rt△EFD和Rt△DBA中
因为EF= EC,EC=2BD,所以EF=BD.
又FD=BC=AB所以Rt△EFD≌Rt△DBA ,故DE=DA.
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,所以BG⊥平面PAD.
核心素养
逻辑推理
逻辑推理
学习目标
课程目标
1.理解直线和平面、平面和平面垂直的性质定理并能运用其解决相关问题.
2.通过对性质定理的理解和应用,培养学生的空间转化能力和逻辑推理能力.
数学学科素养
1.逻辑推理:探究归纳直线和平面、平面和平面垂直的性质定理,线线垂直、线面垂直、
变式训练
3.如图所示,在四棱锥PABCD中,底面ABCD是边长为a的菱形,且∠DAB=60°,G为AD边
的中点,侧面PAD为正三角形,其所在的平面垂直于底面ABCD.
(1)求证:BG⊥平面PAD;(2)求证:AD⊥PB.
证明
(1)因为在菱形ABCD中,G为AD的中点, ∠DAB=60° ,所以BG⊥AD.
复习引入
直线与平面垂直的定义:
如果直线与平面内的任意一条直线都垂直,我们说直
线与平面互相垂直,记作 ⊥ .
直线与平面垂直的判定定理:
一条直线与一个平面内的两条相交直线都垂直,则该直线与此平
面垂直.
复习引入
平面与平面垂直的定义
一般地,两个平面相交,如果它们所成的二面角是直二面角,就说
这两个平面互相垂直.
求证:(1)DE=DA;(2)平面BDM⊥平面ECA;(3)平面DEA⊥平面ECA.
证明
(1)如图,取EC的中点F,连接DF.
因为EC⊥平面ABC,BC⊂平面ABC,所以EC⊥BC.
易知DF//BC,所以DF⊥EC.
在Rt△EFD和Rt△DBA中
因为EF= EC,EC=2BD,所以EF=BD.
又FD=BC=AB所以Rt△EFD≌Rt△DBA ,故DE=DA.
又平面PAD⊥平面ABCD,平面PAD∩平面ABCD=AD,所以BG⊥平面PAD.
人教高中数学必修二2.3直线、平面垂直的判定与性质 -三垂线定理 课件
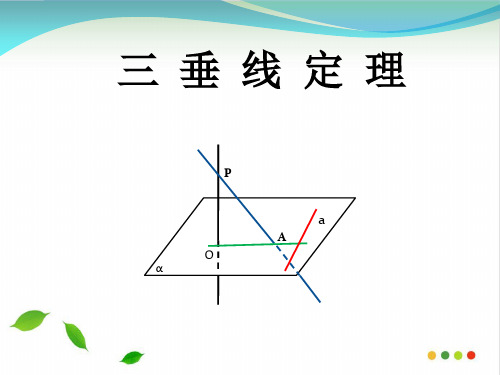
结论:a⊥OA
P
线斜垂直
线射垂直
逆定理
O α
定理
线射垂直
线斜垂直
逆定理
a
A
例1:如图,在正方体中,O是AC与BD的交点,直线D1O与AC
垂直吗?说明你的理由。
D1
C1
D1O在平面ABCD内的射影是DO
AC与BD垂直
A1
B1
D1O与AC垂直(三垂线定理 )
你知道吗? D1B⊥AC
D
C
线射垂直
线斜垂直 A
射影OA和a直线之间的垂直关系
α
O
2、直线a可以移动,但只能在平面内移
动。因此,直线a和斜线PA可以相交也
可以异面。
P
3、三垂线定理的实质是平面的一条斜 线和平面内的一条直线垂直的判定定理。
O α
a
A
a
A
新知探究 • 逆定理
思考:
如果将定理中的条件a⊥OA改成a⊥PA,你会得到
怎样的结果?命题一定成立吗?
P
定理
即:线射垂直
线斜垂直
O α
a
A
定理中包括三种垂直关系:
①线面垂直 ②线射垂直 ③ 线斜垂直
P PO
P
a OA
P
a PA
O Aa
O Aa
O Aa
α
α
α
直线和 平面垂直
平面内的直线 和平面一条斜 线的射影垂直
平面内的直线 和平面的一条 斜线垂直
对定理的几点说明
P
1、三垂线定理描述的是斜线PA、
如图:请说出下列图形中的垂线、斜线和射影。
P
直线PO是垂线 直线PA是斜线
2020-2021学年数学人教A版必修2课件:2-3-3、4 直线与平面垂直的性质

3.设 α-l-β 是直二面角,直线 a⊂α,直线 b⊂β,a,b 与 l 都不垂直,那么( C )
A.a 与 b 可能垂直,但不可能平行 B.a 与 b 可能垂直,也可能平行 C.a 与 b 不可能垂直,但可能平行 D.a 与 b 不可能垂直,也不可能平行
解析:当 a,b 都与 l 平行时,则 a∥b,所以 A、D 错,如图, 若 a⊥b,过 a 上一点 P 在 α 内作 a′⊥l,因为 α⊥β,所以 a′⊥β, 又 b⊂β,∴a′⊥b,∴b⊥α,而 l⊂α,∴b⊥l,与 b 和 l 不垂直矛 盾,所以 B 错.
掌握线线、线面、面面垂直的性质和判定是三种垂直相互转 化的关键.由线面垂直可知线与面内任何一条直线都垂直;由线 面垂直亦可得到面面垂直面面垂直的判定.因此说线面垂直是 线线垂直和面面垂直的枢纽.
[变式训练 3] 如图所示,A,B,C,D 为空间四点,在△ ABC 中,AB=2,AC=BC= 2,等边三角形 ADB 以 AB 为轴转 动.
[重点] 直线与平面垂直、平面与平面垂直的性质及应用. [难点] 直线与平面垂直、平面与平面垂直的性质定理的理 解,直线与平面垂直、平面与平面垂直的判定和性质的综合应用.
要点整合夯基础 课堂达标练经典
典例讲练破题型 课时作业
知识点一 直线与平面垂直的性质 [填一填]
1.文字语言:垂直于同一个平面的两条直线 平行. 简记 为:若线面垂直则线线平行.
(3)因为 AB⊥AD,而且四边形 ABED 为平行四边形.所以 BE⊥CD,AD⊥CD,
由(1)知 PA⊥底面 ABCD. 所以 PA⊥CD.又 AD∩PA=A, 所以 CD⊥平面 PAD. 所以 CD⊥PD. 因为 E 和 F 分别是 CD 和 PC 的中点, 所以 PD∥EF. 所以 CD⊥EF.又 EF∩BE=E, 所以 CD⊥平面 BEF.又 CD⊂平面 PCD, 所以平面 BEF⊥平面 PCD.
2021版高中数学人教A版必修2课件:2.3.3 直线与平面垂直的性质

求证:MN∥AD1. 证明:因为ADD1A1为正方形,所以AD1⊥A1D. 因为CD⊥平面ADD1A1,所以CD⊥AD1. 因为A1D∩CD=D,所以AD1⊥平面A1DC. 因为MN⊥平面A1DC,所以MN∥AD1.
-10-
-8-
2.3.3 直线与平面垂直的性质 目标导航
知识梳理
重难聚焦
典例透析
反思当题中垂直条件很多,但又需证明两条直线的平行关系时,就 要考虑直线与平面垂直的性质定理,从而完成垂直向平行的转化.
-9-
2.3.3 直线与平面垂直的性质 目标导航
知识梳理
重难聚焦
典例透析
【变式训练】
如图,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点 ,MN⊥平面A1DC.
答案:B
-4-
2.3.3 直线与平面垂直的性质 目标导航
知识梳理
重难聚焦
典例透析
12
1.理解直线与平面垂直的性质定理 剖析:(1)直线与平面垂直的性质定理考查的是在直线与平面垂直 的条件下,可得出什么结论. (2)定理给出了判定两条直线平行的另一种方法(只要判定这两 条直线都与同一个平面垂直). (3)定理揭示了空间中“平行”与“垂直”关系的内在联系,提供了“ 垂直”与“平行”关系相互转化的依据. (4)垂直于同一条直线的两个平面互相平行.
-5-
2.3.3 直线与平面垂直的性质 目标导航
知识梳理
重难聚焦
典例透析
12
-6-
2.3.3 直线与平面垂直的性质 目标导航
知识梳理
重难聚焦
典例透析
【例题】 如图,在正方体ABCD-A1B1C1D1中,EF与异面直线AC,A1D 都垂直相交.求证:EF∥BD1.
-10-
-8-
2.3.3 直线与平面垂直的性质 目标导航
知识梳理
重难聚焦
典例透析
反思当题中垂直条件很多,但又需证明两条直线的平行关系时,就 要考虑直线与平面垂直的性质定理,从而完成垂直向平行的转化.
-9-
2.3.3 直线与平面垂直的性质 目标导航
知识梳理
重难聚焦
典例透析
【变式训练】
如图,在正方体ABCD-A1B1C1D1中,M是AB上一点,N是A1C的中点 ,MN⊥平面A1DC.
答案:B
-4-
2.3.3 直线与平面垂直的性质 目标导航
知识梳理
重难聚焦
典例透析
12
1.理解直线与平面垂直的性质定理 剖析:(1)直线与平面垂直的性质定理考查的是在直线与平面垂直 的条件下,可得出什么结论. (2)定理给出了判定两条直线平行的另一种方法(只要判定这两 条直线都与同一个平面垂直). (3)定理揭示了空间中“平行”与“垂直”关系的内在联系,提供了“ 垂直”与“平行”关系相互转化的依据. (4)垂直于同一条直线的两个平面互相平行.
-5-
2.3.3 直线与平面垂直的性质 目标导航
知识梳理
重难聚焦
典例透析
12
-6-
2.3.3 直线与平面垂直的性质 目标导航
知识梳理
重难聚焦
典例透析
【例题】 如图,在正方体ABCD-A1B1C1D1中,EF与异面直线AC,A1D 都垂直相交.求证:EF∥BD1.
人教版高中数学必修二.线面垂直、面面垂直的性质定理教学课件 共18张PP

1、线面垂直的性质:面面垂直的性质:
2、会利用“转化思想”解决垂直问题
β A
B
线面垂直 α a
面面垂直
人教版高中数学必修二2.3.3-2.3.4线 面垂直 、面面 垂直的 性质定 理教学 课件 共18张PP
线线平行 3、用条件想性质: 证结果想判定:
4、如何举反例?满足条件的线、面 转动
人教版高中数学必修二2.3.3-2.3.4线 面垂直 、面面 垂直的 性质定 理教学 课件 共18张PP
四.知识应用
1、判断下列命题是否正确:正确的是:①④ ①平行于同一条直线的两条直线互相平行;
②垂直于同一条直线的两条直线互相平行;
③平行于同一个平面的两条直线互相平行;
④垂直于同一个平面的两条直线互相平行.
2、a,b表示线, 表示面,正确的是 (3)(4)
(1)a ,ab,则 b/ / (2)a/ /,a b,则 b
证明:假设 a与b不平行.记直线b
和α的交点为o,则可过o作 b’∥a
a
b b’ ∵a⊥α,
α
o
∴b’⊥α.
反证法
∴过点o的两条直线 b和b’都 垂直平面α,这是不可能的,
∴a∥b.
线面垂直的性质定理:
垂直于同一个平面的两条直线平行
符号语言? a ,b a//bBiblioteka 简述: 线面垂直 如何证明?
线线平行
人教版高中数学必修二2.3.3-2.3.4线 面垂直 、面面 垂直的 性质定 理教学 课件 共18张PP
人教版高中数学必修二2.3.3-2.3.4线 面垂直 、面面 垂直的 性质定 理教学 课件 共18张PP
•
1.边塞诗的作者大多一些有切身边塞 生活经 历和军 旅生活 体验的 作家, 以亲历 的见闻 来写作 ;另一 些诗人 用乐府 旧题来 进行翻 新创作 。于是 ,乡村 便改变 成了另 一种模 样。正 是由于 村民们 的到来 ,那些 山山岭 岭、沟 沟坪坪 便也同 时有了 名字, 成为村 民们最 朴素的 方位标 识.
人A版数学必修2课件: 第2章 2.3.3 直线与平面垂直的性质 2.3.4 平面与平面垂直的性质
上一页
返回首页
下一页
[小组合作型] 线面垂直性质定理的应用
如图 2-3-31 所示,在正方体 ABCD-A1B1C1D1 中,
M 是 AB 上一点,N 是 A1C 的中点,MN⊥平面 A1DC.
求证:(1)MN∥AD1;
(2)M 是 AB 的中点.
图 2-3-31
【精彩点拨】 (1)要证线线平行,则先证线面垂直,即证 AD1⊥平面 A1DC.
(2)求证:AD⊥PB. 【精彩点拨】 (1) 菱形ABCD, ∠DAB=60°―→ △ABD为
图 2-3-33 正三角形
―→ BG⊥AD 面―PA―D―⊥―底―面―A―B→CD BG⊥平面PAD
(2)要证 AD⊥PB,只需证 AD⊥平面 PBG 即可.
上一页
返回首页
下一页
【自主解答】 (1)如图,在菱形 ABCD 中,连接 BD, 由已知∠DAB=60°,
上一页
返回首页
下一页
图 2-3-32
面面垂直性质定理的应用
如图 2-3-33 所示,P 是四边形 ABCD 所在平面外的
一点,四边形 ABCD 是边长为 a 的菱形且∠DAB=60°,侧面 PAD
为正三角形,其所在平面垂直于底面 ABCD.
(1)若 G 为 AD 的中点,求证:BG⊥平面 PAD;
上一页
返回首页
下一页
1.直线与平面垂直的性质定理是线线、线面垂直以及线面、 面面平行的相互转化的桥梁,因此必须熟练掌握这些定理,并能 灵活地运用它们.
2.当题中垂直条件很多,但又需证平行关系时,就要考虑 垂直的性质定理,从而完成垂直向平行的转化.
上一页
返回首页
下一页
[再练一题] 1.如图 2-3-32,已知平面 α∩平面 β=l,EA⊥α,垂足为 A,EB⊥β,垂足为 B,直线 a⊂β,a⊥AB.求证:a∥l. 【证明】 因为 EA⊥α,α∩β=l,即 l⊂α,所以 l⊥EA. 同理 l⊥EB.又 EA∩EB=E,所以 l⊥平面 EAB. 因为 EB⊥β,a⊂β,所以 EB⊥a, 又 a⊥AB,EB∩AB=B, 所以 a⊥平面 EAB. 由线面垂直的性质定理,得 a∥l.
高中数学 2.3.3直线与平面垂直的性质课件 新人教A版必修2
3. 如 图 所 示 , 在 长 方 体 ABCD -
A1B1C1D1 中 , E∈ 平 面 ABCD , F∈ 平 面
A1B1C1D1,且EF⊥平面ABCD.
求证:EF∥AA1. [分析] 只需证明AA1⊥平面ABCD即可.
[证明] ∵AA1⊥AB,AA1⊥AD,且AB∩AD=A,AB⊂平面 ABCD,AD⊂平面ABCD,
(2)若SD交平面AEF于G,求证:AG⊥SD.
[分析] (1)要证明AF⊥SC,转化成证明SC⊥平面AEF,充 分利用其中的垂直关系.
(2)要证AG⊥SD,转化成AG⊥平面SDC.
[知识拓展] 直线与平面垂直的性质 (1) bl⊥⊂αα⇒l⊥b; (2) ab⊥ ⊥αα⇒a∥b;
(3) aa∥⊥bα⇒b⊥α; (4) aα⊥∥αβ⇒a⊥β; (5) aa⊥⊥αβ⇒α∥β.
●预习自测
1.从圆柱的一个底面上任取一点(该点不在底面圆周上),
过该点作另一个底面的垂线,则这条垂线与圆柱的母线所在直
∴AA1⊥平面ABCD.
又∵EF⊥平面ABCD, ∴EF∥AA1.
规律总结:证明线线平行可转化为线面垂直,即转 化为证明这两条直线同时垂直于一个平面.
高效课堂
●互动探究
利用线面垂直的性质证明平行问题
如 图 , 正 方 体 A1B1C1D1 - ABCD 中,EF与异面直线AC,A1D都垂直相交.求证:EF∥BD1.
2.直线与平面垂直的判定定理:如果一条直线垂直于一ห้องสมุดไป่ตู้个平面内的两条____相__交__直线,则这条直线垂直于这个平面.
3.如图,长方体AC1中,二面角D1-AB-D的平面角是 ()
A.∠D1AB B.∠D1BA C.∠D1AD D.∠D1DA [答案] C
学练考高中数学2.3.3、2.3.4直线与平面垂直的性质、平面与平面垂直的性质课件新人教A版必修2
解: (1)证明:如图所示,取CD的中点E,连接PE,EM,EA. ∵△PCD为正三角形, ∴PE⊥CD,PE=PDsin∠PDE= 3. ∵平面PCD⊥平面ABCD,∴PE⊥平面ABCD. 又AM⊂平面ABCD,∴PE⊥AM. ∵四边形ABCD是矩形, ∴△ADE,△ECM,△ABM均为直角三角形. 由勾股定理可求得EM= 3,AM= 6,AE=3, ∴EM2+AM2=AE2,∴AM⊥EM. ∵PE∩EM=E,∴AM⊥平面PEM,∴AM⊥PM.
图 2-3-55 证明:过点 A 作 AE⊥PB,垂足为 E, ∵平面 PAB⊥平面 PBC,平面 PAB∩平面 PBC=PB,∴AE⊥平面 PBC. ∵BC⊂平面 PBC,∴AE⊥BC.∵PA⊥平面 ABC,BC⊂平面 ABC,∴PA⊥BC. ∵PA∩AE=A,∴BC⊥平面 PAB.
第二十四页,共28页。
(1)求证:BC⊥平面 ACD; (2)求几何体 D -ABC 的体积.
图 2-3-18
第十五页,共28页。
2.3.4 │ 考点(kǎo diǎn)类析
解:(1)证明:在图(a)中,可得 AC=BC=2 2,从而 AC 2 +BC 2=AB 2,故 AC⊥BC.因为平面 ADC⊥平面 ABC,平面
2.3.4 │ 当堂(dānɡ tánɡ)自测
当堂自测
1.已知直线 b⊥平面 α,直线 a⊂α,则 a 与 b 的位置关系 是( )
A.a∥b B.a⊥b C.a 与 b 垂直相交 D.a 与 b 垂直且异面 [答案]B
第二十五页,共28页。
2.3.4 │ 当堂(dānɡ tánɡ)自测
2.已知平面 α,β,直线 l,若 α⊥β,α∩β=l,则( ) A.垂直于平面 β 的平面一定平行于平面 α B.垂直于直线 l 的直线一定垂直于平面 α C.垂直于平面 β 的平面一定平行于直线 l D.垂直于直线 l 的平面一定与平面 α、β 都垂直
图 2-3-55 证明:过点 A 作 AE⊥PB,垂足为 E, ∵平面 PAB⊥平面 PBC,平面 PAB∩平面 PBC=PB,∴AE⊥平面 PBC. ∵BC⊂平面 PBC,∴AE⊥BC.∵PA⊥平面 ABC,BC⊂平面 ABC,∴PA⊥BC. ∵PA∩AE=A,∴BC⊥平面 PAB.
第二十四页,共28页。
(1)求证:BC⊥平面 ACD; (2)求几何体 D -ABC 的体积.
图 2-3-18
第十五页,共28页。
2.3.4 │ 考点(kǎo diǎn)类析
解:(1)证明:在图(a)中,可得 AC=BC=2 2,从而 AC 2 +BC 2=AB 2,故 AC⊥BC.因为平面 ADC⊥平面 ABC,平面
2.3.4 │ 当堂(dānɡ tánɡ)自测
当堂自测
1.已知直线 b⊥平面 α,直线 a⊂α,则 a 与 b 的位置关系 是( )
A.a∥b B.a⊥b C.a 与 b 垂直相交 D.a 与 b 垂直且异面 [答案]B
第二十五页,共28页。
2.3.4 │ 当堂(dānɡ tánɡ)自测
2.已知平面 α,β,直线 l,若 α⊥β,α∩β=l,则( ) A.垂直于平面 β 的平面一定平行于平面 α B.垂直于直线 l 的直线一定垂直于平面 α C.垂直于平面 β 的平面一定平行于直线 l D.垂直于直线 l 的平面一定与平面 α、β 都垂直
人教A版高中数学必修2第二章2.3.3直线与平面垂直的性质课件(共19张PPT)
(2)若AD=1,AB= 2 ,求EC与平面ABCD
所成的角。 E
Page 17
D
M A
C B
思考:对于三个平面α、β、γ,如果α⊥γ, β⊥γ那么直线l与平面γ的位置关系如何? 为什么?
β l
α
l2
n
m
γ
l1
Page 18
如果两个相交平面都垂直于另一个平面, 那么这两个平面的交线垂直于这个平面.
( ×) (2)垂直于交线l的直线必垂直于平面β (×)
(3)过平面α内任意一点作交线的垂线,则此
√ 垂线必垂直于平面β( )
Page 14
例5. , a , a ,判断a与位置关系
解:设 l
在α内作直线b ⊥l
α
β
b l
A
a
b
bl
l
b 又a
a // b
b
LOGO
直线与平面垂直的性质
由NordriDesign™提供
温故知新
1.直线与平面垂直的定义
如果直线 l与平面 内的任意一条直线都垂直 ,我们说直线 l与平面 互相垂直,记作 l .
2.直线与平面垂直的判定定理 一条直线与一个平面内的两条相交直线都垂直,则 该直线与此平面垂直.
3、两个平行平面中的一个垂直于一条直线, 则另一个平面也垂直于这条直线。
Page 9
Page 10
思考1:如果平面α与平面β互相垂直,直线l在平 面α内,那么直线l与平面β的位置关系有哪几种 可能?
αl β
αl β
α
l β
Page 11
思考:一般地, , CD
AB , AB CD ,垂足为B,那么直
a //
所成的角。 E
Page 17
D
M A
C B
思考:对于三个平面α、β、γ,如果α⊥γ, β⊥γ那么直线l与平面γ的位置关系如何? 为什么?
β l
α
l2
n
m
γ
l1
Page 18
如果两个相交平面都垂直于另一个平面, 那么这两个平面的交线垂直于这个平面.
( ×) (2)垂直于交线l的直线必垂直于平面β (×)
(3)过平面α内任意一点作交线的垂线,则此
√ 垂线必垂直于平面β( )
Page 14
例5. , a , a ,判断a与位置关系
解:设 l
在α内作直线b ⊥l
α
β
b l
A
a
b
bl
l
b 又a
a // b
b
LOGO
直线与平面垂直的性质
由NordriDesign™提供
温故知新
1.直线与平面垂直的定义
如果直线 l与平面 内的任意一条直线都垂直 ,我们说直线 l与平面 互相垂直,记作 l .
2.直线与平面垂直的判定定理 一条直线与一个平面内的两条相交直线都垂直,则 该直线与此平面垂直.
3、两个平行平面中的一个垂直于一条直线, 则另一个平面也垂直于这条直线。
Page 9
Page 10
思考1:如果平面α与平面β互相垂直,直线l在平 面α内,那么直线l与平面β的位置关系有哪几种 可能?
αl β
αl β
α
l β
Page 11
思考:一般地, , CD
AB , AB CD ,垂足为B,那么直
a //
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
∩
B
∩
∩
解题反思
1、面面垂直的性质定理给我们提供了一 种证明线面垂直的方法 2、本题充分地体现了面面垂直与 线面 垂直之间的相互转化关系。
面面垂直
性质定理 判定定理
线面垂直
1、直线和平面垂直的性质定理; 2、平面与平面垂直的性质定理: 两个平面垂直,则一个平面内垂直于交线的直线与另一个 平面垂直。 3、空间垂直关系有那些? 如何实现空间垂直关系的相互转化? 请指出下图中空间垂直关系转化的定理依据?
§2.3.3直线与平 面垂直的性质
1、线面垂直的概念
1、定义 2、判定定理
2、如何判定线面垂直?
3、在空间,过一点,有几条直线与已知 平面垂直?过一点,有几个平面与已知直 线垂直?
4、我们已经知道:
如果两条平行线中的一条垂直于一个平 面,那么另一条也垂直于这个平面.
那么:
如果两条直线同垂直于一个平面,那么 这两条直线是否平行?
O
B
★平面与平面垂直的性质定理的应用★
如图,AB是⊙O的直径,点C是圆上异于A,B的任意一 点,PA⊥平面ABC,AF⊥PC于F.求证:AF⊥平面PBC. 证明: ∵AB是⊙O的直径
∴AC⊥BC P
∵PA⊥平面ABC,BC 平面ABC F .O ∴PA⊥BC ∵PA∩AC=A A ∴BC⊥平面PAC C ∵BC 平面PBC ∴平面PBC⊥平面PAC 又∵AF⊥PC,AF 面PAC ,面PBC∩面PAC=PC ∴AF⊥平面PBC
C B
两个平面垂直,其中 一个平面内垂直于交 线的直线垂直于另一 个平面。
概括结论
b l bl
b
A
b
l
O
严格证明
已知 , CD, AB , AB CD于B.
求证 : AB .
证明:在平面 内作BE⊥CD,
b
l
b l b l 简述为:
b
面面垂直
线面垂直
知识应用举例
(1)若b ,则b 。 × (2)若 =l,b l则b 。 ×
例 1、已知:两个平面与 互相垂直,判断下列命题是否正确:
(3)若b ,则b垂直于平面内的无数条直线。
该命题正确吗?
b
Ⅰ. 观察实验
(1)观察黑板所在的平面 和地面,它们是互相垂直的 ,那么黑板所在的平面里的 任意一条直线是否就一定和 地面垂直?
两个平面垂直,其 中一个平面的直线 不一定垂直于另一 个平面。
D’ A’ B’
C’
D
(2)观察长方体ABCDA`B`C`D`中,平面AA`D`D与 A 平面ABCD垂直,你能否在 平面AA`D`D中找一条直线垂 直于平面ABCD?
① ③
线线垂直
②
线面垂直
④
面面垂直
①线面垂直的判定定理
②线面垂直的定义
③面面垂直的判定定理 ④面面垂直的性质定理
作业: P73练习:1,2.(做书上) P73习题2.3A组:2. P74习题2.3B组:3.
P
Q
α
2)互相平行的直线和平面的距离:
一条直线和一个平面平行时,这条 直线上任意一点到这个平面的距离,叫 做这条直线和这个平面的距离.
P P`
Q
Q`
α
练习1:
P71练习:1,2.(做书上)
1、平面与平面垂直的定义
两个平面相交,如果它们所成的二面角是 直二面角,就说这两个平面互相垂直。
2、平面与平面垂直的判定定理
二、新课讲授:
1、问题:
a ,b a // b 是否成立?
β
a b
b’
α
O
2、直线和平面垂直的性质定理: 如果两条直线同垂直于一个平面,那么 这两条直线平行.
β
图形语言:
a
b
α 符号语言: a ,b a // b
3、直线到平面垂直的距离:
1)点到平面的距离: 从平面外一点引这个平面的垂线,这个点和 垂足间的距离叫做这个点到这个平面的距离.
(1)过点P且垂直于的直线a是否一定在内?
(2)过点P且垂直于的直线l与 是什么位置关系?并证明
n l
P
m
例3、如图,AB是⊙O的直径,C是圆周上不同 于A,B的任意一点,平面PAC⊥平面ABC, (1)求证:BC⊥平面PAC。 (2)判断平面PBC与平面PAC是否垂直,并证明。
P
C
A
(4) 过一个平面内任意一点作交线的垂线,则此垂线 必垂直于另一个平面。
√
√
l
例2、平面与平面互相垂直, m, P , P m, 判断:
(1)过点P且垂直于的直线a是否一定在内?
(2)过点P且垂直于的直线l与 是什么位置关系?并证明
a
P
m
b
例2、平面与平面互相垂直, m, P , P m, 判断:
一个平面过另一个平面的垂 线,则这两个平面垂直。
符号表示:
b
b b 线面垂直
面面垂直
b 中的条件 b 与 如果将 b 结论 的位置调换一下,构造这样的 一个命题: b b
A D
垂足为B.
则∠ABE就是二面角 -CD- 的平面角 ∵
B C
E
, ∴AB⊥BE(平面与平面垂直的定义)
又由题意知AB⊥CD,且BE CD=B
∴AB⊥ (直线与平面垂直的判定定理)
平面与平面垂直的性质定理
两个平面垂直,则一个平 面内垂直于交线的直线 与另一个平面垂直.
符号表示:
