单跨静定梁的三种基本形式
合集下载
2.3.1单跨静定梁的内力分析
二、梁的形式
梁的类型：简支梁（一端固定铰支座一端可动铰支座）、 外伸梁（梁端有部分外伸的简支梁）、悬臂梁（一端固定 端支座一端为自由端）。 梁在两个支座之间的部分称为跨。每跨之间的距离为两 支座作用点之间的距离。
三、剪力和弯矩
如课本所给一简支梁，受到均布荷载q作用，当q足够 大时梁会发生破坏，由日常经验可得破坏位置一般在梁中 间，为什么呢？ 外力：荷载和约束反力。内力：构件内部相连接两部 分之间的相互作用。 研究时采用截面法（截开、代替、平衡）。求在内力 的截面m-m处，用一假想的与梁轴线垂直的平面将梁截成 两部分，取左段为研究对象，由于梁处于平衡状态，因此 左段梁也是处于平衡的。 左段上作用反力根据平衡公式可求得截面上向下的剪 力，根据弯矩平衡可以求得弯矩M。Fs为剪力，M为弯矩
F1 m A
F2
B
m
a FAy a RBy
x
x
l
m Fs
F1
A FБайду номын сангаасy m
M
m M' m Fs'
F2 B FBy
左段：∑Fyi=0 FAy—Fs—F1=0 Fs=FAy+F1 ∑MO（F）=0 M—FAy*a+F1*(x-a)=0 M=FAy*a—F1*(x-a) m-m上的内力值也可以通过右段梁的平衡求得，结果是 一样的，但方向相反。 剪力的单位为N或KN，弯矩的单位为KN∙m或N∙m。 剪力的正负号：使所隔离物体有顺时针转动趋势为正；反 之为负。 弯矩的正负号：使所隔离物体产生下凸变形为正（下部受 拉上部受压），反之为负。 如课本所示。 做题步骤：（1）求支座反力（2）求截面内力（剪力和 弯矩）课本例题2-2、2-3
第二章
静定结构内力分析
结构力学第3章 多跨静定梁课件
（1）选定外力的不连续点（集中力作用点、集中力偶作用点、分布荷载的
始点和终点）为控制截面，首先计算控制截面的弯矩值； （2）分段求作弯矩图。当控制截面间无荷载时，弯矩图为连接控制截面弯
矩值的直线；当控制截面间存在荷载时，弯矩图应在控制截面弯矩值作出的
直线上在叠加该段简支梁作用荷载时产生的弯矩值。 例：利用叠加法求作图示梁结构的内力图。
P=8kN q=4 kN/m
A
P=8kN D 4
MG
r
17 B
7
QG 7 MGr 7
23
G
QG
17 9 A + C D E F G _ B
G
m=16kN.m B
8
7
Q图（kN）
§3-3
多跨静定梁
一、多跨静定梁的几何组成特性
多跨静定梁常用于桥梁结构。从几何组成特点看，它的组成可以区分 为基本部分和附属部分。
如图所示梁，其中 AC 部分不依赖于其它部分，独立地与大地组成一个
几何不变部分，称它为基本部分；而CE部分就需要依靠基本部分AC才能保 证它的几何不变性，相对于AC 部分来说就称它为附属部分。
A
C E A E C
C
E
A
（a）
（b）
（c）
二、分析多跨静定梁的一般步骤
对如图所示的多跨静定梁，应先从附属部分CE开始分析：将支座C 的支反 力求出后，进行附属部分的内力分析、画内力图，然后将支座 C 的反力反向 加在基本部分AC 的C 端作为荷载，再进行基本部分的内力分析和画内力图， 将两部分的弯矩图和剪力图分别相连即得整个梁的弯矩图和剪力图 。
分析下列多跨连续梁结构几何构造关系，并确定内力计算顺序。 q P
A B C D E F G H
始点和终点）为控制截面，首先计算控制截面的弯矩值； （2）分段求作弯矩图。当控制截面间无荷载时，弯矩图为连接控制截面弯
矩值的直线；当控制截面间存在荷载时，弯矩图应在控制截面弯矩值作出的
直线上在叠加该段简支梁作用荷载时产生的弯矩值。 例：利用叠加法求作图示梁结构的内力图。
P=8kN q=4 kN/m
A
P=8kN D 4
MG
r
17 B
7
QG 7 MGr 7
23
G
QG
17 9 A + C D E F G _ B
G
m=16kN.m B
8
7
Q图（kN）
§3-3
多跨静定梁
一、多跨静定梁的几何组成特性
多跨静定梁常用于桥梁结构。从几何组成特点看，它的组成可以区分 为基本部分和附属部分。
如图所示梁，其中 AC 部分不依赖于其它部分，独立地与大地组成一个
几何不变部分，称它为基本部分；而CE部分就需要依靠基本部分AC才能保 证它的几何不变性，相对于AC 部分来说就称它为附属部分。
A
C E A E C
C
E
A
（a）
（b）
（c）
二、分析多跨静定梁的一般步骤
对如图所示的多跨静定梁，应先从附属部分CE开始分析：将支座C 的支反 力求出后，进行附属部分的内力分析、画内力图，然后将支座 C 的反力反向 加在基本部分AC 的C 端作为荷载，再进行基本部分的内力分析和画内力图， 将两部分的弯矩图和剪力图分别相连即得整个梁的弯矩图和剪力图 。
分析下列多跨连续梁结构几何构造关系，并确定内力计算顺序。 q P
A B C D E F G H
结构力学 第三章 静定梁和静定平面钢架
２、截面法 若要求某一横截面上的内力，假想用一平面沿杆轴垂直方向将该 截面截开，使结构成两部分；在截开后暴露的截面上用力（内力）代 替原相互的约束。
对于截开后结构的两部分上，截面上的内力已成为外力，因此，
由任一部分的静力平衡条件，均可列出含有截面内力的静力平衡方程。 解该方程即将内力求出。
３、截面内力 截开一根梁式杆件的截面上有三个内力（分量），即：轴力ＦN 、 剪力ＦQ和弯矩Μ 。
dFN/dx=-qx
dFQ/dx=-qy dM/dx=Q
d2M/dx2=-qy
增量关系： DFN=-FPx
DFQ=-FPy
DM=m
１）微分关系及几何意义： dFN/dx=-qx dFQ/dx=-qy dM/dx=Q d2M/dx2=-qy （１）在无荷载区段，ＦQ图为水平直线；
当ＦQ≠０时，Μ图为斜直线;
右右为正。
ＦQ＝截面一侧所有外力在杆轴垂直方向上投影的代数和。左上为正， 右下为正。
Μ ＝截面一侧所有外力对截面形心力矩代数和。弯矩的竖标画在杆
件受拉一侧。
例3-1-1 求图（a）所示简支梁在图示荷载下截面的内力。
解：1）支座反力 ∑ΜA=0 FBy×4﹣10×4×2﹣100× (4/5)×2=0 Fby=60kN (↑) ∑ΜB=0 FAy=60kN (↑) ∑Fx= 0 FAx+100×(3/5)=0 FAx=－60kN (← ) 由 ∑Ｆy= 0 校核，满 足。
(下侧受拉)
区段叠加法求Ｅ、Ｄ截面弯矩； ΜE＝20×42/8＋120/2＝100kNm ΜＤ＝40×4/4＋120/2＝100kNm
(下侧受拉) (下侧受拉)
内力应考虑
说明：集中力或集中力偶作用点，注意对有突变的 分两侧截面分别计算。
结构力学 第3章静 定梁、平面刚架受力分析
工程中，斜梁和 斜杆是常遇到的，如楼梯梁、刚架中的斜梁等。斜梁 受均布荷载时有两种表示方法： （1）按水平方向分布的形式给出（人群、雪荷载等），用 q 表示。 （2）按沿轴线方向分布方式给出（自重、恒载），用 q’ 表示。
q 与 q’间的转换关系：
qdx qds q q
cos
第3章
[例题] 试绘制图示斜梁内力图。
q
B
C
A
α
D VB
HA
l/3 l/3
l/3
VA
（1）求支座反力：
解：
X 0 MB 0 MA 0
HA 0
VA
ql 6
()
VB
ql 6
()
校核：
Y
qj 6
qj 6
ql 3
0
第3章
（2）AC段受力图：
（3）AD段受力图：
HAcosα HAsinα
HA VAsinα
VA VAcosα
MC
C
NC
α QC
HAcosα
dx
d2M dx2
q(x)
（1）在无荷区段q(x)＝０，剪力图为水平直线，弯矩图为斜直线。
（2）在q(x)＝常量段，剪力图为斜直线，弯矩图为二次抛物线。其凹下去的曲 线象锅底一样兜住q(x)的箭头。
（3）集中力作用点两侧，剪力值有突变、弯矩图形成尖点；集中力偶作用点两 侧，弯矩值突变、剪力值无变化。
解：
10KN/m A HA=0
4m VA=26.25kN
30KN.m
20KN
C
D
B
E
2m
2m
32.5 2.5
3m VB=33.75KN 60
（1）计算支座反力
q 与 q’间的转换关系：
qdx qds q q
cos
第3章
[例题] 试绘制图示斜梁内力图。
q
B
C
A
α
D VB
HA
l/3 l/3
l/3
VA
（1）求支座反力：
解：
X 0 MB 0 MA 0
HA 0
VA
ql 6
()
VB
ql 6
()
校核：
Y
qj 6
qj 6
ql 3
0
第3章
（2）AC段受力图：
（3）AD段受力图：
HAcosα HAsinα
HA VAsinα
VA VAcosα
MC
C
NC
α QC
HAcosα
dx
d2M dx2
q(x)
（1）在无荷区段q(x)＝０，剪力图为水平直线，弯矩图为斜直线。
（2）在q(x)＝常量段，剪力图为斜直线，弯矩图为二次抛物线。其凹下去的曲 线象锅底一样兜住q(x)的箭头。
（3）集中力作用点两侧，剪力值有突变、弯矩图形成尖点；集中力偶作用点两 侧，弯矩值突变、剪力值无变化。
解：
10KN/m A HA=0
4m VA=26.25kN
30KN.m
20KN
C
D
B
E
2m
2m
32.5 2.5
3m VB=33.75KN 60
（1）计算支座反力
单跨静定梁
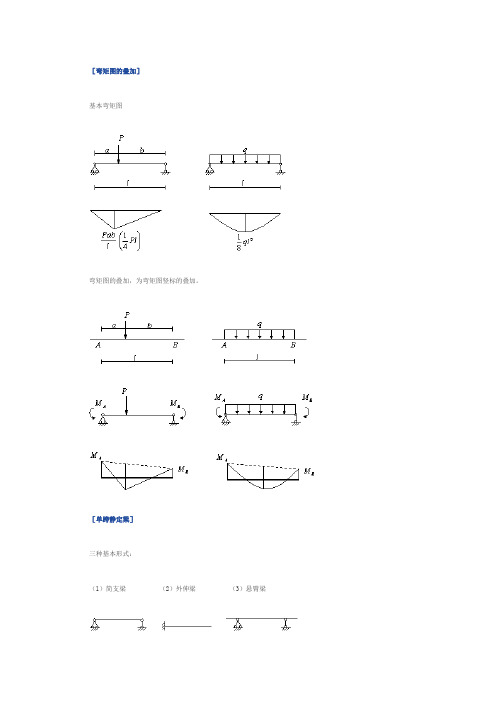
［弯矩图的叠加］
基本弯矩图
弯矩图的叠加，为弯矩图竖标的叠加。
［单跨静定梁］
三种基本形式：
（1）简支梁（2）外伸梁（3）悬臂梁
其它形式：
［作剪力图］
梁的剪力图简易作法：先求出全部的支座反力。
然后根据外力和反力的指向，从梁的左端零点出发，顺着力的方向，依次绘出剪力图，最终到达梁的右端零点。
剪力图绘在梁的上方为正，下方为负。
［作弯矩图］
先求出各控制截面的弯矩，然后根据弯矩图的叠加，分段作出结构的全部弯矩图。
求控制截面弯矩的固定截面法：先求出全部的支座反力。
欲求某控制截面的弯矩，只要将该截面假想固定，可取左半部或右半部为对象，根据悬臂结构的弯矩，判断受拉边，求出弯矩值。
结构力学第3章静定梁的内力计算
➢ 上一步所作的直线为新的基线， 叠加梁中部荷载作用下的弯矩 图。
精品课件
简支梁在两支座端有外力偶作 用时，梁两端截面有等于该端 力偶的弯矩，无外力偶在端部 作用时端部截面的弯矩为零。 所以简支梁两端支座处的弯矩 值竖标可直接绘出。
精品课件
注意：
❖ 图的叠加是弯矩竖标的叠加，而 不是图形的简单叠加。 ❖ 每叠加一个弯矩图，都以紧前一 次弯矩图外包线为新基线，并由此 基线为所叠加的弯矩图的拉压分界 线。见图3-1-6。
精品课件
❖ 又由于区段AB两端的轴力在 弯曲小变形的假设下对弯矩不 产生影响
❖ 所以从弯矩图的角度说， (a)右、(b)右两受力图是相 同的。
精品课件
区段AB的弯矩图可以利用与简支 梁相同的叠加法制作。其步骤相 类似：
➢ 求出直杆区段两端的弯矩值， 在杆轴原始基线相应位置上画出 竖标，并将两端弯矩竖标连直线。
1)求支座反力
去掉支座约束，以整体为隔离 体，由静力平衡条件得
MB 0
MA 0
精品课件
F A y 7 1(1 4 4376)3k0N m(↑)
F B y7 1(1 44471)3k3N m (↑)
FAx=0 FAy=30kN
q=14kN/m
精品课件
(a) FBy=33kN
2)计算控制截面弯矩值
取D截面以左（下侧受拉）
精品课件
➢ 在新的基线上叠加相应简支 梁与区段相同荷载的弯矩图。 （相应简支梁，指与所考虑区段 等长且其上荷载也相同的，相应
于该区段的简支梁）
上述方法即为直杆区段弯矩图的 叠加法。
精品课件
例3-1-3 计算图示简支梁，并作 弯矩图和剪力图。
q=14kN/m
1m 1m
精品课件
简支梁在两支座端有外力偶作 用时，梁两端截面有等于该端 力偶的弯矩，无外力偶在端部 作用时端部截面的弯矩为零。 所以简支梁两端支座处的弯矩 值竖标可直接绘出。
精品课件
注意：
❖ 图的叠加是弯矩竖标的叠加，而 不是图形的简单叠加。 ❖ 每叠加一个弯矩图，都以紧前一 次弯矩图外包线为新基线，并由此 基线为所叠加的弯矩图的拉压分界 线。见图3-1-6。
精品课件
❖ 又由于区段AB两端的轴力在 弯曲小变形的假设下对弯矩不 产生影响
❖ 所以从弯矩图的角度说， (a)右、(b)右两受力图是相 同的。
精品课件
区段AB的弯矩图可以利用与简支 梁相同的叠加法制作。其步骤相 类似：
➢ 求出直杆区段两端的弯矩值， 在杆轴原始基线相应位置上画出 竖标，并将两端弯矩竖标连直线。
1)求支座反力
去掉支座约束，以整体为隔离 体，由静力平衡条件得
MB 0
MA 0
精品课件
F A y 7 1(1 4 4376)3k0N m(↑)
F B y7 1(1 44471)3k3N m (↑)
FAx=0 FAy=30kN
q=14kN/m
精品课件
(a) FBy=33kN
2)计算控制截面弯矩值
取D截面以左（下侧受拉）
精品课件
➢ 在新的基线上叠加相应简支 梁与区段相同荷载的弯矩图。 （相应简支梁，指与所考虑区段 等长且其上荷载也相同的，相应
于该区段的简支梁）
上述方法即为直杆区段弯矩图的 叠加法。
精品课件
例3-1-3 计算图示简支梁，并作 弯矩图和剪力图。
q=14kN/m
1m 1m
《结构力学》第三章 单跨静定梁
l
l/2 l/2
MM
l
l
练习: 利用微分关系等作弯矩图
M
1 ql2 2
P 1 ql2
4
l
l/2 l/2
l
M
2M
MM
l
l
lM
M
l
练习: 利用微分关系等作弯矩图
1 ql2 2
P 1 ql2
4
q
1 ql2
l
l/2 l/2
2l
l
M
2M
M
MM
M
M
M
M MM
M
l
l
MM
练习: 利用微分关系,叠加法等作弯矩图
M图
Q图
例: 作内力图
铰支座有外 力偶,该截面弯矩 等于外力偶.
M图 Q图
无剪力杆的 弯矩为常数.
M图
自由端有外
力偶,弯矩等于外
Q图 力偶
练习: 利用上述关系作弯矩图,剪力图
练习: 利用上述关系作弯矩图,剪力图
5.叠加法作弯矩图
注意:
是竖标相加,不是 图形的简单拼合.
练习:
1 ql2 16
种结构型式?
简支梁(两个并列) 多跨静定梁
连续梁
例.对图示静定梁,欲使AB跨的最大正弯矩与支座B截
面的负弯矩的绝对值相等,确定铰D的位置.
q
A
D
B
C
x
l
l
RD
q
q(l x)2 / 8
RD
B
解: RD q(l x) / 2()
M B qx2 / 2 q(l x)x / 2 q(l x)2 / 8 qx2 / 2 q(l x)x / 2
静定梁、刚架、拱、行架
试用截面法求图示桁架指定杆件的内力。
C
n
m
D
1 4 6m B FP FP
3 A 2.5FP FP
梁上 无外力 均布力作用 集中力作用 (q向下) 情况 处(FP向下) 斜直 剪力图 水平线 线( ) 一般 抛物 弯矩图 为斜 线( 直线 下凸) 为 零 处 有 极 值 集中力 偶M作 用处 铰处
有突 变(突 变值= FP)
有尖 角(向 下）
如 变 号 有 极 值
无变化
无 影 响
有突变 （突变 为零 值=M）
FBx
整体对A、B 取矩，部分 对C取矩。
20
FBx
80
FAy
80
FBy
FN FQ
关键是注意： 取斜杆对杆端取矩求剪力 这样可不解联立方程
例3-8 试作图示刚架的弯矩图 附属 部分
基本 部分
弯矩图如何?
§3-4
少求或不求反力绘制弯矩图
根
据
1.弯矩图的形状特征（微分关系） 2.刚结点力矩平衡 3.外力与杆轴关系(平行,垂直,重合) 4.特殊部分(悬臂部分,简支部分) 5.区段叠加法作弯矩图 6.对称性
静定梁与静定刚架
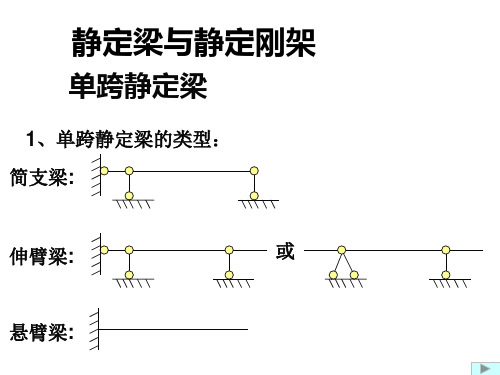
单跨静定梁
1、单跨静定梁的类型：
简支梁:
伸臂梁:
或
悬臂梁:
2、用截面法求指定截面上的内力 若要求某一横截面上的内力，假想用一平面 沿杆轴垂直方向将该截面截开，使结构成两 部分；在截开后暴露的截面上用力（内力） 代替原相互的作用。 对于截开后结构的两部分上，截面上的内 力已成为外力，因此，由任一部分的静力平 衡条件，均可列出含有截面内力的静力平衡 方F
0 Ay
F
0 By
荷载与跨度一定 时，水平推力与 拱高成反比
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
§5.2单跨静定梁的三种基本形式
简支梁、悬臂梁和外伸梁为工程中常见静定梁的三种基本形式。
实际工程中，梁的受力和支座情况都比较复杂。
为了便于分析和计算，需要进行简化，并由此得到梁的计算简图。
梁的简化通常是从梁的结构、支座和荷载等三方面进行。
一、梁的结构简化
梁是具有一定高度和宽度的构件。
在简化时，通常用梁的轴线来代表梁的实体，支座间的距离称为计算跨度。
图5-2
如图5-2(b)所示，用轴线A B代表起重吊车的横梁。
二、支座简化
常见支座形式有三种：可动铰支座、固定铰支座和固定端支座。
梁的实际支座的简化，主要根据每个支座对梁的约束情况来定。
例如图5-2(a)中起重吊车的横梁可简化为一端为可动铰支座，另一端为固定铰支座的梁。
如图5-2(b)所示。
三、荷载简化
作用于梁上的荷载通常可简化为集中力、集中力偶和分布荷载等。
如图5-4所示：
图5-4
通过上述三方面简化即可得到梁的计算简图。
工程中常见单跨静定梁有三种基本形式。
简支梁：一端为固定铰支座，另一端为可动铰支座的梁。
如图
5-5(a)所示。
图5-5
悬臂梁：一端为固定端支座，另一端为自由端的梁。
如图5-5(b)所示。
外伸梁：一端或两端伸出支座外的简支梁。
如图5-5(c)所示。