单跨静定梁
结构力学课件-单跨静定梁的内力分析

FSK
ql 2
qx
cos
0
x
l
FNK
FAy sin
qx sin 0
FNK
ql 2
qx
sin
0
x
l
③作内力图
MK
ql 2
x
qx2 2
0
x
l
FSK
ql 2
qx
cos
0
x
l
ql sinFNKFra bibliotekql 2
qx
sin
0
x
l
2
ql 2 M图 8
ql cos 2
➢将斜梁与相应水平梁作比较:
q 'l
q 'l
2
2
q 'l tan 2
q 'l2
M图 8cos
FS图
q 'l tan
2
FN图
总结斜梁内力分析的特点:
➢截面内力的计算:截面法 ➢沿水平向布置的竖向荷载作用下,简支斜梁的支座反力和相应水平梁的
支座反力相同,弯矩图相同 ➢沿水平向布置的竖向荷载作用下,斜梁的剪力和轴力是相应水平梁剪力
13.805kN
M max 13.805kN.m
单选题 1分
静定结构在荷载作用下均会产生内力,而且内力大小与杆件截面尺 寸及截面材料均无关。
A 正确 B 错误
提交
四、 简支斜梁的计算 1、斜梁应用:楼梯、屋面斜梁、及具有斜杆的刚架结构中
简支斜梁
2、斜梁所受分布荷载
q q' A
沿水平方向均布荷 载q:活载(人群、 雪载)
Fy 0 FA 10 10 4 33.75 10 2 0 FA 36.25kN ()
浅述单跨静定梁弯矩图的快速绘制

浅述单跨静定梁弯矩图的快速绘制摘要:梁是结构的主要受力单元,在计算梁的承载及破坏时,弯矩图的作用至关重要。
而弯矩图的绘制是学生在学习的一个弱点,因此针对静定粱结构的弯矩图快速绘制进行探讨,可以大大提高作图速度和效率。
关键词:静定梁弯矩弯矩图引言:力学课程是工科专业学生的一门必不可少的基础课程,它对于后续钢筋混凝土等课程的学习起十分重要的作用。
就建筑本身来说,就是一个力学模型,要保证结构的安全就必须确保每个受力构件的计算准确。
因此学好力学课程有非常重要的意义,而在日常力学课程的学习中,梁的弯矩图绘制却是学生在学习中的难点,文章通过总结各种弯矩图绘制的方法后,给出一种能够较为快速的绘制弯矩图的方法,对于梁的后续计算打下基础。
1理论知识1、1 单跨静定梁的种类(如图1):(a)悬臂梁(b)简支梁(c) 外伸梁[1]图1 :单跨静定梁的种类(Figure 1: The single-span beam statically determinate types)1、2弯矩出现的原因:弯矩伴随梁的弯曲变形而出现1、3弯矩的位置:弯矩出现在梁的截面上1、4弯矩的正方向规定:弯矩使梁的下侧(以梁的轴线为分界)纤维受拉为正1、5弯矩计算的基本方法:利用截面法计算,通过分段列弯矩图的函数表达式求解1、6 弯矩图绘制的方法:先绘制梁的轴线,弯矩图绘制在梁的受拉侧,不需要标明正负号2静定梁弯矩图绘制的实用结论2、1 弯矩的本质:弯矩是为了平衡所有外界力对截面的转动效果2、2弯矩分段的位置:弯矩作为内力的一种,与外力作用密切相关。
因此,绘制梁的弯矩图时,在有外力()作用的位置分段进行[2]2、3 需要求解弯矩的截面位置:通常出现在梁的两端以及分段位置的截面处2、4 弯矩图形的特点:梁上的荷载分为四种情况:无荷载区段、均布荷载区段、集中力作用点和集中力偶作用点。
可以对梁的弯矩图特点总结出以下规律(如表1):2、4、1、当某段梁上无分布荷载(无荷载区段),即时,是与无关的常数,是的一次函数。
第三章 静定结构的内力计算

FAy
1 3a 4 FP a M q 3a 3a 2 5
第三章
静定结构的内力计算
M
B
0
3a 4 FAy 3a M q 3a FP a 0 2 5 1 3a 4 FAy FP a M q 3a 3a 2 5
第三章
无荷载 平行轴线
Q图
静定结构的内力计算
均布荷载
集中力 发生突变
P
集中力偶
无变化 发生突变
m
斜直线
M图
二次抛物线 凸向即q指向
出现尖点
两直线平行 备 注
Q=0区段M图 Q=0处,M 平行于轴线 达到极值
集中力作用截 集中力偶作用 面剪力无定义 面弯矩无定义
在自由端、铰支座、铰结点处,无集中力偶作用,截面弯矩 等于零,有集中力偶作用,截面弯矩等于集中力偶的值。
第三章 静定结构的内力计算
第三章
静定结构的内力计算
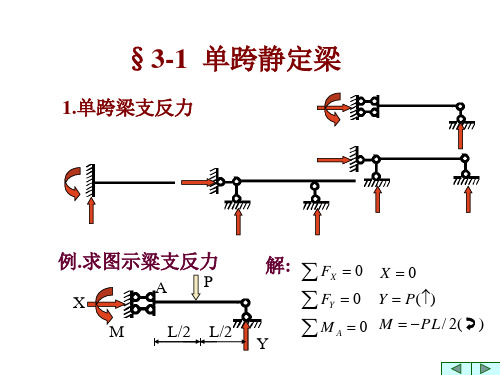
§3-1单跨静定梁
一、静定结构概述 1.概念:是没有多余约束的几何不变体系。 2.特点:在任意荷载作用下,所有约束反力和内力都 可由静力平衡方程唯一确定。 平衡方程数目 = 未知量数目 3.常见的静定结构 常见的静定结构有:单跨静定梁、多跨静定梁、静 定平面刚架、三铰拱、静定平面桁架、静定组合结构等 (如下图)。
0 FYA FYA 0 FYB FYB
A
x
C
L
斜梁的反力与相应简支 梁的反力相同。
第三章
(2)内力
静定结构的内力计算
求斜梁的任意截面C的内力,取隔离体AC: a FP1 A
FYA x Fp1 FYA
0
MC
结构力学二3-静定结构的内力计算

以例说明如下
例 绘制刚架的弯矩图。 解:
E 5kN
由刚架整体平衡条件 ∑X=0 得 HB=5kN← 此时不需再求竖向反力便可 绘出弯矩图。 有:
30
20 20 75 45
40
0
MA=0 , MEC=0 MCE=20kN· m(外) MCD=20kN· m(外) MB=0 MDB=30kN· m(外) MDC=40kN· m(外)
有突变
铰或 作用处 自由端 (无m)
m
Q图
M图
水平线
⊕
⊖㊀
Q=0 处 突变值为P 如变号 无变化
有极值 尖角指向同P 有极值 有突变 M=0 有尖角
斜直线
→
↑
利用上述关系可迅速正确地绘制梁的内力图(简易法)
简易法绘制内力图的一般步骤:
(1)求支反力。 (2)分段:凡外力不连续处均应作为分段点, 如集中力和集中力偶作用处,均布荷载两端点等。 (3)定点:据各梁段的内力图形状,选定控制 截面。如集中力和集中力偶作用点两侧的截面、均 布荷载起迄点等。用截面法求出这些截面的内力值, 按比例绘出相应的内力竖标,便定出了内力图的各 控制点。
说明:
(a)M图画在杆件受拉的一侧。 (b)Q、N的正负号规定同梁。Q、N图可画在杆的 任意一侧,但必须注明正负号。 (c)汇交于一点的各杆端截 面的内力用两个下标表示,例如: MAB表示AB杆A端的弯矩。 MAB
例 作图示刚架的内力图
RB↑
←HA
VA→
CB杆:
由∑ X=0 可得: M = CD RB=42kN↑ HA=48kN←, H (左) A=6×8=48kN← 由∑M144 VA=22kN↓ 48 A=0 可得: MEB=MEC=42×3 ↑ (2)逐杆绘M图 R=126kN = 126 · m (下) B 192 MDC=0 CD杆: M =42 × 6-20 × 3 由 ∑Y=0 可得: CB MCD=48kN·m(左) =192kN· m(下) VA=42-20=22kN↓
结构力学 第三章 静定梁和静定平面钢架

2、截面法 若要求某一横截面上的内力,假想用一平面沿杆轴垂直方向将该 截面截开,使结构成两部分;在截开后暴露的截面上用力(内力)代 替原相互的约束。
对于截开后结构的两部分上,截面上的内力已成为外力,因此,
由任一部分的静力平衡条件,均可列出含有截面内力的静力平衡方程。 解该方程即将内力求出。
3、截面内力 截开一根梁式杆件的截面上有三个内力(分量),即:轴力FN 、 剪力FQ和弯矩Μ 。
dFN/dx=-qx
dFQ/dx=-qy dM/dx=Q
d2M/dx2=-qy
增量关系: DFN=-FPx
DFQ=-FPy
DM=m
1)微分关系及几何意义: dFN/dx=-qx dFQ/dx=-qy dM/dx=Q d2M/dx2=-qy (1)在无荷载区段,FQ图为水平直线;
当FQ≠0时,Μ图为斜直线;
右右为正。
FQ=截面一侧所有外力在杆轴垂直方向上投影的代数和。左上为正, 右下为正。
Μ =截面一侧所有外力对截面形心力矩代数和。弯矩的竖标画在杆
件受拉一侧。
例3-1-1 求图(a)所示简支梁在图示荷载下截面的内力。
解:1)支座反力 ∑ΜA=0 FBy×4﹣10×4×2﹣100× (4/5)×2=0 Fby=60kN (↑) ∑ΜB=0 FAy=60kN (↑) ∑Fx= 0 FAx+100×(3/5)=0 FAx=-60kN (← ) 由 ∑Fy= 0 校核,满 足。
(下侧受拉)
区段叠加法求E、D截面弯矩; ΜE=20×42/8+120/2=100kNm ΜD=40×4/4+120/2=100kNm
(下侧受拉) (下侧受拉)
内力应考虑
说明:集中力或集中力偶作用点,注意对有突变的 分两侧截面分别计算。
结构力学 第3章静 定梁、平面刚架受力分析

q 与 q’间的转换关系:
qdx qds q q
cos
第3章
[例题] 试绘制图示斜梁内力图。
q
B
C
A
α
D VB
HA
l/3 l/3
l/3
VA
(1)求支座反力:
解:
X 0 MB 0 MA 0
HA 0
VA
ql 6
()
VB
ql 6
()
校核:
Y
qj 6
qj 6
ql 3
0
第3章
(2)AC段受力图:
(3)AD段受力图:
HAcosα HAsinα
HA VAsinα
VA VAcosα
MC
C
NC
α QC
HAcosα
dx
d2M dx2
q(x)
(1)在无荷区段q(x)=0,剪力图为水平直线,弯矩图为斜直线。
(2)在q(x)=常量段,剪力图为斜直线,弯矩图为二次抛物线。其凹下去的曲 线象锅底一样兜住q(x)的箭头。
(3)集中力作用点两侧,剪力值有突变、弯矩图形成尖点;集中力偶作用点两 侧,弯矩值突变、剪力值无变化。
解:
10KN/m A HA=0
4m VA=26.25kN
30KN.m
20KN
C
D
B
E
2m
2m
32.5 2.5
3m VB=33.75KN 60
(1)计算支座反力
静定梁与静定刚架

(二)绘内力图:
H A
=0
V
A =130KN
X 0 Y 0 M 0
C
NC 0 QC 130 KN M C 130 KN .M
第3章 例题: 试绘制图示外伸梁的内力图。
解:
10KN/m A HA=0 4m C 2m D B E 30KN.m 20KN
(1)计算支座反力
2m
2kN E
2m F
F
2m
G 2kN
2m
(b)
A
4kN/m B
C
G 2kN
G
B
11kN 4
4kN
4
(d)
8 7
(e) 9
4 M(kN.m) 2 2
Q(kN)
2
第3章 例题2: 图示三跨静定梁,全长承受均布荷载q,试确定铰E、F的位置,使中 间一跨支座的负弯矩与跨中正弯矩数据数值相等。
第3章
3.3 静定平面刚架的内力计算 一、刚架的组成 1、刚架的特征 由若干梁和柱用刚结点联结而成的结构。具有刚结点是 刚架的主要特征。 2、刚架的应用 刚架在工程上有广泛的应用。
(1)斜梁的倾角为常数,而曲梁各截面的的倾角是变量。 (2)计算曲梁的倾角时,可先写出曲梁的轴线方程y=f(x),而后对x求一 阶导数,进而确定倾角:
dy tan ; dx
tan1 (tan )
(3)角以由x轴的正方向逆时针转到切线方向时为正,反时针方向为负。
例题:试求图示曲梁C截面的内力值。已知曲梁轴线方程为:
y 4f 4 4 (l x) x 2 (12 1.5) 1.5 1.75m l2 12
4f 4 4 tan yx 1.5 2 (l 2 x) x1.5 2 (12 2 1.5) 1 l 12 2 450 sin con 0.707 2
《结构力学》第三章 单跨静定梁
l
l/2 l/2
MM
l
l
练习: 利用微分关系等作弯矩图
M
1 ql2 2
P 1 ql2
4
l
l/2 l/2
l
M
2M
MM
l
l
lM
M
l
练习: 利用微分关系等作弯矩图
1 ql2 2
P 1 ql2
4
q
1 ql2
l
l/2 l/2
2l
l
M
2M
M
MM
M
M
M
M MM
M
l
l
MM
练习: 利用微分关系,叠加法等作弯矩图
M图
Q图
例: 作内力图
铰支座有外 力偶,该截面弯矩 等于外力偶.
M图 Q图
无剪力杆的 弯矩为常数.
M图
自由端有外
力偶,弯矩等于外
Q图 力偶
练习: 利用上述关系作弯矩图,剪力图
练习: 利用上述关系作弯矩图,剪力图
5.叠加法作弯矩图
注意:
是竖标相加,不是 图形的简单拼合.
练习:
1 ql2 16
种结构型式?
简支梁(两个并列) 多跨静定梁
连续梁
例.对图示静定梁,欲使AB跨的最大正弯矩与支座B截
面的负弯矩的绝对值相等,确定铰D的位置.
q
A
D
B
C
x
l
l
RD
q
q(l x)2 / 8
RD
B
解: RD q(l x) / 2()
M B qx2 / 2 q(l x)x / 2 q(l x)2 / 8 qx2 / 2 q(l x)x / 2
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
[弯矩图的叠加]
基本弯矩图
弯矩图的叠加,为弯矩图竖标的叠加。
[单跨静定梁]
三种基本形式:
(1)简支梁(2)外伸梁(3)悬臂梁
其它形式:
[作剪力图]
梁的剪力图简易作法:先求出全部的支座反力。
然后根据外力和反力的指向,从梁的左端零点出发,顺着力的方向,依次绘出剪力图,最终到达梁的右端零点。
剪力图绘在梁的上方为正,下方为负。
[作弯矩图]
先求出各控制截面的弯矩,然后根据弯矩图的叠加,分段作出结构的全部弯矩图。
求控制截面弯矩的固定截面法:先求出全部的支座反力。
欲求某控制截面的弯矩,只要将该截面假想固定,可取左半部或右半部为对象,根据悬臂结构的弯矩,判断受拉边,求出弯矩值。
