第四章 多相平衡系统热力学(3)
第4章 多组分热力学

前面所讨论的是:单组分单相(两相)系统或多 组分组成恒定的系统。 但常见系统绝大部分是:多组分变组成系统。因 此必须研究处理多组分系统。
多组分系统除了两个变量之外,还需确定各组分 的物质的量才能确定系统的状态。 多组分系统分为:单相、多相
本章主要讨论多组分单相系统。
1
第四章 多组分系统热力学
B
dA SdT pdV BdnB
B
•适用条件 W ' 0 ,单相系统
31
2.多组分单相系统的热力学公式
•广义定义
B
U nB
S ,V ,nC
H nB
S , p,nC
A nB
T ,V ,nC
G nB
T , p,nC
保持特征变量和除B以外其它组分不变,某热力
学函数随其物质的量 nB的变化率称为化学势。
2 偏摩尔量相对于某一组分而言,本身是强度量;
3 偏摩尔量与浓度有关,与系统的总量无关。
4 偏摩尔量 X B ( nX,B )下T ,标p,n必C 须是
。T , p, nC
15
2.偏摩尔量
•偏摩尔量的物理意义
•两种理解 1 在恒温恒压下,于极大量的某恒定组成的系统中加
入1mol组分B时所引起系统广度量X的改变量。
混合物的摩尔体积:
Vm
xB M B /
B
Vm xBVB
B
21
5.吉布斯—杜亥姆方程
X
X
dX
( T
) p,nB
dT
(
p
)T ,nB
dp
B
X BdnB
•恒温恒压多组分系统
dX X BdnB
B
物理化学:第4章_多组分系统热力学_
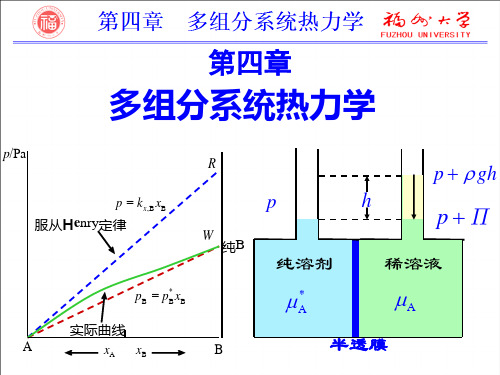
真实混合物:实曲线
Vm xBVB xCVC VB (VC VB)xC
当混合物组成改变时,两组 分偏摩尔体积随之改变,且二者 变化相互关联。
组成接近某纯组分,其偏摩 尔体积也接近该纯组分摩尔体积。
5. 吉布斯 − 杜亥姆方程
对广度量 X (T , p, nB, nC , nD ,) 求全微分:
dX
X T
p,nB
dT
X p
T ,nB
dp
B
X nB
dnB T , p,nC
恒温、恒压
另一方面,由加和公式
,恒温恒压下求导:
比较两式,得
或
或
吉布斯-杜亥姆方程--在一定温度压力下,当混合物
组成变化时,各组分偏摩尔量变化的相互依赖关系。
➢ 系统中各组分的偏摩尔量并非完全独立,而是相 互依存的。
➢ 例:固体溶解、过饱和溶液析出、…
组分B在α、β两相中迁移达平衡的条件:该组分
在两相中的化学势相等。
➢ 物质总是从其化学势高的相向化学势低的相迁移, 直至物质迁移达平衡时为止,此时系统中每个组分在 其所处的相中的化学势相等。
化学势 判据
② 化学平衡
<0:自发不可逆; =0:平衡、可逆
任一化学反应,假定系统已处于相平衡,
任一组分B在每个相中的化学势都相等: Bα B
B
B
整个系统中B组分物质的量的变化量: dnBα dnB
α
BdnB
B
化学平衡时
平衡条件:与化学反应达到平衡的方式无关。
§4.3 气体组分的化学势
1、纯理想气体的化学势 2、理想气体混合物中任一组分的化学势 3、纯真实气体的化学势 4、真实气体混合物中任一组分的化学势
物理化学 第四章 多组分系统热力学

Vm
T,p一定
V*m,C VC
V*m,B VB
d c· b·
0 B
a xC
C
图4.1.2 二组分液态混合物的 偏摩尔体积示意图
若B,C形成真实液态混合物: 则混合物体积为由V*m,B至V*m,C的曲线。对于任一 组成a时,两组分的偏摩尔体积可用下法表示: 过组成点a所对应的系统体积点d作Vm-xC曲线的 切线,此切线在左右两纵坐标上的截距即分别 为该组成下两组分的偏摩尔体积VB,VC。
B
系统中各广度量的偏摩尔量: 对于多组分系统中的组分B,有: 偏摩尔体积: VB=(ƽV/ƽnB)T,p,n C 偏摩尔热力学能: UB=(ƽU/ƽnB)T,p,n C 偏摩尔焓: HB=(ƽH/ƽnB)T,p,n C 偏摩尔熵: SB=(ƽS/ƽnB)T,p,n C 偏摩尔亥姆霍兹函数:AB=(ƽA/ƽnB)T,p,n C 偏摩尔吉布斯函数: GB=(ƽG/ƽnB)T,p,n
C
几点说明: (1)偏摩尔量为两个广度性质之比,所以为强度 性质; (2)偏摩尔量的定义中明确是在恒温、恒压及系 统组成不变的条件下,偏导数式的下标为T,p 时才是偏摩尔量; (3)同一物质在相同温度、压力但组成不同的多 组分均相系统中,偏摩尔量不同; (4)若系统为单组分系统,则该组分的偏摩尔量 与该组分的摩尔量相等,即: XB=X*B,m
C
=VB (数学知识:二阶偏导与求导的顺序无关) 得证。
4.2化学势 4.2化学势
1.化学势的定义 混合物(或溶液中)组分B的偏摩尔吉布斯函数GB 定义为B的化学势,用符号μB表示:
μB = GB=(ƽG/ƽnB)T,p,n
def
C
对于纯物质,其化学势等于它的摩尔吉布斯函 数。
第四章-相平衡-1

考虑水的电离因素。
ii)酸的水溶液,如:HAc + H2O,若不 考虑酸的电离,则 C = 2;
a. 若考虑HAc电离:HAc H+ +Ac
S = 4 ( H2O, HAc, H+, Ac ), R = 1 (有一化学平衡),
且 R´=1 ( [H+] = [Ac] ),
• 以上这些都是我们常见的多相平衡的例 子,这些类型多相平衡各有一定的方法 来研究它们的规律,例如:
拉乌尔定律、亨利定律、分配定律、 平 衡常数及某些其他经验性规则。 而下面要介绍的 “相律”,却不同于上 述这些规律。 相律所反映的是多相平衡中最有普遍性 的规律,即独立变量数、组分数和相数
之间的关系。 “相律”是一种从统一的观点来处理各
现已经有溶液相和冰两个相,所以与其 共存的含水盐相最多只能有一种。
2)同理,在恒定温度下,
f * = C +1 = 3
最多有三相,所以定温下与水蒸气平衡
共存的含水盐最多可有两种。
2. 说明下列平衡系统的自由度 1) 25C 和 1atm 下,固体 NaCl 与其水
溶液成平衡。
答:C = 2, = 2(固相、溶液相)
在保持系统相数不变条件下,可任
意改变的独立变量数。
例如: 水在保持单一液相条件下
f = 2 (压力、温度)
而水在保持:汽 液 两相平衡条件
下,独立变量数为
f = 1 (压力或温度)
§4.2 相律及其热力学推导
一、“ 相律 ” 的完整表述
在平衡系统中,联系系统内相数、组分 数、自由度及影响物质性质的外界因素
(完整版)第四章相平衡思考题(答案)

第四章相平衡思考题1. 纯氮气和空气算一个相吗?【解】纯氮气和空气各算一个相。
2. 当两个相的温度相同但压力不同时,两个相能达到平衡吗?如果两相的压力相同而温度不同,两相能达到平衡吗?【解】一般而言,当系统达到热力学平衡时,系统将同时满足热平衡、力平衡、相平衡和化学平衡。
具体到相平衡,其条件是各物质在两相中的化学势相同。
影响化学势的因素有温度和压力,达到相平衡时一般温度和压力亦相等。
如果温度相同,而压力不等同样有达到相平衡的可能,如渗透系统;同样地,在压力相同而温度不同的情况下,也应该有达到相平衡的可能性。
3. 在抽空的真空容器中,有一定量的NH4HS(s),加热后NH4HS(s)分解,试说明组分数和自由度。
【解】分解反应为NH4HS(s)→ NH3(g)+ H2S(g),组分数K = 3 - 1 – 1 = 1,自由度f = 1 - 2 + 2 = 1。
4. 恒温恒压下,某葡萄糖和氯化钠同时溶于水中,用一张只允许水通过的半透膜将此溶液与纯水分开。
当系统达到平衡后,系统的自由度为多少?【解】f** = 3 - 2 + 1 = 2。
5. 说明物系点和相点的区别,什么时候物系点和相点是统一的?【解】物系点表示系统的组成,而相点表示系统相的组成。
当系统是单相的时候,两者是重合的。
6. 图4-2中,当系统处于临界点C 时,自由度是多少?【解】自由度等于零。
7. 如用二氧化碳超临界流体作萃取剂,最低的工作压力是多少?能在室温下进行此操作吗?【解】二氧化碳的临界参数是t c = 31.26℃、p c = 7.2 MPa,因此最低压力是7.2 MPa。
因为t c = 31.26℃十分接近典型的室温值25℃,因此CO2超临界流体萃取可以在近室温下操作。
8. 在一高压容器中有足够量的水,向容器中充入氮气压力到10 MPa,这时还能用Clausius-Clapeyron 方程计算水的沸点吗?【解】当压力达到10 MPa 时,而水的临界压力为 22.129 MPa,几乎接近一半,此时水的体积不能忽略,水蒸气也不能视为理想气体,所以不能用Clausius-Clapeyron 方程计算水的沸点。
4-3多组分系统热力学-理想液态混合物与理想稀溶液

Physical Chemistry
物理化学(上册)
绪论 第一章 气体 第二章 热力学第一定律 第三章 热力学第二定律 第四章 多组分系统热力学 第五章 化学平衡 第六章 相平衡
第四章 多组分系统热力学
§4-!本章基本要求 §4-1多组分系统热力学概念 §4-2拉乌尔定律与亨利定律 §4-3偏摩尔量 §4-4化学势 §4-5理想液态混合物 §4-6理想稀溶液 §4-7活度活度系数 §4-8化学势小节 §4-$小结与学习指导
d* S*dT V *dp
B
B
B
mixG p
T
B
nBVB
B
nBVB* mixV
2. mixV 0 或 V mix m 0
mix p
G
T
(RT
nB ln xB )
B
p
T
0
§4-5理想液态混合物
四、理想液态混合物混合性质
dG B S B dT VB dp
dG * S * dT V *dp
B
B
6.
mixU mix H P mixV 0
mixU 0 或 mixU m 0
§4-5理想液态混合物
四、理想液态混合物混合性质
小结: 1. mixV=0 , mixU=0 , mixH=0 2. Q=0, W=0 3. mixS=-RnBlnB>0 (绝热 S>0)
mixA=RTnBlnB<0 (恒温恒容W =0 A<0) mixG=RTnBlnB<0 (恒温恒压W =0 G<0)
§4-6理想稀溶液
一、理想稀溶液定义 无限稀溶液,溶质的浓度趋于零的溶液。 对溶剂(A表示)用符合拉乌尔定律
第四章--多组分系统热力学习题
第四章多组分系统热力学选择题1. 在和101325Pa•下水的化学势与水蒸气化学位的关系为(A) μ(水)=μ(汽) (B) μ(水)<μ(汽)(C) μ(水)>μ(汽) (D) 无法确定答案:A。
两相平衡,化学势相等。
2.下列哪种现象不属于稀溶液的依数性(A) 凝固点降低(B)沸点升高(C) 渗透压(D)蒸气压升高^答案:D。
稀溶液的依数性之一为蒸气压下降。
3.98K时,A、B两种气体在水中的亨利常数分别为k1和k2,且k1>k2,则当P1=P2时,A、B在水中的溶解量C1 和C2 的关系为(A) C1>C2 (B) C1<C2 (C) C1=C2 (D) 不能确定答案:B4.将非挥发性溶质溶于溶剂中形成稀溶液时,将引起(A) 沸点升高(B) 熔点升高(C) 蒸气压升高(D) 都不对答案:A。
稀溶液的依数性包括沸点升高、凝固点下降、蒸气压下降和渗透压。
5. 涉及纯物质标准状态的下列说法中不正确的是(A) 纯理想气体的标准状态就是标准压力P(100KPa)下的状态(B) 纯液体物质的标准状态就是标准压力P(100KPa)下的纯液体—(C) 纯固体物质的标准状态就是标准压力P(100KPa)下的纯固体(D) 不同的物质在相同温度下都处于标准状态时,它们的同一热力学函数值都应相同答案:D6. 稀溶液的依数性包括蒸汽压下降、沸点升高、凝固点降低和渗透压,下面的陈述都与它们有关,其中正确的是(A) 只有溶质不挥发的稀溶液才有这些依数性(B) 所有依数性都与溶液中溶质的浓度成正比(C) 所有依数性都与溶剂的性质无关(D) 所有依数性都与溶质的性质有关答案:B7. 关于亨利系数, 下面的说法中正确的是!(A) 其值与温度、浓度和压力有关(B) 其值只与温度、溶质性质和浓度标度有关(C) 其值与溶剂性质、温度和浓度大小有关(D) 其值与温度、溶剂和溶质的性质及浓度标度等因素都有关答案:D8. 定义偏摩尔量时规定的条件是(A) 等温等压 (B) 等熵等压(C) 等温, 溶液浓度不变 (D) 等温等压, 溶液浓度不变答案:D9. 关于偏摩尔量, 下面的说法中正确的是~(A) 偏摩尔量的绝对值都可求算(B) 系统的容量性质才有偏摩尔量(C) 同一系统的各个偏摩尔量之间彼此无关(D) 没有热力学过程就没有偏摩尔量答案:B10. 关于偏摩尔量, 下面的叙述中不正确的是(A) 偏摩尔量是状态函数, 其值与物质的数量无关(B) 系统的强度性质无偏摩尔量(C) 纯物质的偏摩尔量等于它的摩尔量(D) 偏摩尔量的数值只能为整数或零-答案:D11. 影响沸点升高常数和凝固点降低常数值的主要因素是(A) 溶剂本性 (B) 温度和压力 (C )溶质本性(D) 温度和溶剂本性答案:A 。
第四章 相平衡
• 例 :在某温度下 , 体系中 PCl5(g)部分分解产生了一定量的 PCl3(g)
和Cl2(g) 并达到了化学平衡, 体系中独立的化学反应数R为多少?
组分数K是多少?
• 体系中只存在下面一个化学反应:
PCl5(g)= PCl3(g) + Cl2(g) • 该体系中独立的化学反应数R=1
• 该体系中物种数S=3
• 解: 有反应: S=3 R=1 R’= 1 分解反应平衡 [p(NH3)=p(H2S)] NH4HS(s) = NH3(g) + H2S(g)
∴
K=3-1-1=1
f = K- + 2=1-2 + 2=1
• 即此体系的温度和压力两变量中只有一个是独立的 . 体系的温度 固定时, NH4HS的分解压力一定,故体系的压力恒定; 反之,若体系 的压力一定,体系的温度必也被确定.
吉布斯相律
• 相律的物理含义是:
体系的自由度等于体系的独立组分数 K 减去相数 再加上环境变量数2(温度和压力).
• 在某些特殊条件下, 环境变量不仅仅为温度和压力, 可能 存在其它变量, 故相律更一般的可表达为:
f=K– +n
• 式中: f为体系的自由度;
K为组分数;
为相数;
n为环境变量数, 一般情况下n=2(T, p).
• 独立组分数(K), 简称为组分数, 指确定体系组成所必须
的变量数.
• 定义:
K=S-R-R’
• S:物种数, R:独立的化学反应数, R’:浓度限制数
• 独立的化学反应数 (R): 一个多相系统存在多个反应时 ,
• 浓度限制数(R’): 同一相中存在的浓度之间的关系。
独立的化学反应指不能由其他反应组合推导出来的反应.
物理化学第四版 第四章 多组分系统热力学2014.2
)
p,n
(
B
)
,V
(
G P
)T
,n(
B
)
k
dG SdT VdP BdnB
证毕
B 1
14
又 dA d(G PV ) dG pdV Vdp
将上式dG 代入,整理得:
k
dA sdT PdV BdnB ……..(3) B 1
同理可得出另二个热力学基本方程。
因 A=A(T,V,n1,n2…….nk)
B
B
B
........
n B
相平衡条件
有N 个组分,就有N 个这样的式子
19
例:在、 两相中均含有A和B两种物质,达到相平衡时,下列
各式正确的是(
)。
A、
A
B
B、
B
B
C、
A
B
D、
B
A
例:组分B从相扩散入相中,则以下说法正确的有( A、总是从浓度低的相扩散入浓度高的相 B、平衡时两相浓度相等 C、总是从化学势高的相移向低化学势低的相
dA
(
A T
)V
,n
(
B
)
dT
( A V
)T ,n(B)
dV
k B 1
(
A n(B)
)T
,V
,n
(
c,c
B)
dnB
将式(4)和式(3)比较
B
A ( nB
)T ,V ,n(c,cB)
同样可得出
B
U ( nB
)S ,V ,n(c,cB)
H ( nB
)S ,P.n(c,cB)
…..(4)
15
例 2: 下列偏导数中那些是偏摩尔量?那些是化学势?
物理化学第四章
• 但碳的相图中最多只能三相共存,不可能四相共存.
一.克-克方程(Clausius-Clapeyron equation)
• 当单组分体系两相共存时,自由度f=3-2=1, 体系只有一个自由度。 • 单组分的相变温度与压力之间存在一定的关 系, 此关系即为克-克方程. • 设一纯物质在T,p下达两相平衡:
相图:表示体系状态变化的图形
•
• 相(phase): 体系内物理性质和化学性质
完全均匀的部分. • 均匀的要求: •
均匀到分子水平
• 一个体系中可以含有多个相,这些相与相 之间一般存在明显的界面,界面处体系的 热力学性质是间断的.
气体:凡气体成一相.
气体体系无论有多少种气体,一般都达到分子水 平的混合,故为一相。
• (3)式称为克拉贝龙方程. • 克拉贝龙方程适用于纯物质任何平衡相变过 程,应用范围很广.
• 1. 气-液,气-固两相平衡:
• 纯物质的两相平衡中有一相为气相,另一相必为 凝聚相. 以气-液平衡为例,有: • dp/dT=Hm/TVm= Hm/T(Vm,g-Vm,l) (4) • ∵ Vm,g>>Vm,l • ∴ Vm,g-Vm,l≈ Vm,g=RT/p • 代入(4)式: • dp/dT= Hm/[T(RT/p)] •
• 体系的独立变量数f(即自由度)应该等于总变量 数减去关系式总数: • 总变量数:S+2 • 关系式数:+S(-1) • •
f = S+2--S+S
f = S- + 2
(1)
• (1)式就是相律的数学表达式. • 相律的物理含义是:
体系的自由度等于体系的物种数S减去相 数再加上环境变量数2(温度和压力).
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
ii)精馏原理
精馏是多次简 单蒸馏的组合。 将一定组成的 溶液加热到T2, 此时物系点为O, 气相相点G2(组成 为y2),液相相点 L2(组成为x2)。
精馏塔示意图
精馏塔底部是加热区,温度最高,塔顶温度最低。 精馏结果,塔顶冷凝收集的是纯低沸点组分,纯 高沸点组分则留在塔底。
p
p
l
E l+g
O’
O F
* pB
p* A
A+B xf 气相 p A+B xe 液相
g A+B xf 气相 A p
xe xo xf B XB→
Xo’
A+B xe 液相
O
O’
落在EF线上所有物系点的对应的液相和气相 组成,都由E点和F点的组成表示。 f*=2-2+1=1
物系点:是整个系统总的状态点。由p和系统总组成XB确定。 相点:是表示平衡系统中每一个相的状态点。由p和平衡各相 组成XB和YB确定。 例如: ①压力为p1,组分B的摩 尔分数为x1,物系点为O1 此时系统为液相,其相点 也为O1, ②压力为p2,组分B的摩尔分 数为x2,物系点为O2,相点也 为 O2。 在单相区,物系点和相点是重 合的。
TB
B
TA是纯A的沸点,TB是纯B的沸点。
识图
①线 液相线 ②面 液相区 气相区 A 气相线 TA T 气
气相线
气 液 液液相线 X→ TB B
气 液 两相平衡区 ③点 TA是纯A的沸点,TB是纯B的沸点。
识 图
当系统的温度为T,组成 为 X 时,整个系统的状态 用 O 点描述,该点叫做物 系点。 此时系统处于两相平衡, 平衡的液相为 Ol ,气相为 Og , Ol和Og叫做相点。 T g 气相线
设A和B构成理想液态混合物,根据实验测定不同组
成的液态混合物气液两相平衡时,气相的压力p,液相组 成xB和气相组成yB。
p1 ~ xB1 yB 2
气相yB 液相xB
p2 ~ xB 2 yB 2
p3 ~ xB3 yB3
绘制相图
根据上面的数据,由p~xB数据绘制出液相线 由p~yB数据绘制出气相线 p 为什么p~xB为直线? 因为A和B组成的混合物 时理想液态混合物,各个 组分在所有浓度范围内服
2. 部分互溶双液系统
部分互溶:是指一定温度下某液体在另一液体中只有 有限的溶解度。超过一定范围时,就要分成两个液层。 ①部分互溶双液系统液液平衡相图 实验数据的获得:以水—苯酚系统为例 一定温度T时,将一定量的水和 苯酚(苯酚的质量百分数为W%) 混合充分震荡使之达到平衡。。
T2 a” a’ T1
系统始终保持沸腾状态。
T1 T2叫做沸程。
O’ l+g O 液相区 x A XB→
b’ b
B
理想液态混合物 p~x图与T~x图的比较
p T
* pB
p* A
l+g
TA
气相线 l+g 液相线
TB
A
XB
B
A
XB
B
p p
* A * B
是纯A的饱和蒸气压
固定T或p,f*=C-P+1=3-P Pmin=1 , fmax*=2 fmin*=0 ,Pmax=3,即最多允许三相平衡共存。
对于两组分系统,通常固定p绘制T~X图,或固 定T绘制p ~X图。
二、气液平衡相图 1. 完全互溶双液系统 (1)理想液态混合物的相图 ①理想液态混合物的p -x图
• 假设气体为理想气体。
Hm 1 ln p C R T
g l
p2 H m (T2 T1 ) ln p1 RTT 1 2
g l
Clausius-Clapeyron 方程的积分式
p2 H m (T2 T1 ) ln p1 RTT 1 2
p
p1
液 相 O1 区
* pB
l+g O2
p* A
p2 气相区
A
x1
x2 XB→
B
p -x图
物系点与相点
重要概念
物系点:是整个系统总的状态点。由p和系统总组成XB确定。 相点:是表示平衡系统中每一个相的状态点。由p和平衡各相 组成XB和YB确定。 ③压力为p3,组分B的摩尔分数 为x3,物系点为O3,相点分别 为E和F。 EF叫连接线。
液相和气相的数量借助于力 p 学中的杠杆规则求算,即以物系 点O为支点,支点两边连结线OE和 p OF为力臂,计算液相和气相的物 p* 质的量或质量,这就是杠杆规则。 A 可用于任意两相平衡区。
l
E l+g
O’
O F
* pB
nl EO ng OF
nl OF x f xO ng OE xO xe
气
B XB→
p -x图
理想液态混合物 p~x图
p
* pB
p* A
l+g
液相线 气相线
A
XB
B
p p
* A * B
是纯A的饱和蒸气压 是纯B的饱和蒸气压
②理想液态混合物的T -x图
定压下,将不同组成的理想 T 混合物加热至沸,测得沸点与 TA 气、液相组成的关系,可绘制 出T~x图。 依据两相平衡时T~x的关系, 可绘制出液相线。 依据两相平衡时T~y的关系, 可绘制出气相线。 A X→
p
p3
液 相 区
E O3 F l+g
* pB
p* A
A+B xf p A+B xe
g
x3
l
气相区
A
xe XB→
x3 xf
B
p -x图
落在EF线上所有物系点的对应的液相和气相 组成,都由E点和F点的组成表示。 f*=2-2+1=1 O和O’两个物系的异同
对应的两个相的组成是相同 的,只是数量是多少不同。
具有最低恒沸点的相图可以看作由两个简单的T-x 图的组合。对具有最高、低恒沸点的实际溶液精馏 时,不能将两组分完全分离,其精馏结果可得到一 个纯物质,另一个是恒沸混合物。
组成为X1时:塔顶为恒沸混合物
塔底为纯B 组成为X2时:塔顶为恒沸混合物 塔底为纯A
* B * A
* A
p~xB为直线!
A
XB→
B
由Dalton和Raoult定律
pB pyB p x
* B * A
* B B
* A
p ( p p ) xB p
p
p p p * * pB ( p pA ) yB
p ~ yB
* A * B
1. 自由度 在一个平衡体系中,在不消失旧相
也不产生新相的条件下,在有限的范围
内可以任意改变的独立变量(T、p、xi)的 数目称为自由度,用f表示。
www.theBiblioteka
2. 相律表达式 f =C–P+2 Gibbs相律表达式
条件:相律适用于热力学平衡系统
②实际混合物的p~X图T~X图
正偏差
负偏差
最大正偏差
最大负偏差
最低恒沸点
T2 T1
最大正偏差
O点对应的温度:最低恒沸点 O点对应的组成:恒沸混合物
③ 精馏原理
蒸馏与精馏是分离液体混合物常用的方法,在实验 室和工厂应用很广。 i)简单蒸馏
A
f=2
T
4. Clapeyron 方程
dp H m dT T Vm
条件:纯物质两相平衡
5 Clausius-Clapeyron 方程 在Clapeyron方程基础上加了三个条件: • 只考虑气液或气固两相平衡; • 忽略液体或固体的体积;
* B
液相线
p* A
* pB
气相线
A
XB→
B
①线
液相线 p~xB ②面 液相区 气相区
识 图
气相线p~yB
p
液相区
液相线
p* A
l+g
* pB
气液两相平衡区
气相线
气相区 A XB→ B
③点
p* A 是纯A的饱和蒸气压
* pB 是纯B的饱和蒸气压
p -x图
g
A
xe xo xf B XB→
Xo’
相律分析
在液相区或气相区:C=2, p=1,f*=2-1+1=2,系统有两个 p 自由度,p和组成x可在一定范 围内独立变化而维持单相不变。 p
l 液 E l+g F
* pB
p* A
在气液两相平衡区:C=2, p=2,f*=2-2+1=1,系统只有 一个自由度,p和组成x只有一 个是独立变量,当指定p时, 两相的组成也就一定了。 g A
p* A
液相线
* pB
气相线
从拉乌尔定律。
A
0
0.2
XB→ YB→
0.4 0.6
0.8 1.0
B
p pB p A
p x p x
* B B
* B B * A
* A A
p x p (1 xB )
p 液相线
p* A
* pB
( p p ) xB p
是纯B的饱和蒸气压
TA是纯A的沸点, TB是纯B的沸点。
(2) 实际液态混合物的相图 ①正偏差与负偏差
p
p~XCH3OH pCH3OH*
pCH OH xCH3OH
3
pCH3OH p
