梅涅劳斯定理在中学数学中的应用
一道初三课外练习的证明——梅涅劳斯定理和塞瓦定理的应用

一道初三课外练习的证明——梅涅劳斯定理和塞瓦定
理的应用
梅涅劳斯定理:梅涅劳斯定理是一个关于圆的定理,它告诉我们,如果一个圆的外接的正多边形的各个角度都是相等的,那么,这个正多边形的每条边都是等边的。
塞瓦定理:塞瓦定理是一个关于圆的定理,它告诉我们,如果一个圆的内接正多边形的每条边都是等边的,那么,这个正多边形的每个角度也是相等的。
证明:为了证明梅涅劳斯定理和塞瓦定理之间的关系,我们使用反证法。
假设正多边形的每个角度都是相等的,而它的每条边不是等边的。
根据梅涅劳斯定理,我们知道这个正多边形的每条边都是等边的,而这与我们的假设矛盾,因此该假设是错误的。
反之,假设正多边形的每条边都是等边的,而它的每个角度不是相等的。
根据塞瓦定理,我们知道这个正多边形的每个角度都是相等的,而这与我们的假设矛盾,因此该假设也是错误的。
由此可见,梅涅劳斯定理和塞瓦定理之间有着密切的联系。
即正多边形的每个角度都是相等的,那么它的每条边也都是等边的;反之,正多边形的每条边都是等边的,那么它的每个角度也都是相等的。
综上所述,梅涅劳斯定理和塞瓦定理之间是成立的。
(2)点共线、线共点的一般证明方法及梅涅劳斯定理、塞瓦定理的应用

2012年高中数学竞赛讲座在本小节中包括点共线、线共点的一般证明方法及梅涅劳斯定理、塞瓦定理的应用。
1. 点共线的证明点共线的通常证明方法是:通过邻补角关系证明三点共线;证明两点的连线必过第三点;证明三点组成的三角形面积为零等。
n(n≥4)点共线可转化为三点共线。
例1 如图,设线段AB的中点为C,以AC和CB为对角线作平行四边形AECD,BFCG。
又作平行四边形CFHD,CGKE。
求证:H,C,K三点共线。
证连AK,DG,HB。
由题意,AD EC KG,知四边形AKGD是平行四边形,于是AK DG。
同样可证AK HB。
四边形AHBK是平行四边形,其对角线AB,KH互相平分。
而C是AB中点,线段KH过C点,故K,C,H三点共线。
例2如图所示,菱形ABCD中,∠A=120°,为△ABC外接圆,M为其上一点,连接MC交AB于E,AM交CB延长线于F。
求证:D,E,F三点共线。
证如图,连AC,DF,DE。
因为M在O上,则∠AMC=60°=∠ABC=∠ACB,有△AMC∽△ACF,得FA BCDEFHKG第 3 页 共 23 页。
CDCFCA CF MA MC ==又因为∠AMC =BAC ,所以△AMC ∽△EAC ,得。
AEADAE AC MA MC ==所以,又∠BAD =∠BCD =120°,知△CFD ∽AEADCD CF =△ADE 。
所以∠ADE =∠DFB 。
因为AD ∥BC ,所以∠ADF =∠DFB =∠ADE ,于是F ,E ,D 三点共线。
例3 四边形ABCD 内接于圆,其边AB 与DC 的延长线交于点P ,AD 与BC 的延长线交于点Q 。
由Q 作该圆的两条切线QE 和QF ,切点分别为E ,F 。
求证:P ,E ,F 三点共线。
证 如图。
连接PQ ,并在PQ 上取一点M ,使得B ,C ,M ,P 四点共圆,连CM ,PF 。
设PF 与圆的另一交点为E ’,C E (E')ABDF PMQ G并作QG丄PF,垂足为G。
初中数学奥林匹克中的几何问题:第1章梅涅劳斯定理及应用附答案

初中数学奥林匹克中的几何问题:第1章梅涅劳斯定理及应用附答案第一章涅劳斯定理及应用[基础知识]梅涅劳斯定理设a?,b?,c?分别是△abc的三边bc,ca,ab或其延长线上的点,若a?,b?,文学士?cb?交流电?C如果三个点是共线的,那么① 1.a?bb?ac?bab′c′c′b′abca′d图1-1bcda'如图1-1所示,通过a画一条直线?A.交叉口BC的延长线是D,然后是CB?ca?交流电?爸爸因此Baa?华盛顿?文学士?工商管理学士?cb?交流电?文学士?ca?爸爸1.a?cb?交流电?文学士?ca?爸爸?注:该定理的证明还包括以下正弦定理证明和面积证明正弦定理证法设∠bc?a,∠cb?a,∠b?a?b??,在△ba?c?中,有文学士?罪类似地,C?bsin?cb?罪交流电?罪这三种形式的乘法就是证据?ca?罪ab?罪文学士?s△A.Cbcb?s△cb?Cs△ca?Bs△cb?Cs△ca?Bs△Cca?交流电?s△交流电?A.面积证书方法由以下三部分组成:?反恐精英△b?像△B交流电?s△A.ab?s△B交流电??s△A.防抱死制动系统△交流电?A.C学士学位△C文学士?形式的乘法就是证明梅涅劳斯定理的逆定理设a?,b?,c?分别是△abc的三边bc,ca,ab或其延长线上的点,若ba?cb?ac?②1,A.cb?交流电?B然后a?,BC三个点是共线的ba?cb?ac11.证明设直线a?b?交ab于c1,则由梅涅劳斯定理,得到A.cb?Ac1a由问题和答案组成ac1ac?ba?cb?ac??.1,即有c1bc?文学士?cb?交流电?bac1ac那么AC1呢?交流电?,那么C1和C呢?巧合,即a?,BC三个点是共线的吗?ABAB有时把以上两个定理写成:let a?,BC是直线上的点(包括三条边的延长线)△ ABC,然后a?,BC三点共线的充要条件是Ba?cb?交流电1. Acbacb使用上述公式① 和② 是给△ ABC,如图1-1所示(整个图中有四个三角形)。
梅涅劳斯定理在中学数学中的应用

2.2 利用平行线分线段成比例定理进行证明
平行线分线段成比例定理是研究相似形和比例
关系的最重要和最基本的理论,它一方面可以直接
判定线段成比例,另一方面,当不能直接证实要证的
比例成立时,常用这个定理把两条线段的比“转移”
成另两条线段的比.
证 明:过 点 C作 CG
∥DF交 AB于 G,如图,则
CEEA=GFFA,BDDC=BGFF,
则易得BCNP=BDDC,
故FAFB·BDDC·CEEA=BAQN·BCNP·CAQP=1.
2.1 运用相似三角形的知识进行证明
由于梅涅劳斯定理涉及到比例关系,而且还是
针对于三角形,故我们想到九年级数学的相似三角
形相关知识,通过作辅助线,创造出可以利用相似三
角形知识的条件,然后一一分析作答.
证 明:(法平 行 线 交
DF的延长线于 G,则 ∠G=
∠D,∠BAG = ∠B.因 此
△AFG∽△BFD.
从而FAFB=BAGD.又因为∠AEG=∠CED,
所以△AEG∽△CED.故CEEA=CAGD.
从而BDDC·CEEA·FAEB=BDDC·CAGD·BAGD=1.
因此结论成立.
那么sins∠inCDED=CCDE,ssiin n∠ ∠A AE FF E=A EFA,sins∠inBDFD=BFDB.
∵∠CED=∠AFE,∠BFD=180°-∠AFE,
∴sin∠BFD=sin∠AFE,sin∠CED=sin∠AEF,
故sins∠inCDED·
ssiinn∠∠AAE FF E·
《数学之友》 2020年第 20期
梅涅劳斯定理在中学数学中的应用
高中数学巧用梅涅劳斯定理求解向量的线性相关系数

巧用梅涅劳斯定理求解向量的线性相关系数某某某某市第三高级中学 金小欣 467000一、梅涅劳斯〔Menelaus 〕定理简介:如果一直线顺次与三角形ABC 的三边AB 、BC 、CA 或其延长线交于M 、N 、K 三点,那么:1=⋅⋅KACKNC BN MB AM 。
证明:过顶点B 作AC 的平行线与截线交于E ,那么有:BE AK MB AM = ,CKBENC BN =,∴1=⋅⋅=⋅⋅KACKCK BE BE AK KA CK NC BN MB AM对该定理的几点说明:①证明的方法:过其中一个顶点作其对边的平行线与截线相交,利用“平行线截线段成比例定理〞或相似Δ性质,将其中的两个比例式等价转化。
②定理的实质:三个比例式的乘积等于1,每一个比例式的三个字母是共线的两个顶点和一个分点;其结构特征为:顶点分点分点顶点→→ ,呈现“首尾相接〞;整体看,从某一个顶点出发,最后又回到该顶点。
③该定理常与“塞瓦定理〞结合使用。
二、梅涅劳斯定理的一个应用例子题目:在△OAB 的边OA 、OB 上分别取点M 、N ,使|→--OM |∶|→--OA |=1∶3,|→--ON |∶|→--OB |=1∶4,设线段AN 与BM 交于点P ,记→--OA = a →,→--OB =b →,用 a →,b →表示向量OP --→.先给出高中常规解法〔待定系数法〕如下: 解法一:∵ B 、P 、M 共线∴ 记→--BP =s →--PM∴1111113(1)13(1)s s s OP OB OM OB OA b a s s s s s s --→--→--→--→--→→→=+=+=+++++++--------① 同理,记AP t PN --→--→= ,得: →--OP =114(1)t a b t t →→+++--------② ∵a →,b →不共线∴ 由①、②得113(1)114(1)s t s ts t ⎧=⎪++⎪⎨⎪=⎪++⎩解之得:9283s t ⎧=⎪⎪⎨⎪=⎪⎩∴321111OP a b --→→→=+上述解法的基本思想是:先设法求出点P 分AN 、BM 的比,理论依据:一个是教材例题的结论〔可作为定理直接使用〕,一个就是平面向量基本定理。
初中数学奥林匹克几何问题梅涅劳斯定理及应用

初中数学奥林匹克几何问题-梅涅劳斯定理及应用第一章涅劳斯定理及应用【基础知识】梅涅劳斯定理设,,分别是的三边,,或其延长线上的点,若,,三点共线,则.①证明如图,过作直线交的延长线于,则,,故.注此定理的证明还有如下正弦定理证法及面积证法.正弦定理证法设,,,在中,有,同理,,,此三式相乘即证.面积证法由,,,此三式相乘即证.梅涅劳斯定理的逆定理设,,分别是的三边,,或其延长线上的点,若,②则,,三点共线.证明设直线交于,则由梅涅劳斯定理,得到.由题设,有,即有.又由合比定理,知,故有,从而与重合,即,,三点共线.有时,也把上述两个定理合写为:设,,分别是的三边,,所在直线(包括三边的延长线)上的点,则,,三点共线的充要条件是.上述①与②式是针对而言的,如图(整个图中有4个三角形),对于、、也有下述形式的充要条件:;;.③第一角元形式的梅涅劳斯定理设,,分别是的三边,,所在直线(包括三边的延长线)上的点,则,,共线的充分必要条件是.④证明如图,可得.同理,,.以上三式相乘,运用梅涅劳斯定理及其逆定理,知结论成立.第二角元形式的梅涅劳斯定理设,,分别是的三边,,所在直线上的点,点不在三边所在直线上,则,,三点共线的充要条件是.⑤证明如图,由,有.同理,,.于是.故由梅涅劳斯定理知,,共线.从而定理获证.注(1)对于④、⑤式也有类似③式(整个图中有4个三角形)的结论.(2)于在上述各定理中,若采用有向线段或有向角,则①、②、③、④、⑤式中的右端均为,③、④、⑤式中的角也可以按①或②式中的对应线段记忆.特别要注意的是三边所在直线上的点为一点或者三点在边的延长线上.【典型例题与基本方法】1.恰当地选择三角形及其截线(或作出截线),是应用梅涅劳斯定理的关键例1如图,在四边形中,,,的面积比是3∶4∶1,点,分别在,上,满足∶∶,并且,,共线.求证:与分别是和的中点.(1983年全国高中联赛题)证明设(),交于.,,..又因,,三点共线,可视为的截线,故由梅涅劳斯定理,得,即.化简整理,得,解得,(舍去).故与分别是和的中点.例2如图1-5,在四边形中,对角线平分,在上取一点,与相交于,延长交于.求证:.(1999年全国高中联赛题)证明记,,,直线与相截,由梅涅劳斯定理,有.故.即,亦即,且只可能为0,故.例3设、分别为四边形的边、上的点,与交于点.若,则.证明如图1-6,只需证得当关于的等角线交于时,、、共线即可.事实上,、、分别为三边所在直线上的三点,且不在其三边所在直线上.又,,,由第二角元形式的梅涅劳斯定理,有.故、、三点共线.注当平分时,即为1999年全国高中联赛题.2.梅涅劳斯定理的逆用(逆定理的应用)与迭用,是灵活应用梅氏定理的一种方法例2另证如图1-5,设,关于的对称点分别为,,易知,,三点共线,连,,只须证明,,三点共线.设,,,则.对,应用梅涅劳斯定理的逆定理,知,,三点共线.故.注在图1-5中,*式也可为,若在的延长上,则*式为.例4如图1-7,与和的三边所在的3条直线都相切,,,,为切点,直线与交于点.求证:.(1996年全国高中联赛题)证法1过作于,延长交直线于点.对及截线应用梅涅劳斯定理,有.由,有.显然,,三点共线,连,,,,则由,有,从而,即.又,则.对,应用梅涅劳斯定理的逆定理,知,,三点共线,即为直线与的交点.故点与点重合,从而.证法2延长交于,直线与的三边延长线都相交,直线与的三边延长线都相交,分别应用(迭用)梅涅劳斯定理,有,.上述两式相除,则有.而,,于是,即.连,,,,,,而,,共线,则,,且,从而,于是.故,即.【解题思维策略分析】梅涅劳斯定理是三角形几何学中的一颗明珠,它蕴含着深刻的数学美,因而它在求解某些平面几何问题,特别是某些平面几何竞赛题中有着重要的应用.1.寻求线段倍分的一座桥梁例5已知的重心为,是边的中点,过作边的平行线交边于,交边于,且与交于点,与交于点.证明:.(1991年第3届亚太地区竞赛题)证明如图1-8,延长交于,则为的中点.由,知,而.对及截线,应用梅涅劳斯定理,有,故.从而,且.同理,,且.由此可知,与的两边分别平行且方向相反,从而,且,故.例6是一个等腰三角形,,是的中点;是的延长线上的一点,使得;是线段上不同于和的任意一点,在直线上,在直线上,使得,,是不同的和共线的,求证:(Ⅰ)若,则;(Ⅱ)若,则.(1994年第35届试题)证明(1)如图1-9,连,,.由,易证,,,四点共圆,,,,四点共圆.则,因此.故.(Ⅱ)由,,对及截线运用梅涅劳斯定理,有,即.于是可证,得,故.例7在凸四边形的边和上取点和,使线段和把对角线三等分,已知,求证:是平行四边形.(1990年第16届全俄竞赛题)证明如图1-10,设,分别交于,,两对角线交于.要证是平行四边形,若证得(或),且即可.由,(等底等高),知,而,故有,从而有.对及截线,及截线,分别应用梅涅劳斯定理,有,①.②由①,②两式相除得.而,故,即有.此时,又有.又由,知,于是①式可写为,即有,亦即.故为平行四边形.2.导出线段比例式的重要途径例8在中,为边上的中线,为的平分线,且交于,为上的点,使.证明.(1997年第58届莫斯科竞赛题)证明如图1-11,延长交于,只须证.由平分,有.①由,有.注意到,对及截线运用梅涅劳斯定理,得.故,由合比定理,有,即为.②由①,②式有,故.例9给定锐角,在边上取点,(位于与之间),在边上取点,(位于与之间),在边上取点,(位于与之间),使得,直线,与可构成一个三角形,直线,与可构成另一个三角形.证明:(1995年第36届1mo预选题)这两个三角形的六个顶点共圆.证明如图1-12,设题中所述两个三角形分别为与.由已知条件,有,,,得,,,此三式相乘得.①对及截线,及截线,分别应用梅涅劳斯定理,得,②,③①,②,③三式相乘化简,得.故.同理,.故.从而点在的外接圆上.同理,可证得,也在的外接圆上.证毕.例10如图1-13,以的底边为直径作半圆,分别与边,交于点和,分别过点,作的垂线,垂足依次为,,线段和交于点.求证:.(-37中国国家队选拔赛题)证法1设直线与交于,连,,则知,直线与相截,直线与相截,迭用梅涅劳斯定理,有,.两式相除,得.在与中,有,,即.将其代入①式,得.又由,有.将其代入②式,得,从而,.而,则,故.证法2作高,连,,则,于是,,..又,,,即,故.对应用梅涅劳斯定理的逆定理,知,,三点共线.由,知.例11如图1-14,设点,分别为锐角的内心和垂心,点,分别为边,的中点.已知射线交边于点(),射线交的延长线于点,与相交于,为的外心.试证:,,三点共线的充分必要条件是和的面积相等.(-2003试题)分析首先证,,三点共线.设为的外心,连,,则.又,因此,,,,四点共圆在的外接圆上与重合,,三点共线.其次,再证.并在三角函数式中,用、、分别表示三内角.证法1设的外接圆半径为,的延长线交于,对及截线,应用梅涅劳斯定理,有.①注意到,则.而,由①式,有.从而.②又对及截线,应用梅涅劳斯定理,有.注意到,有,,即.从而.③由,注意②,③,且为锐角.证法2如图1-14,设直线交于,直线交的延长线于.对及截线,应用梅涅劳斯定理,有.④又由及角平分线性质,即有.令,,,则.由④式,有,即.而,则.又,(由题设知).从而.对及截线,应用梅涅劳斯定理,有.将⑤式代入上式,得,.⑥同理.由,注意⑥,⑦.注例11还有其他证法,可参见笔者另文《关于20XX年中国数学奥林匹克第一题》(《中等数学》20XX年第6期).例12如图1-15,凸四边形的一组对边与的延长线交于,且,过作截线交另一组对边所在直线于,,交对角线所在直线于,.求工业化:.证法1如图1-15,对及直线由梅涅劳斯定理得.对及直线由梅涅劳斯定理得.对及直线由梅涅劳斯定理得.由①②③得,所以,所以,故.证法2设与的延长线相交于.和均被直线所截,迭用梅涅劳斯定理,有,①,②由①②,得.③注意到(直线上的托勒密定理),则③式变为.④又由截和截,迭用梅涅劳斯定理,有,.将此结果代入④式整理,即得欲证结论.注当,④式显然成立,故仍有结论成立.此题是二次曲线蝴蝶定理的推论.3.论证点共直线的重要方法例13如图1-16,的内切圆分别切三边,,于点,,,点是的一个内点,的内切圆也在点处与边相切,并与,分别相切于点,.证明:是圆内接四边形.(1995年第36届预选题)证明由切线长定理,知,,,.设的延长线与的延长线交于,对及截线,应用梅涅劳斯定理,有.对应用梅涅劳斯定理的逆定理,知,,三点共线,故由切割线定理有,.以而,即是圆内接四边形.例14如图1-17,中,内的旁切圆切的两边于和,直线与交于;类似地定义,,和,,.求证:,,三点共线.证明由切线长定理,知,,.对与直线,,分别应用梅涅劳斯定理,有,,.上述三式相乘,有.设切于,切于,则由,可得.同理.又由两内公切线长相等,即,故.同理,,.从而,故对用梅涅劳斯的逆定理,知,,三点共直线.例15如图1-18,设的三边,,所在的直线上的点,,共线,并且直线,,关于,,平分线的对称直线,,分别与,,所在直线交于,,,则,,也共线.证明对及截线应用第一角元形式的梅涅劳斯定理,有.由题设知,,,,,,,从而有,即.故由第一角元形式的梅涅劳斯定理,知,,共线.例16在筝形中,,.过上的一点作一条直线分别交、于、,再过点作一条直线分别交、于、.设与分别与交于、,求证:.证明如图1-19,过作的平行线交直线于,再过作的平行线交直线于,则,.进而.所以.又、、分别为三边所在直线上的点,且点不在三边所在的直线上.由第二角元形式的梅涅劳斯定理的逆定理知、、共线.于是,由,.有.因此,.故.注当,为中点时,即为1989年12月冬令营选拔赛试题.例17如图1-20,四边形内接于圆,其边,的延长线交于点,和的延长线交于点,过作该圆的两条切线,切点分别为,.求证:,,三点共线.(1997年试题)证明设圆心为,连交于,连,,,,则由切割线定理和射影定理,有,从而,,,四点共圆,即有,亦即为的内角的外角平分线.又,则平分.设分别交,于,,于是.同理,.于是,,,所以,,.直线与的三边延长线相交,由梅涅劳斯定理,有.对应用梅涅劳斯定理的逆定理,知,,三点共线.所以,,三点共线.注此例的其他证法,可参见第二章例9,第九章例15等.例18已知的内切圆分别切、、于点、、,线段、分别与该内切圆交于点、,若直线与交于圆外一点.证明、、三点共线.(20XX年香港奥林匹克题)证明如图1-21,由切线长定理有.对及截线应用梅涅劳斯定理,有,即有.设与交于点,由,,,有,,.又对及所在边上的点、、,有.于是,由梅涅劳斯定理的逆定理,知、、三点共线.4.注意与其他著名定理配合运用例19在中,已知,,是处接圆的圆心,直线、分别切于点、,与直线、与直线分别交于点、,与交于点,与直线交于点,又设是直线上的点,且使得,(不同于点)是与的交点,是与的交点,令与直线交于点.证明:.(20XX年韩国奥林匹克题)证明如图1-22,设的延长线与(过点)的切线交于点.由帕斯卡定理知、、三点共线,从而点与重合.由切割线窄弹知,.所以,.①设与交于点,对及截线,截线分别应用梅涅劳斯定理,有,.②注意相交弦定理,有.③由①、②、③,得.例20在梯形中,已知、分别为上、下底,为腰上一点,与交于点,为边上一点,满足,与交于点,与交于点.证明:、、三线共点.(20XX年乌克兰奥林匹克题)证明如图1-23,设直线与、与分别交于点、.先证、、三点共线.由,知,,.有.上述三式相乘,有.对应用梅涅劳斯定理的逆定理,知、、三点共线.考虑和,注意到直线与,与、与分别交于点、、,于是由戴沙格定理,知、、三线共点.【模拟实战】习题A1.在中,点在上,,,分别在,上,,,交于点,求.2.在中,,分别是,的中点,与相交于,与相交于,求∶∶.3.是内一点,引线段,和,使在上,在上,在上.已知,,,,,求的面积.(第7届题)4.设凸四边形的对角线和交于点,过作的平行线分别交,于点,,交的延长线于点,是以为圆心,以为半径的圆上一点,求证:.(1996年全国初中联赛题)5.已知,分别是的边,上的点,且,连交边的延长线于点,求.6.设为等腰()的直角边的中点,在上,且,求证:.7.在中,点和顺次三等分,点和顺次三等分,与,分别交于点,,求四边形与的面积之比.8.,,,分别为四边形的四条边,,,上的点,若,,三直线共点,则,,三直线共点或平行.9.设,,分别是的边,和延长线上的点,又,和分别是外接圆的切线.证明:,,三点共线.(1989年新加坡竞赛题)10.求证:三角形两角的平分线与第三角的外角平分线各与对边所在直线的交点共线.11.已知直径为的圆和圆上一点,设,和分别是这个圆在,,处的切线.设是直线与的交点,是直线与的交点,证明:,,三直线共点.(第6届加拿大竞赛题)12.是中任一点,过作的平行线分别交,于,,又过作的平行线,分别交,于,.求证:,,三线共点.13.在中,为中线,为角平分线,为上的点,使.证明:.(第58届莫斯科奥林匹克题)14.直线交直线,分别于,,点与是线段两侧的直线上两点,且.过的直线交于,交于;过的直线交于,交于.连结和,交直线分别于,.求证:.15.设四边形外切于一圆,,,,分别是,,,边上的切点,若直线与相交于点,则,,三点共线.16.设为的内点,过点的直线,,分别垂直于,,,若交于,交于,交于,证明:,,共线.(-28预选题)17.已知的与它的内切圆相切于点.证明:该圆的圆心在与的两个中点,的连线上.18.已知凸四边形内接于,对角线,相交于点,过分别作直线,,,的垂线,垂足分别是,,,.求证:,,三直线共点或互相平行.19.设为圆外切四边形,又,,,与该圆的切点为,,,.求证:,,,共点.习题B1.是内一点,,分别过,且分别与,交于点,,且分别与,交于点,.求证:,,三线共点.2.在中,为锐角,从上任一点作于,于,点是的垂心,求当点在线段上移动时,点的轨迹.(-7试题)3.在正的边,,上有内分点,,将边分成3∶,线段,,相交所成的(交于,交于)是的面积的时,求的值.(1992年日本奥林匹克预选题)4.在中,,点在上,点在上,的延长线交于.若∶∶,则.5.已知点,,在()的边上,,交于,又与的延长线交于,交于,又与的延长线交于.求证:.(《数学通报》问题1353题)6.圆外切四边形中,,,,边上的切点分别为,,,.与的延长线交于点,与延长线相交于点.求证:(Ⅰ),,,四线共点;(Ⅱ),,,四线共点;(Ⅲ),,,四线共点(假定).7.若凸四边形的对角线与互相垂直,且相交于,过点分别作边,,,的垂线,垂足依次为,,,,并分别交,,,边于,,,,再顺次连接,.,,则;.(-22试题的推广)8.面积为1的的边,上分别有点,,线段,相交于点.点,分别在,上移动,但满足四边形的面枳是面积的两倍这一条件,求面积的最大值.(1992年日本奥林匹克题)9.是边长为2的正方形,为的中点,是的中点,和相交于,和相交于.求四边形的面积.10.是凸四边形所在平面上一点,,,,的平分线分别交,,,于点,,,.(Ⅰ)寻找一点,使是平行四边形;(Ⅱ)求所有这样的点的轨迹.(1995年世界城市际联赛题)11.中,,为内角平分线,点在的内部,且,,求证:射线平分边.(《数学教学》问题536题)12.设为非等腰三角形,内心为,(,2,3)为过与和相切的小圆(增加的下标作模3同余),(,2,3)为圆和的另一交点,证明:,,的外心共线.(-38预选题)。
中学数学竞赛中常用的几个重要定理
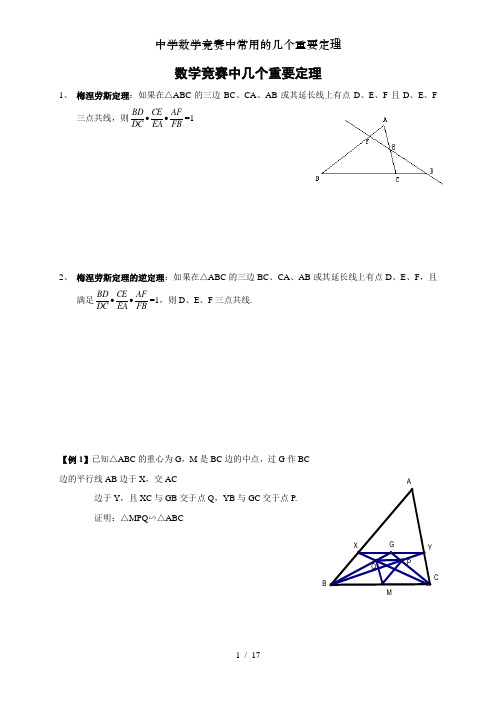
数学竞赛中几个重要定理1、 梅涅劳斯定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F 且D 、E 、F三点共线,则FBAFEA CE DC BD ••=12、 梅涅劳斯定理的逆定理:如果在△ABC 的三边BC 、CA 、AB 或其延长线上有点D 、E 、F ,且满足FBAFEA CE DC BD ••=1,则D 、E 、F 三点共线.【例1】已知△ABC 的重心为G ,M 是BC 边的中点,过G 作BC 边的平行线AB 边于X ,交AC边于Y ,且XC 与GB 交于点Q ,YB 与GC 交于点P. 证明:△MPQ ∽△ABCj MQGAC BXY P【例2】以△ABC的底边BC为直径作半圆,分别与边AB,AC交于点D和E,分别过点D,E作BC的垂线,垂足依次为F,G,线段DG和EF交于点M.求证:AM⊥BC【例3】四边形ABCD内接于圆,其边AB,DC的延长线交于点P,AD和BC的延长线交于点Q,过Q作该圆的两条切线,切点分别为E,F.求证:P,E,F三点共线.【练习1】设凸四边形ABCD 的对角线AC 和BD 交于点M ,过M 作AD 的平行线分别交AB ,CD于点E ,F ,交BC 的延长线于点O ,P 是以O 为圆心,以OM 为半径的圆上一点. 求证:∠OPF=∠OEP【练习2】 在△ABC 中,∠A=900,点D 在AC 上,点E 在BD 上,AE 的延长线交BC 于F. 若BE :ED=2AC :DC ,则∠ADB=∠FDCD塞瓦定理:设O是△ABC内任意一点,AO、BO、CO分别交对边于N、P、M,则1=••PACPNCBNMBAM塞瓦定理的逆定理:设M、N、P分别在△ABC的边AB、BC、CA上,且满足1=••PACPNCBNMBAM,则AN、BP、CM相交于一点.【例1】B E是△ABC的中线,G在BE上,分别延长AG,CG交BC,AB于点D,F,过D作DN∥CG交BG于N,△DGL及△FGM是正三角形.求证:△LMN为正三角形.GCLMEDFN【例2】在△ABC 中,D 是BC 上的点DC BD =31,E 是AC 中点.AD 与BE 交于O ,CO 交AB 于F 求四边形BDOF 的面积与△ABC 的面积的比【练习1】设P 为△ABC 内一点,使∠BPA=∠CPA ,G 是线段AP 上的一点,直线BG ,CG 分别交边AC ,AB 于E ,F.求证:∠BPF=∠CPE【练习2】 在△ABC 中,∠ABC 和∠ACB 均为锐角.D 是BC 边BC 上的内点,且AD 平分∠BAC ,过点D 作垂线DP ⊥AB 于P ,DQ ⊥AC 于Q ,CP 于BQ 相交于K. 求证:AK ⊥BCCCC托勒密定理:四边形ABCD 是圆内接四边形,则有AB ·CD+AD ·BC=AC ·BD【例1】 已知在△ABC 中,AB >AC ,∠A 的一个外角的平分线交△ABC 的外接圆于点E ,过E 作EF ⊥AB ,垂足为F.求证:2AF=AB -AC【例2】经过∠XOY 的平分线上的一点A ,任作一直线与OX 及OY 分别相交于P ,Q.求证:OP 1+OQ1为定值HABCEFAXYPOQ【例3】 解方程42-x+12-x=x 7【练习1】 设AF 为⊙O1与⊙O2的公共弦,点B ,C 分别在⊙O1,⊙O2上,且AB=AC ,∠BAF ,∠CAF 的平分线交⊙O1,⊙O2于点D ,E. 求证:DE ⊥AF【练习2】⊙O 为正△ABC 的外接圆,AD 是⊙O 的直径,在弧BC 上任取一点P (与B ,C不重合).设E ,F 分别为△PAB ,△PAC 的内心.证明:PD=∣PE-PF ∣西姆松定理:点P 是△ABC 外接圆周上任意一点,PD ⊥BC ,PE ⊥AC ,PF ⊥AB ,D 、E 、F 为垂足,则D 、E 、F 三点共线,此直线称为西姆松线.【例1】过正△ABC 外接圆的弧AC 上点P 作P D ⊥直线AB 于D,作PE ⊥AC 于E,作PF ⊥BC 于F.求证:PF 1+PD 1=PE1【练习1】设P 为△ABC 外接圆周上任一点,P 点关于边BC ,AC 所在的直线的对称点分别为P 1,P 2.求证:直线P 1P 2经过△ABC 的垂心.CABPEFD HABP1P2CP三角形的五心内心【例1】设点M 是△ABC 的BC 边的中点,I 是其内心,AH 是BC 边上的高,E 为直线IM 与AH 的交点.求证:AE 等于内切圆半径r【例2】在△ABC 中,AB=4,AC=6,BC=5,∠A 的平分线AD 交△ABC的外接圆于K.O ,I 分别为△ABC 的外心,内心.求证:OI ⊥AK【练习】 在△ABC 中,∠BAC=300,∠ABC=700,M 为形内一点,∠MAB=∠MCA=200求∠MBA 的度数.B外心【例1】锐角△ABC的外心为O,线段OA,BC的中点为M,N,∠ABC=4∠OMN,∠ACB=6∠OMN.求∠OMN【例2】在等腰△ABC中,AB=BC,CD是它的角平分线,O是它的外心,过O作CD的垂线交BC于E,再过E作CD的平行线交AB于F,证明:BE=FD.【练习】1、⊙O 1与⊙O 2相交于P ,Q ,⊙O 1的弦PA 与⊙O 2相切,⊙O 2的弦PB 与⊙O 1相切.设△PAB 的外心为O ,求证:OQ ⊥PQ重心【例1】在△ABC 中,G 为重心,P 是形内一点,直线PG 交直线BC ,CA ,AB 于F ,E ,D.求证:FG FP +EG EP +DGDP=3【例2】已知△ABC 的重心G 和内心I 的连线GI ∥BC ,求证:AB+AC=2BCC【练习】1、设M 为△ABC 的重心,且AM=3,BM=4,CM=5,求△ABC 的面积.2、设O 是△ABC 的外心,AB=AC ,D 是AB 的中点,G 是△ACD 的重心,求证:OG ⊥CD垂心三角形任一顶点到垂心的距离,等于外心到对边的距离的2倍.BCB【例1】△ABC 的外接圆为⊙O ,∠C=600,M 是弧AB 的中点,H 是△ABC 的垂心.求证:OM ⊥OH【例2】已知AD ,BE ,CF 是锐角△ABC 的三条高,过D 作EF 的平行线RQ ,RQ 分别交AB 和AC 于R ,Q ,P 为EF 与CB 的延长线的交点.证明:△PQR 的外接圆通过BC 的中点M.旁心【例1】在锐角∠XAY 内部取一点,使得∠ABC=∠XBD ,∠ACB=∠YCD.证明:△ABC 的外心在线段AD 上.CD【例2】AD是直角△ABC斜边BC上的高(AB<AC),I1,I2分别是△ABD,△ACD的内心,△A I1 I2的外接圆⊙O分别交AB,AC于E,F,直线FE与CB的延长线交于点M.证明:I1,I2分别是△ODM的内心与旁心.相交两圆的性质与应用【例1】证明:若凸五边形ABCDE中,∠ABC=∠ADE,∠AEC=∠ADB. 证明:∠BAC=∠DAEE【例2】已知⊙O1与⊙O2相交于A,B,直线MN垂直于AB且分别与⊙O1与⊙O2交于M,N,P 是线段MN的中点,Q1,Q2分别是⊙O1与⊙O2上的点,∠AO1Q1=∠AO2Q2求证:PQ1=PQ2【练习】梯形ABCD中,AB∥CD,AB>CD,K,M分别是腰AD,CB上的点,∠DAM=∠CBK,求证:∠DMA=∠CKBA其他的一些数学竞赛定理1、 广勾股定理的两个推论:推论1:平行四边形对角线的平方和等于四边平方和.推论2:设△ABC 三边长分别为a 、b 、c ,对应边上中线长分别为m a 、m b 、m c 则:m a =2222221a c b -+;m b =2222221b c a -+;m c =2222221c b a -+2、 三角形内、外角平分线定理:内角平分线定理:如图:如果∠1=∠2,则有ACABDC BD =外角平分线定理:如图,AD 是△ABC 中∠A 的外角平分线交BC 的延长线与D ,则有ACABDC BD =3、 三角形位似心定理:如图,若△ABC 与△DEF 位似,则通过对应点的三直线AD 、BE 、CF 共点于P4、 正弦定理、在△ABC 中有R CcB b A a 2sin sin sin ===(R 为△ABC 外接圆半径) 余弦定理: a 、b 、c 为△ABC 的边,则有: a 2=b 2+c 2-2bc ·cosA;b 2=a 2+c 2-2ac ·cosB; c 2=a 2+b 2-2ab ·cosC;5、欧拉定理:△ABC 的外接圆圆心为O ,半径为R ,内切圆圆心为I ,半径为r,记OI=d,则有:d 2=R 2-2Rr.6、巴斯加线定理:圆内接六边形ABCDEF (不论其六顶点排列次序如何),其三组对边AB 与DE 、BC 与EF 、CD 与FA 的交点P 、Q 、R 共线.。
模型38 梅涅劳斯定理、塞瓦定理(原卷版)-2023年中考数学重难点解题大招复习讲义-几何模型篇
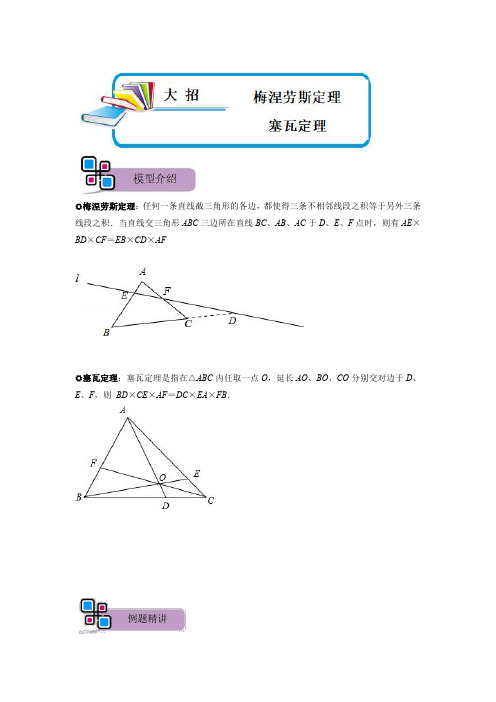
梅涅劳斯定理:任何一条直线截三角形的各边,都使得三条不相邻线段之积等于另外三条线段之积.当直线交三角形ABC三边所在直线BC、AB、AC于D、E、F点时,则有AE×BD×CF=EB×CD×AF塞瓦定理:塞瓦定理是指在△ABC内任取一点O,延长AO、BO、CO分别交对边于D、E、F,则BD×CE×AF=DC×EA×FB.例题精讲考点一:梅涅劳斯定理【例1】.如图,等边△ABC的边长为2,F为AB中点,延长BC至D,使CD=BC,连接FD交AC于E,则四边形BCEF的面积为.变式训练【变式1-1】.如图,D、E、F内分正△ABC的三边AB、BC、AC均为1:2两部分,AD、BE、CF相交成的△PQR的面积是△ABC的面积的()A.B.C.D.【变式1-2】.梅涅劳斯定理梅涅劳斯(Menelaus)是古希腊数学家,他首先证明了梅涅劳斯定理,定理的内容是:如图(1),如果一条直线与△ABC的三边AB,BC,CA或它们的延长线交于F、D、E三点,那么一定有••=1.下面是利用相似三角形的有关知识证明该定理的部分过程:证明:如图(2),过点A作AG∥BC,交DF的延长线于点G,则有=.任务:(1)请你将上述材料中的剩余的证明过程补充完整;(2)如图(3),在△ABC中,AB=AC=13,BC=10,点D为BC的中点,点F在AB上,且BF=2AF,CF与AD交于点E,则AE=.考点二:塞瓦定理【例2】.如图:P,Q,R分别是△ABC的BC,CA,AB边上的点.若AP,BQ,CR相交于一点M,求证:.变式训练【变式2-1】.请阅读下列材料,并完成相应任务如图,塞瓦定理是指在△ABC内任取一点O,延长AO,BO,CO分别交对边D,E,F 于,则××=1.任务:(1)当点D,E分别为边BC,AC的中点时,求证:点F为AB的中点;(2)若△ABC为等边三角形,AB=12,AE=4,点D是BC边的中点,求BF的长.【变式2-2】.请阅读下列材料,并完成相应任务塞瓦定理定理内容:如图1,塞瓦定理是指在△ABC内任取一点O,延长AO,BO,CO分别交对边于D,E,F,则.数学意义:使用塞瓦定理可以进行直线形中线段长度比例的计算,其逆定理还可以用来进行三点共线、三线共点等问题的判定方法,是平面几何学以及射影几何学中的一项基本定理,具有重要的作用.任务解决:(1)如图2,当点D,E分别为边BC,AC的中点时,求证:点F为AB的中点;(2)若△ABC为等边三角形(如图3),AB=12,AE=4,点D是BC边的中点,求BF 的长,并直接写出△BOF的面积.1.如图,在△ABC中,M是AC的中点,E是AB上一点,AE=AB,连接EM并延长,交BC的延长线于D,则=()A.B.2C.D.2.如图,在△ABC中,D、E分别是BC、AC上的点,AD与BE相交于点G,若AG:GD =4:1,BD:DC=2:3,则AE:EC的值是()A.B.C.D.3.如图,在△ABC中,AD是BC边上的中线,F是AD边上一点.射线CF交AB于点E,且,则等于.4.如图,在△ABC中,点D是AB边上的一点,且AD=3BD,连接CD并取CD的中点E,连接BE,若∠ACD=∠BED=45°,且CD=6,则AB的长为.5.如图,在△ABC中,∠ACB=90°,AC=8,BC=16,AD是边BC的中线,过点C 作CE⊥AD于点E,连接BE并延长交AC于点F,则AD的长是,EF的长是.6.如图,△ABC中,D、E是BC边上的点,BD:DE:EC=3:2:1,M在AC边上,CM:MA=1:2,BM交AD、AE于H、G,则BH:HG:GM等于.7.如图,▱ABCD的对角线相交于点O,在AB的延长线上任取一点E,连接OE交BC于点F.若AB=a,AD=c,BE=b,则BF=.8.在△ABC中,∠ACB=90°,AC=BC,AM为BC边上的中线,CD⊥AM于点D,CD 的延长线交于点,求的值.9.如图,在△ABC中,M是AC的中点,E、F是BC上的两点,且BE=EF=FC,求BN:NQ:QM的值.10.如图,△ABC中,∠ACB=90°,CD⊥AB于点D,E为BC上一点,AE交CD于点F,EH⊥AB于点H,若CF=2FD,EH=,求CE•BE的值.11.如图,△ABC中,AD⊥BC于点D,E是AB上一点,连接DE,2∠C+∠BDE=180°.(1)求证:∠BDE=2∠CAD;(2)若AC=BD,∠AED=∠ACB,求证BE=2CD;(3)若AE=kBE,BD=mCD,则的值为.(用含m,k的式子表示).12.如图1,Rt△ABC中,∠BAC=90°,AD是中线,BE⊥AD,垂足为E,点F在AD上,∠ACF=∠DBE.(1)求证:∠ABD=∠CFD;(2)探究线段AF,DE的数量关系,并证明你的结论;(3)如图2,延长BE交CF于点P,AB=AF,求的值.13.如图1,△ABC中,AB=AC,点D在BA的延长线上,点E在BC上,DE=DC,点F 是DE与AC的交点,且DF=FE.(1)图1中是否存在与∠BDE相等的角?若存在,请找出,并加以证明,若不存在,说明理由;(2)求证:BE=EC;(3)若将“点D在BA的延长线上,点E在BC上”和“点F是DE与AC的交点,且DF=FE”分别改为“点D在AB上,点E在CB的延长线上”和“点F是ED的延长线与AC的交点,且DF=kFE”,其他条件不变(如图2).当AB=1,∠ABC=a时,求BE的长(用含k、a的式子表示).14.阅读以下材料,并按要求完成相应的任务.塞瓦(GiovanniCeva,1648~1734)意大利水利工程师,数学家,塞瓦定理载于1678年发表的《直线论》一书,塞瓦定理是指如图1,在△ABC内任取一点O,延长AO,BO,CO分别交对边于D,F,E,则.下面是该定理的部分证明过程:如图2,过点A作BC的平行线分别交BE,CF的延长线于点M,N.则∠N=∠FCB,∠NAF=∠FBC.∴△NAF∽△CBF.∴①.同理可得△NOA∽△COD.∴②.任务一:(1)请分别写出与△MOA,△MEA相似的三角形;(2)写出由(1)得到的比例线段;任务二:结合①②和(2),完成该定理的证明;任务三:如图3,△ABC中,∠ACB=90°,AC=4,BC=3,CD⊥AB,垂足为D,点E 为DC的中点,连接AE并延长,交BC于点F,连接BE并延长,交AC于点G.小明同学自学了上面定理之后解决了如图3所示的问题,并且他用所学知识已经求出了BF与FC的比是25:16,请你直接写出△ECG与△EAG面积的比.15.问题提出如图(1),在△ABC中,AB=AC,D是AC的中点,延长BC至点E,使DE=DB,延长ED交AB于点F,探究的值.问题探究(1)先将问题特殊化.如图(2),当∠BAC=60°时,直接写出的值;(2)再探究一般情形.如图(1),证明(1)中的结论仍然成立.问题拓展如图(3),在△ABC中,AB=AC,D是AC的中点,G是边BC上一点,=(n<2),延长BC至点E,使DE=DG,延长ED交AB于点F.直接写出的值(用含n的式子表示).16.阅读下面材料,完成(1)﹣(3)题数学课上,老师出示了这样一道题:如图1,△ABC中,∠BAC=90°,点D、E在BC上,AD=AB,AB=kBD(其中<k<1)∠ABC=∠ACB+∠BAE,∠EAC的平分线与BC相交于点F,BG⊥AF,垂足为G,探究线段BG与AC的数量关系,并证明.同学们经过思考后,交流了自己的想法:小明:“通过观察和度量,发现∠BAE与∠DAC相等.”小伟:“通过构造全等三角形,经过进一步推理,可以得到线段BG与AC的数量关系.”……老师:“保留原题条件,延长图1中的BG,与AC相交于点H(如图2),可以求出的值.”(1)求证:∠BAE=∠DAC;(2)探究线段BG与AC的数量关系(用含k的代数式表示),并证明;(3)直接写出的值(用含k的代数式表示).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
中,过 C作 DF边上的高 CP,在中,过 B作 DF边 上的高 BN.
A N
F Q
E P
则我们可以得到
B
C
D
S△CDF =12DF·CP=CP, S△AFD 12DF·AQ AQ
利于培养学生的独立思考能力与创造能力,增强学
生的数学能力.本文以梅涅劳斯定理为例,来探讨将
高等数学中的部分定理引入中学课堂.
梅涅劳斯定理:若直线 l
A
分别截三角形 ABC三边 BC、
F
CA、AB及延长线于点 D、E、
E
F,则FAFB·BDDC·CEEA=1.
B
CD
如图,我 们 称 直 线 DEF为 三 角 形 ABC的 梅
氏线.
2 运用中学数学知识证明梅涅劳斯定理
S△AFD S△BDF
=112DDFF··BAQN=BAQN,SS△△BCDDFF
△AFG∽△BFD.
B
CD
从而FAFB=BAGD.又因为∠AEG=∠CED,
所以△AEG∽△CED.故CEEA=CAGD.
从而BDDC·CEEA·FAEB=B DDC·CAGD·BAGD=1.
因此结论成立.
2.2 利用平行线分线段成比例定理进行证明
平行线分线段成比例定理是研究相似形和比例
关系的最重要和最基本的理论,它一方面可以直接
5 展望
运用高等数学的思想方法来剖析中学数学问 题,这样能使一部分学有余力的学生从中体验到智 力探险的乐趣,也能使另一部分学生不会因为害怕 高等数学而在进入高校学习时感觉到困难.像此类 高观点下的数学问题还有很多,期待更多学者加入 研究.
参考文献: [1]黄家礼.几 何 明 珠 (第 三 版 )[M].北 京:国 家行政学院出版社,2013:37-43. [2]杨春波.梅涅劳斯 (Menelaus)定理的十种 证明[J].中学数学杂志,2015,(9):27-28.
理不同方法的证明,不仅可以让学生了解、掌握梅涅 劳斯定理对于学生已有的知识也可以起到一个巩固 的作用,还可以激发学生对课本以外的知识产生浓 厚的兴趣,让学生体会数学的奥妙,在一定程度上发 展了学生的数学思维,拓展了学生的数学视野.
3 梅涅劳斯定理在中学数学中的应用
上文用中学学过的知识点来对梅涅劳斯定理进
判定线段成比例,另一方面,当不能直接证实要证的
比例成立时,常用这个定理把两条线段的比“转移”
成另两条线段的比.
证 明:过 点 C作 CG
A
∥DF交 AB于 G,如图,则
F
CEEA=GFFA,BDDC=BGFF,
G
E
故FAFB·BDDC·CEEA
B
=FAFB·BGFF·GAFF=1.
CD
因此结论成立.
那么sins∠inCDED=CCDE,s si in n∠ ∠A AE FF E=A EFA,sins∠inBDFD=BFDB.
∵∠CED=∠AFE,∠BFD=180°-∠AFE,
∴sin∠BFD=sin∠AFE,sin∠CED=sin∠AEF,
故sins∠inCDED·
s si in n∠ ∠A AE FF E·
例 4 在 △ABC中,点 D、E、F分 别 是 边 AB、
BC、AC的三等分点,且 EC=2BE,BD=2AD,AF=
2FC,设 AE与 CD交于 P点,AE与 BF交于 Q点,
BF与 CD交于 R点.若 S△ABC =1,求 S△PQR.
解:如 图,对 于 △AEC,直
A
线 BQF为梅氏线, ∵EC=2BE,∴BC=3BE, 又 BD=2AD,AF=2FC,
故DEEA·FAFB=12,从而可以得到EAED=2FABF.
注:若该题不用梅涅劳斯定理,做法如下:
·72·
《数学之友》 2020年第 20期
过点 D作 CF的平行线交 AB于点 G,因为 CF
∥DG,则 EAED=FAFG,B CD D=B GG F,又因为 D为 BC的中
《数学之友》 2020年第 20期
梅涅劳斯定理在中学数学中的应用
解题探索
龙仲城,侯万君
(云南师范大学数学学院,650000)
1 引言
近年来,越来越多的中学题目中出现高等数学 的背景,高观点下的中等数学在中学数学中有着越 来越广泛的应用,因此在平时的教学中,对于在数学 学习中学有余力的同学,鼓励他们学习一些高等数 学的知识和定理,用它来解决各种中学中的问题,有
由于梅涅劳斯定理涉及到比例关系,而且还是
针对于三角形,故我们想到九年级数学的相似三角
形相关知识,通过作辅助线,创造出可以利用相似三
角形知识的条件,然后一一分析作答.
证 明:(法 一 )如 图 所 G
A
示,过 A作 BC的平 行 线 交
F
DF的延长线于 G,则 ∠G=
E
∠D,∠BAG = ∠B.因 此
代数式的 运 算 联 系 起 来,其 中 最 重 要 的 思 想 就 是
“角化边”,“边化角”.因此,我们也可以巧用它来对
梅涅劳斯定理进行证明.
证 明: 在 △CED、
A
△AEF和△BFD中,由正弦
F
定理可得sCinED=sin∠CDCED,
E
sin∠EAAFE=sin∠AFAEF, B
CD
sFinBD=sin∠BDBFD.
=121DDFF··BCNP=BCNP.
2
2
又因为∠AQE=∠CPE,∠AEQ=∠CED,
故 Rt△AQE∽Rt△CPE,因此CAQP=CEEA.
同理可得BAQN=FAFB,由于 CP//BN,
则易得BCNP=BDDC,
故FAFB·BDDC·CEEA=BAQN·BCNP·CAQP=1.
2.1 运用相似三角形的知识进行证明
S△PQR
=S△ABC
-3S△AQB
=1-3·
2 7
=17.
4 在中学数学教学中引入梅涅劳斯定理的建议
梅涅劳斯定理可以解决平面几何中角、线段、边 长等问题.通过分析我们不难看出,可以用中学最基 础的知识来对该定理进行证明,例如:相似三角形, 正弦定理等;同时我们知道,利用梅涅劳斯定理可以 解决中学数学的有关问题,尤其是在中学数学中涉 及到特殊角度及比例关系的题目.
·73·
点,所以 BD=CD,故 BG=GF,那么 FG=1 2FB,故
EAED=2FABF.相比较而言,用梅涅劳斯定理思路简洁,
方法直观.
例 3 证明三角形的三条中线交于一点.
证 明:如 图,中 线
A
BE、CF、交 于 O,D为 BC 的中点,如图,把△AFC看 成梅式 三 角 形,BOE看 成
FБайду номын сангаас
E
O
梅氏 线,则 有 BABF· F OOC· B
■C→E=λλ+1■C→A,
■A→F=■A→B-■F→B⇒■A→F=λλ+1■A→B,
■A→E=■A→C-■C→E⇒■A→E=-γ1+1■A→C,
故■D→E=■D→C+■C→E=μ1-1■C→B+λλ+1■C→A
( ) =μ1-1■A→B- μ1-1+γγ+1■A→C.
■E→F=■A→F-■A→E=λλ+1■A→B-λ1+1■A→C.
sins∠inBDFD=CCDE·
AF EA
·BFDB=1,那么可得FAFB·B DDC·CEEA=1.
因此结论成立.
2.4 利用向量法证明
向量是现代数学中的一个重要概念,已经成为
研究几何代数问题的重要工具.所谓向量法,即从问
题条件入手,找到与向量知识相关点,转化为向量背
景下的形式,借助向量运算法则求解,然后回到原问
D D′
C
OCEC=1.
又因为 AB=2BF,CE=EA,
代入上式,得 2FO=OC.
连接 AO延长交 BC于 D′,将△ABC看成梅式
三角形 AOD′看成梅氏线,则有DBD′C′·C OOF·F ABA=1.
又因为 OC=2OF,AB=2FA,
所以 BD′=D′C,所以 D与 D′重合,
因而三角形的三条中线交于一点.
梅涅劳斯定理是射影几何学的一门基本定理, 它不仅在提高认识层次方面具有独特作用,而且在 论证方法,思考问题的方式等方面都很灵活,可是在 中学数学中没有涉及到,若能将此定理引入中学数 学教学中,可以引导学生居高临下的认识数学,有利 于学生思维能力和数学情操的培养.同时,探讨它对 中学数学的教学以及学生核心素养的培养具有十分 重要的指导意义.
行了证明,那么我们是否可以利用它来解答中学试
题呢?
例 1 若一直线和三角形 ABC的边 AB、AC及
BC的延长线分别相交于点 E、D及 F,并 且 AD=
DC,求证:BAEE=CBFF.
证明:视直线 EDF为 G
A
△ABC的 梅 氏 线,则 由 梅 涅劳斯定理得 CBDC· DEEA·
F D
FAFB=1.
在运用该定理进行计算时,恰当地选择三角形 和梅氏线是解决问题的关键,在解决线段比的问题 时,恰当地选择三或多点共线的直线作为梅氏线,应 用梅涅劳斯定理解决;由于存在线段比例关系,就会 存在面积比,因此我们也可以它来解决面积的相关 问题;在解决特殊角问题中,可以借助它推导出相应 的线段关系,将问题引向全等三角形或相似三角形 方面来考虑.总之,梅涅劳斯定理的应用很广泛,更 由于其叙述本身就简洁明了,关于对复杂命题中的 数形结合,能 使 复 杂 的 推 理,转 化 为 简 单 的 计 算 问 题,能极大地促进问题的解决.
2.3 利用正弦定理证明
因此梅涅劳斯定理得证.
正弦定理是三角形中的一个重要定理,揭示了
