第四稳恒磁场剖析
合集下载
四稳恒磁场PPT课件

Idl r2
sin
B
dB
0 I 4R
2 sin
1
d
0 I 4R
(cos
1
cos 2 )
,方向为:
。
[讨论] (1)设载流直导线线长 , 则2 L
ห้องสมุดไป่ตู้
中垂面上:因
cos1 , 而c有os 2
B 0I 4R
延长线上:
2L R2 L2
B0
L R2 L2
第16页/共57页
若导线无限长,则
2
d
0
0 4
2IR 2 ,方向沿:
(R2
Z
2
)
3 2
k
[讨论]
(1) 环心处的
B
B0
0 I
2R
k
(2) 磁偶极子的磁场 当Z>>R时,载流圆环可视为磁偶极矩为
的磁偶极m子。IS
第18页/共57页
B
0
2R2 I
k
4 Z 3
令
m
I(R磁2偶k 极 矩IS),则其轴线上场点的
为
B
B
0
2m
,
即
0
dl
dl
l
代入上式给出
B
dl
0I
dl
4
又因 具dl有任意性,故
(2) 再看
LB dl
B
0I
4
上述场点P为指定点,在P处一元位移 一周,则
所引起结果。d现l P点沿安培环路L移动
第26页/共57页
a、若
b、若
L与L不套链,则因立体角改变总量 L与L相套链,则因立体角改变总量
、 1 ,0有
大学物理稳恒磁场解读

2018/9/27
24
r the displacement from
I dl
I
Idl toward P.
dB
the contribution of Idl to the magnetic induction at point P.
r
P
B
the magnetic field of I at point P.
I
S
2018/9/27 5
I
Magnetic field lines surrounding a long and straight wires
2018/9/27
6
I
Magnetic field lines for a tightly wound solenoid of finite length carrying a steady current.
Gauss’ theorem
B dS 0
Ampere’s circulation theorem (Ampere’s Law) L B d l 0 Ii
i
11
2018/9/27
Affect of magnetic field force on currents
right hand rule
26
Superposition Principle of Magnetic Induction
B d B
L
B Bi
u Idl r B d B= 4 r
L
0
L
3
2018/9/27
27
DISCUSSION
稳恒磁场
二、电流的磁效应 二、电流的磁效应
I
S N •磁针和磁针 •在磁场 中运动的 电荷受到 的磁力 •磁铁与载流导 线的相互作用 S N S N
•电流的磁效应
I I
•载流导 线与载流 导线的相 互作用
三、磁场 三、磁场
1、概念
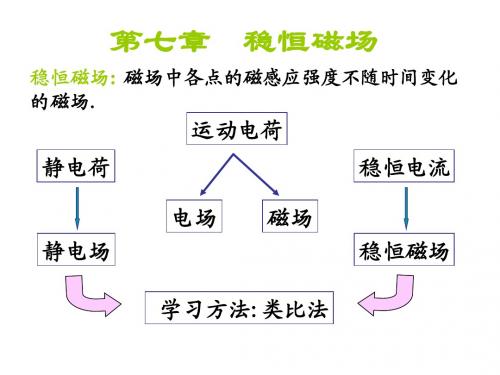
在运动电荷(或电流)周围空间存在的一种特殊形式的物质。
2、磁场的特性
•磁场对磁体、运动电荷或载流导 线有磁场力的作用; •载流导线在磁场中运动时,磁场 力要作功——磁场具有能量。
∧
Idl
r
R Idl’ θ
dB ⊥
dB dB//
P dB’
μ0 Idl sin(d l r ) μ0 Idl dB = = sin 90° 4π r2 4π r 2
分解 dB
dB ⊥ = dB cos θ
dB// = dB sin θ
电流对称
2
∫ dB
⊥
=0
μ0 I B = ∫ dB // = 4π
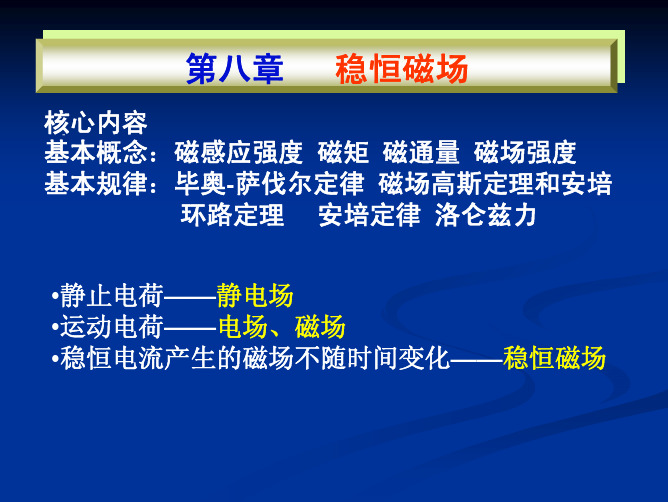
第八章 第八章
稳恒磁场 稳恒磁场
核心内容 基本概念:磁感应强度 磁矩 磁通量 磁场强度 基本规律:毕奥-萨伐尔定律 磁场高斯定理和安培 环路定理 安培定律 洛仑兹力 •静止电荷——静电场 •运动电荷——电场、磁场 •稳恒电流产生的磁场不随时间变化——稳恒磁场
一、电流 一、电流
8.1 电流 current
线圈所包围的面积
I
en
pm
其中 e n 与电流环绕方向符合右手螺旋法则
μ 0 IπR μ 0 pm B = (1)当x=0时,有 BO = = = 3 3 2( R 2 + x 2 ) 3 2 2R 2πR 2πR
2
μ0 I
物理学-稳恒磁场

l B
I
由磁通连续 原理可得
B内>> B外
l B
取过场点的每个边都相当小的矩形环路abcdIa
B dl B内 dl B dl B外 dl Bdl
L
ab
bc
cd
da
B内ab 由安培环路定理
0
N l
abI
n N l
b B内a
c d
B 0nI
磁场的宏观性质:
对运动电荷(或电流)有力的作用
磁场有能量
二.磁感强度
运动电荷在电磁场中受力: f qE qv B
洛仑兹力公式
f qE qv B
电场力,与电荷 的运动状态无关பைடு நூலகம்
磁场力,运动 电荷才受磁力
洛仑兹力是力的基本关系式
洛 仑兹力是相对论不变式 B 磁感强度
(Magnetic Induction)
或称磁通密度 (magnetic flux density) 单位:特斯拉(T)
§3 磁力线 磁通量 磁场的高斯定理
一.磁力线
1. 典型电流的磁力线
2. 磁力线的性质
无头无
与电流
与电流成右
尾 闭 套连
手螺旋关系
合二曲. 线磁通量
m
B ds
S
单位:韦伯(Wb)
三. 磁通连续原理(磁场的高斯定理)
B dS 0
微分形式 B 0
无源场
S
§4 毕-萨-拉定律及应用
一. 毕萨拉定律
电流元 current element Idl
dB
0 Idl r
4 r 2
Idl r
P
I
dB
0 真空中的磁导率
第四讲_稳恒磁场讲解

L
B
1 2
0i
0i
0
0i
60
【例】求无限长螺线管内外的磁感应强度。设电 流强度为I,单位长度的匝数为n。
【解】作如图所示的积分回路,由对称性,管外
B=0,管内B为 常数:
B l BL 0nIL
B 0nI
【例】表面绝缘的细导线密
绕成一个“蚊香”型平面环 带,总匝数为N匝,内外半径 分别为a和b,当导线中通有 电流I时,求圆心处的磁感应 强度。
通常
k 0 4
0 4 10 7 N A2
电流元之间的相互作用力不一定满足牛顿 第三定律,原因是实际上不存在孤立的稳 恒电流元,它们总是闭合回路的一部分。
闭合线圈总的作用力总是与反作用力大小 相等,方向相反。
F12 0
F21
k
I1l1I 2 l2 r122
无限长直导线对l长导线的作用力为:
L1
I I1 I2
L2
L1 : I 8I
L2:
L1
I 0
L2
【例】一圆形的无限长直导线,截面半径R,电流
I均匀地流过导体的截面,求导线内外的磁场分 布。
【解】根据对称性,可以判定磁感应强度B的大 小只与观察点到园柱体轴线的距离有关,方 向沿圆周的切线。
B
B1 S1 B2 S2
B1S1 B2S2
B1 S2 B2 S1
磁场的高斯定理对线电流、面电流和体 电流产生的磁场均成立,因为磁场服从 叠加原理。
高斯定理表明磁场是无源场,或自然 界不存在磁荷。
磁场处处无源。
3.安培环路定理
安培环路定理:沿任何闭合曲线L磁感应强度的
B
1 2
0i
0i
0
0i
60
【例】求无限长螺线管内外的磁感应强度。设电 流强度为I,单位长度的匝数为n。
【解】作如图所示的积分回路,由对称性,管外
B=0,管内B为 常数:
B l BL 0nIL
B 0nI
【例】表面绝缘的细导线密
绕成一个“蚊香”型平面环 带,总匝数为N匝,内外半径 分别为a和b,当导线中通有 电流I时,求圆心处的磁感应 强度。
通常
k 0 4
0 4 10 7 N A2
电流元之间的相互作用力不一定满足牛顿 第三定律,原因是实际上不存在孤立的稳 恒电流元,它们总是闭合回路的一部分。
闭合线圈总的作用力总是与反作用力大小 相等,方向相反。
F12 0
F21
k
I1l1I 2 l2 r122
无限长直导线对l长导线的作用力为:
L1
I I1 I2
L2
L1 : I 8I
L2:
L1
I 0
L2
【例】一圆形的无限长直导线,截面半径R,电流
I均匀地流过导体的截面,求导线内外的磁场分 布。
【解】根据对称性,可以判定磁感应强度B的大 小只与观察点到园柱体轴线的距离有关,方 向沿圆周的切线。
B
B1 S1 B2 S2
B1S1 B2S2
B1 S2 B2 S1
磁场的高斯定理对线电流、面电流和体 电流产生的磁场均成立,因为磁场服从 叠加原理。
高斯定理表明磁场是无源场,或自然 界不存在磁荷。
磁场处处无源。
3.安培环路定理
安培环路定理:沿任何闭合曲线L磁感应强度的
稳恒磁场
安培定律
一、安培力
安培力:电流元在磁场中受到的磁力. 安培力:电流元在磁场中受到的磁力. 一个自由电子受的洛仑兹力为: 一个自由电子受的洛仑兹力为
f 洛 = qv × B = −ev × B
电流元所受磁力: 电流元所受磁力
方向: 方向:×
v
dl
B
I
设截面积为S,单位体积电子数为 设截面积为 单位体积电子数为n 单位体积电子数为
1 2 m = NISn = NI πR n 2
方向:与 B 成600夹角. 夹角. 方向: (2)此时线圈所受力矩的大小为: )此时线圈所受力矩的大小为:
)60
0
B
3 2 πR M = mB sin60 = NIB 4 方向: m× B 方向: ×
0
n
即垂直于 B向上,从上往下俯视,线圈是逆时针转动。 向上,从上往下俯视,线圈是逆时针转动。
1T = 1N ⋅ S ⋅ m−1 ⋅ C−1
磁通量
一、磁力(感)线 磁力( 直线电流的磁力线
磁场的高斯定理
圆电流的磁力线
通电螺线管的磁力线
I
I
I
I
通量(通过一定面积的磁力线数目) 二、磁通量(通过一定面积的磁力线数目)
v v dΦ = B ⋅ dS
v v Φ = ∫s B ⋅ dS
单位
1Wb= 1T ⋅ m
I
该式对任意形状的线圈都适用. 该式对任意形状的线圈都适用.
例1如图,求圆心O点的 B . 如图,求圆心 点的 I O
• × R
B=
µ0 I
4R
I
O• •
R
B=
µ0 I
8R
R
• •O
稳恒磁场

另解: C 4 R , 0
We
q
2
q
2
2C
8 0R
5 5
第四章 稳恒磁场的分析
半径 R 带电 q 的均匀带电球面和均匀带电球体:
W面
q
2
8 0R
W体
3q
2
20 0 R
W面 W体
6 6
第四章 稳恒磁场的分析
§1 电流的稳恒条件和导电规律
一、电流密度 电流密度矢量
S
J dS 0
(积分形式)
9 9
第四章 稳恒磁场的分析
§1 电流的稳恒条件和导电规律
由稳恒条件可得出几个结论
1)稳恒电流的电路必须闭合 2)导体表面电流密度矢量无法向分量 3)对一段无分支的稳恒电路 其各横截面的电流强度相等 4)在电路的任一节点处 流入的电流强度之和等于流出节点的 电流强度之和 --- 节点电流定律(基尔霍夫第一定律)
E — 静电场场强;
— 电介质的电容率。
上式表明: 电容器储有的能量与电场的存在相联系。 大量实验证明: 电容器能量的携带者是电场, 对静电场,也可认为能量携带 者是电荷,两者等价。但对于变化的电磁场, 只能说能量的携带 者是电场和磁场。凡是电场所在的空间,就有电场能量的分布。
电场具有能量, 正是电场物质性的表现之一。
dFm Idl B
三、毕奥-萨伐尔定律
若 B 由电流元 Id l 产生, 产生的磁感应强度为:
0 dB 4
Id l r0 r
2
Idl
r
说明:l 、 、 三者满足右手螺旋关系。 d r B
0 为真空磁导率。
稳恒磁场4

q q qv I T 2R / v 2R
二、带电粒子在电场或磁场中的运动 1、洛仑兹力的特点
Fm
Fm
+q
大小: Fm qvB sin
特点: Fm v , 不作功,只能改变速度的方向, 不能改变速度的大小。
q 0 , Fm 与 v B 同向 Fm B + v
B
S v
I
-
-e
常见错误: 认为金属中的载流子是正电荷。
I I nSev ev nS IB fm nS
f m evB
练习:学习指导“磁学” 4、35-39
- - - - -
b
自由电子受洛仑兹力作用导致正、负电荷相对 集中,产生Hall电场 E H .
Fm ev B
B
_ _ _ _ EH + _ + _ + _ + _ + + + + + +
+ + + + + + + + + + +
b
I
Fe eE H
h
- - - - E H v B
磁 聚 焦 现 象
三、 霍尔效应(Hall effect) 1879年Hall [美]发现:把一载流导体放在磁场中, 若磁场方向与电流方向⊥ ,则在与磁场和电流二 者都⊥的方向上出现横向电势差——Hall效应。 B 以金属导体为例: 金属中的电流就是自 I 由电子的定向移动 + + + + + + h + _ + _ + _ + _ + (与电流反向)。 EH + _ + _ + _ + _ + v -e + + + + + B
二、带电粒子在电场或磁场中的运动 1、洛仑兹力的特点
Fm
Fm
+q
大小: Fm qvB sin
特点: Fm v , 不作功,只能改变速度的方向, 不能改变速度的大小。
q 0 , Fm 与 v B 同向 Fm B + v
B
S v
I
-
-e
常见错误: 认为金属中的载流子是正电荷。
I I nSev ev nS IB fm nS
f m evB
练习:学习指导“磁学” 4、35-39
- - - - -
b
自由电子受洛仑兹力作用导致正、负电荷相对 集中,产生Hall电场 E H .
Fm ev B
B
_ _ _ _ EH + _ + _ + _ + _ + + + + + +
+ + + + + + + + + + +
b
I
Fe eE H
h
- - - - E H v B
磁 聚 焦 现 象
三、 霍尔效应(Hall effect) 1879年Hall [美]发现:把一载流导体放在磁场中, 若磁场方向与电流方向⊥ ,则在与磁场和电流二 者都⊥的方向上出现横向电势差——Hall效应。 B 以金属导体为例: 金属中的电流就是自 I 由电子的定向移动 + + + + + + h + _ + _ + _ + _ + (与电流反向)。 EH + _ + _ + _ + _ + v -e + + + + + B
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
载流导体也具有磁极 ?
N
载流螺线管 与磁铁的作用
SN
S
I
I
载流螺线管磁极的确定方法: 右手法则
总结:各种磁作用
磁铁 磁场 磁铁
电流
电流
分析 上述各种作用应该具有相同的作用机理
电荷之间的相互作用力通过电场来传递 上述各种作用也应该通过场来传递 这种场就是磁场
3.磁场
问题
磁铁 电流
磁场
是一种?
磁场 还是两种产生方式
分析 载流螺线管
条形磁铁
实验表明:磁性特征相同
产生磁场的源应该相同
环向电流
安培分子 环流假说
环向电流
1822安培提出:组成磁铁的最小单元(磁分子)就 是环形电流,这些分子环流定向排列,在宏观上 就会显示出N、S极。
图示 N
等效宏观表面电流 S
磁铁内部分子电流抵消
为什么是假说?
安培提出了分子环流,但在安培时代,还没有建立 物质的分子、原子模型。因此,安培的模型为假说。
现代观点 物质组成:分子、原子
原子:原子核(正电)+ 电子(负电)
电子:绕核旋转,自旋
分子环流 经典模型
磁场的本源
运动的电荷
导线中的传导电流 磁铁中的分子环流
相互作用模型 的统一
电流
分子 传导 环流 电流
磁场
电流
分子 传导 环流 电流
库仑力 磁力
的区别
静止、相对运动电荷之间 运动的电荷之间
库仑力、磁力对比
安培的四个示零实验
实验一 电流反向
实验二 矢量和
F?
无定向秤 弧形导体
水银槽
C
垂直结构
固定绝缘柄
I II III
d1 d2
R1: R2: R3=
1 n
:1:n
d1: d2=
运动限制
1:n
实验三:作用力方向 实验四:作用力与几何尺度
安培假设:两个电流元之间的相互作用力 沿它们的连线
安培定律数学表达: 安培最初的数学表达式 dF12 kI1I2r12 ( ) 错误之一:作用力沿电流元之间的连线
4
r122
0 4
I1I2dl1 (dl2 rˆ21) r221
0
I1dl1
dF21
0 I1I2dl1ex [dl2ez (ex )]
4 0
4
r221
I1I2dl1dl2ex r221
正确的安培定律数学表达式
dF12
k
I1I 2 dl2
(dl1 rˆ12 ) r122
该公式与安培实验结果相符(自行验证)
安培定律数学 表达式说明
I 1 dl1
r12 dF12
dF12
k
I1I 2 dl2
(dl1 rˆ12 ) r122
dl2 I2
dF12与电流元空间位置的关系
第四章 稳恒磁场
§1 磁的基本现象和基本规律 §2 载流回路的磁场 §3 磁场的“高斯定理”与安培环路定理 §4 磁场对载流导线的作用 §5 带电粒子在磁场中的运动
§1 磁的基本现象和基本规律
1. 磁现象研究发展概要
1820年之前,磁学和电学是独立的学科, 人们认为磁和电是没有关系的物理问题。库 仑甚至断言电和磁是完全不同的实体,不可 能互相转化。由于库仑的影响,长时间内上 述观点被人们所信奉。安培也曾认为库仑的 观点是正确的。
物质成分
天然磁铁:Fe3O4 人工磁铁: 铷铁硼合金
钴镆合金
磁铁分区
中性区 磁极
条形磁铁的两端磁性强,称作磁极, 中部磁性弱,称作中性区
作用规律:同性相斥、异性相吸
指南针指南原理 N
S
(2)电流 磁铁(奥斯特实验)
实验现象
实验结论 电流对磁铁有作用
分析
对比磁铁间的作用,电 流产生了磁。
电流的本质是运动的电荷
I2 r12
dF12
z
dl2
4 0
r122 I1I2dl1dl2ez ey
0
I1I2dl1dl2ex
y
x
4
r122
4
r122
同向电流相互吸引
相同分析:反向电流相互排斥
安培定律分析垂直电流元受力
dF12
0 4
I1I2dl2 (dl1 rˆ12 )
r122
dF21
0 I1I2dl2ez (dl1ex ex )
平面 I
问题: dF12的最大值条件?
dF12
k
I1dl1 I2dl2 r122
1
/
2,2
/2
dl1
r12
dl2
电流元与连线垂直
且在同一平面
dF21的表达式
dF21 k
I1I
2dl1
(dl2 r221
rˆ21 )
k 的取值
k 0 4
量纲
[0]
[F] [I 2]
数值 4 107 牛顿 / 安培2
dF12
0 4
I1I2dl2 (dl1 rˆ12 )
r122
问题: 库仑定律有文字表述,为什么安培定律 没有文字表述?
安培定律分析平行电流元受力
dF12
0 4
I1I2dl2 (dl1 rˆ12 )
r122
0 I1I2dl2ez (dl1ez ex )
I1dl1
dF21
丹麦人奥斯特坚信电和磁是统一的观点,经过二 十年努力,终于在1860年发现了电流的磁效应。
随后的半年,法国阿拉果、安培、毕奥、萨伐尔 、 拉普拉斯对稳恒电流的磁场进行了研究,即基本建立 了电流磁场的知识体系。电学、磁学合并成为一个新 的学科:电磁学
2. 磁的基本现象 (不同磁作用形式) (1)磁铁 磁铁
2
nˆ dl2
1 dl1
r12 dF12
平面 I
dF12垂直
nˆ dl2
dF12
在平面I内 垂直 dl2
dF12与电流元参量(I1 dl1, I2 dl2 )之间的关系
dF12
I1dl1
I2dl2 sin1 sin2
r122
对比 库仑定律
F12
q1 q2 r122
2
1 dl1
nˆ dl2
r12 dF12
运动的电荷产生磁场
电流方向变化、磁 针转动方向也变化
磁与电的关系
问题 电流对磁铁有作用,磁铁对电流是否有作用?
实验 结论
N 极向内
载流导线和磁铁具
有相同的磁特性
I=0 I
I
(3)电流 电流(应该存在作用力) 实验
结论 同向电流相吸 I
II
I
异向电流相斥
问题 磁铁 磁铁 磁作用具有极性特点
电流 电流 磁作用具有极性特点
库仑力
磁作用力
定量描 述定律
库仑定律
?
定律 地位
基本规律 (应该为)基本规律
高斯 环路
?
?
研究 方法
点电荷模型 分割、叠加
研究 难易
相对简单
3.安培定律
电流元模型 分割、叠加
相对复杂
电流元 闭合回路
回路形状
3.安培定律
研究内容:两个电流元之间的磁相互作用力
dl1
I1
dl2
I2
研究过程:不同于库仑定律的发现,安培没有能 直接通过实验得到电流元之间磁相互 作用力。(原因?) 安培提出了一个假设,设计了四 个实验,根据实验结果,通过数 学分析得到了安培定律。
