10.3.3旋转对称图形【野渡横舟精编】
合集下载
华师大版七年级数学下册课件:10.3.3 旋转对称图形

A.4个
B.3个
C.2个
D.1个
5.(3分)如图,其中不是旋转对称图B 形的是( )
A.(2)
B.(1)
C.(3)
D
.(4)
A
6.(3分)下列图形中,旋转60°后可以和原图
形重合的是( )
A.正六边形
B.正五边形C.正方形D Nhomakorabea正三角形
旋转对称图形的应用 7.(3分)国旗上的五角星是旋转对称图形,它 的五旋角转星中中心心是___________7_2_°_,它的旋转角是 ________.(填最小度数) 8.B (3分)如图所示,绕其图形中心旋转90°不 能和自身重合的是( )
9.(3分)如图所示是某一轮船的舵的示意图,这个船
舵的旋转中心是舵轴A,最小的旋转角度是( )
A.30° B.60°
C.90° D.120°
10.(6分)下列图形中,哪些是旋转对称图形?是旋转
对称图形的,请指出旋转中心,并指出该图形绕着旋转
中(心1)旋是转,多旋少转度90后°能,与18自0°身重合? 或270°
2 . (3 分 ) 正 6方0 形 绕 它 的 ______________ 旋 转 ________度与自身重合;正六边形至少旋转________ 度能与自身重合.
3.(2分)下列图形中是旋转对称图形,但不是轴C 对 称图形的是( )
4.(3分)如图,在图(1)~(4)中是旋转对B称图形 的有( )
旋转一定角度后能与自身重合的图旋形转就对称称为图形 ____________.
旋转对称图形的特征
1 . (3 分 ) 一 条 线 段 是 旋 转 对 称 图中形点, 因 为1它80绕° ________旋转________后能与原线段重合;等边三角 形角平是分线旋(或转中线对或高称线)图的交形点 ,12因0° 为 它 绕 ________________________________ 至 少 旋 转 ________后与原等边对三角角线形的重交合点. 90
华师版10.3.3旋转对称图形(1)

能与自身重合.
(2)将图形绕中心旋转 90,180,270度后都能与自
身重合
你能设计一个旋转30度后能与 自身重合的图形吗?
八(上)数学
五 课堂小结
1.什么是旋转对称图形? 2.会找旋转对称图形的旋转中心和旋转度数;
3.旋转对称图案的设计;
4.一个图形旋转一定的角度后能与自身重合,这 样的旋转角度可能不止一个.
什么是旋转对称图形
在平面内,将一个图形绕着 某一定点旋转一定的角度(小于 周角)后能与自身重合,这种图 形就称为旋转对称图形.
旋转中心在图形的哪个位置?怎 样确定旋转角度?
▪ 旋转中心在图形的正中心或两组对称点连 线垂直平分线的交点
▪ 旋转角度的最小值是360度除以基本图案的 个数
1.下列英文字母中属于旋转对称图形的是( )
旋转对称图形与以前学过的轴对 称图形有何关系?
旋转对称图形与轴对称图形是两种 不同的对称图形,旋转对称图形不一定是 轴对称图形,轴对称图形不一定是旋转对 称图形,它们是两个不同的概念.
一个是旋转一定的角度得到,一个是翻折得到。
(做一做)在纸 上画△ABC和
旋转对称图形
过点P的两条
直线PQ、PR。 画出△ABC关 于PQ 对称三
C
绕着某一定点转动一定
O
的角度后能与自身重合。
请举例说明
A
B
旋转对称图形
·
120°
180°
(或240°) 如图11.2.8所示,电扇的叶片转动120 、螺旋桨转动180
后,都能与自身重合
旋转对称图形
60° ·
该图形绕圆心旋转60°或_1_2_0_°__,或1_8_0_°___ 或_2_4_0_°__或_3_0_0_°_后,都能与自身重合.
(2)将图形绕中心旋转 90,180,270度后都能与自
身重合
你能设计一个旋转30度后能与 自身重合的图形吗?
八(上)数学
五 课堂小结
1.什么是旋转对称图形? 2.会找旋转对称图形的旋转中心和旋转度数;
3.旋转对称图案的设计;
4.一个图形旋转一定的角度后能与自身重合,这 样的旋转角度可能不止一个.
什么是旋转对称图形
在平面内,将一个图形绕着 某一定点旋转一定的角度(小于 周角)后能与自身重合,这种图 形就称为旋转对称图形.
旋转中心在图形的哪个位置?怎 样确定旋转角度?
▪ 旋转中心在图形的正中心或两组对称点连 线垂直平分线的交点
▪ 旋转角度的最小值是360度除以基本图案的 个数
1.下列英文字母中属于旋转对称图形的是( )
旋转对称图形与以前学过的轴对 称图形有何关系?
旋转对称图形与轴对称图形是两种 不同的对称图形,旋转对称图形不一定是 轴对称图形,轴对称图形不一定是旋转对 称图形,它们是两个不同的概念.
一个是旋转一定的角度得到,一个是翻折得到。
(做一做)在纸 上画△ABC和
旋转对称图形
过点P的两条
直线PQ、PR。 画出△ABC关 于PQ 对称三
C
绕着某一定点转动一定
O
的角度后能与自身重合。
请举例说明
A
B
旋转对称图形
·
120°
180°
(或240°) 如图11.2.8所示,电扇的叶片转动120 、螺旋桨转动180
后,都能与自身重合
旋转对称图形
60° ·
该图形绕圆心旋转60°或_1_2_0_°__,或1_8_0_°___ 或_2_4_0_°__或_3_0_0_°_后,都能与自身重合.
10.3.3.旋转对称图形

3.如图是一个旋转对称图形,以点 O 为旋转中心,以下列哪一个角为旋转
角旋转,能使旋转后的图形与原图形重合( C )
A.60° B.90° C.120° D.180°
课件目录
首页
末页
3 旋转对称图形
4.[2018·和平区一模]把图中的五角星图案,绕着它的中心点 O 进行旋 转,若旋转后与自身重合,则至少旋转( C )
A.36° B.45° C.72° D.90°
课件目录
首页
末页
3 旋转对称图形
分 层 作 业 [学生用书P103]
1.[2018 春·宁德期末]如图所示的图案,其外轮廓是一个正五边形,绕
它的中心旋转一定的角度后能够与自身重合,则这个旋转角可能是( B )
A.90° B.72° C.60° D.36°
3 旋转对称图形
2019年春华师版数学七年级下册课件
第10章 轴对称、平移与旋转
3. 旋转
课件目录
首页
末页
3 旋转对称图形
第10章 轴对称、平移与旋转
3. 旋转 3. 旋转对称图形
学习指南
知识管理 归类探究 当堂测评 分层作业
课件目录
首页
末页
3 旋转对称图形
学 习 指 南 [教用专有]
教学目标 1.理解旋转对称图形的概念. 2.能作旋转对称图形. 情景问题引入 用一张透明的薄纸,覆盖在如图所示的图纸上,在这个薄纸上画这个图 形,使它与如图所示的图形重合,然后用事先准备的图钉钉在圆心,将薄纸 绕着图钉旋转,观察旋转多少度(小于周角)后,薄纸上的图形能与原图形再 一次重合.
课件目录
首页
末页
3 旋转对称图形
当 堂 测 评 [学生用书P103]
角旋转,能使旋转后的图形与原图形重合( C )
A.60° B.90° C.120° D.180°
课件目录
首页
末页
3 旋转对称图形
4.[2018·和平区一模]把图中的五角星图案,绕着它的中心点 O 进行旋 转,若旋转后与自身重合,则至少旋转( C )
A.36° B.45° C.72° D.90°
课件目录
首页
末页
3 旋转对称图形
分 层 作 业 [学生用书P103]
1.[2018 春·宁德期末]如图所示的图案,其外轮廓是一个正五边形,绕
它的中心旋转一定的角度后能够与自身重合,则这个旋转角可能是( B )
A.90° B.72° C.60° D.36°
3 旋转对称图形
2019年春华师版数学七年级下册课件
第10章 轴对称、平移与旋转
3. 旋转
课件目录
首页
末页
3 旋转对称图形
第10章 轴对称、平移与旋转
3. 旋转 3. 旋转对称图形
学习指南
知识管理 归类探究 当堂测评 分层作业
课件目录
首页
末页
3 旋转对称图形
学 习 指 南 [教用专有]
教学目标 1.理解旋转对称图形的概念. 2.能作旋转对称图形. 情景问题引入 用一张透明的薄纸,覆盖在如图所示的图纸上,在这个薄纸上画这个图 形,使它与如图所示的图形重合,然后用事先准备的图钉钉在圆心,将薄纸 绕着图钉旋转,观察旋转多少度(小于周角)后,薄纸上的图形能与原图形再 一次重合.
课件目录
首页
末页
3 旋转对称图形
当 堂 测 评 [学生用书P103]
10.3.3旋转对称图形课件 华东师大版

试一试:
用一张半透明的薄纸,覆盖在如教材图15.2.9所示 的图形上,在薄纸上画这个图形,使它与原图完全 重合.然后固定圆心,将薄纸旋转,猜想旋转多少度 (小于周角)后,薄纸上的图形能与原图再一次重合?
一个图形绕着一个定点旋转 一定角度后,能与自身重合的 图形称为旋转对称图形.
这个角度必须小于周角
一般来说,旋转角度可以有多个,但旋转中心只有一个。
例1.观察下图,判断它是不是旋转对称图形? 如果是,请找出旋转中心在何处,旋转角度是 多少?另外该图形是轴对称图形吗?
解:这个图形是旋转对称图形,旋转中心是外框 正方形对角线的交点(如图中的点O),旋转角度 是90°,但它不是轴对称图形.
四、旋转作图
⑷如图,画△ABC关于直线a,b 连续两次对称的图形, 并观察与原图形的关系.
a
b
A B
C
O
练一练
正三角形、正方形、线段、正六边形、圆
找一找:
找找看,下面图形中 有几匹马?它们的位 置关系大致如何?
⑴绕着某一点转动一定角度后,能与自身重 合的图形称为旋转对称图形, 其中这一点就是 旋转中心,这个角度的最小值就是旋转角. ⑵如果一个图形既是旋转对称图形,又是轴对 称图形,那么它的旋转中心就是对称轴的交点. ⑶正n边形既是旋转对称图形,又是轴对称图 形,所以它的旋转中心就是对称轴的交点,并
ห้องสมุดไป่ตู้
例5.下列各图形是不是旋转对称图形?如果是, 请找出旋转中心在何处。旋转角度至少是多少 度?这些图形是轴对称图形吗?
60°
120°
90°
正三角形是旋转对 正方形是旋转对称 称图形, 它的旋转中 图形, 它的旋转中心 心是两条高线的交 是两条对角线的交 点, 旋转角度是120° 点, 旋转角度是90° 它也是轴对称图形. 它也是轴对称图形.
【最新】华师大版七年级数学下册第十章《10.3.3旋转对称图形》公开课 课件.ppt
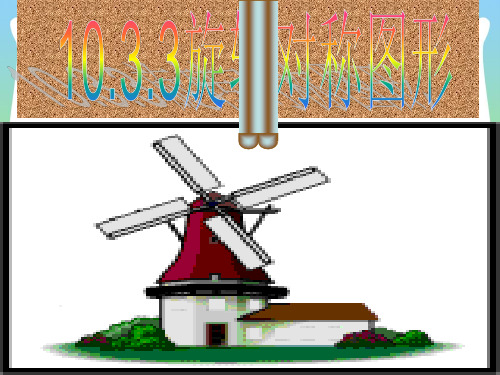
像这样,把一个平面图形绕着某一定点按某个方 向转动一定的角度,这样的图形运动就叫做旋
转.
这个定点O称为旋转中心
转动的角∠AOB
旋转方向:顺时针
称为旋转角
A
B
图形旋转的三要素:
旋转中心.
旋转角
旋转角度.
旋转方向.
o
旋转中心
观察下旋列旋转转的,探特索征对应元素的关系
A′B′=AB, B′C′=BC, A′C′=AC, ∠A′=∠A, ∠B′=∠B, ∠C=′ ∠C
观察下面图形旋转的特点:
1
·
注意旋转的方向
观察下面图形旋转的特点:
AA
·
注意旋转的方向
以上图形都是旋转对称图形,你 能说说定义吗?
定义:
把一个图形绕着某一定点旋转一
定角度后能与自身重合的图形就称为 旋转对称图形。
我们再看一组图形的旋转
探索发现 注意旋转的方向
探索发现
1
你有何发现呢?
以上图形,顺时针或 逆时针旋转360。,都 能与自身重合。那么 这些图形是不是旋转 对称图形呢?
(1)将图形绕圆心旋转 60,120,180,240,300度 后都能与自身重合。
(2)将图形绕中心旋转 90,180,270度后都能与 自身重合。
习题10.3
1.答:将如图所示的五角星绕中心旋转72°、 144°、216°、 288°后都能与自身重合。
72°
2.如图,四边形ABCD是正方形,△ADE经
以上图形都不是 旋转对称图形。
注意旋转的方向
定义:
把一个图形绕着某一定点旋转一定角度后能 与自身重合的图形就称为旋转对称图形。
请注意: 1、0°<旋转角<360°.
转.
这个定点O称为旋转中心
转动的角∠AOB
旋转方向:顺时针
称为旋转角
A
B
图形旋转的三要素:
旋转中心.
旋转角
旋转角度.
旋转方向.
o
旋转中心
观察下旋列旋转转的,探特索征对应元素的关系
A′B′=AB, B′C′=BC, A′C′=AC, ∠A′=∠A, ∠B′=∠B, ∠C=′ ∠C
观察下面图形旋转的特点:
1
·
注意旋转的方向
观察下面图形旋转的特点:
AA
·
注意旋转的方向
以上图形都是旋转对称图形,你 能说说定义吗?
定义:
把一个图形绕着某一定点旋转一
定角度后能与自身重合的图形就称为 旋转对称图形。
我们再看一组图形的旋转
探索发现 注意旋转的方向
探索发现
1
你有何发现呢?
以上图形,顺时针或 逆时针旋转360。,都 能与自身重合。那么 这些图形是不是旋转 对称图形呢?
(1)将图形绕圆心旋转 60,120,180,240,300度 后都能与自身重合。
(2)将图形绕中心旋转 90,180,270度后都能与 自身重合。
习题10.3
1.答:将如图所示的五角星绕中心旋转72°、 144°、216°、 288°后都能与自身重合。
72°
2.如图,四边形ABCD是正方形,△ADE经
以上图形都不是 旋转对称图形。
注意旋转的方向
定义:
把一个图形绕着某一定点旋转一定角度后能 与自身重合的图形就称为旋转对称图形。
请注意: 1、0°<旋转角<360°.
10.3.3旋转对称图形课件(共29张PPT)

2700都能与自身重合。
下列各图形是不是旋转对称图形?如果是, 请找出旋转中心。旋转角度至少是多少度? 这些图形是轴对称图形吗?
120°
90°
60°
正三角形是旋转对 正方形是旋转对称 称图形, 它的旋转中 图形, 它的旋转中心 心是两条高线的交 是两条对角线的交 点, 旋转角度是120° 点, 旋转角度是90° 它也是轴对称图形. 它也是轴对称图形.
观察下面图形旋转的特点:
1
·
注意旋转的方向
观察下面图形旋转的特点:
AA
·
注意旋转的方向
以上图形都是旋转对称图形,你 能说说定义吗?
定义:
把一个图形绕着某一定点旋转一
定角度后能与自身重合的图形就称为 旋转对称图形。
我们再看一组图形的旋转。
探索发现 注意旋转的方向
探索发现
1
你有何发现呢?
以上图形,顺时针或 逆时针旋转360。,都 能与自身重合。那么 这些图形是不是旋转 对称图形呢?
3
4.答:若考虑颜色,将如图所示图形绕中心旋转40°、 80°、120°、 160° 、200°、 240°、 280°、 320°后都能与自身重合。
40°
4
•1、书籍是朋友,虽然没有热情,但是非常忠实。2022年3月3日星期四2022/3/32022/3/32022/3/3 •2、科学的灵感,决不是坐等可以等来的。如果说,科学上的发现有什么偶然的机遇的话,那么这种‘偶然的机遇’只能给那些学有素养的人,给那些善于独 立思考的人,给那些具有锲而不舍的人。2022年3月2022/3/32022/3/32022/3/33/3/2022 •3、书籍—通过心灵观察世界的窗口.住宅里没有书,犹如房间里没有窗户。2022/3/32022/3/3March 3, 2022 •4、享受阅读快乐,提高生活质量。2022/3/32022/3/32022/3/32022/3/3
10.3.3旋转对称图形ppt

(A)是旋转对称图形,肯定不是轴对称图形;
(B) 是轴对称图形,肯定是旋转对称图形;
(C)一些图形可能既是旋转对称图形,又是轴对称 图形;
(D)既不是旋转对称图形,又不是轴对称图形的 图形不存在.
6.在梯形、正三角形、等腰三角形、正方形、线 段、正六边形、圆中是旋转对称图形的是 _正__三__角__形__、___正__方__形__、__线__段__、__正__六__边__形__、__圆___.
第19页,共25页。
7.五角星至少旋转多少度后能与自身重合 ( )
(A)36° (B) 60°
(C)72°
(D)120°
8.如右图所示,此标志图形是( )
(A)旋转对称图形;
(B)轴对称图形;
!
(C)既是旋转对称图形,又是轴
对称图形;
(D)既不是旋转对称图形,也不是轴对称图形.
第20页,共25页。
第1页,共25页。
观察下面图形旋转的特点:
1
·
注意旋转的方向
第2页,共25页。
观察下面图形旋转的特点:
AA
·
注意旋转的方向
第3页,共25页。
以上图形都是旋转对称图形,你能 说说定义吗定义?:
把一个图形绕着某一定
点旋转一定角度后能与自身 重合的图形就称为旋转对称 图形。
我们再看一组图形的旋转。
第4页,共25页。
下列图形旋转多少度后能与自身重合?
(9)
(10)
(11)
(12)
(13)
第11页,共25页。
(14)
旋转对称图形
如图,(1)它是不是旋转对称图形?
(2)旋转中心在何处?
(3)该图形需要旋转多少度后,
(B) 是轴对称图形,肯定是旋转对称图形;
(C)一些图形可能既是旋转对称图形,又是轴对称 图形;
(D)既不是旋转对称图形,又不是轴对称图形的 图形不存在.
6.在梯形、正三角形、等腰三角形、正方形、线 段、正六边形、圆中是旋转对称图形的是 _正__三__角__形__、___正__方__形__、__线__段__、__正__六__边__形__、__圆___.
第19页,共25页。
7.五角星至少旋转多少度后能与自身重合 ( )
(A)36° (B) 60°
(C)72°
(D)120°
8.如右图所示,此标志图形是( )
(A)旋转对称图形;
(B)轴对称图形;
!
(C)既是旋转对称图形,又是轴
对称图形;
(D)既不是旋转对称图形,也不是轴对称图形.
第20页,共25页。
第1页,共25页。
观察下面图形旋转的特点:
1
·
注意旋转的方向
第2页,共25页。
观察下面图形旋转的特点:
AA
·
注意旋转的方向
第3页,共25页。
以上图形都是旋转对称图形,你能 说说定义吗定义?:
把一个图形绕着某一定
点旋转一定角度后能与自身 重合的图形就称为旋转对称 图形。
我们再看一组图形的旋转。
第4页,共25页。
下列图形旋转多少度后能与自身重合?
(9)
(10)
(11)
(12)
(13)
第11页,共25页。
(14)
旋转对称图形
如图,(1)它是不是旋转对称图形?
(2)旋转中心在何处?
(3)该图形需要旋转多少度后,
华师版七年级下数学课件:10.3.3 旋转对称图形(共15张PPT)

2020/6/7
C O
D E
3
定义:
在平面内,将一个图形绕着一定点旋转一定角度 (小于周角)后能与自身重合,这样的图形叫做旋转对 称图形. 旋转的度数称为旋转角度.
一般来说,旋转角度可以有多个,但旋转中心 只有一个.
2
4
例1 下列各图形是不是旋转对称图形?如果是,请 找出旋转中心在何处.旋转角度是多少?这些图形是 轴对称图形吗?
O
2020/6/7
12
旋转对称图形的画法: 1.任意定一点旋转中心O; 2.按设计需要,把周角360°分成n等份; 3.以O为旋转中心,360°除以n的商为旋转角做顺
时针或逆时针旋转n-1次即可得到一个旋转对称图 形.
2020/6/7
13
旋转对 称图形
小结
定义 特点 与轴对称图形的区别 画法
2020/6/7
120°
90°
72°
60°
2020/6/7
正三角形正四边形正五边形正六边形
5
(1)绕着某一点转动一定角度后,能与自身重合的图形 称为旋转对称图形.其中这一点就是旋转中心,这 个角度就是旋转角度;
(2)如果一个图形既是旋转对称图形,又是轴对称图形, 那么它的旋转中心就是对称轴的交点; (3)正n边形既是旋转对称图形,又是轴对称图形,
旋转对称图形
————锦州市第四初级中学
2020/6/7
1
3.图形上的每一点都绕旋转中心沿相同的方向转 动了相同大小的角度.
4.对应点到旋转中心的距离相等.
2
2
特征
60°,120°,180提°醒,:24若0°顺,时3针00或°逆A时
该图形绕哪一点旋针形转旋都转能?O一与点定原角图度形,重该合图,
C O
D E
3
定义:
在平面内,将一个图形绕着一定点旋转一定角度 (小于周角)后能与自身重合,这样的图形叫做旋转对 称图形. 旋转的度数称为旋转角度.
一般来说,旋转角度可以有多个,但旋转中心 只有一个.
2
4
例1 下列各图形是不是旋转对称图形?如果是,请 找出旋转中心在何处.旋转角度是多少?这些图形是 轴对称图形吗?
O
2020/6/7
12
旋转对称图形的画法: 1.任意定一点旋转中心O; 2.按设计需要,把周角360°分成n等份; 3.以O为旋转中心,360°除以n的商为旋转角做顺
时针或逆时针旋转n-1次即可得到一个旋转对称图 形.
2020/6/7
13
旋转对 称图形
小结
定义 特点 与轴对称图形的区别 画法
2020/6/7
120°
90°
72°
60°
2020/6/7
正三角形正四边形正五边形正六边形
5
(1)绕着某一点转动一定角度后,能与自身重合的图形 称为旋转对称图形.其中这一点就是旋转中心,这 个角度就是旋转角度;
(2)如果一个图形既是旋转对称图形,又是轴对称图形, 那么它的旋转中心就是对称轴的交点; (3)正n边形既是旋转对称图形,又是轴对称图形,
旋转对称图形
————锦州市第四初级中学
2020/6/7
1
3.图形上的每一点都绕旋转中心沿相同的方向转 动了相同大小的角度.
4.对应点到旋转中心的距离相等.
2
2
特征
60°,120°,180提°醒,:24若0°顺,时3针00或°逆A时
该图形绕哪一点旋针形转旋都转能?O一与点定原角图度形,重该合图,
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
C C B
B
B C
A
P
预习目标
1.什么叫旋转对称图形? 2.你能找出图形的旋转中心和旋转 角吗?
观察下面图形旋转的特点:
1
·
注意旋转的方向
观察下面图形旋转的特点:
A A
·
注意旋转的方向
以上图形都是旋转对称图形,你 能说说定义吗?
定义:
把一个图形绕着某一定点旋转一 定角度后能与自身重合的图形就称为 旋转对称图形。
观察下列旋转 ,探索对应元素的关系 旋转的特征
即 ⑴: 对应线段相等 对应角相等 C′ ′ ′ ′ OA=OA, OB=OB, OC=OC 还有相等的线段和角吗 ? ⑵ 即 : 对应点到旋转中 心的距离相等 0·
′ ∠COC ′ ′ ∠BOB= ∠AOA=
B′
A′ C
⑶ 即: 每一点都绕旋转中 心按同一方向转过相 A 等的角度
1 1
是。旋转900、1800、 2700都能与自身重合。
下列各图形是不是旋转对称图形?如果是, 请找出旋转中心。旋转角度至少是多少度? 这些图形是轴对称图形吗?
60° 120°
90°
正三角形是旋转对 正方形是旋转对称 称图形, 它的旋转中 图形, 它的旋转中心 心是两条高线的交 是两条对角线的交 点, 旋转角度是120° 点, 旋转角度是90° 它也是轴对称图形. 它也是轴对称图形.
旋转对称图形
如图,(1)它是不是旋转对称图形? (2)旋转中心在何处? (3)该图形需要旋转多少度后,
·O
能与自身重合?
(4)该图形是轴对称图形吗? (1)这个图形是旋转对称图形; (2)如图所示,点O为旋转中心;
(3)该图形需要旋转90度或180度或270 度后,能与自身重合;
(4)该图形不是轴对称图形。
1.答:将如Biblioteka 所示的五角星绕中心旋转72°、 144°、216°、 288°后都能与自身重合。
72°
2.如图,四边形ABCD是正方形,△ADE经 顺时针旋转后与△ABF重合。 (1)旋转中心是哪一点? (2)旋转了多少度? (3)若连结FE,则 △AEF是怎样的三角形?
┖ F B C A D ┖ E
旋转对称图形
如图, (1)它是不是旋转对称图形? (2)旋转中心在何处? (3)该图形需要旋转多少度后,
· · O
能与自身重合?
(4)该图形是轴对称图形吗? (1)这个图形是旋转对称图形;
(2)如图所示,点O为旋转中心;
(3)该图形需要旋转180度后,能与自身重合; (4)该图形是轴对称图形,有两条对称轴.(如图)
B
“两次翻折”与“旋转”的关系
结论:
如图,在纸上画△ABC和过点P的两条直线PQ、 PR.画出△ABC关于PQ对称的△A B C ,再画出 △A B C关于PR对称的△A B C . 观察△ABC和△A B C ,你能发现这两个三角 形有什么关系吗? Q A R
A
当对称轴相 交时,两次 翻折相当于 一次旋转.
分析:若顺时针或逆时针旋转一定角度,该图形 都能与原图形重合,则可以淡化旋转方向。
旋转对称图形
·
120°
180°
如图11.2.8所示,电扇的叶片转动120° (或240°) 后,都能与自身重合。 、螺旋桨转动180°
旋转对称图形
60°
·
该图形绕圆心旋转 60°或______, 120° 或______ 180° 或______ 后,都能与自身重合。 240°或_____ 300°
旋转对称图形与轴对称图形有何关系? 旋转对称图形与轴对称图形是两种 不同的对称图形,旋转对称图形不一定是 轴对称图形,轴对称图形不一定是旋转对 称图形,它们是两个不同的概念.
一个是旋转一定的角度得到,一个是翻折得到。
这个图形是不是 旋转对称图形? 如果是,这个图 形旋转多少度能 与自身重合呢? 想一想它的旋转 中心在哪?
3.答:旋转120°、 240°后都能与自身 重合。
3
4.答:若考虑颜色,将如图所示图形绕中心旋转40°、 80°、120°、 160° 、200°、 240°、 280°、 320°后都能与自身重合。
40°
4
(1)将图形绕圆心旋转 60,120,180,240,300度 后都能与自身重合。
(2)将图形绕中心旋转 90,180,270度后都能与 自身重合。
这节课你学到了什么?
1.我知道了什么叫旋转对称图形; 2.我能找出图形的旋转中心和旋转 角; 注意:旋转对称图形是一个具有旋 转特征的特殊图形。
习题10.3
我们再看一组图形的旋转。
探索发现
注意旋转的方向
探索发现
1
你有何发现呢?
以上图形,顺时针或 。 逆时针旋转360 ,都 能与自身重合。那么 这些图形是不是旋转 对称图形呢?
以上图形都不是 旋转对称图形。
注意旋转的方向
定义: 把一个图形绕着某一定点旋转一定角度后能 与自身重合的图形就称为旋转对称图形。 请注意: 1、0°<旋转角<360°. 2、旋转对称图形是一个具有旋转特征的 特殊图形。 3、旋转的方向不用考虑!
像这样,把一个平面图形绕着某一定点按某个方
向转动一定的角度,这样的图形运动就叫做旋
转. 这个定点O称为旋转中心 转动的角∠AOB 称为旋转角
旋转方向:顺时针
A B
图形旋转的三要素: 旋转中心. 旋转角度. 旋转方向.
旋转角
o
旋转中心
′ ′ ′ ′ ′ ′ ′ ∠A, ∠B= ′ ∠B, ∠C= ′ ∠C AB=AB, BC=BC, AC=AC, ∠A=
正六边形是旋转对称 图形, 它的旋转中心 是两条对角线的交 点, 旋转角度是60° 它也是轴对称图形.
课堂练习
·
2.答:图形中有4匹马。绕矩形两条对角线的交点 旋转180°,两匹马能够分别与另两匹马大致重合, 这个图形可以近似地看作是旋转对称图形。
3.如图所示的图形绕哪一点旋转多少度后与 自身重合?
