材料力学学生习题解答
材料力学课后习题答案详细

变形厚的壁厚:
(R r) | (R r) | 30 0.009 29.991(mm)
[习题 2-11] 受轴向拉力 F 作用的箱形薄壁杆如图所示。已知该材料的弹性
常数为 E, ,试求 C 与 D 两点间的距离改
22
N 22 A
10 103 N 400mm 2
25MPa
33
N 33 A
10 103 N 400mm 2
25MPa
[习题 2-3] 试求图示阶梯状直杆横截面 1-1、2-2 和平 3-3 上的轴力,并作
轴力图。若横截面面积 A1 200mm2 , A2 300mm2 , A3 400mm2 ,并求各横截 面上的应力。
A1 11.503cm2 1150.3mm2
AE
N EA A
366.86 103 N 2 1150.3mm2
159.5MPa
EG
N EG A
357.62 103 N 2 1150.3mm2
155.5MPa
[习题 2-5] 石砌桥墩的墩身高 l 10m ,其横截面面尺寸如图所示。荷载
22
N 22 A2
10 103 N 300mm 2
33.3MPa
3
33
N 33 A
10 103 N 400mm 2
25MPa
[习题 2-4] 图示一混合屋架结构的计算简图。屋架的上弦用钢筋混凝土制
成。下面的拉杆和中间竖向撑杆用角钢构成,其截面均
为两个 75mm 8mm 的等边角钢。已知屋面承受集度为
同济大学-材料力学-习题解答3(练习册P71-P74等)

R
zC
O R
z1
z2
Iz = IzC+Ab2
yC
4R yC = 3p
P282:附录A 第四项
IzC = Iz1 -
1 2
pR2×yC2
Iz2 = IzC +
1 2
pR2×( R+yC )2
=( 5 p + 8
4 )R4 3
= 3.30R4
P111 58-4 等边角钢 (型钢)
查表:导学篇 附录B-1 P374中L 100×10
=-
1 2
qx2
+
2qax
-
2qa2
=-
1 2
q×(2a-x)2
P74 40-2-3
xx
xF
x
A
C
FA
1F 3
mA = 0
Fy = 0
1
1
DB
FB = 3 F
FA = 3 F
F
FB
AC段: FS(x) = FA
=
1 3F
1F 3
M(x) = FA×x
=
1 3
Fx
CD段:FS(x) = FA-F
=-
1 q 23
截面法!
错误较多!
A
B
1
M1
q 23
A FS1
B M2
B
FS2 M3
FS3
C Fy = 0 FS1 + F - q×2 = 0
F
FS1 = q×2 - F = 10 kN
C mA = 0 F×4 - M1 - 2q×1 = 0
F
M1 = F×4 - 2q×1 = 20 kN·m
材料力学习题及答案
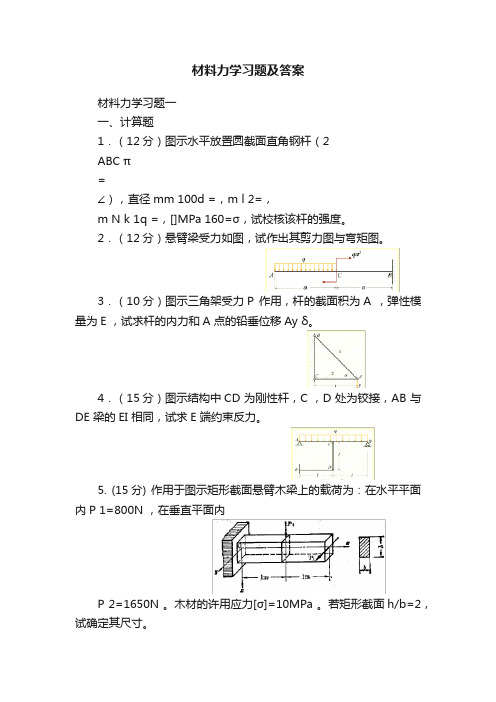
材料力学习题及答案材料力学习题一一、计算题1.(12分)图示水平放置圆截面直角钢杆(2ABC π=∠),直径mm 100d =,m l 2=,m N k 1q =,[]MPa 160=σ,试校核该杆的强度。
2.(12分)悬臂梁受力如图,试作出其剪力图与弯矩图。
3.(10分)图示三角架受力P 作用,杆的截面积为A ,弹性模量为E ,试求杆的内力和A 点的铅垂位移Ay δ。
4.(15分)图示结构中CD 为刚性杆,C ,D 处为铰接,AB 与DE 梁的EI 相同,试求E 端约束反力。
5. (15分) 作用于图示矩形截面悬臂木梁上的载荷为:在水平平面内P 1=800N ,在垂直平面内P 2=1650N 。
木材的许用应力[σ]=10MPa 。
若矩形截面h/b=2,试确定其尺寸。
三.填空题(23分)1.(4分)设单元体的主应力为321σσσ、、,则单元体只有体积改变而无形状改变的条件是__________;单元体只有形状改变而无体积改变的条件是__________________________。
2.(6分)杆件的基本变形一般有______、________、_________、________四种;而应变只有________、________两种。
3.(6分)影响实际构件持久极限的因素通常有_________、_________、_________,它们分别用__________、_____________、______________来加以修正。
4.(5分)平面弯曲的定义为______________________________________。
5.(2分)低碳钢圆截面试件受扭时,沿____________截面破坏;铸铁圆截面试件受扭时,沿____________面破坏。
四、选择题(共2题,9分)2.(5分)图示四根压杆的材料与横截面均相同,试判断哪一根最容易失稳。
答案:()材料力学习题二二、选择题:(每小题3分,共24分)1、危险截面是______所在的截面。
材料力学_范钦珊_习题参考解答
OB
B F P 60kN
Ea
1 .2 m
A
FP
x
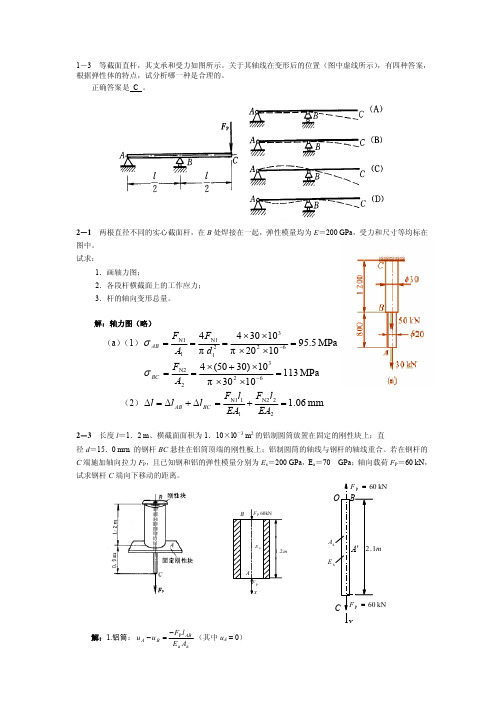
解:1.铝筒: u A − u B
=
−FPl AB Ea Aa
(其中 uA = 0)
As
A' 2.1m
Es
C FP = 60 kN
x
uB
=
60 ×103 ×1.2 ×103 70 ×103 ×1.10 ×10−3 ×106
= 0.935 mm
Mx1= Mx2 2.确定轴和薄壁管横截面上的最大剪应力 设轴受 T = 73.6N·m 时,相对扭转角为 ϕ0 ,于是,有
dφ0 = M x = T dx GIp1 GIp1
(a)
焊接后卸载,管承受扭转,其相对扭转角为 ϕ 2 ,轴上没有恢复的相对扭转角为 ϕ1 = ϕ0 − ϕ2 ,即
其中
ϕ1 + ϕ2 = ϕ0
×103 × 10 −6
= 95.5 MPa
σ BC
=
FN2 A2
=
4 × (50 + 30) ×103 π × 302 ×10−6
= 113 MPa
(2) ∆l = ∆l AB
+ ∆lBC
=
FN1l1 EA1
+ FN2l2 EA2
= 1.06 mm
2-3 长度 l=1.2 m、横截面面积为 1.10×l0-3 m2 的铝制圆筒放置在固定的刚性块上;直 径 d=15.0 mrn 的钢杆 BC 悬挂在铝筒顶端的刚性板上;铝制圆筒的轴线与钢杆的轴线重合。若在钢杆的 C 端施加轴向拉力 FP,且已知钢和铝的弹性模量分别为 Es=200 GPa,Ea=70 GPa;轴向载荷 FP=60 kN, 试求钢杆 C 端向下移动的距离。
材料力学习题解答

解: (3) 梁可简化, 为图示简朴支梁。
B
(m / 2)a 6EI
ma 12EI
(逆时针)
wC 0
mm
m
2
B
C
m
m
2a a a a a 2a
4.如图所示各梁旳抗弯刚度为EI,试用叠加法计算梁 B截面旳转角以及C点旳挠度。
解: (4) 梁可简化,为图示简朴支梁。 B
q
2qqaa22
C
B
qa3 24EI
φ w3 w2
q EI a
A a/4
θ w1
w1
a 4
qa3 a qa4 24EI 4 96EI
w2
q 8EI
a 4
4
qa 4 2048EI
φ w3
w3
a 4
a 3EI
1 2
q
a 4
2
a 4
qa 4 384EI
w2
w
w1
w2
w3
15qa 4 2048EI
7.试用叠加法计算图示各梁C点旳挠度。
解: (1) 梁可简化, 为图示悬臂梁。
A
B
F (2a)2 2EI
Fa 2 2EI
B
3Fa 2 2EI
(逆时针)
wC
wA
F (2a)3 3EI
( Fa3 3EI
Fa 2 2EI
a)
F
F
B C
Fa
a
a
F
a
BF
C
F
11Fa3 wC 6EI (向下)
4.如图所示各梁旳抗弯刚度为EI,试用叠加法计算梁 B截面旳转角以及C点旳挠度。
A
先考虑载荷作用下梁旳变形。
材料力学完整课后习题答案

习题2-2一打入基地内的木桩如图所示,杆轴单位长度的摩擦力fkx2,试做木桩的后力图。
解:由题意可得:l 1 0 fdx F 有kl 3 F k 3F / l 3 3 l FN x1 3Fx 2 / l 3dx F x1 / l 3 0习题2-3 石砌桥墩的墩身高l 10m ,其横截面面尺寸如图所示。
荷载 F 1000kN ,材料的密度2.35kg / m 3 ,试求墩身底部横截面上的压应力。
解:墩身底面的轴力为:N F G F Alg 2-3 图1000 3 2 3.14 12 10 2.35 9.8 3104.942kN 墩身底面积: A 3 2 3.14 12 9.14m 2 因为墩为轴向压缩构件,所以其底面上的正应力均匀分布。
N 3104.942kN 339.71kPa 0.34MPa A 9.14m 2习题2-7 图示圆锥形杆受轴向拉力作用,试求杆的伸长。
2-7 图解:取长度为dx 截离体(微元体)。
则微元体的伸长量为:Fdx l F F l dx d l ,l dx EA x 0 EA x E 0 A x r r1 x r r d d1 d ,r 2 1 x r1 2 x 1 ,r2 r1 l l 2l 2 d d1 d d1 d d1 2 d d A x 2 x 1 u2 ,d 2 x 1 du 2 dx 2l 2 2l 2 2l 2l 2l dx d d 2l du dx du ,2 2 1 du 2 d 2 d1 A x u d1 d 2 u l F F l dx 2 Fl l du 因此,l dx 0 u 2 0 EA x E 0 A x E d1 d 2 l 2 Fl 1 l 2 Fl 1 u E d d d d E d1 d 2 0 2 2 d 1 1 x 1 2l 2 0 2 Fl 1 1 E d1 d 2 d 2 d 1 dd1 l 1 2l 2 2 2 Fl 2 2 4 Fl E d1 d 2 d 2 d1 Ed 1 d 2习题2-10 受轴向拉力 F 作用的箱形薄壁杆如图所示。
大学材料力学习题及答案

大学材料力学习题及答案(题库)(总12页)--本页仅作为文档封面,使用时请直接删除即可----内页可以根据需求调整合适字体及大小--一.是非题:(正确的在括号中打“√”、错误的打“×”) (60小题) 1.材料力学研究的主要问题是微小弹性变形问题,因此在研究构件的平衡与运动时,可不计构件的变形。
( √ )2.构件的强度、刚度、稳定性与其所用材料的力学性质有关,而材料的力学性质又是通过试验测定的。
( √ )3.在载荷作用下,构件截面上某点处分布内力的集度,称为该点的应力。
(√ )4.在载荷作用下,构件所发生的形状和尺寸改变,均称为变形。
( √ ) 5.截面上某点处的总应力p 可分解为垂直于该截面的正应力σ和与该截面相切的剪应力τ,它们的单位相同。
( √ )6.线应变ε和剪应变γ都是度量构件内一点处变形程度的两个基本量,它们都是无量纲的量。
( √ )7.材料力学性质是指材料在外力作用下在强度方面表现出来的性能。
( ) 8.在强度计算中,塑性材料的极限应力是指比例极限p σ,而脆性材料的极限应力是指强度极限b σ。
( )9.低碳钢在常温静载下拉伸,若应力不超过屈服极限s σ,则正应力σ与线应变ε成正比,称这一关系为拉伸(或压缩)的虎克定律。
( )10.当应力不超过比例极限时,直杆的轴向变形与其轴力、杆的原长成正比,而与横截面面积成反比。
( √ )11.铸铁试件压缩时破坏断面与轴线大致成450,这是由压应力引起的缘故。
( )12.低碳钢拉伸时,当进入屈服阶段时,试件表面上出现与轴线成45o 的滑移线,这是由最大剪应力max τ引起的,但拉断时截面仍为横截面,这是由最大拉应力max σ引起的。
( √ )13.杆件在拉伸或压缩时,任意截面上的剪应力均为零。
( ) 14.EA 称为材料的截面抗拉(或抗压)刚度。
( √ )15.解决超静定问题的关键是建立补充方程,而要建立的补充方程就必须研究构件的变形几何关系,称这种关系为变形协调关系。
(完整版)材料力学课后习题答案
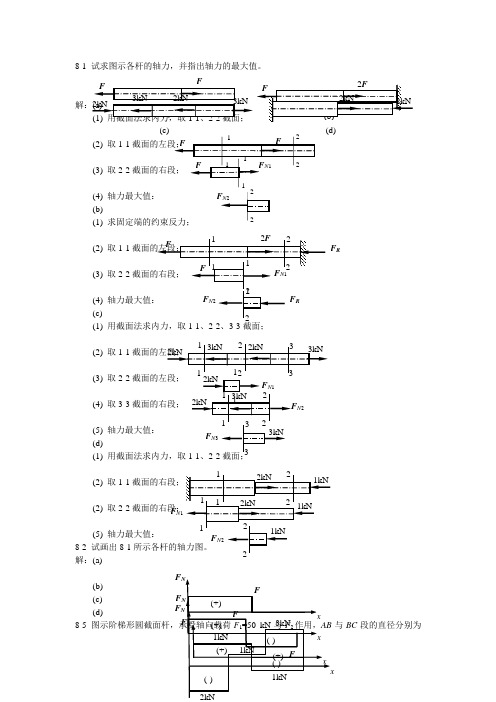
8-1 试求图示各杆的轴力,并指出轴力的最大值。
(2) 取1-1(3) 取2-2(4) 轴力最大值: (b)(1) 求固定端的约束反力; (2) 取1-1(3) 取2-2(4) (c)(1) 用截面法求内力,取1-1、2-2、3-3截面;(2) 取1-1(3) 取2-2 (4) 取3-3截面的右段;(5) 轴力最大值: (d)(1) 用截面法求内力,取1-1、(2) 取1-1(2) 取2-2(5) 轴力最大值: 8-2 试画出8-1解:(a) (b) (c) (d) 8-5与BC 段的直径分别为(c) (d)F RN 2F N 3 F N 1F F Fd 1=20 mm 和d 2=30 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求载荷F 2之值。
解:(1) 用截面法求出(2) 求1-1、2-28-6 题8-5段的直径d 1=40 mm ,如欲使AB 与BC 段横截面上的正应力相同,试求BC 段的直径。
解:(1)用截面法求出1-1、2-2截面的轴力;(2) 求1-1、2-2截面的正应力,利用正应力相同;8-7 图示木杆,承受轴向载荷F =10 kN 作用,杆的横截面面积A =1000 mm 2,粘接面的方位角θ= 450,试计算该截面上的正应力与切应力,并画出应力的方向。
解:(1) (2) 8-14 2=20 mm ,两杆F =80 kN 作用,试校核桁架的强度。
解:(1) 对节点A(2) 列平衡方程 解得: (2) 8-15 图示桁架,杆1A 处承受铅直方向的载荷F 作用,F =50 kN ,钢的许用应力[σS ] =160 MPa ,木的许用应力[σW ] =10 MPa 。
解:(1) 对节点A (2) 84 mm 。
8-16 题8-14解:(1) 由8-14得到的关系;(2) 取[F ]=97.1 kN 。
8-18 图示阶梯形杆A 2=100 mm 2,E =200GPa ,试计算杆AC 的轴向变形 解:(1) (2) AC 8-22 图示桁架,杆1与杆2的横截面面积与材料均相同,在节点A 处承受载荷F 作用。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
E F N1F N3F N2β(c)2-1 试绘出下列各杆的轴力图。
2-2 求下列结构中指定杆内的应力。
已知(a)图中杆的横截面面积A 1=A 2=1150mm 2; 解:(1)分析整体,作示力图∑=0)(i BF M:041088=⨯⨯-⨯A F 40kN A F =(2)取部分分析,示力图见(b )∑=0)(i CF M:02442.22=⨯+⨯-⨯q F F A N2(404402)36.36kN 2.2N F ⨯-⨯==3262236.361031.62MPa 115010N F A σ-⨯===⨯杆(3)分析铰E ,示力图见(c )∑=0ixF:0sin 12=-βN N F F22122140.65kN 2N N F F +=⨯= 3161137.961035.3MPa 115010N F A σ-⨯===⨯杆F 2F F N 2F F N A ECDB F AF BCF A F CyF CxN2(b)2-3 求下列各杆内的最大正应力。
(3)图(c)为变截面拉杆,上段AB 的横截面积为40mm 2,下段BC 的横截面积为30mm 2,杆材料的ρg =78kN/m 3。
解:1.作轴力图,BC 段最大轴力在B 处6N 120.530107812.0kN B F -=+⨯⨯⨯=AB 段最大轴力在A 处6N 1212(0.5300.540)107812.0kN A F -=++⨯+⨯⨯⨯=3N 2612.010400MPa 30mm 3010B B F σ--⨯===⨯ 3N 2612.010300MPa 40mm4010AA F σ--⨯===⨯杆件最大正应力为400MPa ,发生在B 截面。
2-4 一直径为15mm ,标距为200mm 的合金钢杆,比例极限内进行拉伸试验,当轴向荷载从零缓慢地增加58.4kN 时,杆伸长了0.9mm ,直径缩小了0.022mm ,确定材料的弹性模量E 、泊松比ν。
解:加载至58.4kN 时,杆件横截面中心正应力为3N 2458.410330.48MPa 1.5104F A σπ-⨯==⨯⨯= 线应变:333Δ0.9104.51020010llε--⨯===⨯⨯弹性模量:33330.48MPa73.410MPa 4.510E σε-===⨯⨯侧向线应变:310467.115022.0-⨯==,ε泊松比:,0.326εμε==2-6图示短柱,上段为钢制,长200mm ,截面尺寸为100×100mm 2;下段为铝制,长300mm ,截面尺寸为200×200mm 2。
当柱顶受F 力作用时,柱子总长度减少了0.4mm ,试求F 值。
已知E 钢=200GPa ,E 铝=70GPa 。
解:柱中的轴力都为F ,总的变形(缩短)为:120.20.3Δg l F Fl E A E A =+ 12399Δ0.20.30.4100.20.3200100.10.170100.20.21931.0kNg l lF E A E A -=⎡⎤+⎢⎥⎢⎥⎣⎦⨯=⎡⎤+⎢⎥⨯⨯⨯⨯⨯⨯⎣⎦= A BC12.012.0F N (kN)2-7 图示等直杆AC ,材料的容重为ρg ,弹性模量为E ,横截面积为A 。
求直杆B 截面的位移ΔB 。
解: AB 段内轴力 N1F F gAx ρ=-- BC 段内轴力 N22F F gAx ρ=--B 点位移为杆BC 的伸长量: 22(2)d 2 1.5lB lF gAx x Fl gAl EA EAρρ∆-++==-⎰2-8 图示结构中,AB 可视为刚性杆,AD 为钢杆,面积A 1=500mm2,弹性模量E 1=200GPa ;CG 为铜杆,面积A 2=1500mm 2,弹性模量E 2=100GPa ;BE 为木杆,面积A 3=3000mm 2,弹性模量E 3=10GPa 。
当G 点处作用有F =60kN 时,求该点的竖直位移ΔG 。
解:(1)求①、②杆轴力 由平衡方程可以求出:N1N3N2240kN320kN 360kNF F F F F F =-=-=-=-==(2)求杆的变形34N11961140101Δ410m 2001050010AD F l l E A ---⨯⨯===-⨯⨯⨯⨯(压缩) 34N22962260100.5Δ210m 10010150010CG F l l E A --⨯⨯===⨯⨯⨯⨯(拉伸) 36N33963320101Δ 6.6710m 1010300010BE F l l E A ---⨯⨯===-⨯⨯⨯⨯(压缩) (3)由几何关系:421321ΔΔΔ 6.8910m 33G l l l ∆-=-⨯-=(下降)2-11 图示一挡水墙示意图,其中AB 杆支承着挡水墙,各部分尺寸均已示于图中。
若AB 杆为圆截面,材料为松木,其容许应力[σ]=11MPa ,试求AB 杆所需的直径。
解:(1)求水压力的合力:21240kN P h b γ==(2)作示力图(a )由平衡方程求轴力2N 3N ()0:0.60.4011.11kNOi MF F P F =⨯⨯-⨯==∑ (3)由强度条件,设计截面尺寸:N 3632[]411.1110/(1110) 1.28610m 3.58cmF A d d σσπ-=≤≥⨯⨯⋅⨯=⨯≥2-12 图示结构中的CD 杆为刚性杆,AB 杆为钢杆,直径d =30mm ,容许应力[σ]=160MPa ,弹性模量E =2.0×105MPa 。
试求结构的容许荷载F 。
解:(1)求AB 杆的轴力F N∑=0)(i CF M:N N sin 302 2.502.5F F F F⨯-⨯==(2)由强度条件求[]F[][][]N 462.591016010445.2kN2.5F F A A F σσσπ-=≤⇒≤⨯⨯⨯⨯==3-1 试作下列各杆的扭矩图。
3-2 一直径d =60mm 的圆杆,其两端受外力偶矩T =2kN ·m 的作用而发生扭转。
试求横截面上1,2,310010 Mx(N·m) 21 Mx (kN·m) 5 3点处的切应力和最大切应变,并在此三点处画出切应力的方向。
(G =80GPa )。
解:横截面上切应力大小沿半径线性分布,方向垂直半径33P 213200047.2MPa 3.140.06/160.02/331.4MPaT W ττττ===⨯===4max 3/ 5.910rad G γτ-==⨯3-3 从直径为300mm 的实心轴中镗出一个直径为150mm 的通孔而成为空心轴,问最大切应力增大了百分之几?解:实心轴max13P116x xM M W d τπ== 空心轴max 234P216(10.5)x x M M W d τπ==- 最大切应力增大了4343max 2max14max1316160.5(10.5)100%100%100% 6.67%1610.5x xx M M d d M d ττππτπ---⨯=⨯=⨯=-3-4 一端固定、一端自由的钢圆轴,其几何尺寸及受力情况如图所示(空心处有两段,内径10mm ,外径30mm ),试求:(1)轴的最大切应力。
(2)两端截面的相对扭转角(G =80GPa)。
解:(1)作扭矩图, AB 段中最大切应力max36P6035.56MPa 31016xM W πτπ-===⨯⨯CD 段中最大切应力()()max 946P644031101616401024MPa 2713x M W πτπα---==⨯⨯-⨯⨯=⨯=-所以轴中,MPa 56.35max =τ (2)相对扭转角分四段计算P1P1P2P2400.2300.1300.1600.15ΔΔΔΔΔDC CE EB BA GI GI GI GI ππππϕϕϕϕϕ⨯⨯⨯⨯=+++=+++P1P2P1P211121112GI GI G I I πππ⎛⎫=+=+ ⎪⎝⎭3τ1τ60лл30л40лAB C D()94844811120.011426rad 118010310133103232πππ---⎛⎫⎪=+= ⎪⨯⨯⨯-⨯⨯ ⎪⎝⎭3-5 一圆轴AC 如图所示。
AB 段为实心,直径为50mm ;BC 段为空心,外径为50mm ,内径为35mm 。
要使杆的总扭转角为0.12°,试确定BC 段的长度a 。
设G =80GPa 。
解:(1)作扭矩图 100N m x M =⋅ (2)杆件A 、C 截面相对扭转角分两段计算()()4P P ΔΔΔ0.91AC BC BAx x M a M aGI GI ϕϕϕα=+-=+-P 4P 948Δ350.9,0.7501Δ0.315960.980100.12510180320.91000.315960.405mAC x ACxGI aa M GI a M a a ϕααϕππ-=+--=-⎡⎤⨯⨯⨯⨯⨯⨯⎢⎥-⎢⎥⎢⎥⎣⎦==其中==3-8 传动轴的转速为n =500转/分,主动轮输入功率P 1=500kW ,从动轮2、3分别输出功率P 2=200kW ,P 3=300kW 。
已知[τ]=70MPa ,[θ]=1°/m ,G =8×104MPa 。
(1)确定AB 段的直径d 1和BC 段的直径d 2。
(2)若AB 和BC 两段选用同一直径,试确定直径d 。
解:(1)由输入和输出功率求等效力偶,作扭矩图1235009.559.55kN m 5002009.55 3.82kN m 5003009.55 5.73kN m500T T T ==⋅==⋅==⋅由强度条件:[]max max P x MW ττ=≤3311633226169.5510,0.089m 701016 5.7310,0.075m7010d d d d ππ⨯⨯≥=⨯⨯⨯≥=⨯由刚度条件:[]max max Px MGI θθ=≤⊕100N·m M xAC5.739.55M xAB34111023422102329.5510,0.091m81018032 5.3710,0.080m 810180d d d d ππ⨯⨯≥=⨯⨯⨯⨯≥=⨯⨯为满足强度和刚度条件,AB 段的直径d 取91mm ;BC 段的直径d 取80mm 。
(2)若AB 和BC 两段选用同一直径,直径d 取91mm 。
A-2 试求图形水平形心轴z 的位置,并求影阴线部分面积对z 轴的面积矩S z 。
解:分三块计算 215050501501505022500mm iA A ==⨯+⨯+⨯=∑ 形心轴位置()12331257517591.67mm25500.025cm z A A A h A S A h ⨯+⨯+⨯===⨯-=A-3 试计算(b)图形对y ,z 轴的惯性矩和惯性积。
