正弦交流电的瞬时值表达式与三要素
合集下载
第2章 正弦稳态电路的分析
u
l
L是一个与i、ψ无关的常数。若线圈中含有铁磁物质，则 L与i、ψ有关，不是常数。 线圈的电感与线圈的形状，几何尺寸，匝数以及周 围物质的导磁性质有关，即 SN 2 L l l为密绕长线圈的长度（m），截面为S（m2)， 匝数为N，μ为介质的磁导率。
2．自感电动势
i(t)变化
ψ变化
产生eL(t)
波形图中 正半周 u ＞ 0 , i ＞ 0 (正值),说明实际方向与参考方向相同 负半周 u ＜ 0 , i ＜0 (负值),说明实际方向与参考方向相反
+
u
_
i,u T Um O
波形： Im
wt
可见:没有设定参考方向,正负值就没有意义,波形图也表达不出 它们的变化规律
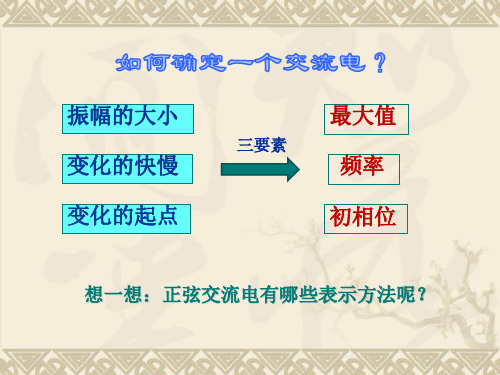
2.1.2 正弦交流电量的三要素：
u U m cos( t + ) w U m e j (wt + )的实部 正弦电压u正好等于复数
u Re [U m e j (wt + ) ] Re [U m e jwt e j ] e jwt ] (令U U e j ) Re [U m m m
现在就把பைடு நூலகம்U m U m e j U m 称为正弦电压u的最大值相量
除法：模相除，角相减。
正弦交流电量的表示法 1、瞬时表达式(即时间的正弦或余弦函数式) 2、波形图(即时间的正弦或余弦函数曲线) 3、相量法(用复数表示正弦电量的方法) (1)复数与正弦量的关系
U m e j (wt + ) U m [cos(wt + ) + j sin(wt + )]
特殊相位关系：
u, i
u i O u, i u O u, i u iw t
交流电瞬时电压表达式
交流电瞬时电压表达式交流电是我们日常生活中常见的一种电流形式。
与直流电不同，交流电的电流方向随时间变化，因此交流电的电压也会随时间变化。
为了描述交流电的瞬时电压，我们需要使用特定的表达式。
瞬时电压是指在某一时刻的电压值，它能够描述电压在时间轴上的变化情况。
在交流电中，电压的变化是周期性的，即电压值会按照一定的规律不断重复。
为了表达这种周期性变化的瞬时电压，我们可以使用三角函数来进行描述。
在交流电中，电压的周期性变化可以用正弦函数来表示。
正弦函数是一种周期性变化的函数，它的图像呈现出一条连续的波形。
正弦函数的表达式为：V(t) = Vm * sin(ωt + φ)其中，V(t)表示在时刻t的瞬时电压值；Vm表示电压的最大值，也称为峰值电压；ω表示角频率，它与电压的频率有关；t表示时间；φ表示相位差。
正弦函数的图像是一条波形，波形的形状和特征与正弦函数的参数有关。
其中，Vm决定了波形的振幅，即波形的最大值和最小值之间的差异；ω决定了波形的周期，即波形重复出现的时间间隔；φ决定了波形在时间轴上的位置，即波形相对于原点的偏移量。
通过正弦函数的表达式，我们可以计算出交流电在任意时刻的瞬时电压值。
例如，假设电压的最大值为220V，频率为50Hz，相位差为0，我们可以得到交流电在某一时刻的瞬时电压值。
在实际应用中，我们通常使用有效值来描述交流电的电压。
有效值是指在一定时间内，交流电的平均功率与直流电相同所需的电压值。
有效值可以通过峰值电压除以根号2来计算：Veff = Vm / √2有效值是交流电的一种重要描述方式，它可以更好地反映交流电的实际能量传输情况。
总结一下，交流电的瞬时电压可以使用正弦函数来进行表达，通过正弦函数的参数可以描述交流电的振幅、频率和相位差。
交流电的有效值是一种重要的描述方式，它可以更好地反映交流电的实际能量传输情况。
通过对交流电瞬时电压的表达式的理解，我们可以更好地理解交流电的特点和应用。
单相正弦交流电路三要素
正弦交流电的三要素
角频率：
i＝Imsin（ωt+ ）
0
i
Im
角频率
T
ωt
i
Im
T
表示正弦电流变化的快慢，还有周期T和频率f。
正弦交流电的三要素
初相位：
i＝Imsin（ωt+ ）
0
i
Im
相位
初相位就是波形起点至坐标原点的角度。 >0,波形“起点”在原点的左边， <0,波形“起点”在原点的右边， 初相位的绝对值不大于π。
φ i
φ u
φ
两个同频率交流电的相位之差。用来φ表示。
φ=φu- φi
相位差等于初相位之差。
u
若φ>0，则电压u先到达正（或负）的最大值，称电压u超前电流i，或称电流i滞后电压u。
02
若φ<0，则电流i先到达正（或负）的最大值，称电流i超前电压u，或称电压u滞后电流i。
03
若φ=0，则电压u与电流i同时到达正（或负）的最大值，称电压u与电流i同相。
正弦电压和电流
实际方向和参考方向一致
实际方向和参考方向相反
＋
－
正半周 实际方向和参考方向一致
负半周 实际方向和参考方向相反
正弦交流电的电压和电流是按照正弦规律周期性变化的。
数学表达式：
i＝Imsin（ωt+ ）
0
i
Im
T
ωt
i
Im
T
在正弦交流电路中各支路的电流、电压都是时间t的正弦函数，分别用英文小写字母“i”和“u”表示。
ωt
i
Im
相位：表示正弦量的变化进程，也称相位角。 初相位：t =0时的相位。
正弦交流电的瞬时值表达式与三要素
正弦交流电的瞬时值表达式与三要素
一正弦电流的波形，其数学表达式为：正弦电流的波形i=Imsin（ωt+φ）
式中Im——幅值；
φ——初相位；
ω——角频率。
幅值、初相位和角频率统称为正弦量的三要素。
正弦量在任一瞬间的值称为瞬时值，已知正弦量的三要素，即可确定正弦量的瞬时值。
（1）幅值
正弦量瞬时值中的最大值称为幅值，表示交流电的强度，用Im表示。
（2）角频率
在单位时间内正弦量变化的角度称为角频率，反映了正弦量的变化快慢程度，用W表示，单位为弧度每秒（rad/s）。
正弦量变化快慢还可用频率和周期表示。
正弦量变化一次所需时间称为周期，用T表示，单位为秒（s）。
每秒内正弦量变化的次数称为频率，用f表示，单位为赫兹（Hz）。
（3）初相位
随时间变化的角度（ωt+φ）称为正弦量的相位。
如果已知正弦量在某一时刻的相位，就可以确定这个正弦量在该时刻的数值、方向及变化趋势，因此相位表示了正弦量在某一时刻的状态。
不同的相位对应正弦量的不同状态，所以相位还反映出正弦量变化的进程。
电工技术：正弦交流电的相量表示法
同频率正弦量的相量运算：知识点小结
两个同频率的正弦交流电相加（减）： 方法一：都化成相量，变为复数的相加（减） 方法二：相量图法（平行四边形或首尾相接法）
正弦交流电的相量表示法
正弦交流电有哪些表达形式？
（1）正弦函数（瞬时值表达式）如
i I m sin (ω t ψ )
Im
（2）正弦曲线波形，如
i
-Im
O
2
T
t
t
这两种表达形式直观，但运算繁琐，绘制困难。
正弦交流电为什么要用相量表示？
两个正弦量
i1 2 I1m sin ( t 1 )
实际应用更多的是有效值形式的相量表示！
一、正弦量的相量表示法
2.注意事项 （1）表示正弦量的复数称相量
（2）相量只是表示正弦量，而不等于正弦量。
u U m sin ( ω t ψ) ＝
（3）一个正弦量与一个复数是一一对应的关系。 （4）只有正弦周期量才能用相量表示，相量不能表示非正弦周期量。
u2 110 2sin(ω t 450 ) V
(2) 相量图
+j
U 2
U2
超前 U1
U 1
+1
45 20
正弦交流电的相量表示法（1）：知识点小结
（1）正弦交流电用相量（复数）表示方法
u U m sin ( ω t ψ )
（2）相量图
U U ψ
U
ψ
正弦交流电的相量运算
同频率正弦量的相量运算
• 同频率正弦量相加减
同频率的两个正弦量相位差为一些 特殊角时，用相量图中的几何关系 很方便求相量和、相量差。 例:题3： 已知 解：
正弦电路的电压电流及相量表示
解：电压u（t）与电流i1（t）的相位差为
=（-180o）-（- 45o ）= -135o＜0
所以u（t）滞后i1（t）135o 。
电压u（t）与电流i2（t）的相位差为
= -180o - 60o = -240o 由于规定||≤π，所以u（t）与i2（t）的相位 差应为 = -240o+360o = 120o＞0，因此u（t）超前 i2（t）120o 。
四、正弦量的有效值 有效值的提出： 正弦量的有效值是根据它的热效应确定的。以正 弦电压u（t）为例，它加在电阻R两端，如果在一个 周期T内产生的热量与一个直流电压U加在同一电阻上 产生的热量相同，则定义该直流电压值为正弦电压 u （t）的有效值。用大写字母“U”表示。 有效值的定义式：
1 U T
本讲作业
1、复习本讲内容；
2、预习下一讲内容——正弦电路的相量分析法； 3、书面作业：习题8-1，8-2，8-4，8-5。
8.2 正弦量的相量表示
一、相量表示法的提出 前面学过的解析式（三角函数表示法）和正弦量 的波形图（正弦曲线表示法）都不便于分析计算正弦 电路。为了解决这个问题，引入了正弦量的第三种表 示方法——相量表示法。 二、相量表示法采用的形式 相量表示法，实际上采用的是复数表示形式。
三、相量表示方法 模等于正弦量的有效值（或振幅），幅角等于 正弦量的初相的复数，称为该正弦量的相量。相量 用该正弦量的符号上加一圆点“ · ”来表示，说明它 是时间的函数，以便与一般复数相区别。 振幅相量 相量的模为正弦量的振幅，称振幅相量，以 I m 、 Um 等表示。其振幅相量表达式为
将u3（t）的解析式整理如下： u3（t）= 5cos（100πt + 60o） = 5sin（100πt + 60o + 90o） = 5sin（100πt + 150o ）V 所以得到
正弦交流电的三种表示法
u2 U m sin(t ) V 200sin(100 t
u1 U m sin(t ) 250sin (100 t )
3
)V
小结：
i I m sin
最大值
t 0
初相位
角频率
周期
i
最大值
Im
T
t
初相位 0
I m 最大值
0
初相位
作业：
i/A 1.6
I m 1.6A
0
最大值
i I m sin(t ) 1.6sin (100 t )
0.02
0.01
初相位 i 0
周期T
T 0.02 Hz
注意： t/s 在波形图 中一般不能直 接读出角频率 ω。 可通过周 期T或频率f来 求出角频率ω。
3、矢量图表示法：用有向线段表示
u1
u2
3
0.01 0 0.02
t/s
u/V 250
200
u1 u2
0.01
3
0
0.02
t/s
解：1）
U m1 250V
u1 0
2） U m2 200V
u 2
3
2 2 1 100 rad / s T 0.02
T1 0.02S
2 1 100 rad / s
u Um sin（ t +/2）
u Um
u Um sin（ t -/2）
t
-/2 /2 3/2 2 5/2
小规律： 若起点在坐标原点（或纵轴）的左侧， 0 >0； 若起点在坐标原点（或纵轴）的右侧， 0 <0。
u1 U m sin(t ) 250sin (100 t )
3
)V
小结：
i I m sin
最大值
t 0
初相位
角频率
周期
i
最大值
Im
T
t
初相位 0
I m 最大值
0
初相位
作业：
i/A 1.6
I m 1.6A
0
最大值
i I m sin(t ) 1.6sin (100 t )
0.02
0.01
初相位 i 0
周期T
T 0.02 Hz
注意： t/s 在波形图 中一般不能直 接读出角频率 ω。 可通过周 期T或频率f来 求出角频率ω。
3、矢量图表示法：用有向线段表示
u1
u2
3
0.01 0 0.02
t/s
u/V 250
200
u1 u2
0.01
3
0
0.02
t/s
解：1）
U m1 250V
u1 0
2） U m2 200V
u 2
3
2 2 1 100 rad / s T 0.02
T1 0.02S
2 1 100 rad / s
u Um sin（ t +/2）
u Um
u Um sin（ t -/2）
t
-/2 /2 3/2 2 5/2
小规律： 若起点在坐标原点（或纵轴）的左侧， 0 >0； 若起点在坐标原点（或纵轴）的右侧， 0 <0。
正弦交流电基本概念
310sin(314t 300 )(V )
i Im sin(t i ) Im sin(2 ft i )
14.1sin(314t 600 )( A)
(2) u i 300 (600 ) 900
答：电压和电流的瞬时值表达式分别是310sin(314t+300)V， 14.1sin(314t-600A ，正弦电压和电流的相位差是900 。
u1与u4同相，即相位差为零。
【例】某正弦电压的最大值Um=310V,初相 φ u=300;某正ቤተ መጻሕፍቲ ባይዱ电流的最大值Im=14.1A,初相
φ i=-600。它们的频率均为50Hz。（1）分别 写出电压和电流的瞬时值表达式。（2）正弦电 压和电流的相位差。
解： (1) u Um sin(t u ) Um sin(2 ft u )
《正弦交流电的基本概念》
轮机系
单相交流电路的基本概念
大小和方向均随时间变化的电压或电流称为交流电。如
等腰三角波
矩形脉冲波
正弦波
其中，大小和方向均随时间按正弦规律变化的电压或电 流称为正弦交流电。
了解和掌握正弦交流电的特点，学会正弦交流电路的基 本分析方法，是本节课学习的目的。
1. 正弦交流电的频率、周期和角频率
则: i 1.84sin(100t 2 ) 当t=0.5s时： i 1.84sin(50 23)
3 1.84sin(1200 ) 1.59(A)
答：初相位是2π/3 rad，t=0.5s时的瞬时值是1.59A。
4 正弦交流电的表示方法
前提：在分析正弦交流电路时，同一电路中的 所有电压、电流都是同频率的正弦量， 且频率与电源的频率相同。
i Im sin(t i ) Im sin(2 ft i )
14.1sin(314t 600 )( A)
(2) u i 300 (600 ) 900
答：电压和电流的瞬时值表达式分别是310sin(314t+300)V， 14.1sin(314t-600A ，正弦电压和电流的相位差是900 。
u1与u4同相，即相位差为零。
【例】某正弦电压的最大值Um=310V,初相 φ u=300;某正ቤተ መጻሕፍቲ ባይዱ电流的最大值Im=14.1A,初相
φ i=-600。它们的频率均为50Hz。（1）分别 写出电压和电流的瞬时值表达式。（2）正弦电 压和电流的相位差。
解： (1) u Um sin(t u ) Um sin(2 ft u )
《正弦交流电的基本概念》
轮机系
单相交流电路的基本概念
大小和方向均随时间变化的电压或电流称为交流电。如
等腰三角波
矩形脉冲波
正弦波
其中，大小和方向均随时间按正弦规律变化的电压或电 流称为正弦交流电。
了解和掌握正弦交流电的特点，学会正弦交流电路的基 本分析方法，是本节课学习的目的。
1. 正弦交流电的频率、周期和角频率
则: i 1.84sin(100t 2 ) 当t=0.5s时： i 1.84sin(50 23)
3 1.84sin(1200 ) 1.59(A)
答：初相位是2π/3 rad，t=0.5s时的瞬时值是1.59A。
4 正弦交流电的表示方法
前提：在分析正弦交流电路时，同一电路中的 所有电压、电流都是同频率的正弦量， 且频率与电源的频率相同。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
i
T
0.03
t
0.04
0
0.01
0.02
T
T=0.02s
2 2 f 2 50 100 T
1 1 f 50 Hz T 0.02
3.初相位
5.1.3 正弦交流电的三要素
i I m sin t
i
i
Im
t
称为初相位或初相角。
i
Im
i1
Im
0
u/V 250 200 u2 u1
3
0.01 0 0.02
t/s
u/V 250
5.1.3 正弦交流电的三要素
200
u2
u1
3
0.01 0 0.02
t/s
解：1）
U m1 250V
u1 0
2） U m2 200V
u 2
3
2 2 1 100 rad / s T 0.02
T1 0.02S
2 1 100 rad / s
u2 U m sin(t ) V 200sin(100 t
u1 U m sin(t ) 250sin (100 t )
3
)V
5.1.3 正弦交流电的三要素
小结：
正弦交流电的三要素:
i I m sin
Im为正弦电流的最大值， 又称振幅值。
i(A )4 Im
0
注意： 电量名称必 须大写,下标加m， 如： Im、
Em
Um 、
e(V)
Im =4A
t （s）
14.1
Em =14.1V t(s)
-14.1
5.1.3 正弦交流电的三要素
2.角频率ω
i I m sin t
角频率ω
交流电每秒内变化的电度数称为角频率，用 字母“ω”表示。单位：弧度/秒（rad/s）
i/A
Im
注意： 在波形图中 一般不能直接读 出角频率ω。 可通过周期 T或频率f来求出 角频率ω。
T
0
0.01
T
0.02
0.03
t/s
2 2 f T
1 f T
周期T： 变化一周所需的时间。 频率f：每秒变化的周期数。
单位：秒(s) 单位：赫兹（Hz）
5.1.3 正弦交流电的三要素
角频率
周期 T
初相位
t
作业：
课本160页
5-1-6
谢谢！
i=Imsin(ωt -π/3)
小规律： 若起点在坐标原点（或纵轴）的左侧，
> 0； < 0。 若起点在坐标原点（或纵轴）的右侧，
5.1.3 正弦交流电的三要素
总结：
正弦交流电的三要素
i I m sin t
最大值
i
最大值 Im
角频率
2 2f T
周期T
初相位
i/A 1.6
I m 1.6A
0.01 0
最大值
i I m sin(t ) 1.6sin (100 t )
0.02
t/s
初相位 i 0
周期T
T 0.02 Hz
5.1.3 正弦交流电的三要素
例
已知两个同频正弦交流电压的波形图
如下图所示, 试写出u1及u2的瞬时值表达式。
)
6
小技巧：i I m sin t sin前面的值为最大值； t前面的值为角频率ω ； t后面的值为初相位 。
5.1.3 正弦交流电的三要素
例
已知某正弦交流电流的波形图如下图
解： 2 2 100 rad / s T 0.02
i
所示, 试写出电流的三要素和瞬时值表达式i。
正弦交流电的表示方法：
瞬时值表达式 （一般形式）
u U m sin t u e Em sin t e
必须小写
i I m sin t i
i
波形图
t
矢量表示法
5.1.3 正弦交流电的三要素
1.最大值或振幅
i I m sin t
6
, 请写出瞬时值表达式。
5.1.3 正弦交流电的三要素
课堂巩固练习
习题2：已知某正弦交流电流的振幅为2A,频率为50Hz，
初相角为
6 解：已知
, 请写出瞬时值表达式。
I m 2A
i
6
f 50Hz
2f 2 50 100 rad / s
i I m sin t 2sin (100
量的三要素。 解：根据 u U m sin t u
最大值： Um =220 2 V, 角频率：ω=314 rad/s, 初相位： u
4
小技巧：
i I m sin t
sin前面的值为最大值； t前面的值为角频率ω ； t后面的值为初相位
。
习题2：已知某正弦交流电流的振幅为2A,频率为50Hz， 初相角为
正弦交流电的三要素
5.1.3 正弦交流电的三要素
目的与要求：
掌握正弦交流电的三要素
重点与难点：
重点：正弦交流电的三要素 难点：交流电的波形图
5.1.3 正弦交流电的三要素
正弦交流电
正弦交流电：电流或电压、电动势的大小和 方向随时间按正弦规律变化的交流电。
想一想：正弦交流电有哪些表示方法呢？
5.1.3 正弦交流电的三要素
i2
i3
0
t
0
t
说明：
给出了观察正弦波的起点或参考点。
几种不同起点的正弦电流波的初相位：
i
i I m sin t
i
5.1.3 正弦交流电的三要素
Im
i1
i
Im
0
i2
Im
t
i3
0
t
3
0
3
t
0
3
3
i=Imsin(ωt)
i=Imsin(ωt+π/3)
初相位
t
找到问题了吗？
I 5 sin100t A 6
u U sin1000 t A 3
例
已知： i 3 sin1000 t A 6
写出表达式的三要素。
5.1.3 正弦交流电的三要素
幅度：
I m 3A
6
小技巧：
i I m sin t
角频率： 1000 rad/s 初相位：
sin前面的值为最大值； t前面的值为角频率ω ； t后面的值为初相位
。
5.1.3 正弦交流电的三要素
习题1：已知u=220 2 sin(314t- ) V, 请写出这个正弦
课堂巩固练习
4