数学归纳法证明整除
数学归纳法及应用举例

数学归纳法及应用举例重点难点分析:(1)第一步递推基础,第二步是递推依据,密切相关缺一不可。
(2)归纳思想充分体现了特殊与一般的思想,数学归纳法体现了有限与无限的辩证关系与转化思想。
(3)归纳—猜想—证明是经常运用的数学方法,观察是解决问题的前提条件,需要进行合理的试验和归纳,提出合理猜想,从而达到解决问题的目的。
(4)数学归纳法的应用通常与数学的其它方法联系在一起,如比较、放缩、配凑、分析和综合法等。
典型例题:例1.证明:=-n(n+1)(4n+3)。
证明:①当n=1时,左,右=-1(1+1)(4+3)=-14,等式成立。
②假设n=k时等式成立,即=-k(k+1)(4k+3)。
n=k+1时,+[(2k+1)(2k+2)2-(2k+2)(2k+3)2] =-k(k+1)(4k+3)-2(k+1)(4k2+12k+9-4k2-6k-2) =-(k+1)[4k2+3k+2(6k+7)]=-(k+1)(4k2+15k+14)=-(k+1)(k+2)(4k+7)=-(k+1)[(k+1)+1][4(k+1)+3],等式成立。
由①②知,当n∈N′时等式成立例2.试证S n=n3+(n+1)3+(n+2)3能被9整除。
证明:①n=1时,S1=4×9,能9整除。
②假设,n=k时,S k能被9整除,则S k+1=(k+1)3+(k+2)3+(k+3)3=S k+(k+3)3-k3=S k+9(k3+3k+3)由归纳假设知S k+1能被9整除,也就是说n=k+1时命题也成立。
综上所述:命题成立。
点评:用数学归纳法证明整除问题时,关键是把n=k+1时的式子分成两部分,其中一部分应用归纳假设,另一部分经过变形处理,确定其能被某数(某式)整除。
例3.通过一点有n个平面,其中没有任何3个平面交于同一条直线,用数学归纳法证明这些平面把空间分成(n2-n+2)个部分。
证明:设适合条件的n个平面把空间分成p n个部分,∴p n=n2-n+2①当n=1时,p1=1-1+2=2,显然符合条件,故命题成立。
数学归纳法

5.由 k 到 k+1 这一步,要善于分析题目的结构特点,进行适 当的变形,常用分析、添项、拆项、作差等方法.
6.用不完全归纳法给出结论,用数学归纳法给出证明是高考题 中经常出现的题型,希望同学们用心体会.
7.本节内容是选修与选考内容,在复习时要注意把握好难度 能证明一些简单的数学命题就可以了.
用数学归纳法证明与正整数n有关的等式 用数学归纳法证明:2×1 4+4×1 6+6×1 8+…+2n21n+2 =4nn+1. 【思路分析】 本题主要考查用数学归纳法证明等式的步骤, 注意当 n=k+1 时,两边加上的项和结论各是什么.
【证明】 (1)当 n=1 时,左边=2×1 4=18,右边=18等式成立. (2)假设 n=k 时,2×1 4+4×1 6+6×1 8+…+2k21k+2=4k+k 1成立. 当 n=k+1 时, 2×1 4+4×1 6+6×1 8+…+2k21k+2+2k+212k+4 =4k+k 1+4k+11k+2=4kk+k+12k++12 =4k+k+11k+2 2=4kk++12=4[k+k+11+1] ∴n=k+1 时,等式成立. 由(1)(2)可得对一切正整数 n∈N*,等式成立.
【名师点睛】 数学归纳法证题的两个步骤缺一不可.证 n=k+1 成立时,必须用 n=k 成立的结论,否则,就不是数学 归纳法证明.
1.用数学归纳法证明: 1·n+2(n-1)+3(n-2)+…+(n-1)·2+n·1=16n(n+1)(n+2). 证明:(1)当 n=1 时,左边=1, 右边=16(1+1)(1+2)=1,等式成立. (2)假设 n=k 时,1·k+2(k-1)+3(k-2)+…+(k-1)·2+k·1= 16k(k+1)(k+2)成立.
(2)假设 n=2k(k∈N*)时,命题成立, 即 x2k-y2k 能被 x+y 整除. 当 n=2k+2 时,x2k+2-y2k+2=x2·x2k-y2·y2k =x2(x2k-y2k)+y2k(x2-y2) =x2(x2k-y2k)+y2k(x+y)(x-y). ∵x2(x2k-y2k)、y2k(x+y)(x-y)都能被 x+y 整除, ∴x2k+2-y2k+2 能被 x+y 整除,即 n=2k+2 时命题成立. 由(1)(2)知原命题对一切正偶数均成立. 【名师点睛】 因证明的命题对所有正偶数成立,所以归纳假 设中采用了 n=2k(k∈N*)与它相邻的是 n=2k+2.要注意体会 n =2k+2 时的变形方法.
数学归纳法教案

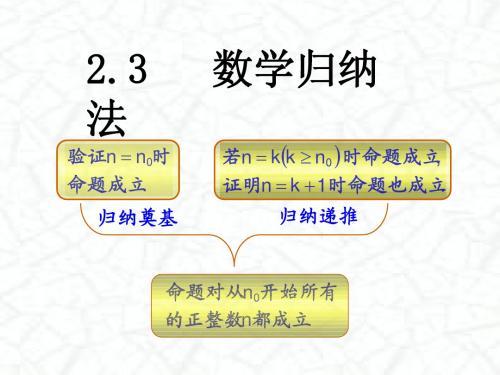
数 学 归 纳 法要点回顾:归纳法是一种由特殊到一般的推理方法,它可以分为完全归纳法和不完全归纳法两种,完全归纳法只局限于有限个元素,而不完全归纳法得出的结论不一定可靠,数学归纳法属于完全归纳法;应用数学归纳法证明的两个步骤: (1)证明当n 取第一个值n 0时结论正确,(2)假设n=k (k ∈N ※,k ≥n 0)时结论正确,证明当n=k+1时结论也正确。
用数学归纳法证题的两个步骤缺一不可,在完成了以上两个步骤以后,就可以断定命题对于从n 0开始的所有正整数n 都正确。
数学归纳法的核心:在验证命题n=n 0正确的基础上,证明命题具有传递性,而第二步实际上是以一次逻辑的推理代替了无限的验证过程.所以说数学归纳法是一种合理、切实可行的科学证题方法,实现了有限到无限的飞跃。
“数学归纳法”中包含着递推思想、类比思想、分类思想、归纳思想.由于数学归纳法是证明与正整数有关的命题,数列是定义在正整数集或其子集上的特殊函数,而导数又是研究函数的重要工具,另外不等式具备传递性,正是这一条知识链注定了数学归纳法必然以数列、不等式、函数与导数等内容为背景。
分析近几年与数学归纳法相关的高考试题,不难得出其命题特点:(1)数学归纳法中的 “归纳—猜想—证明”这一基本思想与方法,考试中可以以各种题型出现,复习中仍需加以重视.但很少单独命制大题,往往作为解答题中某一小问的形式出现,重在体现它的工具性作用。
且常与数列结合去考查,有时还与函数、导数、不等式等内容相关联,以体现“在知识交汇处设计试题”的命题原则。
(2)试题特别注重加强对不完全归纳法的考查,既要求归纳发现结论,又要求能证明结论的正确性,初步形成“观察—归纳—猜想—证明”的思维模式。
(3)高考对数学归纳法主要是‘隐形’考查,也就是说这种方法在题目中往往是“藏而不露”,不明说要用“数归法”,但通常可用“数归法”,也可用其它方法来解决(如果能找到其它解决方法的话)。
数学归纳法证明经典事例

数学归纳法证明经典事例数学中的归纳法是很有作用的,关于这些的整除证明是怎样的呢?下面就是店铺给大家整理的数学归纳法证明整除内容,希望大家喜欢。
数学归纳法事例1当n=1 的时候上面的'式子 = 3^4-8-9=64成立假设当n=k 的时候3^(2k+2)-8k-9能够被64整除当n=k+1式子= 3^(2k+4)-8k-17=9[3^(2k+2) -8k-9] +64k+64因为 3^(2k+2)-8k-9能够被64整除∴ 9[3^(2k+2) -8k-9] +64k+64 能够被64整除n=k+1 时,成立根据上面的由数学归纳法3的2n+2次方-8n-9(n属于N*)能被64整除。
数学归纳法事例2n=1时 3^4-8-9=81-17=64 能被4整除·····(特殊性)设当n=k时,仍然成立。
当n=k+1时,·····················(一般性)3^(2(k+1)+2)-8(k+1)-9=3^(2K+2+2)-8K-17 =9*3^(2K+2)-72K+64K-81+64=9(3^(2k+2)-8k-9)+64k+64因为3^(2k+2)-8k-9能被64整除不用写了吧··正确请采纳数学归纳法当n=1 的时候上面的式子 = 3^4-8-9=64成立假设当n=k (k>=1)数学归纳法事例3当3^(2k+2)-8k-9能够被64整除当n=k+1(k>=1)式子= 3^(2k+4)-8k-17=9[3^(2k+2) -8k-9] +64k+64由9[3^(2k+2) -8k-9] +64k+64-(3^(2k+2)-8k-9)可以被64整出n=k+1 时,成立根据上面的由数学归纳法3的2n+2次方-8n-9(n属于N*)能被64整3.证明:对于任意自然数n (3n+1)*7^n-1能被9整除数学归纳法(1)当n=1时 (3*1+1)*7-1=27能被9整除(2)假设当n=k时 (3k+1)*7^k-1能被9整除则当n=k+1时 [3(k+1)+1]*7^(k+1)-1=[21k+28]*7^k-1=(3k+1)*7^k-1+(18k+27)*7^k=[(3k+1)*7^k-1]+9(2k+3)*7^k括号中的代数式能被9整除 9(2k+3)*7^k能被9整除所以当n=k+1时 [3(k+1)+1]*7^(k+1)-1能被9整除综合(1)(2)可知对于任意自然数n 有(3n+1)*7^n-1能被9整除【数学归纳法证明经典事例】。
2.3数学归纳法(1)
n∈ N
*
成立。
二、数学归纳法 证明整除性问题
(3
例1:证明
1
n+
1 ) 7
n
能被9 − 能被9整除
1
(
n∈ N
*
)
1 ,( 3 1 ) 7 1 (3 1 1 ) 71 1 = 2 7 3 9 , n n+ 证 明 :( ) 当 n = 时 − = × + − = ×
分奇偶讨论: 分奇偶讨论:
= 2
(
k+
*
1 )[(
k+
1 )
+
1 ]
个部分,所以对n=k+1时,猜想成立。
根据(1)和(2)可知猜想对于任何 n∈ N
都成立。
证明不等式问题(适当放缩) 四、数学归纳法 证明不等式问题(适当放缩)
五、数学归纳法 证明数列中的猜想与不等式问题
例1:课本P84 课本P84 B组 B组 1.
五、数学归纳法 证明数列中的猜想与不等式问题
(
k+ 1 ∴ n = k+ 时命题成立。
根据(1)和(2)可知等式对任何
=
1 -1 ] = k 2 + ( k+ ) 2 1 = k + k+ ( 1 )2
+ [+ 2 2
+ ⋅⋅⋅+ (
2
[2 - 1 1 - 1 ] k )+ ( k + )
n∈ N
*
成立。
一、数学归纳法 证明等式
2 例 .
用数学归纳法证明 1 2 2 1 * n + 1 1 . an + 1 + a+ a + + a = ( a≠ n∈ N ),
连加号 整数的整除性理论 数学归纳法

首页
上页
下页
返回
结束
22
设a 0, b是a的因数, 如果b a, b 1, 则称 b是a的真因子.
定义 设a是大于1的整数, 如果除去1和本身外, a没有其它因子(即a没有真因子), 则称a为素数(或质 数), 否则a叫做合数.
由定义可知, 如果素数 p表示成 p a b, 则必有 a 1, b p或a p, b 1.
设a, b是两个整数. 如果整数d 适合 : d | a, d | b, 则 称d 是a, b的一个公因子(公因数).
定义 设d 是a, b的一个公因子, 如果a, b的任一公 因子都是d的因子, 则称d 是a, b的一个最大公因子(最 大公因数).
最大公因子可描述为:
d 是a, b的最大公因子 (1) d | a, d | b; (2) 若h | a, h | b, 则h | d .
首页 上页 下页 返回 结束
18
辗转相除法
设a, b是任意两个正整数, 反复运用带余除法: a q1b r1 , 0 r1 b,
b q2 r1 r2 , r1 q3 r2 r3 ,
rk 2 qk rk 1 rk ,
0 r2 r1 , 0 r3 r2 ,
第一型数学归纳法原理 设有一个与自然数n 有关的命题, 如果 : 1 当n 1时命题成立; 2 假设n k时命题成立, 则n k 1时命题也 成立, 那么这个命题对于一切自然数n都成立.
首页 上页 下页 返回 结束
6
注:
1) 数学归纳法就是一种用“有限”解决“无限” 的数学思维方法,它是一种既重要又很有用的数学证 明方法. 2) 用数学归纳法证明命题的两个步骤是缺一不 可的,第一步是递推的基础,第二步是递推的依据.第 一步说明n从何数起,命题成立,起奠基作用,如果只有 步骤二而没有步骤一,就有可能得出不正确的结论.
数学归纳法的原理及应用

浅谈数学归纳法的原理及应用姓名:王磊峰单位:砀山县豆集学区范套小学浅谈数学归纳法的原理及应用摘要:数学归纳法是证明与自然数有关命题的一种论证方法,也是数学证明中的一个强有力的工具,无论在初等数学还是高等数学中都有广泛的应用。
本文讨论了数学归纳法的理论依据、应用功能以及应用数学归纳法应注意的问题等。
关键词:数学归纳法;匹阿诺公理;应用;推理;命题;类型数学归纳法是数学中最基本也是最重要的证明方法之一,它在各个数学领域分支中都有极大的应用,因为使用面比较广,所以涉及的知识和技巧比较多,在本文中将介绍数学归纳法的产生、发展和确立并分别举例说明数学归纳法在各个方面的应用。
1数学归纳法的产生、发展和确立1.1数学归纳法的产生数学归纳法的产生经历了一个较长的历史时期,一般认为归纳推理可追溯公元六世纪的毕达哥拉斯时代。
这一时代杰出的数学家毕达哥拉斯利用点子数对级数求和问题进行了探讨,利用经过剖分后的正方形的直观形象,他确信无疑地得出:135+++ (2)-=,这里n n(21)有明显的推理过程,但这种推理只是简单枚举而没有碰到矛盾事实的归纳结果,因此是不完全的归纳推理,或者说只是一种寻求结论的手段,它只是作为一种猜想或假说,而不是可靠的,尽管如此,他仍为数学归纳法的产生奠定了一定的基础。
可靠的归纳推理是欧几里得对系数个数无穷的证明,虽然其中递推过程不甚明显,但基本思想却是按递推归纳原理指导的。
肯定地说,这一关于系数个数无穷的具体证明为后人对数学归纳法的认识提供了原形,促使人们加深了对数学归纳法的理解。
16世纪,经过文艺复兴洗礼的欧洲学者越来越意识到数学的重要性。
意大利数学家毛罗利科首先对全体自然数有关的命题的证明做了深入考察,他认为递归推理是指首先确定命题对于第一个自然数是真的,然后再去验证命题具有后继数也是真的。
于是,根据递推特性,命题对于第一个自然数的后继数为真,则对于第二个自然数也为真;对于第二个自然数为真,则对于第三个自然数也为真。
数学归纳法证明的原理

数学归纳法证明的原理2020-12-07数学归纳法证明的原理数学归纳法证明的原理数学归纳法证明的是与自然数有关的命题,它的依据是皮亚诺提出的自然数的序数理论,就是通常所说的自然数的皮亚诺公理,内容是:(1)l是自然数。
(2)每个自然数a有一个确定的“直接后继”数a’,a也是自然数。
(2)a’≠1,即1不是任何自然数的“直接后继”数。
(4)由a’=b’,推得a=b,即每个自然数只能是另外的唯一自然的“直接后继”数。
(5)任一自然数的集合,如果包含1,并且假设包含a,也一定包含a的“直接后继”数a’,则这个集合包含所有的自然数。
皮亚诺公理中的(5)是数学归纳法的依据,又叫归纳公理数学归纳法的应用及举例。
因为由假设知42k+1+3k+2能被13整除,1342k+1也能被13整除,这就是说,当n=k+1时,f(k+l)能被13整除。
根据(1)、(2),可知命题对任何n∈N都成立。
下面按归纳步中归纳假设的形式向读者介绍数学归纳法的几种不同形式以及它们的应用。
(l)简单归纳法。
即在归纳步中,归纳假设为“n=k时待证命题成立”。
这是最常用的一种归纳法,称为简单归纳法,大家都比较熟悉,这里不再赘述。
(2)强归纳法。
这种数学归纳法,在归纳步中,其归纳假设为“n≥k时待证命题成立”。
我们称之为强归纳法,又叫串值归纳法。
通常,如果在证明p(n+l)成立时,不仅依赖于p(n)成立,而且还可能依赖于以前各步时,一般应选用强归纳法,下面举例说明其应用。
例有数目相等的两堆棋子,两人轮流从任一堆里取几项棋子,但不能不取也不能同时从两堆里取,规定凡取得最后一项者胜。
求证后者必胜。
证:归纳元n为每堆棋子的数目。
设甲为先取者,乙为后取者。
奠基n=l,易证乙必胜。
归纳设Nn≤k时,乙必胜。
现证n=k+l时也是乙必胜。
设甲在某堆中先取r颗,O<r≤k。
乙的对策是在另一堆中也取r颗。
有二种可能:(1)若r<k,经过两人各取一次之后,两堆都只有k-r颗,k-r<k,现在又轮到甲先取,依归纳假设,乙必胜。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
数学归纳法证明整除
数学归纳法证明整除数学归纳法
当n=1 的时候
上面的式子 = 3^4-8-9=64
成立
假设当n=k 的时候
3^(2k+2)-8k-9能够被64整除
当n=k+1
式子= 3^(2k+4)-8k-17
=9[3^(2k+2) -8k-9] +64k+64
因为 3^(2k+2)-8k-9能够被64整除
∴ 9[3^(2k+2) -8k-9] +64k+64 能够被64整除
n=k+1 时,成立
根据上面的由数学归纳法
3的2n+2次方-8n-9(n属于N*)能被64整除。
2
当n=1时 3^4-8-9=81-17=64 能被4整除·····(特殊性)
设当n=k时,仍然成立。
当n=k+1时,·····················(一般性)
3^(2(k+1)+2)-8(k+1)-9=3^(2K+2+2)-8K-17 =9*3^(2K+2)-72K+64K-
81+64=9(3^(2k+2)-8k-9)+64k+64
因为3^(2k+2)-8k-9能被64整除
不用写了吧··
正确请采纳
数学归纳法
当n=1 的时候
上面的式子 = 3^4-8-9=64
成立
假设当n=k (k>=1)
3^(2k+2)-8k-9能够被64整除
当n=k+1(k>=1)
式子= 3^(2k+4)-8k-17
=9[3^(2k+2) -8k-9] +64k+64
由9[3^(2k+2) -8k-9] +64k+64-(3^(2k+2)-8k-9)可以被64整出n=k+1 时,成立
根据上面的由数学归纳法
3的2n+2次方-8n-9(n属于N*)能被64整
3.证明:对于任意自然数n (3n+1)*7^n-1能被9整除
数学归纳法
(1)当n=1时 (3*1+1)*7-1=27能被9整除
(2)假设当n=k时 (3k+1)*7^k-1能被9整除
则当n=k+1时 [3(k+1)+1]*7^(k+1)-1=[21k+28]*7^k-1
=(3k+1)*7^k-1+(18k+27)*7^k
=[(3k+1)*7^k-1]+9(2k+3)*7^k
括号中的代数式能被9整除 9(2k+3)*7^k能被9整除
所以当n=k+1时 [3(k+1)+1]*7^(k+1)-1能被9整除
综合(1)(2)可知对于任意自然数n 有(3n+1)*7^n-1能被9整除4证明:
(1)n=1时,3^(6n)-2^(6n) =3^6-2^6=665=19*35,命题成立
(2)假设n=k时命题成立,即
35能整除3^(6k)-2^(6k)
即3^(6k)-2^(6k)=35m (m∈Z+)
则n=k+1时
3^(6n)-2^(6n)
=3^(6k+6)-2^(6k+6)
=(3^6)*3^(6k)-(2^6)*2^(6k)
=64*[3^(6k)-2^(6k)]+(729-64)*3^(6k)
=64*[3^(6k)-2^(6k)]+665*3^(6k)
=64*35m+19*35*3^(6k)
=35*[64m+19*3^(6k)]
即n=k+1时,35能整除3^(6n)-2^(6n)
综合(1)(2)由数学归纳法知:
对于一切正整数n,35能整除3^(6n)-2^(6n)
===============
给定任意正整数n,设d(n)为n的约数个数,证明d(n)证明:
若n存在一个约数a则n/a=b是n的另一个约数,且b>√n
显然a,b是一一对应的
∵a∴a的个数∴b的个数∴d(n)=a的个数+b的个数3^(6k+1)-
2^(6k+1)-3^(6k)+2^(6k)
=(3^6-1)3^(6k)-(2^6-1)*2^(6k)
=728*3^(6k)-63*2^(6k)
=63*(3^(6k)-2^(6k))+665*3^(6k)
因为665/35=19 所以 3^(6k+1)-2^(6k+1)-3^(6k)+2^(6k)可以被35整除
那么由3^(6k+1)-2^(6k+1)-3^(6k)+2^(6k)+3^(6k)-2^(6k)
=3^(6k+1)-2^(6k+1)
可得到
3^(6k+1)-2^(6k+1)
必定可以被35整除
当n=1时3^(6n)-2^(6n)能被35整除
所以证明完成。
