高中数学:直线、平面平行的判定与性质练习
高中数学必杀1-4线面平行与面面平行的判定及性质
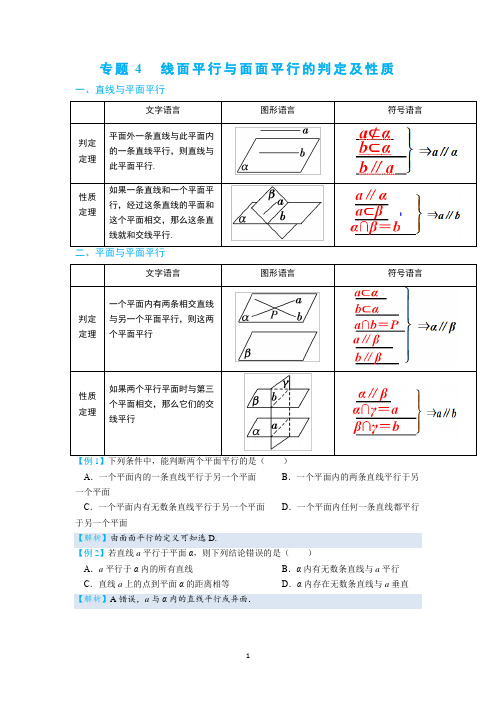
专题4 线面平行与面面平行的判定及性质一、直线与平面平行下列条件中,能判断两个平面平行的是()A.一个平面内的一条直线平行于另一个平面B.一个平面内的两条直线平行于另一个平面C.一个平面内有无数条直线平行于另一个平面D.一个平面内任何一条直线都平行于另一个平面【解析】由面面平行的定义可知选D.【例2】若直线a平行于平面α,则下列结论错误的是()A.a平行于α内的所有直线B.α内有无数条直线与a平行C.直线a上的点到平面α的距离相等D.α内存在无数条直线与a垂直【解析】A错误,a与α内的直线平行或异面.【例3】已知不重合的直线a ,b 和平面α,①若a ∥α,b ⊂α,则a ∥b ;②若a ∥α,b ∥α,则a ∥b ;③若a ∥b ,b ⊂α,则a ∥α;④若a ∥b ,a ∥α,则b ∥α或b ⊂α,上面命题中正确的是________(填序号).【解析】 ①中a 与b 可能异面;②中a 与b 可能相交、平行或异面;③中a 可能在平面α内,④正确.【例4】已知α、β是平面,m 、n 是直线,给出下列命题:①若m ⊥α,m ⊂β,则α⊥β.②若m ⊂α,n ⊂α,m ∥β,n ∥β,则α∥β.③如果m ⊂α,α⊄n ,m 、n 是异面直线,那么n 与α相交.④若α∩β=m ,n ∥m ,且α⊄n ,β⊄n ,则n ∥α且n ∥β其中正确命题的个数是( )A .1B .2C .3D .4【解析】对于①,由定理“如果一个平面经过另一个平面的一条垂线,那么这两个平面垂直”得知,①正确;对于②,注意到直线m ,n 可能是两条平行直线,此时平面α,β可能是相交平面,因此②不正确;对于③,满足条件的直线n 可能平行于平面α,因此③不正确;对于④,由定理“如果平面外一条直线平行于平面内一条直线,那么这条直线平行于这个平面”得知,④正确.综上所述,其中正确的命题是①④,故选B.【例5】已知m ,n 表示两条不同直线,α,β,γ表示不同平面,给出下列三个命题: ①n m n m //⇒⎩⎨⎧⊥⊥αα;①αα//n n m m ⇒⎩⎨⎧⊥⊥;①n m n m ⊥⇒⎩⎨⎧⊥αα//其中真命题的个数为( ) A .0 B .1 C .2 D .3【解析】若⎩⎨⎧⊥⊥ααn m ,则m ①n ,即命题①正确;若⎩⎨⎧⊥⊥n m m α,则n ①α或n ①α,即命题①不正确;若⎩⎨⎧⊥αα//n m ,则m ①n ,即命题①正确;综上可得,真命题共有2个.故选C .【例6】已知m 、n 、l 1、l 2表示直线,α、β表示平面.若m ⊂α,n ⊂α,l 1⊂β,l 2⊂β,l 1∩l 2=M ,则以下条件中,能推出α∥β的是( ) A .m ∥β且l 1∥α B .m ∥β且n ∥βC .m ∥β且n ∥l 2D .m ∥l 1且n ∥l 2【解析】由定理“如果一个平面内有两条相交直线分别与另一个平面平行,那么这两个平面平行”可得,由选项D 可推知α∥β.【例7】在下列条件中,可判断平面α与β平行的是( ) A .α、β都平行于直线l B .α内存在不共线的三点到β的距离相等C .l 、m 是α内两条直线,且l ①β,m ①βD .l 、m 是两条异面直线,且l ①α,m ①α,l ①β,m ①β【解析】排除法,A 中α、β可以是相交平面;B 中三点可面平面两侧;C 中两直线可以不相交.故选D ,也可直接证明.【例8】经过平面外的两点作该平面的平行平面可以作( )A .0个B .1个C .0个或1个D .1个或2个【解析】这两点可以是在平面同侧或两侧.故选C .达标训练11.(2019•延安一模)已知m ,n 表示两条不同的直线,α表示平面.下列说法正确的是( )A .若//m α,//n α,则//m nB .若m α⊥,n α⊥,则//m nC .若m α⊥,m n ⊥,则//n αD .若//m α,m n ⊥,则n α⊥ 2.(2019•湖北期中)平面α与平面β平行的条件可以是( )A .α内有无数多条直线都与β平行B .直线a α⊂,b β⊂,且//a β,//b αC .直线//a α,//a β,且直线a 不在α内,也不在β内D .一个平面α内两条不平行的直线都平行于另一个平面β3.(2019•深圳二模)己知正方体1111ABCD A B C D -,P 为棱1CC 的动点,Q 为棱1AA 的中点,设直线m 为平面BDP 与平面11B D P 的交线,以下关系中正确的是( ) A .1//m D Q B .//m 平面11B D QC .1m B Q ⊥D .m ⊥平面11ABB A4.(2019•聊城二模)在长方体1111ABCD A B C D -中,F ,F ,G ,H 分别为棱11A B ,1BB ,1CC ,11C D 的中点,则下列结论中正确的是( )A .1//AD 平面EFGHB .1//BD GHC .//BD EFD .平面//EFGH 平面11A BCD5.(2019•汕头月考)如图,在正方体1111ABCD A B C D -中,M ,N 分别是1BC ,1CD 的中点,则下列判断错误的是( ) A .1MN CC ⊥B .MN ⊥平面11ACC AC .//MN 平面ABCDD .11//MN A B6.(2019•大连一模)已知m ,n 为两条不重合直线,α,β为两个不重合平面,下列条件中,可以作为//αβ的充分条件的是( ) A .//m n ,m α⊂,n β⊂ B .//m n ,m α⊥,n β⊥ C .m n ⊥,//m α,//n βD .m n ⊥,m α⊥,n β⊥7.(2019•汕头一模)在正方体1111ABCD A B C D -中,点O 是四边形ABCD 的中心,关于直线1A O ,下列说法正确的是( )A .11//AO D C B .1AO BC ⊥C .1//A O 平面11B CDD .1A O ⊥平面11AB D8.(2019•青云月考)如图,四棱锥P ABCD -中,M ,N 分别为AC ,PC 上的点,且//MN 平面PAD ,则( ) A .//MN PD B .//MN PAC .//MN ADD .以上均有可能9.(2019•上饶一模)设m ,n 表示不同的直线,α,β表示不同的平面,且m ,n α⊂.则“//αβ”是“//m β且//n β”的( ) A .充分但不必要条件 B .必要但不充分条件C .充要条件D .既不充分又不必要条件10.(2018•沧州一模)如图,在下列四个正方体中,P ,R ,Q ,M ,N ,G ,H 为所在棱的中点,则在这四个正方体中,阴影平面与PRQ 所在平面平行的是( )A .B .C .D .11.(2017•洛南期末)已知平面//α平面β,直线m α⊂,直线n β⊂,下列结论中不正确的是( ) A .//m βB .//n αC .//m nD .m 与n 不相交12.(2018•杭州期中)如图,四棱锥P ABCD -的底面ABCD 是平行四边形,M 、N 分别为线段PC 、PB 上一点,若:3:1PM MC =,且//AN 平面BDM ,则:PN NB =( )A .4:1B .3:1C .3:2D .2:113.(2018•厦门二模)如图,在正方体1111ABCD A B C D -中,M ,N ,P 分别是11C D ,BC ,11A D 的中点,则下列命题正确的是( )A .//MN APB .1//MN BDC .//MN 平面11BBD DD .//MN 平面BDP14.(2018•辛集期中)在四棱锥P ABCD -中,底面ABCD 为菱形,60BAD ∠=︒,Q 为AD 的中点,点M 在线段PC 上,PM tPC =,//PA 平面MQB ,则实数t 的值为( ) A .15B .14 C .13D .1215.(2018•四川模拟)如图是某几何体的平面展开图,其中四边形ABCD 为正方形,E ,F 分别为PA ,PD 的中点.在此几何体中,以下结论一定成立的是( ) A .直线//BE PFB .直线//EF 平面PBCC .平面BCE ⊥平面PAD D .直线PB 与DC 所成角为60︒16.(2017•万州期末)平面α与ABC ∆的两边AB ,AC 分别交于点D ,E ,且::AD DB AE EC =,如图,则BC 与α的位置关系是( )A .异面B .相交C .平行或相交D .平行17.(2018•桃城模拟)如图,各棱长均为1的正三棱柱111ABC A B C -,M ,N 分别为线段1A B ,1B C 上的动点,且//MN 平面11ACC A ,则这样的MN 有( )A .1条B .2条C .3条D .无数条18.(2018•雁江月考)已知P 为ABC ∆所在平面外一点,平面//α平面ABC ,且α交线段PA ,PB ,PC 于点A ',B ',C ',若:2:3PA AA ''=,则:A B C ABC S S '''=△△( )A .2:3B .2:5C .4:9D .4:2519.(2018•香坊四模)对于不重合的两个平面α和β,给定下列条件: ①存在直线l ,使得l α⊥,且l β⊥; ①存在平面γ,使得αγ⊥且βγ⊥; ①α内有不共线的三点到β的距离相等;①存在异面直线l ,m ,使得//l α,//l β,//m α,//m β. 其中,可以判定α与β平行的条件有( ) A .1个B .2个C .3个D .4个20.(2018•西城期末)在直三棱柱111ABC A B C -中,D 为1AA 中点,点P 在侧面11BCC B 上运动,当点P 满足条件 时,1//A P 平面BCD (答案不唯一,填一个满足题意的条件即可达标训练21.(2017•新课标①)如图,在下列四个正方体中,A ,B 为正方体的两个顶点,M ,N ,Q 为所在棱的中点,则在这四个正方体中,直线AB 与平面MNQ 不平行的是( )A .B .C .D .2.(2011•浙江)若直线l 不平行于平面α,且l α⊂/,则( ) A .α内存在直线与l 异面 B .α内存在与l 平行的直线C .α内存在唯一的直线与l 平行D .α内的直线与l 都相交 3.(2010•浙江)设l ,m 是两条不同的直线,α是一个平面,则下列命题正确的是( ) A .若l m ⊥,m α⊂,则l α⊥ B .若l α⊥,//l m ,则m α⊥C .若//l α,m α⊂,则//l mD .若//l α,//m α,则//l m 4.(2010•江西)如图,M 是正方体1111ABCD A B C D -的棱1DD 的中点,给出下列命题 ①过M 点有且只有一条直线与直线AB 、11B C 都相交; ①过M 点有且只有一条直线与直线AB 、11B C 都垂直; ①过M 点有且只有一个平面与直线AB 、11B C 都相交; ①过M 点有且只有一个平面与直线AB 、11B C 都平行. 其中真命题是( ) A .①①①B .①①①C .①①①D .①①①5.(2008•湖南)已知直线m 、n 和平面α、β满足m n ⊥,m α⊥,αβ⊥,则( ) A .n β⊥ B .//n β,或n β⊂ C .n α⊥D .//n α,或n α⊂6.(2007•北京)平面//α平面β的一个充分条件是( ) A .存在一条直线a ,//a α,//a β B .存在一条直线a ,a α⊂,//a βC .存在两条平行直线a ,b ,a α⊂,b β⊂,//a β,//b αD .存在两条异面直线a ,b ,a α⊂,b β⊂,//a β,//b α7.(2011•福建)如图,正方体1111ABCD A B C D -中,2AB =,点E 为AD 的中点,点F 在CD 上,若//EF 平面1AB C ,则线段EF 的长度等于 .。
专题2:平面与平面平行的判定与性质基础知识与典型例题2020-21学年高中数学平行和垂直证明常见题型

专题2:平面与平面平行的判定与性质平面与平面的位置关系:平行——没有公共点:符号α∥β相交——有一条公共直线: 符号α∩β=a1.平面与平面平行的判定(1)定义:两个平面没有公共点,称这两个平面平行;(2)判定定理:一个平面内的两条相交直线与另一个平面平行,则这两个平面平行。
简记为:线面平行,则面面平行.符号:,,a ba b Aa bαααβββ⊂⊂⎫⎪=⇒⎬⎪⎭1.如图所示,四棱锥P ABCD-中,底面ABCD为平行四边形,E、F分别为PD、PA的中点,AC、BD交于点O.(1)求证:平面//PBC平面EFO;2.如图,正方体1111ABCD A B C D-中,E,F,P,Q分别是BC,11C D,1AD,BD的中点.(1)求证:平面PQB //平面11CB D ;3.如图,在棱长为2的正方体1111ABCD A B C D 中,E ,F 分别为11A D ,11B C 的中点.(1)求证:平面1//AB E 平面1BD F ;4.如图所示,在三棱柱ABC -A 1B 1C 1中,E ,F ,G ,H 分别是AB ,AC ,A 1B 1,A 1C 1的中点,求证:(1)平面EF A 1∥平面BCHG .(2)5.如图,三棱锥P ABC -中,,,PC AC BC 两两垂直,1BC PC ==,2AC =,,,E F G 分别是,,AB AC AP 的中点.(1)证明:平面//GEF 面PCB ;6.如图,在四棱锥P ABCD -中,底面ABCD 为平行四边形,点M ,N ,Q 分别在PA ,BD ,PD 上(不与端点重合),且:::PM MA BN ND PQ QD ==.求证:平面//MNQ 平面PBC .7.如图所示,在正三棱柱ABC-A 1B 1C 1中,E ,F ,G 是侧面对角线上的点,且BE=CF=AG ,平面与平面平行的性质定理:如果两个平行的平面同时与第三个平面相交,那么它们的交线平行。
2020版高中数学(理)一轮复习:第8章 第39讲 直线、平面平行的判定与性质

(2)
所以在△EF M 中,由余弦定理得 |EF |= |ME|2+|MF |2-2|ME|·|MF |·cos∠EMF
= 32+22±2×3×2×12= 13±6, 即|EF |= 7或|EF |= 19.
平行关系中的探索性问题 如图(1)所示,在三棱柱 ABC-A1B1C1 中,若 D 是棱 CC1 的中点,问在棱 AB 上是否存在一点 E,使 DE∥平面 AB1C1?若存在,请确定点 E 的位置;若不存在, 请说明理由. 【思维引导】取 AB,BB1 的中点分别为 E,F ,证明平面 DEF ∥平面 AB1C1 即可.
【解答】 如图(2)所示,连接 A1C 交 AC1 于点 M, 因为四边形 A1ACC1 是平行四边形,
所以 M 是 A1C 的中点,连接 MD.
因为 D 为 BC 的中点,所以 A1B∥DM.
因为 A1B⊂平面 A1BD1,DM⊄平面 A1BD1,
所以 DM∥平面 A1BD1.
(2)
又由三棱柱的性质知,D1C1 BD,
所以四边形 BDC1D1 为平行四边形,所以 DC1∥BD1. 又 DC1⊄平面 A1BD1,BD1⊂平面 A1BD1, 所以 DC1∥平面 A1BD1. 又因为 DC1∩DM=D,DC1,DM⊂平面 AC1D, 所以平面 A1BD1∥平面 AC1D. 【精要点评】证明面面平行时,要利用“线线平行”“线面平行”“面面平行” 的相互转化.面面平行的性质定理的应用问题,往往涉及面面平行的判定、线面平行 的判定与性质的综合应用,解题时,要准确地找到解题的切入点,灵活地运用相关定 理来解决问题.
高中数学必修二2.2-直线、平面平行的判定及其性质课堂练习及答案

2.2.直线、平面平行的判定及其性质2.2.1 直线与平面平行的判定●知识梳理1、直线与平面平行的判定定理:平面外一条直线与此平面内的一条直线平行,则该直线与此平面平行。
简记为:线线平行,则线面平行。
符号表示:a αb β => a∥αa∥b●知能训练一.选择题1.已知m,n是两条不同直线,α,β,γ是三个不同平面,下列命题中正确的是()A.若m∥α,n∥α,则m∥n B.若α⊥γ,β⊥γ,则α∥βC.若m∥α,m∥β,则α∥βD.若m⊥α,n⊥α,则m∥n2.若直线l不平行于平面α,且l⊄α,则()A.α内存在直线与l异面B.α内存在与l平行的直线C.α内存在唯一的直线与l平行D.α内的直线与l都相交3.如图,M是正方体ABCD-A1B1C1D1的棱DD1的中点,给出下列命题①过M点有且只有一条直线与直线AB、B1C1都相交;②过M点有且只有一条直线与直线AB、B1C1都垂直;③过M点有且只有一个平面与直线AB、B1C1都相交;④过M点有且只有一个平面与直线AB、B1C1都平行.其中真命题是()A.②③④B.①③④C.①②④D.①②③4.正方体ABCD-A1B1C1D1中M,N,Q分别是棱D1C1,A1D1,BC的中点.P在对角线BD1上,且BP=BD1,给出下面四个命题:(1)MN∥面APC;(2)C1Q∥面APC;(3)A,P,M三点共线;(4)面MNQ∥面APC.正确的序号为()A.(1)(2)B.(1)(4)C.(2)(3)D.(3)(4)5.在正方体ABCD-A1B1C1D1的各个顶点与各棱中点共20个点中,任取两点连成直线,所连的直线中与A1BC1平行的直线共有()A.12条B.18条C.21条D.24条6.直线a∥平面α,P∈α,那么过P且平行于a的直线()A.只有一条,不在平面α内B.有无数条,不一定在平面α内C.只有一条,且在平面α内D.有无数条,一定在平面α内7.如果直线a∥平面α,那么直线a与平面α内的()A.一条直线不相交B.两条直线不相交C.无数条直线不相交D.任意一条直线不相交8.如图在正方体ABCD-A1B1C1D1中,与平面AB1C平行的直线是()A.DD1B.A1D1C.C1D1D.A1D9.如图,在三棱柱ABC-A1B1C1中,点D为AC的中点,点D1是A1C1上的一点,若BC1∥平面AB1D1,则等于()A.1/2B.1 C.2 D.310.下面四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形是()A.①②B.①④C.②③D.③④11.如图,正方体的棱长为1,线段B′D′上有两个动点E,F,EF=,则下列结论中错误的是()A.AC⊥BEB.EF∥平面ABCDC.三棱锥A-BEF的体积为定值D.异面直线AE,BF所成的角为定值二.填空题12.如图,在正方体ABCD-A1B1C1D1中,E,F,G,H,M分别是棱AD,DD1,D1A1,A1A,AB的中点,点N在四边形EFGH的四边及其内部运动,则当N只需满足条件时,就有MN⊥A1C1;当N只需满足条件时,就有MN∥平面B1D1C.13.如图,正方体ABCD-A1B1C1D1中,AB=2,点E为AD的中点,点F在CD上,若EF∥平面AB1C,则线段EF的长度等于.三.解答题14.如图,在三棱柱ABC-A1B1C1中,侧棱AA1⊥底面ABC,AB⊥BC,D为AC的中点,AA1=AB=2.(1)求证:AB 1∥平面BC1D;(2)若BC=3,求三棱锥D-BC1C的体积.2.2.2 平面与平面平行的判定●知识梳理1、两个平面平行的判定定理:一个平面内的两条交直线与另一个平面平行,则这两个平面平行。
高中数学:点线面关系知识总结和练习(附答案)

//a α//a b点线面位置关系总复习知识梳理一、直线与平面平行 1.判定方法(1)定义法:直线与平面无公共点。
(2)判定定理:(3)其他方法://a αββ⊂ 2.性质定理://a abαβαβ⊂⋂=二、平面与平面平行 1.判定方法(1)定义法:两平面无公共点。
(2)判定定理:////a b a b a b Pββαα⊂⊂⋂=//αβ(3)其他方法:a a αβ⊥⊥//αβ; ////a γβγ//αβ 2.性质定理://a bαβγαγβ⋂=⋂=三、直线与平面垂直(1)定义:如果一条直线与一个平面内的所有直线都垂直,则这条直线和这个平面垂直。
(2)判定方法 ① 用定义.//a b a b αα⊄⊂//a α//a b//a b② 判定定理:a b a cb c A bc αα⊥⊥⋂=⊂⊂a α⊥③ 推论://a a bα⊥b α⊥ (3)性质 ①a b αα⊥⊂a b ⊥ ②a b αα⊥⊥四、平面与平面垂直(1)定义:两个平面相交,如果它们所成的二面角是直线二面角,就说这两个平面互相垂直。
(2)判定定理a a αβ⊂⊥αβ⊥ (3)性质①性质定理la a lαβαβα⊥⋂=⊂⊥αβ⊥ ②lP P A A αβαβαβ⊥⋂=∈⊥垂足为A l ∈ ④lP PA αβαβαβ⊥⋂=∈⊥PA α⊂“转化思想”面面平行 线面平行 线线平行 面面垂直 线面垂直 线线垂直●求二面角1.找出垂直于棱的平面与二面角的两个面相交的两条交线,它们所成的角就是二面角的平面角.2.在二面角的棱上任取一点O,在两半平面内分别作射线OA⊥l,OB⊥l,则∠AOB叫做二面角的平面角例1.如图,在三棱锥S-ABC中,SA⊥底面ABC,AB⊥BC,DE垂直平分SC,且分别交AC于D,交SC于E,又SA=AB,SB=BC,求以BD为棱,以BDE和BDC为面的二面角的度数。
●求线面夹角定义:斜线和它在平面内的射影的夹角叫做斜线和平面所成的角(或斜线和平面的夹角)方法:作直线上任意一点到面的垂线,与线面交点相连,利用直角三角形有关知识求得三角形其中一角就是该线与平面的夹角。
高中数学练习题 线面、面面平行的判定与性质

线面、面面平行的判定与性质基础巩固强化1.已知l是直线,α、β是两个不同平面,下列命题中的真命题是()A.若l∥α,l∥β,则α∥βB.若α⊥β,l∥α,则l⊥βC.若l⊥α,l∥β,则α⊥βD.若l∥α,α∥β,则l∥β2.已知m、n是两条直线,α、β是两个平面,给出下列命题:①若n⊥α,n⊥β,则α∥β;②若平面α上有不共线的三点到平面β的距离相等,则α∥β;③若n、m为异面直线,n⊂α,n∥β,m⊂β,m∥α,则α∥β.其中正确命题的个数是()A.3个B.2个C.1个D.0个一个正方体纸盒展开后如图,在原正方体纸盒中有下列结论:①AB⊥EF②AB与CM成60°③EF与MN是异面直线④MN∥CD其中正确的是()A.①②B.③④C.②③D.①③3.已知平面α∩β=l,m是α内不同于l的直线,那么下列命题中错误..的是()A.若m∥β,则m∥l B.若m∥l,则m∥βC.若m⊥β,则m⊥l D.若m⊥l,则m⊥β4.设a、b是两条不同的直线,α、β是两个不同的平面,则下列命题错误的是()A.若a⊥α,b∥α,则a⊥bB.若a⊥α,b∥a,b⊂β,则α⊥βC.若a⊥α,b⊥β,α∥β,则a∥bD.若a∥α,a∥β,则α∥β对于平面α和共面的直线m、n,下列命题是真命题的是()A.若m,n与α所成的角相等,则m∥n B.若m∥α,n∥α,则m∥nC.若m⊥α,m⊥n,则n∥αD.若m⊂α,n∥α,则m∥n5.设α、β是两个不同的平面,a、b是两条不同的直线,给出下列四个命题,其中真命题是() A.若a∥α,b∥α,则a∥b B.若a∥α,b∥β,a∥b,则α∥βC.若a⊥α,b⊥β,a∥b,则α∥βD.若a、b在平面α内的射影互相垂直,则a⊥b 6.设两个平面α、β,直线l,下列三个条件:①l⊥α;②l∥β;③α⊥β.若以其中两个作为前提,另一个作为结论,则可构成三个命题,这三个命题中正确命题的个数为()A .3B .2C .1D .07.正方体ABCD -A 1B 1C 1D 1的棱长为1cm ,过AC 作平行于对角线BD 1的截面,则截面面积为________.8.在空间中,有如下命题:①互相平行的两条直线在同一个平面内的射影必然是互相平行的两条直线; ②若平面α∥平面β,则平面α内任意一条直线m ∥平面β;③若平面α与平面β的交线为m ,平面α内的直线n ⊥直线m ,则直线n ⊥平面β; ④若平面α内的三点A 、B 、C 到平面β的距离相等,则α∥β. 其中正确命题的序号为________.9.已知m 、n 是两条不重合的直线,α、β、γ是三个两两不重合的平面,给出下列命题: ①若m ∥α,n ∥α,m ∥β,n ∥β,则α∥β; ②若α⊥γ,β⊥γ,α∩β=m ,n ⊂γ,则m ⊥n ; ③若m ⊥α,α⊥β,m ∥n ,则n ∥β; ④若n ∥α,n ∥β,α∩β=m ,那么m ∥n . 其中正确命题的序号是________.10.如图,直三棱柱ABC -A ′B ′C ′,∠BAC =90°,AB =AC =2,AA ′=1,点M 、N 分别为A ′B 和B ′C ′的中点.(1)证明:MN ∥平面A ′ACC ′;(2)求三棱锥A ′-MNC 的体积(锥体体积公式V =13Sh ,其中S 为底面面积,h 为高).如图,在侧棱垂直底面的四棱柱ABCD -A 1B 1C 1D 1中,AD ∥BC ,AD ⊥AB ,AB =2,AD =2,BC =4,AA 1=2,E 是DD 1的中点,F是平面B1C1E与直线AA1的交点.(1)证明:①EF∥A1D1;②BA1⊥平面B1C1EF;(2)求BC1与平面B1C1EF所成角的正弦值.能力拓展提升11.如图,正方体ABCD-A1B1C1D1中,E、F分别为棱AB、CC1的中点,在平面ADD1A1内且与平面D1EF平行的直线()A.不存在B.有1条C.有2条D.有无数条12.如图,若Ω是长方体ABCD—A1B1C1D1被平面EFGH截去几何体EFGHB1C1后得到的几何体,其中E为线段A1B1上异于B1的点,F为线段BB1上异于B1的点,且EH∥A1D1,则下列结论中不正确...的是()A.EH∥FG B.四边形EFGH是矩形C.Ω是棱柱D.Ω是棱台下列命题中,是假命题的是()A.三角形的两条边平行于一个平面,则第三边也平行于这个平面B.平面α∥平面β,a⊂α,过β内的一点B有唯一的一条直线b,使b∥aC.α∥β,γ∥δ,α、β与γ、δ的交线分别为a、b和c、d,则a∥b∥c∥dD.一条直线与两个平面成等角是这两个平面平行的充要条件13.(2012·南昌二模)若P是两条异面直线l、m外的任意一点,则下列命题中假命题的序号是________.①过点P有且仅有一条直线与l、m都平行;②过点P有且仅有一条直线与l、m都垂直;③过点P有且仅有一条直线与l、m都相交;④过点P有且仅有一条直线与l、m都异面.14.下列四个正方体图形中,A、B为正方体的两个顶点,M、N、P分别为其所在棱的中点,能得出AB∥平面MNP的图形的序号是______(写出所有符合要求的图形序号).15.(2011·广东揭阳一模)如图,已知平行四边形ABCD中,BC=6,正方形ADEF所在平面与平面ABCD垂直,G、H分别是DF、BE的中点.(1)求证:GH∥平面CDE;(2)若CD=2,DB=42,求四棱锥F-ABCD的体积.[解析](1)证法1:∵EF∥AD,AD∥BC,∴EF∥BC.又EF=AD=BC,∴四边形EFBC是平行四边形,∴H为FC的中点.又∵G是FD的中点,∴GH∥CD.∵GH⊄平面CDE,CD⊂平面CDE,∴GH∥平面CDE.证法2:连接EA,∵ADEF是正方形,∴G是AE的中点.∴在△EAB中,GH∥AB.又∵AB∥CD,∴GH∥CD.∵HG⊄平面CDE,CD⊂平面CDE,∴GH∥平面CDE.(2)∵平面ADEF⊥平面ABCD,交线为AD,且F A⊥AD,∴F A⊥平面ABCD.∵AD=BC=6,∴F A=AD=6.又∵CD=2,DB=42,CD2+DB2=BC2,∴BD⊥CD. ∵S▱ABCD=CD·BD=82,∴V F-ABCD=13S▱ABCD·F A=13×82×6=16 2.(理)如图,在多面体ABCDEF中,四边形ABCD是正方形,AB=2EF=2,EF∥AB,EF⊥FB,∠BFC=90°,BF=FC,H为BC的中点.(1)求证:FH∥平面EDB;(2)求证:AC⊥平面EDB;(3)求四面体B-DEF的体积.[解析](1)证明:设AC与BD交于点G,联结EG、GH.则G为AC中点,∵H是BC中点,∴GH綊12AB,又∵EF綊12AB,∴四边形EFHG为平行四边形.∴FH∥EG.又EG⊂平面EDB,而FH⊄平面EDB,∴FH∥平面EDB.(2)证明:∵EF∥AB,EF⊥FB.∴AB⊥FB.又四边形ABCD为正方形,∴AB⊥BC,又FB∩BC=B,∴AB⊥平面BFC.∵FH⊂平面BFC,∴AB⊥FH.又∵FB=FC,H是BC中点,∴FH⊥BC.又AB∩BC=B,∴FH⊥平面ABCD,∴FH⊥AC. 又EG∥FH,∴EG⊥AC,又AC⊥BD,BD∩EG=G,∴AC⊥平面EDB.(3)∵EF⊥BF,BF⊥FC且EF∩FC=F,∴BF⊥平面CDEF,∴BF 为四面体B —DEF 的高. 又∵BC =AB =2,∴BF =FC = 2.四边形CDEF 为直角梯形,且EF =1,CD =2. ∴S △DEF =12(1+2)×2-12×2×2=22∴V B —DEF =13×22×2=13. 16.(2012·辽宁大连市、沈阳市联考)如图,在四棱锥P -ABCD 中,P A ⊥底面ABCD ,四边形ABCD 为长方形,AD =2AB ,点E 、F 分别是线段PD 、PC 的中点.(1)证明:EF ∥平面P AB ;(2)在线段AD 上是否存在一点O ,使得BO ⊥平面P AC ,若存在,请指出点O 的位置,并证明BO ⊥平面P AC ;若不存在,请说明理由.[解析] (1)证明:∵EF ∥CD ,CD ∥AB ,∴EF ∥AB , 又∵EF ⊄平面P AB ,AB ⊂平面P AB ,(2)在线段AD上存在一点O,使得BO⊥平面P AC,此时点O为线段AD的四等分点,且AO=14AD,∵P A⊥底面ABCD,∴P A⊥BO,又∵长方形ABCD中,AD=2AB,∴△ABO△DAC,∴∠ABO+∠BAC=∠DAC+∠BAC=90°,∴AC⊥BO,又∵P A∩AC=A,∴BO⊥平面P AC.1.(2012·四川文,6)下列命题正确的是()A.若两条直线和同一个平面所成的角相等,则这两条直线平行B.若一个平面内有三个点到另一个平面的距离相等,则这两个平面平行C.若一条直线平行于两个相交平面,则这条直线与这两个平面的交线平行D.若两个平面都垂直于第三个平面,则这两个平面平行[答案] C[解析]本题考查了线面角,面面垂直,线面平行,面面平行等位置关系的判定与性质,对于A选项,两条直线也可相交,B选项若三点在同一条直线上,平面可相交.D选项这两个平面可相交(可联系墙角),而C项可利用线面平行的性质定理,再运用线面平行的判定与性质可得.本题需要我们熟练掌握各种位置关系的判定与性质.2.(2012·石家庄二模)三棱锥的三组相对的棱(相对的棱是指三棱锥中成异面直线的一组棱)分别相等,且长分别为2、m 、n ,其中m 2+n 2=6,则该三棱锥体积的最大值为( )A.12B.8327 C.33 D.23[答案] D[解析] 令m =n ,由m 2+n 2=6得m =n =3,取AB 的中点E ,则BE =22,PB =3,∴PE =102,CE =102,∴EF =2,∴V P -ABC =13S △PEC ·AB =13×(12×2×2)×2=23,∵23>12,∴23>33,23>8327,故选D.3.如图,正四棱柱ABCD -A 1B 1C 1D 1中,AA 1=2,AB =1,M ,N 分别在AD 1、BC 上移动,且始终保持MN ∥平面DCC 1D 1,设BN =x ,MN =y ,则函数y =f (x )的图象大致是( )[答案] C[解析] 过M 作ME ⊥AD 于E ,连接EN ,则平面MEN ∥平面DCC 1D 1,所以BN =AE =x (0≤x <1),ME =2x ,MN 2=ME 2+EN 2,则y 2=4x 2+1,y 2-4x 2=1(0≤x <1,y >0),图象应是焦点在y 轴上的双曲线的一部分.故选C.4.(2012·东营市期末)设m 、n 是两条不同的直线,α、β是两个不同的平面,给出下列四个命题:①若m ⊥n ,m ⊥α,n ⊄α,则n ∥α;②若α⊥β,α∩β=m ,n ⊥m ,则n ⊥α或n ⊥β; ③若m ⊥β,α⊥β,则m ∥α; ④若m ⊥n ,m ⊥α,n ⊥β,则α⊥β. 其中真命题的序号是________. [答案] ①④⎭⎪⎬⎪⎫ ⎭⎪⎬⎪⎫[解析] m ⊥n m ⊥α⇒n ∥α或n ⊂α n ⊄α⇒n ∥α,故①真; 正方体ABCD -A 1B 1C 1D 1中,平面ABCD 与ADD 1A 1分别取作平面α,β,其交线AD 为m ,取直线AB 1为n ,则满足n ⊥m ,知②错;m ⊥β,α⊥β时,可能m ∥α,也可能m ⊂α,知③错;⎭⎬⎫ ⎭⎪⎬⎪⎫m ⊥n m ⊥α⇒n ∥α或n ⊂αn ⊥β⇒α⊥β,故④真.。
线面平行的判定定理与性质定理练习

高中数学必修二学案(034)班级_________姓名_________组别_____ 编写人 朱永 审核人 赵春梅线面平行的判定定理与性质定理练习1.下列命题正确的是 ( ) A 一直线与平面平行,则它与平面内任一直线平行B 一直线与平面平行,则平面内有且只有一个直线与已知直线平行C 一直线与平面平行,则平面内有无数直线与已知直线平行,它们在平面内彼此平行D 一直线与平面平行,则平面内任意直线都与已知直线异面2.若直线l 与平面α的一条平行线平行,则l 和α的位置关系是( ) A α⊂l B α//l C αα//l l 或⊂ D 相交和αl3.若直线a 在平面α内,直线a,b 是异面直线,则直线b 和α平面的位置关系是 ( ) A .相交 B 。
平行 C 。
相交或平行 D 。
相交且垂直 4.下列各命题:(1) 经过两条平行直线中一条直线的平面必平行于另一条直线; (2) 若一条直线平行于两相交平面,则这条直线和交线平行;(3) 空间四边形中三条边的中点所确定平面和这个空间四边形的两条对角线都平行。
其中假命题的个数为 ( ) A 0 B 1 C 2 D 35.E 、F 、G 分别是四面体ABCD 的棱BC 、CD 、DA 的中点,则此四面体中与过E 、F 、G 的截面平行的棱的条数是( ) A .0 B 1 C 2 D36.直线与平面平行的充要条件是 ( ) A .直线与平面内的一条直线平行 B 。
直线与平面内的两条直线不相交C .直线与平面内的任一直线都不相交D 。
直线与平行内的无数条直线平行7.若直线上有两点P 、Q 到平面α的距离相等,则直线l 与平面α的位置关系是 ( ) A 平行 B 相交 C 平行或相交 D 或平行、或相交、或在内 8.a,b 为两异面直线,下列结论正确的是 ( ) A 过不在a,b 上的任何一点,可作一个平面与a,b 都平行 B 过不在a,b 上的任一点,可作一直线与a,b 都相交 C 过不在a,b 上任一点,可作一直线与a,b 都平行 D 过a 可以并且只可以作一个平面与b 平行 9.判断下列命题是否正确:(1)过平面外一点可作无数条直线与这个平面平行 ( ) (2)若直线α⊄l ,则l 不可能与α内无数条直线相交 ( ) (3)若直线l 与平面α不平行,则l 与α内任一直线都不平行 ( )(4)经过两条平行线中一条直线的平面平行于另一条直线 ( ) (5)若平面α内有一条直线和直线l 异面,则α⊄l ( )【本课小结】从知识上学到________________________________________从方法上学到________________________________________还有哪些疑惑________________________________________下节目标解读____________________________________________包铁一中引导行三线教学法高中数学必修一配餐(034)班级_____ 姓名_________组别_____ 编写人朱永审核人赵春梅10. 三棱柱ABC—A1B1C1中,若D为BB1上一点,M为AB的中点,N为BC的中点.求证:MN∥平面A1C1D;11. 平面外的两条平行直线中的一条平行于这个平面,那么另一条直线也平行于这个平面.已知:直线ba//,//a平面α,α⊄b.求证:α//b.12、如图,在底面为平行四边形的四棱锥 P—ABCD 中,点 E 是 PD 的中点.求证:PB//平面 AEC;13. 如图,求证:如果一条直线和两个相交平面都平行,那么这条直线和它们的交线平行.已知:l=βα ,α//a,β//a,求证:la//.【总结与反思】____________________________________________________________________________ ___________________________________________________________________________________ 【老师批语】______________________________________________________________________包铁一中引导行三线教学法。
高中数学百大经典例题——两平面平行判定和性质(新课标)
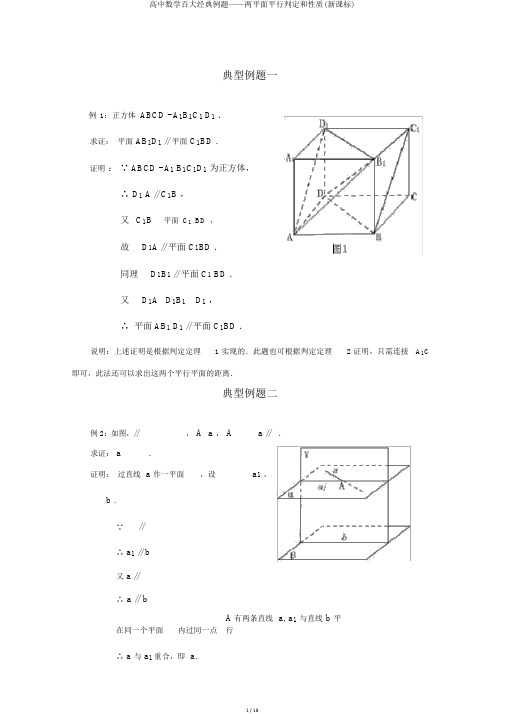
典型例题一例1:正方体ABCD - A1B1C1D1.求证:平面 AB1D1 // 平面 C1BD .证明:∵ ABCD - A1 B1C1D1为正方体,∴D1 A // C1B ,又C1B平面C1BD,故D1A // 平面 C1BD .同理D1B1 // 平面 C1 BD .又D1A D1B1 D1,∴平面 AB1 D1 // 平面 C1BD .说明:上述证明是根据判定定理 1 实现的.此题也可根据判定定理 2 证明,只需连接A1C 即可,此法还可以求出这两个平行平面的距离.典型例题二例 2:如图,// , A a , A a // .求证: a .证明:过直线 a 作一平面,设a1,b .∵//∴ a1 // b又 a //∴ a // b在同一个平面内过同一点A有两条直线a, a1与直线 b 平行∴ a 与 a1重合,即 a.说明:此题也可以用反证法进行证明.典型例题三例 3:如果一条直线与两个平行平面中的一个相交,那么它和另一个也相交.:如图,// ,l A .求证: l 与相交.证明:在上取一点 B ,过 l 和 B 作平面,由于与α有公共点A ,与有公共点B.∴与、都相交.设 a , b .∵//∴a // b又 l 、a、 b 都在平面内,且l和a交于A.∵ l 与 b 相交.所以 l 与相交.典型例题四例 4:平面// ,AB,CD为夹在 a ,间的异面线段, E 、 F 分别为 AB 、CD 的中点.求证: EF // , EF // .证明:连接 AF 并延长交于 G .∵AG CD F∴AG CD确定平面,且AC ,,DG .∵// ,所以AC // DG ,∴ACF GDF ,又AFC DFG , CF DF ,∴ △ ACF ≌△ DFG .∴ AF FG .又AE BE ,∴EF // BG ,BG.故EF // .同理 EF //说明:此题还有其它证法,要点是对异面直线的处理.典型例题六例 6如图,矩形ABCD 的四个顶点在平面上的射影分别为A1、 B1、 C1、 D1,且A1、 B1、 C1、 D1互不重合,也无三点共线.求证:四边形A1B1C1 D1是平行四边形.证明:∵ AA1 , DD 1∴ AA1 // DD1不妨设 AA1和 DD1确定平面.同理 BB1 和 CC1确定平面.又AA1 // BB1,且 BB1∴ AA1 //同理 AD //又 AA1 AD A∴ //又A1D1,B1C1同∴A1D1 // B1C1.理A1B1 // C1D1.∴四边形 A1B1C1D1是平行四边形.典型例题七例 7 设直线l 、m ,平面、,以下条件能得出// 的是〔〕.A.l , m ,且l // , m // B.l , m ,且 l // mC.l , m ,且 l // m D.l // , m // ,且l // m分析:选项 A 是错误的,因为当l // m 时,与可能相交.选项 B 是错误的,理由同A.选项 C 是正确的,因为l , m// l ,所以m ,又∵m ,∴// .选项 D 也是错误的,满足条件的可能与相交.答案: C说明:此题极易选A,原因是对平面平行的判定定理掌握不准确所致.本例这样的选择题是常见题目,要正确得出选择,需要有较好的作图能力和对定理、公理的准确掌握、深刻理解,同时要考虑到各种情况.典型例题八例 8 设平面平面,平面平面,且、分别与相交于 a 、b,a// b.求证:平面// 平面.上找到两条相交直线,或作出相交直线,分析:要证明两平面平行,只要设法在平面它们分别与平行〔如图〕.证明:在平面内作直线PQ直线a,在平面内作直线MN直线b.∵平面平面,∴ PQ平面,MN平面,∴PQ // MN .又∵ a // p, PQ a Q ,MN b N ,∴平面 // 平面.说明:如果在、内分别作 PQ ,MNMN ,这样就走了弯路,还需证明 PQ 、在、内,如果直接在、内作a 、b的垂线,就可推出 PQ // MN .由面面垂直的性质推出“线面垂直〞,进而推出“线线平行〞、“线面平行〞,最后得到“面面平行〞,最后得到“面面平行〞.其核心是要形成应用性质定理的意识,在立体几何证明中非常重要.典型例题九例 9 如下图,平面// 平面,点A 、C ,点B、 D , AB a 是、的公垂线,CD 是斜线.假设AC BD b , CD c , M 、 N 分别是AB 和 CD 的中点,(1)求证:MN // ;(2)求MN 的长.分析:〔 1〕要证MN // ,取AD 的中点P ,只要证明MN 所在的平面PMN // .为此证明PM // , PN // 即可.(2)要求MN 之长,在CMA 中,CM 、 CN 的长度易知,关键在于证明MN证明: (1) 连结CD ,从而由勾股定理可以求解.AD ,设 P 是 AD 的中点,分别连结PM 、 PN .∵M 是 AB 的中点,∴ PM // BD .又 BD,∴ PM //.同理∵N 是 CD 的中点,∴ PN // AC .∵ AC ,∴ PN // .∵ // , PN PM P ,∴平面PMN // .∵ MN 平面 PMN ,∴MN // .(2)分别连结MC、MD.1a ,∵ AC BD b , AM BM2又∵ AB 是、的公垂线,∴CAM DBM 90 ,∴ Rt ACM ≌ Rt BDM ,∴ CM DM ,∴ DMC 是等腰三角形.又 N 是 CD 的中点,∴ MN CD .CN 21 4b2 a 2 c2.在 Rt CMN 中, MN CM 22说明: (1)证“线面平行〞也可以先证“面面平行〞,然后利用面面平行的性质,推证“线面平行〞,这是一种以退为进的解题策略.(2)空间线段的长度,一般通过构造三角形、然后利用余弦定理或勾股定理来求解.(3)面面平行的性质:①面面平行,那么线面平行;②面面平行,那么被第三个平面所截得的交线平行.典型例题十例 10如果平面内的两条相交直线与平面所成的角相等,那么这两个平面的位置关系是 __________.分析:按直线和平面的三种位置关系分类予以研究.解:设 a 、b是平面内两条相交直线.(1)假设a、b都在平面内,a、b与平面所成的角都为0 ,这时与重合,根据教材中规定,此种情况不予考虑.(2)假设a、b都与平面相交成等角,且所成角在(0 , 90 ) 内;∵ a 、b与有公共点,这时与相交.假设 a 、b都与平面成90角,那么a // b,与矛盾.此种情况不可能.(3)假设a、b都与平面平行,那么a、b与平面所成的角都为0,内有两条直线与平面平行,这时//.综上,平面、的位置关系是相交或平行.典型例题十一例11 试证经过平面外一点有且只有一个平面和平面平行.: A平面,求证:过 A 有且只有一个平面//.分析:“有且只有〞要准确理解,要先证这样的平面是存在的,再证它是惟一的,缺一不可.证明:在平面内任作两条相交直线 a 和b,那么由A知,A a , A b .点A和直线a可确定一个平面 M ,点 A 和直线 b 可确定一个平面 N .在平面 M 、 N 内过 A 分别作直线a'// a、b'// b,故 a ' 、 b'是两条相交直线,可确定一个平面.∵ a' , a , a ' // a ,∴a' // .同理 b ' // .又 a' , b' , a' b' A ,∴// .所以过点 A 有一个平面// .假设过 A 点还有一个平面// ,内取一直线 c ,A c ,点 A 、直线 c 确定一个平面,由公理 2 知:那么在平面m ,n ,∴m // c , n// c ,又 A m , A n ,这与过一点有且只有一条直线与直线平行相矛盾,因此假设不成立,所以平面只有一个.所以过平面外一点有且只有一个平面与平面平行.典型例题十二例 12 点S是正三角形ABC所在平面外的一点,且SA SB SC, SG为 SAB 上的高, D 、 E 、 F 分别是 AC 、 BC 、 SC 的中点,试判断 SG 与平面DEF 内的位置关系,并给予证明SG // 平面DEF ,要证明结论成立,只需证明SG与分析 1:如图,观察图形,即可判定平面 DEF 内的一条直线平行.观察图形可以看出:连结CG 与DE 相交于H ,连结FH , FH 就是适合题意的直线.怎样证明 SG// FH ?只需证明 H 是 CG 的中点.证法 1:连结CG交DE于点H,∵DE 是 ABC 的中位线,∴ DE // AB .在 ACG 中, D 是 AC 的中点,且 DH // AG ,∴ H 为 CG 的中点.∵FH 是 SCG的中位线,∴ FH // SG .又 SG平面DEF,FH平面DEF,∴SG// 平面 DEF .分析 2:要证明SG//平面DEF,只需证明平面SAB // 平面 DEF ,要证明平面 DEF // 平面 SAB,只需证明 SA// DF , SB// EF 而 SA// DF , SB// EF 可由题设直接推出.证法 2:∵EF为SBC的中位线,∴EF // SB.∵ EF 平面 SAB , SB 平面 SAB,∴EF // 平面.SAB同理: DF // 平面 SAB, EF DF F ,∴平面 SAB // 平面 DEF ,又∵ SG 平面 SAB,∴ SG// 平面 DEF .典型例题十三例 13 如图,线段PQ 分别交两个平行平面、于 A 、B 两点,线段PD 分别交、PA 9, AB 12 ,BQ 12 ,于 C 、 D 两点,线段QF 分别交、于 F 、 E 两点,假设ACF 的面积为72,求BDE 的面积.分析: 求BDE 的面积,看起来似乎与本节内容无关,事实上,ACF 的面积,假设BDE 与 ACF 的对应边有联系的话,可以利用 ACF 的面积求出BDE 的面积.解: ∵平面 QAFAF ,平面 QAF BE ,又∵// ,∴ AF // BE .同理可证:AC // BD ,∴ FAC 与 EBD 相等或互补,即 sin FAC sin EBD .由 FA // BE ,得 BE ∶AFQB ∶QA 12∶24 1∶2 ,∴ BE1AF 2由 BD // AC ,得: AC ∶BDPA ∶PB 9∶21 3∶7 ,∴ BD7AC .ACF 的面积为 72,即 1AF AC3又∵sin FAC 72 .2∴SDBE1BE BD sin EBD21 1 7FAC2 AF AC sin2 3 7 1AF AC sin FAC 6 27 72 84 . 6∴ BDE 的面积为 84 平方单位.说明: 应用两个平行的性质一是可以证明直线与直线的平行,二是可以解决线面平行的问题.注意使用性质定理证明线线平行时,一定第三个平面与两个平行平面相交,其交线互相平行.典型例题十四例 14 在棱长为 a 的正方体中,求异面直线BD 和 B 1C 之间的距离.分析: 通过前面的学习,我们解决了如下的问题:假设 a 和 b 是两条异面直线,那么过 a 且平 行于 b 的平面必平行于过b 且平行于 a 的平面. 我们知道, 空间两条异面直线, 总分别存在于两个平行平面内.因此,求两条异面直线的距离,有时可以通过求这两个平行平面之间的距离来解决.具体解法可按如下几步来求:①分别经过BD 和 B 1C 找到两个互相平等的平面;②作出两个平行平面的公垂线;③计算公垂线夹在两个平等平面间的长度.解:如图,根据正方体的性质,易证:BD // B1D1平面 A1 BD // 平面 CB1D1A1B // D1C连结 AC1,分别交平面A1BD 和平面 CB1 D1于M和N因为 CC1和 AC1分别是平面ABCD 的垂线和斜线,AC 在平面 ABCD 内, AC BD 由三垂线定理:AC1BD ,同理: AC1A1D∴AC1平面 A1 BD ,同理可证: AC1平面 CB1 D1∴平面 A1 BD 和平面 CB1D1间的距离为线段MN 长度.如下图:在对角面 AC1中, O1为 A1C1的中点,O为AC的中点1 AC13 a .∴ AM MN NC13 3∴ BD 和B1C的距离等于两平行平面A1 BD 和 CB1D1的距离为 3 a .3说明:关于异面直线之间的距离的计算,有两种根本的转移方法:①转化为线面距.设 a 、b 是两条异面直线,作出经过 b 而和a平行的平面,通过计算a和的距离,得出a和 b 距离,这样又回到点面距离的计算;②转化为面面距,设 a 、b是两条异面直线,作出经过 b 而和 a 平行的平面,再作出经过 a 和b平行的平面,通过计算、之间的距离得出 a 和b之间的距离.典型例题十五例 15正方体ABCD A1B1C1 D1棱长为 a ,求异面直线AC 与BC1的距离.解法 1:〔直接法〕如图:取 BC 的中点 P ,连结 PD 、PB1分别交 AC 、BC1于 M 、 N 两点,易证: DB1 // MN , DB1 AC , DB1 BC1.∴ MN 为异面直线 AC 与BC11 3 的公垂线段,易证: MN DB1 a .3 3小结:此法也称定义法,这种解法是作出异面直线的公垂线段来解.但通常寻找公垂线段时,难度较大.解法 2:〔转化法〕如图:∵AC // 平面A1C1B,∴ AC 与BC1的距离等于AC 与平面A1C1B的距离,在 Rt OBO1中,作斜边上的高OE ,那么 OE 长为所求距离,∵ OB 2a , OO1 a ,2∴ O1 B 3a ,∴OEOO1OB3a.2 O1 B 3小结:这种解法是将线线距离转化为线面距离.解法 3:〔转化法〕如图:∵平面ACD1 // 平面A1C1B,∴ AC 与BC1 的距离等于平面ACD 1与平面 A1C1B 的距离.∵ DB1平面 ACD1,且被平面 ACD1和平面 A1C1 B 三等分;∴所求距离为1B D3a.3 1 3小结:这种解法是线线距离转化为面面距离.解法 4:〔构造函数法〕如图:任取点 Q BC1,作 QR BC 于R点,作PK AC 于 K 点,设 RC x ,那么 BR QR a x ,CK KR ,且KR2 CK 2 CR 2∴ KR2 1 CR2 1 x2.2 2那么 QK 2 1 x2 (a x)223( x 2 a)2 1 a2 1 a2,2 3 3 3故 QK 的最小值,即AC 与BC1的距离等于3a .3小结:这种解法是恰当的选择未知量,构造一个目标函数,通过求这个函数的最小值来得到二异面直线之间的距离.解法 5:〔体积桥法〕如图:当求 AC 与BC1的距离转化为求AC 与平面A1C1B的距离后,设 C 点到平面A1C1B的距离为 h ,那么V C A1 C1 B VA1 BCC1.∵1 h 3 ( 2a) 21a 1 a2 ,3 4 3 2∴ h 3a .即AC与 BC1的距离等于3a .3 3小结:本解法是将线线距离转化为线面距离,再将线面距离转化为锥体化为锥体的高,然后用体积公式求之.这种方法在后面将要学到.说明:求异面直线距离的方法有:(1)〔直接法〕当公垂线段能直接作出时,直接求.此时,作出并证明异面直线的公垂线段,是求异面直线距离的关键.(2)〔转化法〕把线线距离转化为线面距离,如求异面直线 a 、b距离,先作出过 a 且平行于 b 的平面,那么b 与距离就是 a 、b距离.〔线面转化法〕.也可以转化为过 a 平行b的平面和过b平行于 a 的平面,两平行平面的距离就是两条异面直线距离.〔面面转化法〕.(3)〔体积桥法〕利用线面距再转化为锥体的高用何种公式来求.(4)〔构造函数法〕常常利用距离最短原理构造二次函数,利用求二次函数最值来解.两条异面直线间距离问题,教科书要求不高〔要求会计算已给出公垂线时的距离〕面的问题的其他解法,要适度接触,以开阔思路,供学有余力的同学探求.,这方典型例题十六例16 如果// , AB 和AC 是夹在平面与之间的两条线段,AB AC ,且AB 2 ,直线 AB 与平面所成的角为30 ,求线段AC 长的取值范围.解法 1:如下图:作 AD 于 D ,连结 BD 、 CD 、 BC∵ AB BD , AC DC ,AB2 AC 2 BC 2,∴在BDC 中,由余弦定理,得:BD 2 CD 2 BC 2 AB 2 AC 2 BC 2cos BDC 2BD CD 2BD CD 0 .∵ AD ,∴ ABD 是 AB 与所在的角.又∵// ,∴ABD 也就等于 AB 与所成的角,即ABD 30 .∵AB 2 ,∴ AD 1 ,BD 3 ,DC AC 2 1 , BC 4 AC2,∴ 1 3 AC 2 1 4 AC 2 0,即:0 1 3 .2 3 AC2 1 AC 2 1∴ AC 2 3 ,即 AC 长的取值范围为 2 3 , .3 3解法 2:如图:∵AB AC∴ AC 必在过点 A 且与直线 AB 垂直的平面内设l ,那么在内,当AC l 时, AC 的长最短,且此时AC AB tan ABCAB tan 30 2 3 3而在内, C 点在 l 上移动,远离垂足时,AC 的长将变大,2 3从而 AC ,3即 AC 长的取值范围是2 3,.3说明: (1)此题考查直线和直线、直线和平面、平面和平面的位置关系,对于运算能力和空间想象能力有较高的要求,供学有余力的同学学习.(2)解法 1 利用余弦定理,采用放缩的方法构造出关于AC 长的不等式,再通过解不等式得到 AC 长的范围,此方法以运算为主.(3)解法 2 从几何性质角度加以解释说明,防止了繁杂的运算推导,但对空间想象能力要求很高,根据此解法可知线段AC 是连结异面直线AB 和 l 上两点间的线段,所以 AC 是 AB 与l的公垂线段时,其长最短.典型例题十七例 17如果两个平面分别平行于第三个平面,那么这两个平面互相平行.://,//,求证://.分析:此题考查面面平行的判定和性质定理以及逻辑推理能力.由于两个平面没有公共点称两平面平行,带有否认性结论的命题常用反证法来证明,因此此题可用反证法证明.另外也可以利用平行平面的性质定理分别在三个平面内构造平行且相交的两条直线,利用线线平行来推理证明面面平行,或者也可以证明这两个平面同时垂直于某一直线.证明一:如图,和相交.假设、不平行,那么∴和至少有一个公共点 A ,即A , A .∵// ,// ,∴ A .于是,过平面外一点 A 有两个平面、都和平面平行,这和“经过平面外一点有且只有一个平面与平面平行〞相矛盾,假设不成立。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
高中数学:直线、平面平行的判定与性质练习
(时间:30分钟)
1.已知直线a和平面α,那么a∥α的一个充分条件是( C )
(A)存在一条直线b,a∥b且b⊂α
(B)存在一条直线b,a⊥b且b⊥α
(C)存在一个平面β,a⊂β且α∥β
(D)存在一个平面β,a∥β且α∥β
解析:在A,B,D中,均有可能a⊂α,错误;在C中,两平面平行,则其中一个平面内的任意一条直线都平行于另一个平面,故C正确.
2.(全国Ⅰ卷)如图,在下列四个正方体中,A,B为正方体的两个顶点,M,N,Q为所在棱的中点,则在这四个正方体中,直线AB与平面MNQ不平行的是( A )
解析:如图,O为正方形CDBE的两条对角线的交点,从而O为BC的中点,在△ACB中,OQ为中位线,所以OQ∥AB,OQ∩平面MNQ=Q,所以,AB与平面MNQ相交,而不是平行,故选A.
3.已知a,b是两条不重合的直线,α,β是两个不重合的平面,则下列命题中正确的是( C )
(A)a∥b,b⊂α,则a∥α
(B)a,b⊂α,a∥β,b∥β,则α∥β
(C)a⊥α,b∥α,则a⊥b
(D)当a⊂α,且b⊄α时,若b∥α,则a∥b
解析:由a∥b,b⊂α,也可能a⊂α,A错;B中的直线a,b不一定相交,平面α,β也可能相交,B 错;C正确;D中的直线a,b也可能异面,D错.故选C.
4.过直线l外两点,作与l平行的平面,则这样的平面( D )
(A)不存在(B)只能作出1个
(C)能作出无数个(D)以上都有可能
解析:设直线l外两点确定直线AB,①当AB与l相交时,满足题意的平面不存在;②当AB与l 异面时,满足题意的平面只能作一个;③当AB∥l时,满足题意的平面有无数多个.
5.(咸宁模拟)如图,在三棱柱ABC-A
1B
1
C
1
中,点D为AC的中点,点D
1
是A
1
C
1
上的一点,若DC
1
∥平
面AB
1D
1
,则等于( B )
(A)(B)1 (C)2 (D)3
解析:因为DC
1∥平面AB
1
D
1
,DC
1
⊂平面ACC
1
A
1
,平面ACC
1
A
1
∩平面AB
1
D
1
=AD
1
,所以DC
1
∥AD
1
,又AD
∥C
1D
1
,所以四边形ADC
1
D
1
是平行四边形,所以AD=C
1
D
1
.又D为AC的中点,所以D
1
为A
1
C
1
的中点,
所以=1.
6.(丽江模拟)若正n边形的两条对角线分别与平面α平行,则这个正n边形所在的平面一定平行于平面α,那么n的取值可能是( A )
(A)5 (B)6 (C)8 (D)12
解析:因为正五边形的对角线都相交,所以正五边形所在的平面一定与平面α平行.
7.(益阳模拟)设a,b为不重合的两条直线,α,β为不重合的两个平面,给出下列命题:
①若a⊂α,b⊄α,a,b是异面直线,那么b∥α;
②若a∥α且b∥α,则a∥b;
③若a⊂α,b∥α,a,b共面,那么a∥b;
④若α∥β,a⊂α,则a∥β.
上面命题中,所有真命题的序号是.
解析:①中的直线b与平面α也可能相交,故不正确;②中的直线a,b可能平行、相交或异面,故不正确;由线面平行的性质得③正确;由面面平行的性质可得④正确.
答案:③④
8.(达州月考)α,β,γ是三个平面,a,b是两条直线,有下列三个条件:
①a∥γ,b⊂β;②a∥γ,b∥β;③b∥β,a⊂γ.
如果命题“α∩β=a,b⊂γ,且,则a∥b”为真命题,则可以在横线处填入的条件是(填上你认为正确的所有序号).
解析:①a∥γ,a⊂β,b⊂β,β∩γ=b⇒a∥b(线面平行的性质).
②如图所示,在正方体中,α∩β=a,b⊂γ,a∥γ,b∥β,而a,b异面,故②错.
③b∥β,b⊂γ,a⊂γ,a⊂β,β∩γ=a⇒a∥b(线面平行的性质).
答案:①③
能力提升(时间:15分钟)
9.(三明模拟)设α,β是两个不同的平面,m,n是平面α内的两条不同的直线,l
1,l
2
是平面β内
的两条相交直线,则α∥β的一个充分而不必要条件是( D )
(A)m∥β且l
1∥α(B)l
1
∥α且l
2
∥α
(C)m∥β且n∥β(D)m∥l
1且n∥l
2
解析:m∥l
1,且n∥l
2
⇒α∥β,但α∥β⇒/ m∥l
1
且n∥l
2
,所以“m∥l
1
,且n∥l
2
”是“α
∥β”的一个充分而不必要条件.
10.(亳州模拟)设平面α∥平面β,A∈α,B∈β,C是AB的中点,当点A,B分别在平面α,β内运动时,所有的动点C( D )
(A)不共面
(B)当且仅当A,B分别在两条直线上移动时才共面
(C)当且仅当A,B分别在给定的两条异面直线上移动时才共面
(D)无论A,B如何移动都共面
解析:因为平面α∥平面β,A∈α,B∈β,且C为AB的中点,所以点C在同一平面内,这个平面夹在平面α与β的正中间.
11.如图,L,M,N分别为正方体对应棱的中点,则平面LMN与平面PQR的位置关系是( C )
(A)垂直 (B)相交不垂直 (C)平行 (D)重合
解析:如图,分别取另三条棱的中点A,B,C 将平面LMN 延展为平面正六边形AMBNCL,因为PQ ∥AL,PR ∥AM,且PQ 与PR 相交,AL 与AM 相交,所以平面PQR ∥平面AMBNCL,即平面LMN ∥平面PQR.故选C.
12.(舟山模拟)如图所示,在正四棱柱ABCD-A 1B 1C 1D 1中,E,F,G, H 分别是棱CC 1,C 1D 1,D 1D,DC 的中点,N 是BC 的中点,点M 在四边形EFGH 及其内部运动,则M 只需满足条件 时,就有MN ∥平面B 1BDD 1. (注:请填上你认为正确的一个条件即可,不必考虑全部可能情况)
解析:连接HN,FH,FN,则FH ∥DD 1,HN ∥BD,
所以平面FHN ∥平面B 1BDD 1,只需M ∈FH,则MN ⊂平面FHN,所以MN ∥平面B 1BDD 1. 答案:点M 在线段FH 上
13. (保定模拟)在如图所示的多面体中,四边形ABB 1A 1和ACC 1A 1都为矩形.设D,E 分别是线段BC,CC 1的中点,在线段AB 上是否存在一点M,使直线DE ∥平面A 1MC?请证明你的结论.
解:取线段AB 的中点M,连接A 1M,MC,A 1C,AC 1,设O 为A 1C,AC 1的交点.
由已知,O为AC
1
的中点.
连接MD,OE,则MD,OE分别为△ABC,△ACC
1
的中位线, 所以MD AC,OE AC,
因此MD OE.
连接OM,从而四边形MDEO为平行四边形,
则DE∥MO.
因为直线DE⊄平面A
1MC,MO⊂平面A
1
MC,
所以直线DE∥平面A
1
MC.
即线段AB上存在一点M(线段AB的中点),使直线DE∥平面A
1
MC.
14.如图,四棱锥P-ABCD中,AB∥CD,AB=2CD,E为PB的中点.
(1)求证:CE∥平面PAD;
(2)在线段AB上是否存在一点F,使得平面PAD∥平面CEF?若存在,证明你的结论,若不存在,请说明理由.
(1)证明:取PA的中点H,连接EH,DH,
因为E为PB的中点,
所以EH∥AB,EH=AB,
又AB∥CD,CD=AB,
所以EH∥CD,EH=CD,
因此四边形DCEH是平行四边形,
所以CE∥DH,
又DH⊂平面PAD,CE⊄平面PAD,
因此CE∥平面PAD.
(2)解:存在点F为AB的中点,使平面PAD∥平面CEF, 证明如下:
取AB的中点F,连接CF,EF,
所以AF=AB,
又CD=AB,所以AF=CD,
又AF∥CD,
所以四边形AFCD为平行四边形,
因此CF∥AD,
又CF⊄平面PAD,
所以CF∥平面PAD,
由(1)可知CE∥平面PAD,
又CE∩CF=C,
故平面CEF∥平面PAD,
故存在AB的中点F满足要求.。
