永续年金现值公式例题
财务管理第二章练习题

财务管理第二章练习题第二章练习题1、资金的时间价值的实质是资金周转使用后的增值额,是资金所有者让渡资金使用权而参与社会财富分配的一种形式。
2、时间价值只产生与生产领域和流通领域。
3、只有运动着的资金才能产生时间价值。
4、时间价值的大小取决于资金周转速度的快慢。
5、一次性收付款项、终值(本利)、现值(未来某一时点上的一定量的现金折合到现在的价值)一些公式:1、单利:I=P×i ×n2、单利终值:F=P(1+i×n )3、单利现值:P=F/(1+i×n )4、复利终值:F=P(1+i)n 或:P (F/P,i ,n )5、复利现值:P=F×(1+i)-n或: F (P/F,i ,n )6、普通年金终值:F=A[(1+i)n-1]/i或:A (F/A,i ,n )7、年偿债基金:A=F×i/[(1+i)n-1] 或:F (A/F,i ,n )8、普通年金现值:P=A{[1-(1+i)-n]/i}或:A (P/A,i ,n )9、年资本回收额:A=P{i/[1-(1+i)-n]}或:P (A/P,i ,n )10、即付年金的终值:F=A{[(1+i)n+1-1]/i -1}或:A[(F/A,i ,n+1)-1]11、即付年金的现值:P=A{[1-(1+i)-n-1]/i+1}或:A[(P/A,i ,n-1)+1]12、递延年金现值:第一种方法:P=A{[1-(1+i)-m-n]/i-[1-(1+i)-m]/i}或:A[(P/A,i ,m+n)-(P/A,i ,m )]第二种方法:P=A{[1-(1+i)-n]/i× [(1+i)-m]}或:A[(P/A,i ,n )×(P/F,i ,m )]= A( F/A ,i ,n )(P/F,i ,m+n)第三种方法:P= A( P/A ,i ,n )(P/F,i ,m )13、永续年金现值:P=A/i14、折现率:i=[(F/p)1/n]-1(一次收付款项)i=A/P(永续年金)比如,若银行存款年利率为10%,将今天的1元钱存入银行,一年以后就会是1.10元。
永续年金现值的计算
○理解并掌握各Leabharlann 年金现值、年金终值的含义与计算方法; 掌握利率、期限、年金以及名义利率与实际利率的互算;
能力目标
○能够根据普通年金的计算公式推算出预付年金、递延年金、 永续年金时间价值的计算;
○能进行利率、期间和各种系数之间的换算;能利用内插值 求解利率、求期限;
○能利用资金时间价值原理进行相应理财活动的应用决策。
分析提示:P=0.46÷5%=9.20元
假设一年期的国债的平均利率为3%。那么,该企业 要向学校捐赠多少款项才能创建该爱心基金呢?
分析提示:
P=10÷3%=333.33万元
【例2-16】对佛山照明投资价格的确定
佛山照明自1993年上市以来,一直十分重视对股东 的回报,自1994~2009年期间每10股平均现金 分红达4.60元,被誉为国内资本市场的“现金奶 牛”。如果你的期望报酬率为5%。请问,若该 公司继续保持分红能力,你在愿意在多少的价位 以下购入并长期持有该股股票?
永续年金是指无限期等额收付的年金。 永续年金因为没有终止期,只有现值没有终值。 永续年金现值计算公式:
0
1
2
3
4
5…
n→∞
【例2-15】创建一个永久性的爱心基金
江南公司想给学校创立一个永久性的爱心基金,希 望每年能从该基金中拿出10万元用于经济困难 学生的生活补助。
考虑到基金资金的安全性,基金管理人计划将基金 的购买近乎无风险的国债,用其产生的利息收入 用于学生的补助。
年金现值怎么计算例题

年金现值怎么计算例题
年金现值通常为每年投资收益的现值总和,它是一定时间内每期期末收付款项的复利现值之和。
每年取得收益1元,年利率为10%,为期5年,上例逐年的现值和年金现值,可计算如下:1年1元的现值=0.909(元)
2年1元的现值=0.826(元)
3年1元的现值=0.751(元)
4年1元的现值=0.683(元)
5年1元的现值=0.621(元)
1元年金5年的现值=3.790(元)
计算普通年金现值的一般公式为:
P=A/(1+i)1+A/(1+i)2…+A/(1+i)n,(1)
等式两边同乘(1+i)
P(1+i)=A+A/(1+i)1+…+A/(1+i)(n-1),(2)
(2)式减(1)式
P(1+i)-P=A-A/(1+i)n,
剩下的和上面一样处理就可以了。
普通年金1元、利率为i,经过n期的年金现值,记作(P/A,i,n),可查年金现值系数表。
另外,预付年金、递延年金的终值、现值以及永续年金现值的计算公式都可比照上述推导方法,得出其一般计算公式。
扩展资料:
普通年金终值指一定时期内,每期期末等额收入或支出的本利和,也就是将每一期的金额,按复利换算到最后一期期末的终值,然后加总,就是该年金终值.例如:每年年初存款1元,年利率为10%,经过5年,逐年的终值和年金终值,可计算如下:
1元1年的终值=(1+10%)^0=1.00(元)
1元2年的终值=(1+10%)^1=1.10(元)
1元3年的终值=(1+10%)^2=1.21(元)
1元4年的终值=(1+10%)^3=1.331(元)
1元5年的终值=(1+10%)^4=1.4641元
,1,。
(完整版)现值和终值的计算

客观题企业现在需购进一台设备,买价为 20000元,其应用年数为 10年,如果租用,则每年年初付租金 2500 元,不考虑其余的因素,如果利率 为 10%,则应采用购入的方式()。
答案:×解析:租金现值为 2500+2500( P/A ,10%,9)=2500+2500*5.7590=16897.5 (元),所以应该选择租赁的方式。
A 、 10×[( P/A , 10%, 15) - ( P/A , 10%, 5)] B 、 10×( P/A , 10%, 10) ( P/F 10%,5) C 、 10×[ ( P/A , 10%, 16) - ( P/A , 10%, 6)] D 、 10×[ ( P/A , 10%, 15) - ( P/A , 10%, 6)] 答案:AB解析:按递延年金求现值公式:递延年金现值 =A ×( P/A ,i ,n )×( P/F ,i ,m )=A ×[ ( P/A ,i , m+n )- ( P/A,i,m )],m 表示递延期,n+m 表示总期数,一定注意应将期初问题转化为期末,所以 m=5,n+m=15。
某企业向租赁公司租入设备一套,价值 200 万元,租期为 3 年,综合租赁费率为 10%,则每年年末支付的等额租金为( )A 、 60.42 万元 B 、 66.66 万元 C 、 84.66 万元 D 、 80.42 万元 答案: D解析:企业每年年末支付的租金 =200/ (P/A ,10%, 3)=200/2.4869=80.42 (万元)下列说法中正确的有()。
A 、复利终值系数和复利现值系数互为倒数B 、普通年金终值系数和偿债基金系数互为倒数C 、偿债基金系数和资本回收系数互为倒数D 、普通年金现值系数和资本回收系数互为倒数 答案: ABD解析:注意各种系数之间的对应关系。
复利现值、终值、年金现值终值公式、实例

解:本例因为涉及到年金当中的递延年金,所以将年金系列一起先介绍,然后解题年金,是指一定时期内每次等额收付款的系列款项,通常记作A 。
如保险费、养老金、折旧、租金、等额分期收款、等额分期付款以及零存整取或整存零取储蓄等等。
年金按每次收付发生的时点不同,可分为普通年金、即付年金、递延年金、永续年金等。
结合本例,先介绍普通年金与递延年金,其他的在后面介绍。
一、普通年金,是指从第一期起,在一定时期内每期期末等额发生的系列收付款项,又称后付年金。
1.普通年金现值公式为:ii A i A i A i A i A P nn n ------+-⨯=+⨯++⨯+++⨯++⨯=)1(1)1()1()1()1()1(21Λ 式中的分式ii n -+-)1(1称作“年金现值系数”,记为(P/A ,i ,n ),可通过直接查阅“1元年金现值表”求得有关的数值,上式也可写作:P=A (P/A ,i ,n ). 2.例子:租入某设备,每年年末需要支付租金120元,年复利利率为10%,则5年内应支付的租金总额的现值为:%10%)101(1120)1(15--+-⨯=+-⨯=i i A P n 4557908.3120≈⨯=(元) 二、递延年金,是指第一次收付款发生时间与第一期无关,而隔若干期(假设为s 期,s ≥1),后才开始发生的系列等额收付款项。
它是普通年金的特殊形式,凡不是从第一期开始的年金都是递延年金。
1.递延年金现值公式为:[]),,/(),,/()1(1)1(1s i A P n i A P A i i i i A P s n -⨯=⎥⎦⎤⎢⎣⎡+--+-⨯=-- (1) 或),,/(),,/()1()1(1)(s i F P s n i A P A i ii A P s s n ⨯-⨯=+⨯+-⨯=--- (2) 上述(1)公式是先计算出n 期的普通年金现值,然后减去前s 期的普通年金现值,即得递延年金的现值,公式(2)是先将些递延年金视为(n-s)期普通年金,求出在第s 期的现值,然后再折算为第零期的现值。
1、某企业使用M零件,可以自制也可以外购,年需用量为72000件,
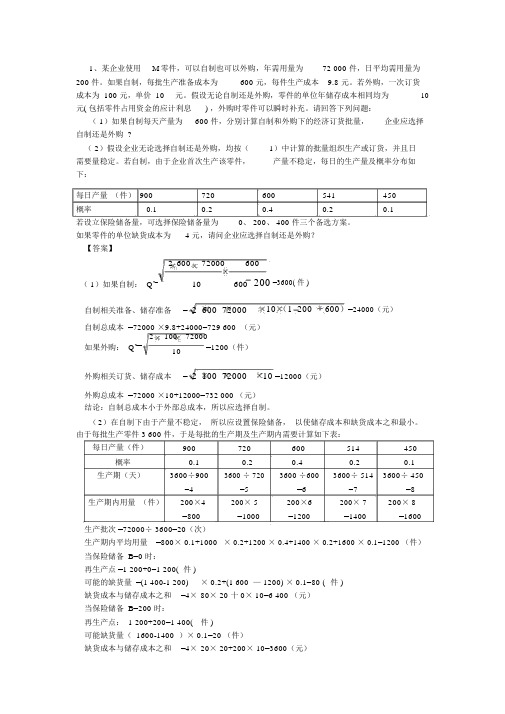
1、某企业使用M零件,可以自制也可以外购,年需用量为72 000 件,日平均需用量为200 件。
如果自制,每批生产准备成本为600 元,每件生产成本9.8 元。
若外购,一次订货成本为 100 元,单价 10元。
假设无论自制还是外购,零件的单位年储存成本相同均为10元( 包括零件占用资金的应计利息) ,外购时零件可以瞬时补充。
请回答下列问题:( 1)如果自制每天产量为600 件,分别计算自制和外购下的经济订货批量,企业应选择自制还是外购 ?( 2)假设企业无论选择自制还是外购,均按(1)中计算的批量组织生产或订货,并且日需要量稳定。
若自制,由于企业首次生产该零件,产量不稳定,每日的生产量及概率分布如下:每日产量(件) 900720600541450概率0.10.20.40.20.1若设立保险储备量,可选择保险储备量为0、 200、 400 件三个备选方案。
如果零件的单位缺货成本为 4 元,请问企业应选择自制还是外购?【答案】260072000600( 1)如果自制: Q*=10600200 =3600( 件 )自制相关准备、储存准备= 2 600 7200010 (1 200600)=24000(元)自制总成本 =72000 ×9.8+24000=729 600 (元)210072000=1200(件)如果外购: Q*==10外购相关订货、储存成本= 2 100 7200010 =12000(元)外购总成本 =72000 ×10+12000=732 000 (元)结论:自制总成本小于外部总成本,所以应选择自制。
(2)在自制下由于产量不稳定,所以应设置保险储备,以使储存成本和缺货成本之和最小。
由于每批生产零件 3 600 件,于是每批的生产期及生产期内需要计算如下表:每日产量(件)900720600514450概率0.10.20.40.20.1生产期(天)3600÷9003600 ÷ 7203600 ÷6003600÷ 5143600÷ 450=4=5=6=7=8生产期内用量(件)200×4200× 5200×6200× 7200× 8=800=1000=1200=1400=1600生产批次 =72000÷ 3600=20(次)生产期内平均用量=800× 0.1+1000× 0.2+1200 × 0.4+1400 × 0.2+1600 × 0.1=1200 (件)当保险储备 B=0 时:再生产点 =1 200+0=1 200( 件 )可能的缺货量 =(1 400-1 200)× 0.2+(1 600 — 1200) × 0.1=80 (件 )缺货成本与储存成本之和=4×80× 20 十 0× 10=6 400 (元)当保险储备 B=200 时:再生产点: 1 200+200=1 400(件 )可能缺货量( 1600-1400)× 0.1=20 (件)缺货成本与储存成本之和=4×20× 20+200× 10=3600(元)当保险储备 B=400 时:再生产点 =1 200+400=1 600( 件 )可能的缺货量 =0缺货成本与储存成本之和 =4× 0× 20+400× 10=4000(元)因为当保险储备B=200 时,缺货成本与储存成本之和最小,所以,保险储备应为200 件。
练习讲解及递延永续年金

某人从第四年末起, 每年年末支付100元, 利率为10%,问第 七年末共支付利息多 少?
答案:
例题
01
F=A(F/A,10%,4)
单击此处添加正文,文字是您思想的提炼,请尽量言简意赅地阐述 观点。
02
=100×4.641=464.1(元)
100 100 100 100
(一)递延年金现值
结论:按现值比较,仍是方案2
较好
F5 =800 000 (1+7%)5=1 122 080 或F5 =800 000 (F/P,7%,5) =1 122 080
03
方案二的终值:
F5 =1 000 000 所以应选择方案二。 现在一次性付80万 元;另一方案是5年 后付100万
例题
例.某人拟购房,开 发商提出两种方案, 一是5年后付120万 元,另一方案是从现 在起每年末付20万, 连续5年,若目前的 银行存款利率是7%, 应如何付款?
○ 答案:
问题
有一项年金,前3年无流入, 后5年每年年初流入500万元, 假设年利率为10%,现值为 ( )万元。 1994.59 1565.68 1813.48 1423.21
解答
有一项年金,前3年无流入,后5年每年年初 流入500万元,假设年利率为10%,现值为 ( )万元。
A.1994.59 B.1565.68 C.1813.48 D.1423.21 P=500×(P/A,10%,5)×(P/F,10%, 2) =1565.68 答案:B
方案一的终值:
F=120(万元)
方案二的终值:
○ F=20×(F/A,7%,5) =20 × (5.7507) =115.014(万元)
第二专题家庭理财计算基础1

C×(1+g) C ×(1+g)2
2 3
…
C C (1 g ) C (1 g ) 2 PV 2 3 (1 r ) (1 r ) (1 r )
(期末)增长型永 续年金的现值计算 公式(r>g)为:
C PV rg
恩碧教学
例题:增长型永续年金的现值
• 某增长型永续年金明年将分红1.30元,并将以5%的 速度增长下去,年贴现率为10%, 那么该年金的现值 是多少?
恩碧教学
案例2
• 假设刘先生将10万元投资在某建筑工程公司, 期限5年,年投资回报率为8%。 • 问:5年后的本息和为多少?
FV = PV×(1 + r)n FV = 10×(1+8%)5 FV = 14.69万元
恩碧教学
“利滚利”演示
假如你买彩票中奖100万,将其存为10年期, 年利率为6%的定期存款,按复利计算。或者, 你将其交给表兄打理,10年中,每年按7.5%的 单利计算。10年后,哪种方式获利多? A. 定期存款的终值是1,000,000 x (1+6%)10 = 1,790,847.70 元 B. 从表兄那里获得的终值是 1,000,000 + 1,000,000 x 7.5% x 10 = 1,750,000.00 元
1.30 0 1
1.30×(1.05) 2
1.30 ×(1.05)2
…
3
1.30 PV 26.00元 0.10 0.05
恩碧教学
3.5 期末年金与期初年金
• 期末年金:工资薪金收入、利息收入,红利收入, 房贷本息支付,储蓄等。 C 0 C C C C T
1 2
3
