第三章 固体材料中的扩散作业答案
材料化学作业考研题目及答案

材料化学作业考研题目及答案题目:材料化学中的扩散现象在材料化学中,扩散是指物质在固体、液体或气体中的运动过程,它在材料加工和性能优化中起着至关重要的作用。
扩散现象可以通过Fick's定律来描述,该定律指出扩散通量与浓度梯度成正比。
本题旨在考察学生对扩散现象的理解以及如何应用扩散定律解决实际问题。
一、简答题(共20分)1. 简述扩散现象的定义及其在材料科学中的重要性。
(5分)2. 解释Fick's第一定律,并给出扩散通量的表达式。
(5分)3. 扩散系数是如何影响扩散速率的?(5分)4. 扩散过程在金属材料的哪些应用中至关重要?(5分)二、计算题(共30分)1. 假设一个纯金属棒,其初始温度为T0,一端加热至T1,另一端保持在T0。
如果已知扩散系数D(T)随温度变化的函数为D(T) = D0 * exp(-Q/kT),其中D0和Q是常数,k是Boltzmann常数。
求在时间t 后,该棒中某点x处的浓度分布。
(15分)2. 给定一个扩散系统,其扩散系数D为常数,初始条件为C(x,0) = C0,边界条件为C(0,t) = C1,C(L,t) = 0。
求该系统的浓度分布C(x,t)。
(15分)三、论述题(共50分)1. 论述扩散在合金化过程中的作用及其对合金性能的影响。
(20分)2. 描述扩散在半导体材料制备过程中的应用,并讨论其对器件性能的影响。
(20分)3. 扩散在陶瓷材料中的应用及其对材料性能的贡献。
(10分)答案:一、简答题1. 扩散现象是指物质在空间中的自发运动,它在材料科学中的重要性体现在材料的制备、加工和性能优化等方面。
2. Fick's第一定律表达式为J = -D * (dC/dx),其中J是扩散通量,D是扩散系数,C是浓度,x是位置。
3. 扩散系数D越大,表示物质的扩散能力越强,扩散速率也就越快。
4. 扩散在金属材料的合金化、热处理、腐蚀防护等应用中至关重要。
二、计算题1. 根据题目所给条件,可以推导出该棒中某点x处的浓度分布函数为C(x,t) = C0 + (C1 - C0) * erf(x/(2 * sqrt(D0 * D * t)) *sqrt(1/k * (1/T0 - 1/T1)))。
固体的扩散习题与答案

固体的扩散习题与答案固体的扩散习题与答案扩散是指物质在空间中自发的、无宏观流动的传递过程。
在固体中,扩散现象常常发生,它对于材料的性能和应用具有重要影响。
下面将介绍一些固体扩散的习题和答案,帮助读者更好地理解和掌握这一概念。
习题一:某金属材料的扩散系数为2.5×10^-5 cm^2/s,温度为800℃。
若在1小时内,该金属材料中某种元素的浓度从表面向内部下降了0.1%,求该元素在1小时内的扩散深度。
解答:根据扩散定律,扩散深度可以用以下公式计算:L = √(D × t)其中,L表示扩散深度,D表示扩散系数,t表示时间。
代入已知数据,得到:L = √(2.5×10^-5 cm^2/s × 3600 s)计算结果约为0.3 cm。
所以,在1小时内,该元素的扩散深度约为0.3 cm。
习题二:某金属材料的扩散系数为1.8×10^-6 m^2/s,温度为900K。
若在10小时内,该金属材料中某种元素的扩散深度为0.5 mm,求该金属材料的扩散系数。
解答:根据扩散定律,扩散系数可以用以下公式计算:D = (L^2)/(4t)其中,D表示扩散系数,L表示扩散深度,t表示时间。
代入已知数据,得到:D = (0.5×10^-3 m)^2 / (4 × 10 × 3600 s)计算结果约为2.08×10^-7 m^2/s。
所以,该金属材料的扩散系数约为2.08×10^-7 m^2/s。
习题三:某金属材料的扩散系数为1.2×10^-9 cm^2/s,温度为500℃。
若在5小时内,该金属材料中某种元素的扩散深度为0.2 mm,求该元素的扩散时间。
解答:根据扩散定律,扩散时间可以用以下公式计算:t = (L^2)/(4D)其中,t表示扩散时间,L表示扩散深度,D表示扩散系数。
代入已知数据,得到:t = (0.2 mm)^2 / (4 × 1.2×10^-9 cm^2/s)计算结果约为2.78×10^7 s。
第三章 固体中的扩散

d i G iQ iO dx dx
3-2 扩散热力学
一摩尔 i 组元原子扩散驱动力的表达式为:
d i Fi dx
式中负号表示驱动力与化学位下降的方向一致,也就是扩
散总是向化学位减小的方向进行。
3-2 扩散热力学
二、扩散定律的热力学说明
(一)原子迁移率 在化学位梯度的驱动下,i 组元原子在固体中的平均扩 散速度vi正比于驱动力Fi,即:
设原子的振动频率为,间隙原子最邻近的间隙位置
数为Z(即间隙配位数),则:
Zp Z exp( G
kT )
3-3 扩散机制和扩散激活能
由于 G E TS ,故有: Z exp( 因此: D Pd Pd Z exp(
2 2
S
k
) exp(
i i0 kT lnai i0 kT ln iCi
3-2 扩散热力学
1 d ln i d i kT ( )dCi Ci dCi J i Ci Bi kT ( 1 d ln i dCi ) Ci dCi dx d ln i dCi ) d lnCi dx
n1 C1d n2 C2d
dC d 其中: C 2 C1 dx dC 2 d 故: ( n1 n2 ) dx
因而: J Pd 2
dC dx
3-3 扩散机制和扩散激活能
扩散系数的表达式为:
D Pd
距离d 的平方成正比。
2
扩散系数与原子跳跃频率、跳跃方向几率 P和跳跃
vi Bi Fi
Bi为 i 组元原子在单位驱动力作用下的迁移速度,称为 原子迁移率。
3-2 扩散热力学
(二)扩散系数的表达式
【材料科学基础习题】固体中的扩散(可编辑)

【材料科学基础习题】固体中的扩散1.能否说扩散定律实际上只要一个,而不是两个?2.要想在800℃下使通过α-Fe箔的氢气通气量为2×10-8mol/(m2??s),铁箔两侧氢浓度分别为3×10-6mol/m3和8×10-8?mol/m3,若D=2.2×10-6m2/s,试确定:(1)(2)3.在硅晶体表明沉积一层硼膜,再在1200℃下保温使硼向硅晶体中扩散,已知其浓度分布曲线为若M=5×1010mol/m2,D=4×10-9m2/s;求距表明8μm处硼浓度达到 1.7×1010mol/m3所需要的时间。
4.若将钢在870℃下渗碳,欲获得与927℃下渗碳10h相同的渗层厚度需多少时间(忽略927℃和870℃下碳的溶解度差异)?若两个温度下都渗10h,渗层厚度相差多少?5.Cu-Al组成的互扩散偶发生扩散时,标志面会向哪个方向移动?6.设A,B元素原子可形成简单立方点阵固溶体,点阵常数a=0.3nm,若A,B原子的跳动频率分别为10-10s-1和10-9s-1,浓度梯度为1032原子/m4,计算A,B原子通过标志界面的通量和标志面移动速度。
7.根据无规行走模型证明:扩散距离正比于。
8.将一根高碳钢长棒与纯铁棒对焊起来组成扩散偶,试分析其浓度分布曲线随时间的变化规律。
9.以空位机制进行扩散时,原子每次跳动一次相当于空位反向跳动一次,并未形成新的空位,而扩散激活能中却包含着空位形成能,此说法是否正确?请给出正确解释。
10.??间隙扩散计算公式为,为相邻平行晶面的距离,为给定方向的跳动几率,为原子跳动频率;(1)(2)(3)925℃下,20℃下,讨论温度对扩散系数的影响。
11.??为什么钢铁零件渗碳温度一般要选择γ相区中进行?若不在γ相区进行会有什么结果? 12.??钢铁渗碳温度一般选择在接近但略低于Fe-N系共析温度(500℃),为什么? 13.??对掺有少量Cd2+的NaCl晶体,在高温下与肖脱基缺陷有关有关的Na+空位数大大高于与Cd2+有关的空位数,所以本征扩散占优势;低温下由于存在Cd2+离子而造成的空位可使Na+离子的扩散加速。
固体中的扩散 作业

一、名词解释1.上坡扩散2.柯肯达尔效应3.菲克第一定律4.自扩散5.反应扩散二、简答题1.为什么钢铁零件渗碳温度一般要选择γ相区中进行?若不在γ相区进行会有什么结果?2.三元系发生扩散时,扩散层内能否出现两相共存区域,三相共存区?为什么?三、综合题1.以空位机制进行扩散时,原子每次跳动一次相当于空位反向跳动一次,并未形成新的空位,而扩散激活能中却包含着空位形成能,此说法是否正确?请给出正确解释。
2.指出以下概念中的错误。
(1)如果固溶体中不存在扩散流,则说明原子没有扩散。
(2)因固体原子每次跳动方向是随机的,所以在没有任何扩散情况下扩散通量为零。
(3)晶界上原子排列混乱,不存在空位,所以空位机制扩散的原子在晶界处无法扩散。
(4)间隙固溶体中溶质浓度越高,则溶质所占的间隙越多,供扩散的空余间隙越少,即z值越小,导致扩散系数下降。
(5)体心立方比面心立方的配位数要小,故由关系式可见,α-Fe 中原子扩散系数要小于γ-Fe中的扩散系数。
3.一块0.1%C的钢在930℃渗碳,渗到0.5mm的地方碳浓度达到0.45%,在t >0的全部时间内,渗碳气氛始终保持在表面成分为1%,假设D=1.4×10-7cm2/s。
P142a)计算渗碳时间。
b)若将渗层增加一倍所需时间。
c)设D=0.25exp(-34500/RT)cm2/s。
若在某温度渗碳在0.1cm 处为0.45%C与930℃在0.05cm处达同样浓度所需时间相同,渗碳温度为多少?4. 在950℃下对纯铁进行渗碳,并希望在0.1mm的深度得到ω(C)=0.9%的碳含量。
假设表面碳含量保持在ω(C)2=1.20%,扩散系数Dγ-Fe=10-10m2/s。
计算为达到此要求至少要渗碳多少时间。
P142 查表P141 表3-15.有两种激活能分别为Q1=83.7kJ/mol和Q2=251kJ/mol的扩散反应。
观察在温度从25℃高到60℃对这两种扩散的影响,并对结果做出评述。
材料化学-第三章无机材料化学习题及答案
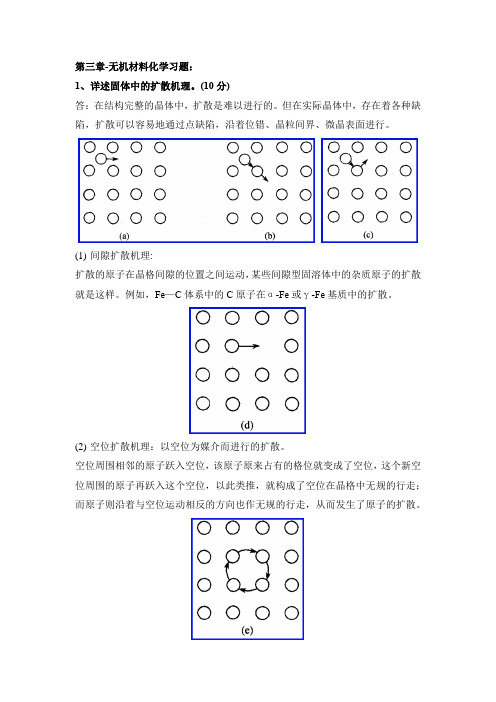
第三章-无机材料化学习题:1、详述固体中的扩散机理。
(10分)答:在结构完整的晶体中,扩散是难以进行的。
但在实际晶体中,存在着各种缺陷,扩散可以容易地通过点缺陷,沿着位错、晶粒间界、微晶表面进行。
(1)间隙扩散机理:扩散的原子在晶格间隙的位置之间运动,某些间隙型固溶体中的杂质原子的扩散就是这样。
例如,Fe—C体系中的C原子在α-Fe或γ-Fe基质中的扩散。
(2)空位扩散机理:以空位为媒介而进行的扩散。
空位周围相邻的原子跃入空位,该原子原来占有的格位就变成了空位,这个新空位周围的原子再跃入这个空位,以此类推,就构成了空位在晶格中无规的行走;而原子则沿着与空位运动相反的方向也作无规的行走,从而发生了原子的扩散。
(3)环形扩散机理:是指在密堆积的晶格中,两个相邻的原子同时互相直接地调换位置,即处于对等位置上的两个原子同时跃迁而互换位置。
这种情况发生的几率是很低的,因为这将引起晶格的变形,且需要很高的活化能。
但是如果有三个或更多个原子同时发生环形的互换位置,则活化能较低,因而这种环形扩散机制是可能的。
上述机理都属于通过点缺陷体扩散。
晶体位错、晶粒间界面和表面上都是结构组分活动剧烈的地方。
低温微晶体试样或位错密度大的试样,主要是晶粒间界和表面上的扩散。
这时处于界面上的原子和杂质原子,沿晶面运动,发生吸着或化学吸附,扩散现象是很显著的。
并且由于临近晶粒间界面和相间界面处的结构比内部的结构要松弛些,这里的原子扩散活化能也要小一些,大约相当于固体的气化热。
高温扩散机理是体扩散,而低温扩散机理是晶粒间界扩散。
2、详述固相反应机理。
(10分)答:固相反应比气相或液相反应复杂,其反应机理为:(1)吸着现象:吸附和解析(2)在界面上或均相区内原子进行反应(3)在固体界面上或内部形成新物相的核,即成核反应(4)物质通过界面和相区的输运,包括扩散和迁移。
3、详述固体热分解反应的动力学过程。
(10分)答:固体化合物的热分解是一个常见且获得广泛应用的固相反应,例如石灰石分解为CaO和CO2就属于这类反应。
【精品】第三章 固体材料中的扩散作业答案.doc

第三章固体材料中的扩散Chapter3 The Diffusion in Solid Materials 作业1:原版教材第143页第22题22. Which type of diffusion do you think will be easier (have a lower activation energy)?a.C in HCP Tib.N in BCC Tic.Ti in BCC TiExplain your choice.Solution:A and b interstitial solid solutions, but c is a substitutional solid solution・ So the mechanism of diffusion of a and b is interstitial diffusion, and the mechanism of diffusion of c is the vacancy exchange. We have known that the activation energy for vacancy-assisted diffusion Q v are higher than those for interstitional diffusion Qi. So c is the most difficult one comparing a and b, HCP Ti is a close-packed structure, much closer than BCC, so b is the answer. The diffusion of N in BCC Ti will be easier (have a lower activation energy).作业2:原版教材第143页第19题19. Consider the possibility of solid solutions with Au acting as the solvent.a.Which elements (N, Ag,or Cs) is most likely toform an interstitial solid solution with Au?b.Which elements (N,Ag9 or Cs) is most likely toform a substitutional solid solution with Au? Solution:a.N is most likely to form an interstitial solid solution with Au;b.Ag is most likely to for a substitutional solid solution with Au.作业3:原版教材第143页第23题23・At one instant in time there is 0.19 atomic % Cu at the surface of Al and 0.18 atomic % Cu at a depth of 1.2mm below the surface. The diffusion coefficient of Cu in Al is 4xio-14m2/5 at the temperature of interest. The lattice parameter of FCC Al is 4.049A. What is the flux of Cu atoms from the surface to the interior?Solution:(Density (DensityJ = atoms ! cm 1 - s已矢口: Cu 的原子量(atomic mass) 63.55 ofsolid(g/cm 3)) 8.93Al 的原子量(atomic mass)26.98of solid(g/cm 3)) 2.70换算成重量百分 Cu%wt -Cu%at x Cu 原子量 Cu%at x Cu 原子量+ M%at x 4/原故(Cu%wtxdensity.of.FCC.AlS / 八小 .八“ ■ 3-------------------- ---- ------------ x2.7x6.02xl0^3 =l.\4\lx\0A)atoms/cm 3v Mol.wt.Cuc 2 = 1.08176 x IO 20 atoms / cm y+A ■/=_Dgj = _4xI(T 叫“2/s)x (108176-l .⑷ 7)x10% 讪 $/c"RX x 1.2mm=1.99Sx\0U}atoms/cm 2 -s 另一种算法:每个Al 晶胞有4个原子,晶胞体积为故Al 的原 子密度为:4 = 7 ------------ -------- 百=6.026 xlO 22 个 / cm 3a (4.049x10")已知Cu 的原子百分数为0.18%和0.19%,即0.0018, 0.0019Sic, = 0.0019 x 6.026x1022个/cvn' c2 = 0.0018 x 6.026 x 1022个/CM'0.12cmWe know that-QRTC\-C[ 14 4( 2 / \ -0.000lx 6.026xio 22 个/cm' J =_D ― =-4x10 xlO (cv/r/"x x=2.0087 xlO 1(,原子/(cm 2 •s) 作业4:原版教材第143页第27题27. Consider the diffusion of C into Fe. Atapproximately what temperature would a specimen of Fe have to be carburized for 2 hours to produce the same diffusion result as at 900°C for 15 hours ?Solution:The same diffusion result means that other variables are the same and Dit]=D 2t2900°CDl xl5 = D 2x2 T? 仓表可知:D Q 9OO °C =0.20X 10-\H 2 I SQ900 C 二 84 x 1 O ' J / molD ()>912 C = 2.0xl0 s m 2 /sQ>912°C = i40 x 103J/mol R 二&314J/mol-KD T = D900 x -— In D T = In Dg) + In 15 - In 2D T 15ln2.0-5-140x1()38.314T15~2lnO.2-5-84xl038.314x1173 )Then:x = 0.4/nm c =0.5%wtt = 4Shours0.5 = 1.0 - (1.0 -0.2 财0.4xlQ-3m270x48x360()50.5oi=0.625Z = 0.625 =0.4x10-3£> = 5.9259xl()T3 加2/$ T=18918k=1618.8°C作业5:原版教材第143页第30题(该题已知条件不全,取消)30. A Ti rod (HCP) is to be placed in a furnace in order to increase its carbon content. If the initial carbon content of the rod is 0.2 weight % and the carbon content in the furnace is the equivalent of 1.0 weight %,find the temperature required to yield a carbon content of 0.5 weight % at a depth of 0.4mm below the surface of the rod in 48 hours.Solution:We know that = i.o%wt5c{) = 0.2%vvZ作业6:将含碳0.2%的碳钢零件置于1.2%碳势的渗碳气氛中加热至930°C,经10小时保温后随炉冷却至室温,试分析在930°C和室温零件从表层到心部成分和组织的变化规律,并画出示意图。
材料科学基础扩散题库及答案

材料科学基础扩散题库及答案1、 简要说明影响溶质原子在晶体中扩散的因素。
答: 影响扩散的因素主要有温度,温度越高,扩散越快;晶体缺陷如界面、晶界位错容易扩散;不同致密度的晶体结构溶质原子扩散速度不一样,低致密度的晶体中溶质原子扩散快,各向异性也影响溶质原子扩散;在间隙固溶体中溶质原子扩散容易;扩散原子性质与基体金属性质差别越大,扩散越容易;一般溶质原子浓度越高,扩散越快;加入其它组元与溶质原子形成化合物阻碍其扩散。
2、Ni 板与Ta 板中有0.05mm 厚MgO 板作为阻挡层,1400℃时Ni +通过MgO 向Ta 中扩散,此时Ni +在MgO 中的扩散系数为D=9×10-12cm 2/s ,Ni 的点阵常数为3.6×10-8cm 。
问每秒钟通过MgO 阻挡层在2×2cm 2的面积上扩散的Ni +数目,并求出要扩散走1mm 厚的Ni 层需要的时间。
答:Ni 为fcc 结构,一个晶胞中的原子个数为4,依题意有:在Ni/MgO 界面镍板一侧的Ni 的浓度C Ni 为100%,每cm 3中Ni 原子个数为: N Ni/MgO =(4原子/晶胞)/(3.6×10-8cm 3)=8.57×1022原子/cm 3,在Ta/MgO 界面Ta 板一侧的Ni 的浓度0%,这种扩散属于稳态扩散,可以利用菲克第一定律求解。
故浓度梯度为dc/dx =(0-8.57×1022原子/cm 3)/(0.05cm )=-1.71×1024原子/(cm 3.cm ), 则Ni 原子通过MgO 层的扩散通量: J =-D (dc/dx )=-9×10-12cm 2/s ×(-1.71×1024原子/(cm 3.cm ))=1.54×1013Ni 原子/(cm 2.s)每秒钟在2×2cm 2的面积上通过MgO 层扩散的Ni 原子总数N 为 N =J ×面积=[1.54×1013Ni 原子/(cm 2.s)]×4cm 2=6.16×1013Ni 原子/s 。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
第三章固体材料中的扩散
Chapter3 The Diffusion in Solid Materials
作业1:原版教材第143页第22题
22. Which type of diffusion do you think will be easier (have a lower activation energy)?
a. C in HCP Ti
b. N in BCC Ti
c. Ti in BCC Ti
Explain your choice.
Solution:
A and b are interstitial solid solutions, but c is a substitutional solid solution. So the mechanism of diffusion of a and b is interstitial diffusion, and the mechanism of diffusion of c is the vacancy exchange. We have known that the activation energy for vacancy-assisted diffusion Q v are higher than those for interstitional diffusion Q i. So c is the most difficult one comparing a and b, HCP Ti is a close-packed structure, much closer than BCC, so b is the answer. The diffusion of N in BCC Ti will be easier (have a lower activation energy).
作业2:原版教材第143页第19题
19. Consider the possibility of solid solutions with Au acting as the solvent.
a. Which elements (N, Ag, or Cs) is most likely to form an interstitial solid solution with Au?
b. Which elements (N, Ag, or Cs) is most likely to form a substitutional solid solution with Au? Solution:
a. N is most likely to form an interstitial solid solution with Au;
b. Ag is most likely to for a substitutional solid solution with Au.
作业3:原版教材第143页第23题
23.At one instant in time there is 0.19 atomic % Cu at the surface of Al and 0.18 atomic % Cu at a depth of 1.2mm below the surface. The diffusion coefficient of Cu in Al is
s m /104214-⨯
at the temperature of interest.
The lattice parameter of FCC Al is 4.049Å. What is the flux of Cu atoms from the surface to the interior?
Solution:
已知:Cu 的原子量(atomic mass )63.55 (Density of solid(g/cm 3)) 8.93
Al 的原子量(atomic mass )26.98 (Density of solid(g/cm 3)) 2.70 换
算成重量百分数:
原子量
原子量原子量
Al at l Cu at Cu Cu at Cu wt Cu ⨯+⨯⨯=
%A %%%
当Cu 故321231
/1096.681002.6.....%cm atoms Cu wt Mol Al FCC of density wt Cu c
⨯=⨯⨯⎪⎭
⎫ ⎝⎛⨯= 3212/1002.19cm atoms c ⨯=
故
()
()s
cm atoms mm
cm atoms s m x c c D J -⨯=⨯-⨯
⨯-=--=-2103212
1412/10988.12.1/1002.1996.68/104
另一种算法:
每个Al 晶胞有4个原子,晶胞体积为a 3,故Al 的原子密度为:
()
322383/10026.610049.444cm cm
a 个⨯=⨯=- 已知Cu 的原子百分数为0.18%和0.19%,即0.0018,0.0019 故3221
/10026.60019.0cm c 个⨯⨯=
3222/10026.60018.0cm c 个⨯⨯=
()
()
s
cm cm
cm s cm x c c D J ∙⨯=⨯⨯-⨯
⨯⨯-=--=-2103222
41412/100087.212.0/10026.60001.0/10104原子个
作业4:原版教材第143页第27题
27. Consider the diffusion of C into Fe. At approximately what temperature would a specimen of Fe have to be carburized for 2 hours to produce the same diffusion result as at 900℃ for 15 hours ? Solution:
()⎪⎪⎭
⎫
⎝⎛--=Dt x erf c c c c s s 20 The same diffusion result means that other variables are the same and D 1t 1=D 2t 2 900℃
21521⨯=⨯D D T?
15
2
900=T D D We know that
RT
Q
D D -=exp
RT
Q D D -
=0ln ln
查表可知: D 0900℃ =s m /1020.025
-⨯
Q 900℃=mol J /10
843
⨯
D 0>912℃=s m /100.225
-⨯
Q>912℃=mol J /101403
⨯
R=8.314J/mol-K
D T =2
15900⨯
D
2ln 15ln ln ln 900-+=D D T
⎪⎪⎭⎫
⎝⎛⨯⨯--=⨯--1173
314.8108452.0ln 215314.81014050.2ln 3
3T T=1891.8k=1618.8℃
The same diffusion result means that other variables are the same and D 1t 1=D 2t 2 即:
0102exp(
)2
15
exp()Q
D RT Q
D RT -=- 121115
ln 2.0152
Q R T T ⎛⎫-== ⎪⎝⎭ 查表可知:
Q 1=mol J /10
843
⨯
R=8.314J/mol-K
计算可得:
T 2=1453.73K=1180.73℃
作业5:
作业6:将含碳0.2%的碳钢零件置于1.2%碳势的渗
碳气氛中加热至930℃,经10小时保温后随炉冷却至室温,试分析在930℃和室温零件从表层到心部成分和组织的变化规律,并画出示意图。
解答:
过共析共析亚共析
作业7:一根足够长的共析钢棒在800℃强脱碳气氛中从一端脱碳一段时间后,试画出沿长度方向
碳浓度分布曲线及组织示意图。
若将其缓慢冷
却至室温,画出室温下组织示意图。
解答:
1.
作业8:设有一个厚为0.1cm 的Si 图片,初始时有1千万个Si 原子中含有一个磷原子。
经加工处理后,在表面的每1千万个Si 原子中含有400个磷原子。
Si 的晶体结构为金刚石结构,每个晶胞中含有8个原子,晶胞常数nm a 543.0=,试计算该硅圆片的线浓度梯度和体积梯度。
解答: 1) 计算P%: 内部:%00001.0%10010
11
7
=⨯⨯=
i C
%004.0%10010
14007=⨯⨯=s C
线浓度梯度cm X C /%0399.01
.0%004.0%00001.0-=-=∆∆
体积浓度梯度:()
3223
8cm 106.1cm 104307.5--⨯=⨯=晶胞
V
107
个Si
原子的体积:3167
cm 102V 8
10-⨯=⨯晶胞
此体积中的P 浓度:3
15316
cm /105cm /10
21C 个个⨯=⨯=
-i
3
1836
cm /102cm /102400C 个个⨯=⨯=-s 体积浓度梯度:cm cm /10995.11
.0102105C 31918
15∙⨯-=⨯-⨯=
∆∆原子X
个磷原子
7
400。
