正弦函数、余弦函数、正切函数的图像和性质
正弦,余弦,正切函数的图像 与性质

性
典例一:1.函数y=sin(π+x),x∈的单调增区间是____________. 2. 求下列函数的单调增区间.
(1)y=1-sin ; (2)y=log(cos 2x).
典例二:1.函数y=的定义域是____________. 2.函数y=的定义域是________________. 3. 求函数f(x)=lg sin x+的定义域. 典例三:1.函数y=3tan的对称中心的坐标是 ________________________________ 2.函数y=sin的最小正周期是,则ω=______. 典例四:1.怎样由函数y=sin x的图象变换得到y=sin的图象,试叙述这 一过程.
课后作业 1.某同学给出了以下论断: ①将y=cos x的图象向右平移个单位,得到y=sin x的图象; ②将y=sin x的图象向右平移2个单位,可得到y=sin(x+2)的图象; ③将y=sin(-x)的图象向左平移2个单位,得到y=sin(-x-2)的图象; ④函数y=sin的图象是由y=sin 2x的图象向左平移个单位而得到的. 其中正确的结论是______(将所有正确结论的序号都填上).
4.下列函数中,不是周期函数的是( ) A.y=|cos x| B.y=cos|x| C.y=|sin x| D.y=sin|x|
5.定义在R上的函数f(x)既是奇函数又是周期函数,若f(x)的最小正周期 为π,且当x∈时,f(x)=sin x,则f的值为( ) A.- B. C.- D.
6.为了得到函数y=sin的图象,只需把函数y=sin的图象( ) A.向左平移个长度单位 B.向右平移个长度单位 C.向左平移个长度单位 D.向右平移个长度单位
2.函数y=tan(sin x)的值域为( ). A. B. C.[-tan 1,tan 1] D.以上均不对
余弦函数和正切函数的图像及性质课件

-4π
-3π
-2π
-π
o-1Biblioteka 余弦函数的单调性y
1
-3π
5π 2
-2π
3π 2
-π
π
2
o
-1
π
2
π
3π 2
2π
5π 2
3π
7π 2
4π
x
y=cosx (x∈R) ∈ π π ∈ 增区间为 [ π +2kπ, 2kπ],k∈Z π π ∈ 减区间为 [2kπ, 2kπ + π], k∈Z , 其值从-1增至 其值从 增至1 增至 减至-1 其值从 1减至 减至
π
x= 2kπ时 ymax=1 x= 2kπ+ π时 ymin=-1 周期为T=2π 偶
π
在x∈[2kπ, 2kπ+ π ] 上都是增函数 , 在x∈[2kπ- π , 2kπ ] 上都是减函数 。 (kπ+ π ,0) 2
对称中心 对称轴
π
2
x = kπ
正切函数的图像和性质
回忆: 回忆:怎样利用单位圆中的正弦线作出 图像的? y = sin x 图像的?
一、y=sinx 与 y=cosx 的性质
函 数 y= sinx 性质
(k∈z) ∈
y= cosx x∈ R [-1,1]
(k∈z) ∈
定义域 值域 最值及相应的 x 的集合 周期性 奇偶性 单调性
x∈ R [-1,1] x= 2kπ+ 2 时 ymax=1 x=2kπ- π 时 ymin=-1 2 周期为T=2π 奇 在x∈[2kπ- π, 2kπ+ ]2上 2 都是增函数 , 在 π 3 x∈[2kπ+ ,2kπ+ ]上π 2 2 都是减函数. (kπ,0) x = kπ+
正弦余弦正切函数图象

1-
643 34 6
y 3 1 3 3 1 3 0
3
3
o
1 -
2
-
3
2
x
2
(2) 描点
2-
(3) 连线
正切函数图像: ytanx,
y
xxR,且 xk2,kZ
思考:
2
正切函数 ytanx
1
图像是否有渐近线?
3 2
2
o
1 2
3 2
x
渐近线方程:
2
xk,(kZ)
2
二、三角函数图象的性质
上平移一个
单位得到的
.●
2
x
y=sinx
(2)按五个关键点列表
x
0
2
3 2
2
cosx 1 0 -1 0 1
-cosx
.y
1
o
-1 ●
-1 0 1 0 -y1= -cosx和
y=cosx 关
. y= cosx x [0,2 ] 于X轴对称 ●
.●
2
.
.3●
2
2
●
x
y= - cosx x [0, 2]
y=cosx
左移
2
y=cosx y=sinx
余弦曲线
返回目录
二、正弦函数的“五点画图法”
(0,0)、( , 1)、( ,0)、( 3 ,-1)、 (2 ,0)
2
2
y
1
●
●
0Hale Waihona Puke 2-1●3
2
●
●
2
x
y
●
1
●
0
2
-1
常见三角函数图像及其性质
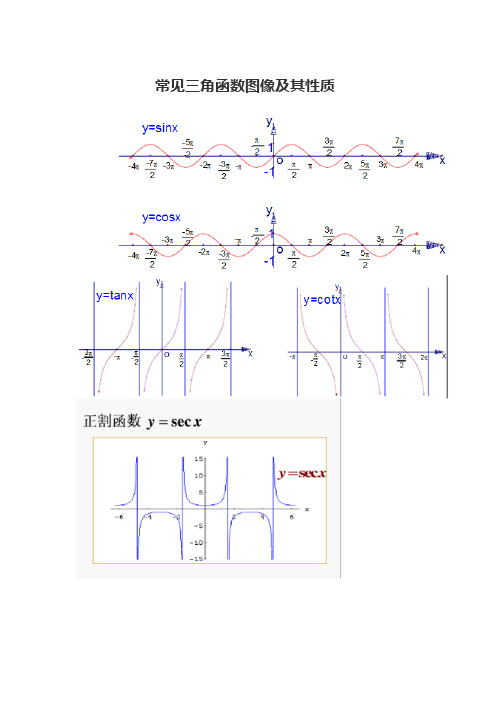
常见三角函数图像及其性质三角函数介绍正弦函数主词条:正弦函数格式:sin(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角对边长度比斜边长度的比值求出,函数值为上述比的比值,也是csc(θ)的倒数函数图像:波形曲线值域:[]1,1-余弦函数主词条:余弦函数格式:cos(θ)作用:在直角三角形中,将大小为(单位为弧度)的角邻边长度比斜边长度的比值求出,函数值为上述比的比值,也是sec(θ)的倒数函数图像:波形曲线值域:[]1,1-正切函数主词条:正切函数格式:tan(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角对边长度比邻边长度的比值求出,函数值为上述比的比值,也是cot(θ)的倒数。
函数图像:上图平面直角坐标系反映值域:()∞-∞,+余切函数主词条:余切函数格式:cot(θ)作用:在直角三角形中,将大小为θ(单位为弧度)的角邻边长度比对边长度的比值求出,函数值为上述比的比值,也是tan(θ)的倒数值域:()∞-∞,+正割函数主词条:正割函数格式:sec(θ)作用:在直角三角形中,将斜边长度比大小为θ(单位为弧度)的角邻边长度的比值求出,函数值为上述比的比值,也是cos(θ)的倒数函数图像:上图平面直角坐标系反映值域:(][)∞-1-,1∞,+余割函数主词条:余割函数格式:csc(θ)作用:在直角三角形中,将斜边长度比大小为θ(单位为弧度)的角对边长度的比值求出,函数值为上述比的比值,也是sin(θ)的倒数值域:(][)∞-1-∞,+,1。
1.3.2余弦、正切函数的图象与性质

π π y = 3tan u在u ?(kπ ,kπ + ),k Z 上单调递增. 2 2 1 π π 1 π π \ y = 3tan( x + )在kπ - 〈 x + 〈kπ + 2 4 2 2 4 2
即x ?(2kπ
3 π π,kπ + )上单调递增. 2 2 2
课堂小结
π π 1、y = tanx的作图是平移在( - , )上的图象得到的. 2 2
π y 例4:求下列函数的周期, = 3tan(2 x + ). 4
分析:利用周期函数定义及正切函数最小正周 期为π.
4 解:f(x) 3tan(2 x + ) = π
π = 3tan(2 x + + π) 4 轾 π π = 3tan 犏 x + ) + 2( 犏 2 4 臌
π \ 周期T = 2
π 周期T 2
π (1) y 3 tan(2 x ); 4
π f (x ) 2
1 π (2)变题y=3tan( x + ) 2 4
1 π 解: f ( x) 3tan( x ) 2 4 1 π 3tan( x π) 2 4
1 π 3tan[ ( x 2π) ] 2 4
新课导入
提问: 1、正弦函数 性质?
y sin x, x R
都有哪些
2、正弦函数的两个代数性质:
sin( x 2 ) sin x,sin( x) sin x
反映了正弦函数图象的什么几何特征?
教学目标
知识与能力
利用正切函数已有的知识(如定义、诱 导公式、正切线等)研究性质,根据性质探 究正切函数的图象.
三角函数的图像和性质

(ω>0)的最小正周期为π,则函数 ( π B.关于直线x= 对称 8 π D.关于点8 ,0对称 )
π 2π 解析:∵f(x)=sin ωx+4 的最小正周期为π,∴ ω =π,ω=2, π π π 3π ∴f(x)=sin 2x+4 .当x= 时,2x+ = ,∴A、C错误;当x 4 4 4
[即时应用] 求函数 y=cos x+sin
2
π x|x|≤ 4的最大值与最小值.
π 2 2 解:令 t=sin x,∵|x|≤ ,∴t∈- , . 4 2 2
∴y=-t
2
1 2 5 +t+1=-t-2 + , 4
1- 2 1 5 2 ∴当 t= 时,ymax= ,当 t=- 时,ymin= . 2 4 2 2 ∴函数 y=cos x+sin
2.求三角函数单调区间的 2 种方法 (1)代换法: 就是将比较复杂的三角函数含自变量的代 数式整体当作一个角 u(或 t),利用基本三角函数的单调性 列不等式求解. (2)图象法:画出三角函数的正、余弦曲线,结合图象 求它的单调区间.
[演练冲关] π 1.最小正周期为π且图象关于直线x= 对称的函数是( 3
π π B,因为sin2×3-6 =sin
π =1,所以选B. 2
答案:B
2.函数
π y=cos4-2x的单调减区间为____________. π π y=cos4-2x=cos2x-4 得
解析:由
π 2kπ≤2x- ≤2kπ+π(k∈Z), 4 π 5π 解得 kπ+ ≤x≤kπ+ (k∈Z). 8 8
π π π π 3 在 3,2 上单调递减知, = ,∴ω= . 2ω 3 2
三角函数的图象与性质
-
;
-1
y=cosx
2 3
4 5 4 5
6 x 6 x
五.定义域 、值域及取到最值时相应的x的集合:
-6 -5
-4 -3
复习回顾
-2 -
y y=sinx
1 o
-1
2 3
y
si-n6x的对称-5轴:x
k -4
2-,3对 称点-:2(k
,0);
-
y cosx的对称轴:x k , 对称点:(k ,0);
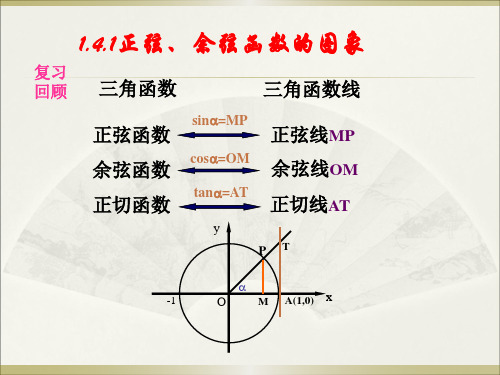
1.4.1正弦、余弦函数的图象
复习
回顾 三角函数
三角函数线
正弦函数 余弦函数 正切函数
sin=MP
正弦线MP cos=OM 余弦线OM tan=AT 正切线AT
y PT
-1
O
M A(1,0) x
正弦、余弦函数的图象
问题:如何作出正弦、余弦函数的图象?
途径:利用单位圆中正弦、余弦线来解决。
描图:用光滑曲线
复习回顾
一.正弦余弦函数的作图: 几何描点法(利用三角函数线) 五点法作简图
二.周期性:
函数y Asin(x )和y Acos(x ),x R的周期T 2 | |
三.奇偶性:
y sin x为奇函数,图像关于原点对称; y cosx为偶函数图像关于y轴对称。
-6 -5
-4 -3
复习回顾 y y=sinx
(0,11)
3
( 2 ,1)
-
(-o12 ,0)
( 2 ,0)
2
( ,-1)
3
线
4
5 6 x
正弦、余弦函数的图象
y
五点画图法
1
(
2
,1)
三角函数的图像与性质

三角函数的图像与性质三角函数是数学中的重要概念,它们在几何、物理、工程等领域中都有广泛的应用。
本文将介绍三角函数的图像与性质,包括正弦函数、余弦函数和正切函数。
正弦函数的图像与性质正弦函数是最基本的三角函数之一,它表示一个周期性变化的曲线。
正弦函数的图像可以通过在单位圆上取点来得到。
在单位圆上,我们可以将角度与坐标点联系起来,从而得到正弦函数的图像。
正弦函数的图像是一个连续的曲线,它在每个周期内都会经过最高点和最低点。
正弦函数的周期是360度或2π弧度,即在一个周期内,正弦函数的值会重复出现。
正弦函数的最高点和最低点分别为1和-1,它们对应于角度为90度或π/2弧度和270度或3π/2弧度。
正弦函数还具有以下性质: - 正弦函数是奇函数,即f(-x)=-f(x)。
- 正弦函数在0度或0弧度时取得最小值0。
- 正弦函数在90度或π/2弧度时取得最大值1。
- 正弦函数在180度或π弧度时取得最小值0。
- 正弦函数在270度或3π/2弧度时取得最大值-1。
余弦函数的图像与性质余弦函数是另一个常见的三角函数,它也表示一个周期性变化的曲线。
余弦函数的图像可以通过在单位圆上取点来得到。
与正弦函数类似,余弦函数的图像也是一个连续的曲线,它在每个周期内都会经过最高点和最低点。
余弦函数的周期也是360度或2π弧度,即在一个周期内,余弦函数的值会重复出现。
余弦函数的最高点和最低点分别为1和-1,它们对应于角度为0度或0弧度和180度或π弧度。
余弦函数还具有以下性质: - 余弦函数是偶函数,即f(-x)=f(x)。
- 余弦函数在0度或0弧度时取得最大值1。
- 余弦函数在90度或π/2弧度时取得最小值0。
- 余弦函数在180度或π弧度时取得最大值-1。
- 余弦函数在270度或3π/2弧度时取得最小值0。
正切函数的图像与性质正切函数是三角函数中的另一个重要概念,它表示一个周期性变化的曲线。
正切函数的图像可以通过在单位圆上取点来得到。
