2020年江西省中考数学模拟试题 (含案)
【2020精品】江西省九年级数学中考模拟试题含答案

2020江西省九年级数学中考模拟试题一、选择题(本大题共6小题,每小题3分,共18分) 1.下列计算正确的是 ( )A. -3-(-3) =-6B. -3-3=0C.-3÷3×3=-3D. -3÷3÷3=-32. 在△ABC 中,∠B =∠C ,与△ABC 全等的三角形有一个角是100°,那么在△ABC 中与这100°角对应相等的角是( )A.∠AB.∠BC.∠CD.∠B 或∠C3.下面说法中,不.正确的是 ( ) A .绝对值最小的实数是0 B .立方根最小的实数是0 C .平方最小的实数是0 D .算术平方根最小的实数是04.下列计算结果为正数的是 ( ) A .21()2-- B.01()2-- C. 31()2- D.-125.在下列说法中,菱形对角线不具有的性质是 ( ) A .对角线互相垂直; B.对角线所在的直线是对称轴; C .对角线相等; D.对角线互相平分.6.如图抛物线2y=ax bx c ++与x 轴交于A 、B 两点,其中B 点坐标为(4,0),直线DE 是抛物线的对称轴,且与x 轴交于点E ,C D⊥DE 于D ,现有下列结论:① a <0, ② b <0, ③ 2b -4ac >0, ④ AE+CD=4下列选项中选出的结论完全正确..............的.是. . (第6题) A .①②③ B. ①②④ C. ① ③ ④ D. ①②二、填空题 (本大题共6小题,每小题3分,共18分) 7.化简:188-= . 8. .一次体检中,某班学生视力情况如下表: 视力情0.7以下 0.7 0.80.91.01.0以上况人数所占的百分比5﹪8﹪15﹪20﹪40﹪12﹪从表中看出全班视力情况的众数是9.已知命题“关于x的一元二次方程x2+bx+14=0,当b<0时必有实数解”,能说明这个命题是假命题的一个反例可以是.10.如图,BC是一条河的直线河岸,点A是河岸BC对岸上的一点,AB⊥BC于B,站在河岸BC的C处测得∠BCA=50 ,BC=10m,则桥长AB= m(用计算器计算,结果精确到0.1米)11.如图是由棱长相等的小立方体摆成的几何体的主视图与俯视图,根据视图可以判断组成这个几何体至少要个小立方体.(第10题) (第11题) (第12题)12.如图,在直角坐标系中,ABCD的四个顶点的坐标分别为A(0,8),B(-6,8),C(-6,0),D(0,0),现有动点P在线段CB上运动,当△ADP为等腰三角形时,P点坐标为 .三、(本大题共5小题, 每小题6分,共30分)13. (本题共2小题,每小题3分)(1)解方程:12222x x x++=--(2)如图,在⊙O 中,OA ⊥OB ,∠A=20°,求∠B 的度数.14.已知2(2a ++与2b +-互为相反数,求22(2)(2)(2)2a b b a b a a +-+--的值.(第(2)题)15,.关于x 的不等式组.;01234⎪⎩⎪⎨⎧<-+>+a x x x (1)当3=a 时,解这个不等式组; (2)若不等式组的解集是1<x ,求a 的值.16.如图,点A 、B 在⊙O 上,点O 是⊙O 的圆心,请你只用无刻度的直尺,分别画出图①和图②中∠A 的余角. (1)图①中,点C 在⊙O 上; (2)图②中,点C 在⊙O 内;17.一个不透明的布袋里装有16个只有颜色不同的球,其中红球有x个,白球有2x个,其他均为黄球,现甲从布袋中随机摸出一个球,若是红球则甲同学获胜,甲同学把摸出的球放回并搅匀,由乙同学随机摸出一个球,若为黄球,则乙同学获胜。
2020年江西省中等学校中考数学模拟试卷(3)(含答案解析)
2020年江西省中等学校中考数学模拟试卷(3)一、选择题(本大题共6小题,共18.0分)1.两千多年前,中国人就开始使用负数,且在世界上也是首创《九章算术》的“方程”一章,在世界数学史上首次正式引入负数.如果收入100元记作+100,那么支出40元应记作()A. −60B. −40C. +40D. +602.下列运算正确的是()A. a2⋅a3=a5B. a5+a5=a10C. (−3a3)2=6a6D. (a3)2⋅a=a63.数据3、6、7、1、7、2、9的中位数和众数分别是()A. 1和7B. 1和9C. 6和7D. 6和94.如图是由7个小正方体组合成的几何体,则其左视图为()A.B.C.D.5.如图,先将正方形ABCD对折,折痕为MN,再把点B折叠在MN上,折痕为AE,点B在MN上的对应点为点H,则∠AEB等于()A. 60°B. 45°C. 70°D. 75°6.抛物线y=x2+bx+3的对称轴为直线x=1.若关于x的一元二次方程x2+bx+3−t=0(t为实数)在−1<x<4的范围内有实数根,则t的取值范围是()A. 2≤t<11B. t≥2C. 6<t<11D. 2≤t<6二、填空题(本大题共6小题,共18.0分)7.(−0.7)2的平方根是______.8.在函数y=√x+1−5,自变量x的取值范围是________.x−29.如图,点P在△ABC的边AC上,请你添加一个条件,使得△ABP∽△ACB,这个条件可以是______.10.已知m,n是方程x2+2x−5=0的两个实数根,则m−mn+n=.11.如图,已知⊙O的直径为8cm,A、B、C三点在⊙O上,且∠ACB=30°,则AB的长为.12.▱ABCD中,AD=12,BD=10,AC=26,则▱ABCD的面积是______ .三、计算题(本大题共1小题,共8.0分)13.小芳身高1.6米,此时太阳光线与地面的夹角为45°.(1)若小芳正站在水平地面A处上时,那么她的影长为多少米?(2)若小芳来到一个坡度i=√3的坡面底端B处,当她在坡面上至少前进多少米时,小芳的影子3恰好都落在坡面上?四、解答题(本大题共10小题,共76.0分)14.如图,AC//BD,AD、BC相交于E,EF//BD,求证:1AC +1BD=1EF.15.解不等式组:{12x+1≥−1x−2(x−2)>0并将该不等式的解集在数轴上表示出来.16.国家实施高效节能电器的财政补贴政策,某款空调在政策实施后,每购买一台,客户可获得500元财政补贴.某校用6万元购买此款空调,补贴后可购买的台数是补贴前的1.2倍,则该款空调补贴前的售价为每台多少元?17.如图,D为等腰三角形ABC的边AB的中点,BC=12.(1)用尺规作图找出AC的中点E;(保留作图痕迹)(2)连接DE,求DE的长.18.某学校在‘小小数学家’的课堂练习中,甲、乙、丙、丁四人表现优秀,现决定从这四名同学中任选两名参加全国数学大赛,请用列表法或画树状图法,求恰好同时选中甲、丁两位同学的概率.19.某校举行全体学生“汉字听写”比赛,每位学生听写汉字39个.随机抽取了部分学生的听写结果,绘制成如下的图表.组别正确字数x人数A0≤x<810B8≤x<1615C16≤x<2425D24≤x<32mE32≤x<40n根据以上信息完成下列问题:(1)统计表中的m=_____,n=_____,并补全条形统计图;(2)扇形统计图中“C组”所对应的圆心角的度数是_____;(3)已知该校共有900名学生,如果听写正确的字的个数少于24个定为不合格,请你估计该校本次听写比赛不合格的学生人数.20.如图,已知反比例函数y=k的图象经过点A(−1,a),过点A作AB⊥x轴,垂足为点B,△AOB的x.面积为√32(1)求k的值;(2)若一次函数y=mx+n图象经过点A和反比例函数图象上另一点C(t,−√3),且与x轴交于M3点,求AM的值;(3)在(2)的条件下,如果以线段AM为一边作等边△AMN,顶点N在另一个反比例函数y=k′上,x 则k′=______.21.如图,已知AB是⊙P的直径,点C在⊙P上,D为⊙P外一点,且∠ADC=90°,2∠B+∠DAB=180°.(1)证明:直线CD为⊙P的切线;(2)若DC=2√6,AD=4,求⊙P的半径.22.已知二次函数y=ax2+bx−3的图象经过点A(2,−3),B(−1,0).(1)求二次函数的解析式;(2)要使该二次函数的图象与x轴只有一个交点,应把图象沿y轴怎样平移?平移几个单位?23.如图,在四边形ABCD中,∠BAD=∠BCD=90°,BC=D C. 延长AD到E点,使DE=AB.求证:CA=CE.【答案与解析】1.答案:B解析:本题考查了正数和负数,解题关键是理解“正”和“负”的相对性,确定一对具有相反意义的量.在一对具有相反意义的量中,先规定其中一个为正,则另一个就用负表示.解:根据题意,收入100元记作+100,则支出40元应记作−40.故选B.2.答案:A解析:解:A、a2⋅a3=a5,正确,符合题意;B、a5+a5=2a5,故此选项错误,不合题意;C、(−3a3)2=9a6,故此选项错误,不合题意;D、(a3)2⋅a=a7,故此选项错误,不合题意;故选:A.直接利用同底数幂的乘法运算法则、积的乘方与幂的乘方运算法则、合并同类项法则分别计算得出答案.此题主要考查了同底数幂的乘法运算、积的乘方与幂的乘方运算、合并同类项,正确掌握运算法则是解题关键.3.答案:C解析:解:将数据重新排列为1、2、3、6、7、7、9,则这组数据的中位数为6、众数为7,故选:C.中位数是一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数);众数是一组数据中出现次数最多的数据,据此可得答案.本题考查众数与中位数的意义.将一组数据从小到大(或从大到小)重新排列后,最中间的那个数(或最中间两个数的平均数)叫做这组数据的中位数;如果中位数的概念掌握得不好,不把数据按要求重新排列,就会出错.解析:解:从左面看易得其左视图为:故选:A.找到从左面看所得到的图形即可,注意所有的看到的棱都应表现在左主视图中.本题考查了三视图的知识,左视图是从物体的左面看得到的视图.5.答案:D解析:解:由折叠的性质可得出AB=AH=AD=DH,∴△ADH是等边三角形,∴∠DAH=60°,∴∠BAH=30°,∠BAE=∠HAE=15°,∴∠AEB=90°−∠BAE=75°.故选:D.根据折叠的性质可得出AB=AH=AD=DH,从而可得出△ADH是等边三角形,继而可得出∠DAH=60°,也可得出∠BAE的度数,在Rt△AEB中可求出∠AEB的度数.此题考查了翻折变换的知识,解答本题的关键是掌握翻折前后对应的边、对应角分别相等,难度一般.6.答案:A解析:本题考查二次函数的图象及性质;能够将方程的实数根问题转化为二次函数与直线的交点问题,借助数形结合解题是关键.根据给出的对称轴求出函数解析式为y=x2−2x+3,将一元二次方程x2+ bx+3−t=0的实数根可以看做y=x2−2x+3与函数y=t的有交点,再由−1<x<4的范围确定y的取值范围即可求解.解:∵y=x2+bx+3的对称轴为直线x=1,∴y=x2−2x+3,∴一元二次方程x2+bx+3−t=0的实数根可以看做y=x2−2x+3与函数y=t的有交点,∵方程在−1<x<4的范围内有实数根,当x=−1时,y=6;当x=4时,y=11;函数y=x2−2x+3在x=1时有最小值2;∴2≤t<11.故选:A.7.答案:±0.7解析:本题考查了平方根的概念.注意一个正数有两个平方根,它们互为相反数.根据平方根的定义解答即可.解:∵(−0.7)2=(±0.7)2,∴(−0.7)2的平方根是±0.7.故答案为:±0.7.8.答案:x≥−1且x≠2解析:本题考查了函数自变量的取值范围问题,函数自变量的范围一般从三个方面考虑:(1)当函数表达式是整式时,自变量可取全体实数;(2)当函数表达式是分式时,考虑分式的分母不能为0;(3)当函数表达式是二次根式时,被开方数非负.根据二次根式有意义的条件和分式有意义的条件,被开方数大于或等于0,分母不等于0,可以求出x的范围.解:根据题意得:x+1≥0且x−2≠0,解得:x≥−1且x≠2.故答案为x≥−1且x≠2.9.答案:∠ABP=∠C(答案不唯一)。
江西省2020年中考数学模拟试题及答案3套

江西省2020年中考数学模拟试题及答案3套江西省2020年中等学校招生考试数学模拟试题卷(一)说明:1.全卷满分120分,考试时间120分钟。
2.请将答案写在答题卡上,否则不给分。
一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项) 1.-2的相反数是( A )A .2B .-2C .12D .-122.下列图案中,是中心对称图形但不是轴对称图形的是( C ),A,B ,C,D3.下列运算正确的是(B)A.2a2+3a2=5a4B.a2·a=a3C.(a2)3=a5D.a2=a4.如图是由一个长方体和一个球组成的几何体,它的主视图是(C)(第4题)ABCD5.图1、图2分别是某厂六台机床10月份第一天和第二天生产零件数的统计图,与第一天相比,第二天六台机床生产零件数的平均数与方差的变化情况是(D)A.平均数变大,方差不变B.平均数变小,方差不变C.平均数不变,方差变小D.平均数不变,方差变大(第5题),(第6题)6.如图,在平面直角坐标系xOy 中,直线y =12x 与双曲线y =kx交于A ,B 两点,且点A 的坐标为(4,a),将直线y =12x 向上平移m 个单位,交双曲线y =kx(x >0)于点C ,交y 轴于点F ,且△ABC 的面积是323.给出以下结论:①k =8;②点B 的坐标是(-4,-2);③S △ABC <S △ABF ;④m =83.其中正确的结论有( C )A .1个B .2个C .3个D .4个二、填空题(本大题共6小题,每小题3分,共18分) 7.因式分解:x 3-9x =__x(x +3)(x -3)__.8.我国古代数学著作《九章算术》中记载了一个问题:“今有邑方不知大小,各开中门,出北门三十步有木,出西门七百五十步见木,问:邑方几何?”.其大意是:如图,一座正方形城池,A 为北门中点,从点A 往正北方向走30步到B 处有一树木,C 为西门中点,从点C 往正西方向走750步到D 处正好看到B 处的树木,则正方形城池的边长为__300__步.,(第8题),(第10题)9.设m ,n 是方程x 2-x -2 019=0的两实数根,则m 3+2 020n -2 019=__2__020__.10.如图1,点F 从菱形ABCD 的顶点A 出发,沿A→D→B 以1 cm /s 的速度匀速运动到点B ,图2是点F 运动时,△FBC 的面积y(cm 2)随时间x(s )变化的关系图象,则a 的值为__52__.11.如图,已知∠XOY =60°,点A 在边OX 上,OA =2.过点A 作AC ⊥OY 于点C ,以AC 为一边在∠XOY 内作等边三角形ABC ,点P 是△ABC 围成的区域(包括各边)内的一点,过点P 作PD ∥OY 交OX 于点D ,作PE ∥OX 交OY 于点E.设OD =a ,OE =b ,则a +2b 的取值范围是__2≤a +2b≤5__.,(第11题),(第12题)12.定义:若抛物线的顶点与x 轴的两个交点构成的三角形是直角三角形,则这种抛物线被称为“直角抛物线”.如图,直线l :y =15x +b 经过点M ⎝⎛⎭⎫0,14,一组抛物线的顶点B 1(1,y 1),B 2(2,y 2),B 3(3,y 3),…,B n (n ,y n )(n 为正整数),依次是直线l 上的点,第一条抛物线与x 轴正半轴的交点A 1(x 1,0)和A 2(x 2,0),第二条抛物线与x 轴交点A 2(x 2,0)和A 3(x 3,0),以此类推,若x 1=d(0<d <1),当d 为__1120或1320或320__时,这组抛物线中存在直角抛物线. 三、(本大题共5小题,每小题6分,共30分)13.(1)计算:(-2)2-|2-2|-2cos 45°+(3-π)0;解:原式=4-(2-2)-2×22+1 2分=4-2+2-2+1 =3;3分(2)如图,点E 在AB 上,∠CEB =∠B ,∠1=∠2=∠3,求证:CD =CA.证明:∵∠1=∠2,∴∠1+∠ACE =∠2+∠ACE ,即∠DCE =∠ACB.1分 ∵∠CEB =∠B ,∴CE =CB.∵∠2=∠3,∠CEB =∠B ,∴∠DEC =∠B.2分 ∴△DCE ≌△ACB(ASA ).∴CD =CA.3分14.解方程组:⎩⎪⎨⎪⎧x -y =1,x +3y =9.解:⎩⎪⎨⎪⎧x -y =1, ∴x +3y =9.∴∴-∴,得4y =8,解得y =2.2分把y =2代入∴,得x -2=1,解得x =3.4分∴原方程组的解为⎩⎪⎨⎪⎧x =3,y =2.6分15.在10×10的网格中,A ,B ,C 均在格点上,请用无刻度的直尺作直线MN ,使得直线MN 平分∴ABC 的周长(保留作图痕迹).(1)请在图1中作出符合要求的一条直线MN ;(2)如图2,点M 为BC 上一点,BM =5.请在AB 上作出点N 的位置.解:(1)图1中,直线MN 即为所求; 3分 (2)图2中,点N 即为所求.6分16.为弘扬中华传统文化,某校举办了学生“国学经典大赛”,比赛项目为:A .唐诗;B .宋词;C .元曲;D .论语,比赛形式分为“单人组”和“双人组”.(1)小明参加“单人组”,他从中随机抽取一个比赛项目,则抽到“唐诗”的是________事件,其概率是________;(2)若小亮和小丽组成一个小组参加“双人组”比赛,比赛规则是:同一小组的两名队员的比赛项目不能相同,且每人只能随机抽取一次,则小亮和小丽都没有抽到“元曲”的概率是多少?请用画树状图或列表的方法进行说明.解:(1)随机;14;3分(2)画树状图:由图可知,共有12种等可能的结果,其中小亮和小丽都没有抽到“元曲”的结果有6种,5分∴小亮和小丽都没有抽到“元曲”的概率为612=12.6分17.如图,在平面直角坐标系中,边长为2的正方形ABCD 在第一象限内,AD∴y 轴,点A 的坐标为(5,3),已知直线l :y =12x -2.(1)将直线l 向上平移m 个单位,使平移后的直线恰好经过点A ,求m 的值;(2)在(1)的条件下,平移后的直线与正方形的边长BC 交于点E ,求∴ABE 的面积.解:(1)设平移后的直线解析式为y =12x +b.∴y =12x +b 过点A(5,3),∴3=12×5+b ,即b =12.1分∴平移后的直线解析式为y =12x +12.∴m =12-(-2)=52;3分(2)∴正方形ABCD 中,AD∴y 轴,点A 的坐标为(5,3), ∴点E 的横坐标为5-2=3.4分把x =3代入y =12x +12,得y =12×3+12=2.∴点E 的坐标为(3,2).∴BE =1.5分∴∴ABE 的面积为12×2×1=1.6分四、(本大题共3小题,每小题8分,共24分)18.在创客教育理念的指引下,国内很多学校都纷纷建立创客实践室及创客空间,致力于从小培养孩子的创新精神和创造能力,某校开设了“3D ”打印、数学编程、智能机器人、陶艺制作四门创客课程,分别记为A ,B ,C ,D ,为了解学生对这四门创客课程的喜爱情况,数学兴趣小组对全校学生进行了随机问卷调查,将调查结果整理后绘制成两幅均不完整的统计图表.请根据图表中提供的信息回答下列问题: (1)统计表中的a =________b =________; (2)“陶艺制作”对应扇形的圆心角为________;(3)根据调查结果,请你估计该校3 000名学生中最喜欢“智能机器人”创客课程的人数;(4)学校为开设这四门课程预计每生A ,B ,C ,D 四科投资比为4∴3∴6∴7,若“3D ”打印课程每人投资200元,求学校为开设创客课程需为学生人均投入多少元.解:(1)80;0.20; 2分 (2)36°; 3分(3)估计该校3 000名学生中最喜欢“智能机器人”创客课程的人数为3 000×0.2=600(人);5分(4)依题意得每生A ,B ,C ,D 四门课程的投资分别为200元、150元、300元、350元,则学校为开设创客课程需为学生人均投入200×36+150×20+300×16+350×880=222.5(元).8分19.如图,∴O 是∴ABC 的外接圆,∴BAC 的平分线交∴O 于点D ,交BC 于点E ,过点D 作直线DF∴BC.(1)判断直线DF 与∴O 的位置关系,并说明理由;(2)若AB =6,AE =1235,CE =475,求BD 的长.解:(1)直线DF 与∴O 相切.理由:连接OD.∴∴BAC 的平分线交∴O 于点D ,∴∴BAD =∴CAD.∴BD ︵=CD ︵.2分 ∴OD∴BC.∴DF∴BC, ∴OD∴DF.∴直线DF 与∴O 相切;4分 (2)∴∴BAD =∴CAD ,∴ADB =∴C.∴∴ABD∴∴AEC. ∴AB AE =BD CE ,即61235=BD 475.6分 ∴BD =2213.8分20.将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P 时停止倒入,图2是它的平面示意图,请根据图中的信息解答下列问题:(1)填空:AP =______cm ,PF =______cm ; (2)求出容器中牛奶的高度CF.解:(1)5;152;4分(2)∴EF∴AB ,∴∴BPF =∴ABP =30°.又∴∴BFP =90°,∴tan 30°=BFPF.∴BF =152×33=532(cm ). 6分∴CF =BC -BF =12-532(cm ).答:容器中牛奶的高度CF 为⎝⎛⎭⎫12-532 cm .8分五、(本大题共2小题,每小题9分,共18分)21.如图,反比例函数y =kx(x >0)过点A(3,4),直线AC :y =mx +n 与x 轴交于点C(6,0),过点C 作x 轴的垂线交反比例函数图象于点B.(1)求反比例函数的解析式和直线AC 的解析式; (2)求∴ABC 的面积;(3)在平面内有点D ,使得以A ,B ,C ,D 四点为顶点的四边形为平行四边形,请直接写出符合条件的所有点D 的坐标.解:(1)把点A(3,4)代入y =kx (x >0),得k =xy =3×4=12.∴反比例函数的解析式为y =12x.1分把A(3,4),C(6,0)代入y =mx +n ,得⎩⎪⎨⎪⎧3m +n =4,6m +n =0.解得⎩⎪⎨⎪⎧m =-43,n =8.∴直线AC 的解析式为y =-43x +8;2分(2)∴点C(6,0),BC∴x 轴,∴把x =6代入y =12x ,得y =126=2.3分∴B(6,2).∴∴ABC 的面积为12×(6-3)×2=3;4分(3)∴如图,当四边形ABCD 为平行四边形时,AD 綊BC.∴A(3,4),B(6,2),C(6,0),∴x D =3,y A -y D =y B -y C 即4-y D =2-0,则y D =2.∴D(3,2);6分∴如图,当四边形ACBD′为平行四边形时,AD′綊CB.∴A(3,4),B(6,2),C(6,0),∴x D′=3,y D′-y A =y B -y C ,即y D′-4=2-0,则y D′=6.∴D′(3,6);7分∴如图,当四边形ACD″B 为平行四边形时,AC 綊BD″.∴A(3,4),B(6,2),C(6,0),∴x D″-x B =x C -x A ,即x D″-6=6-3,则x D″=9;y D″-y B =y C -y A ,即y D″-2=0-4,则y D″=-2.∴D″(9,-2).8分综上所述,符合条件的点D 的坐标是(3,2)或(3,6)或(9,-2).9分22.已知正方形ABCD 中,∴EAF =45°.(1)如图1,当点E ,F 分别在边BC ,CD 上,连接EF ,求证:EF =BE +DF ; 童威同学是这样思考的,请你和他一起完成如下解答:证明:将∴ADF 绕点A 顺时针旋转90°,得∴ABG ,则∴ADF∴∴ABG.(2)如图2,点M ,N 分别在边AB ,CD 上,且BN =DM.当点E ,F 分别在BM ,DN 上,连接EF ,探究三条线段EF ,BE ,DF 之间满足的数量关系,并证明你的结论;(3)如图3,当点E ,F 分别在对角线BD 、边CD 上.若FC =2,则BE 的长为________.(1)证明:将∴ADF 绕点A 顺时针旋转90°,得∴ABG ,则∴ADF∴∴ABG.∴AF =AG ,DF =BG ,∴DAF =∴BAG ,∴ABG =∴D =90°=∴ABC ,即G ,B ,C 在同一直线上. 在正方形ABCD 中,∴D =∴BAD =∴ABE =90°,AB =AD. ∴∴EAF =45°,∴∴DAF +∴BAE =90°-45°=45°.∴∴EAG =∴BAG +∴BAE =∴DAF +∴BAE =45°,即∴EAG =∴EAF.2分 在∴EAG 与∴EAF 中, ⎩⎪⎨⎪⎧EA =EA ,∴EAG =∴EAF ,AG =AF ,∴∴EAG∴∴EAF(SAS ).∴EG =EF.∴BE +DF =BE +BG =EG ,∴EF =BE +DF ;3分 (2)解:EF 2=BE 2+DF 2. 4分证明:图2中,将∴ADF 绕点A 顺时针旋转90°,得∴ABH ,则∴ADF∴∴ABH.∴AF =AH ,DF =BH ,∴DAF =∴BAH ,∴ADF =∴ABH. ∴∴EAF =45°,∴∴DAF +∴BAE =90°-45°=45°. ∴∴EAH =∴BAH +∴BAE =∴DAF +∴BAE =45°, 即∴EAH =∴EAF.连接EH.在∴EAH 与∴EAF 中,⎩⎪⎨⎪⎧EA =EA ,∴EAH =∴EAF ,AH =AF ,∴∴EAH∴∴EAF(SAS ),∴EH =EF.6分∴BN =DM ,BN∴DM ,∴四边形BMDN 是平行四边形.∴∴ABE =∴MDN. ∴∴EBH =∴ABH +∴ABE =∴ADF +∴MDN =∴ADM =90°.∴EH 2=BE 2+BH 2, 即EF 2=BE 2+DF 2;7分(3) 2.9分[图3中,作∴ADF 的外接圆∴O ,连接EF ,EC ,过点E 分别作EM∴CD 于点M ,EN∴BC 于点N.∴∴ADF =90°,∴AF 为∴O 直径.∴BD 为正方形ABCD 对角线,∴∴EDF =∴EAF =45°. ∴点E 在∴O 上.∴∴AEF =90°.∴∴AEF 为等腰直角三角形.∴AE =EF.由正方形的对称性可得AE =CE ,∴CE =EF.∴EM∴CF ,CF =2,∴CM =12CF =1.∴EN∴BC ,∴NCM =90°,∴四边形CMEN 是矩形.∴EN =CM =1. ∴∴EBN =45°,∴BE =2EN = 2.]六、(本大题共12分)23.如图1,抛物线C :y =x 2经过变换可得到抛物线C 1:y 1=a 1x(x -b 1),C 1与x 轴的正半轴交于点A 1,且其对称轴分别交抛物线C ,C 1于点B 1,D 1,此时四边形OB 1A 1D 1恰为正方形;按上述类似方法,如图2,抛物线C 1:y 1=a 1x(x -b 1)经过变换可得到抛物线C 2:y 2=a 2x(x -b 2),C 2与x 轴的正半轴交于点A 2,且其对称轴分别交抛物线C 1,C 2于点B 2,D 2,此时四边形OB 2A 2D 2也恰为正方形;按上述类似方法,如图3,可得到抛物线C 3:y 3=a 3x(x -b 3)与正方形OB 3A 3D 3.请探究以下问题:(1)填空:a 1=________,b 1=________; (2)求出C 2与C 3的解析式;(3)按上述类似方法,可得到抛物线C n :y n =a n x(x -b n )与正方形OB n A n D n (n≥1). ∴请用含n 的代数式直接表示出C n 的解析式;∴当x 取任意不为0的实数时,试比较y 2 018与y 2 019的函数值的大小关系,并说明理由.解:(1)1;2;4分(2)当y 2=0时,a 2x(x -b 2)=0,解得x 1=0,x 2=b 2.∴A 2(b 2,0).由正方形OB 2A 2D 2得OA 2=B 2D 2=b 2,∴B 2⎝⎛⎭⎫b 22,b 22,D 2⎝⎛⎭⎫b 22,-b 22. ∴B 2在抛物线C 1上,∴b 22=b 22⎝⎛⎭⎫b 22-2,可得b 2=0(不符合题意,舍去)或b 2=6.∴D 2(3,-3). 把D 2(3,-3)代入C 2:y 2=a 2x(x -6),得-3=3a 2(3-6),即a 2=13.∴C 2的解析式为y 2=13x(x -6)=13x 2-2x.6分当y 3=0时,a 3x(x -b 3)=0,解得x 1=0,x 2=b 3.∴A 3(b 3,0).由正方形OB 3A 3D 3得OA 3=B 3D 3=b 3,∴B 3⎝⎛⎭⎫b 32,b 32,D 3⎝⎛⎭⎫b 32,-b 32. ∴点B 3在抛物线C 2上,则b 32=13⎝⎛⎭⎫b 322-2×b 32,可得b 3=0(不符合题意,舍去)或b 3=18.∴D 3(9,-9).把D 3(9,-9)代入C 3:y 3=a 3x(x -18),得-9=9a 3(9-18),即a 3=19.∴C 3的解析式为y 3=19x(x -18)=19x 2-2x ;8分(3)∴C n 的解析式为y n =13n -1x 2-2x(n≥1); 9分∴由∴可得抛物线C 2 018的解析式为y 2 018=132 017x 2-2x ,10分 抛物线C 2 019的解析式为y 2 019=132 018x 2-2x.11分∴两抛物线的交点为(0,0).如图,由图象可得当x≠0时,y 2 018>y 2 019.12分江西省2020年中等学校招生考试数学模拟试题卷(二)说明:1.全卷满分120分,考试时间120分钟。
2020年江西省中考数学模拟试卷

2020年江西省中考数学训练试卷一、选择题(本大题共6小题,每题3分,共18分) 1.(3分)2-的绝对值是( ) A .2-B .2C .2±D .122.(3分)下列计算正确的是( ) A .4373()a b a b = B .232(4)82b a b ab b --=-- C .32242aa a a a +=D .22(5)25a a -=-3.(3分)某公司年前缴税20万元,今年缴税24.2万元.若该公司这两年的年均增长率相同,设这个增长率为x ,则列方程( ) A .320(1)24.2x += B .220(1)24.2x -= C .22020(1)24.2x ++=D .220(1)24.2x +=4.(3分)如图,点A 在反比例函数3(0)y x x=>的图象上,过点A 作AB x ⊥轴,垂足为点B ,点C 在y 轴上,则ABC ∆的面积为( )A .3B .2C .32D .15.(3分)如图,在菱形ABCD 中,点E 是BC 的中点,以C 为圆心、CE 为半径作弧,交CD 于点F ,连接AE 、AF .若6AB =,60B ∠=︒,则阴影部分的面积为( )A .933πB .932πC .1839πD .1836π6.(3分)若一元二次方程220x x m ++=有实数解,则m 的取值范围是( )A .1m -B .1mC .4mD .12m二.填空题(本大题共6小题,每题3分,共18分) 7.(3分)分解因式:244m m -+= .8.(3分)一个扇形的圆心角是120︒.它的半径是3cm .则扇形的弧长为 cm . 9.(3分)如图,在Rt ABC ∆中,90C ∠=︒,点D 是AC 边上的一点,DE 垂直平分AB ,垂足为点E .若8AC =,6BC =,则线段DE 的长度为 .10.(3分)如图,在ABC ∆中,AC BC =,将ABC ∆绕点A 逆时针旋转60︒,得到ADE ∆.若2AB =,30ACB ∠=︒,则线段CD 的长度为 .11.(3分)甲、乙两人分别从A ,B 两地相向而行,匀速行进甲先出发且先到达B 地,他们之间的距离()s km 与甲出发的时间()t h 的关系如图所示,则乙由B 地到A 地用了 h .12.(3分)以线段AC 为对角线的四边形ABCD (它的四个顶点A 、B 、C 、D 按顺时针方向排列),已知AB BC CD ==,100ABC ∠=︒,40CAD ∠=︒;则BCD ∠的大小为 . 三.解答题(本大题共5小题,每题6分,共30分) 13.(6分)按要求解方程 (1)2320x x --=.(方法自选) (2)22410x x --=(配方法)14.(6分)先化简,再求值:22111211x x x x x +÷-++++,其中31x =. 15.(6分)如图,A ,B ,C 是O 上的三上点,且四边形OABC 是菱形,请用无刻度直尺完成下列作图.(1)如图①,作出线段OA 的垂直平分线;(2)如图②,作出线段BC 的垂直平分线.16.(6分)如图,在Rt ABC ∆中,90C ∠=︒,正方形CDEF 的三个顶点D ,E ,F 分别在边AC ,AB ,BC 上.若7.5AC =,5BC =,求正方形的边长.17.(6分)如图,在四边形ABCD 中,//AD BC ,点O 是对角线AC 的中点,过点O 作AC 的垂线,分别交AD 、BC 于点E 、F ,连接AF 、CE .试判断四边形AECF 的形状,并证明.四、(本大题共3小题,每题8分,共24分) 18.(8分)如图,已知反比例函数1(0)k y k x =≠的图象经过点1(8,)2-,直线2y x b =+与反比例函数图象相交于点A 和点(,4)B m . (1)求上述反比例函数和直线的解析式; (2)当12y y <时,请直接写出x 的取值范围.19.(8分)如图,AB 、CD 是O 的两条直径,过点C 的O 的切线交AB 的延长线于点E ,连接AC 、BD .(1)求证;ABD CAB ∠=∠;(2)若B 是OE 的中点,12AC =,求O 的半径.20.(8分)工艺商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等. (1)该工艺品每件的进价、标价分别是多少元?(2)若每件工艺品按(1)中求得的进价进货,标价售出,工艺商场每天可售出该工艺品100件.若每件工艺品降价1元,则每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天获得的利润最大?获得的最大利润是多少元? 五、(本大题共2小题,共18分)21.(9分)如图,ABC ∆在平面直角坐标系中,顶点的坐标分别为(4,4)A -,(1,1)B -,(1,4)C -. (1)画出与ABC ∆关于y 轴对称的△111A B C .(2)将ABC ∆绕点B 逆时针旋转90︒,得到△22A BC ,画两出△22A BC . (3)求线段AB 在旋转过程中扫过的图形面积.(结果保留)π22.(9分)如图,抛物线22y ax ax c =-+的图象经过点(0,2)C -,顶点D 的坐标为8(1,)3-,与x 轴交于A 、B 两点. (1)求抛物线的解析式.(2)连接AC ,E 为直线AC 上一点,当AOC AEB ∆∆∽时,求点E 的坐标和AEAB的值.六、(本大题共1小题,共12分)23.(12分)如图,已知90AOB ∠=︒,30OAB ∠=︒,反比例函数3(0)y x x =-<的图象过点(3,)B a -,反比例函数(0)ky x x=>的图象过点A .(1)求a 和k 的值;(2)过点B 作//BC x 轴,与双曲线ky x=交于点C .求OAC ∆的面积.2020年江西省中考数学训练试卷参考答案与试题解析一、选择题(本大题共6小题,每题3分,共18分) 1.(3分)2-的绝对值是( ) A .2-B .2C .2±D .12【解答】解:2-的绝对值是:2. 故选:B .2.(3分)下列计算正确的是( ) A .4373()a b a b = B .232(4)82b a b ab b --=-- C .32242aa a a a +=D .22(5)25a a -=-【解答】解:A 、43123()a b a b =,故此选项不合题意;B 、232(4)82b a b ab b --=-+,故此选项不合题意;C 、32242aa a a a +=,故此选项符合题意;D 、22(5)1025a a a -=-+,故此选项不合题意;故选:C .3.(3分)某公司年前缴税20万元,今年缴税24.2万元.若该公司这两年的年均增长率相同,设这个增长率为x ,则列方程( ) A .320(1)24.2x += B .220(1)24.2x -= C .22020(1)24.2x ++= D .220(1)24.2x +=【解答】解:设这个增长率为x , 由题意得,220(1)24.2x +=. 故选:D .4.(3分)如图,点A 在反比例函数3(0)y x x=>的图象上,过点A 作AB x ⊥轴,垂足为点B ,点C 在y 轴上,则ABC ∆的面积为( )A .3B .2C .32D .1【解答】解:连结OA ,如图,AB x ⊥轴, //OC AB ∴, OAB CAB S S ∆∆∴=,而13||22OAB S k ∆==, 32CAB S ∆∴=, 故选:C .5.(3分)如图,在菱形ABCD 中,点E 是BC 的中点,以C 为圆心、CE 为半径作弧,交CD 于点F ,连接AE 、AF .若6AB =,60B ∠=︒,则阴影部分的面积为( )A .933π-B .932π-C .1839π-D .1836π-【解答】解:连接AC ,四边形ABCD 是菱形, 6AB BC ∴==,60B ∠=︒,E 为BC 的中点,3CE BE CF ∴===,ABC ∆是等边三角形,//AB CD , 60B ∠=︒,180120BCD B ∴∠=︒-∠=︒,由勾股定理得:AE =11622AEB AEC AFC S S S ∆∆∆∴==⨯⨯==,∴阴影部分的面积212033360AEC AFC CEFS S S S ππ∆∆⨯=+-==扇形,故选:A .6.(3分)若一元二次方程220x x m ++=有实数解,则m 的取值范围是( ) A .1m -B .1mC .4mD .12m【解答】解:一元二次方程220x x m ++=有实数解, 224240b ac m ∴-=-,解得:1m ,则m 的取值范围是1m . 故选:B .二.填空题(本大题共6小题,每题3分,共18分) 7.(3分)分解因式:244m m -+= 2(2)m - . 【解答】解:原式2(2)m =-, 故答案为:2(2)m -8.(3分)一个扇形的圆心角是120︒.它的半径是3cm .则扇形的弧长为 2π cm . 【解答】解:根据题意,扇形的弧长为12032180ππ⨯=, 故答案为:2π9.(3分)如图,在Rt ABC ∆中,90C ∠=︒,点D 是AC 边上的一点,DE 垂直平分AB ,垂足为点E .若8AC =,6BC =,则线段DE 的长度为154.【解答】解:90C∠=︒,8AC=,6BC=,22228610AB AC BC∴=+=+=,DE垂直平分AB,90DEA∴∠=︒,1110522AE AB==⨯=,DEA C∴∠=∠,又A A∠=∠,AED ACB ∴∆∆∽,∴AE DE AC BC=,即586DE =154DE∴=.故答案为:154.10.(3分)如图,在ABC∆中,AC BC=,将ABC∆绕点A逆时针旋转60︒,得到ADE∆.若2AB=,30ACB∠=︒,则线段CD的长度为2.【解答】解:连接CE,如图,ABC∆绕点A逆时针旋转60︒,得到ADE∆,2AD AB∴==,AE AC=,60CAE∠=︒,30AED ACB∠=∠=︒,ACE∴∆为等边三角形,60AEC∴∠=︒,DE∴平分AEC∠,DE∴垂直平分AC,2DC DA∴==.故答案为2.11.(3分)甲、乙两人分别从A ,B 两地相向而行,匀速行进甲先出发且先到达B 地,他们之间的距离()s km 与甲出发的时间()t h 的关系如图所示,则乙由B 地到A 地用了 10 h .【解答】解:由图可得,甲的速度为:3666(/)km h ÷=,则乙的速度为:366 4.5 3.6(/)4.52km h -⨯=-, 则乙由B 地到A 地用时:36 3.610()h ÷=,故答案为:10.12.(3分)以线段AC 为对角线的四边形ABCD (它的四个顶点A 、B 、C 、D 按顺时针方向排列),已知AB BC CD ==,100ABC ∠=︒,40CAD ∠=︒;则BCD ∠的大小为 80︒或100︒ .【解答】解:AB BC =,100ABC ∠=︒,1240CAD ∴∠=∠=∠=︒,//AD BC ∴,(1)如图1,过点C 分别作CE AB ⊥于E ,CF AD ⊥于F ,1CAD ∠=∠,CE CF ∴=,在Rt ACE ∆与Rt ACF ∆中,AC AC CE CF =⎧⎨=⎩, Rt ACE Rt ACF ∴∆≅∆,在Rt BCE ∆与Rt DCF ∆中,CB CD CE CF =⎧⎨=⎩,Rt BCE Rt DCF ∴∆≅∆,ACE ACF ∴∠=∠,BCE DCF ∠=∠∆,240ACD ∴∠=∠=︒,80BCD ∴∠=︒;(2)如图2,//AD BC ,AB CD =',∴四边形ABCD '是等腰梯形,100BCD ABC ∴∠'=∠=︒.综上所述,80BCD ∠=︒或100︒.三.解答题(本大题共5小题,每题6分,共30分)13.(6分)按要求解方程(1)2320x x --=.(方法自选)(2)22410x x --=(配方法)【解答】解:(1)原方程可化为:(1)(3)0x x +-=(1)0x ∴+=或(3)0x -=11x ∴=-,23x =;(2)原方程可化为:2122x x -= 23212x x ∴-+=23(1)2x ∴-= 3612x ∴-=±= 161x ∴=+,261x =-. 14.(6分)先化简,再求值:22111211x x x x x +÷-++++,其中31x =-. 【解答】解:原式221(1)(1)(1)x x x x +=+--+ 221111x x x x +-=-++ 21x =+, 当31x =-时,原式233==. 15.(6分)如图,A ,B ,C 是O 上的三上点,且四边形OABC 是菱形,请用无刻度直尺完成下列作图.(1)如图①,作出线段OA 的垂直平分线;(2)如图②,作出线段BC 的垂直平分线.【解答】解:(1)BE 是OA 的垂直平分线;(2)OF 为BC 的垂直平分线.16.(6分)如图,在Rt ABC∆中,90C∠=︒,正方形CDEF的三个顶点D,E,F分别在边AC,AB,BC上.若7.5AC=,5BC=,求正方形的边长.【解答】解:90C∠=︒,四边形CDEF是正方形,//DE BC∴,ADE ACB∴∆∆∽,∴DE AD CB AC=,设正方形CDEF的边长为x,又7.5AC=,5BC=,可得:7.557.5x x-=,解得:3x=,即正方形CDEF的边长为3.17.(6分)如图,在四边形ABCD中,//AD BC,点O是对角线AC的中点,过点O作AC 的垂线,分别交AD、BC于点E、F,连接AF、CE.试判断四边形AECF的形状,并证明.【解答】解:四边形AECF为菱形.证明如下://AD BC,12∴∠=∠.O是AC中点,AO CO∴=.在AOE∆和COF∆中12AOE COF AO CO ∠=∠⎧⎪∠=∠⎨⎪=⎩()AOE COF AAS ∴∆≅∆.AE CF ∴=.又//AE CF ,∴四边形AECF 为平行四边形,EF AC ⊥,∴平行四边形AECF 为菱形.四、(本大题共3小题,每题8分,共24分)18.(8分)如图,已知反比例函数1(0)k y k x =≠的图象经过点1(8,)2-,直线2y x b =+与反比例函数图象相交于点A 和点(,4)B m . (1)求上述反比例函数和直线的解析式;(2)当12y y <时,请直接写出x 的取值范围.【解答】解:(1)反比例函数1(0)k y k x =≠的图象经过点1(8,)2A -, 128K ∴-=, 4k ∴=-,∴反比例函数解析式为14y x=-.点(,4)B m 在反比例函数解析式为14y x=-上, 44m∴=-, 1m ∴=-,又(1,4)B -在2y x b =+上,41b ∴=-+,5b ∴=,∴直线的解析式为25y x =+.(2)由图象可知,当12y y <时x 的取值范围41x -<<-或0x >.19.(8分)如图,AB 、CD 是O 的两条直径,过点C 的O 的切线交AB 的延长线于点E ,连接AC 、BD .(1)求证;ABD CAB ∠=∠;(2)若B 是OE 的中点,12AC =,求O 的半径.【解答】解:(1)证明:AB 、CD 是O 的两条直径,OA OC OB OD ∴===,OAC OCA ∴∠=∠,ODB OBD ∠=∠,AOC BOD ∠=∠,OAC OCA ODB OBD ∴∠=∠=∠=∠, 即ABD CAB ∠=∠;(2)连接BC . AB 是O 的两条直径,90ACB ∴∠=︒, CE 为O 的切线,90OCE ∴∠=︒, B 是OE 的中点,BC OB ∴=,OB OC =,OBC ∴∆为等边三角形,60ABC ∴∠=︒,30A ∴∠=︒, 343BC AC ∴==, 43OB ∴=,即O 的半径为43.20.(8分)工艺商场按标价销售某种工艺品时,每件可获利45元;按标价的八五折销售该工艺品8件与将标价降低35元销售该工艺品12件所获利润相等.(1)该工艺品每件的进价、标价分别是多少元?(2)若每件工艺品按(1)中求得的进价进货,标价售出,工艺商场每天可售出该工艺品100件.若每件工艺品降价1元,则每天可多售出该工艺品4件.问每件工艺品降价多少元出售,每天获得的利润最大?获得的最大利润是多少元?【解答】解:(1)设该工艺品每件的进价是x 元,标价是y 元.依题意得方程组:4580.858(35)1212y x y x y x -=⎧⎨-=--⎩解得:155200x y =⎧⎨=⎩. 故该工艺品每件的进价是155元,标价是200元.(2)设每件应降价a 元出售,每天获得的利润为W 元.依题意可得W 与a 的函数关系式:(45)(1004)W a a =-+,24804500W a a =-++,配方得:24(10)4900W a =--+,当10a =时,4900W =最大.故每件应降价10元出售,每天获得的利润最大,最大利润是4900元.五、(本大题共2小题,共18分)21.(9分)如图,ABC ∆在平面直角坐标系中,顶点的坐标分别为(4,4)A -,(1,1)B -,(1,4)C -. (1)画出与ABC ∆关于y 轴对称的△111A B C .(2)将ABC ∆绕点B 逆时针旋转90︒,得到△22A BC ,画两出△22A BC .(3)求线段AB 在旋转过程中扫过的图形面积.(结果保留)π【解答】解:(1)如图,△11l A B C 为所作;(2)如图,△22A BC 为所作;(3)223332AB =+=,所以线段AB 在旋转过程中扫过的图形面积290(32)93602ππ==. 22.(9分)如图,抛物线22y ax ax c =-+的图象经过点(0,2)C -,顶点D 的坐标为8(1,)3-,与x 轴交于A 、B 两点.(1)求抛物线的解析式.(2)连接AC ,E 为直线AC 上一点,当AOC AEB ∆∆∽时,求点E 的坐标和AE AB的值.【解答】解:(1)由题意可列方程组:2823c a a c =-⎧⎪⎨-+=-⎪⎩, 解得:232a c ⎧=⎪⎨⎪=-⎩.故抛物线解析式为:224233y x x =--; (2)连结BE ,由题意有90AOC ∠=︒,5AC 4AB =,设直线AC 的解析式为:y kx b =+,则02k b b -+=⎧⎨=-⎩, 解得:22k b =-⎧⎨=-⎩. ∴直线AC 的解析式为:22y x =--; 当AOC AEB ∆∆∽时2255()()16AOC AEB SAC S AB ∆∆===, 1AOC S ∆=,165AEB S ∆∴=, ∴116||25E AB y ⨯=,4AB =,则85E y =-, 则点1(5E -,8)5-; 由AOC AEB ∆∆∽得:5AO AE AC AB ==, ∴5AE AB =.六、(本大题共1小题,共12分)23.(12分)如图,已知90AOB ∠=︒,30OAB ∠=︒,反比例函数3(0)y x x=-<的图象过点(3,)B a -,反比例函数(0)k y x x=>的图象过点A . (1)求a 和k 的值;(2)过点B 作//BC x 轴,与双曲线k y x=交于点C .求OAC ∆的面积.【解答】解:(1)比例函数3(0)y x x=-<的图象过点(3,)B a -, 313a ∴=-=-, 3OE ∴=,1BE =,分别过点A 、B 作AD x ⊥轴于D ,BE x ⊥轴于E , 90BOE OBE ∴∠+∠=︒,90AOB ∠=︒,30OAB ∠=︒,90BOE AOD ∴∠+∠=︒,3tan 30OB OA ︒==, OBE AOD ∴∠=∠,90OEB ADO ∠=∠=︒,BOE OAD ∴∆∆∽ ∴3OE BE OB AD OD OA ===, 33333AD OE ∴==⨯=,3313OD BE ==⨯ (3A ∴,33),反比例函数(0)k y x x=>的图象过点A , 3339k ∴=;(2)由(1)可知33AD =,3OD =,//BC x 轴,(3,1)B -,C ∴点的纵坐标为1,过点C 作CF x ⊥轴于F ,点C 在双曲线9y x =上, 91x∴=,解得9x =, (9,1)C ∴,1CF ∴=,AOC AOD COF ADFC ADCF S S S S S ∆∆∆∴=+-=梯形梯形 1()()2AD CF OF OD =+- 1(331)(93)2=+- 133=.。
【2020精品】江西省九年级数学中考模拟试题含答案

2020年江西省九年级数学中考模拟试题考生须知:1 .全卷共六大题,23小题.满分为120分.考试时间120分钟.2 .本卷答案必须做在答题纸的对应位置上,做在试题卷上无效^温馨提示:请仔细审题,细心答题,相信你一定会有出色的表现!一、选择题(本大题共有6小题,每小题3分,共18分。
请选出各题中一个符合题意的正确 选项,不选、多选、错选,均不给分 )1、在0 ,-2,1, 5这四个数中,最小的数是 ()A.0 B . -2 C . 1 D.5 2、下列三条线段不能构成三角形的三边的是()4、为了调查瑞州市2016年初三年级学生的身高,从中抽取出200名学生进行调查,这个问题中样本容量为( )A .被抽取的200名学生的身高 身高5、平行四边形、矩形、正方形之间的关系是()6、下面几何体的主视图是(A . 3cm^ 4cm, 5cmB 5cm , 6cm, 11cmC . 5cm, 6cm, 10cmD 25 3cm, 4cm3、已知sin =走,且 2 是锐角,则等于()A.75 0B.60 0C.45D.30B . 200C . 200名D .初三年级学生的希匕皿士 [ A B C二、填空题(本大题共6个小题,每小题3分,共18分.)7、2016年我市经济依然保持了平稳增长。
据统计,截止到今年4月底,我市金融机构存款余额约为1193亿元,用科学计数法一应记为元8、分解因式:a3-16a= ____________ 。
“9、有两名学员小林和小明练习射击,A轮10枪打完后两人打靶的环数如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小林和小明两人中新手是_________ 。
DQ ■■♦ 1 ■ 1 立上」■1 2 3 4 5 6 7 8 "0叫硼谷小将筐喔图10、定义新运算R”,规则:a^ b=ab-a-b,如1:X1,X 2,则X1 X X2 = ____________________ o11、如图a是长方形纸带,/ DEF=20 ,将纸带沿图c中的/ CFE的度数是_____________ 。
江西省2020年中考数学模拟试卷试题卷(一)

江西省2020年中考数学模拟试卷试题卷(一)说明:1.本卷共有六个大题,23个小题,全卷满分120分,考试时间120分钟.2.本卷分为试题卷和答题卷,答案要求写在答题卷上,不得在试题卷上作答,否则不给分.一、选择题(本大题共6小题,每小题3分,共18分.每小题只有一个正确选项)1.下列各数中,比﹣2小的数是()A.2 B.0 C.﹣1 D.﹣3【考点】18:有理数大小比较.【分析】根据负数的绝对值越大负数反而小,可得答案.【解答】解:|﹣3|>|﹣2|,∴﹣3<﹣2,故选:D.2.下列计算正确的是()A.a2•a3=a6B.2a+3b=5ab C.a8÷a2=a6D.(a2b)2=a4b【考点】48:同底数幂的除法;35:合并同类项;46:同底数幂的乘法;47:幂的乘方与积的乘方.【分析】A、利用同底数幂的乘法法则计算得到结果,即可做出判断;B、原式不能合并,错误;C、原式利用同底数幂的除法法则计算得到结果,即可做出判断;D、原式利用积的乘方及幂的乘方运算法则计算得到结果,即可做出判断.【解答】解:A、a2•a3=a5,本选项错误;B、2a+3b不能合并,本选项错误;C、a8÷a2=a6,本选项正确;D、(a2b)2=a4b2,本选项错误.故选C.3.如图所示的几何体的俯视图是()A.B.C.D.【考点】U1:简单几何体的三视图.【分析】找到从上面看所得到的图形即可,注意所有的看到的棱都应表现在俯视图中.【解答】解:从上往下看,易得一个长方形,且其正中有一条纵向实线,故选:B.4.已知点P(3﹣3a,1﹣2a)在第四象限,则a的取值范围在数轴上表示正确的是()A.B.C.D.【考点】CB:解一元一次不等式组;C4:在数轴上表示不等式的解集;D1:点的坐标.【分析】由点P在第四象限,可得出关于a的一元一次不等式组,解不等式组即可得出a 的取值范围,再对照四个选项即可得出结论.【解答】解:∵点P(3﹣3a,1﹣2a)在第四象限,∴,解不等式①得:a<1;解不等式②得:a>.∴a的取值范围为<a<1.故选C.5.如图,▱ABCD中,∠C=120°,AB=AE=5,AE与BD交于点F,AF=2EF,则BC的长为()A.6 B.8 C.10 D.12【考点】S9:相似三角形的判定与性质;L5:平行四边形的性质.【分析】根据平行四边形的性质得到∠ABC=60°,得到△ABE是等边三角形,求出BE=AB=5,根据相似三角形的性质列出比例式,计算即可.【解答】解:在▱ABCD中,∠C=120°,∴∠ABC=60°,∵AB=AE,∴△ABE是等边三角形,∴BE=AB=5,∵AD∥BC,∴==2,∴BC=10,故选:C.6.已知两点A(﹣5,y1),B(3,y2)均在抛物线y=ax2+bx+c(a≠0)上,点C(x0,y0)是该抛物线的顶点.若y1>y2≥y0,则x0的取值范围是()A.x0>﹣5 B.x0>﹣1 C.﹣5<x0<﹣1 D.﹣2<x0<3【考点】H5:二次函数图象上点的坐标特征.【分析】先判断出抛物线开口方向上,进而求出对称轴即可求解.【解答】解:∵点C(x0,y0)是抛物线的顶点,y1>y2≥y0,∴抛物线有最小值,函数图象开口向上,∴a >0;∴25a ﹣5b+c >9a+3b+c , ∴<1, ∴﹣>﹣1,∴x 0>﹣1∴x 0的取值范围是x 0>﹣1. 故选:B .二、填空题(本大题共6小题,每小题3分,共18分)7.分解因式:x 3-x = . 【答案】x (x +1)(x -1)【解析】利用提公因式法及公式法因式分解8.如图,AB 是⊙O 的直径,弦CD ⊥AB ,垂足为E .若∠A =36°,则∠C 的度数为 .【答案】18°【解析】连接OD ,由∠A =36°,得到∠ODA =36°,由直径AB ⊥弦CD ,可求得 ∠ADC 的度数为54°,即∠ODC =18°,由圆的轴对称性即可求得∠C 的度数. 9. 从分别写着0,π,0.101001,2,722,38的六张无明显差别的卡片中,随机抽 取1张,则所抽卡片上的数是无理数的概率是 . 【答案】31 【解析】利用有理数和无理数的概念,判断哪些是无理数,并求事件A 的概率. 10. 已知a ,b 是一元二次方程x 2+4x +2=0的两个实数根,且点P (a ,b )在反比例函数y =xk, 的图像上,则k = .(第8题)O DCBA【答案】2【解析】利用根与系数的关系2ab =,即k =ab =2.11. 将一张边长为2的正方形纸片按照图①~④的过程折叠后再展开,则四边形AMCN的面积为 .【答案】424-【解析】由折叠可得对应角相等,即可得出AF 、AC 、AE 、CG 、CH 为角平分线,利用角平分线的性质或三角形的内切圆,求出点M 到AC 的距离,再利用菱形的面积公式对角线对角线菱形⨯⨯=21S ,可得最终结果. 12. 菱形ABCD 中,∠B =60°,AB =4,点E 在BC 上,CE =32.若点P 是菱形上异于 点E 的另一点,CE =CP ,则EP 的长为 .【答案】 6,6-2362或(每填对一个得1分,每填错一个扣1分,扣完为止,其中也对)写成33-62623-【解析】根据点P 是菱形上异于点E 的另一点,易得BC 边上存在一点P ,的长,可得三线合一”及三角函数为等腰三角形,利用“由于EP ECP ∆;为了确定AD 上是否存在符合题意的点P ,过点C 作AD 的垂线段,易得垂线段长为32,即垂足就是所要的点P ,由于PEC ∆为∆Rt ,利用勾股定理可求EP 的长;同理,在AB 边也存在符合题意的一点P ,过点P 作M BC PM 于点⊥,利用勾股定理可求PM 、CM ,从而求出EM ,因为PEM ∆是∆Rt ,利用勾股定理,可求PE 的长.本题共分三类. 三、(本大题共5小题,每小题6分,共30分) 13.(本题共2小题,每小题3分) (1)计算: .81)1()14.3(2017+---+-π④③②①NMH G F ED C BAF E D C B A321【答案】解:原式=221-1-1+ ……2分 1-22=. ……3分 【解析】先分别计算出0(3.14)π-、2017(1)-、1-8的值,然后从左到右依次进行运算.(2)如图,在△ABC 中,点D ,E ,F 分别在边AB ,BC ,AC 上,∠1=∠2,∠3=63°,求∠A 的度数.【答案】解:∵∠1=∠2,∴ AB ∥EF. ……1分∴∠A =∠3. ……2分∵∠3=63°,∴∠A =63° ……3分【解析】先根据∠1=∠2这一条件判定AB ∥EF.,然后运用平行线的性质求解。
2020年江西省中考数学仿真试卷(四) (含答案解析)
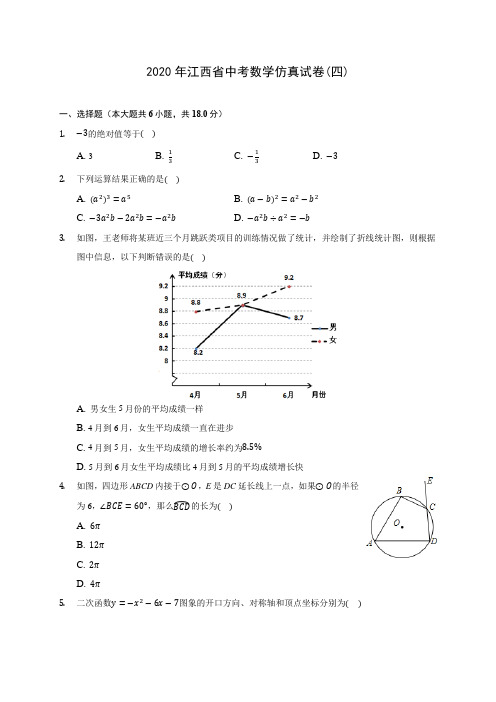
2020年江西省中考数学仿真试卷(四)一、选择题(本大题共6小题,共18.0分)1.−3的绝对值等于()A. 3B. 13C. −13D. −32.下列运算结果正确的是()A. (a2)3=a5B. (a−b)2=a2−b2C. −3a2b−2a2b=−a2bD. −a2b÷a2=−b3.如图,王老师将某班近三个月跳跃类项目的训练情况做了统计,并绘制了折线统计图,则根据图中信息,以下判断错误的是()A. 男女生5月份的平均成绩一样B. 4月到6月,女生平均成绩一直在进步C. 4月到5月,女生平均成绩的增长率约为8.5%D. 5月到6月女生平均成绩比4月到5月的平均成绩增长快4.如图,四边形ABCD内接于⊙O,E是DC延长线上一点,如果⊙O的半径为6,∠BCE=60°,那么BCD⏜的长为()A. 6πB. 12πC. 2πD. 4π5.二次函数y=−x2−6x−7图象的开口方向、对称轴和顶点坐标分别为()A. 向下,直线x=3,(3,2)B. 向下,直线x=−3,(3,2)C. 向上,直线x=−3,(3,2)D. 向下,直线x=−3,(−3,2)6.下列图形(包括数)按照一定的规律排列,依此规律,第300个图形是()A. B. C. D.二、填空题(本大题共6小题,共18.0分)7.要使x在实数范围内有意义,x的取值范围是.1−x8.已知x1、x2是一元二次方程x2+x−3=0的两个根,则x1+x2=______.9.如果函数y=(m−3)x+1−m的图象经过第二、三、四象限,那么常数m的取值范围为______ .10.甲、乙两人在一条笔直的道路上相向而行,甲骑自行车从A地到B地,乙驾车从B地到A地,他们分别以不同的速度匀速行驶,已知甲先出发6分钟后,乙才出发,在整个过程中,甲、乙两人的距离y(千米)与甲出发的时间x(分)之间的关系如图所示,当乙到达终点A时,甲还需分钟到达终点B.11.二次函数y=x2+bx+c经过(5,3)和(−2,3),则当x=_______时,函数取到最小值.12.如图,在平面直角坐标系xOy中,一次函数y=−x+2与反比例函数y=k(x<0)相交于点B,与x轴相交于点A,点B的横坐标为−2,设点Mx(x<0)是直线AB上的一点,过点M作MN//x轴,交反比例函数y=kx的图象于点N,若以A、O、M、N为顶点的四边形为平行四边形,则点M的坐标为______.三、解答题(本大题共12小题,共84.0分))−1−(√2)213.(1)计算:|−3|−20180+(14(2)计算:(2√3−5√8)−(√75−√18)14. 如图,△ABC 中,AB =AC ,AD 是△ABC 的角平分线,点O 为AB的中点,连接DO 并延长到点E ,使OE =OD ,连接AE 、BE ,求证:四边形AEBD 是矩形.15. 解不等式组{2(x +2)>3x,1−3x 2≤−1,并将它的解集在数轴上表示出来.16. 如图,在四边形ABCD 中,AB//CD ,对角线BD 的垂直平分线分别与DC 、AB 、BD 相交于点E 、F 、O ,求证:四边形DFBE 是菱形.17.某商场举办抽奖活动,规则如下:在不透明的袋子中有2个红球和2个黑球,这些球除颜色外都相同.顾客每次摸出1个球,若摸到红球,则获得1份奖品;若摸到黑球,则没有奖品.(1)如果小芳只有一次摸球机会,那么小芳获得奖品的概率为;(2)如果小芳有两次摸球机会(摸出后不放回),求小芳获得2份奖品的概率.(请用“画树状图”或“列表”等方法写出分析过程)18.如图,已知反比例函数y1=k1与一次函数y2=k2x+b的图象交于点A(1,8),B(m,−2).x(1)求这两个函数的表达式;(2)求△AOB的面积.19.2014年11月,绵阳某中学结合语文阅读素养评估活动,以“我最喜爱的书籍”为主题,对学生最喜爱的一种书籍类型进行随机抽样调查,收集整理数据后,绘制出以下两幅未完成的统计图,请根据图①和图②提供的信息,解答下列问题:(1)在这次抽样调查中,一共调查了多少名学生?(2)请把折线统计图(图1)补充完整;(3)求出扇形统计图(图2)中,体育部分所对应的圆心角的度数;(4)如果这所中学共有学生3600名,那么请你估计最喜爱科普类书籍的学生人数.20.如图,将笔记本电脑水平放置在桌子上,显示屏OB与底板OA所在水平线形成的角为120°(如图1),侧面示意图为图2.使用时为了散热,在底板下垫入散热架ACO′(ACO′是直角三角形)后,电脑绕点A旋转到AO′B′位置(如图3),侧面示意图为图4.此时B′,O′,C共线,已知OA=OB= 26cm。
江西2020年中考数学模拟试卷 四(含答案)

江西2020年中考数学模拟试卷四一、填空题1.如图,P是正三角形ABC内的一点,且PA=6,PB=8,PC=10.若将△PAC绕点A逆时针旋转后,得到△MAB,则点P与点M之间的距离为,∠APB= °.2.如图为6个边长相等的正方形的组合图形,则∠1+∠2+∠3=________.3.若关于x的方程3x2﹣kx+k=0有两个相等的实数根,则常数k的值为.4.计划用x kg化肥给一块y亩的麦地施肥,若每亩麦地用化肥23kg,则还差90kg;若每亩麦地用18kg,则还多110kg.故可列方程组为___________.5.如图,一等腰三角形,底边长是18厘米,底边上的高是18厘米,现在沿底边依次从下往上画宽度均为3厘米的矩形,画出的矩形是正方形时停止,则这个矩形是第个.二、选择题6.下列各运算中,计算正确的是( )A.a2+2a2=3a4 B.b10÷b2=b5 C.(m﹣n)2=m2﹣n2 D.(﹣2x2)3=﹣8x67.若|a|=3,|b|=2,且a+b>0,那么a-b的值是()A.5或1B.1或-1C.5或-5D.-5或-18.计算的正确结果是()A.0B.C.D.9.如图是由5个完全相同的小正方形搭成的几何体,如果将小正方体A放到小正方体B的正上方,则它的( )A.主视图会发生改变 B.俯视图会发生改变C.左视图会发生改变 D.三种视图都会发生改变10.下列说法中错误的是( )A.给定一组数据,那么这组数据的平均数一定只有一个B.给定一组数据,那么这组数据的中位数一定只有一个C.给定一组数据,那么这组数据的众数一定只有一个D.如果一组数据存在众数,那么该众数一定是这组数据中的某一个11.反比例函数y=﹣,下列说法不正确的是( )A.图象经过点(1,﹣3) B.图象位于第二、四象限C.图象关于直线y=x对称 D.y随x的增大而增大12.如图,在一单位长度为1cm的方格纸上,依如图所示的规律,设定点A、A2、A3、A4、A5、A6、1A7、…、A n,连接点O、A1、A2组成三角形,记为△1,连接O、A2、A3组成三角形,记为△2…,连O、A n、A n+1组成三角形,记为△n(n为正整数),请你推断,当n为50时,△n的面积=()cm2.A.1275B.2500C.1225D.1250三、计算题13.计算:9+7﹣5+2.四、作图题14.如图,在7×6的方格中,△ABC的顶点均在格点上.试按要求画出线段EF(E,F均为格点),各画出一条即可.五、解答题15.如图,菱形ABCD的对角线AC、BD相交于点O,分别延长OA、OC到点E、F,使AE=CF,依次连接B、F、D、E各点.(1)求证:△BAE≌△BCF;(2)若∠ABC=50°,则当∠EBA=________°时,四边形BFDE是正方形.16.已知│3a+5│+(a-2b+)2=0,求关于x的不等式3ax-(x+1)<-4b(x-2)的最小非负整数解.17.在一只不透明的袋子中装有2个白球和2个黑球,这些球除颜色外都相同.(1)若先从袋子中拿走m个白球,这时从袋子中随机摸出一个球是黑球的事件为“必然事件”,则m的值为;(2)若将袋子中的球搅匀后随机摸出1个球(不放回),再从袋中余下的3个球中随机摸出1个球,求两次摸到的球颜色相同的概率.18.居民区内的“广场舞”引起媒体关注,辽宁都市频道为此进行过专访报道.小平想了解本小区居民对“广场舞”的看法,进行了一次抽样调查,把居民对“广场舞”的看法分为四个层次:A.非常赞同;B.赞同但要有时间限制;C.无所谓;D.不赞同.并将调查结果绘制了图1和图2两幅不完整的统计图.请你根据图中提供的信息解答下列问题:(1)求本次被抽查的居民有多少人?(2)将图1和图2补充完整;(3)求图2中“C”层次所在扇形的圆心角的度数;(4)估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有多少人.19.如图,已知△ABC,以AB为直径的⊙O交AC于点D,∠CBD=∠A.(1)求证:BC为⊙O的切线;(2)若E为中点,BD=6,,求BE的长.20.如图,在一次综合实践活动中,小亮要测量一楼房的高度,先在坡面D处测得楼房顶部A的仰角为30°,沿坡面向下走到坡脚C处,然后向楼房方向继续行走10米到达E处,测得楼房顶部A的仰角为60°.已知坡面CD=10米,山坡的坡度i=1: (坡度i是指坡面的铅直高度与水平宽度的比),求楼房AB高度.(结果精确到0.1米)(参考数据:≈1.73,≈1.41)21.喝绿茶前需要烧水和泡茶两个工序,即需要将电热水壶中的水烧到100℃,然后停止烧水,等水温降低到适合的温度时再泡茶,烧水时水温y(℃)与时间x(min)成一次函数关系;停止加热过了1分钟后,水壶中水的温度y(℃)与时间x(min)近似于反比例函数关系(如图).已知水壶中水的初始温度是20℃,降温过程中水温不低于20℃.(1)分别求出图中所对应的函数关系式,并且写出自变量x的取值范围;(2)从水壶中的水烧开(100℃)降到80℃就可以进行泡制绿茶,问从水烧开到泡茶需要等待多长时间六、综合题22.如图,点A的坐标是(-2,0),点B的坐标是(6,0),点C在第一象限内且△OBC为等边三角形,直线BC交y轴于点D,过点A作直线AE⊥BD,垂足为E,交OC于点F.(1)求直线BD的函数表达式;(2)求线段OF的长;(3)连接BF,OE,试判断线段BF和OE的数量关系,并说明理由.23.如图,在△ABC中,AB=AC,AD⊥BC于点D,BC=12cm,AD=8cm.点P从点B出发,在线段BC上以每秒3cm的速度向点C匀速运动,与此同时,垂直于AD的直线m从底边BC出发,以每秒2cm的速度沿DA方向匀速平移,分别交AB,AC,AD于E,F,H,当点P到达点C时,点P与直线m同时停止运动,设运动时间为t秒(t>0).(1)连接DE、DF,当t为何值时,四边形AEDF为菱形?(2)连接PE、PF,在整个运动过程中,△PEF的面积是否存在最大值?若存在,试求当△PEF的面积最大时,线段BP的长.(3)是否存在某一时刻t,使点F在线段EP的中垂线上?若存在,请求出此时刻t的值;若不存在,请说明理由.24.已知,如图,抛物线y=ax2+bx+c(a≠0)的顶点为M(1,9),经过抛物线上的两点A(﹣3,﹣7)和B(3,m)的直线交抛物线的对称轴于点C.(1)求抛物线的解析式和直线AB的解析式.(2)在抛物线上A、M两点之间的部分(不包含A、M两点),是否存在点D,使得S△DAC=2S△DCM?若存在,求出点D的坐标;若不存在,请说明理由.(3)若点P在抛物线上,点Q在x轴上,当以点A,M,P,Q为顶点的四边形是平行四边形时,直接写出满足条件的点P的坐标.参考答案1.答案为6,150.2.答案为:135°3.答案为:0或12.4.答案为:5.答案为:56.答案为:D.7.答案为:A;8.C9.答案为:A.10.C11.答案为:D.12.A13.答案为:;14.解:如图:从图中可得到AC边的中点在格点上设为E,过E作AB的平行线即可在格点上找到F,则EG平分BC;EC=,EF=,FC=,借助勾股定理确定F点,则EF⊥AC;借助圆规作AB的垂直平分线即可;15. (1)证明:在菱形ABCD中,BA=BC,∴∠BAC=∠BCA,∴∠BAE=∠BCF.在△BAE与△BCF中,BA=BC,∠BAE=∠BCF,AE=CF∴△BAE≌△BCF(SAS).(2)20.16.解:17.解:(1)∵在一只不透明的袋子中装有2个白球和2个黑球,这些球除颜色外都相同,从袋子中拿走m个白球,这时从袋子中随机摸出一个球是黑球的事件为“必然事件”,∴透明的袋子中装的都是黑球,∴m=2,故答案为:2;(2)设红球分别为H1、H2,黑球分别为B1、B2,列表得:第二球第一球 H1 H2 B1B2H1(H1,H2)(H1,B1)(H1,B2)H2(H2,H1)(H2,B1)(H2,B2)B1(B1,H1)(B1,H2)(B1,B2)B2(B2,H1)(B2,H2)(B2,B1)总共有12种结果,每种结果的可能性相同,两次都摸到球颜色相同结果有4种,所以两次摸到的球颜色相同的概率=.18.【解答】解:(1)90÷30%=300(人),答:本次被抽查的居民有300人;(2)D所占的百分比:30÷300=10% B所占的百分比:1﹣20%﹣30%﹣10%=40%,B对应的人数:300×40%=120(人), C对应的人数:300×20%=60(人),补全统计图,如图所示:(3)360°×20%=72°,答:“C”层次所在扇形的圆心角的度数为72°;(4)4000×(30%+40%)=2800(人),答:估计该小区4000名居民中对“广场舞”的看法表示赞同(包括A层次和B层次)的大约有2800人.19.(1)证明:∵AB是⊙O的直径,∴∠ADB=90°.∴∠A+∠ABD=90°.又∵∠A=∠CBD,∴∠CBD+∠ABD=90°.∴∠ABC=90°.∴AB⊥BC.又∵AB是⊙O的直径,∴BC为⊙O的切线.(2)解:连接AE.如图所示:∵AB是⊙O的直径,∴∠AEB=∠ADB=90°.∵∠BAD=∠BED,∴.∴在Rt△ABD中,.∵BD=6,∴AB=10.∵E为中点,∴AE=BE.∴△AEB是等腰直角三角形.∴∠BAE=45°.∴.20.解:过D作DG⊥BC于G,DH⊥AB于H,交AE于F,作FP⊥BC于P,如图所示:则DG=FP=BH,DF=GP,∵坡面CD=10米,山坡的坡度i=1:,∴∠DCG=30°,∴FP=DG=CD=5,∴CG=DG=5,∵∠FEP=60°,∴FP=EP=5,∴EP=,∴DF=GP=5+10+=+10,∵∠AEB=60°,∴∠EAB=30°,∵∠ADH=30°,∴∠DAH=60°,∴∠DAF=30°=∠ADF,∴AF=DF=+10,∴FH=AF=+5,∴AH=FH=10+5,∴AB=AH+BH=10+5+5=15+5≈15+5×1.73≈23.7(米),答:楼房AB高度约为23.7米.21.一、综合题22.23.24.解:(1)二次函数表达式为:y=a(x﹣1)2+9,将点A的坐标代入上式并解得:a=﹣1,故抛物线的表达式为:y=﹣x2+2x+8…①,则点B(3,5),将点A、B的坐标代入一次函数表达式并解得:直线AB的表达式为:y=2x﹣1;(2)存在,理由:二次函数对称轴为:x=1,则点C(1,1),过点D作y轴的平行线交AB于点H,(3)设点Q(m,0)、点P(s,t),t=﹣s2+2s+8,①当AM是平行四边形的一条边时,点M向左平移4个单位向下平移16个单位得到A,同理,点Q(m,0)向左平移4个单位向下平移16个单位为(m﹣4,﹣16),即为点P,即:m﹣4=s,﹣6=t,而t=﹣s2+2s+8,解得:s=6或﹣4,故点P(6,﹣16)或(﹣4,﹣16);②当AM是平行四边形的对角线时,由中点公式得:m+s=﹣2,t=2,而t=﹣s2+2s+8,解得:s=1,故点P(1,2)或(1﹣,2);综上,点P(6,﹣16)或(﹣4,﹣16)或(1,2)或(1﹣,2).。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
2020年江西省中考数学模拟试题含答案考生须知:1.全卷共六大题,23小题.满分为120分.考试时间120分钟.2.本卷答案必须做在答题纸的对应位置上,做在试题卷上无效. 温馨提示:请仔细审题,细心答题,相信你一定会有出色的表现!一、选择题(本大题共有6小题,每小题3分,共18分。
请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分) 1、在0 ,-2,1,5这四个数中,最小的数是() A .0 B .-2 C .1 D .5 2、下列三条线段不能构成三角形的三边的是() A .3cm ,4cm ,5cm B .5cm ,6cm ,11cm C .5cm ,6cm ,10cm D .2cm ,3cm ,4cm 3、已知sin α=23,且α是锐角,则α等于( ) A.750B.600C.450D.3004、为了调查瑞州市2016年初三年级学生的身高,从中抽取出200名学生进行调查,这个问题中样本容量为( )A .被抽取的200名学生的身高B .200C .200名D .初三年级学生的身高5、平行四边形、矩形、正方形之间的关系是( )6、下面几何体的主视图是( )二、填空题(本大题共6个小题,每小题3分,共18分.)7、2016年我市经济依然保持了平稳增长。
据统计,截止到今年4月底,我市金融机构存款余额约为1193亿元,用科学计数法应记为元8、分解因式:a3-16a=____________。
9、有两名学员小林和小明练习射击,第一轮10枪打完后两人打靶的环数如图所示,通常新手的成绩不太稳定,那么根据图中的信息,估计小林和小明两人中新手是。
10、定义新运算“※”,规则:a※b=ab-a-b,如1※2=1×2-1-2=-1。
若x2+x-1=0的两根为x1,x2,则x1※x2=。
11、如图a是长方形纸带,∠DEF=20°,将纸带沿EF折叠成图b,再沿BF折叠成图c,则图c中的∠CFE的度数是。
12、如图,以O为圆心的两个同心圆中,大圆的弦AB与小圆相切于点C,若大圆半径为10cm,小圆半径为6cm,则弦AB的长为 cm三、解答题(本大题共5个小题,每小题6分,共30分.解答应写出文字说明、证明过程或演算步骤.)13、1)计算:00245sin 2)1()21(2--++-2)求满足⎩⎨⎧≤+=+227152x y y x 的x 、y 的正整数解。
14、 如图,以AB 为直径的⊙O 交△ABC 的BC 、AC 边与D 、E 两点,在图中仅以没有刻度的直尺画出三角形的三条高(简单叙述你的画法)15、先化简: (1+x1)÷x x 12 再从1、-1、0、2中选择一个合适的数代入求值:16、如图,已知△ABC 中,AB=AC ,BD 、CE 是高,BD 与CE 相交于点O , 1)求证:OB=OC2)如果∠ABC=50o,求∠BOC 的度数。
17、甲、乙、丙、丁四人参加某校招聘教师考试,试后甲、乙两人去询问成绩。
请你根据下面回答者对甲、乙两人回答的内容进行分析:(1)列举出这四人的名次排列所有可能出现的不同情况 (2)求甲排在第一名的概率?四.(本大题共4小题,每小题8分共32分。
)18、如图,在3×3的方阵图中,填写了一些数和代数式(其中每个代数式 都表示一个数),使得每行的3个数、每列的3个数、斜对角的3个数之 和均相等. (1)求x ,y 的值;(2)在备用图中完成此方阵图.19、一次函数y =kx +b 的图象与x 、y 轴分别交于点A (2,0),B (0,4). (1)求该函数的解析式;(2)O 为坐标原点,设OA 、AB 的中点分别为C 、D ,P 为OB 上一动点,求PC +PD 的最小值,并求取得最小值时P 点的坐标.–23 4(备用图)2y –x–2 34 x y (第18题)a bc20、某商场将每件进价为80元的某种商品原来按每件100元出售,一天可售出100件.后来经过市场调查,发现这种商品单价每降低1元,其销量可增加10件.(1)求商场经营该商品原来一天可获利润多少元?(2)设后来该商品每件降价x元,,商场一天可获利润y元.①若商场经营该商品一天要获利润2160元,则每件商品应降价多少元?②求出y与x之间的函数关系式,结合题意写出当x取何值时,商场获利润不少于2160元?=的解,请你仿照他的方法求出下面另外两个方21、小明用下面的方法求出方程30程的解,并把你的解答过程填写在下面的表格中.230x -=令x t =, 则230t -=32t =302t => 32x =, 所以94x =230x x +-= 240x x +--=五.(本大题共1小题,共10分)。
22.阅读下列材料,并解决后面的问题。
材料:我们知道,n 个相同的因数a 相乘可记为a n ,如23=8,此时,3叫做以2为底8的对数,记为log 28(即log 28=3)一般地,若a n=b (a>0且a ≠1,b>0),则n 叫做以a 为底b 的对数,记为log a b(即log a b=n).如34=81,则4叫做以3为底81的对数,记为log 381(即log 381=4) (1)计算以下各对数的值:log 24=,log 216=,log 264=.(2)观察(1)中三数4、16、64之间满足怎样的关系式?log 24、log 216、log 264之间又满足怎样的关系式?(3)根据(2)的结果,我们可以归纳出:log a M+log a N=log a M N (a>0且a ≠1,M>0,N>0) 请你根据幂的运算法则:a m=a n+m以及对数的定义证明该结论。
六、(本大题共1小题,共12分)23、如图,抛物线223y x x =--与x 轴交A 、B 两点(A 点在B 点左侧),直线l 与抛物线交于A 、C 两点,其中C 点的横坐标为2.(1)求A 、B 两点的坐标及直线AC 的函数表达式;(2)P 是线段AC 上的一个动点,过P 点作y 轴的平行线交抛物线于E 点,求线段PE 长度的最大值;(3)点G抛物线上的动点,在x轴上是否存在点F,使A、C、F、G这样的四个点为顶点的四边形是平行四边形?如果存在,求出所有满足条件的F点坐标;如果不存在,请说明理由.参考答案一、选择题(本大题共有6小题,每小题3分,共18分。
请选出各题中一个符合题意的正确选项,不选、多选、错选,均不给分)1、B2、B3、B4、B5、A6、A二、填空题(本大题共6个小题,每小题3分,共18分.) 7、1.193×10118、a(a+4)(a+2)(a-2) 9、小林 10、0 11、120o12、16三、解答题(本大题共5个小题,每小题6分,共30分.解答应写出文字说明、证明过程或演算步骤.)13、1) 原式=+5 ………………………………………………………………………………3分. 2)解得x ≤7/5 ………………………………………………………………………2分所以x=1,y=13………………………………………………………………………3分 14、 如图:连AD 、BE 交于点G ,连CG 延长交AB 于F 。
AD 、BE 、 C F 即为高。
…………………3分 (有文字叙述,图画对即可) 15、解:2111(1)(1)1x x x x x x x x -+-+⎛⎫+÷=÷ ⎪⎝⎭1(1)(1)x x x x x +=⨯-+11x =- ···················· 4分取2x =时,原式1121==- ························· 6分16、 证到OB=OC …………………………………………………………………3分 求到∠ BOC=100o…………………………………………………………………6分 17、(1)列举如下:……………… …………… …………… …………… 4分(甲、乙、丁、丙 )、(甲、丁、乙、丙)、( 丁、乙、甲、丙)、( 丁、甲、乙、丙) (2)甲排在第一名的概率为二分之一……………… … …………… …………… 6分 四、(本大题共4小题,每小题8分共32分。
)18、(1)求x=-1,y=2 ;……… ………………………………3分(2)在备用图中完成此方阵图.………8分(除X、y外填错一个扣1分)19、解:(1)将点A、B的坐标代入y=kx+b并计算得k=-2,b=4.∴解析式为:y=-2x+4;………………………………………………………3分(2)设点C关于点O的对称点为C′,连结PC′、DC′,则PC=PC′.∴PC+PD=PC′+PD≥C′D,即C′、P、D共线时,PC+PD的最小值是C′D.连结CD,在Rt△DCC′中,C′D=22;。
5分易得点P的坐标为(0,1).………………………………………………………………8分 (亦可作Rt△AOB关于y轴对称的△)20、解:⑴若商店经营该商品不降价,则一天可获利润100×(100-80)=2000(元)。
2分⑵①依题意得:(100-80-x)(100+10x)=2160即x2-10x+16=0 -解得:x1=2,x2=8经检验:x1=2,x2=8都是方程的解,且符合题意.答:一天要获利润2160元,则每件商品应降价2元或8元.。
5分②依题意得:y=(100-80-x)(100+10x)∴函数关系式:y= -10x2+100x+2000 。
7分当2≤x≤8 时商场获利润不少于2160元。
8分21、原方程的解求出即给满分,未检验扣1分。
解:方程换元法得新方程解新方程检验求原方程的解230x x +-= 令x t =,则2230t t +-=……1分1213t t ==-,……2分 110t =>, 230t =-<(舍去) ……3分 1x =,所以1x =. ……4分240x x +--=令2x t -=,则220t t +-=……5分1212t t ==-, ……6分 110t =>, 220t =-<(舍去) ……7分 21x -=,所以213x x -==,. ……8分五.(本大题共1小题,共10分)。
