基于囚徒困境模型的博弈论的日常应用
博弈论经典案例

博弈论经典案例在我们的生活中,博弈论的应用无处不在。
从商业竞争到政治决策,从人际关系到体育比赛,博弈论的智慧都在发挥着作用。
接下来,让我们一起来探讨几个经典的博弈论案例。
案例一:囚徒困境假设有两个犯罪嫌疑人 A 和 B 被警察抓住,但警察并没有足够的证据证明他们有罪。
于是,警察将两人分别关押在不同的房间进行审讯,并给出了以下的条件:如果 A 和 B 都保持沉默(不认罪),那么他们都会被判刑 1 年。
如果 A 认罪并指证 B,而 B 保持沉默,那么 A 将被无罪释放,B将被判刑 10 年。
如果 B 认罪并指证 A,而 A 保持沉默,那么 B 将被无罪释放,A将被判刑 10 年。
如果 A 和 B 都认罪并互相指证,那么他们都会被判刑 8 年。
从理性的角度来看,对于 A 来说,如果 B 保持沉默,那么自己认罪可以无罪释放;如果B 认罪,那么自己认罪也能少判刑2 年。
所以,A 会选择认罪。
同样的,B 也会做出相同的选择。
最终的结果是,两人都认罪,都被判刑 8 年。
然而,从整体的最优结果来看,如果两人都保持沉默,那么他们总共只需要判刑 2 年。
但由于双方无法信任对方,都为了自身利益做出了看似最优的选择,却导致了次优的结果。
这个案例在现实生活中有很多应用。
比如在商业竞争中,两个企业可能会为了争夺市场份额而采取降价策略。
如果双方都不降价,可能都能获得一定的利润;但如果一方降价,另一方不降价,那么降价的一方就能获得更多的市场份额;如果双方都降价,虽然都能获得一些市场份额,但利润都会大幅减少。
案例二:智猪博弈假设猪圈里有一头大猪和一头小猪。
猪圈的一头有猪食槽,另一头安装着控制猪食供应的按钮。
按一下按钮会有 10 个单位的猪食进槽,但谁按按钮就会首先付出 2 个单位的成本。
若大猪先到槽边,大猪吃到 9 个单位,小猪只能吃到 1 个单位;若同时到槽边,大猪吃 7 个单位,小猪吃 3 个单位;若小猪先到槽边,大猪吃 6 个单位,小猪吃 4个单位。
现实中囚徒困境的实例

现实中囚徒困境的实例【实用版】目录1.囚徒困境的定义和概念2.囚徒困境在现实中的实例3.解决囚徒困境的方法和策略正文正文囚徒困境是博弈论中的一个经典模型,它描述了两个罪犯被捕后,警方分别与他们单独进行审讯。
如果两人都保持沉默,那么警方无法证明他们有罪,两人都将获得轻判;如果其中一个人供认,而另一个人保持沉默,那么沉默者将被判重刑,而另一个人则不被惩罚;如果两人都供认,则两人都将被判处较轻的刑期。
这个模型反映了在自私的情况下,合作可能导致更好的结果,而不合作则可能导致更差的结果。
尽管囚徒困境是一个抽象的模型,但在现实生活中,我们可以找到许多类似的实例。
例如,在商业竞争中,两家公司可能会陷入囚徒困境。
如果它们都降低价格,那么双方都将失去利润,但如果它们都保持高价,那么可能会有其他竞争者进入市场。
另一个例子是环境问题。
各国都知道减少排放将有利于全球环境,但如果其他国家不采取行动,那么单个国家采取行动将损害其经济。
这些实例都反映了在现实中,囚徒困境是一种常见的现象。
那么,如何解决囚徒困境呢?一种方法是通过合作。
在商业竞争中,如果两家公司可以达成协议,共同维持价格,那么双方都将受益。
在环境问题中,各国可以通过国际协议来共同减少排放。
然而,建立信任是合作面临的一个挑战。
在警方审讯的例子中,罪犯们很难相信对方会保持沉默。
因此,为了解决囚徒困境,我们需要找到方法来建立信任。
另一种方法是通过惩罚和奖励。
如果警方可以向罪犯们提供奖励,以鼓励他们保持沉默,或者制定严厉的惩罚措施,以阻止他们供认,那么囚徒困境就可以得到解决。
同样,在商业竞争中,如果一家公司可以向另一家公司提供奖励,以鼓励它们保持高价,或者制定严厉的惩罚措施,以阻止它们降低价格,那么囚徒困境也可以得到解决。
总的来说,囚徒困境在现实生活中很常见,而解决囚徒困境的方法包括合作和惩罚奖励。
博弈论经典案例

博弈论经典案例在我们的日常生活中,博弈论的应用无处不在。
从商业竞争到政治决策,从体育比赛到人际关系,博弈论为我们理解和预测各种策略互动提供了有力的工具。
接下来,让我们一起探讨几个经典的博弈论案例。
案例一:囚徒困境假设有两个犯罪嫌疑人 A 和 B 被警方抓获,但警方缺乏足够的证据指控他们。
于是,警方将两人分别关押在不同的房间进行审讯,并分别向他们提出相同的条件:如果一人认罪并揭发对方的罪行,而对方保持沉默,那么认罪的人将被从轻处罚,只判 1 年有期徒刑,而沉默的人将被判处 10 年有期徒刑;如果两人都保持沉默,那么他们都将因证据不足而被判处 2 年有期徒刑;如果两人都认罪,那么他们都将被判处 8 年有期徒刑。
对于嫌疑人 A 来说,如果 B 认罪,那么自己认罪将被判 8 年,不认罪将被判 10 年,所以认罪是更好的选择;如果 B 不认罪,那么自己认罪将被判 1 年,不认罪将被判 2 年,还是认罪更好。
同样的逻辑对于嫌疑人 B 也适用。
因此,从个体理性的角度出发,两人都会选择认罪,最终都被判处 8 年有期徒刑。
但从整体的角度来看,如果两人都保持沉默,那么他们总共只需要服刑4 年,这显然是一个更好的结果。
囚徒困境揭示了个体理性与集体理性之间的冲突。
在许多现实情况中,人们往往只考虑自己的利益最大化,而忽视了共同合作可能带来的更优结果。
案例二:智猪博弈猪圈里有一头大猪和一头小猪。
猪圈的一侧有一个食槽,另一侧有一个控制食物供应的按钮。
按一下按钮,会有 10 份食物进入食槽,但按按钮需要付出 2 份食物的成本。
如果大猪先去按按钮,然后小猪去吃,大猪能吃到 6 份食物,小猪能吃到 4 份食物;如果小猪先去按按钮,然后大猪去吃,大猪能吃到 9 份食物,小猪只能吃到 1 份食物;如果大猪和小猪同时去按按钮,大猪能吃到 7 份食物,小猪能吃到 3份食物;如果大猪和小猪都不去按按钮,那么它们都没有食物吃。
对于小猪来说,如果大猪去按按钮,自己等待可以吃到 4 份食物,自己去按按钮只能吃到 1 份食物;如果大猪等待,自己去按按钮没有食物吃,等待也没有食物吃,所以小猪的最优策略是等待。
博弈论经典案例

博弈论经典案例博弈论是研究决策者之间策略和利益的数学理论,它在经济学、政治学、生物学等领域有着广泛的应用。
在博弈论中,经典案例是帮助我们理解和应用博弈论理论的重要工具。
下面,我们将介绍几个经典的博弈论案例,帮助大家更好地理解博弈论的核心概念和应用。
第一个经典案例是囚徒困境。
囚徒困境是指两个犯罪嫌疑人被分开审讯,如果两人都沉默不发言,警方只能以轻罪定罪,每人判刑一年;如果其中一人选择认罪举证,而另一人沉默不发言,认罪者将免于刑事处罚,而另一人将被判十年重刑;如果两人都选择认罪举证,警方将以共同犯罪定罪,每人判刑八年。
在这个案例中,每个囚徒都面临着合作和背叛的选择,他们的最佳策略取决于对方的选择。
囚徒困境案例展示了合作和背叛之间的博弈,以及如何在利益最大化和风险最小化之间进行权衡。
第二个经典案例是孩子分糖果。
假设有两个孩子,他们要平分一袋糖果。
如果他们能够达成一致,那么每个人都会得到一半的糖果;但如果他们无法达成一致,糖果将被拿走。
在这个案例中,每个孩子都需要考虑对方的利益和策略,以及如何最大化自己的利益。
这个案例展示了博弈论在日常生活中的应用,以及如何在博弈中进行合作和谈判。
第三个经典案例是价格竞争。
假设有两家公司在同一个市场上销售相似的产品,它们需要决定产品的定价策略。
如果它们选择相同的价格,那么它们将平分市场份额;但如果它们选择不同的价格,价格较低的公司将获得更多的市场份额。
在这个案例中,每家公司都需要考虑对方的定价策略,以及如何最大化自己的利润。
这个案例展示了博弈论在市场竞争中的应用,以及如何在竞争中制定最佳策略。
以上三个经典案例展示了博弈论在不同领域的应用,以及博弈论理论对于理解和解决现实生活中的冲突和竞争问题的重要性。
通过学习这些经典案例,我们可以更好地理解博弈论的核心概念和方法,为我们在实际问题中的决策和策略制定提供有益的启示。
希望大家能够通过这些案例,深入了解博弈论的精髓,为自己的决策和行为提供更加理性和有效的指导。
博弈论的囚徒困境模型

博弈论的囚徒困境模型引言博弈论是研究决策制定者在多方面利益冲突下进行选择的一门学科。
而囚徒困境模型是博弈论中最经典的模型之一,用于描述两个合作者之间存在利益冲突时可能出现的情况。
本文将详细介绍囚徒困境模型的基本概念、策略和解决方法,并探讨其在现实生活中的应用。
1. 囚徒困境模型的基本概念囚徒困境模型最早由美国数学家Melvin Dresher和Merrill Flood于1950年提出。
它是一个非零和博弈模型,意味着合作者之间的利益不完全一致,他们可以选择合作或背叛对方,从而获得不同的收益。
在囚徒困境模型中,通常有两名犯人被关押在不同的牢房里,无法相互沟通。
检察官给每个犯人提供了一个选择:如果两个人都保持沉默(即合作),那么他们将分别被判处较轻的刑期;如果其中一个人背叛(即不合作),而另一个人保持沉默,那么背叛者将被释放,而保持沉默者将被判处重刑;如果两个人都背叛,那么他们将各自被判处较重的刑期。
2. 囚徒困境模型的策略在囚徒困境模型中,每个犯人都有两种基本策略:合作和背叛。
根据对方的选择和自己的选择,可以得出四种不同的结果:互相合作、互相背叛、自己合作对方背叛、自己背叛对方合作。
这些结果对应着不同的收益。
为了量化这些收益,通常使用一个称为支付矩阵的工具。
支付矩阵是一个2x2的矩阵,其中每个元素表示在不同情况下每个合作者获得的收益。
在标准囚徒困境模型中,支付矩阵可以表示为:合作背叛合作R,R S,T背叛T,S P,P其中R表示互相合作时的收益,T表示自己背叛对方合作时的收益,S表示自己合作对方背叛时的收益,P表示互相背叛时的收益。
通常,R > T > P > S。
3. 囚徒困境模型的解决方法在囚徒困境模型中,每个犯人都希望获得最大的个人利益。
然而,如果两个犯人都追求个人利益,那么最终的结果将是两败俱伤。
如何选择合适的策略成为了一个关键问题。
在博弈论中,有许多不同的解决方法可以用于囚徒困境模型。
现实中的囚徒困境现实案例

现实中的囚徒困境现实案例-优势策略均衡-免费搭车(博弈策略)1、家电价格战:由于彩电行业是寡头控制的,9大厂商控制了70%的市场份额,这样的博弈互动特征更为突出。
1999年4月,长虹为扩大市场宣布彩电产品降价,各整个行业市场造成巨大震动,随即康佳、TCL、创维达成默契:建立彩电联盟。
直到4月20日上午,康佳仍然表示不降价,但是当晚即改变主意,使得TCL和创维措手不及,价格战立即蔓延开来。
大家都降价对于各自的扩大市场没有多大帮助,反而使得利润都被削弱了,1996~2000年,彩电行业发生大的价格战达到8次以上,整个行业的利润被极大削减,全行业进入亏损,信息产业部统计价格战使行业利润减少147亿元。
价格战于人于己都不利,为什么还打价格战呢?这是一个简单的囚徒困境博弈形势。
双方作好的结果都是降价,降价都是“优势策略”。
大家可能会想到成立价格联盟,但是事实是:2000年6月9日,TCL、海信、创维、厦华、乐华、金星、熊猫、西湘9家厂商歃血结盟,召开了彩电联盟峰会,实际上是一纸空文,当年8月康佳响应长虹的降价20%口号,率先脱离9家同盟会,价格战在次开打。
所以,任何同盟都敌不过“先下手为强”的背义利益来的真实。
2、军备竞赛:冷战时期的美苏军备竞赛都是各自的优势策略,双方都无法信任对方不搞军事发展,都担心自己被设计而陷入危险,所以即使曾经出现了“盟约”,最后还是不得不撕毁。
3、公共资源的过度使用:哈丁(Hardin)于1968年在《科学》杂志上发表的论文《公共地悲剧》经常被引用,表达了这样一个思想:如果人们都只关注个人福利,公共资源就会被过度使用。
例如:《公共草地牧羊》一片公共草地可以养羊,但是随着羊的数量增加,草地对羊的贡献价值再下降,假设养2只羊,每只可以带来100元的价值,养3只羊,则每只可以得到60元的价值,到了养4只以后,每只的价值只有40元。
如果共有2个养殖户,可以各自选择养1只还是2只时,盈利表显示各自的优势策略是养2只,共4只,所以草地作为公共资源只能产生4x40=160远的价值,远低于2x100=200的贡献,这就是公共资源过度利用,而最后各人利益也被消减了。
浅谈生活中的“囚徒困境”

浅谈生活中的“囚徒困境”博弈论(game theory)在我们生活中是无处不在的,大大小小的事情中都可从看到博弈论的影子。
外面下雨了,你就应根据小雨这一信息采取对应的策略,出去就要打伞,如果外面艳阳高照,你大可选择不带伞出门。
这就是博弈论在生活中的例子,只是很少有人去关注它博弈论对人的基本假定是:人是理性的或者说自私的,理性的人是指他在具体策略选择时的目的是使自己的利益最大化,博弈论研究的是理性的人之间如何进行策略选择的。
“囚徒困境”是博弈论经典案例之一,讲的是一位富翁在家中被杀,财物被盗。
警方在此案的侦破过程中,抓到两个犯罪嫌疑人,斯卡尔菲丝和那库尔斯,并从他们的住处搜出被害人家中丢失的财物。
但是,他们矢口否认曾杀过人,辩称是先发现富翁被杀,然后只是顺手牵羊偷了点儿东西。
为防止串供,警方将两人隔离,分别关在不同的房间进行审讯。
检察官说,“由于你们的偷盗罪已有确凿的证据,所以可以判你们一年刑期。
但是,我可以和你做个交易。
如果你单独坦白杀人的罪行,我只判你三个月的监禁,但你的同伙要被判十年刑。
如果你拒不坦白,而被同伙检举,那么你就将被判十年刑,他只判三个月的监禁。
但是,如果你们两人都坦白交代,那么,你们都要被判5年刑。
”一般的博弈问题由三个要素所构成:即局中人又称当事人、参与者、策略等等的集合,策略集合以及每一对局中人所做的选择和赢得集合。
其中所谓赢得是指如果一个特定的策略关系被选择,每一局中人所得到的效用。
所有的博弈问题都会遇到这三个要素。
在这个例子里,博弈的参加者就是两个嫌疑犯A和B,他们每个人都有两个策略即坦白和不坦白,判刑的年数就是他们的支付。
可能出现的四种情况:A和B均坦白或均不坦白、A坦白B不坦白或者B坦白A不坦白,是博弈的结果。
A和B均坦白是这个博弈的纳什均衡。
这是因为,假定A选择坦白的话,B最好是选择坦白,因为B坦白判8年而抵赖却要判十年;假定A选择抵赖的话,B最好还是选择坦白,因为B坦白判不被判刑而抵赖确要被判刑1年。
囚徒困境--博弈论在谈判中的应用
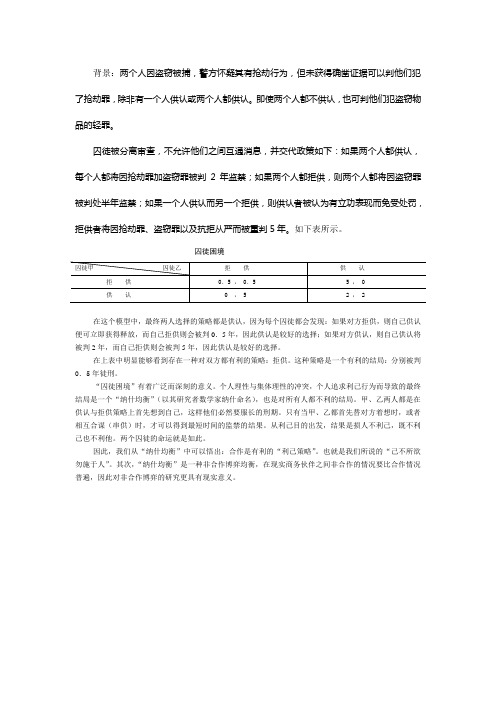
背景:两个人因盗窃被捕,警方怀疑其有抢劫行为,但未获得确凿证据可以判他们犯了抢劫罪,除非有一个人供认或两个人都供认。
即使两个人都不供认,也可判他们犯盗窃物品的轻罪。
囚徒被分离审查,不允许他们之间互通消息,并交代政策如下:如果两个人都供认,每个人都将因抢劫罪加盗窃罪被判2年监禁;如果两个人都拒供,则两个人都将因盗窃罪被判处半年监禁;如果一个人供认而另一个拒供,则供认者被认为有立功表现而免受处罚,拒供者将因抢劫罪、盗窃罪以及抗拒从严而被重判5年。
如下表所示。
囚徒困境在这个模型中,最终两人选择的策略都是供认,因为每个囚徒都会发现:如果对方拒供,则自己供认便可立即获得释放,而自己拒供则会被判0.5年,因此供认是较好的选择;如果对方供认,则自己供认将被判2年,而自己拒供则会被判5年,因此供认是较好的选择。
在上表中明显能够看到存在一种对双方都有利的策略:拒供。
这种策略是一个有利的结局:分别被判0.5年徒刑。
“囚徒困境”有着广泛而深刻的意义。
个人理性与集体理性的冲突,个人追求利己行为而导致的最终结局是一个“纳什均衡”(以其研究者数学家纳什命名),也是对所有人都不利的结局。
甲、乙两人都是在供认与拒供策略上首先想到自己,这样他们必然要服长的刑期。
只有当甲、乙都首先替对方着想时,或者相互合谋(串供)时,才可以得到最短时间的监禁的结果。
从利己目的出发,结果是损人不利己,既不利己也不利他。
两个囚徒的命运就是如此。
因此,我们从“纳什均衡”中可以悟出:合作是有利的“利己策略”。
也就是我们所说的“己不所欲勿施于人”。
其次,“纳什均衡”是一种非合作博弈均衡,在现实商务伙伴之间非合作的情况要比合作情况普遍,因此对非合作博弈的研究更具有现实意义。
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
基于囚徒困境模型的博弈论的日常应用
作者:张育弘
来源:《消费导刊》2017年第04期
摘要:本文旨在引入博弈论的基本概念、基本内容以及基本方法。
并对囚徒困境模型进行分析、研究。
将该博弈模型与日常生活相结合。
将决策模型应用到日常生活中的两个案例中:购买火车票时的应用、马路行驶违章问题研究。
并针对其产生的问题提出一定的建议。
关键词:博弈论囚徒困境日常生活最优化
一、博弈论基础
(一)博弈的基本概念
博弈论,又名“对策论”,它研究的是决策者为获得最大利益如何选择适当的策略的理论和方法。
作为应用数学的一个分支,博弈论在运筹学领域也有重要地位。
它研究的是在彼此依赖的条件下,决策者为获得最大利益如何抉择适当的策略的理论和方法。
(二)博弈的基本内容
博弈的构成要素有五个,分别是:参与者、行动、支付、规则以及均衡。
参与者是博弈的决策主体;行动指参与者可以采取的行动方案;支付指根据决策结果获得的收益;规则指对参与者行动的先后次序等内容的规定;均衡指一切参与者的最优策略的组合。
(三)纳什均衡
纳什均衡是指参与者在作出决策后,所得到的支付结果是稳定的,并且任一方都不能通过改变自己的策略得到更大的收益,因此,参与者都不会改变策略来打破这个均衡。
博弈的结果总为纳什均衡,因此,我们用纳什均衡来表示博弈的结果。
二、囚徒困境模型
囚徒困境是博弈论中具典型的案例。
警察抓捕两个作案嫌疑犯,并将其关在不同的房间受审。
警察告诉每个嫌疑犯:若两人都抵赖,各判刑一年;两人都坦白,各判八年;一人坦白而另一人抵赖,则释放坦白嫌疑犯,对抵赖嫌疑犯判刑十年。
在这个博弈中,每个嫌疑犯都有两种选择:坦白或抵赖。
然而,每个嫌疑犯的最优选择是坦白:如果同伙抵赖、自己坦白,则被释放,不坦白则会判刑一年,总之,坦白要比抵赖好;如果同伙坦白、自己坦白的话判八年,抵赖则被判十年,坦白还是比抵赖更好。
结果,两个嫌疑犯都选择坦白,各判刑八年。
这就是囚徒困境。
运用博弈论分析,参与者为嫌疑犯甲和嫌疑犯乙;行动集分别为嫌疑犯坦白或者抵赖。
若两名嫌疑犯均选择坦白,其支付结果为(-8,-8);若嫌疑犯甲坦白而乙抵赖,其支付结果为(0,-10);若嫌疑犯甲抵赖,乙坦白,支付结果为(-10,0);若嫌疑犯甲、乙均选择抵赖,其支付结果为(-1,-1)。
运用下划线法进行分析,支付矩阵为表2-1:
由囚徒困境案例得知,一个人在追求自身利益最大化的行为不一定可以满足集体利益的最大化,这就导致了个人选择和集体理性的矛盾。
三、囚徒困境模型在日常生活中的应用
(一)购买火车票时的应用
火车出行方便快捷、价格合理,因此乘坐火车出行已成为人们内剧增,火车票的购买难度便明显增加。
因此,抢票是无法避免的。
假设学生甲和学生乙同时购买仅剩的一张火车票,运用博弈论进行分析,该博弈的参与者为学生甲和学生乙;行动集为学生选择放弃或者继续坚持;若学生甲坚持,学生乙放弃,其支付结果为(1,-1);若学生甲坚持,学生乙坚持,其支付结果为(-∞,-∞);若学生甲放弃,学生乙坚持,其支付结果为(-1,1);若学生甲放弃,学生乙放弃,其支付结果为(0,0);运用下划线法进行分析:划线后的支付矩阵为表3-1:
(二)马路行驶中的违章问题研究
为了节省时间,大部分驾驶员会选择加速、超车甚至闯红灯,所以造成了日益突出的城市交通问题和交通拥堵现象。
运用博弈论对该现象进行分析。
假定在不全违章的情况下,违章的成本低于不违章的成本,违章成本为1,不违章成本为2;若驾驶员同时违章,会造成交通堵塞,产生额外的成本2。
假设马路上有两名驾驶员:驾驶员甲和乙,即为该博弈的参与者。
行动集为:驾驶员违章或不违章;若驾驶员甲违章,乙不违章,则支付表示为(-1,-4);若驾驶员甲违章,乙违章,支付表示为(-3,-3);若驾驶员甲不违章,乙违章,支付表示为(-4,-1);若驾驶员甲不违章,乙不违章,他们的支付表示为(-2,-2),运用下划线法分析后的支付矩阵为表3-2:
从支付矩阵看,该博弈的策略组合:驾驶员甲不违章且驾驶员乙不违章为唯一的纳什均衡。
但是,由于每位驾驶员都会追求个人利益最大化,因此他们都会不约而同的选择违章,从而引发交通问题,既损害了个人利益,也损害了整个社会的利益。
四、结论与建议
以上案例直接明了的让我们看到了博弈论的用途。
博弈是决策与对应结果的互动过程。
决策结果不仅依赖于我们自身的决策,同时也离不开他人的决策选择。
因此在生活中我们要运用理性的思维方式去思考问题、解决问题,要善于避开各种各样的社会准则,加深对于对手的认识和理解,最终根据对方的选择做出明智的决策,让自己的人生之路走得更顺利。
