光电子技术安毓英版答案
光电子技术安毓英第五章课后习题参考答案1
5.1以图中p型半导体器件为例，栅极加正电压超过MOS晶体管的开启电压时，在半导体金属界面会形成深度耗尽层，称为电子的势阱。
当有光照时，光生电子会聚集在势阱中，形成电荷存储。
以图中三相CCD结构为例，相邻三个栅极电压从高电平依次降低到低电平，为一个周期。
每个栅极电压降低过程与下一个栅极高电平重合。
这样三个栅极位置的电子势阱会依次减小，消失与出现。
存储电子会随着势阱位置的移动发生转移。
电荷输出：外加放大电路，利用电荷电势进行放大，输出信号CCD输出信号的特点：1.信号电压是在浮置电平基础上的负电压2.每个电荷包的输出占有一定的时间长度3.在输出信号总叠加有复位期间的高电平脉冲根据这些特点，对CCD的输出进行处理时，较多地采用了取样技术，以去除浮置电平，复位高脉冲及抑制噪声。
5.2光电成像系统利用的都是帧扫描方式，完成一帧扫描所需要的时间称为帧时T，单位时间完成的帧数称为帧速 F, 它们的关系是T=1/F5.3(1)F=0.3m(2) W=n*α=128*a/f=128x100um/0.3m=4.26x10-2 rad5.5从目标调制度（对比度）到人眼观察到，总的调制函数为各个调制函数的乘积，光学体统调制传递函数为MTF O, 人眼能感知的极限调制度为0.026，则0.5×MTF O×0.9×0.5×0.95×0.5≥0.026MTF O≥0.245.7(1)像增强器CCD (ICCD)可以探测微光图像，但是其内经过光子-电子的多次转换，图像质量会有损失，光锥中光纤光栅干涉波纹，折断和耦合损失都将使ICCD输出噪声增加，对比度下降，动态范围减小，影响成像质量。
（2）薄型背向CCD器件灵敏度高，噪声低，但当照度低于10-6 lx 时，只能依赖图像增强来提高增益，克服噪音（3）电子轰击型CCD简化了光子多次转换过程，信噪比大大提高，与ICCD相比，电子轰击型CCD具有体积小，重量轻，可靠性高，分辨率高及对比度好等优点。
最新光电子技术(安毓英)习题课后答案
第一章1. 设在半径为R c 的圆盘中心法线上，距盘圆中心为l 0处有一个辐射强度为I e 的点源S ，如图所示。
试计算该点源发射到盘圆的辐射功率。
解：因为，且()⎪⎪⎭⎫ ⎝⎛+-=-===Ω⎰22000212cos 12sin c R R l l d d rdS d c πθπϕθθ 所以⎪⎪⎭⎫ ⎝⎛+-=Ω=Φ220012c e e e R l lI d I π2. 如图所示，设小面源的面积为∆A s ，辐射亮度为L e ，面源法线与l 0的夹角为θs ；被照面的面积为∆A c ，到面源∆A s 的距离为l 0。
若θc 为辐射在被照面∆A c 的入射角，试计算小面源在∆A c 上产生的辐射照度。
解：亮度定义:强度定义:ΩΦ=d d I ee 可得辐射通量：Ω∆=Φd A L d s s e e θcos 在给定方向上立体角为：2cos l A d cc θ∆=Ω 则在小面源在∆A c 上辐射照度为：20cos cos l A L dA d E cs s e e e θθ∆=Φ=ΩΦd d ee I =r r ee A dI L θ∆cos =3.假如有一个按朗伯余弦定律发射辐射的大扩展源（如红外装置面对的天空背景），其各处的辐亮度L e 均相同，试计算该扩展源在面积为A d 的探测器表面上产生的辐照度。
答：由θcos dA d d L e ΩΦ=得θcos dA d L d e Ω=Φ，且()22cos rl A d d +=Ωθ 则辐照度：()e e e L d rlrdrl L E πθπ=+=⎰⎰∞20022224. 霓虹灯发的光是热辐射吗？不是热辐射。
霓虹灯发的光是电致发光，在两端放置有电极的真空充入氖或氩等惰性气体，当两极间的电压增加到一定数值时，气体中的原子或离子受到被电场加速的电子的轰击，使原子中的电子受到激发。
当它由激发状态回复到正常状态会发光，这一过程称为电致发光过程。
光电子技术第三版安毓英刘继芳等著习题答案完整版
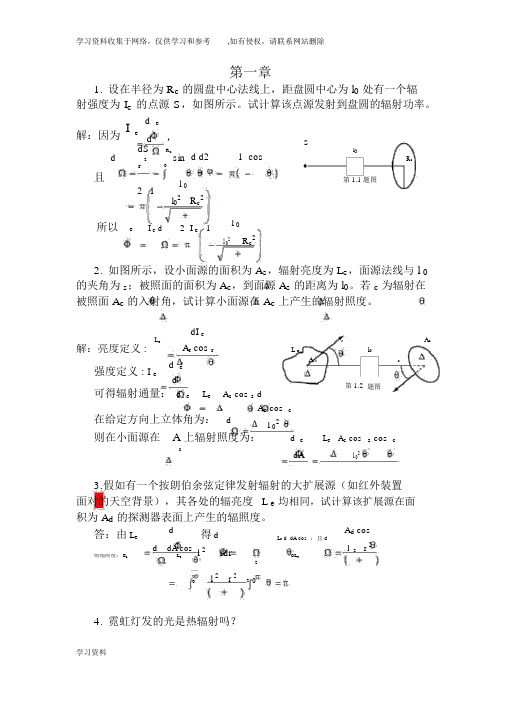
学习资料收集于网络，仅供学习和参考 ,如有侵权，请联系网站删除第一章1. 设在半径为 R c 的圆盘中心法线上，距盘圆中心为 l 0 处有一个辐射强度为 I e 的点源 S ，如图所示。
试计算该点源发射到盘圆的辐射功率。
解：因为 Ie d ed，SdSR c d d21 cosl 0d2sin R cr且l 0第 1.1 题图2 1l 02R c 2所以 eI e d2 I e 1l 0R c 2l 022. 如图所示，设小面源的面积为 A s ，辐射亮度为 L e ，面源法线与 l 0 的夹角为 s ；被照面的面积为 A c ，到面源 A s 的距离为 l 0。
若 c 为辐射在被照面 A c 的入射角，试计算小面源在 A c 上产生的辐射照度。
dI e L e A r cos rsA c解：亮度定义 :L el 0强度定义 : I ed e A scd第 1.2 题图可得辐射通量： d e L e A s cos s d在给定方向上立体角为： A c cos cdl 02则在小面源在 A 上辐射照度为：d eL e A s cos s cos ccdAl 023.假如有一个按朗伯余弦定律发射辐射的大扩展源（如红外装置面对的天空背景），其各处的辐亮度 L e 均相同，试计算该扩展源在面 积为 A d 的探测器表面上产生的辐照度。
答：由 L ed得 dA d cosdA cosL e d dA cos ，且 d2 r 2d l2rdrl 则辐照度： E eL ed L e2l 2 r 22 04. 霓虹灯发的光是热辐射吗？学习资料收集于网络，仅供学习和参考,如有侵权，请联系网站删除不是热辐射。
霓虹灯发的光是电致发光，在两端放置有电极的真空充入氖或氩等惰性气体，当两极间的电压增加到一定数值时，气体中的原子或离子受到被电场加速的电子的轰击，使原子中的电子受到激发。
当它由激发状态回复到正常状态会发光，这一过程称为电致发光过程。
光电子技术课后答案
第二章:⒉在玻璃( 2.25,1)r r εμ==上涂一种透明的介质膜以消除红外线(0.75)m λμ=的反射。
⑴求该介质膜应有的介电常量及厚度。
⑵如紫外线(0.42)m λμ=垂直照射至涂有该介质膜的玻璃上，反射功率占入射功率百分之多少？⑴1.5n = 正入射时，当n =时，膜系起到全增透作用5 1.225n ==，正入射下相应的薄膜厚度最薄为 00.750.15344 1.225h m nλμ===⨯⑵正入射时，反射率为222200002222000022()cos ()sin 22()cos ()sin G G G G n n nhnhn n n n n n nh nhn n n n ππλλρππλλ-+-=+++正220022220002()cos 3.57%22()cos ()sin G G G nhn n n n nhnhn n n n πλππλλ-==+++⒌一束波长为0.5 m μ的光波以045角从空气入射到电极化率为20.6j ＋的介质表面上，求⑴此光波在介质中的方向（折射角）。
⑵光波在介质中的衰减系数。
⑴2123n =+=n = 由112sin sin n n θθ=得2sin 6θ=2arcsin 6θ= ⑵衰减系数72(0.6)0.6 1.310nr k πλ=-⨯-=⨯=⨯⒍输出波长λ＝632.8nm 的He-Ne 激光器中的反射镜是在玻璃上交替涂覆ZnS 和2ThF 形成的，这两种材料的折射率系数分别为1.5和2.5。
问至少涂覆多少个双层才能使镜面反射系数大于99.5％？设玻璃的折射率G n ＝1.5 由题意： 02220220()0.995()P H H LG P H H L Gn n n n n n n n n n λρ⎡⎤-⎢⎥⎢⎥=≥⎢⎥+⎢⎥⎣⎦正，，即22222.5 1.51()1.5 1.50.99752.5 1.51()1.5 1.5P P -≤-+ 即 250.0025() 1.5 1.99753P ⨯⨯≥25()532.73P≥ 212.3P = 7P ≈ 故至少涂覆7个双层。
光电子技术课后习题答案
第一章1. 设在半径为R c 的圆盘中心法线上，距盘圆中心为l 0处有一个辐射强度为I e 的点源S ，如图所示。
试计算该点源发射到盘圆的辐射功率。
解：因为ΩΦd d ee I =， 且 ()⎪⎪⎭⎫ ⎝⎛+-=-===Ω⎰22000212cos 12sin c R R l l d d rdSd c πθπϕθθ 所以⎪⎪⎭⎫ ⎝⎛+-=Ω=Φ220012c e e e R l l I d I π2. 如图所示，设小面源的面积为∆A s ，辐射亮度为L e ，面源法线与l 0的夹角为θs ；被照面的面积为∆A c ，到面源∆A s 的距离为l 0。
若θc 为辐射在被照面∆A c 的入射角，试计算小面源在∆A c 上产生的辐射照度。
解：亮度定义:r r ee A dI L θ∆cos =强度定义:ΩΦ=d d I ee可得辐射通量：Ω∆=Φd A L d s s e e θcos在给定方向上立体角为：20cos l A d c c θ∆=Ω则在小面源在∆A c 上辐射照度为：20cos cos l A L dA d E cs s e e e θθ∆=Φ=3.假如有一个按朗伯余弦定律发射辐射的大扩展源（如红外装置面对的天空背景），其各处的辐亮度L e 均相同，试计算该扩展源在面积为A d 的探测器表面上产生的辐照度。
答：由θcos dA d d L e ΩΦ=得θcos dA d L d e Ω=Φ，且()22cos rl A d d +=Ωθ 则辐照度：()e e e L d rlrdrl L E πθπ=+=⎰⎰∞20022224. 霓虹灯发的光是热辐射吗？l 0SR c第1.1题图L e ∆A s ∆A cl 0 θsθc第1.2题图不是热辐射。
霓虹灯发的光是电致发光，在两端放置有电极的真空充入氖或氩等惰性气体，当两极间的电压增加到一定数值时，气体中的原子或离子受到被电场加速的电子的轰击，使原子中的电子受到激发。
光电子技术安毓英习题答案(完整版)
第一章2. 如图所示，设小面源的面积为∆A s ，辐射亮度为L e ，面源法线与l 0的夹角为θs ；被照面的面积为∆A c ，到面源∆A s 的距离为l 0。
若θc 为辐射在被照面∆A c 的入射角，试计算小面源在∆A c 上产生的辐射照度。
解：亮度定义:r r ee A dI L θ∆cos =强度定义:ΩΦ=d d I e e可得辐射通量：Ω∆=Φd A L d s s e e θcos在给定方向上立体角为：2cos l A d cc θ∆=Ω 则在小面源在∆A c 上辐射照度为：2cos cos l A L dA d E cs s e e e θθ∆=Φ=3.假如有一个按朗伯余弦定律发射辐射的大扩展源（如红外装置面对的天空背景），其各处的辐亮度L e 均相同，试计算该扩展源在面积为A d 的探测器表面上产生的辐照度。
答：由θcos dA d d L e ΩΦ=得θcos dA d L d e Ω=Φ，且()22cos r l A d d +=Ωθ则辐照度：()e e e L d rlrdrl L E πθπ=+=⎰⎰∞20022227.黑体辐射曲线下的面积等于等于在相应温度下黑体的辐射出射度M 。
试有普朗克的辐射公式导出M 与温度T 的四次方成正比，即 M=常数4T ⨯。
这一关系式称斯特藩-波耳兹曼定律，其中常数为 5.6710-8W/m 2K 4解答：教材P9，对公式2151()1e C TC M T eλλλ=-进行积分即可证明。
第二章3．对于3m 晶体LiNbO3，试求外场分别加在x,y 和z 轴方向的感应主折射率及相应的相位延迟（这里只求外场加在x 方向上）解：铌酸锂晶体是负单轴晶体，即n x =n y =n 0、n z ＝n e 。
它所属的三方晶系3m 点群电光系数有四个，即γ22、γ13、γ33、γ51。
电光系数矩阵为：L e∆A s∆A cl 0θsθc第1.2题图⎥⎥⎥⎥⎥⎥⎥⎥⎦⎤⎢⎢⎢⎢⎢⎢⎢⎢⎣⎡--=0000000002251513313221322γγγγγγγγγij 由此可得铌酸锂晶体在外加电场后的折射率椭球方程为：12)(2)1()1()1(2251233121322202152220=-++++++++-xy E xz E yz E z E n y E E n x E E n x x z z ez y z y γγγγγγγ （1）通常情况下，铌酸锂晶体采用450－z 切割，沿x 轴或y 轴加压，z 轴方向通光，即有E z =E y =0,且E x ≠0。
光电子技术安毓英第一章课后习题参考答案1
(t)
2
− A21t
20
20 − s
因此
s
=
1 A 21
1.19 该电矢量方程写成实数形式：
E=(-2i+2 3 j) cos (6x108t-(- 3 x-y)
E0= (-2, 2 3 , 0), k=(- 3 , -1, 0), = 6108
平面波电矢量的振动方向为 X 和 Y 轴面内, 一，三象限内，与 X 轴成 60°角 传播方向为与 X 和 Y 轴平面内，第三象限，与 X 轴成 30°角负向传播
类似于一个完全吸收的黑体，所以室外看窗口感觉较黑。
1.8 （1）根据维恩位移定律：
m
=
2897.9m 3K
K
= 966m
（2）根据斯忒潘-波尔兹曼定律，黑体的辐射出射度为
Meb (T ) = T 4 = 5.67 10−8 J （/ m2 s K4）T 4
所以 3K 辐射背景的辐射出射度为：
s
1 ln10
=
4.80 3 103 K ln10
=
6254K
1.13 证明：自发辐射，一个原子由高能级 自发跃迁到 ，单位时间内能级 减少的粒子数为：
dn2 =−( dn21) dt dt
sp
自发跃迁几率
A21
=(
dn21) dt
1 n2
sp
可得：
dn2 dt
=−
A21
n2
t
n =n e n e 解得：
r sin
hr
Le
=
dIe ds cos
,
dIe = Le ds cos
,
ds = rd r sin d cos
第二版《光电子技术》课后习题答案
1・1可见光的波长.频率和光子的能量范围分别是多少？波长：380~780nm 400-760nm频率：385T~790THz 400T-750THz能量：l ・6~3・2cV1.2辐射度量与光度量的根本区别是什么？为什么量子流速率的计算公式中不能出现光度 戢？为了泄量分析光与物质相互作用所产生的光电效应，分析光电敏感器件的光电特 性，以及用光电敏感器件进行光谱、光度的左量计算，常需要对光辐射给出相应的计量参 数和量纲。
辐射度量与光度量是光辐射的两种不同的度量方法。
根本区別在于：前者是物 理（或客观）的讣量方法，称为辐射度量学计量方法或辐射度参数，它适用于整个电磁辐 射谱区，对辐射量进行物理的计量：后者是生理（或主观）的计量方法，是以人眼所能看 见的光对大脑的刺激程度来对光进行计算，称为光度参数。
因为光度参数只适用于 O.38~O.78um 的可见光谱区域，是对光强度的主观评价，超过这个谱区，光度参数没有任何 意义。
而量子流是在整个电磁辐射，所以量子流速率的il •算公式中不能出现光度量.光源在 给定波长入处，将入〜X+dX 范囤内发射的辐射通M d<Pe,除以该波长入的光子能量h V,就得到光源在入处每秒发射的光子数，称为光谱量子流速率。
1.3 -只白炽灯，假设齐向发光均匀，悬挂在离地而l ・5m 的髙处，用照度计测得正下方地 而的照度为301X,求出该灯的光通量。
0>=L*4 n R A 2=30*4*3.14* 1.5A 2=848.2引x1・4 一支氨■就激光器（波长为632.8nm ）发出激光的功率为2mW.该激光束的平而发散角 为lmrad,激光器的放电毛细管为1mm 。
求出该激光束的光通呈:、发光强度、光亮度、光出射度。
若激光束投射在10m 远的白色漫反射屏上，该漫反射屏的发射比为0.85,求该屏 上的光亮度。
= 683x0.265x2x107 = 0.3 62/,77 "令・(>1) _ 0.362 7lS _ XO.OOO52 Z = 10/zz » r = O.OOO5ZZ7 (P6), d /• 2 A7 = O.85^v = 0.85——:——— = 0.85 ・疋厶 — v v as cose v /2c 如0.85 £厶,升 r —= =1 55cd / m dGdS cos 3 dG 2兀 1.6从黑体辐射曲线图可以看书，不同温度下的黑体辐射曲线的极大值处的波长随温度T 的升2兀Rh s Q =-—— = 2兀(1 — cos △e、（几） 2兀（1 — cos &） 0.362 2兀(1 — cos 0.00 1) "40)= △e 。
- 1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。
习 题11. 设在半径为R c 的圆盘中心法线上，距盘圆中心为l 0处有一个辐射强度为I e 的点源S ，如图所示。
试计算该点源发射到盘圆的辐射功率。
解：ΩΦd d e e I =， 202πd l R c =Ω202e πd d l R I I c e e ==ΩΦ2. 如图所示，设小面源的面积为∆A s ，辐射亮度为L e ，面源法线与l 0的夹角为θs ；被照面的面积为∆A c ，到面源∆A s 的距离为l 0。
若θc 为辐射在被照面∆A c 的入射角，试计算小面源在∆A c 上产生的辐射照度。
解：用定义r r e e A dI L θ∆cos =和AE ee d d Φ=求解。
3.假设有一个按郎伯余弦定律发射辐射的大扩展源（如红外装置面对的天空背景），其各处的辐亮度e L 均相同。
试计算该扩展源在面积为d A 的探测器表面上产生的辐照度。
解：辐射亮度定义为面辐射源在某一给定方向上的辐射通量，因为余弦辐射体的辐射亮度为 eoe eo dI L L dS== 得到余弦辐射体的面元dS 向半空间的辐射通量为 0e e e d L dS L dS ππΦ==又因为在辐射接收面上的辐射照度e E 定义为照射在面元上的辐射通量e d Φ与该面元的面积dA 之比，即ee d E dAΦ= 所以该扩展源在面积为d A 的探测器表面上产生的辐照度为e e dL dS E A π=单位是2/W m 4. 霓虹灯发的光是热辐射吗？ 解： 不是热辐射。
5刚粉刷完的房间从房外远处看，它的窗口总显得特别黑暗，这是为什么？解：因为刚粉刷完的房间需要吸收光线，故从房外远处看它的窗口总显得特别黑暗第1题图第2题图6. 从黑体辐射曲线图可以看出，不同温度下的黑体辐射曲线的极大值处的波长λm 随温度T 的升高而减小。
试由普朗克热辐射公式导出常数=T m λ。
这一关系式称为维恩位移定律，其中常数为2.898⨯10-3m •K 。
解：普朗克热辐射公式求一阶导数，令其等于0，即可求的。
7.黑体辐射曲线下的面积等于在相应温度下黑体的辐射出射度M 。
试由普朗克热辐射公式导出M 与温度T 的四次方成正比，即4*M =常数T这一关系式被称为斯忒藩—玻尔兹曼定律，其中常数为-85.67*10W(24m K ⋅)。
解：黑体处于温度T 时，在波长λ处的单色辐射出射度有普朗克公式给出： 252[exp(/)1]e bB hc M hc k λπλλ=- 式中h 为普朗克常数，c 为真空中光速，B k 为玻尔兹曼常数。
令212C hc π=,2Bhc k C =则上式可改写为152[exp(/)1]e b C M C T λλλ=-将此式积分得 245002[exp(/)1]eb e b B hc M M d d T hc k λπλλσλλ∞∞===-⎰⎰此即为斯忒藩—玻尔兹曼定律。
式中24824322 5.67010/15Bk J m h cπσ-==⨯••为斯忒藩—玻尔兹曼常数。
8．宇宙大爆炸遗留在宇宙空间的均匀背景热辐射相当于3K 黑体辐射。
（1）此辐射的单色辐射出射度在什么波长下有意义？ （2）地球表面接收到此辐射的功率是多大？解：答（1）由维恩位移定律2897.9*m T m k λμ=（）得2897.9965.973λ==m μ （2）由e e d M dSΦ=和普朗克公式152[exp(/)1]e b C M C T λλλ=-及地球面积24S R π=得出地球表面接收到此辐射的功率。
9. 常用的彩色胶卷一般分为日光型和灯光型。
你知道这是按什么区分的吗？解：按色温区分。
10. v dv ρ为频率在()vv dv +间黑体辐射的能量密度，d λρλ为波长在d λλ间黑体辐射能量密度。
已知338/[exp(/)1]v B hv c hv k T ρπ=-，试求λρ。
解：由v dv ρ=d λρλ得λρ= 11.如果激光器和微波激射器分别在m μλ10=，nm 500=λ和MHz 3000=υ输出1W 连续功率，问每秒钟从激光上能级向下能级跃迁的粒子数是多少？解：chp h p n λυ== （1）个10*03.510*3*10*626.610*1191834≈=--msJs mW n μ（2）个10*52.210*3*10*626.6500*1181834≈=--msJs nm W n （3）个10*03.53000*10*626.612334≈=-MHzJs W n12．设一对激光能级为E 2和E 1（21g g=），相应频率为υ（波长为λ），各能级上的粒子数为n 2和n 1，求：（1）当MHz 3000=υ，T=300K 时，=n n 12？（2）当mμλ1=，T=300K 时，=n n 12？（3）当m μλ1=，1.012=n n 时，温度T=?解： e e f f n n kT h kT E E ==---υ121212（1）110*8.4300*10*38.110*300010*626.64236*3412≈≈=-----ee n n（2）10*4.1216238341210*8.410*1*300*10*38.110*3*10*626.6≈≈==-------e e e n n kT hcλ（3）1.010*1*10*38.110*3*10*626.662383412===-----e e n n TkT hc λ得：KT 10*3.63≈13试证明，由于自发辐射，原子在E 2能级的平均寿命As 211=τ证明：自发辐射，一个原子由高能级E 2自发跃迁到E 1，单位时间内能级E 2减少的粒子数为：)(212dt dn dt dn sp -= ， 自发跃迁几率n dt dn A sp 2211)(21=n A dtdn 2212-=， en e n n stt A t τ--≡=2020221)(因此 21s A 1=τ14焦距f 是共焦腔光束特性的重要参数，试以f 表示0000,,,z Z w w R V 。
由于f 和0w 是一一对应的，因而也可以用0w 作为表征共焦腔高斯光束的参数，试以0w 表示f ，000,,z Z w R V 。
解：0w =,()z ωω=20000()z f f R z f z f z =+=+，202000122s L V L λπω==15今有一球面腔，m R 5.11=，m R 12-=，L ＝0.8m 。
试证明该腔为稳定腔；求出它的等价共焦腔的参数。
解：g 1=1-1R L =0.47 g 2=1-2R L =1.8 ，g 1•g 2=0.846即：0< g 1•g 2<1，所以该腔为稳定腔。
由公式（2.8.4） Z 1=()()()212R L R L L R L -+--=-1.31mZ 2=()()()211R L R L L R L -+---=-0.15mf 2=()()()()()[]2212121R L R L L R R L R L R L -+--+--=0.25m 2f=0.5m16某高斯光束0 1.2mm ω=，求与束腰相距0.3m 、m 10、m 1000远处的光斑ω的大小及波前曲率半径R 。
解：2)(1)(fz z +=ωω，z f z z R 2)(+= 其中，m f 385.02≈=λπω cm z 30=： mm cm 45.1)30(≈ω，m cm R 79.0)30(≈ m z 10= ： mm m 6.29)10(≈ω， m m R 0.10)10(≈ m z 1000=：m m 96.2)1000(≈ω，m m R 1000)1000(≈17有频率为1υ，2υ的二束光入射，试求在均匀加宽及非均匀加宽两种情况下(1) 频率为υ的弱光的增益系数表达式； (2) 频率为1υ的强光的增益系数表达式；解：对于均匀加宽物质，当频率为v ，光强为v I 的准单色光入射时，其小信号增益系数和饱和增益系数分别为22200()()()/[()()]22H H H H v vG v G v v v =-+ 022200(,)()()/[()()(1)]22H v H H H v SI v vG v I G v v v I =-++ 式中00()H G v 为中心频率处的小信号增益系数，H v ∆为增益曲线的宽度。
对于非均匀加宽物质，当频率为v ，光强为v I 的准单色光入射时，其小信号增益系数和饱和增益系数分别为0(4ln2)200()()[(/]i i D G v G v e v v v -=-∆0(4ln 2)2()[(/](,)i v G v e v v v G v I --∆=式中00()i G v 为中心频率处的小信号增益系数，D v ∆为增益曲线的宽度。
若1υ，2υ二强光同时入射，则此时反转集居数)1()2()()2()()1()2()()2()()1()2()()2()(11121220222022202201022022202SH H S H H SH H I I I I n I I n n υυυυυυυυυυυυυυυυυυυυυυ+∆+-∆+-⋅+∆+-∆+-∆=+∆+-∆+-∆=∆（1） 弱光υ的增益系数2202122012122021)2()(28),(8),(),,(21H H H H A vng A v nn I I g υυυπυπυυυπυυυσυυυ∆+-∆∆=∆=∆=（2） 强光1υ的增益系数)1()2()(2)1()2()()2()(8),(8),(),,(12212201220222022122001212201211SH HS H H H H I I I I A v ng A v nn I I g υυυυυυυπυυυυυυυπυυυπυυυσυ+∆+-∆⋅+∆+-∆+-∆=∆=∆=18长为1m 的He-Ne 激光器中，气体温度T=400K 。
若工作波长λ=3.39um 时的单程小信号增益为30dB ，试求提供此增益的反转集居数密度。
解：氦氖激光器的小信号增益系数可表示为2/12120000)2ln (4)(πυπλυD A n G ∆∆= （1）式中16211087.2--⨯=s A 为自发辐射跃迁几率，而多普勒加宽线宽071016.7υυMT D -⨯≈∆ 式中氖原子量M=20,而T=400K ，由此有Z D MH 283≈∆υ根据题中给出条件 dB elG 30log 10)(00=υ （即：单程小信号增益为30dB ）式中腔长m l 1=，由此可得到100069.0)(-=cm G υ于是由（1）式，求出反转集居数 392/121200001058.1)/2(ln )(4-⨯=∆=∆cm A G n D πλυυπ19计算由下式表示的平面波电矢量的振动方向、传播方向、相位速度、振幅、频率和波长。