四川省广安、眉山2018届毕业班第一次诊断性考试数学(文)试题(附答案精品)

合集下载

四川省广安、眉山2018届毕业班第一次诊断性考试文科综合试题(pdf版)

A.① ③
B。
①④
C。
②③
D。
②④
15.⒛ 17年 8月 23日 ,国务院常务会议提出 ,要扩大国有科技型企业股权期权和分红等激励政策实施范围、放宽实施条件 ,完善股权激励和技术入股相关所得税政策。上述举措 ①是对按劳分配原则的坚持和完善 ③ 体现了对劳动、知识和创造的尊重 ② 旨在增加科技人才的财产性收人 ④ 有利于促进科技成果转化为生产力
A。
②减轻企业负担 ,激发市场活力 ④ 推进政务公开 ,防止权力滥用
①②
②③ ・教考联盟文科综合试题第 4页 (共 14页 )
B。
①④
C。
D。
③④
19.2017年 11月 ,S省人大常委会制定了《关于建立预算审查前听取人大代表和社会各界意
,E为冰激凌原来的均衡点 ,则
A。
E1
B。
E2
C.E3
D。
E4
,
13.法国哲学家布利丹讲过一个寓言故事 :“ 一头饥饿至极的毛驴站在两捆相同的草料中间
” 可是它却始终犹豫不决 ,不知道应该先吃哪一捆才好 ,结果被活活饿死了。后来人们便 “ ” 把这种现象称为布利丹效应。这启示生产经营者
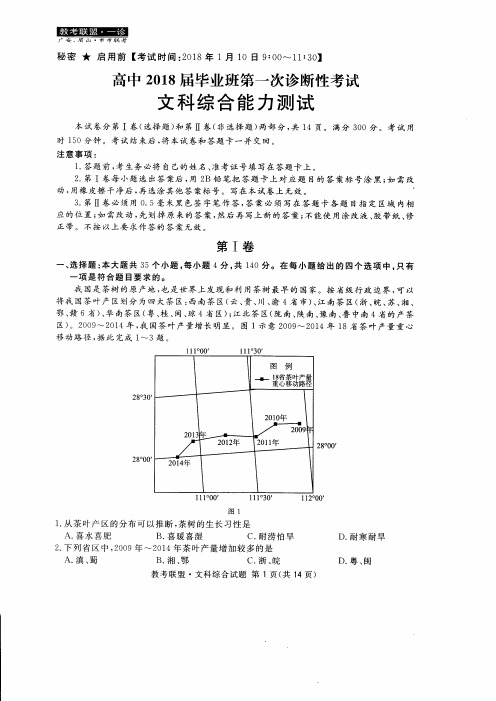
我国是茶树的原产地 ,也是世界上发现和利用茶树最早的国家。按省级行政边界 ,可以将我国茶叶产区划分为四大茶区 :西南茶区 (云、川、贵、渝 4省市 )、江南茶区 (浙、皖、苏、湘、 (粤 (陇 6省、 )、 4省区鄂赣、琼区 );江北茶区华南茶桂、闽、陕南、南、豫南、鲁中南 4省的产茶区)。 ⒛ 09~⒛ 14年 ,我国茶叶产量增长明显。图 1示意 ⒛ 09~⒛ 1钅年 18省茶叶产量重心移动路径 ,据此完成 1~3题。

四川省广安市眉山市高中届毕业班第一次诊断性考试数学理含答案

一、选择题 :本题共 12小题 ,每小题 5分 ,共 60分。在每小题给出的四个选项中 ,只有一项是
符合题目要求的。
1.已知集合 A=(∝ J)1),函数 y=lg(2一安)的定义域为 B,则
A.A∪ B=(￡ 1(J(2)
B。 A∪ B=R
C.A∩ B=(J|J>1)
附 :对于一组数据(扌 1,γ 1),(彦 2,y2),… ,(扌″,丿″),其回归直线 3=劭 +a的斜率和截距的最
小二乘估计公式分别为 :3=⊥∑±飞(∑莎 i丁-(7~△)~(—丿~莎~氵)2一~,γ)a=J一
浙 .
⒛ .(12分 )
如图 ,ABCD是菱形 ,zABC=60° ,AC与 BD相交于点 O, 平面 AEFC⊥ 平面 ABCD,且 AEFC是直角梯形 ,zEAC= 90° ,CF∥ AE,AE=AB=2,CF=4。
#!" # r s t u C j v w . 1 h i x y z ' P G e 2 { | C j $!} $ ~ j C : \ : 4 $ C
!%&!"%&!#%'!$%&!(%'!)%&!*%+!,%'!-%.!!/%.!!!%'!!"%+
!#!"*(! !!$!!! !!(!"# ! !!)!#
(r为参数 ),其中 α≠ 号,以原
点为极点 ,J轴正半轴为极轴建立极坐标系 ,曲线 C2的极坐标方程为 ρ2-6ρcos汐 +4=0。

2018年四川省广安市、眉山市高考数学一诊试卷(理科)

2018年四川省广安市、眉山市高考数学一诊试卷（理科）一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）已知集合A={x|x＞1}，函数y=lg（2﹣x）的定义域为B，则（）A．A∪B={x|1＜x＜2}B．A∪B=R C．A∩B={x|x＞1}D．A∩B={x|x＜2} 2．（5分）若z=1+i，则=（）A．﹣i B．，C．﹣1 D．13．（5分）执行如图所示的程序框图，若输出的y=2，则输入的x=（）A．1 B．2 C．4 D．1或44．（5分）（x﹣y）（x+y）5的展开式中，x2y4的系数为（）A．﹣10 B．﹣5 C．5 D．105．（5分）为了解某高校学生使用手机支付和现金支付的情况，抽取了部分学生作为样本，统计其喜欢的支付方式，并制作出如下等高条形图：根据图中的信息，下列结论中不正确的是（）A．样本中的男生数量多于女生数量B．样本中喜欢手机支付的数量多于现金支付的数量C．样本中多数男生喜欢手机支付D．样本中多数女生喜欢现金支付6．（5分）已知△ABC是边长为1的等边三角形，点D在边BC上，且BD=2DC，则的值为（）A．B．C．D．7．（5分）若将函数的图象向左平移个单位长度，则平移后图象的对称轴方程为（）A．B．C．D．8．（5分）从0，1，2，3这4个数字中选3个数字组成没有重复数字的三位数，则该三位数能被3整除的概率为（）A．B．C．D．9．（5分）已知定义在R上的函数f（x）满足f（x）=f（﹣x），当0≤x≤3时，f （x）=|x﹣2|；当x≥3时，f（x）=f（x﹣2），则函数y=f（x）﹣|ln|x||的零点个数是（）A．1 B．2 C．4 D．610．（5分）已知椭圆的左焦点为F1，y轴上的点P在椭圆外，且线段PF1与椭圆E交于点M，若，则E椭圆的离心率为（）A．B．C．D．11．（5分）已知SC是球O的直径，A，B是球O球面上的两点，且，若三棱锥S﹣ABC的体积为1，则球O的表面积为（）A．4πB．13πC．16πD．52π12．（5分）已知函数f（x）=（x2﹣x﹣1）e x，设关于x的方程有n个不同的实数解，则n的所有可能的值为（）A．3 B．1或3 C．4或6 D．3或4或6二、填空题（每题5分，满分20分，将答案填在答题纸上）13．（5分）已知，则=．14．（5分）已知直线l：y=kx+2与圆C：x2+y2﹣2x﹣2y=0相交于A，B两点，若，则实数k的值为．15．（5分）如图，已知A，B是函数f（x）=log2（16x）图象上的两点，C是函数g（x）=log2x图象上的一点，且直线BC垂直于x轴，若△ABC是等腰直角三角形（其中A为直角顶点），则点A的横坐标为．16．（5分）如图，表示正方体表面的一种展开图，则其中的四条线段AB，CD，EF，GH在原正方体中为异面直线且所成角为60°的有对．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．（12分）已知数列{a n}的前n项和为S n，a1=1，且．（1）求数列{a n}的通项公式；（2）设数列的前n项和为T n，求满足不等式的最小正整数n．18．（12分）在△ABC中，内角A，B，C所对的边分别为a，b，c，已知△ABC 的面积为．（1）求a；（2）求sinB+sinC的值．19．（12分）全民健身倡导全民做到每天参加一次以上的体育健身活动，旨在全面提高国民体质和健康水平．某部门在该市2011﹣2016年发布的全民健身指数中，其中的“运动参与”的评分值进行了统计，制成如图所示的散点图：（1）根据散点图，建立y关于t的回归方程=t；（2）从该市的市民中随机抽取了容量为120的样本，其中经常参加体育锻炼的人数为40，以频率为概率，若从这120名市民中随机抽取4人，记其中“经常参加体育锻炼”的人数为X，求X的分布列和数学期望．附：对于一组数据（t1，y1），（t2，y2），…，（t n，y n），其回归直线=t的斜率和截距的最小二乘估计公式分别为：=，=．20．（12分）如图，ABCD是菱形，∠ABC=60°，AC与BD相交于点O，平面AEFC ⊥平面ABCD，且AEFC是直角梯形，∠EAC=90°，CF∥AE，AE=AB=2，CF=4．（1）求证：BD⊥EF；（2）求二面角B﹣DE﹣F的余弦值．21．（12分）已知函数．（1）当a≥0时，求函数f（x）的极值；（2）若函数f（x）有两个零点x1，x2，求a的取值范围，并证明x1+x2＞2．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.[选修4-4：坐标系与参数方程]22．（10分）在直角坐标系xOy中，曲线C1的参数方程为（t为参数），其中．以原点为极点，x轴正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ2﹣6ρcosθ+4=0．（1）写出曲线C1的普通方程和曲线C2的直角坐标方程；（2）已知曲线C2与C1交于两点，记点A，B相应的参数分别为t1，t2，当t1+t2=0时，求|AB|的值．[选修4-5：不等式选讲]23．已知不等式|2x+1|+|x﹣1|＜3的解集M．（1）求M；（2）若m，n∈M，求证：．2018年四川省广安市、眉山市高考数学一诊试卷（理科）参考答案与试题解析一、选择题：本大题共12个小题，每小题5分，共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1．（5分）已知集合A={x|x＞1}，函数y=lg（2﹣x）的定义域为B，则（）A．A∪B={x|1＜x＜2}B．A∪B=R C．A∩B={x|x＞1}D．A∩B={x|x＜2}【解答】解：由A={x|x＞1}=（1，+∞），由2﹣x＞0解得x＜2，即B=（﹣∞，2）．所以A∪B=R，A∩B={x|1＜x＜2}．观察选项，只有选项B符合题意．故选：B．2．（5分）若z=1+i，则=（）A．﹣i B．，C．﹣1 D．1【解答】解：∵z=1+i，∴==，故选：B．3．（5分）执行如图所示的程序框图，若输出的y=2，则输入的x=（）A．1 B．2 C．4 D．1或4【解答】解：由已知中的程序框图可知：该程序的功能是计算并输出分段函数y=的值，若y=2，则x=4，或x=1，故选：D．4．（5分）（x﹣y）（x+y）5的展开式中，x2y4的系数为（）A．﹣10 B．﹣5 C．5 D．10【解答】解：（x+y）5的通项公式为：T r+1=•x5﹣r•y r，令5﹣r=1，得r=4；令5﹣r=2，得r=3；∴（x﹣y）（x+y）5的展开式中x2y4的系数为：×1+（﹣1）×=﹣5．故选：B．5．（5分）为了解某高校学生使用手机支付和现金支付的情况，抽取了部分学生作为样本，统计其喜欢的支付方式，并制作出如下等高条形图：根据图中的信息，下列结论中不正确的是（）A．样本中的男生数量多于女生数量B．样本中喜欢手机支付的数量多于现金支付的数量C．样本中多数男生喜欢手机支付D．样本中多数女生喜欢现金支付【解答】解：由左图知，样本中的男生数量多于女生数量，A正确；由右图知样本中喜欢手机支付的数量多于现金支付的数量，B正确；由右图知，样本中多数男生喜欢手机支付，C正确；由右图知样本中女生喜欢现金支付与手机支付的一样多，D错误．故选：D．6．（5分）已知△ABC是边长为1的等边三角形，点D在边BC上，且BD=2DC，则的值为（）A．B．C．D．【解答】解：=•（+）=2+•=2+•=1﹣×1×1×cos60°=1﹣×=．故选：B．7．（5分）若将函数的图象向左平移个单位长度，则平移后图象的对称轴方程为（）A．B．C．D．【解答】解：将函数=2sin（2x+）的图象向左平移个单位长度，可得y=2sin（2x++）=2sin（2x+）的图象，令2x+=kπ+，可得x=﹣，k∈Z，则平移后图象的对称轴方程为x=﹣，k∈Z，故选：A．8．（5分）从0，1，2，3这4个数字中选3个数字组成没有重复数字的三位数，则该三位数能被3整除的概率为（）A．B．C．D．【解答】解：从0，1，2，3这4个数字中选3个数字组成没有重复数字的三位数，基本事件总数n==18，该三位数能被3整除包含的基本事件个数：m==10，∴该三位数能被3整除的概率为p=．故选：D．9．（5分）已知定义在R上的函数f（x）满足f（x）=f（﹣x），当0≤x≤3时，f （x）=|x﹣2|；当x≥3时，f（x）=f（x﹣2），则函数y=f（x）﹣|ln|x||的零点个数是（）A．1 B．2 C．4 D．6【解答】解：定义在R上的函数f（x）满足f（x）=f（﹣x），可得f（x）为偶函数，图象关于y轴对称，又当0≤x≤3时，f（x）=|x﹣2|；当x≥3时，f（x）=f（x﹣2），可得x≥3时的图象，可将f（x）在[1，3]的图象向右平移2k（k为正整数）个单位；在y轴左边的图象与右边的图象关于y轴对称，作出f（x）的图象和函数y=|ln|x||的图象，可得它们有4个交点，则函数y=f（x）﹣|ln|x||的零点个数是4．故选：C．10．（5分）已知椭圆的左焦点为F1，y轴上的点P在椭圆外，且线段PF1与椭圆E交于点M，若，则E椭圆的离心率为（）A．B．C．D．【解答】解：如图所示|OM|=|MF1|=|OP|，不妨设|OP|=，则|OM|=|MF1|=1，设∠MF1O=θ，在△MOF1中由余弦定理可得cosθ===，∴sinθ==，∴tanθ===，∵tanθ==，∴=，解得c=1，∴△MOF1为等边三角形，∴M（﹣，），∴+=1，①∵a2﹣b2=c2=1，②，由①②可得4a4﹣8a2+1=0，解得a2=＜1（舍去），a2=，∴a2===（）2，∴a==，∴e===﹣1，故选：C．11．（5分）已知SC是球O的直径，A，B是球O球面上的两点，且，若三棱锥S﹣ABC的体积为1，则球O的表面积为（）A．4πB．13πC．16πD．52π【解答】解：∵SC是球O的直径，A，B是球O球面上的两点，且，∴∠SAC=∠SBC=90°，cos∠ACB==﹣，∴∠ACB=120°，∴∠CAB=∠CBA=30°，∴∠ASB=60°，∴SA=SB=AB=，∴SC==2，∴球半径R=1，∴球O的表面积S=4πR2=4π．故选：A．12．（5分）已知函数f（x）=（x2﹣x﹣1）e x，设关于x的方程有n个不同的实数解，则n的所有可能的值为（）A．3 B．1或3 C．4或6 D．3或4或6【解答】解：f′（x）=e x（2x﹣1）+）+（x2﹣x﹣1）e x=e x（x2+x﹣2），∴当x＜﹣2或x＞1时，f′（x）＞0，当﹣2＜x＜1时，f′（x）＜0，∴f（x）在（﹣∞，﹣2）上单调递增，在（﹣2，1）上单调递减，在（1，+∞）上单调递增，f（x）的极大值为f（﹣2）=，f（x）的极小值为f（1）=﹣e．作出f（x）的函数图象如图所示：∵，∴f2（x）﹣mf（x）﹣=0，△=m2+＞0，令f（x）=t则，则t1t2=﹣．不妨设t1＜0＜t2，（1）若t1＜﹣e，则0＜t2＜，此时f（x）=t1无解，f（x）=t2有三解；（2）若t1=﹣e，则t2=，此时f（x）=t1有一解，f（x）=t2有两解；（3）若﹣e＜t1＜0，则t2＞，此时f（x）=t1有两解，f（x）=t2有一解；综上，f2（x）﹣mf（x）=有三个不同的实数解．故选：A．二、填空题（每题5分，满分20分，将答案填在答题纸上）13．（5分）已知，则=．【解答】解：∵，∴==．故答案为：．14．（5分）已知直线l：y=kx+2与圆C：x2+y2﹣2x﹣2y=0相交于A，B两点，若，则实数k的值为﹣1．【解答】1解：圆C：x2+y2﹣2x﹣2y=0，转化为：（x﹣1）2+（y﹣1）2=2，所以圆的直径为2．由于|AB|=2，则：直线l：y=kx+2，经过圆心（1，1）．所以：1=k+2，解得：k=﹣1．故答案为：﹣1．15．（5分）如图，已知A，B是函数f（x）=log2（16x）图象上的两点，C是函数g（x）=log2x图象上的一点，且直线BC垂直于x轴，若△ABC是等腰直角三角形（其中A为直角顶点），则点A的横坐标为．【解答】解：设A（x1，y1），B（x2，y2），C（x3，y3），则y1=log2（16x1），y2=log2（16x2），y3=log2x3，x2=x3，△ABC是等腰直角三角形（其中A为直角顶点），可得y2﹣y3=2（x2﹣x1），y2+y3=2y1，即有log2（16x2）﹣log2x3=2（x2﹣x1），log2（16x2）+log2x3=2log2（16x1），化简可得x2﹣x1=2，log2x2=2+log2x1，即为2+x1=4x1，解得x1=，故答案为：．16．（5分）如图，表示正方体表面的一种展开图，则其中的四条线段AB，CD，EF，GH在原正方体中为异面直线且所成角为60°的有3对．【解答】解：把正方体的展开图还原成正方体，如下图：则四条线段AB，CD，EF，GH在原正方体中为异面直线且所成角为60°的有：AB与CD，AB与GH、EF与GH，共3组．故答案为：3．三、解答题（本大题共5小题，共70分.解答应写出文字说明、证明过程或演算步骤.）17．（12分）已知数列{a n}的前n项和为S n，a1=1，且．（1）求数列{a n}的通项公式；（2）设数列的前n项和为T n，求满足不等式的最小正整数n．【解答】解：（1）由，﹣a n=n+1，又a1=1，则：a n+1所以n≥2时，a n=（a n﹣a n﹣1）+（a n﹣1﹣a n﹣2）+…+（a2﹣a1）+a1=．当n=1时，也满足，所以数列{a n}的通项公式为．（2）由（1）知，所以令，解得n≥19，所以满足不等式的最小正整数n为19．18．（12分）在△ABC中，内角A，B，C所对的边分别为a，b，c，已知△ABC的面积为．（1）求a；（2）求sinB+sinC的值．【解答】解：（1）由△ABC的面积为，得．因，所以，所以，得bc=35，又b﹣c=2，由余弦定理得：，=，所以a=8．（2）法一：由（1）中b﹣c=2，bc=35．解得b=7，c=5，由正弦定理得：，所以，法二：由（1）有（b+c）2=（b﹣c）2+4bc=22+4×35=144，所以b+c=12．由正弦定理得，所以．19．（12分）全民健身倡导全民做到每天参加一次以上的体育健身活动，旨在全面提高国民体质和健康水平．某部门在该市2011﹣2016年发布的全民健身指数中，其中的“运动参与”的评分值进行了统计，制成如图所示的散点图：（1）根据散点图，建立y关于t的回归方程=t；（2）从该市的市民中随机抽取了容量为120的样本，其中经常参加体育锻炼的人数为40，以频率为概率，若从这120名市民中随机抽取4人，记其中“经常参加体育锻炼”的人数为X，求X的分布列和数学期望．附：对于一组数据（t1，y1），（t2，y2），…，（t n，y n），其回归直线=t的斜率和截距的最小二乘估计公式分别为：=，=．【解答】解：（1）由题，==3.5，==75，则（t i﹣）（y i﹣）=（1﹣3.5）（65﹣75）+（2﹣3.5）（71﹣75）+（3﹣3.5）（73﹣74）+（4﹣3.5）（77﹣75）+（5﹣3.5）（80﹣75）+（6﹣3.5）（84﹣75）=63．（t i﹣）2=（1﹣3.5）2+（2﹣3.5）2+（3﹣3.5）2+（4﹣3.5）2+（5﹣3.5）2+（6﹣3.5）2=17.5，==3.6，=75﹣3.6×3.5=62.4，∴运动参与y关于t的回归方程是=3.6t+62.4．（2）以频率为概率，从这120名市民中随机抽取1人，经常参加体育锻炼的概率为，由题，X的可能取值为0，1，2，3，4．则，，，．分布列如下：X01234P数学期望或．20．（12分）如图，ABCD是菱形，∠ABC=60°，AC与BD相交于点O，平面AEFC ⊥平面ABCD，且AEFC是直角梯形，∠EAC=90°，CF∥AE，AE=AB=2，CF=4．（1）求证：BD⊥EF；（2）求二面角B﹣DE﹣F的余弦值．【解答】证明：（1）在棱形ABCD中，可得DB⊥AC，∵平面AEFC⊥平面ABCD，且交线为AC，∴DB⊥平面AEFC，∵EF⊂平面AEFC，∴BD⊥EF．解：（2）直角梯形AEFC中，由∠EAC=90°，CF∥AE，AE=AB=2，得EA⊥平面ABCD．取EF的中点M，以O为坐标原点，以OA为x轴，OB为y轴，OM为z轴，建立空间直角坐标系，则．∴=（0，2，0），=（1，，2）．设平面BDE的法向量=（x，y，z），则，取x=2，得=（2，0，﹣1），由=（﹣1，，4）．设平面DEF的法向量为=（a，b，c），则，取a=1，得=（1，﹣，1）．则cos＜＞===，即二面角B﹣DE﹣F的余弦值为．21．（12分）已知函数．（1）当a≥0时，求函数f（x）的极值；（2）若函数f（x）有两个零点x1，x2，求a的取值范围，并证明x1+x2＞2．【解答】解：（1）由，得，当a≥0时，ax+1＞0，若0＜x＜1，f'（x）＞0；若x＞1，f'（x）＜0，故当a≥0时，f（x）在x=1处取得的极大值；函数f（x）无极小值．（2）当a≥0时，由（1）知f（x）在x=1处取得极大值，且当x趋向于0时，f（x）趋向于负无穷大，又f（2）=ln2﹣2＜0，f（x）有两个零点，则，解得a＞2．当﹣1＜a＜0时，若0＜x＜1，f'（x）＞0；若；若，则f（x）在x=1处取得极大值，在处取得极小值，由于，则f（x）仅有一个零点．当a=﹣1时，，则f（x）仅有一个零点．当a＜﹣1时，若；若；若x＞1，f'（x）＞0，则f（x）在x=1处取得极小值，在处取得极大值，由于，则f（x）仅有一个零点．综上，f（x）有两个零点时，a的取值范围是（2，+∞）．两零点分别在区间（0，1）和（1，+∞）内，不妨设0＜x1＜1，x2＞1．欲证x1+x2＞2，需证明x2＞2﹣x1，又由（1）知f（x）在（1，+∞）单调递减，故只需证明f（2﹣x1）＞f（x2）=0即可．，又，所以f（2﹣x1）=ln（2﹣x1）﹣ln（x1）+2x1﹣2，令h（x）=ln（2﹣x）﹣lnx+2x﹣2（0＜x＜1），则，则h（x）在（0，1）上单调递减，所以h（x）＞h（1）=0，即f（2﹣x1）＞0，所以x1+x2＞2．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分.[选修4-4：坐标系与参数方程]22．（10分）在直角坐标系xOy中，曲线C1的参数方程为（t为参数），其中．以原点为极点，x轴正半轴为极轴建立极坐标系，曲线C2的极坐标方程为ρ2﹣6ρcosθ+4=0．（1）写出曲线C1的普通方程和曲线C2的直角坐标方程；（2）已知曲线C2与C1交于两点，记点A，B相应的参数分别为t1，t2，当t1+t2=0时，求|AB|的值．【解答】解：（1）线C1的参数方程为（t为参数），所以：C1的普通方程：y=（x﹣2）tanα+1，其中；曲线C2的极坐标方程为ρ2﹣6ρcosθ+4=0．所以：C2的直角坐标方程：（x﹣3）2+y2=5．（2）由题知直线恒过定点P（2，1），又t1+t2=0，由参数方程的几何意义知P是线段AB的中点，曲线C2是以C2（3，0）为圆心，半径的圆，且．由垂径定理知：．[选修4-5：不等式选讲]23．已知不等式|2x+1|+|x﹣1|＜3的解集M．（1）求M；（2）若m，n∈M，求证：．【解答】解：（1）当时，不等式即为﹣2x﹣1﹣x+1＜3，解得；当时，不等式即为2x+1﹣x+1＜3，解得；当x＞1时，不等式即为2x+1+x﹣1＜3，此时无解，综上可知，不等式解集M={x|﹣1＜x＜1}．（2）m，n∈（﹣1，1），欲证，需证|m﹣n|＜|mn﹣1|，即证（m﹣n）2＜（mn﹣1）2，即m2+n2﹣2mn＜m2n2﹣2mn+1，即证（m2﹣1）（n2﹣1）＞0，因为m，n∈（﹣1，1），所以（m2﹣1）（n2﹣1）＞0显然成立．所以成立．。

2017-2018届四川省眉山市高三第一次诊断性考试文科数学试题及答案

眉山市高中2017-2018届第一次诊断性考试数学(文史类) 01注意事项：1.答题前，务必将自乙的姓名、准考证号填写在答题卡规定的位置上.2.答选择题时，必须使用2B 格笔把答题卡上对应题目的答案标号涂黑.如需改动，用橡皮擦干净后，再选涂其他答案标号。

3.答非选择题时，必须使用0.5毫米的黑色签字笔，将答案书写在答题卡规定的位置上。

4.所有题有必须在答题卡上作答，在试题卷上答题无效。

5.考试结束，将答题卡上交。

一、选择题：本大题共10小题，每小题5分，共50分。

在每小题给出的四个选项中，只有一个是符合题目要求的。

1、复数2)1(i -等于A ．2+2i B.﹣2i C. 2﹣2i D. 2i2、对于以下判断（1）命题“已知R y x ∈,”，若x ≠2或y ≠3，则x + y ≠5”是真命题。

（2）设f (x )的导函数为f' (x )，若f' (x 0)，则x 0是函数f (x )的极值点。

（3）命题“R x ∈∀,e x ﹥0”的否定是：“R x ∈∃,e x﹥0”。

（4）对于函数f (x )，g (x )，恒成立的一个充分不必要的条件是f (x )min ≥g (x )max 。

其中正确判断的个数是A ．1B ．2C ．3D ．03、执行如右图所示的程序框图，输出的S 值为 A ．21 B ．43 C ．1411 D ．107 4、以下茎叶图记录了甲乙两组各五名学生在一次英语听力测试中的成绩（单位：分）已知甲组数据的中位数为15，乙组数据的平均数为16.8，则y x ,的值分别为A ． 5,2B ．5,5C ． 8,5D ．8,85、设n m ,是两条不同的直线，βα,是两个不同的平面，下列命题中正确的是A ．若βα⊥, ,α⊂m ,β⊂n 则n m ⊥B ．若β//,//,n n m a m ⊥ ，则,ββα⊂⊥m C ．若n m ⊥，,α⊂m ,β⊂n 则,ββα⊂⊥m D ．若,//ββα⊂m,αm ,β⊂n 则n m // 6、已知数列{a n }的前n 项和S n =2n +1-2，等差数列{b n }中，b 2 = a 2，面b n +3+b n -1=2b n +4, (n ≥2,n ∈N +), 则b n =A. 2n+2B.2nC. n-2D.2n-27、△ABC 的三内角A ,B ,C 所对边的长分别为a ,b ,c ，设向量),(sin c a B p += ,),sin (sin a b A C q --= .若,R ∈∃λ使,q p λ=则角C 的大小为 A. 6π B. 32π C. 3π D. 2π 8、设f(x)=(1+t e )x-t e 2. 其中R x ∈，t 为常数；集合M={x )(x f ﹤0，R x ∈}，则对任意实常数t ，总有A ．-3∉M ，0∈MB ．-3∉M ，0∉MC ．-3∈M ，0∉MD ．-3∈M ，0∈M9、己知函数f (x )=R a a x ∈+,3在[-1，1]上的最大值为M (a ) ，则函数g (x )=M (x )-12-x 的零点个数为A. 1个B. 2个C. 3个D. 4个10、节日里某家前的树上挂了两串彩灯，这两串彩灯的第一次闪亮相互独立，若接通电后的月秒内任一时刻等可能发生，然后每串彩灯在4秒内间隔闪亮，那么这两串彩灯同时通电后它们第一次闪亮的时刻相差不超过1秒的概率是A ．165B ．169C ．41D ．167 二、填空题：本大题共5小题。

四川省资阳、眉山、遂宁、广安、自贡、广元等六市高2018级第一次诊断性考试文数答案

$2'从
而
"1.
平
面
1$/&所
以
$1."1&所
以
31,"$/
)3/,"1$
)ቤተ መጻሕፍቲ ባይዱ
! $
+
!#1"
+1$+$/)
!$1"+1$!令
1")4&1$)5&则
4#*5#
)%!所
以
31,"$/
)
!$45&
! $
+4#*5# #
)
# $
&其
中
,)-当且仅当 4)5)槡#时取得!
命题意图#本小题主要考查线面垂直(面面垂直(三棱锥的体积(基本不等式等基础知识'考查
+,!#",'!所以+!#"在!,;&'"上单调递减&在!'&* ;"上单调递增&所以 +!#"<+0)+!'") 9',',!)'&所以-#'&9###*!&. 选项正确&- 选项不正确'当 #)$ 时&##)#$)8&##)
$#):&##%##&选项 ( 不正确'因为#,'时&#*#!##&所以选项 6 不正确!
象
关于'
轴
对称
&所以
,%*
%
) # *.&.'&解

四川省广安市眉山市2018届高三第一次诊断性考试文综试题 word版详解

广安、眉山·市市联考秘密★启用前【考试时间：2018年1月10日9：00～11: 30】高中2018届毕业班第一次诊断性考试文科综合能力测试第I卷一、选择题：本大题共35个小题，每小题4分，共140分。

在每小题给出的四个选项中，只有一项是符合题目要求的。

我国是茶树的原产地，也是世界上发现和利用茶树最早的国家。

按省级行政边界，可以将我国茶叶产区划分为四大茶区：西南茶区（云、贵、川、渝4省市）、江南茶区（浙、皖、苏、湘、鄂、赣6省）、华南茶区（粤、桂、闽、琼4省区）；江北茶区（陇南、陕南、豫南、鲁中南4省的产茶区）。

2009～2014年，我国茶叶产量增长明显。

图1示意2009～2014年18省茶叶产量重心移动路径，据此完成l～3题。

1．从茶叶产区的分布可以推断，茶树的生长习性是A.喜水喜肥B．喜暖喜湿 C.耐涝怕旱 D.耐寒耐旱2．下列省区中，2009年～2014年茶叶产量增加较多的是A.滇、蜀B．湘、鄂 C.浙、皖 D.粤、闽3．促使图示茶叶产量重心转移的主导因素是A.气候变化B．科技进步 C.市场需求 D.政策引导新疆阿尔泰山放牧形式因地而异，转场风景也异彩纷呈。

每个转场季节牧道连续过畜量达100万头以上，迁徙路径最远达四、五百千米之遥，一年中平均每四天就得搬家一次，常常导致牛羊大量死亡。

图2为阿尔泰山牧场分布示意图，据此完成4～5题。

4．图中甲牧场是A.春季牧场B．夏季牧场 C.秋季牧场 D.冬季牧场5．导致转场过程中牛羊大量死亡的主要原因可能是A.春夏之交的风沙B．夏秋之交的高温C．秋冬之交的干旱 D.冬春之交的雪灾空气质量指数用于定量描述空气质量状况，指数越大则大气污染越严重。

图3表示某日20时海平面气压(单位：hpa)分布及16～24时北京空气质量指数变化，读图完成6～8题。

6．①②两地的气压差可能是A.0 hPaB.2.5 hPaC.5 hPaD.7.5 hPa7．该日20时前后，北京A.经历降温降水过程B．经历大风扬沙过程C．盛行风向为偏南风 D.气压逐渐降低过程8．当海上风浪较大时，渔船往往需要回港避风，此时下列四地渔船最需回港的是A.黄海海域B．东海海域 C.台湾海峡 D.朝鲜海峡早晨5:00，生活在上海的小丽与在西藏拉萨工作的爸爸通话。

四川省广安、眉山2018届高三第一次诊断性考试语文试题含解析

高中2018届毕业班第一次诊断性考试语文―、现代文阅读（一）论述类文本阅读（本题共3小题，9分）阅读下面的文字，完成小题。

民间文化承载着厚重的历史积淀，散发着清新的泥土芳香，闪烁着朴素的哲理光辉，它的巨大艺术魅力经久不衰。

千百年来，从神话传说、故事、歌谣、谚语等民间文学到民间音乐、舞蹈、戏剧、曲艺等民间艺术，已深深融入了中华民族的血脉，深刻影响着中国人的精神世界。

民间文化具有鲜明的民族性、地域性和群众性，让中华优秀传统文化亮丽多彩。

民间文化又是传统文化遗产中最基本、最生动、最丰富的组成部分，从这个意义上说，它恰是中华文化最丰厚的土壤。

尽管厚植文化的土壤肥沃，但从一部电影《百鸟朝凤》中，仍能看到传统民间艺术在现代化浪潮中受到的巨大冲击。

这并不是个例，由于近些年来工业化、城镇化进程的加快和社会结构的变动，民间文化赖以生存的土壤和环境也在改变，许多民间艺术、民间技艺的生存空间受到压缩，遭遇“边缘化”危机，甚至一些珍责的民间文化遗产随着老一代传承人的相继离去而失传。

“文化土壤”被蚕食，中华传统文化传承将面临严峻挑战，守护民间文化刻不容缓。

民间文化活动生于民间、兴于民间、藏于民间，是群众最真实的生命体验。

传承和振兴民间文化，意味着整理一个民族文化生活的历史。

实施民间典籍搜集、抢救濒危民间文艺、民间历史文化纪录创作等工程须深入民间生活；振兴传统民间技艺，做好现有的民间文化传承保护工作需行走在民间。

在此过程中，还应坚持辩证取舍、扬弃继承，对传统文化进行科学分析、鉴别和梳理，汲取优秀民间文化的精髓精华。

总而言之，生活是民间文化的沃土，不忘本来才能开辟未来，善于继承才能更好发展。

只有深入民间，扎根生活，去粗取精，才能为中华民族优秀文化的生生不息、发展壮大提供丰厚滋养。

民间文化薪火相传，人才是决定因素。

而推动民间文化的现代化转化，首先要做好青少年一代传承人的培养和扶持，创新传统师徒承袭模式，让民间文化事业后继有人。

四川省广安、遂宁、内江、眉山2018届高三上学期第一次诊断考试文数试题含答案

数学（文史类）第Ⅰ卷（共60分）一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.1.已知集合{}|9,*A x x x N =≤∈，集合{}|07B x x =<<，则A B =（）A ．{}|07x x <<B ．{}|16x x ≤≤C ．{}1,2,3,4,5,6D ．{}7,8,92.已知i 是虚数单位，复数131ii+=+（） A ．2i +B ．2i -C ．1i -+D ．1i --3.将函数()sin 2f x x =的图象向右平移6π个单位后得到函数()g x 的图象，则函数()g x 的单调递增区间是（） A ．,36k k ππππ⎡⎤-+⎢⎥⎣⎦（k Z ∈） B ．,63k k ππππ⎡⎤-+⎢⎥⎣⎦（k Z ∈） C ．5,1212k k ππππ⎡⎤-+⎢⎥⎣⎦（k Z ∈） D ．5,1212k k ππππ⎡⎤-+⎢⎥⎣⎦（k Z ∈） 4.供电部门对某社区1000位居民2018年11月份人均用电情况进行统计后，按人均用电量分为[0,10)，[10,20)，[20,30)，[30,40)，[]40,50五组，整理得到如图的频率分布直方图，则下列说法错误的是（）A ．11月份人均用电量人数最多的一组有400人B ．11月份人均用电量不低于20度的有500人C ．11月份人均用电量为25度D ．在这1000位居民中任选1位协助收费，选到的居民用电量在[30,40)一组的概率为1105.已知等比数列{}n a 满足126a a +=，4548a a +=，则数列{}n a 的前10项的和10S =（） A ．1182B ．1183C ．2186D ．21876.“21x>”是“1x > ”的（） A ．充分不必要条件B ．必要不充分条件C ．充要条件D ．既不充分也不必要条件7.如图，是某算法的程序框图，当输出29T >时，正整数n 的最小值是（） A ．2B ．3C ．4D ．58.如图，四边形ABCD 是正方形，延长CD 至E ，使得DE CD =，若点P 为CD 的中点，且AP AB AE λμ=+，则λμ+=（） A ．3B ．52C ．2D ．19．若无论实数a 取何值时，直线10ax y a +++=与圆22220x y x y b +--+=都相交，则实数b 的取值范围为（） A ．(,2)-∞B ．(2,)+∞C ．(,6)-∞-D ．(6,)-+∞10.当,33x ππ⎡⎤∈-⎢⎥⎣⎦时，函数2()cos 444x x x f x =的最小值为（）A ．B ．2C ．1D 11.如图，ABCD 是边长为2的正方形，点E ，F 分别为边BC ，CD 的中点，将ABE ∆，ECF ∆，FDA ∆分别沿AE ，EF ，FA 折起，使B ，C ，D 三点重合于点P ，若四面体PAEF的四个顶点在同一个球面上，则该球的表面积是（）AB ．6πC ．D ．12π12.已知函数()y f x =与()y F x =的图象关于y 轴对称，当函数()y f x =和()y F x =在区间[],a b 同时递增或同时递减时，把区间[],a b 叫做函数()y f x =的“不动区间”．若区间[]1,2为函数|2|xy t =-的“不动区间”，则实数t 的取值范围是（） A ．(0,2]B ．1[,)2+∞C ．1,22⎡⎤⎢⎥⎣⎦D ．1,2[4,)2⎡⎤+∞⎢⎥⎣⎦第Ⅱ卷（共90分）二、填空题（每题5分，满分20分，将答案填在答题纸上） 13.221log log 324+= ．14.学校艺术节对同一类的A ，B ，C ，D 四项参赛作品，只评一项一等奖，在评奖揭晓前，甲、乙、丙、丁四位同学对这四项参赛作品预测如下：甲说：“是C 或D 作品获得一等奖”；乙说：“B 作品获得一等奖”；丙：“A ，D 两项作品未获得一等奖”；丁说：“是C 作品获得一等奖”．若这四位同学中只有两位说的话是对的，则获得一等奖的作品是．15.如图，网格纸上小正方形的边长为1，粗实线画出的是某几何体的三视图，则该几何体的体积为．16.椭圆22221(0)x y a b a b+=>>的一个焦点为F ，该椭圆上有一点A ，满足OAF ∆是等边三角形（O 为坐标原点），则椭圆的离心率是．三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.） 17.已知公差不为零的等差数列{}n a 中，11a =，且1a ，2a ，5a 成等比数列．（1）求数列{}n a 的通项公式；（2）若11n n n b a a +=⋅，求数列{}n b 的前n 项和n T ．18.在ABC ∆中，角A ，B ，C 的对边分别为a ，b ，c ，且满足(2)cos cos 0a b C c B ++=．（1）求角C 的大小；（2）若6c =，求ABC ∆面积的最大值．19.某市对创“市级优质学校”的甲、乙两所学校复查验收，对办学的社会满意度一项评价随机访问了30位市民，根据这30位市民对这两所学校的评分（评分越高表明市民的评价越好），绘制茎叶图如下：（1）分别估计该市的市民对甲、乙两所学校评分的中位数；（2）分别估计该市的市民对甲、乙两所学校的评分不低于90分的概率；（3）根据茎叶图分析该市的市民对甲、乙两所学校的评价． 20.已知()f x 是定义在R 上的奇函数，当0x >时，31()3f x x ax =+（a R ∈），且曲线()f x 在12x =处的切线与直线314y x =--平行．（1）求a 的值及函数()f x 的解析式；（2）若函数()y f x m =-在区间⎡-⎣上有三个零点，求实数m 的取值范围．21.已知函数()xf x ae x =-（a R ∈），其中e 为自然对数的底数， 2.71828e =…．（1）判断函数()f x 的单调性，并说明理由；（2）若[]1,2x ∈，不等式()x f x e -≥恒成立，求a 的取值范围．请考生在22、23两题中任选一题作答，如果多做，则按所做的第一题记分. 22.选修4-4：坐标系与参数方程在平面直角坐标系中，曲线1C ：33cos 2sin x y αα=+⎧⎨=⎩（α为参数）经过伸缩变换',3'2x x yy ⎧=⎪⎪⎨⎪=⎪⎩后的曲线为2C ，以坐标原点为极点，x 轴正半轴为极轴建立极坐标系．（1）求2C 的极坐标方程；（2）设曲线3C 的极坐标方程为sin()16πρθ-=，且曲线3C 与曲线2C 相交于P ，Q 两点，求||PQ 的值．23.选修4-5：不等式选讲已知函数2()|||1|f x x b x =+--+，222()|||2|g x x a c x b =+++-，其中a ，b ，c 均为正实数，且1ab bc ca ++=．（1）当1b =时，求不等式()1f x ≥的解集；（2）当x R ∈，求证：()()f x g x ≤．高中2018届毕业班第一次诊断性考试数学（文史类）答案一、选择题题号 1 2 3 4 5 6 7 8 9 10 11 12 答案 CACCCBCBCBBC二、填空题13.3 14.B 15.3231 三、解答题17.解：（1）设数列{}n a 的公差为d （0d ≠），则11a =，21a d =+，514a d =+，因为1a ，2a ，5a 成等比数列，所以2(1)1(14)d d +=⨯+，解得2d =或0d =（舍），所以数列{}n a 是以1为首项，2为公差的等差数列，所以数列{}n a 的通项公式为21n a n =-．18.解：（1）因为(2)cos cos 0a b C c B ++=，所以2cos (cos cos )a C b C c B =-+，由正弦定理得2sin cos (sin cos sin cos )sin()sin A C B C C B B C A =-+=-+=-，因为在ABC ∆中，sin 0A ≠，所以1cos 2C =-，所以23C π=．（2）由（1）的结论和余弦定理有22222cos3c a b ab π=+-223a b ab ab =++≥，由6c =，所以12ab ≤，当且仅当a b == 由1sin 2ABC S ab C ∆=得此时ABC ∆的面积最大，且最大值为11222ABC S ∆=⨯⨯= 19．解：（1）由题意，根据所给的茎叶图，30位市民对甲学校的评分按由低到高排序，排在第15,16两位的分数是85,85，故样本中位数是85，所以该市的市民对甲学校评分的中位数的估计值是85．30位市民对乙学校的评分按由低到高排序，排在第15,16两位的分数是75,77，故样本中位数是7577762+=，所以该市的市民对乙学校评分的中位数的估计值为76．（2）由所给茎叶图知，30位市民对甲、乙两学校的评分不低于90分的比率分别为61305=，101303=，故该市的市民对甲、乙两所学校的评分不低于90分的概率估计值分别为15，13．（3）由所给茎叶图知，该市的市民对甲学校的评分的中位数高于对乙学校的评分的中位数，而且由茎叶图可以大致看出市民对甲学校的评分标准差要小于对乙学校的评分的标准差，说明该市的市民对甲学校的评价较高、评价较为一致，对乙学校的评价较低、评价差异较大． 20.解：（1）当0x >时，2'()f x x a =+，因为曲线()f x 在12x =处的切线与直线314y x =--平行，所以113'()244f a =+=-，所以1a =-，则当0x >时，31()3f x x x =-．因为()f x 是定义在R 上的奇函数，可知(0)0f =，设0x <，则0x ->，31()3f x x x -=-+，所以3311()()()33f x f x x x x x =--=--+=-，综上所述，函数()f x 的解析式为31()()3f x x x x R =-∈．（2）由31()3f x x x =-（x R ∈），得2'()1f x x =-，令'()0f x =，得1x =±．当31x -<<-时，'()0f x >，()f x 单调递增；当11x -<<时，'()0f x <，()f x 单调递减；当1x <<'()0f x >，()f x 单调递增．又(3)6f -=-，2(1)3f -=，2(1)3f =-，0f =，函数()y f x m =-在区间⎡-⎣上有三个零点，等价于()f x 在⎡-⎣上的图象与y m =有三个公共点．结合()f x 在区间⎡-⎣上大致图象可知，实数m 的取值范围是2(,0]3-．21.解：（1）由题可知，()x f x ae x =-，则'()1x f x ae =-，（i ）当0a ≤时，'()0f x <，()x f x ae x =-为R 上的减函数．（ii ）当0a >时，令10xae -=，得ln x a =-，①若(,ln )x a ∈-∞-，则'()0f x <，此时函数()f x 为单调递减函数； ②若(ln ,)x a ∈-+∞，则'()0f x >，此时函数()f x 为单调递增函数．（2）由题意，问题等价于[]1,2x ∈，不等式xxae x e --≥恒成立，即[]1,2x ≤，21xxxe a e+≥恒成立，令21()xx xe g x e +=，则问题等价于a 不小于函数()g x 在[]1,2上的最大值，由2211()x x x xxe xg x e e e +==+，显然21x y e =在[]1,2上单调递减，令()x x h x e =，[]1,2x ∈，则[]1,2x ∈时，2'()x x xe xe h x e -=10x xe -=≤，所以函数()h x 在[]1,2上也是单调递减函数，所以函数()g x 在[]1,2上单调递减，所以函数()g x 在[]1,2x ∈的最大值为211(1)g e e=+，故[]1,2x ∈，()xf x e -≥恒成立时实数a 的取值范围为211[,)e e++∞． 22.解：（1）由题意得曲线2C 的参数方程'1cos 'sin x y αα=+⎧⎨=⎩（α为参数），则曲线2C 的直角坐标方程为22('1)'1x y -+=，所以曲线2C 的极坐标方程为2cos ρθ=．（2）由（1）知曲线2C 是以(1,0)为圆心，半径为1的圆，而曲线3C为直线，直角坐标方程为20x -=．曲线2C 的圆心(1,0)到直线3C的距离为12d ==，所以弦||PQ ==23.解：（1）由题意，当1b =时，2,1,()2,11,2, 1.x f x x x x -≤-⎧⎪=-<<⎨⎪≥⎩当1x ≤-时，()21f x =-<，不等式()1f x ≥无解；当11x -<<时，()21f x x =≥，解得12x ≥，所以112x ≤<；当1x ≥时，()21f x =≥恒成立．所以()1f x ≥的解集为1[,)2+∞．（2）当x R ∈时，2()|||1|f x x b x =+--+2|(1)|x b x ≤++-+22|1|1b b =+=+；222()|||2|g x x a c x b =+++-222|(2)|x a c x b ≥++--2222a c b =++．而22222(1)a c b b ++-+2221a c b =++-2222221()12a b b c c a =+++++-1(222)12ab bc ac ≥++-10ab bc ac =++-=，当且仅当3a b c ===时，等号成立．即222221a c b b ++≥+，因此，当x R ∈时，2222()12()f x b a c b g x ≤+≤++≤，所以，当x R ∈时，()()f x g x ≤．。

四川省广安市、眉山市、遂宁市2018-2019学年高考文数一诊试卷

四川省广安市、眉山市、遂宁市2018-2019学年高考文数一诊试卷一、单选题 (共12题；共12分)1．（1分）若集合A={1,2，3，4，5}，B={2,4，6，8}，则集合A∪B=()A．2，3，4，5，6，B．3，4，5，C．3，5，6，D．（）2．（1分）复数2−i1+i=A．B．C．D．3．（1分）已知平面向量a⃗=(1,2)，b⃗=(−2,m)，且a⃗⊥b⃗，则m=() A．1B．4C．D．，则cos(π−2α)=()4．（1分）已知sinα=35A．B．C．D．5．（1分）若双曲线x22=1的一条渐近线为x−2y=0，则实数m=（）m−yA．B．C．D．6．（1分）如图，某校一文化墙上的一幅圆形图案的半径为6分米，其内有一边长为1分米的正六边形的小孔，现向该圆形图案内随机地投入一飞镖(飞镖的大小忽略不计)，则该飞镖落在圆形图案的正六边形小孔内的概率为（）A．B．C．D．7．（1分）下列命题错误的是（）A．不在同一直线上的三点确定一个平面B．两两相交且不共点的三条直线确定一个平面C．如果两个平面垂直，那么其中一个平面内的直线一定垂直于另一个平面D．如果两个平面平行，那么其中一个平面内的直线一定平行于另一个平面8．（1分）设a=50.4，b=log0.40.5，c=log50.4，则a，b，c的大小关系是()A．B．C．D．9．（1分）已知函数f(x)=sin(2x+π3)，g(x)=sinx，要得到函数y=f(x)的图象，只需将函数y=g(x)的图象上的所有点（）A．横坐标缩短为原来的，再向左平移个单位得到B．横坐标缩短为原来的，再向左平移个单位得到C．横坐标伸长为原来的倍，再向左平移个单位得到D．横坐标伸长为原来的倍，再向左平移个单位得到10．（1分）《九章算木》中将底面为长方形，且有一条侧棱与底面垂直的四棱锥称之为“阳马”，现有一阳马，其正视图和侧视图是如图所示的直角三角形，该“阳马”的体积为163，若该阳马的顶点都在同一个球面上，则该球的表面积为（）正视图侧视图A．B．C．D．11．（1分）元朝时，著名数学家朱世杰在《四元玉鉴》中有一首诗:“我有一壶酒，携着游春走，与店添一倍，逢友饮一斗，店友经三处，没了壶中酒，借问此壶中,当原多少酒?”用程序框图表达如图所示，即最终输出的x=0时，问一开始输入的x=()A．B．C．D．12．（1分）若对∀x，y∈R，有f(x)+f(y)−f(x+y)=3，函数g(x)=xx2+1+f(x)，则g(2)+g(−2)的值()A．0B．4C．6D．9二、填空题 (共2题；共2分)13．（1分）在ΔABC中，内角A，B，C的对边分别为a，b，c，若a=√7，b=2，A=π3，则c=.14．（1分）某车间租赁甲、乙两种设备生产A，B两类产品，甲种设备每天能生产A类产品8件和B类产品15件，乙种设备每天能生产A类产品10件和B类产品25件，已知设备甲每天的租赁费300元，设备乙每天的租赁费400元，现车间至少要生产A类产品100件，B类产品200件，所需租赁费最少为元.三、解答题 (共7题；共16分)15．（2分）已知等差数列{a n}中，a1=1，a3=5.（1）（1分）求数列{a n}的通项公式；（2）（1分）若等比数列{b n}满足b1=a2，b2=a1+a2+a3，求{b n}的前n项和S n. 16．（3分）今年年初，中共中央、国务院发布《关于开展扫黑除恶专项斗争的通知》，在全国范围部署开展扫黑除恶专项斗争.那么这次的“扫黑除恶”专项斗争与2000年、2006年两次在全国范围内持续开展了十多年的“打黑除恶”专项斗争是否相同呢？某高校一个社团在年后开学后随机调查了80位该校在读大学生，就“扫黑除恶”与“打黑除恶”是否相同进行了一次调查，得到具体数据如表：（1）（1分）根据如上的 2×2 列联表，能否在犯错误的概率不超过 0.05 的前提下，认为“扫黑除恶”与“打黑除恶”是否相同与性别有关"？（2）（1分）计算这 80 位大学生认为“扫黑除恶”与“打黑除恶”不相同的频率，并据此估算该校 10000 名在读大学生中认为“扫黑除恶”与“打黑除恶”不相同的人数；（3）（1分）为了解该校大学生对“扫黑除恶”与“打黑除恶”不同之处的知道情况，该校学生会组织部选取 2 位男生和 3 位女生逐个进行采访，最后再随机选取 3 次采访记录放到该大学的官方网站上，求最后被选取的 3 次采访对象中至少有一位男生的概率.参考公式： K 2=n(ad−bc)2(a+b)(c+d)(a+c)(b+d)(n =a +b +c +d) . 附表：17．（3分）如图，在棱长为 2 的正方体 ACBD −A 1C 1B 1D 1 中， M 是线段 AB 上的动点.（1）（1分）证明： AB// 平面 A 1B 1C ；（2）（1分）若点 M 是 AB 的中点，证明：平面 MCC 1⊥ 平面 ABB 1A 1 ；（3）（1分）求三棱锥 M −A 1B 1C 的体积.18．（2分）已知椭圆 C:x 2a 2+y 2b2=1 (a >b >0) 的离心率为 √32 ，长轴长为 4 ，直线 y =kx +2 与椭圆 C 交于 A 、 B 两点且 ∠AOB 为直角， O 为坐标原点. （1）（1分）求椭圆 C 的方程；（2）（1分）求 |AB| 的长度.19．（2分）已知函数 g(x)=e x−2−ax (a ∈R) （ e 为自然对数的底数）（1）（1分）讨论函数 g(x) 的单调性；（2）（1分）当x>0且x≠1时，f(x)=g(x)−e x−2+xlnx在(1,+∞)上为减函数，求实数a的最小值.20．（2分）已知极点与直角坐标系原点重合，极轴与x轴的正半轴重合，圆C的极坐标方程为ρ=asinθ（a>0），直线l的参数方程为{x=−1+√22t,y=√22t,（t为参数）.（1）（1分）若a=2，直线l与x轴的交点为M，N是圆C上一动点，求|MN|的最小值；（2）（1分）若直线l被圆C截得的弦长等于圆C的半径，求a的值.21．（2分）已知函数f(x)=|x−a|+|2x−1|−1（a∈R）的一个零点为1（1）（1分）求不等式f(x)≤1的解集；（2）（1分）若1m+2n−1=a(m>0,n>1)，求证：m+2n≥11.答案解析部分1．【答案】A【解析】【解答】∵集合A={1,2，3，4，5}，B={2,4，6，8}，∴集合A∪B={1,2，3，4，5，6，8}．故答案为：A．【分析】由并集运算可得结果.2．【答案】B【解析】【解答】因为复数2−i1+i=2−i1+i×1−i1−i=1−3i2，故答案为：B【分析】由复数的乘除运算可得结果.3．【答案】A【解析】【解答】因为平面向量a⃗=(1,2)，b⃗=(−2,m)，所以，由a⃗⊥b⃗，可得a⃗⋅b⃗=0，即有1×(−2)+2m=0，解得m=1．故答案为：A．【分析】由a⃗⊥b⃗，可得a⃗⋅b⃗=0，求解可得m的值. 4．【答案】B【解析】【解答】因为sinα=35，所以cos(π−2α)=−cos2α=−(1−2sin2α)=2sin2α−1=−725，故答案为：B．【分析】化简可得cos(π−2α)=−cos2α，由二倍角的余弦公式可得结果. 5．【答案】B【解析】【解答】∵双曲线的方程为x 2m−y2=1，∴双曲线的渐近线方程为y=± 1√mx又∵一条渐近线方程为y= 12x∴m=4故答案为：B【分析】由双曲线的渐近线方程可求出实数m的值. 6．【答案】B【解析】【解答】半径为6的圆形图案的面积为36π，其圆内接正六边形的面积为：6× 12×1×sin60°= 3√32，故所求的概率为：P= 3√3236π= √324π．故答案为：B．【分析】分别计算半径为6的圆形图案的面积及其圆内接正六边形的面积，可得所求概率.7．【答案】C【解析】【解答】由公理知直线及直线外一点，确定一个平面，A不符合题意；由公理知两两相交且不共点的三条直线确定一个平面，B不符合题意；由面面垂直的性质定理知错误，C错误，符合题意；由面面平行的性质定理知正确，D不符合题意；．故答案为：C．【分析】由空间中直线与平面之间的位置关系逐项判断即可得出错误的命题.8．【答案】B【解析】【解答】∵a=50.4>50=1，0=log0.41<b=log0.40.5<log0.40.4=1，c=log50.4<log51=0，则a，b，c的大小关系为：c<b<a．故答案为：B．【分析】由指数与对数函数的图象与性质，可比较a，b，c的大小关系 .9．【答案】B【解析】【解答】将函数f（x）=sinx图象上所有点的横坐标缩短到原来的12倍，可得y=sin2x的图象；再向左平移π6个单位长度，得到函数y=sin2（x+π6）=sin（2x+π3）的图象，则得出f（x）的解析式．故答案为：B．【分析】由函数y=Asin （ωx+φ）的图象变换可知：横坐标缩短为原来的12，再向左平移 π6 个单位，可得出 f （x ）的解析式．10．【答案】D【解析】【解答】如图所示，该几何体为四棱锥P ﹣ABCD ．底面ABCD 为矩形，其中PD ⊥底面ABCD ．AB=2，AD=4，因为“阳马”的体积为 163，所以VP−ABCD= 13S ABCD ×PD =13×2×4×PD =163所以PD=2．则该阳马的外接球的直径为PB= √4+16+4=2√6 ．所以r= √6 ∴该阳马的外接球的体积 S =4π×(√6)2=24π ．故答案为：D ．【分析】由题意，该几何体为四棱锥P ﹣ABCD ，底面ABCD 为矩形，计算可得该外接球的表面积.11．【答案】B【解析】【解答】第一次输入 x =x ， i =1 ；第二次输入 x =2x −1 ， i =2 ；第三次输入 x =2(2x −1)−1=4x −3 ， i =3 ；第四次输入 x =2(4x −3)−1=8x −7 ， i =4>3 ，输出 8x −7=0 ，解得 x =78 .故答案为：B.【分析】执行该程序，根据最终输出的 8x −7=0可解得输入的x 的值.12．【答案】C【解析】【解答】令 x =y =0 ，可得 f(0)+f(0)−f(0)=3 ，即 f(0)=3 ，可令 y =−x ，可得 f(x)+f(−x)=3+f(0)=6 ，则 g(2)+g(−2)=25+f(2)−25+f(−2)=f(2)+f(−2)=6 ．故答案为：C ．【分析】利用赋值法，令 x =y =0 ，可得f(0)=3，即可得到 f(x)+f(−x)=6，进而可得所求.13．【答案】3【解析】【解答】∵a =√7 ， b =2 ， A =π3 ，∴由余弦定理可得：cosA= c 2+b 2−a 22bc=c 2+4−72×2c =c 2−34c =12所以c=3或c=-1（舍）故答案为：3．【分析】由余弦定理可得边c 的值.14．【答案】3800【解析】【解答】设甲种设备需要生产 x 天，乙种设备需要生产 y 天，该公司所需租赁费为 z 元，则 z =300x +400y ， (2 分 ) 甲、乙两种设备生产A ，B 两类产品的情况为： {4x +5y ≥503x +5y ≥40x ∈N,y ∈N，做出不等式表示的平面区域，由 {4x +5y =503x +5y =40解得 (10,2) 当 z =300x +400y 经过的交点 (10,2) 时，目标函数 z =300x +400y 取得最低为3800元．故答案为 3800 .【分析】由题意列出生产A 类产品与B 类产品所需满足的条件，则利用简单线性规划可求出所需租赁费的最小值.15．【答案】（1）解：设等差数列 {a n } 的公差为 d ，则 a n =a 1+(n −1)d由 a 1=1 ， a 3=5 可得 5=1+2d ，解得 d =2从而 a n =1+(n −1)×2=2n −1 . 即数列 {a n } 的通项公式 a n =2n −1（2）解：设等比数列 {b n } 的公比为 q ，则 b n =b 1q n−1 由 b 1=a 2=3 ， b 2=a 1+a 2+a 3 =1+3+5=9=b 1q ，解得 q =3 ，所以 {b n } 的前 n 项和公式 S n =b 1(1−q n )1−q =3(1−32)1−3=3n+1−32。

四川省广安高2018届第一次诊断语文试题

(摘编自孙金行《传承创新 ,守护民族民间文化》 )
1.下列关于原文内容的理解和分析 ,正确的一项是 (3分 )
A。
民间文化各个门类在我国都有悠久的历史 ,对国人的精神世界产生了深刻的影响。中华文化尽管土壤丰厚 ,但在工业化、城镇化的进程中 ,它的生存仍面临严峻挑战。整理民族文化生活的历史 ,扎根生活 ,是传承和振兴民间文化的一条有效路径。要让民间文化事业后继有人 ,就需要废弃传统的师徒传承模式 ,探索建立新模式。
眉山・市市联考广安、
秘密 ★ 启用前【】
高中 zO18届毕业班第一次诊断性考试
语
:
文
本试卷 10页 ,22小题 ,满分 150分。考试用时 150分钟。注意事项 1.答卷前 ,考生务必将自己的姓名、座位号和准考证号填写在答题卡上。 2.答选择题时 ,选出每小题答案后 ,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动 ,用橡皮擦干净后 ,再选涂其它答案标号。写在本试卷上无效。 3.答主观题时 ,将答案写在答题卡上。写在本试卷上无效。
4.考试结束后 ,将答题卡交回。
-、现代文阅读 (35分
)
(-)论述类文本阅读 (本题共 3小题 ,9分

1、下载文档前请自行甄别文档内容的完整性，平台不提供额外的编辑、内容补充、找答案等附加服务。
2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
3、如文档侵犯您的权益，请联系客服反馈,我们会尽快为您处理(人工客服工作时间：9:00-18:30)。

高中2018届毕业班第一次诊断性考试
数学（文史类）
第Ⅰ卷（共60分）
一、选择题：本大题共12个小题,每小题5分,共60分.在每小题给出的四个选项中，只有一项是符合题目要求的.
1.已知集合}1|{>=x x A ，函数)2lg(x y -=的定义域为B ，则=⋂B A （）
A ．R
B ．),1(+∞
C ．)2,(-∞
D ．)2,1(
2.复数=+-i
i 11（） A ．i - B ．i C ．1- D ．1
3.执行如图所示的程序框图，若输出的2=y ，则输入的=x （）
A ．1
B ．2
C ．4
D ．1或4
4.若y x ,满足约束条件⎪⎩
⎪⎨⎧≤-+≤--≥-+04201022y x y x y x ，则y x z 32+=的最大值为（）
A ．2
B ．6 C. 7 D ．9
5.为了解某高校学生使用手机支付和现金支付的情况，抽取了部分学生作为样本，统计其喜欢的支付方式，并制作出如下等高条形图：
根据图中的信息，下列结论中不正确的是（）
A ．样本中的男生数量多于女生数量
B ．样本中喜欢手机支付的数量多于现金支付的数量
C.样本中多数男生喜欢手机支付 D ．样本中多数女生喜欢现金支付
6.若将函数x y 2sin =的图象向左平移
6π个单位长度，则平移后图象的对称轴方程为（） A ．)(122
Z k k x ∈-=ππ
B ．)(22Z k k x ∈+=ππ C. )(2Z k k x ∈=π D ．)(12
2Z k k x ∈+=ππ 7.已知ABCD 是边长为1的正方形，F E ,分别为边CD BC ,的中点，则→
→⋅AF AE 的值为（）
A ．3
B ．2 C. 1 D ．
2
1 8.已知两个平面垂直，下列命题：
①一个平面内的已知直线必垂直于另一个平面内的任意一条直线.
②一个平面内的已知直线必垂直于另一个平面内的无数条直线.
③一个平面内的任一条直线必垂直于另一个平面.
其中错误命题的序号是（）
A ．①②
B ．①③ C. ②③ D ．①②③
9.在区间]1,1[-上随机取一个数k ，则直线)2(-=x k y 与圆122=+y x 有两个不同公共点的概率为（） A ．92 B ．63 C. 31 D ．3
3 10.已知定义在R 上函数)(x f 满足0)()(=-+x f x f ，且当0<x 时，22)(2-=x x f ，则
=+-)2())1((f f f （）
A ．8-
B ．6- C. 4 D ．6
11.已知椭圆)0(1:22
22>>=+b a b
y a x E 的左焦点为y F ,1轴上的点P 在椭圆外，且线段1PF 与椭圆E 交于点M ，若||3
3||||1OP MF OM ==，则E 椭圆的离心率为（） A ．21 B ．23 C. 13- D ．2
13+
12.已知函数⎩⎨⎧≤≤-+>=0
3|,2|0,log )(x x x x x f a （0>a 且1≠a ），若函数)(x f 的图象上有且仅有两个点关于y 轴
对称，则a 的取值范围是（）
A ．)1,0(
B ．)3,1( C. ),3()1,0(+∞⋃ D ．)3,1()1,0(⋃
第Ⅱ卷（共90分）
二、填空题（每题5分，满分20分，将答案填在答题纸上）
13.已知54)4cos(=-π
α，则=+)4
sin(πα ． 14.若直线l 与直线022=--y x 关于直线04=-+y x 对称，则l 的方程是．
15.如图，已知B A ,是函数)16(log )(2x x f =图象上的两点，C 是函数x x g 2log )(=图象上的一点，且直线BC 垂直于x 轴，若ABC ∆是等腰直角三角形（其中A 为直角顶点），则点A 的横坐标为．
16.如图表示正方体表面的一种展开图，则其中的四条线段GH EF CD AB ,,,在原正方体中为异面直线且所成角为
60的有对．
三、解答题（本大题共6小题，共70分.解答应写出文字说明、证明过程或演算步骤.）
17. 设数列}{n a 满足)(1,1*11N n n a a a n n ∈++==+.
（1）求数列}{n a 的通项公式；
（2）若数列}1{n
a 的前n 项和为n T ，求n T . 18. 全民健身倡导全民做到每天参加一次以上的体育健身活动，旨在全面提高国民体质和健康水平.某部门在该市20162011-年发布的全民健身指数中，其中的“运动参与”的评分值（满分100分）进行了统计，。