理论力学第十三章作业答案
理论力学习题解答(8-13章)

对于一个物体,如果受到的合力为零,则该物体处于力的平衡状态。
力的平衡与运动状态
力的平衡状态下,物体的运动状态保持不变,即速度和方向都不发生变化。
力矩是力和力臂的乘积,表示力对物体转动作用的物理量。
力矩概念
力矩的方向
力矩的几何意义
力矩的方向按照右手定则确定,即右手四指从转动轴指向力的方向,大拇指指向转动方向。
动量定理,描述了物体加速度与其所受合外力之间的线性关系。
详细描述
牛顿第二定律,也被称为动量定理,表述为F=ma,其中F代表合外力,m代表质量,a代表加速度。该定律揭示了物体的加速度与作用在物体上的力成正比,与物体的质量成反比。
牛顿第二定律
作用与反作用定律,描述了作用力和反作用力大小相等、方向相反的特性。
伯努利方程
层流与湍流,定常流动与非定常流动,一维、二维、三维流动。
流体流动的分类
流体质量守恒,流量连续,无质量亏损或增加。
连续性方程
流体动力学基础
03
拉格朗日法
追踪流体质点运动的方法,描述流场中质点位置随时间变化。
01
微元体分析法
对流场中微小体积元进行分析,列出流体运动和力的平衡方程。
02
欧拉法
描述流体运动随时间变化的方法,基于流体质点运动观点。
天体运动的计算方法
天体运动的计算方法通常涉及到对万有引力定律的应用,以及运用运动学和动力学原理。
总结词
在计算天体运动时,首先需要确定天体的质量、位置和速度等参数,然后根据万有引力定律计算出天体之间的相互作用力。接着,运用牛顿第二定律和运动学原理,可以求解出天体的加速度、速度和位移等参数。最后,通过比较理论计算结果和观测数据,可以对天体运动的规律进行验证和预测。
《理论力学》第十三章--虚位移试题及答案
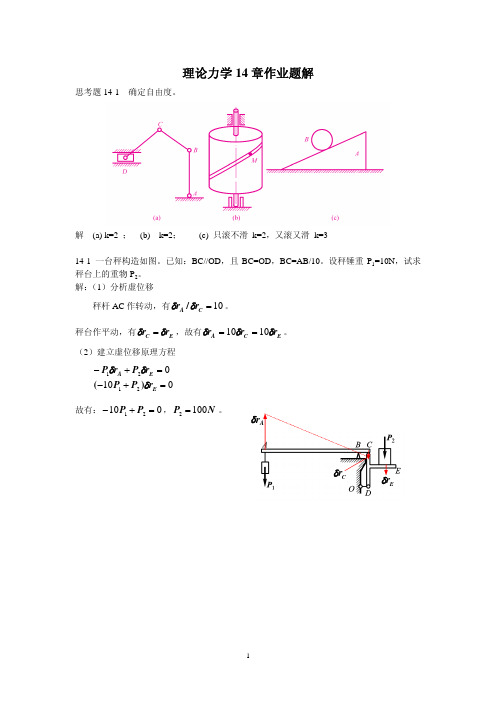
理论力学14章作业题解思考题14-1 确定自由度。
解 (a) k=2 ; (b) k=2; (c) 只滚不滑 k=2,又滚又滑 k=314-1 一台秤构造如图。
已知:BC//OD ,且BC=OD ,BC=AB/10。
设秤锤重P 1=10N ,试求秤台上的重物P 2。
解:(1)分析虚位移 秤杆AC 作转动,有10=C A r r d d /。
秤台作平动,有E C r r d d =,故有E C A r r r d d d 1010==。
(2)建立虚位移原理方程1002121=+-=+-E E A r P P r P r P d d d )(故有:01021=+-P P ,N P 1002=。
Cr d Er14-5 OA=l ,OC=R满足的条件。
解: (用虚位移原理求解)(1) 运动分析(虚位移关系分析)A 处虚位移关系用合成运动的理论分析。
A 为动点,OC 为动系。
r e A r r r r r r d d d +=f d d cos A e r r =另外:R r l r C e /d d = (2) 虚功方程fd f f d d d d cos /)cos /(cos /R l F F r R l F F R r l F r F r F r F C C C A C 21212121000==-=-=-14-9 已知:AC=BC=EC=GC=DE=DG=l ,荷载F 2。
求平衡时的F 1。
解 用解析法,1个自由度,选q 为广义坐标。
建立坐标,如图。
(1) 计算虚位移qdqd q qdq d q sin ,cos cos ,sin l y l y l x l x A A D D 2233-====(2) 计算力的投影 2211F F F F x y -=-= , (3) 建立虚位移原理方程qqdq q q d d sin cos )cos sin (230320212121F F l F l F x F y F D x A y ==×-×=+Oxy14-12 F=4kN, AO=OE=5m. 求D 解:(1) 接触D 处水平约束,代之约束力。
理论力学课后习题与答案解析

第一章习题4-1.求图示平面力系的合成结果,长度单位为m。
解:(1) 取O点为简化中心,求平面力系的主矢:求平面力系对O点的主矩:(2) 合成结果:平面力系的主矢为零,主矩不为零,力系的合成结果是一个合力偶,大小是260Nm,转向是逆时针。
习题4-3.求下列各图中平行分布力的合力和对于A点之矩。
解:(1) 平行力系对A点的矩是:取B点为简化中心,平行力系的主矢是:平行力系对B点的主矩是:向B点简化的结果是一个力R B和一个力偶M B,且:如图所示;将R B向下平移一段距离d,使满足:最后简化为一个力R,大小等于R B。
其几何意义是:R的大小等于载荷分布的矩形面积,作用点通过矩形的形心。
(2) 取A点为简化中心,平行力系的主矢是:平行力系对A点的主矩是:向A点简化的结果是一个力R A和一个力偶M A,且:如图所示;将R A向右平移一段距离d,使满足:最后简化为一个力R,大小等于R A。
其几何意义是:R的大小等于载荷分布的三角形面积,作用点通过三角形的形心。
习题4-4.求下列各梁和刚架的支座反力,长度单位为m。
解:(1) 研究AB杆,受力分析,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(2) 研究AB杆,受力分析,将线性分布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
(3) 研究ABC,受力分析,将均布的载荷简化成一个集中力,画受力图:列平衡方程:解方程组:反力的实际方向如图示。
校核:结果正确。
习题4-5.重物悬挂如图,已知G=1.8kN,其他重量不计;求铰链A的约束反力和杆BC所受的力。
解:(1) 研究整体,受力分析(BC是二力杆),画受力图:列平衡方程:解方程组:反力的实际方向如图示。
习题4-8.图示钻井架,G=177kN,铅垂荷载P=1350kN,风荷载q=1.5kN/m,水平力F=50kN;求支座A的约束反力和撑杆CD所受的力。
理论力学作业本

第一章 静力学公理和物体的受力分析一、选择题(请将答案的序号填入划线内。
)1、若作用在A点的两个大小不等的力1F 和2F ,沿同一直线但方向相反。
则其合力可以表示为 。
①1F -2F;②2F -1F; ③1F+2F 。
2、三力平衡汇交定理是 。
①共面不平行的三个力互相平衡必汇交于一点; ②共面三力若平衡,必汇交于一点;③三力汇交于一点,则这三个力必互相平衡。
3、在下述原理、法则、定理中,只适用于刚体的有 。
①二力平衡原理; ②力的平行四边形法则; ③加减平衡力系原理; ④力的可传性原理; ⑤作用与反作用定理。
4、图示系统只受F作用而平衡。
欲使A支座约束力的作用线与AB成30°角,则斜面的倾角应为 。
①0° ②30° ③45° ④60°二、填空题(请将简要答案填入划线内。
)1、作用在刚体上的两个力等效的条件是。
2、在平面约束中,由约束本身的性质就可以确定约束力方位的约束有 ,可以确定约束力方向的约束有 ,方向不能确定的约束有 (各写出两种约束)。
三、作图题1、画出下列各图中A、B两处反力的方向(包括方位和指向)。
2、图示系统受力F作用而平衡。
若不计各物体重量,试分别画出杆AC、CB和圆C的示力图,并说明C处约束力间的关系。
3、画出下列各图构件AB,CD的受力图。
未画出重力的各物体自重不计,所有接触处均为光滑接触。
4、画出下列每个标注字符的物体(不含销钉与支座)的受力图与系统整体受力图。
未画出重力的各物体自重不计,所有接触处均为光滑接触。
5、画出下列每个标注字符的物体(不含销钉与支座)的受力图与系统整体受力图。
未画出重力的各物体自重不计,所有接触处均为光滑接触。
第二章平面汇交力系和平面力偶系一、选择题(请将答案的序号填入划线内。
)1、已知1F、2F、3F、4F为作用于刚体上的平面共点力系,其力矢关系如图所示为平行四边形,由此可知。
①力系可合成为一个力偶;②力系可合成为一个力;③力系简化为一个力和一个力偶;④力系的合力为零,力系平衡。
理论力学作业答案

解:力系对O点的主矩在轴上的投影为
M Ox M x F F2 cos a .100 F3 sin .300 51.8 N .m M Oy M y F F1 .200 F2 sin a .100 36.64 N .m M Oz M z F F2 cos a .200 F3 cos .300 103.6 N .m
FCy
P1
FDx
解得: FCy 4550 N
P
3、研究杆ABC
FCy
C
M F F
y
C
0
M A 6FAx 3FBx 0 0
B
FCx
FBy
FAy FBy FCy P3 0
x
0
FBx
FAx FBx FCx 0
MA P3 FAy
A
解得: FBx 22800, FBy 17850
M M FAx tan , FAy , M A M a a
3-9(b)
已知:q, M, a,. 不计梁自重,求支座A、B、C约束反力。 FNC FBy FBx
解:BC段梁受力分析如图,平面任意力系平衡方程为
F F
解得:
FNC
x y
0 FBx FNC sin 0 0 FBy qa FNC cos 0
解得: FAx 0, FAy 1 F M , FNB 1 3F M 2 a 2 a
3-5(b)
已知:F, M, q, a, 求支座A、B约束反力。
q
M
解:梁受力分析如 图,平面任意力系 平衡方程为
FAx
南华大学理论力学第13章练习答案

M P 0
又 2a1 a 联立解得
a
ma m ra1 FS 2r 1 r 0 2 4
FS A
P
8 F 11 m
均质圆盘B转动。不计支架和绳子的重量及轴上的摩擦,BC=l,
盘B的半径为r,求固定端的约束力。 解:分析轮及物块,加惯性力如图,由
MA
l
C
B
M
B
0
1 ( m2 m1 )r 2 m1 gr 0 2
Fx
Fy
2m1 g ( m2 2m1 )r
,
1 m2 r 2 m2 g 2 m1a A
M
D
r
C
n 2 r 其中 aa
a r
t n
A
E
B
cos ) 则 F m(r 2 sin r 分析轮,加惯性力矩 J
M
C
r
F
J
M mr(r 2 sin r cos ) sin J mr(r 2 sin r cos ) sin M J
a
m1 g
分析整体,
F
F
X
0
0
Fx 0
Fy m1a m1 g m2 g 0
M A m1 g (l r ) m2 gl
Y
Fy
3m1 m2 m2 g 2m1 m2
MC 0
1 m2 r 2 m1 (l r )a 0 2
MA
3m m2 1 m2 r 2 m1 (l r )r m1 g(l r ) m2 gl 1 m2 gl 2 2m1 m2
曲柄滑块机构如图所示已知圆轮半径为r对转轴的转动惯量为j轮上作用一不变力偶矩mabd滑道的质量为m不计摩擦
理论力学练习册及答案
8-8.图示机构中,设当OA与水平线成450角的瞬时,曲柄OA有反时针方向的匀角速度ω=25 rad/s,连杆AB水平,扇形板BD铅垂。求扇形板绕定轴D转动的角加速度ε。
解:将力系向A点简化,并过A点建立如图所示坐标系。
由矢量式可得力系简化的最终结果为力螺旋,
作用点为:
3-2.已知A(1,0,1),B(0,1,2)(长度单位为米),F= kN。求力F对x、y、z轴的矩?
解:
3-3.如图所示,长方体边长为a、b、c,力F沿BD,试计算力F对AC轴之矩MAC(F)
解:力F对C点的矩为:
4-3.置于铅垂面内的均质正方形簿板重P= 100kN,与地面间的摩擦系数f= 0.5,欲使簿板静止不动,求作用在点A的力F的最大值?
4-4.折梯放在水平地面上,其两脚与地面的摩擦系数分别为fA= 0.2,fB= 0.6,折梯一边AC的中点D上有一重为P= 500N的重物,折梯重量不计,问折梯能否平衡?如果折梯平衡。试求出两脚与地面间的摩擦力。
第六章 刚体基本运动
6-1.在如图所示中,已知ω、。在图上标示出A、B两的速度、加速度。
6-2.在如图所示的平面机构中,半径为r的半圆盘在A和B处与杆铰接,已知 , ,曲柄O1A以匀角速度ω转动。求图示瞬时圆盘上M点的速度和加速度。
6-3.在如图所示的平面机构中,齿轮1紧固在杆AC上, ,齿轮1与半径为r2的齿轮2啮合,齿轮2可绕O2轴转动,。设 , ,试确定 时,轮2的角速度和角加速度。
解:动点取曲柄OA上A点,
理论力学13-2 基本定理综合题

解 (1)以 A 及 B 为系统,由于作用于该系统上的外力无水平分量,因此该系统在水 平方向动量守恒。即 & A + m2 x & B = 常数 m1 x 两边求导得
& &A = − x
m2 & &B x m1
(1)
(2) 以 B 为动系,分析 A 的运动。如图综-5b 所示,根据 aA = ae + ar = aB + ar
M O′ FT O
(a) 图综-1
FN
v
a
ϕ
mg
(b)
解 滑块 M 在下降至任意位置时的运动及受力分析如图综-1b 所示。滑块 M 在下降过 程中 v 与 ϕ 的关系可由动能定理确定:
mg × 2 R cos 2 ϕ +
1 1 k (2 R) 2 − (2 R sin ϕ ) 2 = mv 2 -0 2 2 kR v = 2 cos ϕ gR(1 + ) mg
t maC = ∑ Ft , n maC = ∑ Fn ,
J Cα = ∑ M C
(1) (2) (3)
得
b FBE sin 60° − FBE 2
联立解得
mg cos 60° = maC FAD + FBE − mg sin 60° = 0 b b b cos 60° − FAD sin 60° − FAD cos 60° = 0 2 2 2 g aC = = 4.9 m/s 2 2 FAD = 72 N FBE = 268 N
ρ = R - vt
ϕ=
v0 t R − vt
2 mvϕ
线的张力
&& = F = ma ρ = mρ
- 1、下载文档前请自行甄别文档内容的完整性,平台不提供额外的编辑、内容补充、找答案等附加服务。
- 2、"仅部分预览"的文档,不可在线预览部分如存在完整性等问题,可反馈申请退款(可完整预览的文档不适用该条件!)。
- 3、如文档侵犯您的权益,请联系客服反馈,我们会尽快为您处理(人工客服工作时间:9:00-18:30)。
⇒ mg − FN = 0
∑M (F) = 0 ⇒ L
o
FT
利用质点动量矩定理建立方程:
O1
= LO 2
mv0 r = mv1r / 2
v0 2 = 8m r/2 r
2
⇒ v1 = 2v0
FT = man
2v0 ) ( =m
[13-8]滑轮重W,半径为R,对转轴O的回转半径为ρ;一绳绕在滑轮上, 另一端系一重为P的物体A;滑轮上作用一不变转矩M,忽略绳的质 量,求重物A上升的加速度和绳的拉力。 解:取整体为研究对象:受力分析 FOy 运动分析:滑轮定轴转动,重物向上直线运动 FOx 利用质点动量矩定理建立方程: W
补充方程:
F A = fFNA
2 1 + f ( )r
FB = fFNB
⇒α =
−2 f (1 + f ) g
∫
0
ω0
dω = ∫ α d t
0
t
( 1 + f )rω ⇒t =
2
2 ε2R =
( kM − PR ) R
J 2 + k 2 J1 + PR 2 g
[13-16]如图所示,质量为m的偏心轮在水平面上作平面运动。轮 子轴心为A,质心为C,AC=e,轮子半径为R,对轴心A的转动惯 量为JA;C、A、B三点在同一铅垂上。(1)当轮子纯滚动时,若 vA已知,求轮子的动量及对地面B点的动量矩;(2)当轮子又滚 又滑时,若ω、vA已知,求轮子的动量及对地面B点的动量矩。 解:(1)轮纯滚动时,点B是其速度瞬心。
J1ε 1 = M − Ft R1
P = Ft R2 − PR ⇒ J 2ε 2 + ε 2 R 2 = Ft R2 − PR g
d ( J 2ω2 + PvR g ) dt
ε1 z2 R z2 = =k, = =k ε 2 z1 R1 z1
kM − PR ⇒ ε2 = J 2 + k 2 J1 + PR 2 g
MR + W ρ 2 ⇒ FT = P 2 PR + W ρ 2
[13-9]电动绞车提升重物P,在其主动轴上作用有不变主矩M,主动轴 与从动轴对各自转轴的转动惯量分别为J1和J2,传动比为z2/z1=k,鼓 轮半径为R;不计轴承摩擦及吊索质量,求重物的加速度。 解:分别取两轴为研究对象:受力分析
对主动轴: 对从动轴:
1
J1ε1 = (T1 − T2 ) R1 + M
J 2ε 2 = − (T1 − T2 ) R2 − M
W1 2 其中J1 = R1 2g
W2 2 其中J 2 = R2 2g
W1 T1’
'
M’
ε 1 R1 = ε 2 R2
⇒ ε1 =
2 g ( MR2 − M ' R1 )
(W1 + W2 ) R12 R2
W 2v P ∑ M o ( F ) = M − PR LO = g ρ R + g vR dLO W 2 PR = ρ + a = M − PR dt gR g M − PR ⇒a= Rg 2 2 PR + W ρ
FT
P 取重物为研究对象:受力分析 P
FT − P = Pa / g
Re p mv A , R LB mvc R e J C w
Re vc vA R
2 vA 2 J A me m R e R
(2)轮又滚又滑
p mvc m v A we
LB mvc R e J C w J A meR w m R e v A
[13-12]均质圆柱重P、半径为r,放置如图并给以初角速度ω0。设在 A和B处的摩擦系数均为f,问经过多长时间圆柱才能静止? y 解:取圆柱为研究对象,分析受力情况. x
∑F
∑F
x
= 0 : FNA − FB = 0
= 0 : FNB + FA − P = 0
P 2 rα 2g
y
∑ M 0 = Jα : −(FA + FB )r =
[13-3]质量为m的小球系于细绳的一端,绳的另一端穿过光滑水平面 上的小孔O,令小球在此水平面上沿半径为r的圆周作匀速运动,其速 度为v0.如将绳下拉,使圆周半径缩小为r/2,问此时小球的速度v1和绳 的拉力各位多少? FN 解:取整体为研究对 象:受力分析 r 运动分析:小球在水平面内均速 O F v0 T 圆周运动. aτ=0 mg
[13-7]均质圆轮重W,半径为r1,对转轴的回转半径为ρ,以角速度 ω0绕水平轴O转动。今用闸制动,要求在t秒内停止,问需要加多 大的铅垂力F?设动摩擦系数f’是常数,轴承摩擦忽略不计。 解:(1)取轴为研究对象, 受力分析
FAy FAx Fs’
M
F Fs FN FN’ Foy
A
0 : Fl FN b 0
FN Fl / b
(2)取圆轮为研究对象,受力分析
W 2 dw r f ' FN r1 g dt
ω0
0 w0
dw
t
0
W Fox
W r 2 w0 b f ' F r1 gl dt F ' 2 Wr b f gtr1l
[13-10] 两带轮的半径各为R1和R2,重量分别为W1和W2,如在轮O1 上作用一转矩M,在轮O2上作用一阻力矩;带轮视为均质圆盘,胶 带的质量和轴承的摩擦忽略不计,求轮O1的角加速度。 解:分别取两轮为研究对象,分析 受力情况. F0Y F0X T1 M T2 F0Y F0X T2’ W
